2. 浙江大学建筑工程学院, 杭州 310058
2. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
0 引言
松散堆积土滑坡是主要的滑坡类型之一[1],其稳定性与地下水位的升降变化往往密切相关[2-5]。控制坡体地下水位上升对提高坡体稳定性具有十分重要的意义,但目前边坡地下水排水方法均利用势能原理,缺乏排水过程的主动控制,常常无法满足滑坡抢险的排水需要;因此探索主动疏干或拦截坡体地下水的技术方法,对防止雨季滑坡启动具有迫切性。考虑到防灾需要,杜丽丽等[6-8]于2013年率先提出了松散堆积土边坡充气排水方法,通过物理模型试验证明向土体中充气的方法截水减渗效果明显,并根据理论推导了充气排水启动气压值和充气压力上限值计算公式;另外通过数值模拟方法,探究了渗透系数、充气气压、孔隙率对截排水效果的影响。康剑伟等[9]采用数值模拟方法研究了充气和不充气时一维土柱降雨入渗过程。钱文见等[10]通过数值模拟进一步研究了充气点位置对截排水效果的影响。余文飞等[11]建立了二维长边坡数值模型,研究了充气时坡体内不同阶段水-气二相流具体的运动特征。
这些研究证明了充气截排水的有效性,但均基于理想规则边坡模型,属于基础理论层面的探索,还未见有结合实际滑坡进行充气截排水方法可行性的研究报道。本文以瓯青公路小旦滑坡为例,采用数值模拟方法研究充气截排水控制坡体地下水位的有效性及其对坡体稳定性的影响,以期为充气截排水的工程应用奠定基础。
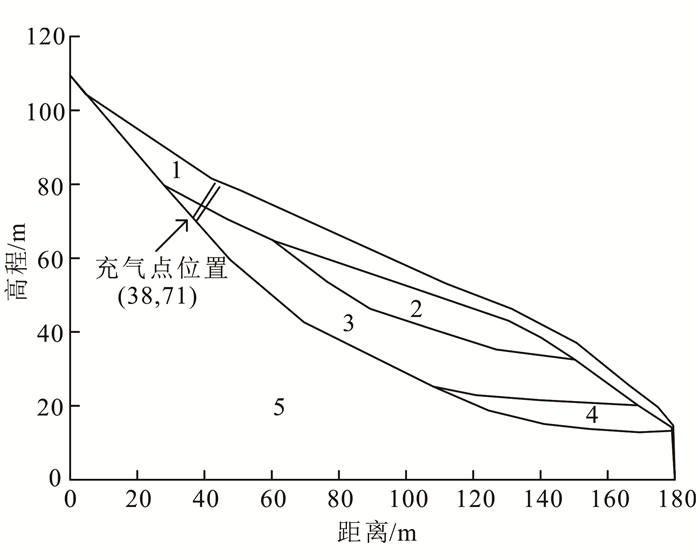
1 滑坡概况及成因分析小旦滑坡由330国道瓯青公路复线开挖坡脚引发,滑坡体纵向最大长度约140 m、最大宽度约135 m,滑体一般厚度15~20 m。滑坡区原始地形坡度15°~20°。坡体主要由4层堆积土组成,工程地质剖面如图 1所示。
|
| 1.坡积粉质黏土混碎块石(Q4dl); 2.冲积黏土(Q3al); 3.古滑坡堆积粉质黏土混碎块石(Q3del); 4.冲积粉质黏土(Q2al); 5.基岩。 图 1 工程地质剖面图 Figure 1 Engineering geological profile |
|
|
滑坡体由表层向深层依次为:坡积灰黄色粉质黏土混碎块石(Q4dl);冲积褐红色黏土(Q3al);古滑坡堆积褐黄色粉质黏土混碎块石(Q3del);冲积杂色粉质黏土(Q2al);底部为基岩。Q4dl和Q3del土层的碎块石体积分数约为50%,碎石块块径一般在数十厘米,其间空隙由粉质黏土充填,为滑坡体中透水性较好的土层。Q3al土层和Q2al土层原始结构紧密,为相对隔水层,由于粉粒体积分数较高,力学强度低,在发生坡体变形时很容易产生裂隙,使地下水沿裂隙流出。
滑坡区路基开挖时正值雨季,坡体地下水丰富。由于开挖后初期没有进行任何支护措施,使得坡脚发生小规模的局部变形破坏,引起坡体水文地质条件发生变化,特别是透水性差的冲积黏土Q3al堆积于坡脚,阻碍了地下水的排泄。滑坡发生变形破坏过程中地下水从坡面渗出,表明坡体地下水位因降雨入渗而大幅上升。正是坡体地下水水位快速抬升,使得坡体稳定性下降,最终发生整体滑动。
综合地形地质资料及边坡的变形破坏机理分析可知:如果在滑坡体后缘区域透水性良好的古滑坡堆积土层Q3del中充入有压气体,形成临时性的非饱和区截水帷幕改变地下水渗流场,使部分地下水直接流向坡面或流向相对隔水层Q3al以上,再通过坡面松散堆积层Q4dl流出坡体,就可降低下游Q3del土层中的地下水位,减小坡脚开挖面附近潜在滑动面上的孔隙水压力,达到阻止坡体发生整体滑动的目的。
2 水-气二相流数学模型充气截排水是土体孔隙中水气相互置换的过程,R.E.Collins[12]很早就研究了气体在土体中的运动,认为土中气体运动必须考虑其压缩性。因此,充气截排水数值模拟必须建立可考虑气体压缩性的水-气二相流数学模型。
2.1 基本控制方程水-气二相流模型的基本控制方程是质量守恒方程,一维可压缩流体质量守恒方程的一般形式[13]为
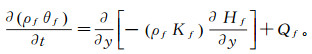 (1)
(1) 式中:下标“f ”代表流体,f=w或a,代表水相或气相;ρf为流体密度;θf为流体的单位体积分数;t为时间;y为距离;Kf为流体的渗透系数;Hf为总水头;Qf为单位时间内的单宽流量。
假设水为不可压缩流体,则密度不变,所以其质量守恒方程可以用体积守恒方程来表示:
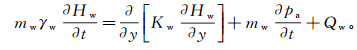 (2)
(2) 式中:mw为土水特征曲线在某一特定孔隙水压力处的斜率;γw为水的重度;Kw为随含水率变化而变化的渗透性系数;Hw为渗流过程中的总水头;pa为孔隙气压力;Qw为水的单宽流量。
而考虑气体可压缩性的质量守恒方程可表示为
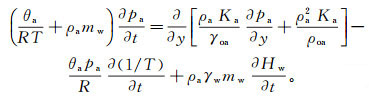 (3)
(3) 式中:θa为空气的单位体积分数;T为温度;ρa为气体密度;Ka为随含水率变化而变化的透气系数;γoa为标准状态下气体重度;ρoa为标准状态下气体密度;R为气体常数。对于干燥空气,R=287 J/(kg·K)。
2.2 土水特征曲线与相对渗透系数曲线根据非饱和土理论,土体的渗透性与土体饱和度正相关,可采用土水特征曲线进行表征。本文采用商业岩土工程软件Geo-Studio中Seep/W和Air/W模块的耦合进行水-气二相流的数值模拟,通过Van Genuchten模型[14]来定义土-水特征曲线和土中水、气渗透率曲线。
土-水特征曲线为
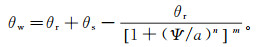 (4)
(4) 式中:θw为体积含水量;θs为饱和体积含水量;θr为残余体积含水量;Ψ为基质吸力;a,n,m均为拟合经验参数,n=1/(1-m)。
水、气的相对滲透系数函数为:
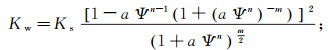 (5)
(5) 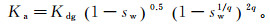 (6)
(6) 式中:Ks为饱和渗透系数;Kdg为干土透气系数;sw为有效饱和度;q为系数,q=2.9。
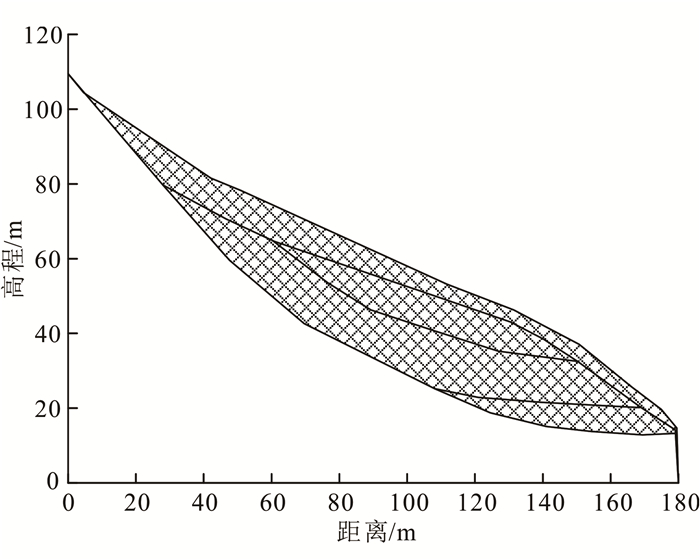
3 数值计算模型参数确定 3.1 模型物理力学参数确定本文采用基于有限元的二维两相模型进行分析,数值模型计算剖面采用实际的典型地质剖面,单元数为1 706,节点数为1 804,网格自动剖分为四边形和三角形单元,图 2为计算网格图。
|
| 图 2 计算网格图 Figure 2 Meshes for FEM analysis |
|
|
各土层材料物理参数的取值:Q3al和Q2al土层按照工程经验结合工程地质手册[15]的推荐值进行选取;而Q4dl和Q3del土层含有碎块石,查阅相关资料[16]发现由于粗颗粒和细颗粒土体积分数的不同以及级配的差异,含碎石土体的渗透性相差较大,数量级一般在10-6~10-2 cm/s,依据滑坡工程地质勘查报告的相关试验成果取值,具体取值结果见表 1。
| 坡体土层 | 饱和渗透系数/(cm/s) | 饱和体积含水量/(m3/m3) | 残余体积含水量/(m3/m3) | 干土透气系数/(cm/s) |
| Q4dl | 3.0×10-4 | 0.40 | 0.040 | 3.0×10-3 |
| Q3al | 1.0×10-6 | 0.50 | 0.050 | 1.0×10-5 |
| Q3del | 2.0×10-4 | 0.45 | 0.045 | 2.0×10-3 |
| Q2al | 6.0×10-5 | 0.46 | 0.046 | 6.0×10-4 |
由于透气系数一般比透水系数大1~2个数量级[17],为保证计算结果可靠性,取Kdg =10 Ks。
坡体后缘设置单位入渗流量q′;坡体前缘为自由出流边界;坡面为透水透气边界。充气点设置在基岩与滑坡体交界面附近。
在文献[5]中,作者采用常用的传递系数法对坡体的稳定性进行了计算分析,获得小旦滑坡在自然稳定状态下的稳定性系数为1.142。在假定滑面强度参数和其他因素不变的情况下,坡脚开挖后稳定性系数降为1.104,降幅为3.3%。而当坡脚附近发生局部变形,地下水渗流管网系统受到破坏,地下水水位抬升到相对隔水的冲积褐红色黏土土层Q3al以上时,边坡的稳定性系数下降到0.910,降幅达17.6%。依据上述资料和计算结果,通过选取合适的后缘单位入渗流量q′进行反演计算,获得各土层的强度参数如表 2所示。
| 坡体土层 | 材料天然重度/(kN/m3) | 内摩擦角/(°) | 黏聚力/(kPa) |
| Q4dl | 19.5 | 26 | 18 |
| Q3al | 19.0 | 23 | 23 |
| Q3del | 19.5 | 32 | 20 |
| Q2al | 19.0 | 22 | 28 |
当坡体处于自然入渗状态下时(取单位入渗流量q′=0.008 3 m3/d),通过滑动面位置最优化,采用M-P法(下同)得到最危险滑动面下坡体的稳定性系数Fs=1.144;开挖完成初期假设渗流场不变,此时计算得到Fs=1.106;而当坡体后缘单位入渗流量增大到q′=0.017 2 m3/d时,地下水水位上升到相对隔水的冲积褐红色黏土土层Q3al以上,计算得到Fs=0.912。数值反演计算结果与已有文献的稳定性分析计算结果相近(表 3),表明确定的模型土体强度参数是合理可靠的。
选择合适的充气点位置和充气气压值,才能取得期望的截排水效果。钱文见等[10]发现:当充气压力相同时,充气点位置离潜在滑坡区越近,则潜在滑坡区的地下水位下降幅度就越大;充气点位置越深,所能采用的充气压力值越大,潜在滑坡区地下水位下降就越大,截排水的效果也越明显。杜丽丽等[8]发现,对坡体充气时存在一个启动充气压力,渗透系数越小,启动气压越大。显然,对于不同边坡,均需要根据坡体地质结构和潜在滑坡特征确定充气点的位置,充气压力大小的确定则需要进行必要的试算确定。
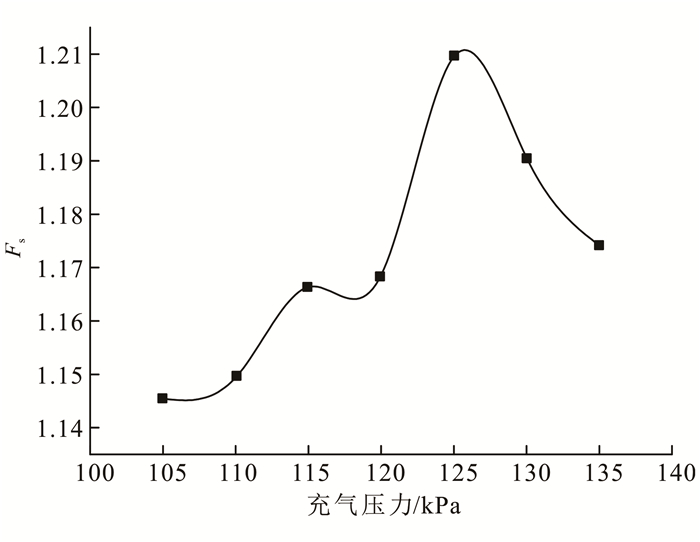
根据小旦滑坡的地质条件,结合反复试算,确定充气点取在图 1所示坐标点(38,71)的位置。取不同的充气压力进行模拟,得到坡体充气稳定后渗流场,计算得到它们对应的稳定性系数,结果如图 3所示。
|
| 图 3 充气压力与稳定性系数关系图 Figure 3 Relationship between inflation pressure and stability coefficient |
|
|
由图 3可以看出,稳定性系数随充气压力的增大呈现出先增大后减小的规律。当充气压力小于105 kPa时,充气对于提高坡体的稳定性几乎没有什么作用;这是因为充气压力较小时,气压不足以驱动后缘来水改变流向。当充气压力大于125 kPa后,继续增大充气压力反而使稳定性系数下降;这是因为土体孔隙中原本被孔隙水封住的气体的逃逸通道增多,充气区中土体的封气性降低,截排水效果变差。所以对于此特定坡体的最佳充气压力值为125 kPa。
4 数值模拟结果分析坡体处于自然稳定入渗状态时(此时单位入渗流量q′=0.008 3 m3/d)的渗流场如图 4所示,计算得Fs=1.144。

|
| 图 4 自然入渗状态下坡体渗流场 Figure 4 Seepage field of slope under natural infiltration |
|
|
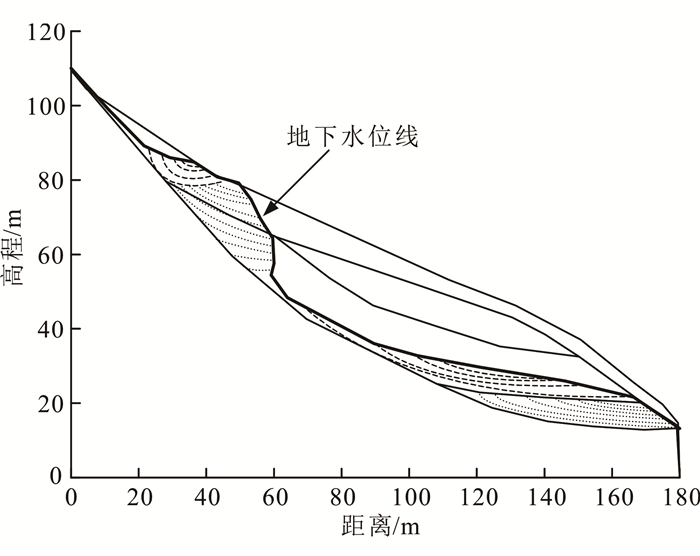
当在坡体后缘采用最佳充气压力值125 kPa进行充气时,得到坡体的稳定渗流场如图 5所示。计算得Fs=1.209,相比于原来自然入渗状态下Fs=1.144时提高了5.7%。
|
| 图 5 充气稳定后的坡体渗流场 Figure 5 Seepage field of slope after inflate stabilization |
|
|
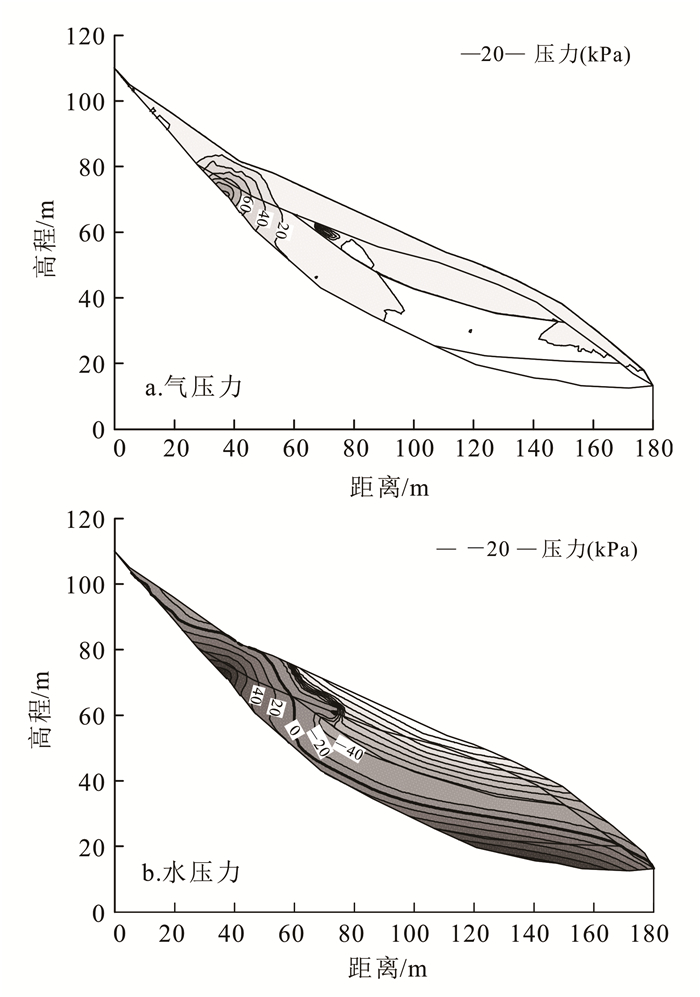
同时可以得到充气稳定后坡体内孔隙气压力等值线图与孔隙水压力等值线图,如图 6所示。据此可以分析充气稳定后坡体内孔隙气压力与孔隙水压力的关系。
|
| 图 6 充气稳定后孔隙压力等值线图 Figure 6 Pore-water pressure contours after inflate |
|
|
由图 6a可以看出,充气点附近区域气压力值向外逐渐减小,充气非饱和区上游侧的压力梯度明显大于下游侧的压力梯度;这是因为后缘来水对非饱和区上游侧孔隙中的空气会有挤压作用,使得上游侧的孔隙气压力等值线更密。图 6b中灰色越深的区域代表孔隙水压力值越大。结合图 6a和图 6b可以看出, 充气非饱和区附近孔隙气压力等值线与孔隙水压力等值线分布非常类似,说明它们之间存在平衡关系,从微观上来看即孔隙中水气分界面维持在稳定状态。
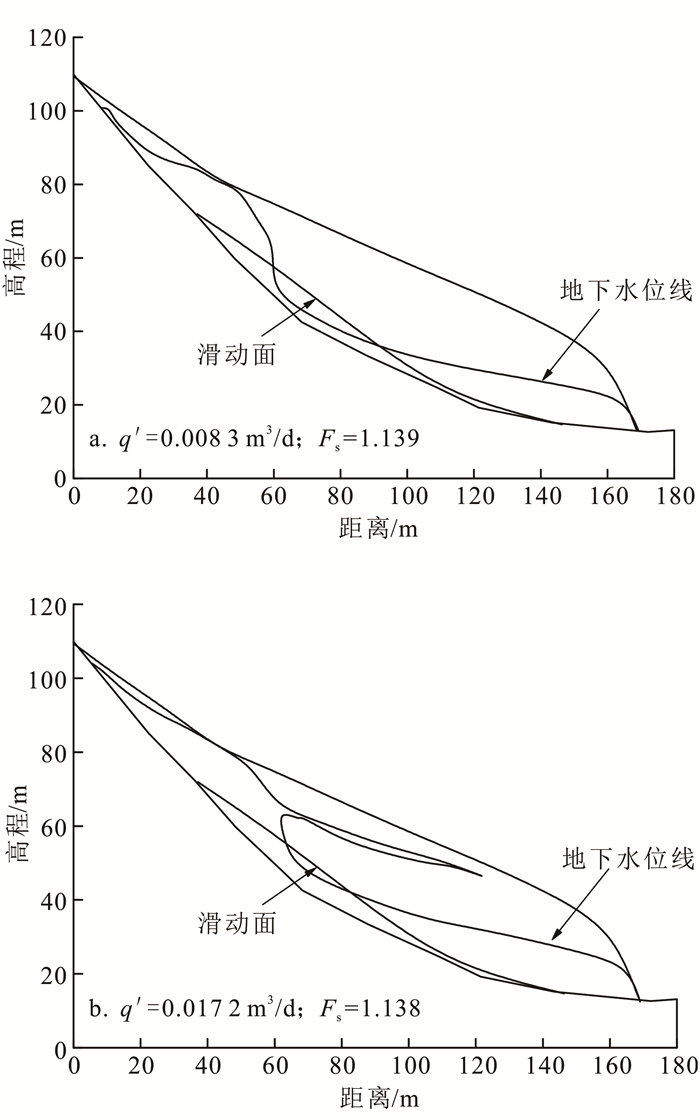
将充气稳定后的坡体进行坡脚开挖,得到不同后缘来水流量情况下坡体的状态,如图 7所示。
|
| 图 7 开挖状态下充气稳定后坡体稳定性分析 Figure 7 Stability analysis of slope after inflate stabilization under excavation statement |
|
|
假设开挖完成初期地下水渗流场不变,此时的坡体稳定性计算结果如图 7a所示,Fs=1.139,相较之前自然状态下开挖后的Fs=1.106,提高了3.0%。而当遇到坡体后缘入渗流量增大的情况时,假设后缘单位入渗流量由q′=0.008 3 m3/d增大到q′=0.017 2 m3/d,在坡体后缘充气形成稳定非饱和截水帷幕的作用下,那么开挖状态下坡体渗流场稳定后的稳定性计算结果如图 7b所示。此时Fs=1.138,可以保障坡体的稳定性系数基本保持不变,与没有进行充气截排水情况的Fs=0.912相比,充气时坡体的稳定性提高了24.8%。
5 结论1) 在滑坡后缘坡体的适当位置进行充气,能够形成稳定的非饱和截水帷幕,有效拦截地下水流向充气点下坡侧潜在滑坡区,达到阻止潜在滑坡区地下水位的大幅上升的目的。
2) 在其他条件固定的情况下,不同充气压力对坡体地下水控制效果有较大的差别,相应的对滑坡稳定性提高作用效果也随充气压力的改变而变化,即存在最佳充气压力值。就小旦滑坡的计算结果看:当充气压力值小于125 kPa时,滑坡的稳定性系数随充气压力的提高而提高;当充气压力值大于125 kPa后,继续增大充气压力反而使稳定性系数下降。小旦滑坡的最佳充气压力值为125 kPa。
3) 在最佳充气压力作用下,小旦滑坡的坡脚未开挖状态下稳定性系数由1.144增大到1.209,提高了5.7%;而开挖状态下的稳定性系数由1.106增大到1.139,提高了3.0%。雨季边坡后缘入渗量增大的情况下,充气截排水对滑坡稳定性的提高作用更为显著,因此充气截排水技术对提高此类含碎石堆积层边坡的稳定性是有效的。
| [1] |
李烈荣. 中国地质灾害与防治[M]. 北京: 地质出版社, 2003. Li Lierong. Geological Hazards and Prevention in China[M]. Beijing: Geological Publishing House, 2003. |
| [2] |
孙红月, 吴红梅, 李焕强, 等. 松散堆积土中的隔水层对边坡稳定性的影响[J]. 浙江大学学报(工学版), 2010, 44(10): 2016-2020. Sun Hongyue, Wu Hongmei, Li Huanqiang, et al. Influence to Slope Stability Caused by Impermeable Layer in Loose Deposited Soil[J]. Journal of Zhejiang University (Engineering Science), 2010, 44(10): 2016-2020. DOI:10.3785/j.issn.1008-973X.2010.10.029 |
| [3] |
俞伯汀, 孙红月, 尚岳全. 含碎石黏性土边坡渗流系统的物理模拟试验[J]. 岩土工程学报, 2006, 28(6): 705-708. Yu Boting, Sun Hongyue, Shang Yuequan. Physical Model Simulation Tests on Seepage System in Debris-Containing Clay Slopes[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 705-708. DOI:10.3321/j.issn:1000-4548.2006.06.006 |
| [4] |
尚岳全, 孙红月, 侯利国, 等. 管网渗流系统对含碎石黏性土边坡的稳定作用[J]. 岩石力学与工程学报, 2005, 24(8): 1371-1375. Shang Yuequan, Sun Hongyue, Hou Liguo, et al. Study on the Stability of Pebbly-Clay Slopes with Pipe Drainage System[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(8): 1371-1375. DOI:10.3321/j.issn:1000-6915.2005.08.015 |
| [5] |
尚岳全, 周建锋, 童文德. 含碎块石土质边坡的稳定性问题[J]. 地质灾害与环境保护, 2002, 13(1): 41-43. Shang Yuequan, Zhou Jianfeng, Tong Wende. The Influence of Pipe Seepage System on the Stability of a Pebbly-Clay Slope[J]. Journal of Geological Hazards and Environment Preservation, 2002, 13(1): 41-43. DOI:10.3969/j.issn.1006-4362.2002.01.011 |
| [6] |
杜丽丽, 孙红月, 尚岳全. 松散堆积土边坡充气排水方法[J]. 吉林大学学报(地球科学版), 2013, 43(3): 877-882. Du Lili, Sun Hongyue, Shang Yuequan. Air-Filled Drainage Method in Loose Accumulation Soil Slope[J]. Journal of Jilin University (Earth Science Edition), 2013, 43(3): 877-882. |
| [7] |
杜丽丽, 孙红月, 尚岳全, 等. 滑坡应急治理充气截水方法[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3954-3960. Du Lili, Sun Hongyue, Shang Yuequan, et al. Method of Intercepting Water by Filting Soil with Air in Emergency Treatment Engineering of Landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(Sup.2): 3954-3960. |
| [8] |
杜丽丽, 孙红月, 尚岳全, 等. 充气截排水滑坡治理数值模拟研究[J]. 岩石力学与工程学报, 2014, 33(增刊1): 2628-2634. Du Lili, Sun Hongyue, Shang Yuequan, et al. Simulation of Numerical Control of Pneumatic Cut-off Method for Landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Sup.1): 2628-2634. |
| [9] |
康剑伟, 孙红月, 刘长殿. 一维土柱高压充气阻渗法的数值模拟[J]. 公路工程, 2013, 38(3): 67-71. Kang Jianwei, Sun Hongyue, Liu Changdian. Numerical Simulation of High-Pressure Infiltration Resistance of One-Dimensional Soil Column[J]. Highway Engineering, 2013, 38(3): 67-71. |
| [10] |
钱文见, 尚岳全, 杜丽丽, 等. 充气位置及压力对边坡截排水效果的影响[J]. 吉林大学学报(地球科学版), 2016, 46(2): 536-542. Qian Wenjian, Shang Yuequan, Du Lili, et al. Influences of Inflation Location and Pressure on Draining of Slope[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(2): 536-542. |
| [11] |
余文飞, 孙红月, 尚岳全, 等. 坡体充气过程中气水两相流数值模拟[J]. 岩石力学与工程学报, 2016(增刊2): 3597-3604. Yu Wenfei, Sun Hongyue, Shang Yuequan, et al. Numerical Simulation of Air-Water Two-Phase Flow in Inflatable Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2016(Sup.2): 3597-3604. |
| [12] |
Collins R E.流体通过多孔材料的流动[M].陈钟祥译.北京: 石油工业出版社, 1984: 63-65. Collins R E. Flow of Fluids Through Porous Materials[M]. Translated by Chen Zhongxiang. Beijing: Petroleum Industry Press, 1984: 63-65. |
| [13] |
Geo-Slope International Ltd. Air Flow Modeling with AIR/W 2007[M]. Calgary: Geo-Slope International Ltd Press, 2008: 117-120.
|
| [14] |
Van Genuchten M T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils[J]. Soil Science Society of America Journal, 1980, 44: 892-898. DOI:10.2136/sssaj1980.03615995004400050002x |
| [15] |
常士骠, 张苏民, 项勃, 等. 工程地质手册[M]. 四版. 北京: 中国建筑工业出版社, 2006: 536-538. Chang Shibiao, Zhang Sumin, Xiang Bo, et al. Engineering Geology Handbook[M]. 4th ed. Beijing: China Architecture and Building Press, 2006: 536-538. |
| [16] |
南京大学水文地质工程地质教研室. 工程地质学[M]. 北京: 地质出版社, 1982. Staff of Hydrogeology and Engineering Geology of Nanjing University. Engineering Geology[M]. Beijing: Geological Publishing House, 1982. |
| [17] |
贝尔J.多孔介质流体动力学[M].李竞生, 陈崇希译.北京: 中国建筑工业出版社, 1983: 346-450. Bear J. Dynamics of Fluids in Porous Media[M]. Translated by Li Jingsheng, Chen Chongxi. Beijing: China Architecture and Building Press, 1983: 346-450. |



