2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东 青岛 266071
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, Shandong, China
0 引言
浊积扇低渗透油藏与常规油藏的地质特征存在明显差异。该储层孔隙结构复杂、细小,再加上后期成岩作用的改造,导致储层物性较差,平面、纵向非均质性较为强烈[1-3]。这些因素综合作用导致低渗透油藏差异性较为明显,区块部分井出现注水开发效果差、含水上升快等问题,影响了研究区的油气勘探与开发。查明低渗透储层层间水驱效果的差异性、流体渗流特征及分布规律,对油藏开发中后期剩余油分布预测意义重大[4-6]。
流动单元的概念最早是由Hearn(1984)提出的,是指垂向及横向上连续的、影响流体流动的、岩石物理性质相似的储集岩体,且随着开发阶段的深入,呈动态性变化[7-10]。低渗透储层强烈的非均质性、复杂的渗流特征对流动单元划分的精度提出了更高的要求。近年来,支持向量机算法越来越多地被运用到复杂岩性识别、测井曲线分层及储层预测等方面[11-13]。然而,在流动单元领域还无人涉及。因此,利用支持向量机算法开展流动单元研究,为流动单元分类评价提供了新的研究方向。
本文以大芦湖油田樊29块湖底浊积扇储层为例,结合低渗透储层的特征,在因子分析法优选参数的基础上,应用支持向量机算法开展流动单元研究,建立研究区流动单元分布模式,以期为油藏开发中后期剩余油分布预测、提高采收率提供理论支撑。
1 研究区地质特征大芦湖油田位于济阳坳陷东营凹陷博兴洼陷,是一被断层切割的简单穹窿背斜构造。研究区樊29块位于大芦湖油田中部鼻状构造的高部位,其主力含油层系为沙三中亚段四砂层组,含油面积为2.9 km2,地质储量为583×104 t。四砂层组主要发育5个小层,其中41小层在研究区不发育,只发育42、43、44、45四个小层;每个小层又可细分为4个单砂层,故全区可以细分为16个单砂层。该油藏储集层为湖底浊积扇沉积,主要发育中扇、外扇亚相,内扇亚相不发育;岩性类型主要包括含砾砂岩、细砂岩、粉砂岩、泥质粉砂岩及泥岩。油藏埋深2 800~3 100 m,平均孔隙度15.9%,平均渗透率11.6×10-3μm2,为中深层低渗透油藏。油藏非均质性强、层间矛盾突出,经过几十年的开发,目前已进入高含水期,含水率达81.3%,采出程度为19.78%,处于低速开发阶段。
2 流动单元划分参数选取 2.1 定性选取研究区为典型的湖底浊积扇沉积体系,形成于沙三段沉积中期。该时期物源供应充足,高青扇三角洲沉积体系范围扩大,一度向博兴断层下降盘推进,东北部受地形的影响,在樊家古鼻状构造部位推进不前,沉积体快速堆积,滑塌浊积扇沉积体系因而形成[14]。大芦湖油田樊29块浊积扇沉积体系主要发育浊积水道、水道间及朵叶体等微相类型,受沉积环境、成岩作用、构造作用等多重因素的影响,储层成因机制复杂。沉积体系内各水道砂体横向、纵向迁移变化快,展布规律及连通程度复杂。此外,成岩作用的改造导致储层非均质强烈,储层物性、渗流能力较差。
由于浊积扇储层特征及成因机制的复杂性,仅仅依靠单一参数难以反映储层流动单元的全部特征。因此,在流动单元评价参数选取过程中应充分考虑影响储层流动单元分布的诸多因素,如储层岩石物理特征、微观孔隙结构特征、储层沉积特征及储层非均质特征等[15-16]。
本文在充分考虑影响流动单元分布的诸多因素基础上,共选取了13个储层特征参数,包括:孔隙度(φ)、渗透率(K)、泥质体积分数(Vsh)、含油饱和度(So)、沉积微相、砂岩厚度(H)、孔喉半径(R35)、流动带指标(Ifz)、油藏品质指数(Irq)、渗透率突进系数(TK)、渗透率级差(JK)、隔夹层厚度(hd)、隔夹层密度(ρd)。其中:φ、K反映储层储集物性特征;So反映储层流体特征;沉积微相、H反映储层沉积特征;Vsh反映储层岩性特征;hd、ρd、TK、JK反映储层非均质特征;Irq反映储层质量特征;R35、Ifz反映储层的微观孔隙结构特征,是体现流体渗流能力的特征参数。
2.2 因子分析法优选 2.2.1 因子分析法原理因子分析的概念最早是由Thurstone于1931年首次系统提出的,是研究变量间相关性、变量内部成因联系及探索产生上述关系内因的一种多元统计学方法[1]。在流动单元研究中,储层评价参数众多且参数间关系复杂。因子分析法通过降维的思想,可以提取几个少数的主因子来涵盖大量的原始储层信息;新因子的提取既无损于原始参数的信息,又能简化众多参数间的复杂关系,便于对原始参数进行分类和解释[17]。因子分析的步骤包括:建立因子分析模型,计算因子载荷;进行因子旋转得到旋转后的因子载荷,计算因子得分。其中,初始因子载荷矩阵往往不唯一,因子地质涵义不明确,故需要进行最大方差旋转得到地质意义明确的主因子。
建立因子分析模型。假设X=(X1, X2, …, Xm)是m×1阶的随机向量,代表每个单砂层的储层参数;F=(F1, F1, …, Fp)是p×1阶的标准化正交主因子向量(p<m)。当前p个主因子能解释原始数据80%以上的信息时,即可得到因子分析模型:
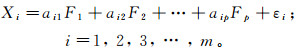 (1)
(1) 式中:ai1, ai2, …, aip是各变量(储层参数)在各主因子上的载荷,反映了变量(储层参数)与主因子之间关系的密切程度;εi为特殊因子。矩阵形式为
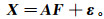 (2)
(2) 式中:
为了得到地质意义明确的主因子,需利用最大方差法对初始载荷进行旋转得到旋转后的因子载荷。计算各主因子得分就需要将主因子F表示为原始变量的线性组合。主因子Fj由原始变量Xi表示的线性组合为
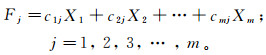 (3)
(3) 式中,cmj为变量系数。
通过因子分析可以探索储层参数间的内在联系,将冗杂的储层参数转化为少数几个反映储层性质的主因子。当每个主因子被赋予客观合理的地质解释后,就可以利用含有地质含义的主因子作为流动单元评价的储层参数,进而完成优选流动单元评价参数的目的。
2.2.2 因子分析法应用本文通过标志层对比、旋回对比、等高程对比等方法建立了包括小层、单砂层在内的多级地层格架,并通过测井解释参数模型的建立,进行了研究区储层测井二次解释。在此基础上选取了10口关键井的13个流动单元评价参数,以单砂层内各参数均值构成122个样本,利用SPSS软件,采用因子分析法对样本数据的13个流动单元评价参数进行了因子分析,分析结果如下。
样本数据的KMO(Kaiser-Meyer-Olkin)检验统计量和Bartlett球形检验统计量是检验样本数据是否适合做因子分析的两个重要指标[18]。对122个样本数据的KMO和Bartlett球形检验结果如表 1所示。其中,KMO值为0.623,Bartlett球形检验显著水平为0.000,非常显著,因此研究区储层参数适合做因子分析。通过方差分析可知,从13个参数中提取5个主因子时可以涵盖84.134%的原始储层信息(表 2),符合因子分析的精度要求。通过因子载荷旋转得到各主因子的载荷系数矩阵(表 3)。
| KMO值 | Bartlett球形检验 | ||
| 统计量 | 自由度 | 显著性 | |
| 0.623 | 1 534.658 | 78 | 0.000 |
| 因子 | 起始 | 提取平方和载入 | 旋转平方和载入 | ||||||||
| 特征值 | 方差贡献率/% | 累加方差贡献率/% | 特征值 | 方差贡献率/% | 累加方差贡献率/% | 特征值 | 方差贡献率/% | 累加方差贡献率/% | |||
| F1 | 3.654 | 28.110 | 28.110 | 3.654 | 28.110 | 28.110 | 3.559 | 27.376 | 27.376 | ||
| F2 | 3.492 | 26.862 | 54.972 | 3.492 | 26.862 | 54.972 | 2.452 | 18.858 | 46.234 | ||
| F3 | 1.761 | 13.549 | 68.522 | 1.761 | 13.549 | 68.522 | 1.774 | 13.648 | 59.882 | ||
| F4 | 1.159 | 8.919 | 77.441 | 1.159 | 8.919 | 77.441 | 1.640 | 12.613 | 72.495 | ||
| F5 | 0.870 | 6.693 | 84.134 | 0.870 | 6.693 | 84.134 | 1.513 | 11.639 | 84.134 | ||
| 储层综合因子 | F1 | F2 | F3 | F4 | F5 |
| 沉积微相 | -0.004 | 0.401 | 0.145 | 0.029 | 0.043 |
| 砂岩厚度 | -0.014 | 0.497 | 0.161 | 0.117 | 0.241 |
| 渗透率 | 0.169 | -0.054 | -0.001 | 0.037 | 0.310 |
| 孔隙度 | -0.169 | -0.053 | -0.024 | 0.053 | 0.461 |
| 含油饱和度 | 0.008 | 0.170 | 0.052 | -0.052 | 0.552 |
| 泥质体积分数 | 0.030 | -0.276 | -0.039 | 0.150 | -0.048 |
| 孔喉半径 | 0.282 | -0.006 | -0.024 | 0.040 | 0.006 |
| 流动带指标 | 0.274 | 0.002 | -0.014 | -0.022 | -0.240 |
| 油藏品质指数 | 0.264 | -0.014 | -0.027 | 0.056 | 0.110 |
| 隔夹层厚度 | -0.027 | 0.237 | 0.696 | -0.079 | 0.057 |
| 隔夹层密度 | -0.011 | -0.056 | 0.487 | -0.134 | -0.064 |
| 渗透率级差 | 0.090 | 0.057 | -0.112 | 0.621 | 0.027 |
| 渗透率突进系数 | -0.031 | 0.000 | -0.094 | 0.505 | -0.049 |
由因子载荷系数矩阵可以得出每个因子的地质意义。对于因子F1,载荷较大的是孔喉半径、流动带指标、油藏品质指数,因此F1反映储层流动特征,命名为流动因子;对于因子F2,正载荷较大的是沉积微相、砂岩厚度,负载荷较大的是泥质体积分数,主要反映储层沉积特征,命名为沉积因子;对于因子F3,载荷较大的是隔夹层厚度、隔夹层密度,主要反映隔夹层特征,命名为隔夹层因子;对于因子F4,载荷较大的是渗透率级差、渗透率突进系数,反映储层非均质特征,命名为非均质因子;而对于因子F5,载荷较大的是孔隙度、渗透率、含油饱和度,反映储层储集特征,命名为储集因子。因此,可以用提取的5个主因子:流动因子(F1)、沉积因子(F2)、隔夹层因子(F3)、非均质因子(F4)、储集因子(F5),作为流动单元评价的地质参数。
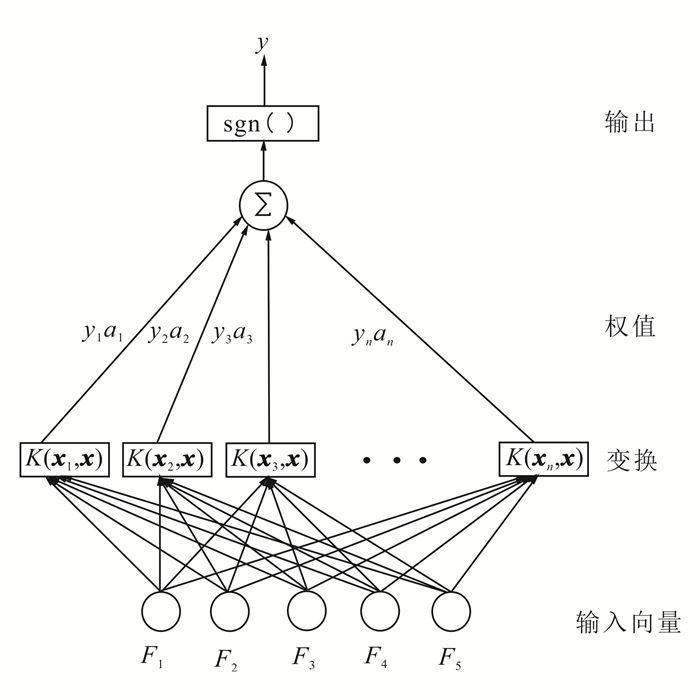
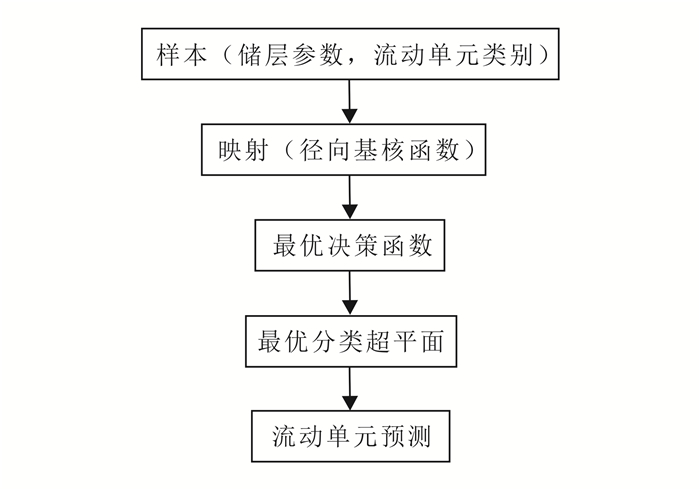
3 支持向量机算法原理及模型构建 3.1 支持向量机算法原理支持向量机(SVM)最早由Vapnik[19]提出,是一种基于统计学理论的新型机器学习方法。其基本实现途径是通过核函数的引入,将非线性问题(输入空间)映射到新的高维特征空间,在高维特征空间中构造最优决策曲面并进行样本分类。支持向量机在解决研究目标与多个不确定特征相关的非线性问题时,具有精度高、速度快、通用性强和理论完善等优点[20]。由于低渗透储层流动单元受多种地质因素的影响,且流动性能好坏与各因素间变化规律不尽相同,因此本文采用非线性处理能力较强的支持向量机算法进行流动单元分类识别。支持向量机算法结构示意图和流动单元划分流程如图 1、2所示。算法实现流程如下:首先,选取已知样本组成学习样本对模型进行训练,从而建立流动单元定量识别模型;其次,通过测试样本对建立的预测模型进行检验;最终,利用验证合格的预测模型实现对未知样本的流动单元预测。
|
| 图 1 支持向量机结构图 Figure 1 Structure of SVM |
|
|
|
| 图 2 支持向量机划分流动单元流程图 Figure 2 Flow chart of flow unit division base on SVM |
|
|
模型构建主要包括核函数和惩罚因子C的确定。SVM中最常见的核函数主要有高斯径向基核函数、多层感知器核函数和多项式核函数3种[21]。高斯径向基核函数拥有较宽的收敛域,对于各种各样的样本情况都有较高的适用性,且只有一个核参数g,灵活性高,是目前运用最广泛且效果最优的分类核函数。本文在实际的SVM模型建立中,通过对不同核函数模型预测精度的对比可知,选用高斯径向基核函数时模型预测精度远远高于其他两类核函数(表 4)。因此,选用高斯径向基核函数来建立支持向量机预测模型。高斯径向基核函数公式为
| 核函数类型 | 预测准确率/% |
| 高斯径向基核函数 | 90.38 |
| 多项式核函数 | 85.25 |
| 多层感知器核函数 | 69.66 |
 (4)
(4) 式中:xi(i=1, 2, 3, …, n)代表样本的输入特征;x是多个行向量xi组成的矩阵;g为高斯核宽度,控制着径向基核函数对非线性样本的映射效果。当g取值很小时,所有样本都成为支持向量,容易出现过拟合现象;当g取值较大时,该核函数映射的空间相当于一个低维的子空间,所有样本被分为一类,对新样本分类能力几乎为零。因此,只有当g取合适值时样本才能取得最优分类效果。
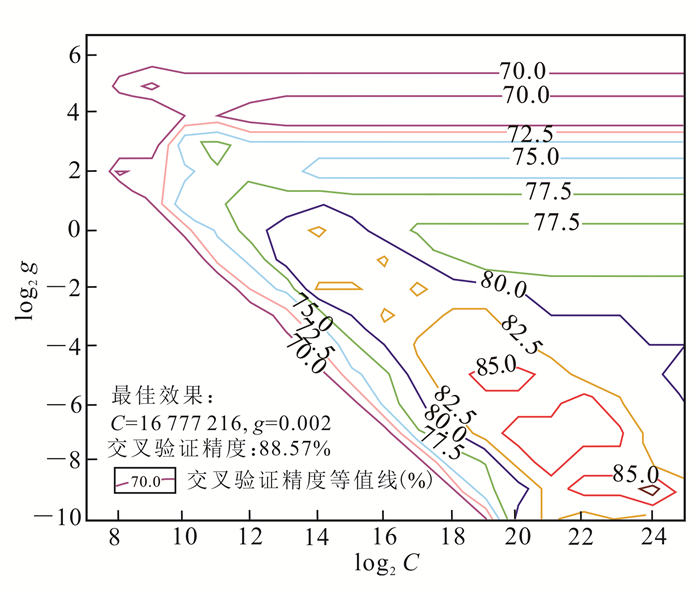
3.3 模型参数寻优核函数建立后还需优选出最优的高斯径向基核参数g和惩罚因子C,从而使SVM模型取得最准确的分类结果。国际上常用的模型参数优化方法主要有留一法、网格搜索、粒子群优化算法及交叉验证法[21]。其中交叉验证法具有应用广泛、精确率高的特点,所以本文选用交叉验证与网格搜索相结合的方法进行参数寻优。首先,凭经验选定一个g和C的网格搜索范围;其次,采用交叉验证法,以学习样本作为训练集训练支持向量机并进行检验,得到每组参数对应的交叉验证精度;最终,选出交叉验证精度最高的一组参数值,即为最优参数。C表示对错误分类惩罚的程度,控制着最优分类面的位置。当多组参数得到交叉验证精度均最高时,为避免因C过高而导致过学习状态(即学习样本分类准确度很高,而预测样本分类准确度却很低),一般选取最小的C。
通过反复搜索和验证,最终确定最优参数(g, C)=(0.002, 16 777 216),此时模型的交叉验证精度为88.57%(图 3)。
|
| 图 3 SVM模型参数寻优 Figure 3 Optimization of SVM model parameters |
|
|
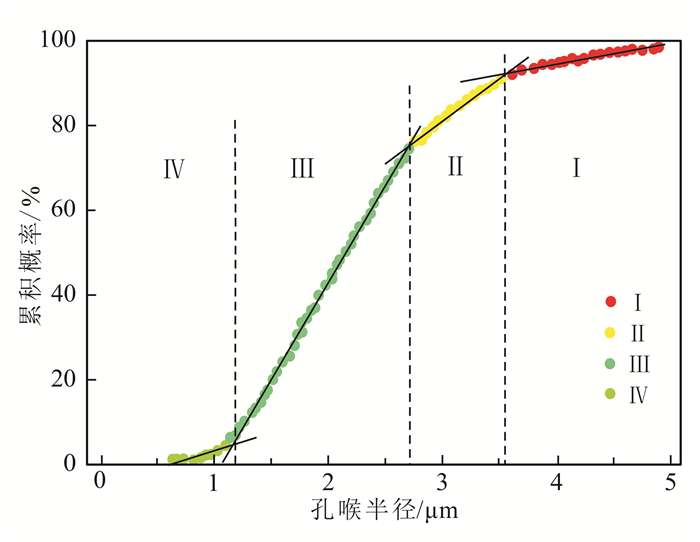
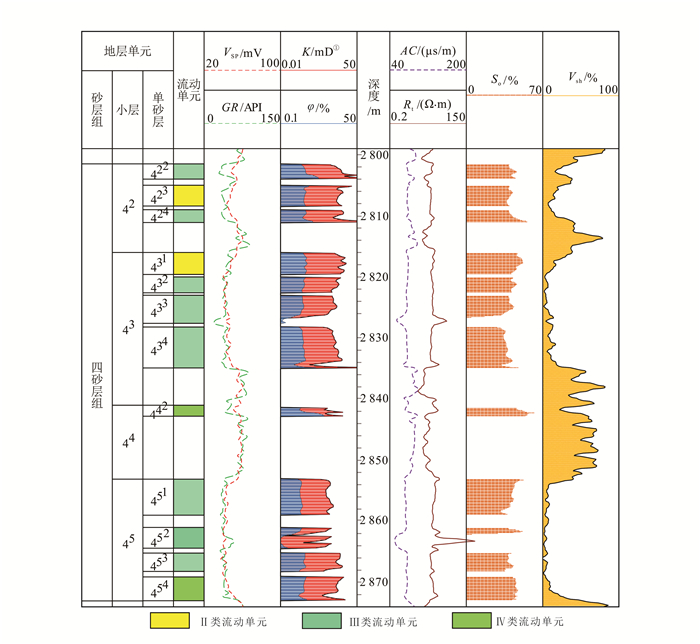
基于因子分析法进行参数优选的基础上,选取5个主因子(流动因子、沉积因子、隔夹层因子、非均质因子、储集因子)作为支持向量机模型的输入特征参数。采用孔喉半径法将研究区10口关键井的122个样本数据分为4类流动单元(图 4),从而获得构建模型所需的已知样本数据集(表 5),并以F29井为例(该井单砂层发育不完整,421、441、443、444单砂层不发育)展示单井流动单元划分结果(图 5)。按照第3节中的算法流程建立研究区流动单元预测模型,进而应用建立的预测模型对研究区未取心井进行流动单元识别与划分[22]。
|
| 图 4 孔喉半径法划分流动单元 Figure 4 Flow unit divided by pore throat method |
|
|
|
| VSP.自然电位;GR.自然伽马;AC.声波时差;Rt.地层电阻率。①毫达西(mD)为非法定计量单位,1 mD=0.987×10-3 μm2,下同。 图 5 F29井流动单元划分 Figure 5 Flow unit division of F29 well |
|
|
| 样本号 | 流动单元评价参数 | 主因子 | SVM预测结果 | 评价结果 | ||||||||||||||||
| H/m | K/(10-3×)μm2 | φ/% | So/% | Vsh/% | R35/μm | Ifz | Irq | 沉积微相 | hd/m | ρd | Jk | Tk | F2 | F3 | F4 | F5 | ||||
| 1 | 1.4 | 4.32 | 26.73 | 37.09 | 68.2 | 0.75 | 3.46 | 1.26 | 中扇侧缘 | 4.08 | 0.74 | 3.38 | 2.1 | 2.67 | 6 | 4.15 | 2.72 | 33 | Ⅳ | Ⅳ |
| 2 | 6.4 | 8.01 | 9.02 | 38.67 | 37.3 | 2.74 | 29.8 | 2.96 | 水道主体 | 4.69 | 0.42 | 17.43 | 2.2 | 7.21 | 12 | 3.98 | 10.82 | 23 | Ⅲ | Ⅱ |
| 3 | 6.3 | 9.56 | 9.02 | 42.78 | 28.7 | 3.04 | 32.6 | 3.23 | 水道主体 | 0.85 | 0.12 | 3.31 | 1.9 | 9.82 | 10 | 2.92 | 1.99 | 24 | Ⅱ | Ⅱ |
| 4 | 5.3 | 11.46 | 8.88 | 64.16 | 20.1 | 3.43 | 36.6 | 3.57 | 水道主体 | 0.6 | 0.1 | 2.65 | 1.3 | 11.85 | 13 | 3.74 | 0.12 | 36 | Ⅰ | Ⅰ |
| 5 | 2.9 | 26.43 | 13.19 | 57.17 | 16.3 | 3.99 | 29.2 | 4.45 | 朵叶体 | 0.95 | 0.25 | 4.81 | 1.6 | 12.09 | 10 | 2.99 | 2.61 | 40 | Ⅰ | Ⅰ |
| 6 | 6.2 | 34.41 | 22.47 | 54.81 | 41.8 | 2.94 | 13.4 | 3.89 | 水道主体 | 3.25 | 0.34 | 32.86 | 1.3 | 4.03 | 13 | 1.95 | 21.32 | 51 | Ⅱ | Ⅱ |
| 7 | 1 | 28.15 | 15.53 | 52.95 | 53.7 | 3.59 | 23 | 4.23 | 朵叶体 | 3 | 0.75 | 2.82 | 1.9 | 10.45 | 9 | 4.36 | 1.68 | 40 | Ⅰ | Ⅰ |
| 8 | 4 | 10.94 | 15.8 | 54.45 | 25.2 | 2.03 | 13.9 | 2.61 | 水道侧缘 | 2.85 | 0.42 | 3.64 | 1.8 | 3.66 | 11 | 4.66 | 1.8 | 38 | Ⅲ | Ⅲ |
| 9 | 3.4 | 11.24 | 13.18 | 51.08 | 4.7 | 2.41 | 19.1 | 2.9 | 水道主体 | 0.8 | 0.19 | 3.98 | 1.5 | 5.84 | 10 | 2.96 | 1.97 | 34 | Ⅱ | Ⅲ |
| 10 | 3.4 | 3.86 | 14.76 | 52.14 | 4.5 | 1.17 | 9.27 | 1.61 | 水道侧缘 | 0.8 | 0.19 | 1.61 | 1.3 | 1.18 | 10 | 3.33 | 0.19 | 35 | Ⅳ | Ⅳ |
| 11 | 3 | 13.72 | 17.07 | 45.69 | 24.3 | 2.17 | 13.6 | 2.82 | 水道侧缘 | 2.9 | 0.49 | 2.72 | 1.4 | 4.11 | 9 | 4.21 | 1.55 | 35 | Ⅲ | Ⅲ |
| 12 | 3.4 | 7.8 | 17.93 | 32.94 | 35.3 | 1.49 | 9.48 | 2.07 | 水道主体 | 3.1 | 0.48 | 8.69 | 2.5 | 0.69 | 8 | 3.19 | 6.41 | 28 | Ⅲ | Ⅲ |
| 13 | 4.2 | 9.03 | 16.61 | 47.5 | 18.1 | 1.74 | 11.6 | 2.32 | 水道主体 | 1.35 | 0.24 | 6.84 | 2.8 | 2.05 | 10 | 2.93 | 4.82 | 35 | Ⅲ | Ⅲ |
| 14 | 2.4 | 0.95 | 7.06 | 38.8 | 30.2 | 0.97 | 15.1 | 1.15 | 中扇侧缘 | 1.4 | 0.29 | 3.41 | 3 | 3.08 | 9 | 3.01 | 2.15 | 22 | Ⅳ | Ⅳ |
| 15 | 5 | 15.16 | 9.62 | 55.02 | 25.7 | 3.77 | 37 | 3.94 | 水道主体 | 2.64 | 0.35 | 22.24 | 2.1 | 10.77 | 13 | 2.44 | 13.12 | 33 | Ⅰ | Ⅰ |
| 16 | 2.5 | 3.6 | 14.39 | 51.46 | 26.5 | 1.14 | 9.34 | 1.57 | 中扇侧缘 | 0.75 | 0.23 | 2.22 | 1.4 | 0.84 | 12 | 3.64 | 0.9 | 35 | Ⅳ | Ⅳ |
| 17 | 3.4 | 16.82 | 11.17 | 49.78 | 23.5 | 3.52 | 30.6 | 3.85 | 朵叶体 | 2.2 | 0.39 | 24.66 | 2.8 | 8.9 | 11 | 1.35 | 15.36 | 32 | Ⅱ | Ⅱ |
| 18 | 1.9 | 12.34 | 16.01 | 52.88 | 19.2 | 2.15 | 14.4 | 2.76 | 水道侧缘 | 2.85 | 0.6 | 2.29 | 1.2 | 4.5 | 9 | 4.52 | 0.53 | 37 | Ⅲ | Ⅲ |
| 19 | 2.8 | 19.75 | 18.01 | 47.66 | 26.4 | 2.56 | 14.9 | 3.29 | 中扇侧缘 | 2.6 | 0.48 | 3.9 | 1.8 | 5.49 | 8 | 3.68 | 2.67 | 38 | Ⅲ | Ⅲ |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 122 | 3.1 | 5.15 | 8.3 | 35.27 | 40.2 | 2.27 | 27.3 | 2.47 | 水道侧缘 | 1.3 | 0.3 | 8.89 | 1.7 | 7.2 | 8 | 1.78 | 5.19 | 19 | Ⅲ | Ⅲ |
为避免各参数间量纲的差异导致运算困难,影响学习效果,所有样本数据在进入支持向量机之前都要进行归一化处理,将样本的特征值映射到[0, 1]。本文采用MATLAB中的mapminmax函数完成样本数据的归一化处理。
4.2 流动单元分类预测研究区取心井数量有限,样本数据较少,而支持向量机在小样本数据分类中具有显著的优势,因此采用该算法进行流动单元分类预测是可靠的。选取4.1节中提取的10口关键井的122个样本数据组成样本集进行SVM训练,样本数据示例如表 5所示。样本数据分配时,为避免训练样本过少而导致模型精度不佳或测试样本不足导致的预测局限性,一般选取样本数据的1/2~2/3作为训练样本进行模型训练。因此,选取70个样本数据作为学习样本组成训练集进行训练(Ⅰ类流动单元10个、Ⅱ类流动单元15个、Ⅲ类流动单元36个、Ⅳ类流动单元9个),并建立SVM模型;选取52个测试样本(Ⅰ类流动单元6个、Ⅱ类流动单元10个、Ⅲ类流动单元30个、Ⅳ类流动单元6个)对流动单元预测模型进行检验(表 6)。
| 流动单元类型 | 训练样本数 | 预测样本数 | SVM预测样本数 | 正判率/% |
| Ⅰ | 10 | 6 | 6 | 100.00 |
| Ⅱ | 15 | 10 | 9 | 90.00 |
| Ⅲ | 36 | 30 | 26 | 86.67 |
| Ⅳ | 9 | 6 | 6 | 100.00 |
| 合计 | 70 | 52 | 47 | 90.38 |
根据模型预测结果可知,测试样本的整体正判率为90.38%,且4类流动单元的预测正判率均在85%以上,具有较高的预测精度(表 6)。错判的5个样本均出现在由一类流动单元向另一类流动单元过渡的地方,但9.62%的错判率已经满足地质上的要求。支持向量机算法为流动单元研究提供了一种新的手段,具有较显著的分类效果,应用该算法开展流动单元研究具有广阔的前景。
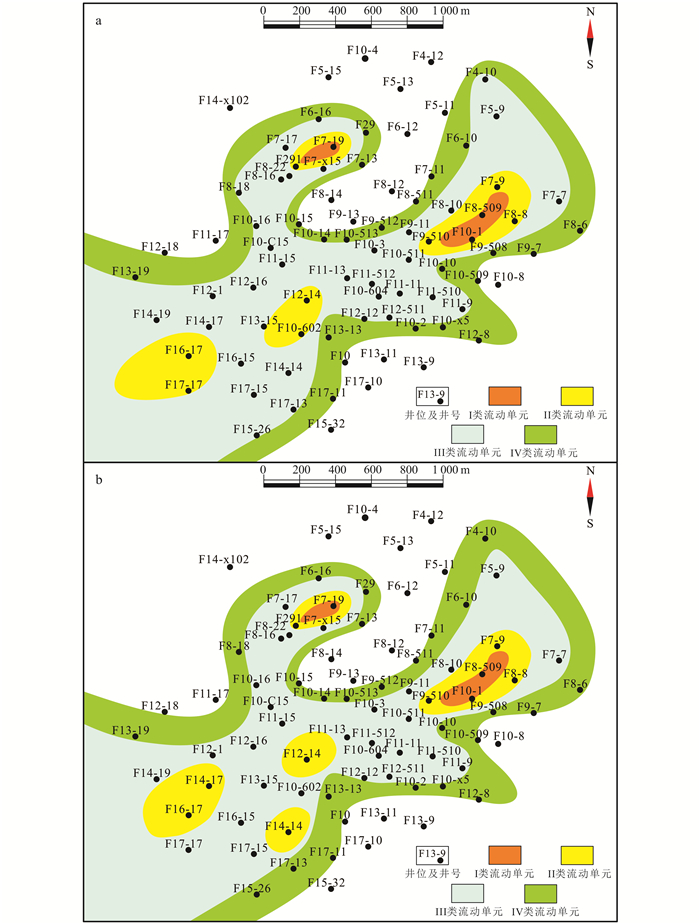
4.3 流动单元平面展布特征本文应用建立的支持向量机预测模型对工区未取心井进行流动单元识别与分类,并在单井流动单元预测的基础上,对浊积扇储层内部进行流动单元井间分布预测[23-24]。以441单砂层为例,将预测结果与定性分析结果进行对比,结果如图 6所示。结果表明:支持向量机预测结果与定性分析结果符合度较高,该算法在流动单元划分中具有显著的分类效果。
|
| a.定性分析结果;b.预测结果。 图 6 441单砂层流动单元识别结果对比图 Figure 6 Correlation of flow unit in 441 single sand layer |
|
|
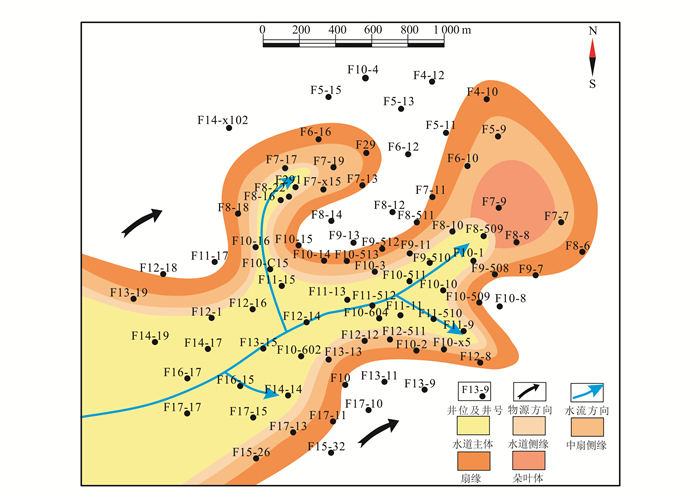
研究区为典型的湖底浊积扇沉积,沉积微相对流动单元展布具有明显的控制作用,但后期成岩作用的改造也可能导致同一沉积微相发育不同的流动单元类型、同一流动单元分布于不同的沉积微相[25]。本文以441单砂层为例研究了流动单元的平面展布规律(图 7)。研究表明:Ⅲ类流动单元分布最为广泛,占全区的65%左右,是研究区最主要的流动单元类型,Ⅰ、Ⅱ、Ⅳ类流动单元分布较少,储层流动性能较差与低渗储层分布特征吻合;另外,平面上流动单元与沉积微相展布规律吻合。Ⅰ类、Ⅱ类流动单元分布局限,仅在浊积水道主流线方向及朵叶体微相发育;Ⅲ类流动单元分布广泛,呈大面积连片分布,在浊积水道、水道侧缘及中扇侧缘均有分布;Ⅳ类流动单元主要分布在浊积扇外缘的扇缘亚相。
|
| 图 7 441单砂层沉积微相平面展布 Figure 7 Distribution of sedimentary microfacies in 441 single sand layer |
|
|
1) 利用因子分析法从13个流动单元评价参数中提取了流动因子、沉积因子、隔夹层因子、非均质因子、储集因子等5个综合因子,这5个主因子较为完整地涵盖了原始储层信息。
2) 基于支持向量机的流动单元预测模型能够较为系统地反映多种地质因素与流动性能之间的复杂映射规律,能够更为精确地划分流动单元,正判率高达90.38%。该方法操作简单、运算速度快、准确率高,为流动单元研究提供了一种新的思路,应用该算法开展流动单元研究具有广阔的前景。
3) 流动单元与沉积微相平面展布规律吻合。Ⅰ类、Ⅱ类流动单元分布局限,仅在浊积水道主流线方向及朵叶体微相发育;Ⅲ类流动单元分布广泛,呈大面积连片分布,在浊积水道、水道侧缘及中扇侧缘均有分布;Ⅳ类流动单元主要分布在浊积扇外缘的扇缘亚相。
| [1] |
宁正福, 赵洋, 程林松. 基于因子分析的流动单元研究[J]. 中国石油大学学报:自然科学版, 2012, 36(4): 107-111,117. Ning Zhengfu, Zhao Yang, Cheng Linsong. Study on Flow Units Based on Factor Analysis[J]. Journal of China University of Petroleum, 2012, 36(4): 107-111,117. |
| [2] |
熊文涛, 师永民, 刘新菊, 等. 致密砂岩储层流动单元研究:以鄂尔多斯盆地延长组长61油层为例[J]. 北京大学学报(自然科学版), 2014, 50(2): 288-294. Xiong Wentao, Shi Yongmin, Liu Xinju, et al. Study on Flow Unit of Tight Sandstone Reservoir:A Case of Yanchang Formation Chang-61 Resrvoir in Erdos Basin[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2014, 50(2): 288-294. |
| [3] |
王亚, 杨少春, 路研, 等. 基于测井岩石物理相识别的低渗透储层评价方法:以东营凹陷高青地区蒙阴组上段为例[J]. 中国矿业大学学报, 2018, 47(6): 1388-1399. Wang Ya, Yang Shaochun, Lu Yan, et al. Evaluation Method of Low Permeability Reservoirs Based on Logging Petrophysical Facies Identification:A Case Study of the Upper Member of Mengyin Formation in Gaoqing Area, Dongying Depression[J]. Journal of China University of Mining & Technology, 2018, 47(6): 1388-1399. |
| [4] |
Yin T J, Zhang C M, Zhang S F, et al. Estimation of Reservoir and Remaining Oil Prediction Based on Flow Unit Analysis[J]. Earth Science, 2009, 52(Sup. Ⅰ): 120-127. |
| [5] |
范子菲, 李孔绸, 李建新, 等. 基于流动单元的碳酸盐岩油藏剩余油分布规律[J]. 石油勘探与开发, 2014, 41(5): 578-584. Fan Zifei, Li Kongchou, Li Jianxin, et al. A Study on Remaining Oil Distribution in a Carbonate Oil Reservoir Based on Reservoir Flow Units[J]. Petroleum Exploration and Development, 2014, 41(5): 578-584. |
| [6] |
苗长盛, 董清水, 张旗, 等. 储层流动单元研究在油田老区挖潜中的应用:以吉林油田乾146区块开发为例[J]. 吉林大学学报(地球科学版), 2011, 41(1): 39-45. Miao Changsheng, Dong Qingshui, Zhang Qi, et al. Application of Reservoir Flow Unit in Potential Finding of Developed Reservoir:A Case Study on Exploitation of Block Qian-146 in Jilin Oil Field, NE China[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(1): 39-45. |
| [7] |
Hearn C L, Ebanks W J, Tye R S, et al. Geological Factors Influencing Reservoir Performance of the Hartzog Draw Field[J]. Wyoming JPT, 1984, 36(9): 1335-1344. |
| [8] |
Ebanks W J Jr. Flow Unit Concept Integrated App-roach to Reservoir Description for Engineering Projects[J]. AAPG Bulletin, 1987, 71(5): 551-552. |
| [9] |
Rodriguez A. Facies Modeling and the Flow Unit Concept as a Sedimentological Tool in Reservoir Description: A Case Study[C]//SPE Annual Technical Conference and Exhibition. Houston: Society of Petroleum Engineers of AIME, 1988: 465-472.
|
| [10] |
Mahjour S K, Al-Askari M K G, Masihi M. Iden-tification of Flow Units Using Methods of Testerman Statistical Zonation, Flow Zone Index, and Cluster Analysis in Tabnaak Gas Field[J]. Journal of Petroleum Exploration & Production Technology, 2016, 6(4): 577-592. |
| [11] |
朱怡翔, 石广仁. 火山岩岩性的支持向量机识别[J]. 石油学报, 2013, 34(2): 312-322. Zhu Yixiang, Shi Guangren. Identification of Lithologic Characteristics of Volcanic Rocks by Support Vector Machine[J]. Acta Petrolei Sinica, 2013, 34(2): 312-322. DOI:10.3969/j.issn.1001-8719.2013.02.020 |
| [12] |
牟丹, 王祝文, 黄玉龙, 等. 基于最小二乘支持向量机测井识别火山岩类型:以辽河盆地中基性火山岩为例[J]. 吉林大学学报(地球科学版), 2015, 45(2): 639-648. Mou Dan, Wang Zhuwen, Huang Yulong, et al. Application of Least Squares Support Vector Machine to Lithology Identification:Taking Intermediate/Basaltic Rocks of Liaohe Basin as an Example[J]. Journal of Jilin University (Earth Science Edition), 2015, 45(2): 639-648. |
| [13] |
王常明, 田书文, 王翊虹, 等. 泥石流危险性评价:模糊c均值聚类-支持向量机法[J]. 吉林大学学报(地球科学版), 2016, 46(4): 1168-1175. Wang Changming, Tian Shuwen, Wang Yihong, et al. Risk Assessment of Debris Flow:A Method of SVM Based on FCM[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(4): 1168-1175. |
| [14] |
韩祥磊, 王文林, 孙红蕾. 博兴洼陷沙三段沉积体系探讨[J]. 油气地质与采收率, 2003, 8(10): 7-18. Han Xianglei, Wang Wenlin, Sun Honglei. Discussion on Sedimentary System of the Es3 Formation in Boxing Sag[J]. Petroleum Geology and Recovery Efficiency, 2003, 8(10): 7-18. |
| [15] |
王志章, 何刚. 储层流动单元划分方法与应用[J]. 天然气地球科学, 2010, 21(3): 362-366. Wang Zhizhang, He Gang. The Classification Method and Application of Reservoir Flow Units[J]. Natural Gas Geoscience, 2010, 21(3): 362-366. |
| [16] |
郑香伟, 吴健, 何胜林, 等. 基于流动单元的砂砾岩储层渗透率测井精细评价[J]. 吉林大学学报(地球科学版), 2016, 46(1): 286-294. Zheng Xiangwei, Wu Jian, He Shenglin, et al. Fine Evaluation of Permeability of Conglomerate Reservoir Based on Flow Unit[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(1): 286-294. |
| [17] |
Davis J C. Statistical and Data Analysis in Geology[M]. 2nd ed. New York: John Wiley & Sons, 1986: 646.
|
| [18] |
赵少卿, 魏俊浩, 高翔, 等. 因子分析在地球化学分区中的应用:以内蒙古石板井地区1:5万岩屑地球化学测量数据为例[J]. 地质科技情报, 2012, 31(2): 27-34. Zhao Shaoqing, Wei Junhao, Gao Xiang, et al. Factor Analysis in the Geochemical Subdivisions:Taking 1:50000 Debris Geochemical Survey in the Shibanjing Area of Inner Mongolia as an Example[J]. Geological Science and Technology Information, 2012, 31(2): 27-34. |
| [19] |
Vapnik V N.统计学习理论的本质[M].张学工, 译.北京: 清华大学出版社, 2000: 85-205. Vapnik V N. The Nature of Statistical Learning Theory[M]. Translated by Zhang Xuegong. Beijing: Tsinghua University Press, 2000: 85-205. |
| [20] |
卢文喜, 郭家园, 董海彪, 等. 改进的支持向量机方法在矿山地质环境质量评价中的应用[J]. 吉林大学学报(地球科学版), 2016, 46(5): 1511-1519. Lu Wenxi, Guo Jiayuan, Dong Haibiao, et al. Evaluating Mine Geology Environmental Quality Using Improved SVM Method[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(5): 1511-1519. |
| [21] |
陈科贵, 吴刘磊, 陈愿愿, 等. 基于支持向量机的川中杂卤石分类识别研究[J]. 地球科学进展, 2016, 31(10): 1041-1046. Chen Kegui, Wu Liulei, Chen Yuanyuan, et al. Classification and Recognition of Polyhalite in Chuanzhong Based on Support Vector Machine[J]. Advances in Earth Science, 2016, 31(10): 1041-1046. |
| [22] |
孙致学, 姚军, 孙治雷, 等. 基于神经网络的聚类分析在储层流动单元划分中的应用[J]. 物探与化探, 2011, 35(3): 249-353. Sun Zhixue, Yao Jun, Sun Zhilei, et al. The Application of Clustering Analysis Based on Neural Network Technology in Reservoir Flow Unit Classification[J]. Geophysical & Geochemical Exploration, 2011, 35(3): 249-353. |
| [23] |
万琼华, 吴胜和, 王石, 等. 深水浊积水道储层多参数流动单元划分方法及其分布规律研究[J]. 高校地质学报, 2014, 20(2): 317-323. Wan Qionghua, Wu Shenghe, Wang Shi, et al. Multi-Parameter Technology on the Study of Flow Units Division and Their Distribution in Deep-Water Turbidity Channel Reservoir[J]. Geological Journal of China Universities, 2014, 20(2): 317-323. DOI:10.3969/j.issn.1006-7493.2014.02.017 |
| [24] |
吴小斌, 侯加根, 孙卫, 等. 基于层次分析方法对姬塬地区流动单元的研究[J]. 吉林大学学报(地球科学版), 2011, 41(4): 1013-1019. Wu Xiaobin, Hou Jiagen, Sun Wei, et al. Study on Flow-Units Based on Hierarchical Analysis in Jiyuan Area, Ordos Basins[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(4): 1013-1019. |
| [25] |
唐民安, 李建明, 孙宝玲, 等. 鄂尔多斯盆地红河油田长8油层组储层流动单元研究[J]. 地质科技情报, 2014, 33(6): 83-87. Tang Min'an, Li Jianming, Sun Baoling, et al. Reservoir Flow Units of Chang-8 Oil-Bearing Formation in Honghe Oilfield, Ordos Basin[J]. Geological Science and Technology Information, 2014, 33(6): 83-87. |



