2. 郑州大学土木工程学院, 郑州 450001
2. School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China
0 引言
全断面隧洞掘进机(TBM)施工具有掘进速度快、成洞质量好、施工环境好及人员安全性高等的技术特点,已在国内的水利水电工程长隧洞的施工中得到了广泛的应用[1-4]。护盾式(shield)TBM是全断面TBM的一种常见机型,其可以分为单护盾(single shield)TBM、双护盾(double shields或telescopic shields)TBM和三护盾(triple shields)TBM,其最大的特点是掘进和支护作业都是在护盾的保护下进行,安全性高,对地质条件的适应范围较广。
隧洞围岩稳定性分类是施工中的一项重要工作,分类结果直接关系到支护、衬砌的强度和型式选择。无论是钻爆法还是TBM施工,隧洞围岩的稳定性均取决于围岩性质及场地工程地质条件,如岩石的单轴抗压强度、岩石质量指标(RQD)、节理间距、节理面性状、地下水、地应力等,以上这些指标均可以通过室内试验、现场测试及调查获得。目前隧洞围岩分类一般采用这些定性、定量、半定量指标通过评分的方法把围岩分为若干等级,每种等级对应围岩的不同稳定性。常用的围岩稳定性分类方法有国外的地质力学分类法(RMR)[5]、Q系统分类法[6],及国内的工程岩体分级方法[7]、水电系统的分类法[8]等。钻爆法施工时可以采用以上这些方法对围岩的稳定性进行分类和评价。
与开敞式TBM不同,护盾式TBM隧洞施工时,刀盘、护盾和衬砌管片将掌子面和洞壁围岩几乎全部遮挡,无法像钻爆法和开敞式TBM那样对围岩进行直接的地质描述,也无法采取原状岩样进行试验,影响围岩稳定性的指标无法直接获得,因此传统的围岩分类方法并不适用护盾式TBM施工。目前,针对护盾式TBM施工隧洞围岩分类尚没有统一的标准;随着护盾式TBM在隧洞施工的广泛应用,迫切需要寻求一种适用于护盾式TBM施工的围岩分类方法。
本文采用模糊综合评判的方法,选择护盾式TBM施工所能获得的围岩稳定性评价指标,对围岩的稳定性进行分类并应用到工程实际中。
1 护盾式TBM隧洞施工围岩稳定性分类模糊综合评判法的建立 1.1 评判因素的选取根据模糊综合评判法的基本原理,对围岩稳定性分类应首先选取合理的评判因素,并对各因素赋予参数值;其值可以是定量的或半定量的,也可是定性描述的。考虑影响围岩稳定性的主要地质因素及护盾式TBM施工的特点,所选取的评判因素应能全面、客观地反映围岩类别,同时要具有可操作性。本文根据相关工程实践及文献[5-14]选取以下6个因素对围岩稳定性进行分类。
1) 回弹值:护盾式TBM施工时,可在停机时采用高强度回弹仪(schmidt hammer)通过滚刀间隙、护盾观察窗口或伸缩护盾连接处对岩石进行回弹值测试。相关研究[10]表明:岩石的回弹值与岩石的单轴抗压强度直接相关;可通过回弹值估算岩石的单轴抗压强度,而岩石的单轴抗压强度直接关系到岩石的稳定;一般情况下岩石的回弹值越高,岩石的单轴抗压强度越高,对围岩稳定越有利。
2) TBM刀盘推力:用所采用推力占额定推力的比例表示。掘进推力是隧洞围岩地质条件的反映,应成为围岩稳定性评判的依据之一。一般情况下,在完整硬岩中掘进时,TBM需要较高的推力;而在软弱破碎围岩中掘进时,TBM需要的推力较小。
3) TBM刀盘扭矩:用所采用扭矩占额定扭矩的比例表示。掘进时刀盘扭矩受地质条件的影响而变化,在硬岩中掘进,滚动阻力小,相应扭矩小;反之在软岩中掘进需要的扭矩大。
4) 片状岩渣质量分数:用片状岩渣质量与岩渣总质量的比值表示。渣料中岩渣的形状、粒径与围岩的强度与节理密度等密切相关,可从较大程度上反映围岩的稳定性。一般情况下,完整硬岩的岩渣主要呈片状,而破碎围岩的岩渣主要呈块状。
5) 地下水:用地下水流渗量参数表示。当围岩中存在地下水时,会软化岩石,降低围岩的稳定性,因此围岩中地下水的发育程度越低对围岩稳定越有利。
6) 地应力:用最大主应力方向与洞轴线的夹角表示。当最大主应力与洞轴线平行时对围岩稳定最有利,当与洞轴线垂直时最不利。
围岩稳定性分类目前尚无统一的标准,不同行业、不同学者所采用的标准均有所差别。考虑模糊综合评判法的需要,并参照国内、外成熟的围岩分类方法,本文将围岩稳定分为5个类别,即稳定、较稳定、局部稳定性差、不稳定和极不稳定,分别对应Ⅰ、Ⅱ、Ⅲ、Ⅳ和Ⅴ类围岩。根据相关工程实践及文献[5-14],选取的因素与围岩分类标准的关系见表 1。
| 围岩稳定性 | 类别 | 回弹值 | 刀盘推力/% | 刀盘扭矩/% | 片状岩渣质量分数/% | 地下水渗流量/(L/(min·10m)) | 最大主应力与洞轴线夹角/(°) |
| 稳定 | Ⅰ | ≥45 | ≥80 | <60 | ≥90 | <1 | <30 |
| 较稳定 | Ⅱ | 35~45 | 70~80 | 60~70 | 80~90 | 1~10 | 30~40 |
| 局部稳定性差 | Ⅲ | 25~35 | 60~70 | 70~80 | 50~80 | 10~25 | 40~50 |
| 不稳定 | Ⅳ | 15~25 | 50~60 | 80~90 | 10~50 | 25~125 | 50~60 |
| 极不稳定 | Ⅴ | <15 | <50 | ≥90 | <10 | ≥125 | ≥60 |
按照表 1,评判围岩稳定性的因素有6个,可以用集合表示为
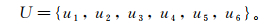 (1)
(1) 式中:u1为回弹值;u2为刀盘推力;u3为刀盘扭矩;u4为片状岩渣质量分数;u5为地下水渗流量;u6为最大主应力方向与隧洞轴线夹角。
1.3 因素权重的确定因素权重的确定采用层次分析法[15-17],其原理是:先把n个评判因素排列成一个n阶矩阵;然后对各因素的重要程度进行两两比较,矩阵中元素值由各因素的重要程度来确定;再计算出判断矩阵的最大特征根和其对应的特征向量,其特征向量即为所求的权重值。两因素之间的重要程度比较和对应值由层次分析法[14-16]确定,如表 2所示。
| 因素ui和uj相比较的重要程度 | f(ui, uj) | f(uj, ui) |
| ui比uj同等重要 | 1 | 1 |
| ui比uj稍微重要 | 3 | 1/3 |
| ui比uj明显重要 | 5 | 1/5 |
| ui比uj强烈重要 | 7 | 1/7 |
| ui比uj绝对重要 | 9 | 1/9 |
| ui比uj处于上述两相邻判断之间 | 2,4 6,8 |
1/2,1/4 1/6,1/8 |
| 注:f为ui和uj的函数,即ui和uj的相比较的值。 | ||
本文根据国、外常用的围岩分类方法及工程经验,得出判断矩阵如下:

1) 计算判断矩阵每行元素的乘积Wi:

即W1=630.000,W2=0.198,W3=0.066,W4=69.300,W5=12.000,W6=0。
2) 计算Wi的n次方根Mi:
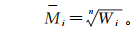
即
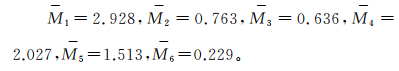
3) 归一化处理向量M为:
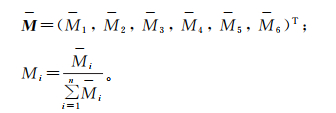
则特征向量A为:
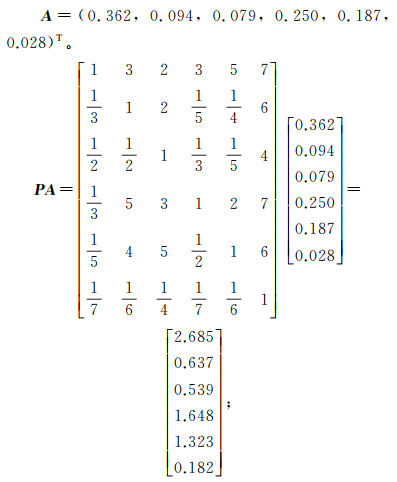
则最大特征根λmax为:

4) 进行一致性检验计算,用一致性指标CI表示:
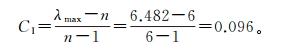
查随机性指标CR数值表[17]可知,当n=6时,CR=1.24,则
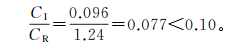 (2)
(2) 式(2)表明判断矩阵的一致性达到了要求,因此向量A的各个分量可以作为相应评判因素的权重系数。
1.5 隶属函数的确定根据所要解决问题的实际特征,参照文献[11]的研究方法,采用岭形隶属函数,按照公式(2)建立代表评判因素隶属度的函数u(x):
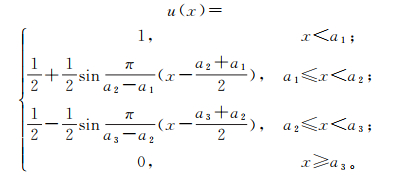 (3)
(3) 式中,a1, a2, a3均为参数,表示各子集的区间边界。
以回弹值为例,建立其对应不同围岩的隶属函数:
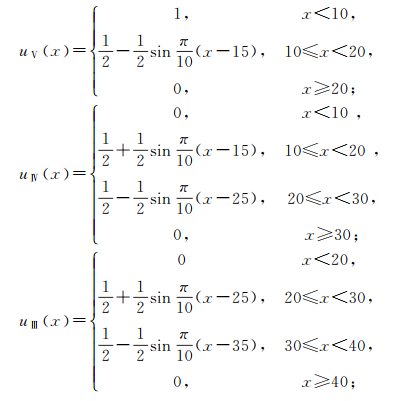
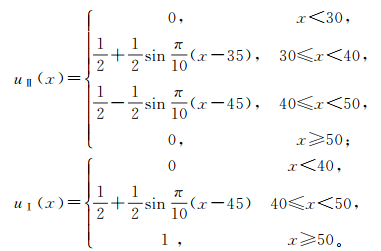
式中,uⅠ(x)、uⅡ(x)、uⅢ(x)、uⅣ(x)、uⅤ(x)分别为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ类围岩的隶属函数。其余因素与其类似,限于篇幅有限,本文略去。
2 工程应用某水电站引水隧洞全长24.8 km,洞径9.11 m,采用双护盾式TBM开挖施工,在掘进过程中获得了若干洞段的掘进参数、渣料成分与地质资料,现选取4组数据(表 3),采用模糊综合评判法,对围岩稳定性进行综合评判。
| 序号 | 隧洞桩号 | 回弹值 | 刀盘推力/% | 刀盘扭矩/% | 片状岩渣质量分数/% | 地下水渗流量/(L/(min·10m)) | 最大主应力与洞轴线夹角/(°) |
| 1 | 17+660—17+685 | 48 | 78 | 64 | 85 | 5 | 53 |
| 2 | 18+212—18+228 | 36 | 72 | 68 | 82 | 8 | 60 |
| 3 | 22+985—22+998 | 28 | 64 | 74 | 63 | 12 | 52 |
| 4 | 23+871—23+886 | 22 | 53 | 82 | 52 | 20 | 55 |
1) 评判因素集合见式(1)。
2) 选择评语集V:
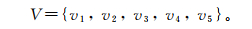
式中:v1表示稳定,对应Ⅰ类围岩;v2表示较稳定,对应Ⅱ类围岩;v3表示局部稳定性差,对应Ⅲ类围岩;v4表示不稳定,对应Ⅳ类围岩;v5表示极不稳定,对应Ⅴ类围岩。
3) 单因素评判。以表 3中序号1洞段为例,将评判因素值代入式(3)隶属函数中,可得各因素对应不同稳定状态的隶属度M:

4) 各因素的权重向量即特征向量A:
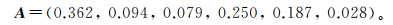
5) 进行综合评判计算,用隶属度向量B表示:
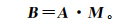
计算其结果并对结果进行归一化处理,用归一化隶属度向量B′表示,则表 3中序号1洞段的归一化隶属度向量B1′为
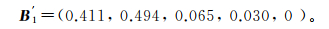
参照以上计算方法,对表 2中序号2、3和4洞段分别进行计算,得:

按照最大隶属度原则,可以判断序号1、2、3和4洞段的最大隶属度分别为0.494、0.403、0.388、0.442,围岩稳定性状态分别为较稳定、较稳定、局部稳定性差和不稳定,分别对应Ⅱ、Ⅱ、Ⅲ和Ⅳ类围岩。该评判结果在工程中已得到验证。
3 结语1) 护盾式TBM隧洞施工时,无法直接对围岩进行地质描述,因此无法采用传统的分类方法对围岩稳定性进行评价。围岩的稳定性受多种因素的影响,本文在研究护盾式TBM施工特点的基础上,参照国内、外常用的围岩分类方法,选择了岩石的回弹值、刀盘推力、刀盘扭矩、片状岩渣质量分数、地下水渗流量和最大主应力与洞轴线的夹角作为围岩稳定性评判因素。
2) 影响因素与隧洞围岩是否稳定具有一定的模糊性质,围岩的稳定性无法采用精确的关系式来表达。采用模糊综合评判方法,建立围岩稳定性多因素评判模型,制定稳定性分类标准,对围岩稳定性进行定量评判,可以得到较为合理的结果。
| [1] |
张镜剑, 傅冰骏. 隧道掘进机在我国应用的进展[J]. 岩石力学与工程学报, 2007, 26(2): 226-238. Zhang Jingjian, Fu Bingjun. Advances in Tunnel Boring Machine Application in China[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 226-238. DOI:10.3321/j.issn:1000-6915.2007.02.002 |
| [2] |
张镜剑. TBM的应用及其有关问题和展望[J]. 岩石力学与工程学报, 1999, 18(3): 363-367. Zhang Jingjian. The Application and Some Problems of TBM and Its Prospects[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(3): 363-367. DOI:10.3321/j.issn:1000-6915.1999.03.029 |
| [3] |
尹俊涛, 尚彦军, 傅冰骏, 等. TBM掘进技术发展及有关工程地质问题分析和对策[J]. 工程地质学报, 2005, 13(3): 389-397. Yin Juntao, Shang Yanjun, Fu Bingjun, et al. Development of TBM-Excavation Technology and Analyses & Countermeasures of Related Engineering Geological Problems[J]. Journal of Engineering Geology, 2005, 13(3): 389-397. DOI:10.3969/j.issn.1004-9665.2005.03.019 |
| [4] |
茅承觉. 我国全断面岩石掘进机(TBM)发展的回顾与思考[J]. 建设机械技术与管理, 2008, 21(5): 81-84. Mao Chengjue. Review and Thoughts of Developmental Full Face Rock Tunnel Boring Machine(TBM) in China[J]. Construction Machinery Technology & Management, 2008, 21(5): 81-84. DOI:10.3969/j.issn.1004-0005.2008.05.022 |
| [5] |
Bieniaski Z T. Classification of Rock Masses for Engineering[M]. New York: Wiley, 1993.
|
| [6] |
Barton N. Some New Q-Value Correlations to Assist in Site Characterization and Tunnel Design[J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39: 185-216. |
| [7] |
工程岩体分级标准GB50218-2014[S].北京: 中国计划出版社, 2014. Standard for Classification of Engineering Rock Masses GB50218-94[S]. Beijing: China Planning Press, 1994. |
| [8] |
水利水电工程地质勘察规范GB50487-2008[S].北京: 中国计划出版社, 2009. Code for Geologic Investigation of Water Resources and Hydropower Engineering GB50487-2008[S]. Beijing: China Planning Press, 2009. |
| [9] |
黄祥志.基于渣料和TBM掘进参数的围岩稳定性分类方法研究[D].武汉: 武汉大学, 2005. Huang Xiangzhi. The Research of the Methods of Surrounding Rock Masses Stability Classification Based on the Geological Documentation of Muck and the Boring Parameters of TBM[D]. Wuhan: Wuhan University, 2005. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y744058 |
| [10] |
黄扬一. 万安工程建基岩体回弹仪测试结果[J]. 大坝观测与土工测试, 1996, 20(3): 39-42. Huang Yangyi. Schmidt Hammer in Foundation of Wan'an Dam[J]. Dam Observation and Geotechnical Tests, 1996, 20(3): 39-42. |
| [11] |
尚彦军, 杨志法, 李丽慧, 等. 黑洞大型古地下洞室群工程地质条件及岩体稳定性分析[J]. 吉林大学学报(地球科学版), 2015, 45(1): 214-224. Shang Yanjun, Yang Zhifa, Li Lihui, et al. Study of the Engineering Geological Conditions and Rock Mass Stability of Heidong Large Ancient Underground Caverns[J]. Journal of Jilin University(Earth Science Edition), 2015, 45(1): 214-224. |
| [12] |
张鹏, 陈剑平, 张丽, 等. 隧道围岩断面轮廓分维数与岩体质量关系[J]. 吉林大学学报(地球科学版), 2010, 40(5): 1110-1114. Zhang Peng, Chen Jianping, Zhang Li, et al. Relationship Between Fractal Dimension of Section Profile & Rock Quality of Tunnel Surrounding Rock Mass[J]. Journal of Jilin University(Earth Science Edition), 2010, 40(5): 1110-1114. |
| [13] |
许传华, 任青文. 地下工程围岩稳定性的模糊综合评判法[J]. 岩石力学与工程学报, 2004, 23(11): 1852-1855. Xu Chuanhua, Ren Qingwen. Fuzzy-Synthetical Evaluation on Stability of Surrounding Rockmassed of Underground Engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(11): 1852-1855. DOI:10.3321/j.issn:1000-6915.2004.11.013 |
| [14] |
盛继亮. 地下工程围岩稳定模糊综合评价模型研究[J]. 岩石力学与工程学报, 2003, 22(增刊1): 2418-2421. Sheng Jiliang. Research on Fuzzy Synthetic Evaluation Model for the Stability of Surrounding Rocks of Underground Project[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(Sup.1): 2418-2421. |
| [15] |
段瑜.地下采空区灾害危险度的模糊综合评价[D].长沙: 中南大学, 2005. Duan Yu. The Fuzzy-Synthetical Evaluation of Goaf Disaster Hazard Degree[D]. Changsha: Central South University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10533-2006036388.htm |
| [16] |
彭祖赠, 孙韫玉. 模糊数学及其应用[M]. 武汉: 武汉大学出版社, 2005. Peng Zuzeng, Sun Yunyu. Fuzzy Mathematics and Its Application[M]. Wuhan: Wuhan University Press, 2005. |
| [17] |
卢有杰, 卢家仪. 项目风险管理[M]. 北京: 清华大学出版社, 1998. Lu Youjie, Lu Jiayi. Project Risk Management[M]. Beijing: Tsinghua University Press, 1998. |


