2. 中石油东方地球物理公司, 河北 涿州 072751;
3. 中国石化页岩油气勘探开发重点实验室, 北京 100083;
4. 中国石化石油勘探开发研究院, 北京 100083
2. Bureau of Geophysical Prospecting INC, CNPC, Zhuozhou 072751, Hebei, China;
3. Key Laboratory of Shale Oil/Gas Exploration and Production Technology, SinoPEC, Beijing 100083, China;
4. Petroleum Exploration and Production Research Institute, SinoPEC, Beijing 100083, China
0 引言
地震反射系数反映地下界面物性特征的变化。对于各向同性介质分界面,平面波反射、透射系数的精确解可由Zoeppritz[1]方程计算。许多学者对Zoeppritz方程进行了不同形式的简化,以此开展地震AVO(amplitude versus offset)技术研究,通过反射波振幅随偏移距的变化规律研究反射界面两侧介质的物性特征。传统的AVO分析都是基于Zoeppritz方程的各自线性近似式提出的[2-4]。1955年,Koefoed[5]不仅简化了Zoeppritz方程,而且在实验中假设上下界面的泊松比不同,所得的纵波反射系数随入射角的改变而变化范围大大增大,这对之后的AVO技术发展具有重大意义。1980年,Aki等[6]将Zoeppritz方程简化为入射角与纵波振幅相关的近似公式。1985年,Shuey[7]根据该简化公式做了进一步研究,将其改写为入射角小角度项、中角度项和广角度项三部分之和的近似公式。
然而,层状介质的AVO特征与单一界面是不同的,因为反射系数与入射波的频率相关。实际地层为非均匀介质,地震波在地下传播时具有传播效应和层间多次波的调谐干涉效应。对此,早在1971年,Fuchs等[8]就应用反射率方法计算了多层介质对点震源的响应。1980年,Aki等[6]提出传播矩阵算法,在理论上可以更好地描述这种层状介质模型。1983年,Kennett[9]给出了地震波在层状各项异性介质中传播的描述。1984年,Fryer等[10]又将传播矩阵用于各向异性介质,制作了合成地震记录。在此之后,有许多学者对层状介质进行了AVO正演响应研究。2001年,Carcione[11]计算了富有机质页岩层的反射系数。2003年,Liu等[12]研究了泊松比和层厚度对薄层AVO响应的影响。2005—2016年,郭智奇等[13-15]基于广义传播矩阵理论计算地震波频变反射系数,完善了频变AVO算法,为含油气储层频变AVO响应的模拟和分析提供了方法。2014年,兰慧田[16]应用广义传播矩阵理论计算了上覆介质与裂缝性孔隙介质分界面的反射系数,为裂缝检测和裂缝参数反演提供地震波振幅信息。
本文针对非均匀地下介质模型,选取薄互层结构和页岩气储层两组实际测井数据,分别比较精确的Zoeppritz方程、Shuey二项近似方程和Shuey三项近似方程以及传播矩阵算法得到的正演模拟响应计算效果,并与实际的地震数据进行对比分析,讨论存在调谐干涉和传播效应的情况下不同方法的精确性和适用性。
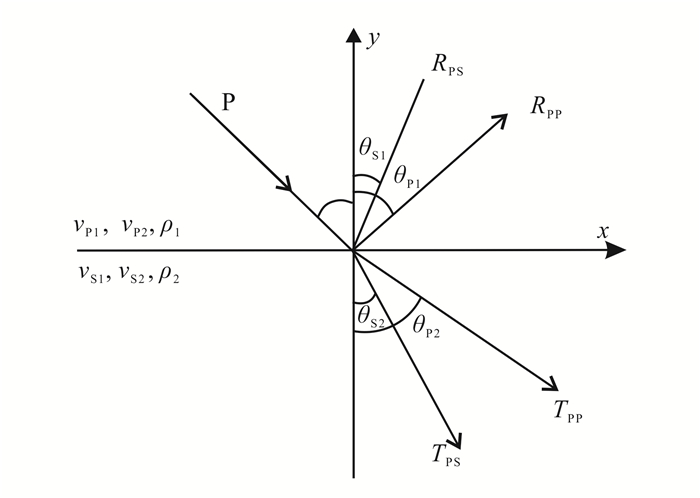
1 AVO正演模拟基本理论 1.1 Zoeppritz方程Zoeppritz方程[1]是AVO分析的基础,该方程通过平面波的入射角和反射界面上下介质的6个弹性参数求取界面的反射系数和透射系数,利用界面两侧应力和位移守恒的原则推导反射波和透射波振幅。反射、透射模式如图 1所示。当平面波入射到界面时,波前面与y轴是平行的,所以与方程、y轴无关。当P波以一定入射角入射到界面时,将会产生反射P波、反射S波、透射P波和透射S波,其Zoeppritz方程表达式为
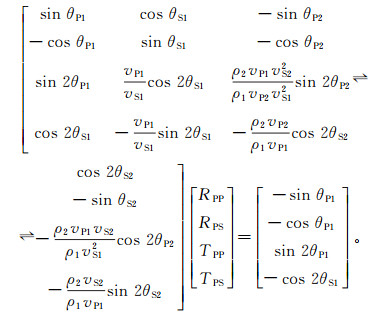 (1)
(1)
|
| vP1、vP2分别为反射界面上下层介质的纵波速度;vS1、vS2分别为反射界面上下层介质的横波速度;ρ1、ρ2分别为反射界面上下层介质的密度。 图 1 入射波、反射波和透射波的关系 Figure 1 Relationship amongincident wave, reflection wave and transmission wave |
|
|
式中:RPP、RPS分别为纵波和横波的反射系数;TPP、TPS分别为纵波和横波的透射系数。
1.2 Shuey二项近似方程及Shuey三项近似方程Shuey[7]将Zoeppritz方程简化为关于入射角θ的函数,并分为小角度项、中角度项和大角度项三部分,利用泊松比来代替横波速度,推导出纵波反射系数(R(θ))公式。
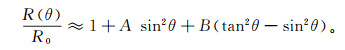 (2)
(2) 其中,
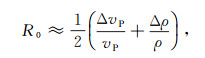 (3)
(3) 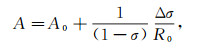 (4)
(4)  (5)
(5)  (6)
(6) 则纵波反射系数公式为
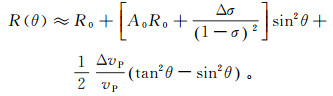 (7)
(7) 式中:ΔvP、Δρ和Δσ分别为反射界面两侧介质纵波速度、密度和泊松比的差值;vP、ρ、σ分别为反射界面两侧介质纵波速度、密度和泊松比的平均值。Shuey三项近似方程(式(7))第一项为垂直入射时的反射系数;第二项主要表示中等角度入射时的反射系数;第三项为大角度入射时的反射系数。当入射角较小、并且vP/vS≈2时,第三项可以忽略(vS为反射界面两侧介质横波速度的平均值),此时式(7)只有前两项,称为Shuey二项近似方程。
1.3 传播矩阵理论对于非均匀地下介质,地震波的反射特征不仅与入射角度、物性差异有关,还与入射波频率、地层厚度、薄互层结构、地层的不均匀性等因素有关[9, 12, 17-18]。
由于干涉、调谐等现象的存在,来自薄互层的反射地震波呈现复合波型,与基于界面模型的Zeoppritz理论相比,传播矩阵理论更适用于非均匀介质情况。根据传播矩阵理论[19],对于P波入射,地层的反射、透射系数向量r=[RPP, RPS, TPP, TPS]T为
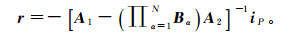 (8)
(8) 式中:矩阵A1与A2分别为与上、下层介质物性参数有关的传播矩阵;Bα(α=1, …, N)为具有N层结构的中间薄互层的传播矩阵;iP为P波入射向量,与入射介质物性参数有关。上述矩阵和向量都是入射波频率和波慢度的函数。
传播矩阵A1和A2分别为:
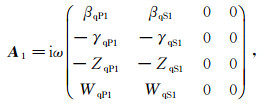 (9)
(9) 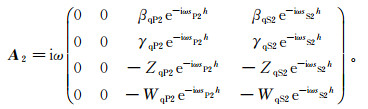 (10)
(10) 式中:i为虚数单位;ω为入射波角频率;s为波慢度;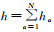
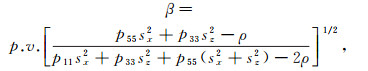 (11)
(11) 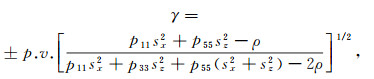 (12)
(12)  (13)
(13) 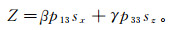 (14)
(14) 式中:p11、p33、p55和p13为相应层位各项异性弹性参数;p.v.意为取复数的主值;对于γ,符号“+”对应准纵波,符号“-”对应准横波;sx为水平波慢度;sz为垂直波慢度。
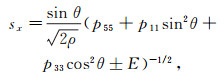 (15)
(15) 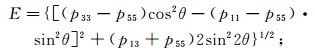 (16)
(16) 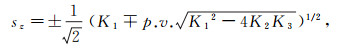 (17)
(17) 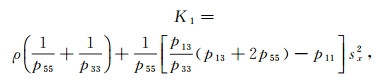 (18)
(18) 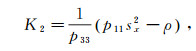 (19)
(19) 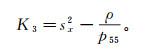 (20)
(20) 其中,sz表达式符号约定为:(+, -)表示向下传播准纵波;(+, +)表示向下传播准横波;(-, -)表示向上传播准纵波;(-, +)表示向上传播准横波。
传播矩阵Bα为
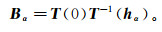 (21)
(21) 其中,
 (22)
(22) P波入射向量iP为
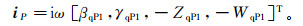 (23)
(23) 由薄互层反射系数的传播矩阵理论,可计算各频率下的反射、透射系数向量r相应反射波的频变反射系数Rf。将频变反射系数与频率域的地震子波Wf相乘可得相应反射波的振幅谱Uf,即
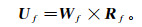 (24)
(24) 对Uf做反傅里叶变换则可以获得时间域的反射波波形ut:
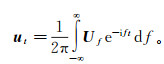 (25)
(25) 式中:f为频率;t为时间。
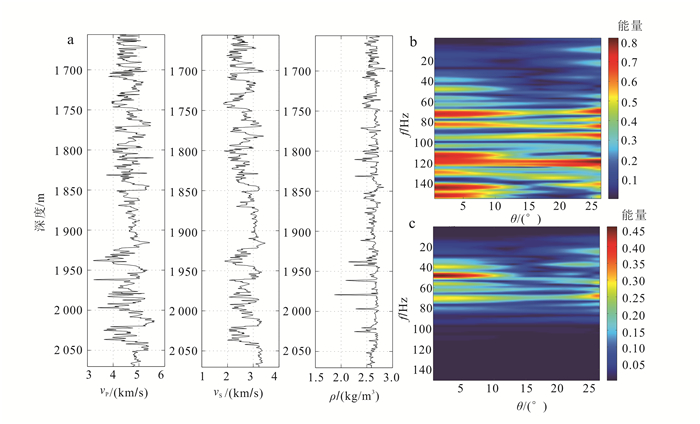
2 地震AVO模拟及分析 2.1 砂泥岩薄互层图 2a为砂泥岩薄互层结构的实际数据测井曲线,包括纵、横波速度和密度。基于传播矩阵理论计算该非均匀地层的地震响应,图 2b为计算得到的频变反射系数。考虑入射波为40 Hz的Ricker子波,进一步计算反射波频谱如图 2c所示。
|
| 图 2 砂泥岩薄互层储层测井曲线(a)、频变反射系数谱(b)和反射波频谱(c) Figure 2 Sand-shale thin interbed logging curve(a), reflection coefficients spectrum (b) and amplitude-spectrum of reflection wave (c) in frequency domain of sand-shale thin interbed |
|
|
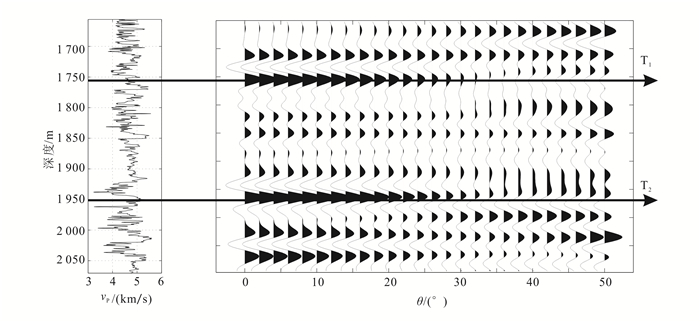
对图 2c所示的反射波频谱进行反傅里叶变换,得到如图 3所示的时间域合成地震记录,从中选取两个强反射界面T1、T2进行井震标定。图 4比较了基于传播矩阵算法、Zoeppritz方程以及Shuey二项近似方程和Shuey三项近似方程计算得到的合成地震记录。从图 4中可以看到,4种方法得到的AVO地震响应在不同入射角范围下波形变化也不同,尽管Zoeppritz算法和传播矩阵方法计算的AVO波形在小角度入射时(入射角 < 20°)比较接近,但是中、大角度(入射角>20°)入射时存在明显差别。如图 4中A、B、C三处可以清晰地看到两种波形在振幅和走向上都有明显的不同,A处Zoeppritz方程计算的振幅明显强于传播矩阵,B和C处两种方法得到的合成记录强反射界面位置和振幅都有差异。分析可知,相比于传播矩阵算法,Shuey二项近似方程和Shuey三项近似方程在大角度入射时与Zoeppritz方程更为接近,对于此数据,入射角为0°~50°时,相比于Shuey二项近似方程,Shuey三项近似方程与Zoeppritz方程吻合度也更高;传播矩阵算法与其他几种方法相比,由于考虑了地震反射的传播效应、调谐效应等动力学特征,可以更加清晰地反映薄互层结构的AVO特征变化,由图 4也可看出其垂向分辨率在这几种正演算法中最高。
|
| 图 3 砂泥岩薄互层结构数据井震标定 Figure 3 Well to seismic calibration of sand-shale thin interbed data |
|
|

|
| a.传播矩阵算法;b. Zoeppritz方程;c. Shuey二项近似方程;d. Shuey三项近似方程。 图 4 砂泥岩薄互层合成地震记录 Figure 4 Synthetic seismogram of sand-shale thin interbed data |
|
|
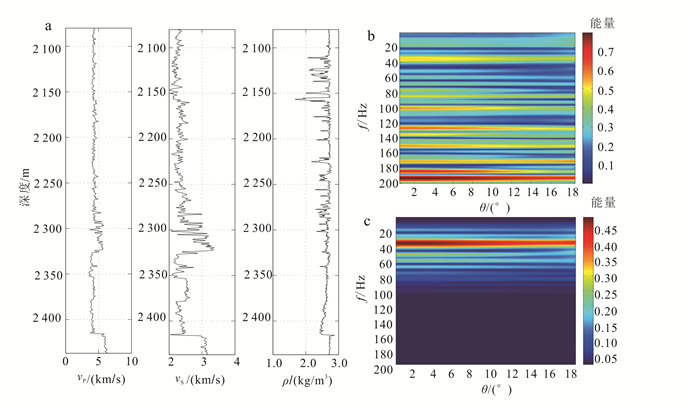
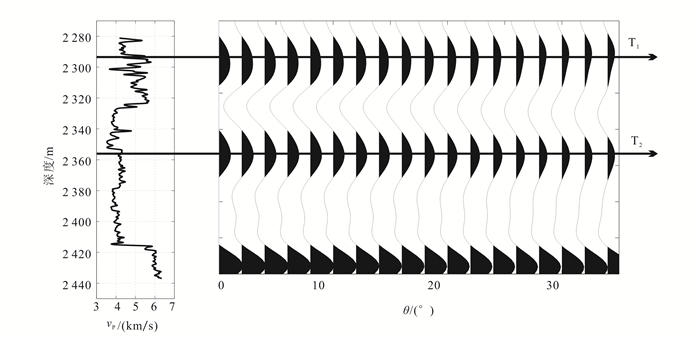
图 5a所示为某页岩气储层的纵、横波速度和密度测井曲线。从图 5a中可以看到,纵、横波速度曲线的相关性很强,图中2 330~2 415 m为页岩地层,含气储层为2 380~2 415 m[20]。基于传播矩阵算法计算的频变反射系数和反射波频谱分别如图 5b和图 5c所示。图 6所示为井震标定结果,选取T1和T2两个标志层进行井震标定。
|
| 图 5 页岩气储层测井曲线(a)、频变反射系数谱(b)和反射波频谱(c) Figure 5 Shale reservoirs loging curve(a), reflection coefficients spectrum (b) and amplitude-spectrum of reflection wave (c) in frequency domain of shale reservoirs |
|
|
|
| 图 6 页岩气储层井震标定 Figure 6 Well to seismic calibration of shale reservoirs data |
|
|
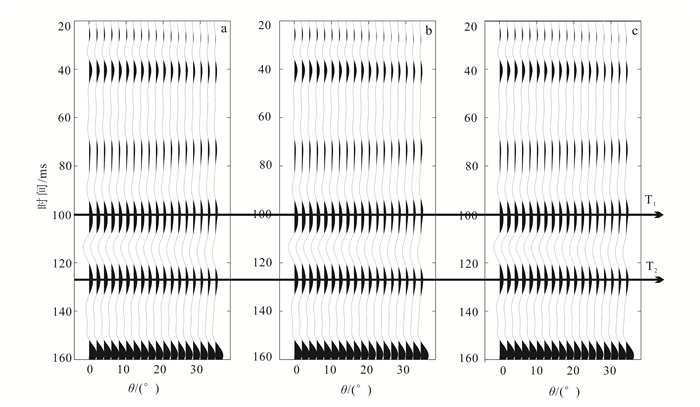
图 7为实际观测数据和基于传播矩阵理论、Zoeppritz方程、Shuey二项近似方程、Shuey三项近似方程的高精度叠前正演合成记录。与Zoeppritz方程、Shuey二项近似方程、Shuey三项近似方程相比,传播矩阵算法在入射角为20°~35°(图 7中T1、T2标志层)时有明显振幅减小的趋势,而其他方法振幅没有该趋势。Zoeppritz方程与Shuey二项近似方程、Shuey三项近似方程在该段入射角范围内区别不是很明显。传播矩阵算法与实际数据吻合度比Zoeppritz方程、Shuey二项近似方程及Shuey三项近似方程的计算结果更高,如T1标志层所示,传播矩阵方法中模拟出与实际数据一致的反射振幅随入射角减弱的现象,而Zoeppritz方程计算结果中振幅随入射角增强,验证了传播矩阵理论在理论上的完备性。与基于单界面反射的Zoeppritz方程算法相比,传播矩阵理论充分考虑了地震波的传播效应,正演结果与实际数据更接近,为进一步研究非均匀储层地震响应提供了精确的模拟方法。为了更加直观地显示以上几种正演算法之间的差异,对4种正演算法进行归一化并计算出差剖面来进行误差分析。如图 8所示,传播矩阵算法在T1、T2标志层处振幅小于其他几种算法。振幅趋势与实际数据振幅趋势一致。

|
| a.实际地震数据;b.传播矩阵算法;c. Zoeppritz方程;d. Shuey二项近似方程;e. Shuey三项近似方程。 图 7 页岩气储层合成地震记录 Figure 7 Synthetic seismogram shale reservoirs data |
|
|
|
| a.Zoeppritz方程与传播矩阵算法差剖面;b. Shuey二项近似方程与传播矩阵算法差剖面;c. Shuey三项近似方程与传播矩阵算法差剖面。 图 8 误差分析 Figure 8 Error analysis |
|
|
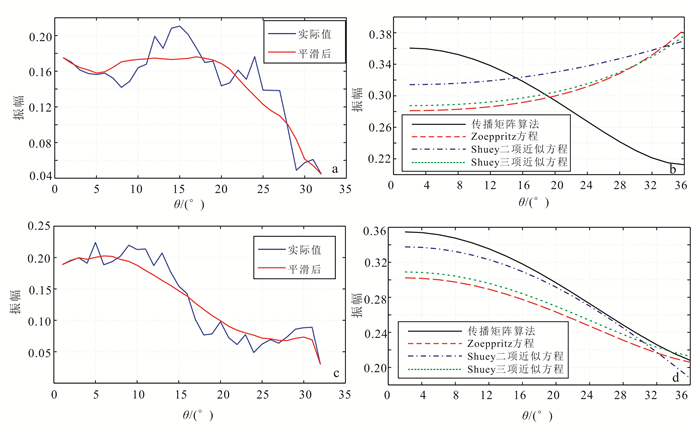
通过以上分析结果,进一步对实际数据得到的地震剖面与传播矩阵算法、Zoeppritz方程、Shuey二项近似方程及Shuey三项近似方程得到的地震剖面进行对比分析。图 9为T1、T2处提取的振幅曲线。由图 9a、b可知,在T1标志层处,传播矩阵算法得到的振幅曲线趋势与实际数据得到的振幅曲线趋势基本一致,而Zoeppritz方程、Shuey二项近似方程及Shuey三项近似方程没能合理预测振幅的变化趋势;由图 9c、d可知,在T2标志层处,这4种算法得到的振幅曲线趋势均与实际数据得到的振幅曲线基本一致,但也存在一定差异。正演算法得到的振幅提取曲线与实际数据得到的振幅提取曲线趋势吻合度越高,说明正演结果越好。Zoeppritz方程、Shuey二项近似方程及Shuey三项近似方程在T1处预测失误可能由于选取的研究区上覆层存在较强的反射界面,而Zoeppritz方程是基于单界面的反射,没有考虑地震波传播时层间多次波传播效应和调谐干涉效应。
|
| a.实际数据T1处振幅曲线和平滑后振幅曲线;b. 4种算法T1处振幅曲线;c.实际数据T2处振幅曲线和平滑后振幅曲线;d. 4种算法T2处振幅曲线。 图 9 振幅曲线 Figure 9 Amplitude-angle curve |
|
|
1) 本文应用传播矩阵、Zoeppritz方程、Shuey二项近似方程及Shuey三项近似方程4种正演算法,计算砂泥岩薄互层和页岩储层非均匀地层的高精度地震合成记录。应用于薄互层实际数据的计算结果表明,与Zoeppritz方程、Shuey二项近似方程及Shuey三项近似方程相比,传播矩阵方法考虑了地震反射的传播效应、调谐效应等动力学特征,可以更加清晰地反映薄互层结构的AVO特征变化,并为薄层、薄互层条件下的地震反射振幅信息提供了更为准确的正演方法。
2) 将上述4种正演方法应用于页岩储层进行对比研究得出,在近垂直入射时(0°~20°),Zoeppritz方程算法及Shuey二项近似方程、Shuey三项近似方程与传播矩阵的结果基本相同,但是在中、远偏移距(入射角>20°)的情况下,传播矩阵算法与实际观测数据吻合度最高。因此,基于传播矩阵理论计算高精度合成地震记录,可以充分考虑地震波动力学特征,为理解非均匀地层地震反射特征、进一步开发AVO反演和分析技术提供方法。
| [1] |
Zoeppritz K. Über Reflexionad Durchgang Seismischer Wellen Durch Unstetigkeitsflächen[J]. Erdbebenwellen, 1919, Ⅶb: 66-84. |
| [2] |
Bortfeld R. Approximations to the Reflection and Transmission Coefficients of Plane Longitudinal and Transverse Waves[J]. Geophysical Prospecting, 1961, 9(4): 485-502. DOI:10.1111/gpr.1961.9.issue-4 |
| [3] |
Chapman C H. Exact and Approximate Generalized Ray Theory in Vertically Inhomogeneous Media[J]. Geophysical Journal International, 1976, 46(2): 201-233. DOI:10.1111/j.1365-246X.1976.tb04154.x |
| [4] |
Richards P G, Frasier C W. Scattering of Elastic Eaves from Depth-Dependent Inhomogeneities[J]. Geophysics, 1976, 41(3): 441. DOI:10.1190/1.1440625 |
| [5] |
Koefoed O. On the Effect of Poission's Ratios of Rock Strata on the Reflection Coefficients of Plane Wave[J]. Geophysical Prospecting, 1955, 3(4): 381-387. DOI:10.1111/gpr.1955.3.issue-4 |
| [6] |
Aki K, Richards P G. Quantitative Seismology:Theory and Methods[M]. San Francisco: Freeman, 1980.
|
| [7] |
Shuey B R T. A Simplification of the Zoeppritz-Equations[J]. Geophysics, 1985, 50(4): 609-614. DOI:10.1190/1.1441936 |
| [8] |
Fuchs K, Müller G. Computation of Synthetic Seis-mograms with the Reflectivity Method and Comparison with Observations[J]. Geophysical Journal of the Royal Astronomical Society, 1971, 23(4): 417-433. DOI:10.1111/j.1365-246X.1971.tb01834.x |
| [9] |
Kennett B L. Seismic Wave Propagation in Stratified Media[M]. Cambridge: Cambrigde University Press, 1983.
|
| [10] |
Fryer G J, Frazer L N. Seismic Waves in Stratified Anisotropic Media[J]. Geophysical Journal International, 1984, 78(3): 691-710. DOI:10.1111/j.1365-246X.1984.tb05065.x |
| [11] |
Carcione J M. AVO Effects of a Hydrocarbon Source-Rock Layer[J]. Geophysics, 2012, 66(2): 419-427. |
| [12] |
Liu Y, Schmitt D R. Amplitude and AVO Responses of a Single Thin Bed[J]. Geophysics, 2003, 68(4): 1161-1168. DOI:10.1190/1.1598108 |
| [13] |
郭智奇, 刘财, 李向阳, 等. 非弹性层状介质地震波频变AVO响应模拟及分析[J]. 地球物理学报, 2016, 59(2): 664-672. Guo Zhiqi, Liu Cai, Li Xiangyang, et al. Modeling and Analysis of Frequency-Dependent AVO Responses in Inelastic Stratified Media[J]. Chinese Journal of Geophysics, 2016, 59(2): 664-672. |
| [14] |
郭智奇, 刘财, 冯晅, 等. 各向异性衰减与AVO分析[J]. 吉林大学学报(地球科学版), 2010, 40(2): 432-438. Guo Zhiqi, Liu Cai, Feng Xuan, et al. Attenuation Anisotropy and AVO Analysis[J]. Journal of Jilin University (Earth Science Edition), 2010, 40(2): 432-438. |
| [15] |
郭智奇, 刘财, 张凤琴. 层状粘弹性介质中SH波的反射、透射问题[J]. 吉林大学学报(地球科学版), 2005, 35(增刊1): 61-65. Guo Zhiqi, Liu Cai, Zhang Fengqin. Reflection and Transmission Problem of SH Waves in Layered Viscoelastic Medium[J]. Journal of Jilin University (Earth Science Edition), 2005, 35(Sup. 1): 61-65. |
| [16] |
兰慧田.裂缝性孔隙介质波场模拟与频变AVO储层参数反演[D].长春: 吉林大学, 2014. Lan Huitian. Wave Field Modeling in Fractured Porous Media and Frequency-Dependent AVO Reservoir Parameters Inversion[D]. Changchun: Jilin University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10183-1014268078.htm |
| [17] |
Rokhlin S I, Wang Y J. Equivalent Boundary Con-ditions for Thin Orthrotropi Clayer Between Two Solids:Reflection, Refraction, and Interface Waves[J]. Journal of Acoustic Society of America, 1992, 91: 1875-1887. DOI:10.1121/1.403717 |
| [18] |
Ursin B, Stovas A. Reflection and Transmission Res-ponses of a Layered Isotropic Viscoelastic Medium[J]. Geophysics, 2002, 67(1): 307-323. DOI:10.1190/1.1451803 |
| [19] |
Carcione J M. AVO Effects of a Hydrocarbon Source-Rock Layer[J]. Geophysics, 2012, 66(2): 419-427. |
| [20] |
逄硕, 刘财, 郭智奇, 等. 基于岩石物理模型的页岩孔隙结构反演及横波速度预测[J]. 吉林大学学报(地球科学版), 2017, 47(2): 606-615. Pang Shuo, Liu Cai, Guo Zhiqi, et al. Estimation of Pore-Shape and Shear Wave Velocity Based on Rock-Physics Model in Shale[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(2): 606-615. |



