2. 西安航天天绘数据技术有限公司, 西安 710054
2. Xi'an Aerors Data Technology Co. Ltd, Xi'an 710054, China
0 引言
传统的测深方法以船舶作为测量仪器的载体,以船舶定位技术和水声技术作为测深技术的主体,对海深和海底障碍物进行测绘。由于技术条件的限制,依然还有大面积的海域存在数据空白,导致人们对大洋底的地貌形态知之甚少,认识还很贫乏[1]。卫星测高技术在研究海洋表面及其内部现象、海底构造、全球重力场等方面具有无可比拟的优势。它可以大范围、周期性、快速地观测海洋上的各种现象及其变化,极大地提高人们对海洋认识的广度和深度,可以使以前几个世纪的测量任务在几个月内完成。
如今,利用卫星测高技术确定重力异常的理论和方法基本成熟[2],通过测高数据获取的重力异常与实测重力异常的差值均方根在几个毫伽范围内[3],使得依据重力数据与海深的关系反演海底地形成为可能[4-11]。目前,海底地形反演技术大多基于Paker[11]异常扰动位公式和Watts[12]的3个板块地壳均衡模型,如Smith等[13]的方法。然而,经典的海底地形反演方法通常需要引入先验模型、考虑海底均衡状况,且计算模型复杂,如Braitenberg等[14]在利用重力数据反演中国南海海底地形的过程中,考虑了地壳均衡、沉积层厚度、有效弹性厚度等因素的影响,过程较为复杂。重力地质法(gravity-geologic method,GGM)与经典方法相比,具有模型简单、易于计算[15]的优点。该方法最初被用于地球物理中反演沉积物基岩深度的研究,由于陆地上地质层的密度变化大,使得该方法在陆地上的应用效果不佳。而在海底地形的探索方面,洋壳密度和海水密度的差异变化较小,通常认为海水内部密度不随深度变化[15]。从而,GGM在反演海洋深度方面有较高的可行性[16]。
以重力异常为数据源,依据GGM反演海底地形的关键在于密度差异常数的确定。欧阳明达等[17]利用GGM模型反演的海深值与检核点海深的相关系数,以及反演海深值与检核点海深差值的标准差,获得该海域密度差异常数为1.32 g/cm3,进而对中国南海海域进行反演分析;胡敏章等[15]应用GGM反演皇帝海山的海底地形时,密度差异常数的获取也是依据检核点处GGM海深与船测海深的相关系数以及海深差值的标准差得到的。本文通过重力异常向下延拓方法确定密度差异常数,进而开展海底地形反演实验,并结合反演结果对研究区域的海底地形特征进行分析。
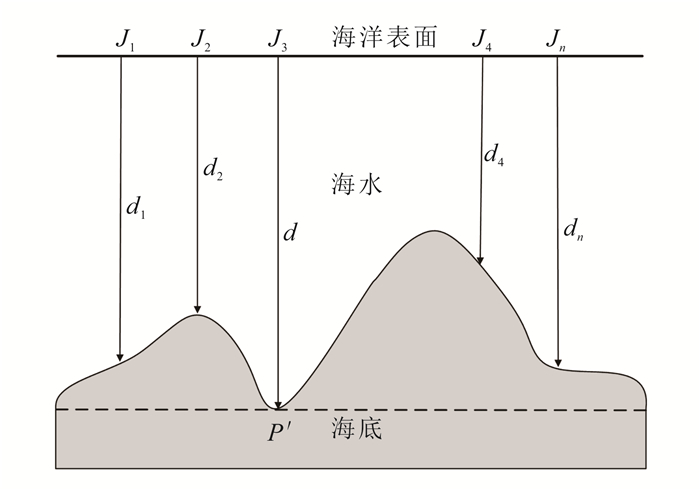
1 原理与方法 1.1 海底地形反演基本原理GGM的原理如图 1所示。海洋表面的测深点分布设为J1, J2, …, Jn,测深点对应的船测海深为d1, d2, d3, …, dn,d为参考深度,对应测量任务中最深点的测量结果,P′为最深测量点对应的海底点。
|
| 图 1 GGM模型原理示意图 Figure 1 Principle of the GGM |
|
|
将测深点上的重力异常Δg分为“长波段重力异常”和“短波段重力异常”2个分量,即
 (1)
(1) 式中:Δglong为长波段重力异常,由地壳下层物质的质量产生;Δgshort为短波段重力异常,由海底地形变化引起。测深点Jn处的海深dn与该点短波段重力异常Δgshortdn的关系[18]为
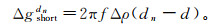 (2)
(2) 式中:Δρ为洋壳与海水的密度之差;f为引力常数(通常取6.672×10-8cm3/(g·s2))。
GGM模型反演海底地形的步骤如下:
1) 依据公式(2)得到测深点的Δgshort;
2) 由Δgshort根据公式(1)得到测深点的Δglong;
3) 将Δglong格网化,得到格网化的长波段重力异常Δglong格;
4) 用格网点上的重力异常Δg格减去格网点的Δglong格得到格网点的短波段重力异常Δgshort格;
5) 根据式(2),得到格网点的海深为
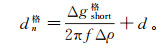 (3)
(3) 测深点的重力异常Δg由重力异常模型内插得到。
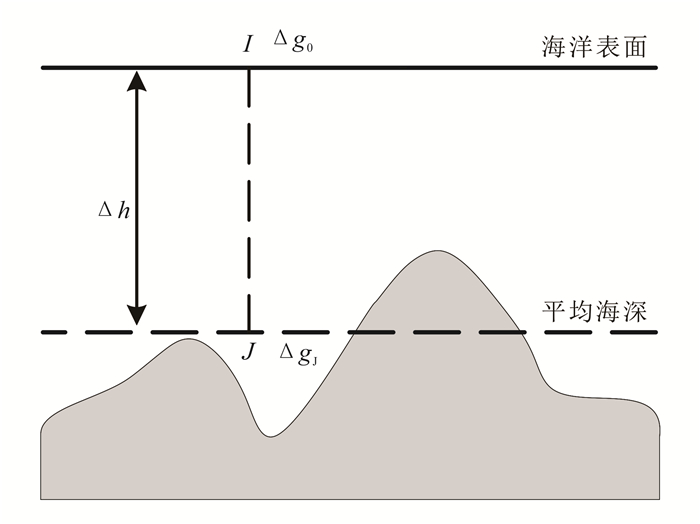
1.2 向下延拓方法如图 2所示,设海水的平均密度为ρsea,海面船测点I处的重力异常为Δg0,I点对应平均海深面上的J点。将I点位置的重力异常Δg0向下延拓到平均海深面上,得到J点的重力异常ΔgJ。那么,根据文献[17]中方法,Δρ可表示为
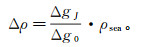 (4)
(4)
|
| 图 2 向下延拓法示意图 Figure 2 Downward continuation |
|
|
常用的向下延拓方法是频率域内的傅里叶变换法[19]。对海面重力异常Δg0进行二维离散傅里叶变换:
式中:j2=-1;(x, y)为重力异常在时域的坐标;Δg0为时域重力异常;G0为频率域重力异常;(fx, fy)为重力异常在频率域上的坐标;M、N为波数[20]。通过式(5),可将重力异常转换到频率域进行处理。海面重力异常在频率域延拓的公式为
式中:Gh为延拓面上的频率域重力异常;Δh为延拓高度。Δh < 0为向下延拓,Δh > 0为向上延拓。
向下延拓是误差放大的过程,特别是高频噪声[21]。为去除噪声的影响,需将Gh(fx, fy)进行降噪处理。本文选取高斯低通滤波器FGau:
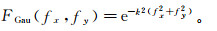 (7)
(7) 式中:k为高斯滤波参数。经过滤波后的重力异常G′h(fx, fy)表示为
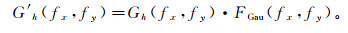 (8)
(8) 然后,对频率域上的重力异常进行傅里叶逆变换得到时域上的重力异常:
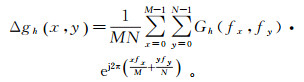 (9)
(9) 实际计算过程中,顾及计算的速度和效率,常采用快速傅里叶变换(FFT)方法进行时频转换。
利用移去恢复技术,首先依据EGM2008重力场模型计算海面上的重力异常和延拓面上的重力异常。在实际操作过程中,由于延拓面上的重力异常涉及到地球内部重力场,因此,考虑了海洋表面到延拓面(平均海深面)间海水层质量的影响。海面实际重力异常减去海面模型重力异常得到海面剩余重力异常;然后,海面剩余重力异常向下延拓得到延拓面重力异常;最后,延拓面重力异常加上延拓面模型重力异常(顾及海洋表面与延拓面间海水层质量的影响)得到最终的延拓面重力异常。由于延拓过程中涉及对重力异常进行傅里叶变换,为消除边缘效应的影响,实际处理时将研究区域分别沿经度和纬度方向向外扩大1°范围。而后,将结果按照研究区域大小进行截取处理得到最终结果。
2 实验结果与分析 2.1 实验区域选择和数据准备板块之间的俯冲、后退、挤压,使得俯冲带上发育了大量构造地形。在西太平洋海域,太平洋板块自东向西俯冲于菲律宾板块之下形成了马里亚纳海沟[22]。海沟呈现近南北延伸、向东弧向凸出的地形走势。北起硫磺列岛,南至雅浦岛附近,全长大约2 550 km,宽70 km左右。马里亚纳海沟因其在地质构造、区域板块和深度构造研究方面的积极作用,成为学者们研究的热点海域。本文选取“挑战者深渊”(因英国测量船“挑战者号”首次在该海域测量而得名[23])附近6°×8°(8°N—14°N、138°E—146°E)海域范围为研究区域。使用的地形模型为2008年8月由美国地球物理数据中心(NGDC)和美国海洋和大气管理局(NOAA)发布的分辨率为1′×1′的ETOPO1模型[24],该模型利用陆地和海洋实测数据,并融合部分其他地形模型生成,以前的ETOPO2v2[25]和ETOPO5[26]全球地形模型现在基本不再使用。重力异常数据来自于丹麦科技大学(technical university of denmark)空间实验室(DTU space)发布的分辨率为1′×1′的DTU10重力场模型[27]。船测海深数据来源于NOAA发布的多波束海深测量数据(船测数据下载网址:http://www.ngdc.noaa.gov/)。
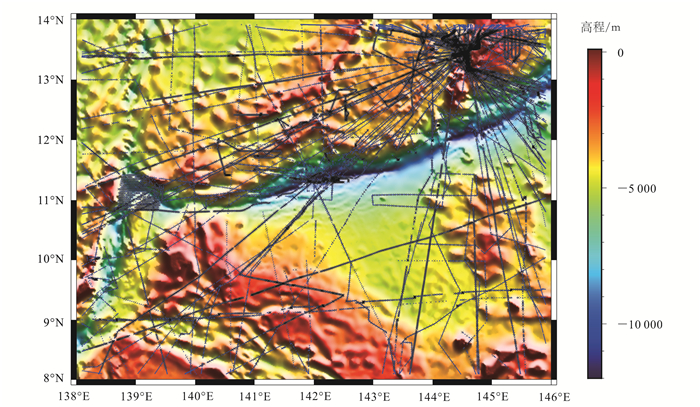
首先依据3σ法则对研究海域的实测数据进行初步剔除,筛选得到75 110个船测点数据。均匀选取实测数据中14 278个数据作为检核点数据,大约占船测数据总数的五分之一;余下60 832个数据作为控制点数据。船测控制点和检核点分布情况如图 3所示。
|
| 黑色标志点为检核点;蓝色标志点为控制点;背景为ETOPO1模型。 图 3 研究区船测点分布 Figure 3 Distribution of ship datum in the study area |
|
|
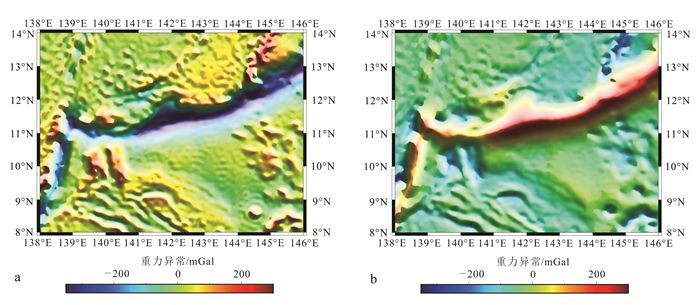
研究海域海面重力异常如图 4a所示(以DTU10模型值作为海面重力异常)。通过计算,得到研究区域平均海深为3 751.5 m,将海面重力异常采用FFT法向下延拓到平均海深面上,高斯滤波参数k取10。滤波后的重力异常经傅里叶逆变换得到延拓面(平均海深面)上的重力异常,如图 4b所示。分别对海面重力异常和延拓面上的重力异常取均值[7],海水密度为1.03 g/cm3,依式(4)求得Δρ=2.32 g/cm3。
|
| a.海面重力异常;b.平均海深面重力异常。 图 4 研究区重力异常 Figure 4 Gravity anomaly in the study area |
|
|
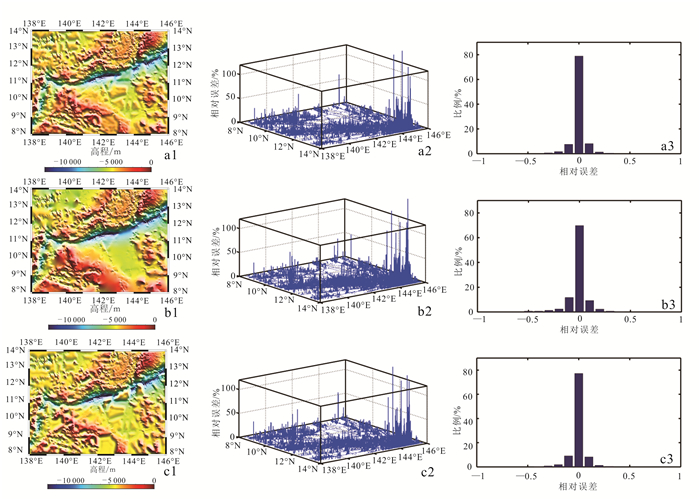
依据GGM模型计算流程,采用四次曲面的局部多项式插值法内插得出控制点的重力异常,与式(2)计算的控制点短波段重力异常作差,使用GMT(generic mapping tools)中的张力样条函数进行格网化处理,得到1′×1′分辨率的长波段重力异常(图 5a);根据式(1)得到1′×1′分辨率的短波段重力异常(图 5b);由式(3)最终得到1′×1′分辨率的GGM海深模型(图 6a1);将GGM海深模型内插到检核点,并统计相对误差(模型与检核点海深的差值与检核点海深之比),结果如图 6a2、图 6a3所示。同理,对ETOPO1模型(图 6b1)内插到检核点,其相对误差统计结果分别如图 6b2、图 6b3所示。使用GMT中的张力样条函数对海深控制点进行网格化处理,生成1′×1′的格网化海深模型(以下称为模型1),结果如图 6c1所示,其相对误差统计结果分别如图 6c2、图 6c3所示。

|
| a.长波段重力异常;b.短波段重力异常。 图 5 研究区重力异常分量 Figure 5 Component of gravity anomaly in the study area |
|
|
|
| a1.GGM海深模型;a2.GGM海深模型相对误差分布; a3.GGM海深模型相对误差; b1.ETOPO1模型; b2.ETOPO1模型相对误差分布; b3.ETOPO1模型相对误差; c1.模型1; c2.模型1相对误差分布; c3.模型1相对误差。 图 6 研究区海深模型与相对误差 Figure 6 Bathymetry model and relative error in the study area |
|
|
将海深模型(图 6a1)与图 5对比可以看出,海深与短波段重力异常(图 5b)之间存在明显的相关性,而与长波段重力异常(图 5a)的相关性不明显;说明利用短波段重力异常反演海底地形在理论上具有可行性。
对比GGM海深模型、ETOPO1模型、模型1(图 6a1、b1、c1)可以看出:GGM海深模型对海底地形的反映比ETOPO1模型更加精细,可以有效填补无船测数据区域的海深空白;模型1在船测点密集的海域对海底地形的反映比较详细,而在船测点稀疏的海域对海底地形的呈现不如GGM海深模型和ETOPO1模型详细,如12°N—14°N、138°E—140°E海域。
3种海深模型与检核点差值的统计结果如表 1所示。由表 1看出,GGM海深模型的精度明显优于另外2个模型,然而,GGM海深模型与检核点差值统计结果中的最值项却超过了千米量级。对数据进行再次检查发现,出现该结果是因为在实验初始阶段有部分粗差未被发现。如本次出现差值最大值的检核点处水深为143 m,而其周围检核点水深基本在1 200 m以上,说明该处测量值明显出现错误,而在粗差剔除初始阶段未被发现,进而影响到最终的统计结果。将该错误数据剔除后,GGM海深模型相对误差最大值由3.053 1减小为1.647 9,相对误差标准差由0.079 5减小为0.075 3。
| m | ||||
| 数据类型 | 最大值 | 最小值 | 平均值 | 均方根 |
| GGM海深模型 | 1 171.70 | -1 232.20 | 1.58 | 150.11 |
| ETOPO1模型 | 1 444.00 | -1 330.10 | 20.27 | 209.12 |
| 模型1 | 1 109.90 | -1 122.40 | 5.97 | 156.31 |
可以看出:若将带有粗差的船测点作为控制点,会影响模型的建立;若将含有粗差的船测点作为检核点,又将对精度统计结果产生误导。基于此,在数据处理初始阶段,对船测海深粗差的剔除和发现显得尤为重要。
如图 6a2、b2、c2所示,在13°N—14°N、144°E—146°E,3个模型的海深差值相对误差普遍很大。探究其原因,对比分析不同海域的相对误差分布情况发现:13°N—14°N、144°E—146°E船测控制点密集(图 3),海底地形变化剧烈,相对误差大;同样船测控制点密集、海底地形变化不剧烈的11°N、142°E周围海域的相对误差小得多;9°N—10°N、143°E—144°E海域,船测控制点分布均匀,海底地形变化平缓,相对误差也很小;船测控制点分布均匀,海底地形变化剧烈海域(如8°N—10°N、139°E—140°E附近),相对误差较大。从而,说明海底地形变化的剧烈程度是影响相对误差的主要原因。
对比图 6a3、b3、c3发现,GGM海深模型的相对误差为-0.01~0.01的占绝大多数,相对误差为-0.05~0.05的比例占78.82%,而在ETOPO1模型和模型1中,相对误差为-0.05~0.05所占比例分别为69.75%和77.83%;可见,GGM海深模型的相对误差小值所占比例明显多于另外2个模型。3种海深模型的相对误差统计结果见表 2。
| 数据类型 | 最大值 | 最小值 | 平均值 | 标准差 |
| GGM海深模型 | 1.647 9 | -0.682 2 | 0.000 2 | 0.075 3 |
| ETOPO1模型 | 1.893 5 | -0.644 2 | -0.006 8 | 0.104 9 |
| 模型1 | 1.598 7 | -0.750 3 | -0.001 7 | 0.077 9 |
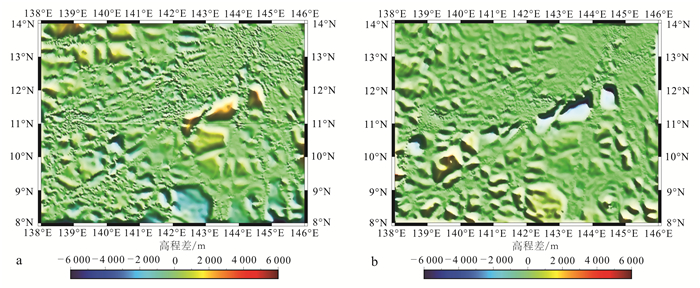
进一步比较GGM海深模型和ETOPO1模型,将GGM海深模型和ETOPO1模型作差,结果如图 7a所示。将图 7a与船测点分布图(图 3)比较分析发现:模型差值较大区域为船测点匮乏或者过于稀疏的海域,如12°N—14°N、138°E—139°E海域。同时,在多海沟、多海山区域模型差值也普遍较大;另外,船测点分布的密集程度对模型差值的影响显著,反映了GGM海深模型和ETOPO1模型在模型建立时源数据的差异,GGM海深模型和ETOPO1模型的测深基准面差异对结果也会产生影响,但不是主要影响。GGM海深模型与船测点格网化模型的差值受船测点的分布情况更加明显(图 7b)。3个海深模型的差值统计结果见表 3。
|
| a.GGM海深模型-ETOPO1模型;b.GGM海深模型-模型1。 图 7 研究区模型较差 Figure 7 Difference of the model in the study area |
|
|
| 数据类型 | 海深/m | |||
| 最大值 | 最小值 | 平均值 | 标准差 | |
| GGM海深模型-ETOPO1模型 | 2 454.20 | -4 443.80 | 33.85 | 418.31 |
| GGM海深模型-模型1 | 3 991.70 | -5 321.60 | 79.36 | 488.59 |
图 7和表 3结果显示,GGM海深模型与ETOPO1更为接近。那么建立综合模型时,应该考虑船测点的分布情况;船测点分布均匀的海域,用GGM海深模型;在船测点匮乏海域,考虑到ETOPO1模型源数据的充分性和来源多样性,选择ETOPO1模型。
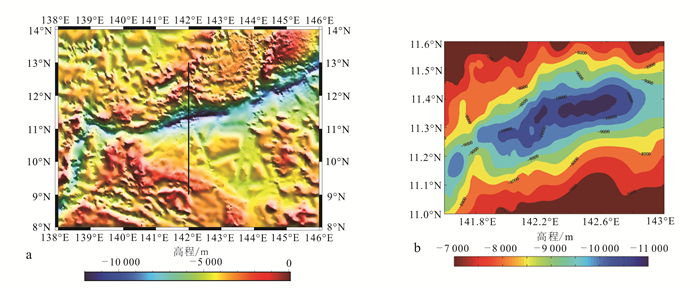
2.4 海底地形分析依据GGM反演的海深模型结果如图 8a所示,从图中能清晰地看出本文实验的马里亚纳海沟海域为东西走势。海沟的平均深度大于8 000 m。在11°N、142°E附近出现10 000 m以上的深度值。“挑战者深渊”就位于该海域,选择最深点周围海域进行分析(11°00′N—11°36′N、141°36′E—143°00′E),海深结果如图 8b所示。
|
| a.依据GGM反演的马里亚纳海沟海深模型;b.“挑战者深渊”附近海底深度。 图 8 马里亚纳海沟 Figure 8 Mariana trench |
|
|
从图 8b可以看出,大于10 000 m的等深线圈东西两端较窄,中间宽,形似纺锤。在万米等深线圈内能清楚地看见3个洼地,从东到西面积逐渐减小。东部洼地呈长条状。洼地的中轴方向和海沟的中轴方向基本一致。但是,洼地的细部轮廓特征描述不够细致。
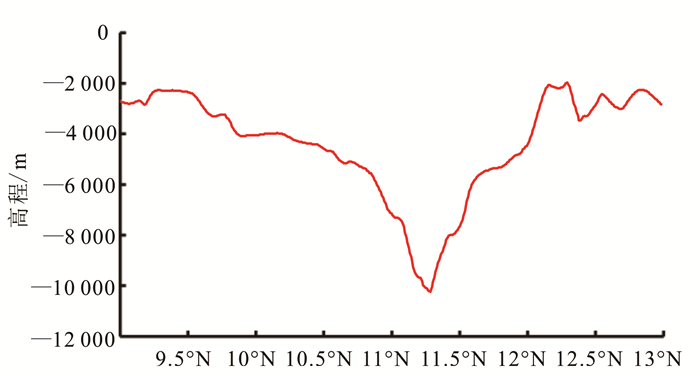
在图 8a中直线所在位置作海沟的剖面图,结果如图 9所示。从图 9中可看到,4 000 m深的海沟南北两侧不同程度地发育了海山。海沟南侧在海深小于5 000 m的浅区坡度较平缓,为2°~5°;海深大于5 000 m以下坡度明显增大,为10°~15°,直抵海沟底部。海沟北测在整个下降阶段,坡度很大,为10°~15°;在北纬11°45′附近出现一个缓冲地带。南北两侧不对称。
|
| 图 9 海沟剖面图 Figure 9 Topography of the trench |
|
|
依据反演的海底地形,能够大概看出海沟的基本形态。但是,对于海沟南北坡的细节反映不够明显。从而,依据模型反演的海底地形只能反映某种大范围的海底地形,对海底地形细节的反映不够清晰。
3 结论文章选取西太平洋板块俯冲菲律宾板块而形成的马里亚纳海沟所在海域作为实验区域,分析比较了GGM海深模型、ETOPO1模型以及直接将船测点海深数据格网化3种海深模型之间的差异,并对所选海域最深点附近的“挑战者深渊”两侧地貌进行了研究,得到结论如下:
1) GGM利用卫星测高重力异常,可以高分辨率地反演海底地形,结果优于ETOPO1模型,优于按本文格网化方法将船测点直接格网化的结果,为大面积地研究地质构造、区域板块和深度构造有积极作用。
2) 相对误差与海深的关系不大,受海底地形变化影响剧烈。海底地形变化平缓,船测点分布均匀,相对误差小。
3) GGM海深模型和ETOPO1模型的差值,以及GGM海深模型与船测点海深格网化的差值受船测点的分布影响明显。船测点匮乏或者过于稀疏的海域模型差值较大。
4) 绘制“挑战者深渊”两侧南北坡剖面图后发现,海沟两侧的地貌有明显差异。在海沟南侧海深小于5 000 m的浅海部分坡度平缓(2°~5°),而在水深大于5 000 m部分坡度明显增大(10°~15°);海沟北侧在整个下降阶段坡度很大(10°~15°),11°45′N附近出现一个缓冲地带。依据模型反演的海底地形,只能大范围地反演某些海底环境,对海底的细节描述依然不够清晰。
向下延拓理论上本应在整个球面上进行,文章在向下延拓过程中,直接在局部范围内将海洋表面的重力异常向下延拓,同时,忽略了海水质量的影响,对最终结果可能有影响,还需进一步论证。
| [1] |
翟国君, 黄谟涛, 欧阳永忠, 等. 卫星测高原理及其应用[J]. 海洋测绘, 2002, 22(1): 57-62. Zhai Guojun, Huang Motao, Ouyang Yongzhong, et al. The Principle of Satellite Altimetry and Its Applications[J]. Hydrographic Surveying and Charting, 2002, 22(1): 57-62. DOI:10.3969/j.issn.1671-3044.2002.01.016 |
| [2] |
许惠平, 刘万崧, 周云轩, 等. 卫星测高重力资料及其在南海莺-琼盆地中的应用[J]. 吉林大学学报(地球科学版), 2003, 33(3): 368-371. Xu Huiping, Liu Wansong, Zhou Yunxuan, et al. Altimetry Gravity and Its Applications in South China Sea[J]. Journal of Jilin University (Earth Science Edition), 2003, 33(3): 368-371. |
| [3] |
梁子亮, 陈路, 解琨, 等. 利用多代卫星测高数据反演海洋重力异常及大地水准面[J]. 大地测量与地球动力学, 2015, 35(1): 40-44. Liang Ziliang, Chen Lu, Xie Kun, et al. Inversion of Marine Gravity Anomalies and Geiod Using Muiti-Satellite Altimeter Data[J]. Journal of Geodesy and Geodynnamics, 2015, 35(1): 40-44. |
| [4] |
聂琳娟, 吴云孙, 金涛勇, 等. 联合测高重力异常与ETOPO5海深数据求解南海海深模型[J]. 湖北民族学院学报(自然科学版), 2011, 29(2): 157-160. Nie Linjuan, Wu Yunsun, Jin Taoyong, et al. Solution of the Ocean Depth Model for the South China Sea by Combining Gravity Altimetry and ETOPO5 Deep-Sea Data[J]. Journal of Hubei University for Nationalities (Natural Science Edition), 2011, 29(2): 157-160. DOI:10.3969/j.issn.1008-8423.2011.02.012 |
| [5] |
Calmant S, Baudry N. Modelling Bathymetry by Inverting Satellite Altimetry Data:A Review[J]. Marine Geophysical Research, 1996, 18(2): 123-134. |
| [6] |
Hwang C. A Bathymetric Model for the South China Sea from Satellite Altimetry and Depth Data[J]. Marine Geodesy, 1999, 22(1): 37-51. DOI:10.1080/014904199273597 |
| [7] |
Kim K B, Hsiao Y S, Kim J W, et al. Bathymetry Enhancement by Altimetry-Derived Gravity Anomalies in the East Sea (Sea of Japan)[J]. Marine Geophysical Researches, 2010, 31(4): 285-298. DOI:10.1007/s11001-010-9110-0 |
| [8] |
Kim J W, Frese R R B V, Bang Y L, et al. Altimetry-Derived Gravity Predictions of Bathymetry by the Gravity-Geologic Method[J]. Pure and Applied Geophysics, 2011, 168(5): 815-826. DOI:10.1007/s00024-010-0170-5 |
| [9] |
Hsiao Y S, Kim J W, Kim K B, et al. Bathymetry Estimation Using the Gravity-Geologic Method:An Investigation of Density Contrast Predicted by the Downward Continuation Method[J]. Terrestrial Atmospheric & Oceanic Sciences, 2011, 22(3): 347-358. |
| [10] |
Sandwell D T, Müller R D, Smith W H, et al. New Global Marine Gravity Model from Cryosat-2 and Jason-1 Reveals Buried Tectonic Structure[J]. Science, 2014, 346(6205): 65. DOI:10.1126/science.1258213 |
| [11] |
Parker R L. The Rapid Calculation of Potential Ano-malies[J]. Geophysical Journal International, 1973, 31(4): 447-455. |
| [12] |
Watts A B. An Analysis of Isostasy in the World's Oceans:1. Hawaiian-Emperor Seamount Chain[J]. Journal of Geophysical Research Solid Earth, 1978, 83(B12): 5989-6004. DOI:10.1029/JB083iB12p05989 |
| [13] |
Smith W H F, Sandwell D T. Bathymetric Prediction from Dense Satellite Altimetry and Sparse Shipboard Bathymetry[J]. Journal of Geophysical Research Solid Earth, 1994, 99(B11): 21803-21824. DOI:10.1029/94JB00988 |
| [14] |
Braitenberg C, Pagot E, Wang Y, et al. Bathymetry and Crustal Thickness Variations from Gravity Inversion and Flexural Isostasy[M]. Berlin: Springer, 2003: 143-149.
|
| [15] |
胡敏章, 李建成, 金涛勇. 应用重力地质方法反演皇帝海山的海底地形[J]. 武汉大学学报:信息科学版, 2012, 37(5): 610-612, 629. Hu Minzhang, Li Jiancheng, Jin Taoyong. Bathymetry Inversion with Gravity-Geologic Method in Emperor Seamount[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5): 610-612, 629. |
| [16] |
黄谟涛, 翟国君, 欧阳永忠, 等. 卫星测高资料在反演海底地形中的应用[J]. 海洋测绘, 2002, 22(1): 3-7. Huang Motao, Zhai Guojun, Ouyang Yongzhong, et al. On the Application of Altimeter Data to the Recovery of Bathymetry[J]. Hydrographic Surveying and Charting, 2002, 22(1): 3-7. DOI:10.3969/j.issn.1671-3044.2002.01.002 |
| [17] |
欧阳明达, 孙中苗, 翟振和. 基于重力地质法的南中国海海底地形反演[J]. 地球物理学报, 2014, 57(9): 2756-2765. Ouyang Mingda, Sun Zhongmiao, Zhai Zhenhe. Predicting Bathymetry in South China Sea Using the Gravity-Geologic Method[J]. Chinese Journal of Geophysics, 2014, 57(9): 2756-2765. |
| [18] |
Hsiao Y S, Hwang C, Cheng Y S, et al. High-Resolution Depth and Coastline over Major Atolls of South China Sea from Satellite Altimetry and Imagery[J]. Remote Sensing of Environment, 2016, 176: 69-83. DOI:10.1016/j.rse.2016.01.016 |
| [19] |
徐世浙. 迭代法与FFT法位场向下延拓效果的比较[J]. 地球物理学报, 2007, 50(1): 285-289. Xu Shizhe. A Comparison of Effects Between the Iteration Method and FFT for Downward Continuation of Potential Fields[J]. Chinese Journal of Geophysics, 2007, 50(1): 285-289. DOI:10.3321/j.issn:0001-5733.2007.01.035 |
| [20] |
Schwarz K P, Sideris M G, Forsberg R. The Use of FFT Techniques in Physical Geodesy[J]. Geophysical Journal International, 1990, 100(3): 485-514. DOI:10.1111/gji.1990.100.issue-3 |
| [21] |
周波阳, 罗志才, 许闯, 等. 航空重力数据向下延拓的FFT快速算法比较[J]. 大地测量与地球动力学, 2013, 33(1): 64-68. Zhou Boyang, Luo Zhicai, Xu Chuang, et al. Comparison Among Fast Fourier Transform Algorithms for Downward Continuation of Airborne Gravity Data[J]. Journal of Geodesy and Geodynamics, 2013, 33(1): 64-68. |
| [22] |
Fryer P, Becker N, Appelgate B, et al. Why is the Challenger Deep so Deep[J]. Earth & Planetary Science Letters, 2003, 211(3-4): 259-269. |
| [23] |
Fujioka K, Okino K, Kanamatsu T, et al. Morp-hology and Origin of the Challenger Deep in the Southern Mariana Trench[J]. Geophysical Research Letters, 2002, 29(10): 10-11. |
| [24] |
Amante C, Eakins B W. Etopo11 Arc-Minute Global Relief Model:Procedures, Data Sources and Analysis[J]. Psychologist, 2009, 16(3): 20-25. |
| [25] |
Center N G D. Etopo2V22 Minute Worldwide Bathy-metry/Topography Grids|Ngdc.Noaa.Gov[EB/OL].[2017-04-15]. https://www.ngdc.noaa.gov/mgg/global/etopo2.html.
|
| [26] |
Center N G D. Etopo5 Data and Documentation|Ngdc.Noaa.Gov.[EB/OL].[2017-04-15]. https://www.ngdc.noaa.gov/mgg/global/etopo5.html.
|
| [27] |
Andersen O B, Jain M, Knudsen P. The Impact of Using Jason-1 and Cryosat-2 Geodetic Mission Altimetry for Gravity Field Modeling[M]. Cham: Springer International Publishing, 2016: 205-210.
|



