Morphing wing strategy of a deformable wing and its cooperative control
-
摘要: 针对可变形机翼的变形及其协同控制问题，本文提出了一种保证变形翼面光滑且便于实施控制的变翼型策略，设计了一种基于交叉耦合的分布式同步控制器，很好地解决了翼型变形过程中的同步问题。通过计算流体力学仿真方法，分析了变翼型对气动参数的影响特性，以及变翼型对变形装置负载的影响。本文建立了翼型变形系统的动力学模型，提出了一种交叉耦合同步偏差生成方法，利用同步偏差表征同步性能，设计了分布式同步控制器使同步偏差收敛到零，在实现翼型变形的同时保证变形同步。通过数值仿真验证了该协同控制方法的有效性和稳定性。相比于并行控制方法，本方法的同步性能和稳态性能均有显著提升。Abstract: Aiming at the morphing and cooperative control of deformable wings, this paper proposes a variable airfoil strategy to ensure the smoothness of the variable airfoil and facilitate the implementation of control. A cooperative controller based on cross-coupling is also designed to solve the synchronous problem in the process of airfoil morphing. First, this paper analyzes the influence characteristics of wing morphing on aerodynamic parameters and the load of the morphing device through the computational fluid dynamics simulation method. Second, a dynamics model of the airfoil morphing system is established in this paper, and a cross-coupling synchronization error generation method, which uses synchronous deviation to represent synchronization performance, is proposed. A distributed synchronous controller is also designed, ensuring the convergence of synchronization errors to zero. The wing is morphed into the desired one, and all morphing devices act cooperatively in the process. Finally, the effectiveness and stability of the cooperative control method are verified by numerical simulation. Compared with the parallel control method, the synchronization and steady-state performances of this proposed method are significantly improved.
-
变形翼的总体思想是使其气动外形适应各种飞行条件，以获得更好的飞行性能[1]。可变形机翼主要由结构骨架、蒙皮、执行系统、传感系统和控制系统组成[2]。可变形机翼不仅要实现机翼变形，而且还必须能够承受外部和内部载荷。这就要求可变形机翼既具有柔性，同时还具有足够的强度[3]。随着材料技术[4-7]、传感技术[8]的发展，变形翼的研究也越来越受到关注。
变形翼根据改变的机翼几何参数的不同，可分为平面形状变形、平面外变形，以及翼型变形，其中平面形状变形包括变翼展、变后掠、变弦长，平面外变形包括扭转、Z形翼、变翼展方向的弯度，变翼型包括变弯度和变厚度[9]。变形翼飞行器的控制包括，对机翼变形的控制和对飞行器整体的控制[10]。
由于对气动效率、机动性、负载控制和减轻、高升力产生等方面的巨大潜力，学者们在变形翼的相关课题开展了大量研究[3]。Kim等[11]采用积分强化学习和基于确定性策略的梯度学习方法对参数化控制输入进行训练，以处理变后掠无人机的动力学控制的非线性和非仿射特性。由于训练数据有限，强化学习方法难以应对复杂的环境不确定性。Kim[12]、陆宇平[13]、江未来[14]、闫彬彬[15]均通过计算流体力学仿真分析了机翼变形对飞行器气动参数的影响，并建立了变形翼飞行器的纵向动力学模型。文献[12]建立了变后掠无人机的纵向动力学模型，设计了一种滑模控制律对无人机的飞行速度、姿态等进行控制。文献[13]建立了伸缩变翼展飞行器的纵向动力学模型，并提出了一种非奇异终端滑模控制律实现了飞行器的速度和姿态控制。文献[14]分析构建了变后掠飞行器的切换线性变参数模型，设计了一种平滑切换鲁棒控制律以抑制系统状态在切换中的抖振，实现在匀速平飞时进行机翼变形的姿态控制。但文献[12-15]都未考虑变形的同步控制问题。吴俊[16]对电动舵机驱动的变翼型机翼构造了一种二次型局部代价函数，通过设计一种最优控制器，实现了翼型变形的分布式同步控制，还分析了信息交换拓扑、信息交换时延对变形控制系统稳定性的影响。但并没有考虑变形过程中气动负载、变形负载对变形的影响。
针对翼型变形，本文提出了一种变形策略，能保证在变形过程中翼面始终光滑且便于实施变形同步控制，为减小变形不协调、不同步等问题的影响，本文提出了一种基于交叉耦合的分布式协同控制方法，通过配置系数矩阵生成交叉耦合偏差，设计分布式控制器使交叉耦合偏差收敛以实现同步控制。
1. 翼型变形分析
1.1 变形策略简介
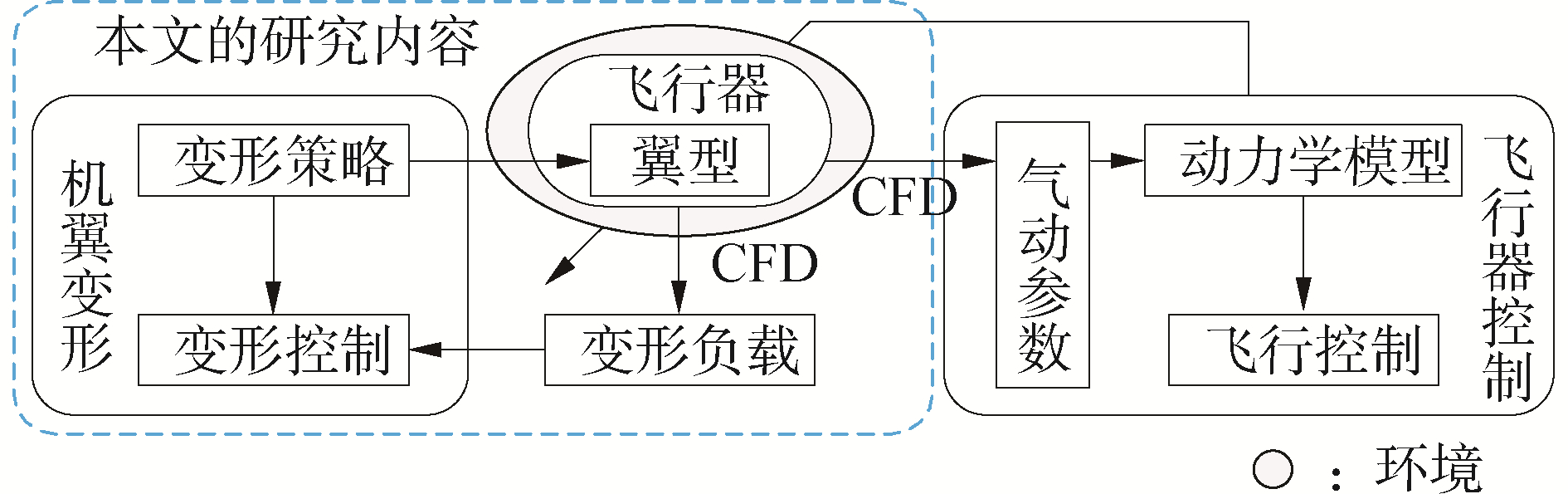
可变形机翼飞行器的控制包括机翼变形控制和飞行器整体的飞行控制，两者相互耦合，如图 1所示。本文主要侧重机翼变形的变形同步控制，提出了一种可保证变形翼面光滑且便于实施同步控制的变形策略。针对该变形策略利用CFD仿真分析了变形对变形负载和气动参数的影响。
图 1 可变形机翼飞行器系统控制架构Fig. 1 Variable-wing aircraft system control architecture
下载:
全尺寸图片
考虑机翼变形的翼面光滑性要求，同时便于进行变形同步控制，本文针对翼型变形设计了一种变形策略。引入变形比函数，即变形后翼型参数与参考翼型参数的比值函数，为保证变形后的翼型光滑，该变形比函数在翼型域内光滑且在前缘点和后缘点处的变形比数值为零。
假设翼型前缘点为原点，前缘点指向后缘点方向为x轴正向，y轴正向垂直x轴指向上翼面方向，则翼型可表示为：
$$ \left\{\begin{array}{l} y^{+}=h^{+}(x), \quad y \geqslant 0 \\ y^{-}=h^{-}(x), \quad y<0 \end{array}\right. $$ (1) 本文中变形比函数R(x)选取三次多项式函数，该变形比函数满足翼面光滑条件：
$$ R(x)=a x(x-b)(x-1), 0 \leqslant x \leqslant 1 $$ (2) 式中：R(x)为变形比，即变形后的翼型值ym+(x)相对于参考翼型值y0+(x)的变形量与参考翼型值之比，为正表示变厚，为负表示变薄；a为待定参数；b为待定参数，满足0 < b < 1，称为不变形点。
本文仅对上翼面进行变形，变形后的翼型为：
$$ \begin{cases}y_{m}^{+}=[1+R(x)] h^{+}(x), & y \geqslant 0 \\ y^{-}=h^{-}(x), & y<0\end{cases} $$ (3) 基于上述变形函数，改变不变形点和变形比的最大值可以实现翼面变形，并且可以保证在变形过程中翼面光滑。
1.2 气动特性影响分析
基于1.1节的变翼型参数定义，本文设计了一种固定不变形点，改变最大变形量的变形策略。结合式(2)和(3)可知，该变形策略在变形过程中各变形点处变形量的比值始终保持不变，这便于变形同步控制器的设计。
飞行器的升力L、阻力D与气动参数、机翼形状的关系满足：
$$ \left\{\begin{array}{l} L=0.5 \rho V^{2} S_{W} C_{L} \\ D=0.5 \rho V^{2} S_{W} C_{D} \end{array}\right. $$ (4) 式中：ρ为大气密度；V飞行器的速度；SW为机翼参考面积；CL、CD分别为升力系数和阻力系数。
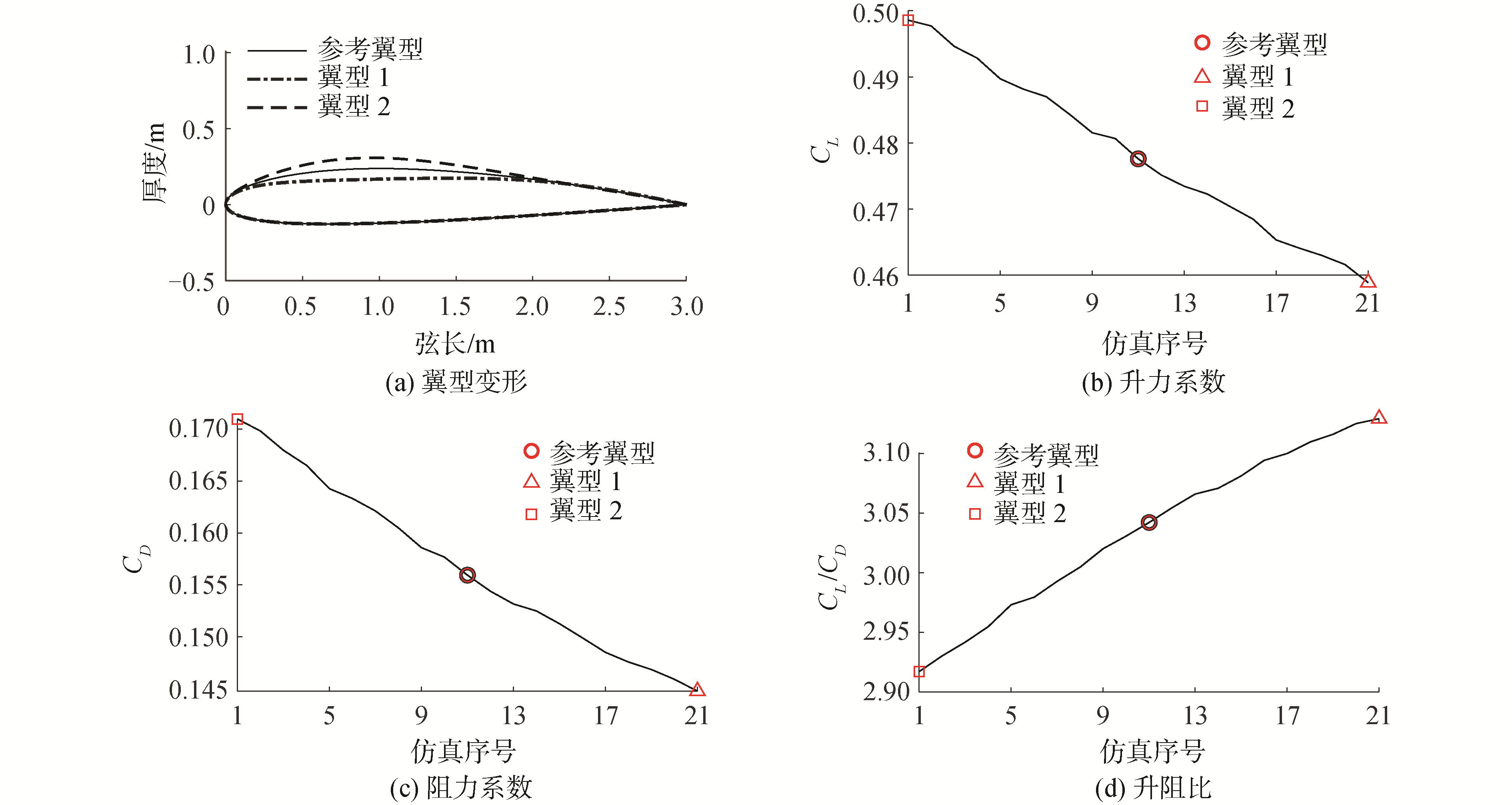
为分析变形对气动参数的影响，利用CFD仿真计算该变形策略下机翼的气动参数(升力系数、阻力系数)。仿真试验中选取NACA2412作为参考翼型，仅对一段机翼进行仿真，该段机翼的翼根弦长为3 m，翼尖弦长为2.7 m，前缘后掠角为26.565°，后缘后掠角为11.31°，翼展为1 m。仿真中设置攻角为20°，流速为0.4Ma。
基于1.1节的定义，保持不变形点为0.75，最大变形比从-0.3~0.3均匀变化，构成一组21个翼型的仿真试验。仿真结果如图 2，由图 2可知变形时升力、阻力和升阻比与最大变形比均近似满足线性关系。这将大大降低飞行器整体控制器设计的难度，这也体现了该变形策略的优越性。本文将基于该变形策略给出一种通用的变形同步控制方案。
图 2 翼型变形对气动参数的影响Fig. 2 Influence of airfoil morphing on aerodynamic parameters下载:
全尺寸图片
1.3 变形方案与负载估计
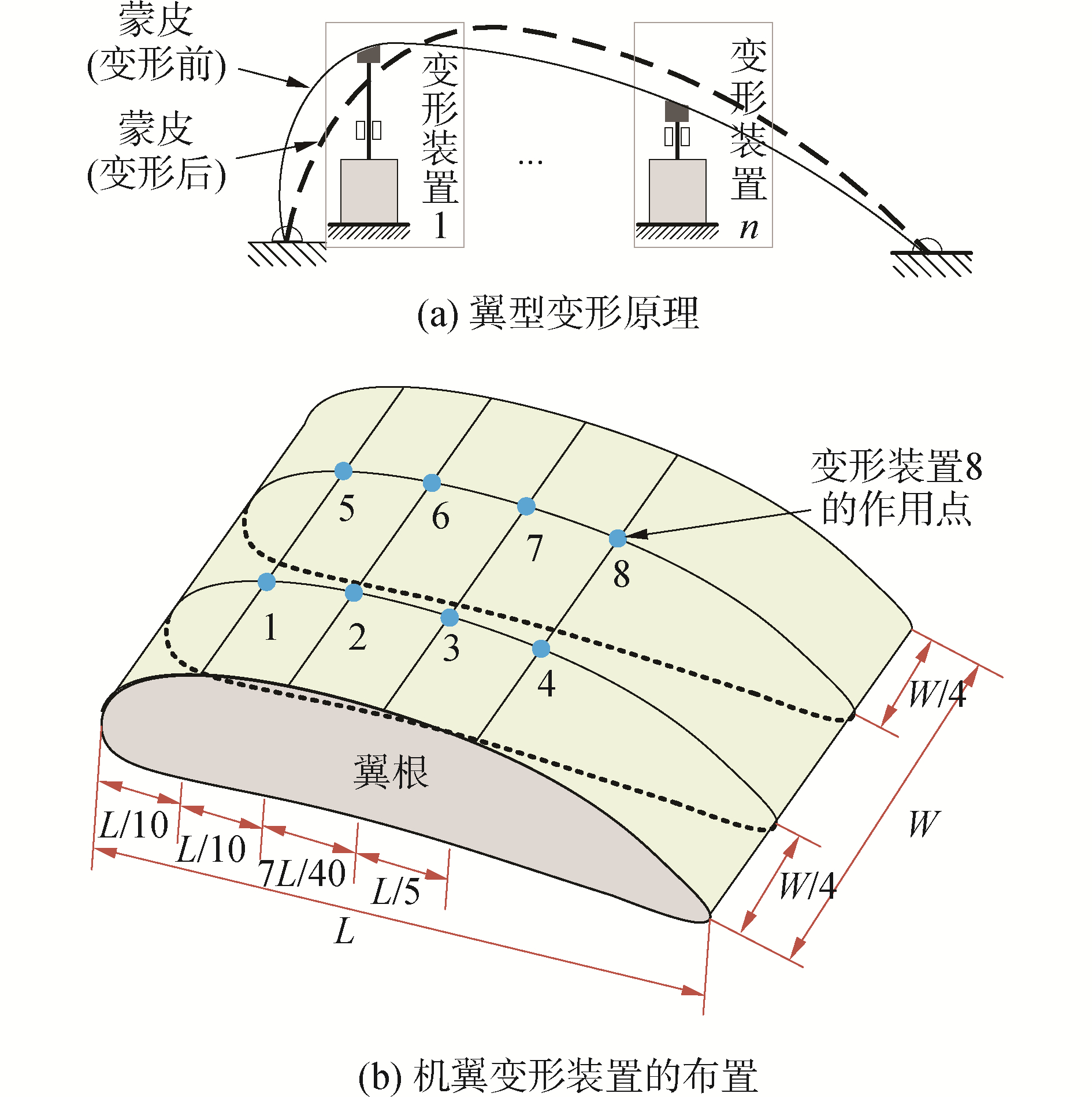
为了实现机翼翼型的改变，需在机翼上布置变形装置。图 3(a)展示了在翼型截面内翼型变形的基本原理[17]，图 3(b)展示了一段机翼上变形装置的布置，变形装置分别沿翼型横截面和沿机翼翼展方向进行阵列布置，共8个变形装置，布置成4×2的阵列。按照从翼根到翼尖，从前缘到后缘依次编号为变形装置1~8和作用点1~8。变形装置由电机、传动装置等部分组成。驱动变形装置阵列协同动作，就能够实现机翼翼型按照指定的规律变化。
图 3 翼型变形原理Fig. 3 Principle of airfoil morphing下载:
全尺寸图片
利用仿真可等效地近似计算出各变形装置作用点处的气动载荷(流体对翼面的压力或吸力等效到变形作用点处的推力或拉力)。进而提取出各变形装置的位移量与载荷之间的关系。采用线性拟合：
$$ \hat{F}_{k}\left(x_{k}\right)=a_{k} x_{k}+b_{k}, k=1, 2, \cdots, 8 $$ (5) 式中：$\hat{F}_k\left(x_k\right)$为第k个变形装置在位移为xk时的等效气动负载力, a、b为拟合系数，N/m、N。xk为位移，m。
拟合结果见表 1。假设式(5)的拟合误差δk满足正态分布δk~$\mathcal{N}$(0, σk2), k=1, 2, …, 8，其中σk代表k个变形装置气动负载力的拟合误差的方差。此处引入随机分布可表征部分不确定性。考虑拟合误差后，变形装置的负载力可以表示为：
$$ \widetilde{F}_{k}\left(x_{k}\right)=\hat{F}_{k}\left(x_{k}\right)+\delta_{k}, \quad k=1, 2, \cdots, 8 $$ (6) 表 1 变形装置等效负载力拟合结果Table 1 Fitting results of equivalent load force序号 拟合系数
ak拟合系数
bk拟合误差的方差 相关系数 1 -2 706.153 1 425.201 8.660 -0.986 843 2 4 015.458 69.918 1.938 0.999 923 3 5 229.864 -312.477 3.788 0.999 860 4 3 464.761 128.100 8.827 0.990 002 5 -2 604.038 1 576.647 12.010 -0.970 394 6 5 381.872 -31.878 4.852 0.999 703 7 6 410.688 -390.128 7.766 0.999 564 8 3 643.843 256.557 4.878 0.996 901 各变形装置的气动负载与机翼整体翼型相关，因此各变形装置的变形量和气动负载是相互耦合的，即第k个变形装置的气动负载不仅与第k个变形装置的变形量有关，还与其余的变形装置的变形量有关。在仿真中不可能考虑到所有的翼型，若翼型变形过程中的过渡翼型恰好就是仿真的插值翼型，则可近似表示第k个变形装置的气动负载力矩：
$$ T_{L}\left(x_{k}\right)=K_{f t} \widetilde{F}_{k}\left(x_{k}\right), \quad k=1, 2, \cdots, 8 $$ (7) 式中：xk为第k个变形装置的位置；Kft为空气负载力的等效力臂，m。
2. 翼型变形控制
2.1 变形系统的数学模型
对于4×2的变形装置阵列，可建立8个相互关联的永磁同步电机的数学模型。对于变形装置k的永磁同步电机，其d-q轴数学模型为：
$$ \left\{\begin{array}{l} u_{\mathrm{d}}=R i_{\mathrm{d}}+L_{\mathrm{d}} \frac{\mathrm{d} i_{\mathrm{d}}}{\mathrm{d} t}-L_{\mathrm{q}} i_{\mathrm{q}} \omega_{e} \\ u_{\mathrm{q}}=R i_{\mathrm{q}}+L_{\mathrm{q}} \frac{\mathrm{d} i_{\mathrm{q}}}{\mathrm{d} t}+\left(L_{\mathrm{d}} i_{\mathrm{d}}+\psi_{f}\right) \omega_{e} \end{array}\right. $$ (8) 式中：ud、uq分别为直轴、交轴下定子线圈两端电压；id、iq为直轴、交轴下通过定子线圈的电流；R为定子电阻；Ld、Lq分别为定子的直轴、交轴电感；ωe为转子的电角速度；ψf为永磁体的磁链。
电机机械角度θm和变形装置的位移xk满足：
$$ x_{k}=G \theta_{m} $$ (9) 式中G为传动增益常数，m/rad。
其电磁转矩方程为：
$$ T_{e}=\frac{3}{2} n_{\mathrm{p}} i_{\mathrm{q}}\left[\psi_{f}+i_{\mathrm{d}}\left(L_{\mathrm{d}}-L_{\mathrm{q}}\right)\right] $$ (10) 式中：Te为电磁转矩；np为极对数。
其动力学方程为：
$$ T_{e}-T_{f}-T_{L}=J \frac{\mathrm{d} \omega_{m}}{\mathrm{~d} t} $$ (11) 式中：Tf为摩擦转矩；TL为气动负载转矩，可通过式(7)近似算得；J为电机转子的转动惯量；ωm为电机机械角速度。
本文采用连续可微的摩擦模型[18]：
$$ T_{f}\left(\omega_{m}\right)=\beta_{1}\left[\tanh \left(\beta_{2} \omega_{m}\right)-\tanh \left(\beta_{3} \omega_{m}\right)\right]+\\ \qquad\qquad \beta_{4} \tanh \left(\beta_{5} \omega_{m}\right)+\beta_{6} \omega_{m} $$ (12) 式中β1~β6为正实数。等号右边第1项代表Stribeck效应，第2项代表库伦摩擦，第3项代表粘滞摩擦。
式(5)~(12)给出了翼型变形系统的控制模型，但此模型中为了得到变形负载，假设各变形负载相互解耦。为了满足负载相互解耦的条件，需要对各变形装置进行协同控制，以保证变形过程中的过渡翼型恰好就是气动负载拟合采样点处的翼型。
2.2 翼型变形协同控制
机翼变形需采用协同控制主要基于2个方面的考虑。1)各变形装置协同动作保证在变形过程中翼面平滑，保证在变形过程中机翼的气动特性不出现突变，保证翼型变形准确、可靠; 2)各变形装置协同动作保证变形过程中的过渡翼型恰好是CFD仿真的“插值点”的翼型，进而使得各变形装置负载转矩的估计实现解耦。当然，对左侧机翼、右侧机翼进行变形同步控制还可以保证变形过程中左右翼始终保持对称。
交叉耦合同步的核心思想是通过构建交叉耦合偏差，使得交叉耦合偏差收敛于零时被控的各状态量实现同步。而使交叉耦合偏差收敛到零则是控制器的工作，即交叉耦合偏差生成器和控制器的设计是相对独立的。
用被控对象状态的加权平均构造交叉耦合偏差是一种常用的方法[19]。对于n个被控对象进行同步，第k个被控对象的交叉耦合偏差为：
$$ e_{k c c}=x_{k}-\bar{x}_{k} $$ (13) 式中：xk为对象k的状态；xk为对象k的状态和与对象k进行状态交互的对象的状态的加权平均。
与对象k进行状态交互的对象的集合，以及加权平均的权值都会影响xk的具体形式。对象k的状态，以及与对象k进行状态交互的对象的状态构成集合记为
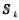
(14) 基于上述定义，xk满足：
$$ \bar{x}_{k}=\sum\limits_{x_{i} \in \mathbb{S} _{k}} w_{k, i} x_{i} $$ (15) 式中：wk, i为对象i的状态xi在构建对象k的交叉耦合偏差ekcc时的权重值，满足wk, i≠0和$\sum\limits_i$wk, i=1。
可证明按上述方法生成的交叉耦合偏差对于n个同步对象的初始状态和期望状态的差值相等，即：
$$ x_{k d}-x_{k 0}=x_{j d}-x_{j 0}, k, j \in\{1, 2, \cdots, n\} $$ (16) 的情形能够实现同步。为了简便，取权值为：
(17) 式中
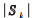
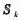
对翼型变形同步，不满足式(16)。各变形装置的初始状态和期望状态的差值满足比例关系：
$$ x_{i d}-x_{i 0}=k_{i j}\left(x_{j d}-x_{j 0}\right), i, j \in\{1, 2, \cdots, n\} $$ (18) 对于此情况，本文提出一种通用的交叉耦合偏差生成方法用于多个被控对象的分布式同步控制。
对n个被控对象的状态x1, x2，…, xn进行同步，构建n个交叉耦合偏差ecc=We，其中W∈$\mathbb{R}^{n \times n}$为待设计的权重矩阵，零元素和非零元素的位置须满足通信拓扑的约束，e=x-xd，x=[x1 x2…xn]T∈$\mathbb{R}^{n}$，xd为期望状态构成的列向量，若权重矩阵W的最简行阶梯形为：
$$ \boldsymbol{Q}=\left[\begin{array}{cccc} 1 & \cdots & 0 & -k_{1} \\ \vdots & & \vdots & \vdots \\ 0 & \cdots & 1 & -k_{n-1} \\ 0 & \cdots & 0 & 0 \end{array}\right], k_{i}>0, $$ $$ i=1, 2, \cdots, n-1 \text {, } $$ 且设计n个分布式控制器使交叉耦合偏差ecc收敛到零，则该控制器可实现被控对象状态的同步，即状态满足(x1-x1d): …: (xn-xnd)=k1: …: …: kn-1: 1。
根据Q的形式可知，对于n被控对象进行同步控制，设计n个分布式同步控制器，若至多有1个控制器发生故障，仍然能够实现所有被控对象状态同步。即交叉耦合同步控制本身具有冗余特性。
权重矩阵W的配置步骤为：
1) 按照初始状态和期望状态的差值相等配置权重系数矩阵，记为W0；
2) 根据初始状态与期望状态的差值的比例关系(x1d-x10): …: (xnd-xn0)=k1: …: kn-1: 1，构造对角矩阵V=diag(v1, v2, vn)，满足vv=viki, i=1, 2, …, n-1且vi>0, i=1, 2, …, n；
3) 待求的权重系数矩阵为W=W0V。
按上述方法配置的权重系数矩阵W的最简行阶梯形满足要求，且矩阵W满足信息交互拓扑对应的零元、非零元约束。考虑到实际应用中矩阵W的元素位数有限，在构造过程中需要对各被控对象初始状态与期望状态的差值的比值进行截断。
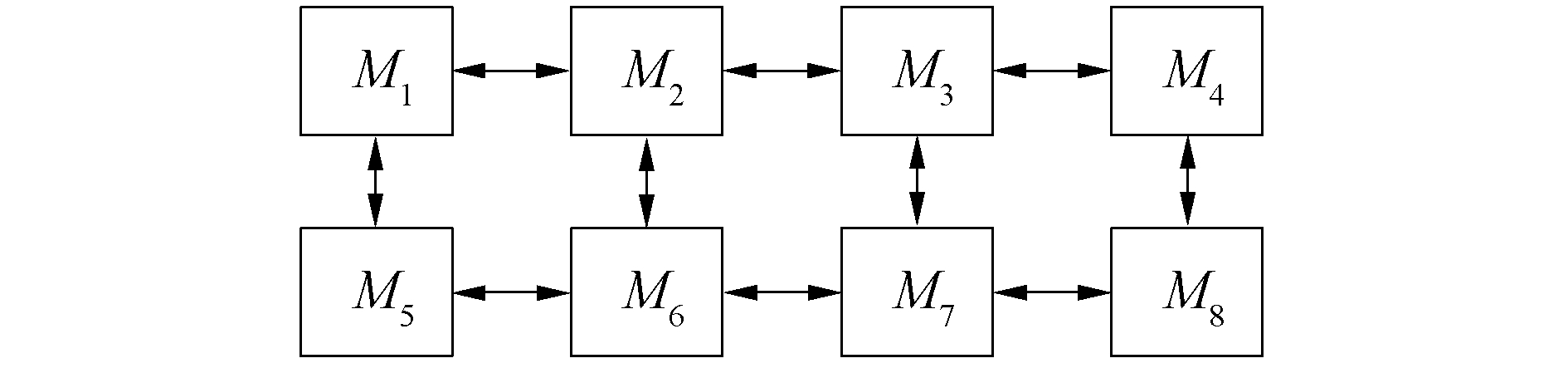
针对图 3中的变形装置阵列，本文采用四边形拓扑进行变形装置间的状态信息交互，对应的状态交互拓扑如图 4。图 4中箭头代表状态信息的流向。按上述步骤矩阵W0为：
$$ \boldsymbol{W}_{0}=\frac{1}{12}\left[\begin{array}{cccccccc} 8 & -4 & 0 & 0 & -4 & 0 & 0 & 0 \\ -3 & 9 & -3 & 0 & 0 & -3 & 0 & 0 \\ 0 & -3 & 9 & -3 & 0 & 0 & -3 & 0 \\ 0 & 0 & -4 & 8 & 0 & 0 & 0 & -4 \\ -4 & 0 & 0 & 0 & 8 & -4 & 0 & 0 \\ 0 & -3 & 0 & 0 & -3 & 9 & -3 & 0 \\ 0 & 0 & -3 & 0 & 0 & -3 & 9 & -3 \\ 0 & 0 & 0 & -4 & 0 & 0 & -4 & 8 \end{array}\right] $$ 
图 4 变形装置交互的拓扑Fig. 4 Topology of morphing devices interaction下载:
全尺寸图片
在设计同步控制器时，可采用不同的状态信息生成交叉耦合偏差，生成同步控制量也可以施加到控制环路的不同部位。对于常见的机电系统，构建交叉耦合偏差可以提取位置、速度信息，生成的同步控制量可以施加到电机控制的电流环、速度环和位置环，不同方案的实现难点和同步效果有所差异。
针对翼型变形控制模型，更关注各变形装置位置的同步，并且由于提取速度需进行微分易受噪声影响，因此选择位置状态生成交叉耦合偏差。系统的控制框图如图 5所示，同步控制器采用PID控制器，综合考虑动态响应，以及抑制启动延时对同步性能的影响，将同步控制量施加到位置环，用于对指令信号进行微小修正。
图 5 交叉耦合同步控制系统Fig. 5 Cross-coupled synchronous control system下载:
全尺寸图片
3. 仿真校验
3.1 仿真条件
针对4×2的变形装置阵列，考虑永磁同步电机的具有分布式的参数，即8个变形装置的电机电磁参数、转动惯量、摩擦参数等均不相同。假设上述参数在某一标称值附近符合正态分布，参数均值近似为标称值，方差为标称值的5%，标称参数见表 2。
表 2 标称值参数Table 2 Nominal value of parameters参数名称 标称值 定子电阻R/Ω 2.875 直轴/交轴电感Ld=Lq/H 8.5×10-3 永磁体磁链ψf/Wb 0.154 37 转子转动惯量J/(kg·m2) 1.7×10-5 摩擦模型的系数β1/(N·m) 0.1 摩擦模型的系数β2 100 摩擦模型的系数β3 5 摩擦模型的系数β4/(N·m) 0.08 摩擦模型的系数β5 100 摩擦模型的系数β6/(N·m·s/rad) 1.5×10-4 按照第1节中的翼面变形定义，结合翼型数据，可以确定8个变形装置处的位移指令。本文以1.2节的翼型1和翼型2作为2种期望的翼型，提取8个变形装置处的期望位置，结果如表 3。
表 3 变形装置在各翼型下的位置Table 3 The position of the morphing device under each airfoil位移指令/m 参考翼型 翼型1 翼型2 变形装置1 0.162 264 0.132 941 0.191 588 变形装置2 0.211 271 0.152 858 0.269 883 变形装置3 0.230 746 0.165 831 0.295 661 变形装置4 0.193 701 0.166 855 0.220 546 变形装置5 0.153 943 0.126 124 0.181 763 变形装置6 0.200 531 0.145 019 0.256 043 变形装置7 0.218 913 0.157 327 0.280 499 变形装置8 0.183 767 0.158 298 0.209 236 根据变形翼型间的位移比例关系，构造生成交叉耦合偏差的权重系数矩阵W，结果为：
$$ \boldsymbol{W}=\left[\begin{array}{cccccccc} 6.948\;536 & -1.741\;084 & 0 & 0 & -3.662\;100 & 0 & 0 & 0 \\ -2.605\;701 & 3.917\;439 & -1.177\;032 & 0 & 0 & -1.376\;406 & 0 & 0 \\ 0 & -1.305\;813 & 3.531\;096 & -2.846\;121 & 0 & 0 & -1.240\;656 & 0 \\ 0 & 0 & -1.569\;376 & 7.589\;656 & 0 & 0 & 0 & -4 \\ -3.474\;268 & 0 & 0 & 0 & 7.324\;200 & -1.835\;208 & 0 & 0 \\ 0 & -1.305\;813 & 0 & 0 & -2.746\;575 & 4.129\;218 & -1.240\;656 & 0 \\ 0 & 0 & -1.177\;032 & 0 & 0 & -1.376\;406 & 3.721\;968 & -3 \\ 0 & 0 & 0 & -3.794\;828 & 0 & 0 & -1.654\;208 & 8 \end{array}\right] $$ 8个变形装置的电流环、速度环、位置环PID控制器采用相同参数，分布式同步PID控制器采用不同参数。为了简化同步控制器的参数整定，设置变形装置8的同步控制器参数作为参照，其他同步控制器的参数与之满足比例关系k1: …: kn-1: 1。控制器参数见表 4。
表 4 控制器参数Table 4 Controller parameters控制器参数 Kp Ki Kd 输出限制 电流环 30 10 000 0 ±300 速度环 0.003 0.03 0 ±12 位置环 5 000 0 50 ±6 000 同步控制(变形装置8) 0.1 100 0 ±0.2 数值仿真条件设置如下：初始翼型为参考翼型，在t=0.1 s时，开始向翼型2变形；在t=3 s时，开始由翼型2向翼型1变形；在t= 7 s时，开始由翼型1向参考翼型变形。按变形装置8的电机速度1 000 r/s，其余变形装置的电机速度与之满足比例关系k1: …: kn-1: 1，生成梯形位置指令。设置传动增益常数G的数值为1×10-3/π，等效力臂Kft的数值为0.001，仿真步长1×10-4 s，仿真总时长10 s。
设置了2组仿真试验。仿真1：在变形装置2的电机上施加一个幅值为0.5 N·m，周期为1 s，初始相位为0的方波信号，用于模拟周期性干扰。仿真2：施加与工况1相同的外部干扰，且将变形装置1、7的电机位置输入指令信号分别滞后和超前100 ms，用于模拟电机的启动延时。
3.2 仿真结果及分析
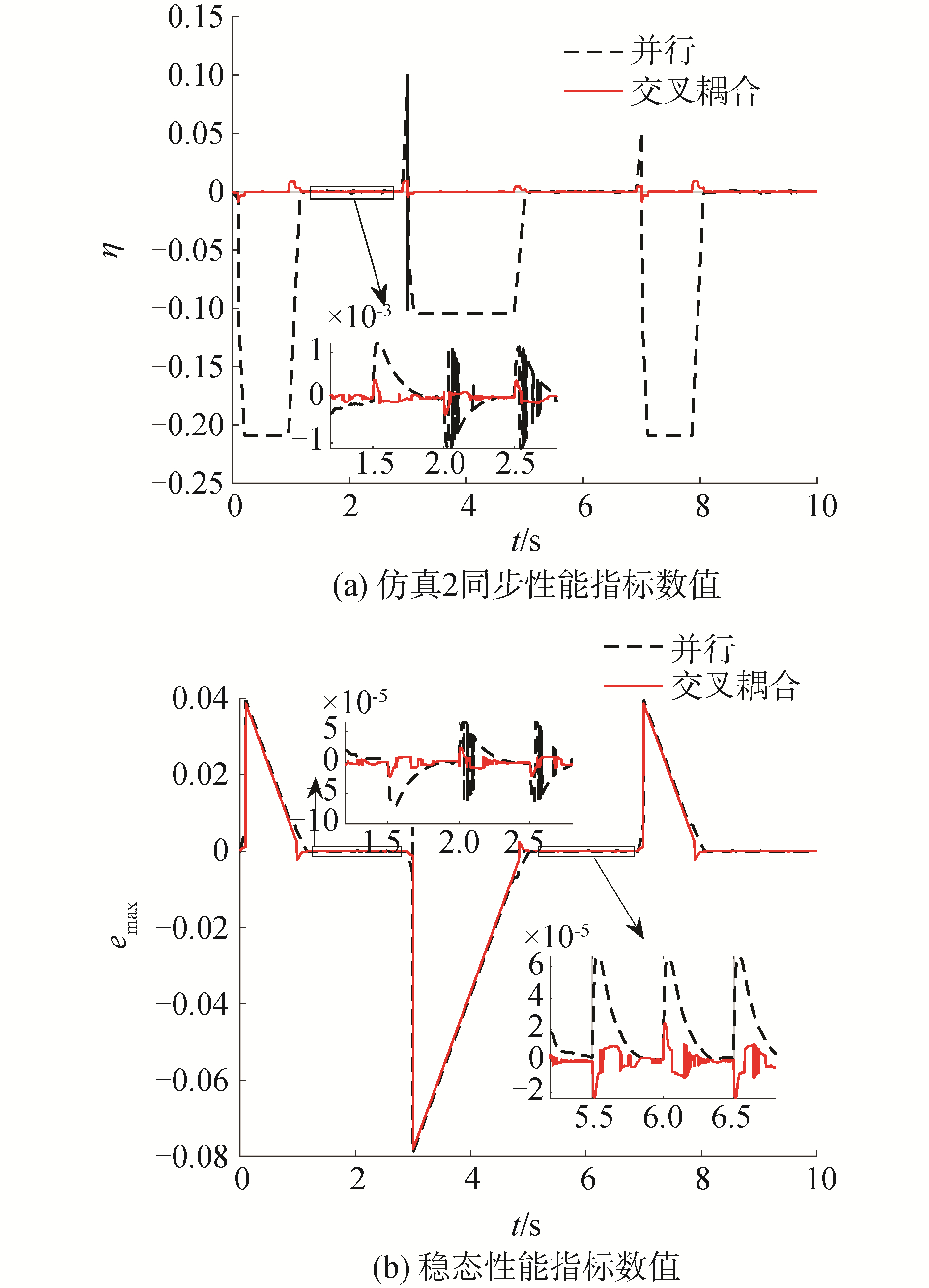
由于变形系统由多个变形装置组成，直接给出8个变形装置的位置曲线无法直接反映性能的差异，且图线太多过于杂乱。为了解决这一问题，引入各变形装置的实时位移占期望位移的百分比的最大差值η作为同步性能的评价指标，引入各变形装置位移误差的最大值emax作为稳态性能的评价指标。η和emax分别体现了8个变形装置间同步差别最大，稳态误差最大的数值，具体定义为：
$$ \eta=\max\limits_{k} \eta_{k}, \quad \eta_{k}=\frac{x_{k}-x_{k 0}}{x_{k d}-x_{k 0}} $$ (19) $$ e_{\max }=\max\limits_{k}\left(x_{k}-x_{k 0}\right) $$ (20) 式中：k代表变形装置k，1≤k≤8且k∈$\mathbb{N}$；xk为变形装置k的实时位置；xkd为变形装置k当前变形任务的期望位置；xk0为变形装置k当前变形任务的初始位置。η单位为1，emax单位为m。
针对仿真1和仿真2，分别进行了并行控制和交叉耦合同步控制，对比了2组试验下2种控制方式的稳态性能和同步性能，仿真结果如图 6~7。
图 6 仿真1性能对比Fig. 6 Simulation 1 performance comparison下载:
全尺寸图片
图 7 仿真2性能对比Fig. 7 Simulation 2 performance comparison下载:
全尺寸图片
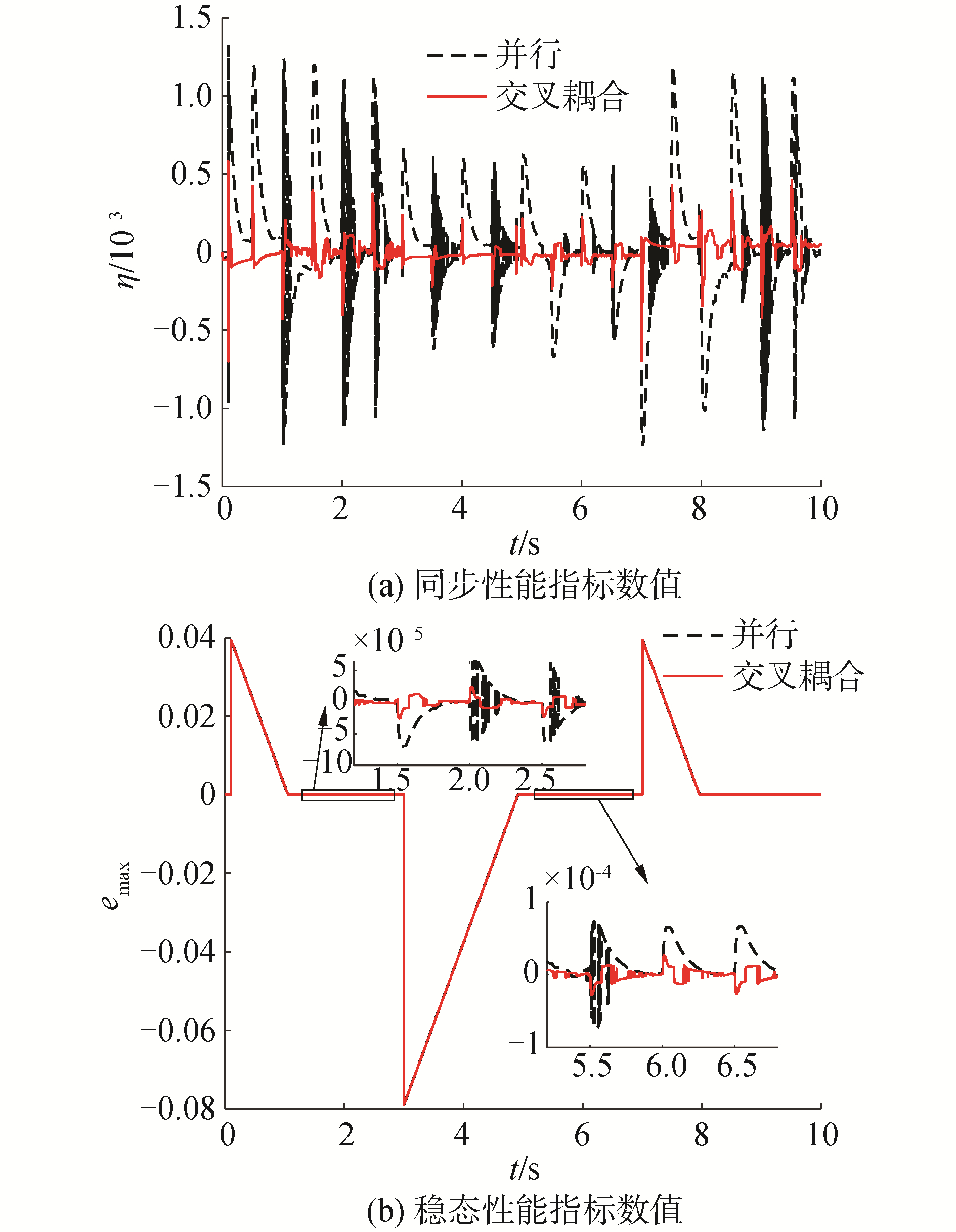
存在外部干扰、没有启动延迟时，仿真结果如图 6，由图 6可知，并行控制和交叉耦合分布式同步控制都能很好地抑制外部干扰，并且能够保证变形同步。但交叉耦合同步控制较并行控制，同步性能提升了56%以上，稳态性能提升了62%以上。
存在外部干扰和启动延迟时，仿真结果如图 7，由图 7可知，并行控制对启动延时非常敏感，同步性能很差。相比之下，交叉耦合分布式同步控制能够很好地抑制启动延时对同步性能的影响。后者的同步性能较前者提升12倍以上。两者控制器的变形量最终都能收敛到期望值，但交叉耦合同步控制的稳态性能较并行控制提升了64%以上。
仿真结果表明本文提出的交叉耦合分布式同步控制能够很好地抑制外部干扰、启动延时对同步性能、稳态性能的影响，对外部干扰、启动延时具有良好的鲁棒性，并且，同步性能和稳态性能较并行控制均有显著提升。
4. 结论
1) 提出的变翼型变形策略，保证变形过程中翼面始终光滑，且各变形点的变形量比值恒定，为翼型变形同步控制器的设计提供了极大的便利。
2) 针对多个被控对象的同步控制问题，提出了一种通用的交叉耦合同步偏差生成方法，该方法将同步问题从同步控制中分离出来，使得同步控制器的设计变得简单，且便于实现分布式控制。
3) 通过2组仿真实例验证了该方法的有效性和鲁棒性，本方法相比于并行控制，同步性能和稳态性能均提升一倍以上。
-
图 1 可变形机翼飞行器系统控制架构
Fig. 1 Variable-wing aircraft system control architecture
下载:
全尺寸图片
图 2 翼型变形对气动参数的影响
Fig. 2 Influence of airfoil morphing on aerodynamic parameters
下载:
全尺寸图片
图 3 翼型变形原理
Fig. 3 Principle of airfoil morphing
下载:
全尺寸图片
图 4 变形装置交互的拓扑
Fig. 4 Topology of morphing devices interaction
下载:
全尺寸图片
图 5 交叉耦合同步控制系统
Fig. 5 Cross-coupled synchronous control system
下载:
全尺寸图片
图 6 仿真1性能对比
Fig. 6 Simulation 1 performance comparison
下载:
全尺寸图片
图 7 仿真2性能对比
Fig. 7 Simulation 2 performance comparison
下载:
全尺寸图片
表 1 变形装置等效负载力拟合结果
Table 1 Fitting results of equivalent load force
序号 拟合系数
ak拟合系数
bk拟合误差的方差 相关系数 1 -2 706.153 1 425.201 8.660 -0.986 843 2 4 015.458 69.918 1.938 0.999 923 3 5 229.864 -312.477 3.788 0.999 860 4 3 464.761 128.100 8.827 0.990 002 5 -2 604.038 1 576.647 12.010 -0.970 394 6 5 381.872 -31.878 4.852 0.999 703 7 6 410.688 -390.128 7.766 0.999 564 8 3 643.843 256.557 4.878 0.996 901 表 2 标称值参数
Table 2 Nominal value of parameters
参数名称 标称值 定子电阻R/Ω 2.875 直轴/交轴电感Ld=Lq/H 8.5×10-3 永磁体磁链ψf/Wb 0.154 37 转子转动惯量J/(kg·m2) 1.7×10-5 摩擦模型的系数β1/(N·m) 0.1 摩擦模型的系数β2 100 摩擦模型的系数β3 5 摩擦模型的系数β4/(N·m) 0.08 摩擦模型的系数β5 100 摩擦模型的系数β6/(N·m·s/rad) 1.5×10-4 表 3 变形装置在各翼型下的位置
Table 3 The position of the morphing device under each airfoil
位移指令/m 参考翼型 翼型1 翼型2 变形装置1 0.162 264 0.132 941 0.191 588 变形装置2 0.211 271 0.152 858 0.269 883 变形装置3 0.230 746 0.165 831 0.295 661 变形装置4 0.193 701 0.166 855 0.220 546 变形装置5 0.153 943 0.126 124 0.181 763 变形装置6 0.200 531 0.145 019 0.256 043 变形装置7 0.218 913 0.157 327 0.280 499 变形装置8 0.183 767 0.158 298 0.209 236 表 4 控制器参数
Table 4 Controller parameters
控制器参数 Kp Ki Kd 输出限制 电流环 30 10 000 0 ±300 速度环 0.003 0.03 0 ±12 位置环 5 000 0 50 ±6 000 同步控制(变形装置8) 0.1 100 0 ±0.2 -
[1] LI Daochun, ZHAO Shiwei, RONCH A D, et al. A review of modelling and analysis of morphing wings[J]. Progress in aerospace sciences, 2018, 100: 46-62. doi: 10.1016/j.paerosci.2018.06.002 [2] CONCILIO A, DIMINO I, LECCE L, et al. Morphing wing technologies: large commercial aircraft and civil helicopters[M]. [S. l. ], Butterworth-Heinemann, 2018. [3] AMEDURI S, CONCILIO A. Morphing wings review: aims, challenges, and current open issues of a technology[J]. Proceedings of the institution of mechanical engineers, Part C: Journal of mechanical engineering science, 2020, 0(0). DOI: 10.1177/0954406220944423. [4] THILL C, ETCHES J, BOND I, et al. Morphing skins[J]. The aeronautical Journal, 2008, 112(1129): 117-139. doi: 10.1017/S0001924000002062 [5] SUN Jian, GUAN Qinghua, LIU Yanju, et al. Morphing aircraft based on smart materials and structures: a state-of-the-art review[J]. Journal of intelligent material systems and structures, 2016, 27(17): 2289-2312. doi: 10.1177/1045389X16629569 [6] BARBARINO S, SAAVEDRA FLORES E I, AJAJ R M, et al. A review on shape memory alloys with applications to morphing aircraft[J]. Smart materials and structures, 2014, 23(6): 063001. doi: 10.1088/0964-1726/23/6/063001 [7] DAYYANI I, SHAW A D, SAAVEDRA F E I, et al. The mechanics of composite corrugated structures: a review with applications in morphing aircraft[J]. Composite structures, 2015, 133: 358-380. doi: 10.1016/j.compstruct.2015.07.099 [8] HUANG Yongan, ZHU Chen, XIONG Wennan, et al. Flexible smart sensing skin for "Fly-by-Feel" morphing aircraft[J]. Science China technological sciences, 2022, 65(1): 1-29. doi: 10.1007/s11431-020-1793-0 [9] BARBARINO S, BILGEN O, AJAJ R M, et al. A review of morphing aircraft[J]. Journal of intelligent material systems and structures, 2011, 22(9): 823-877. doi: 10.1177/1045389X11414084 [10] 陆宇平, 何真. 变体飞行器控制系统综述[J]. 航空学报, 2009, 30(10): 1906-1911. doi: 10.3321/j.issn:1000-6893.2009.10.019 LU Yuping, HE Zhen. A survey of morphing aircraft control systems[J]. Acta aeronautica et astronautica sinica, 2009, 30(10): 1906-1911. doi: 10.3321/j.issn:1000-6893.2009.10.019 [11] KIM S H, LEE Hanna, KIM Y. Continuous-time deterministic policy gradient-based controller for morphing aircraft without exploration[C]//202028th mediterranean conference on control and automation (MED). Piscataway, NJ: IEEE, 2020: 224-229. [12] LEE J, KIM S H, JUNG S, et al. Sliding mode control design for a multidimensional morphing UAV[C]//2018 European control conference (ECC). Piscataway, NJ: IEEE, 2018: 2356-2361. [13] 殷明, 陆宇平, 何真. 变体飞行器LPV建模与鲁棒增益调度控制[J]. 南京航空航天大学学报, 2013, 45(2): 202-208. https://www.cnki.com.cn/Article/CJFDTOTAL-NJHK201302009.htm YIN Ming, LU Yuping, HE Zhen. LPV modeling and robust gain scheduling control of morphing aircraft[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(2): 202-208. https://www.cnki.com.cn/Article/CJFDTOTAL-NJHK201302009.htm [14] 江未来, 董朝阳, 王通, 等. 变体飞行器平滑切换LPV鲁棒控制[J]. 控制与决策, 2016, 31(1): 66-72. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201601009.htm JIANG Weilai, DONG Chaoyang, WANG Tong, et al. Smooth switching LPV robust control for morphing aircraft[J]. Control and decision, 2016, 31(1): 66-72. https://www.cnki.com.cn/Article/CJFDTOTAL-KZYC201601009.htm [15] YAN Binbin, LI Yong, DAI Pei, et al. Aerodynamic analysis, dynamic modeling, and control of a morphing aircraft[J]. Journal of aerospace engineering, 2019, 32(5): 04019058. doi: 10.1061/(ASCE)AS.1943-5525.0001047 [16] 吴俊. 变形翼分布式协同控制技术研究[D]. 南京: 南京航空航天大学, 2012. WU Jun. Research on distributed cooperative control technology of morphing wings[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. [17] POPOV A V, GRIGORIE L T, BOTEZ R, et al. Closed-loop control validation of a morphing wing using wind tunnel tests[J]. Journal of aircraft, 2010, 47(4): 1309-1317. [18] MAKKAR C, HU G, SAWYER W G, et al. Lyapunov-based tracking control in the presence of uncertain nonlinear parameterizable friction[J]. IEEE transactions on automatic control, 2007, 52(10): 1988-1994. [19] 谢炜. 基于BP神经网络PID算法的多电机同步控制研究[D]. 沈阳: 沈阳工业大学, 2017. XIE Wei. Research on control system of multi-motor based on BP neural network with PID algorithm[D]. Shenyang: Shenyang University of Technology, 2017.
