Investigation of the problem of internal waves generated by the movement of a seafloor object
-
摘要: 为研究物体在海底运动产生大幅内孤立波问题，本文基于商业软件STAR-CCM+，选用无粘模型，求解欧拉方程，采用流体体积法监测内波界面，对网格、时间步长开展收敛性分析，得到STAR-CCM+计算的内波波面空间分布收敛结果与全非线性势流模型结果高度吻合。研究了物体形状对于生成内波的影响，对比了上下层液体密度比分别为0.787和0.95时，刚盖假设与自由表面这2种不同边界条件下的内波波面空间分布结果，研究表明: 当上下层液体的密度比不接近1时，必须考虑自由面效应对内波波幅和波速的影响。Abstract: In order to study the problem of large-amplitude internal solitary waves generated by objects moving on the ocean floor, this paper assesses an inviscid model and solves the Euler equation using the commercial software STAR-CCM+. The volume of fluid method is used to monitor the internal wave, and convergence analysis is conducted on the grid and time step. Convergence results of the spatial distribution of the internal wave surface calculated by STAR-CCM+ are in agreement with those of the fully nonlinear potential flow model. The influence of the object's shape on the generation of internal waves is then investigated. Finally, the spatial distribution results of internal solitary waves under two different boundary conditions, namely, the rigid cover assumption and the free surface, are compared when the density ratio of the upper and lower layers is 0.787 and 0.95, respectively. The influence of the free surface effect on the internal wave amplitude and speed must be considered when the density ratio of the upper and lower liquids is not close to 1.
-
海洋内波是指在海水稳定层化的海洋中产生的、最大振幅出现在海洋内部的波动。海洋内波对水下结构物的安全存在巨大威胁，如我国372号潜艇于2014年在远航期间因为遭遇内波而意外下沉，险些造成事故。因此，对内波的生成及其特性进行研究具有重要的意义。
对于物体运动激发内波问题，国内外学者都做了很多研究，可以分为物理实验和数值模拟2个方面。
实验室中的内波模拟以其成本低、可重复性强、容易实现以及容易获得内波相关特征参数的特性受到了更多研究人员的青睐。Schooley等[1]首次实现了关于内波的实验，该实验是针对弱线性分层流体中自驱动物体运动产生的紊流尾迹的研究。Arntsen[2]在分层实验水槽中系统全面地进行了分层流体中圆柱绕流实验，得到不同密度比、不同深度、不同Froude数下圆柱的阻力系数以及升力系数，以及产生的内界面波波高和波长的无量纲数值。马晖扬等[3]通过物理实验，研究了球体在密度突跃层附近运动时导致的自由面的特定变形，讨论了物体的位置和运动速度等因素对波形形态的影响。李万鹏等[4]对分层流体中螺旋桨效应激发内波进行了实验分析。陈科等[5]对1个球体和2个不同长径比细长体在拖曳运动下激发内波的时空特性进行了系列实验。高德宝等[6]在大型分层流水池中开展了拖曳体内波尾迹水下/水面特征试验研究，釆用电导率仪阵列测量了水下波高场及其随时间变化，获取了内波诱导的水面流场，并对内波尾迹水下/水面特征的相关性进行了分析。
相比于物理实验，基于内波的基本方程，利用计算机实现数值模拟内孤立波的生成、传播以及演化等相关特性更加容易。罗恒[7]进行了2层流体中水下运动潜艇激发表面尾迹及其与随机海面相互作用的数值模拟。段菲[8]研究了2层流体中SUBOFF潜艇在不同潜深位置处做非定常运动对内波波动过程的影响。黄璐[9]计算了SUBOFF潜艇在不同工况下近水面航行时产生的kelvin波，分析了不同海况以及姿态调整对自由表面波的影响。黄风来等[10-11]分析了连续密度分层流体中JoubertBB2潜艇在自由表面兴波过程。胡开业等[12]研究了在含跃层的分层流中，运动椭球的速度、潜深以及跃层强度对水面兴波的影响。何广华等[13-18]研究了SUBOFF潜艇在近水面航行时的兴波尾迹、兴波阻力、深水中航行的兴波尾迹、兴波阻力，以及附体对潜艇水动力特性的影响。除了定常运动，于祥等[19]研究了潜体的加减速运动对尾迹特性的影响。
然而，上述研究都没有考虑物体在海底运动时生成内波的情况。Grue等[20]对物体在海底运动激发内波问题进行了数值模拟，发现海底匀速运动的物体会在其前方激发内孤立波，随着运动时间增长，激发内孤立波的数目也变多。但是Grue等[20]没有开展物理实验，也没有经过其他数值模型的验证；此外，海底物体形状对内波产生的影响，尚未开展研究；Grue等[20]研究中上层液体顶部边界条件，用的刚盖近似来代替实际海洋中的这种自由面是否合理，有待进一步研究。针对上述的3个问题，本文给出了数值计算模型，介绍了控制方程、边界条件以及VOF方法监测内波界面和自由表面；给出了本文的数值计算结果以及分析。
1. 数值计算模型
本文基于商业软件STAR-CCM+，对海底物体运动引发内波进行数值模拟研究，所使用的控制方程、流体域体积(volume of fluid，VOF)方法处理内波界面及边界条件将依次进行介绍。
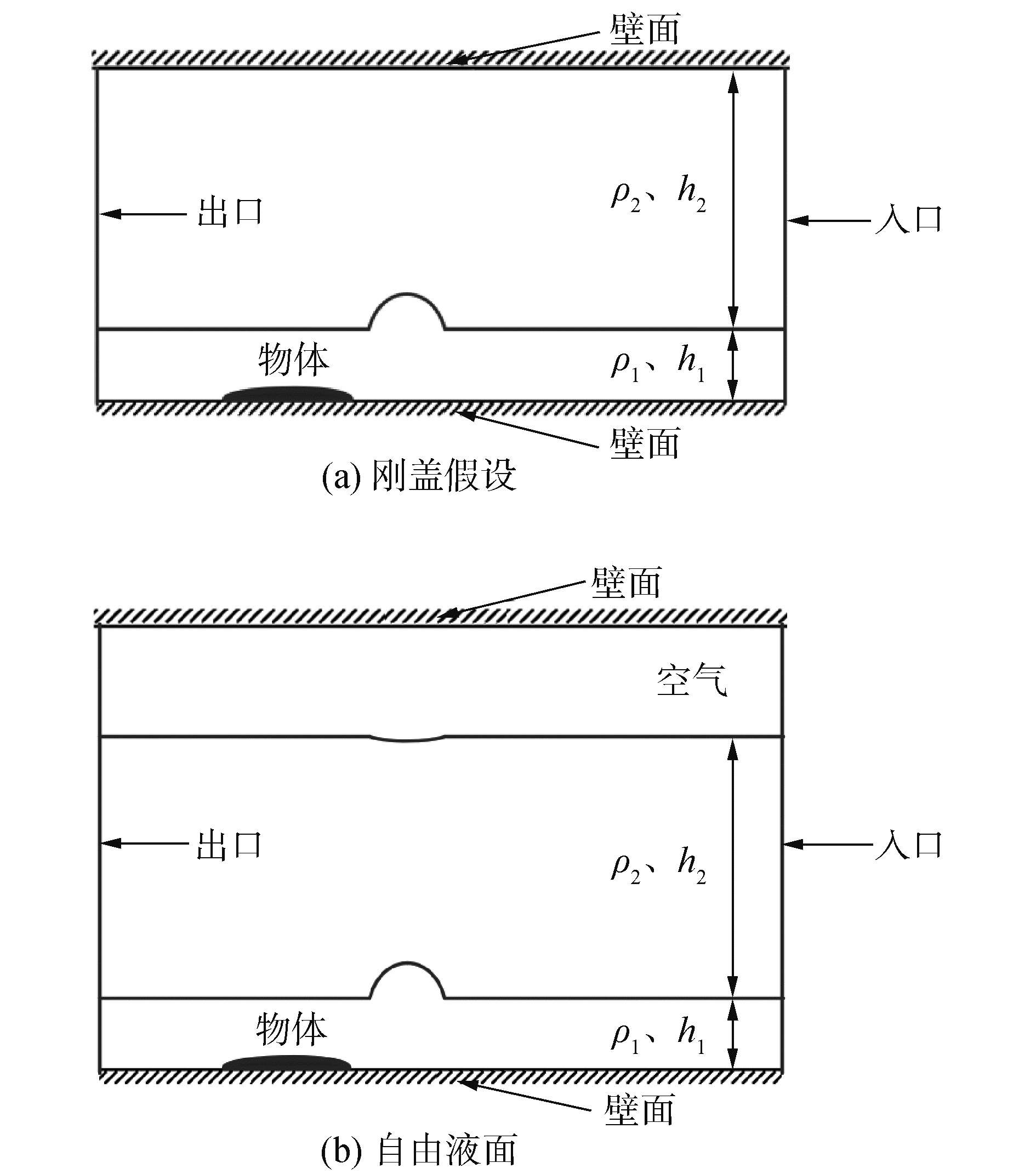
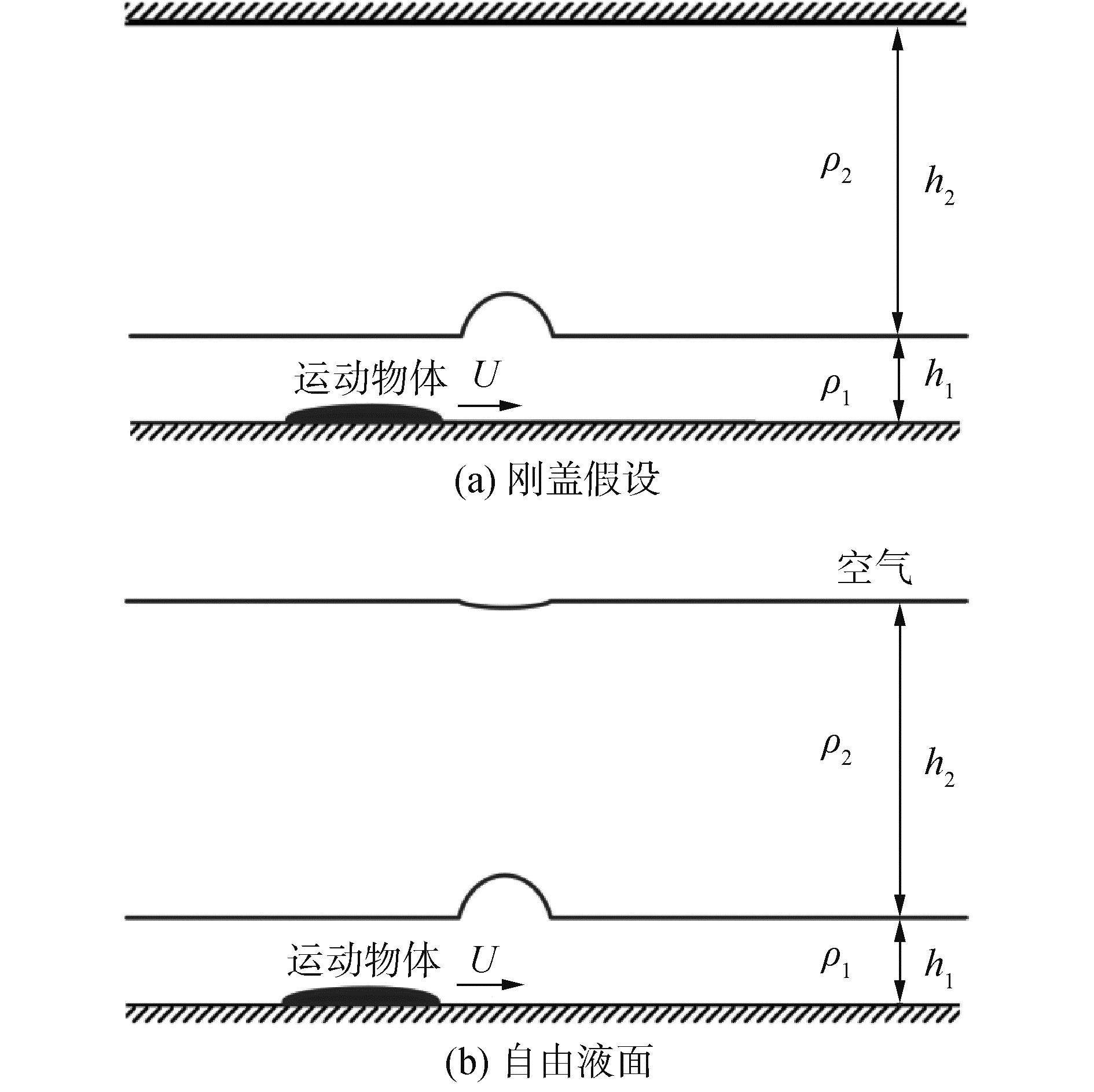
本文研究的是分层流体中一个物体在海底运动激发内孤立波问题(如图 1所示)，上层流体厚度较大为h2，下层流体厚度较小为h1，一个物体(以半椭圆形物体为例)以一定速度在海底运动，物体的运动会对内波界面形成扰动，最终生成内孤立波。当上层液体表面边界条件设置为壁面时是刚盖假设，当在上层液体上方加入一层空气是自由液面，示意图如图 1。
图 1 海底物体运动生成内波示意Fig. 1 Diagram of internal waves generated by the motion of seafloor objects
下载:
全尺寸图片
1.1 控制方程
STAR-CCM+可以选择层流、湍流、无粘的求解器，本文选择的是无粘求解器，对应的是求解无粘的欧拉方程，对应每一层流体其控制方程为：
$$ \frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=0 $$ (1) $$ \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+w \frac{\partial u}{\partial z}=-\frac{1}{\rho} \frac{\partial p}{\partial x} $$ (2) $$ \frac{\partial w}{\partial t}+u \frac{\partial w}{\partial x}+w \frac{\partial w}{\partial z}=-\frac{1}{\rho} \frac{\partial p}{\partial z}-g $$ (3) 式中：u、w分别代表水平、垂直方向的流体质点速度分量；p为压力；ρ为每一层流体的密度；g=9.81m/s2为重力加速度。
1.2 VOF方法处理内波界面
内孤立波形成于流体间的分层界面，可通过VOF法进行界面捕捉。VOF方法是通过计算每一个网格内每种流体所占的体积分数来处理界面问题，目前VOF在有限体积法中得到了广泛的应用[21]。
假设r(k)为第k相在某一单元网格所占的比例，根据质量守恒可得：
$$ \sum\limits_{k=1}^{n} r^{(k)}=1 $$ (4) 体积分数可以通过每一相的体积与总体积求出：
$$ r^{(k)}=V^{(k)} / \sum\limits_{k=1}^{n} V^{(k)} $$ (5) 本文中当上层液体顶部边界条件是自由表面时，有三相，k=1、2、3，通过分别监测空气、下层液体体积分数为50%的等值面的垂向位置，即可知道自由表面、内波界面的起伏。当上层液体顶部边界条件是刚盖假设时，同理可得内界面的起伏变化。
1.3 边界条件
对于数值模拟物体的运动兴波问题，可以采用重叠网格，使物体本身运动，但本文要模拟的时间较长并且物体是匀速平移运动，若采用这种方式，则需要较长的计算域，所以本文采用的是相对运动的方法，让物体本身不动，在速度入口处给定液体一个反向速度，从而可以减少计算域长度。
入口设置为速度入口边界条件，出口设置为自由流出口边界条件，底部和顶部以及物体表面都设置为壁面边界条件，当考虑自由面效应时，在上层液面上方会增加一层空气，从而使上层液体表面成为自由液面，如图 2所示。
图 2 边界条件设置示意Fig. 2 Schematic diagram of boundary condition setting下载:
全尺寸图片
2. 数值计算及分析
首先使用Grue等[20]的算例进行对比验证，然后研究了海底运动物体的形状对生成内孤立波的影响，最后分析了自由表面近似为刚盖假设的合理性。
2.1 半椭圆形物体在海底运动产生内孤立波
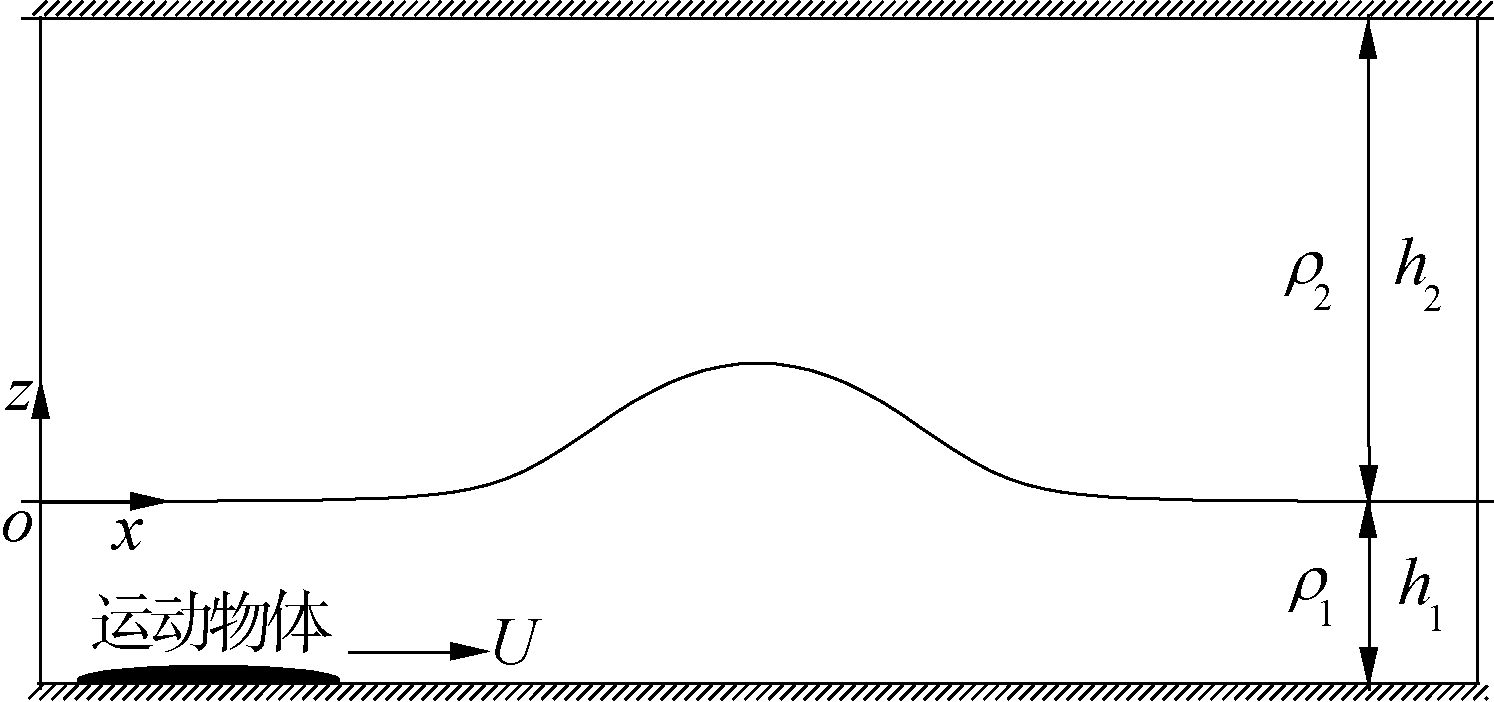
Grue等[20]考虑的是一个二维情况下2层流体中半椭圆形物体在海底运动生成内孤立波问题(如图 3所示)：上层流体厚度h2=0.12 m，密度ρ2=787.3 kg/m3，下层流体厚度h1=0.03 m，密度ρ1=1 000 kg/m3，上下层厚度比为h2/h1=4，密度比是ρ2/ρ1=0.787 3，一个半椭圆形物体以一定速度U在海底运动，物体的运动会对内波界面形成扰动，最终生成内孤立波。
图 3 海底物体运动生成内波示意Fig. 3 Diagram of internal waves generated by the motion of seafloor objects下载:
全尺寸图片
物体的运动速度是U=1.1c0，其中特征波速c0为：
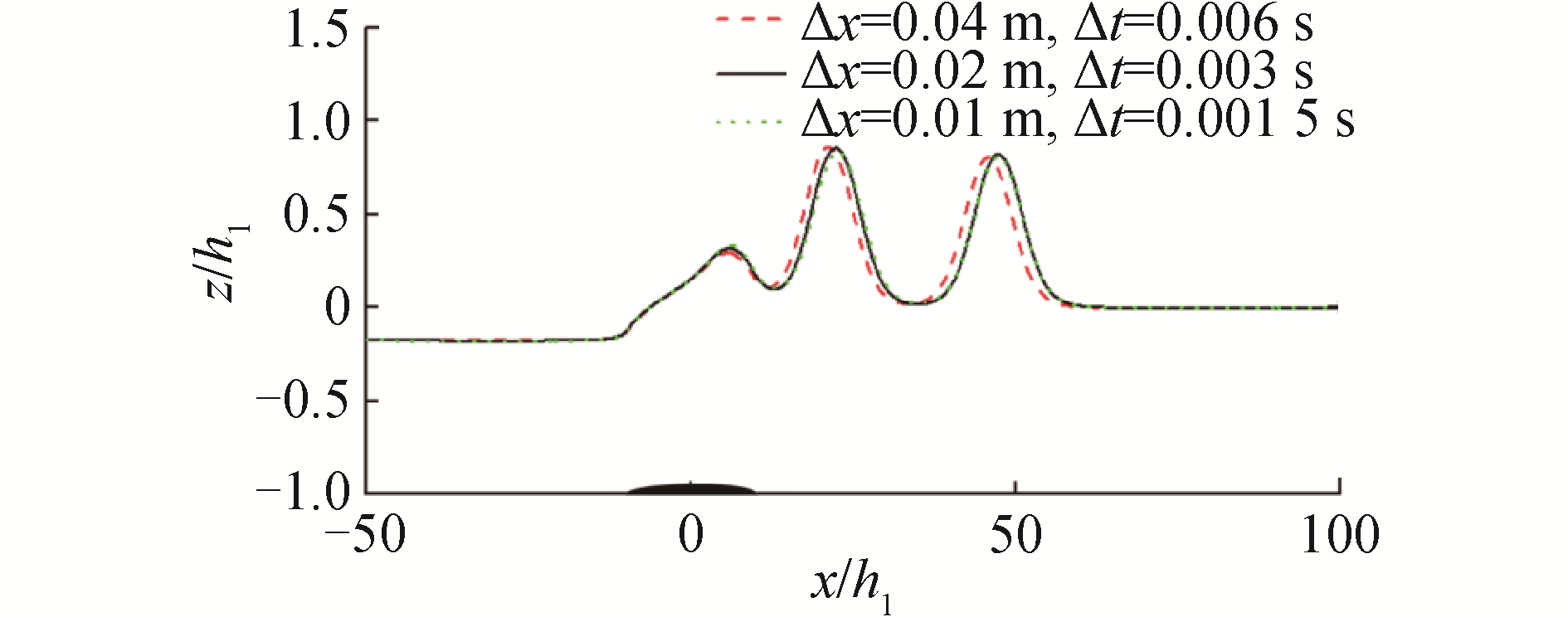
$$ c_{0}^{2}=\frac{g h_{1} h_{2}\left(\rho_{1}-\rho_{2}\right)}{\rho_{1} h_{2}+\rho_{2} h_{1}} $$ (6) 为了验证本文数值计算结果的准确性，首先需要进行数值结果的收敛性分析。本文进行了3种不同数值加密策略的收敛性分析，在基本网格尺寸的基础上再在物体以及内波界面附件进行网格加密，每种策略的网格加密方式都一样，表 1中Δx表示的是基本网格尺寸，Δt表示时间步长。
表 1 收敛性分析Table 1 Convergence analysis参数 数值策略1 数值策略2 数值策略3 Δx/m 0.04 0.02 0.01 Δt/s 0.006 0.003 0.001 5 t(g/h1)1/2=1 080时刻下, 3种数值加密策略的海底物体运动生成内孤立波的内波波面空间分布计算结果如图 4所示。从图 4可以看出，数值策略2和数值策略3得到的结果一样，而数值策略1得到的结果与其他数值策略的结果相差较大，说明本文采用的Δx=0.02 m，Δt=0.003 s可以得到收敛的数值结果。
图 4 内波波面空间分布结果收敛性分析Fig. 4 Convergence analysis of spatial distribution of internal wave surface下载:
全尺寸图片
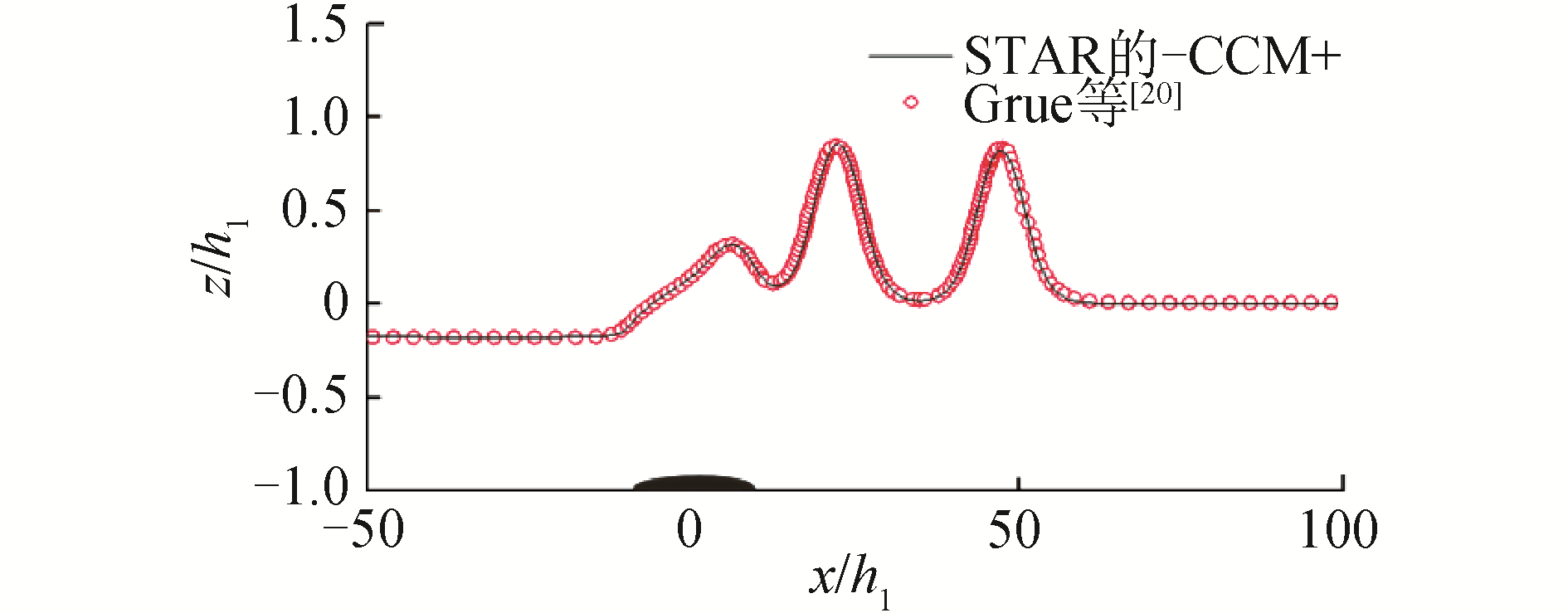
本文将t(g/h1)1/2=1 080时刻下, STAR-CCM+收敛的海底物体运动生成内孤立波的内波波面空间分布计算结果与Grue等[20]的结果进行比较，结果如图 5所示。
下载:
全尺寸图片
从图 5可以看出，本文使用STAR-CCM+计算得到的海底物体运动生成内孤立波的内波波面空间分布计算结果与Grue等[20]的结果吻合得很好，说明本文的数值计算结果是准确的，同时也验证了Grue等[20]的结果。
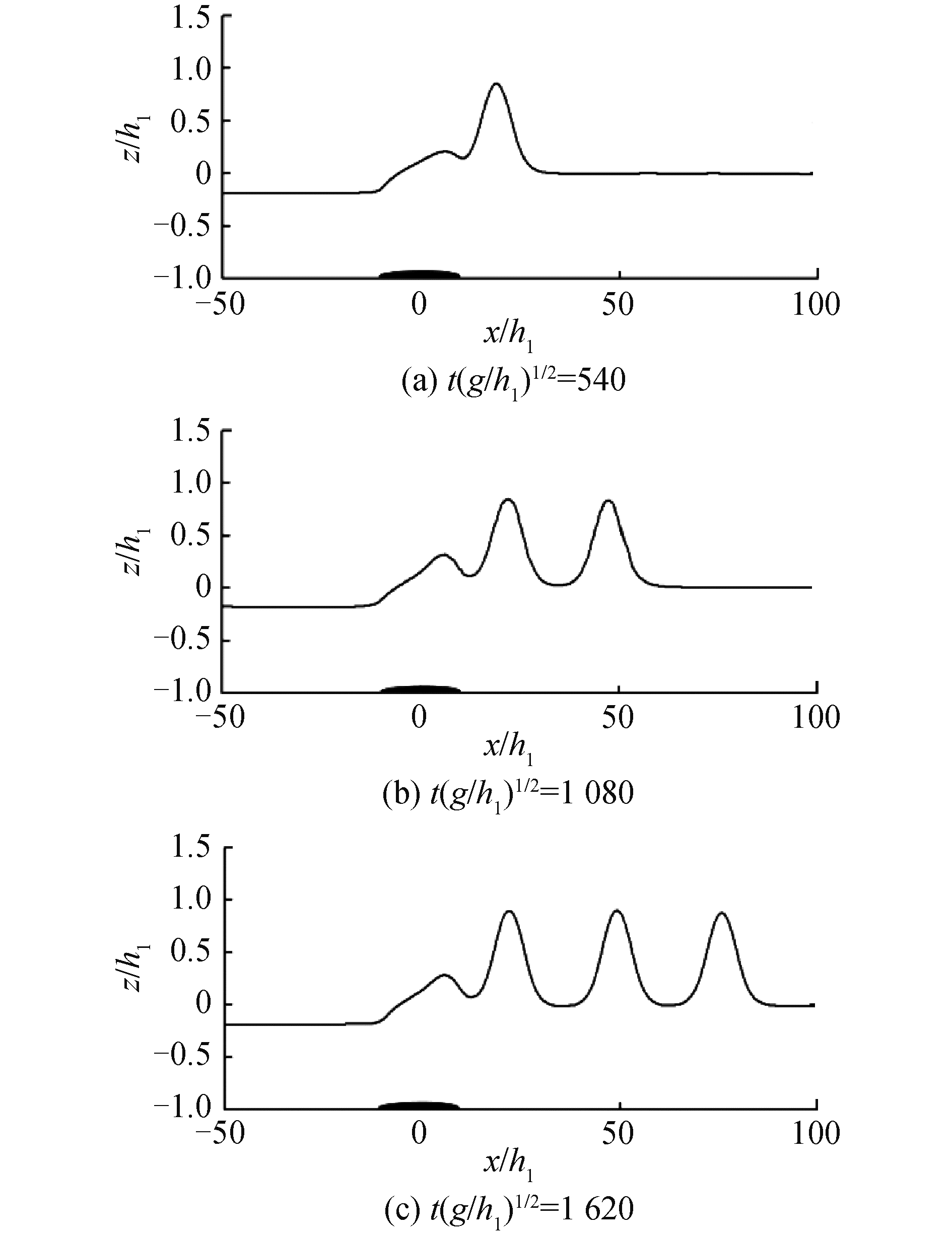
图 6展示了海底物体以一定速度运动，能够在内波界面激发内孤立波，随着时间的推移，产生的内孤立波的数量越来越多的过程。
图 6 不同时刻半椭圆形物体运动激发的内孤立波Fig. 6 Internal solitary waves excited by the motion of a semi-elliptic object at different time下载:
全尺寸图片
2.2 海底运动物体的形状对内波生成影响
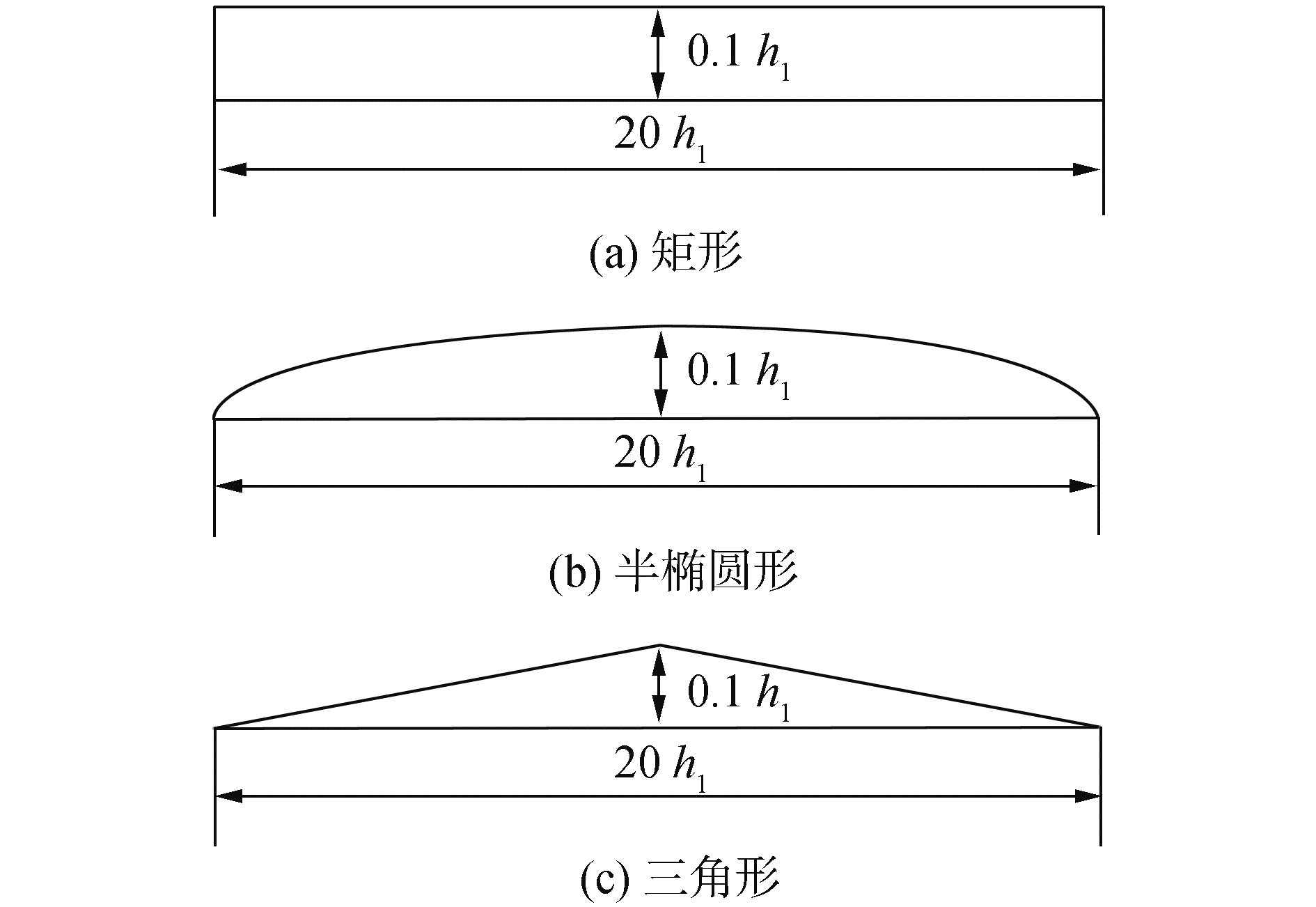
为考虑海底运动物体的形状对内孤立波生成的影响，基于Grue等[20]的算例参数，本文使用矩形、半椭圆形、三角形物体来进行海底物体运动生成内孤立波的数值模拟，各个形状的物体都是左右对称的且长和高的尺寸都一样，分别是20h1和0.1h1(h1为下层液体厚度，算例中的具体值是0.03 m)，如图 7所示。为了更直观地比较矩形、半椭圆形、三角形物体产生的内孤立波的波幅大小以及内孤立波数量关系，可见表 2。
图 7 运动物体的形状示意Fig. 7 A sketch of the shape of a moving object下载:
全尺寸图片
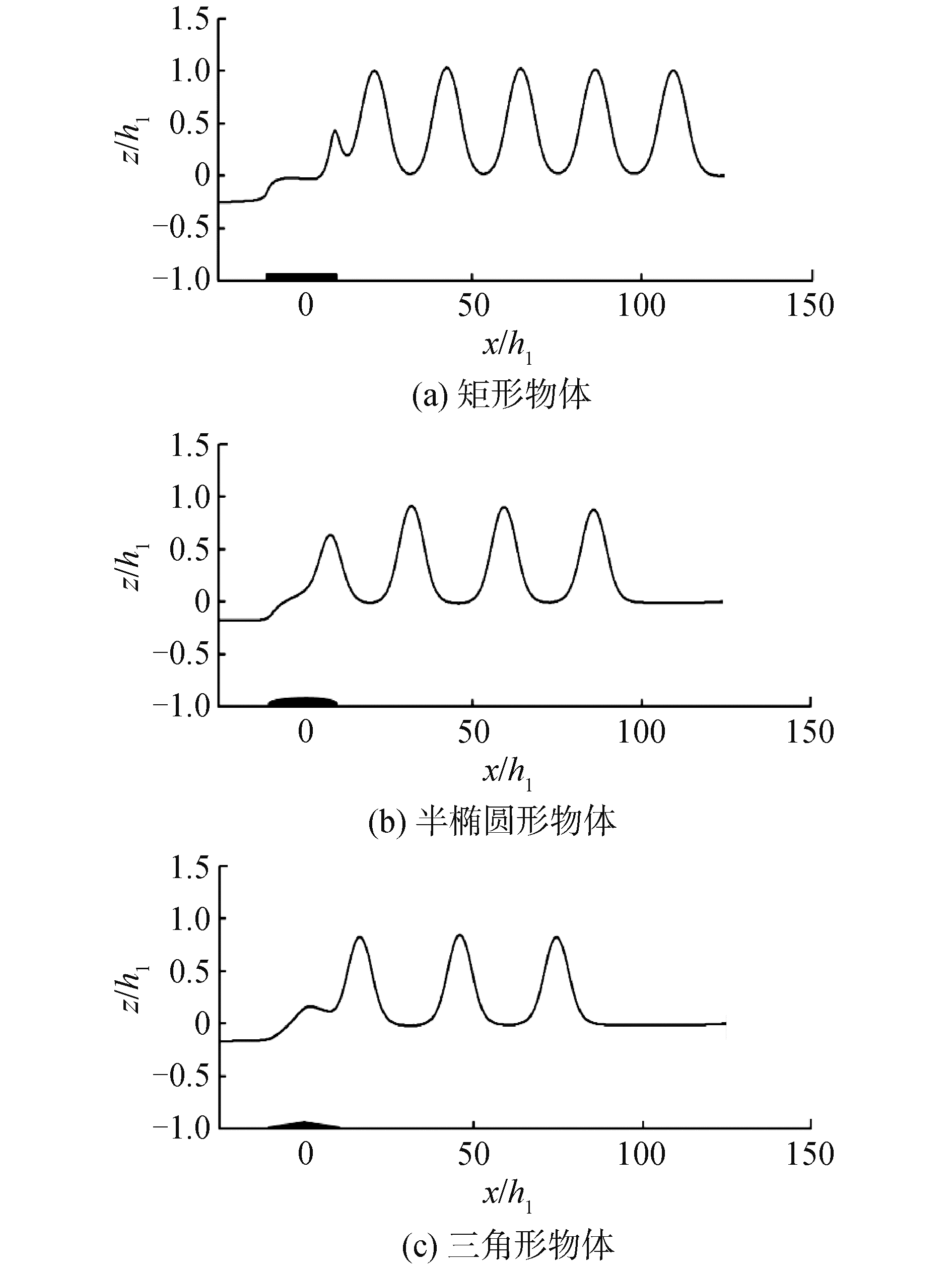
表 2 不同形状物体运动激发的内孤立波波幅和内孤立波数量Table 2 The amplitude and number of internal solitary waves excited by the motion of objects with different shapes参数 矩形 半椭圆形 三角形 z/h1 1.01 0.88 0.83 $ \sqrt{S /\left(2 h_1^2\right)}$ 1.00 0.89 0.71 内孤立波数量 5 3.5 3 图 8为矩形、半椭圆形、三角形这3种形状的物体在海底运动到t(g/h1)1/2=1860时刻下生成的内孤立波波面空间分布的数值计算结果。从图 8可以看出，物体海底在运动，可以在物体前方激发一系列内孤立波，在t(g/h1)1/2=1860时刻，矩形物体前方激发了5个内孤立波，内波波幅为1.01h1；半椭圆形物体前方正在激发第4个内孤立波，内波波幅为0.88h1；半椭圆形物体前方激发了3个内孤立波，内波波幅为0.83h1。
图 8 t(g/h1)1/2=1860时刻下不同形状物体在海底运动激发的内孤立波Fig. 8 Internal solitary waves excited by different shapes of objects at the moment of t(g/h1)1/2=1860下载:
全尺寸图片
从图 8和表 2可以发现，矩形、半椭圆形、三角形这3种形状的物体在海底运动，随着时间的推移，都能在物体前方激发一系列内孤立波，当物体的长宽比确定时，在运动了相同的时间后，面积最大的矩形物体在海底运动激发的内孤立波波幅最大，且矩形物体运动激发的内孤立波数量最多；面积最小的三角形物体在海底运动激发的内孤立波幅最小，且三角形物体运动激发的内孤立波数量最少。
2.3 自由面效应的影响
Grue等[20]考虑的半椭圆形物体在海底运动产生内孤立波算例中，上层液体密度为ρ2=787.3 kg/m3，下层液体密度为ρ1=1 000 kg/m3，上下层液体的密度比是ρ2/ρ1=0.787 3，上层液体表面边界条件使用的是壁面边界条件，也就是采用了刚盖假设，但是Zhao等[22]发现对于2层流体间内孤立波生成问题，只有当上下层密度比ρ2/ρ1接近于1时，刚盖假设才是合理的，否则应该考虑自由面效应的影响。
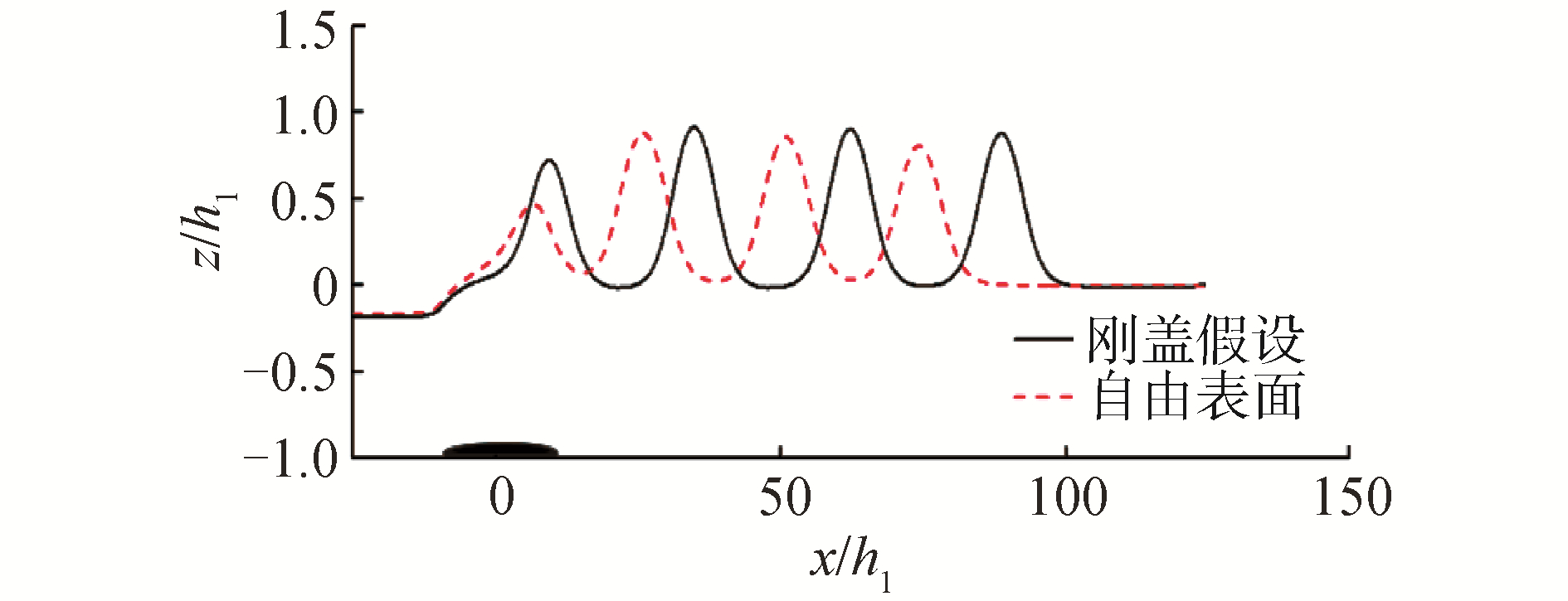
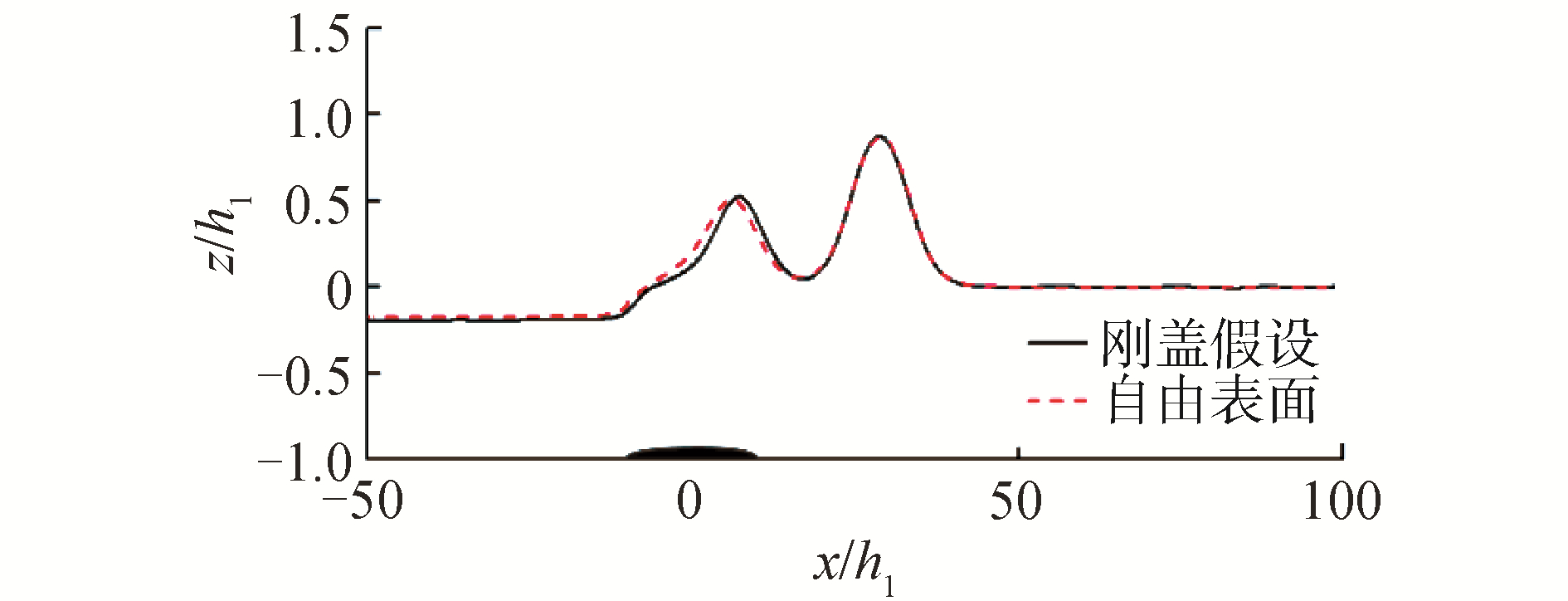
因此，对于半椭圆形物体运动生成内孤立波的算例，本文做了一组保留自由面的对照组，即在上层液体上方增加层空气，从而使上层液体表面成为自由表面，在上下层液体密度比为0.787，t(g/h1)1/2=1 920时刻下的数值模拟结果如图 9所示。
图 9 当ρ2/ρ1=0.787 3时，2种边界条件下半椭圆形物体运动激发的内孤立波Fig. 9 The internal solitary waves under two boundary conditions when ρ2/ρ1=0.787 3下载:
全尺寸图片
从图 9可以看出，当上下层液体密度比为0.787时，海底半椭圆形物体运动到t(g/h1)1/2=1 920时刻，在刚盖假设条件下半椭圆形物体运动激发的内孤立波波幅比在自由表面边界条件下半椭圆形物体运动激发的内孤立波波幅更大，内孤立波传播的距离也更远，也就是自由面效应会减少海底物体运动激发的内孤立波的波幅和波速。
为了进一步研究上下层液体的密度比接近1时刚盖假设的适用情况，本文计算了在上下层液体密度比为0.95时，半椭圆形物体在海底运动同样运动到t(g/h1)1/2=1 920时刻，2种边界条件下物体运动激发的内孤立波波面空间分布结果，如图 10所示。
图 10 当ρ2/ρ1=0.95时，2种边界条件下半椭圆形物体运动激发的内孤立波Fig. 10 The internal solitary waves under two boundary conditions when ρ2/ρ1=0.787 3下载:
全尺寸图片
从图 10可以看出，在上下层液体密度比为0.95时，海底半椭圆形物体运动到t(g/h1)1/2=1 920时刻，刚盖假设和自由表面这2种上层液体顶部边界条件下，物体运动激发的内孤立波波形的空间分布结果几乎重合，所以当上下层液体的密度比接近1时，自由表面可以近似为刚盖。
此外，结合图 9和图 10可以发现，在t(g/h1)1/2=1 920时刻，当上下层液体的密度比为0.787时，半椭圆形物体前方正在激发第4个内孤立波，当上、下层液体的密度比为0.95时，半椭圆形物体前方正在激发第2个内孤立波，2种情况下的内孤立波数量相差1倍。因此，上下层液体的密度比越接近于1时，在同一时刻，海底物体运动激发的内孤立波数量越少。
3. 结论
1) 本文使用STAR-CCM+验证了在刚盖假设条件下，海底半椭圆形物体运动激发内孤立波，Grue等的数值模型计算结果的准确性。
2) 矩形、半椭圆形、三角形物体在海底运动，都能够激发内孤立波。在运动了相同的时间后，矩形物体运动激发的内波波幅最大，内孤立波数量最多，三角形物体运动激发的内孤立波波幅最小，数量最少。
3) 如果上、下层液体的密度比是0.78这样不接近1的情况，对于海底物体运动激发内孤立波问题，不可以将自由表面近似为刚盖，否则，刚盖假设条件下内孤立波的波幅和波速比自由表面条件下内孤立波的波幅和波速更大。
-
图 1 海底物体运动生成内波示意
Fig. 1 Diagram of internal waves generated by the motion of seafloor objects
下载:
全尺寸图片
图 2 边界条件设置示意
Fig. 2 Schematic diagram of boundary condition setting
下载:
全尺寸图片
图 3 海底物体运动生成内波示意
Fig. 3 Diagram of internal waves generated by the motion of seafloor objects
下载:
全尺寸图片
图 4 内波波面空间分布结果收敛性分析
Fig. 4 Convergence analysis of spatial distribution of internal wave surface
下载:
全尺寸图片
下载:
全尺寸图片
图 6 不同时刻半椭圆形物体运动激发的内孤立波
Fig. 6 Internal solitary waves excited by the motion of a semi-elliptic object at different time
下载:
全尺寸图片
图 7 运动物体的形状示意
Fig. 7 A sketch of the shape of a moving object
下载:
全尺寸图片
图 8 t(g/h1)1/2=1860时刻下不同形状物体在海底运动激发的内孤立波
Fig. 8 Internal solitary waves excited by different shapes of objects at the moment of t(g/h1)1/2=1860
下载:
全尺寸图片
图 9 当ρ2/ρ1=0.787 3时，2种边界条件下半椭圆形物体运动激发的内孤立波
Fig. 9 The internal solitary waves under two boundary conditions when ρ2/ρ1=0.787 3
下载:
全尺寸图片
图 10 当ρ2/ρ1=0.95时，2种边界条件下半椭圆形物体运动激发的内孤立波
Fig. 10 The internal solitary waves under two boundary conditions when ρ2/ρ1=0.787 3
下载:
全尺寸图片
表 1 收敛性分析
Table 1 Convergence analysis
参数 数值策略1 数值策略2 数值策略3 Δx/m 0.04 0.02 0.01 Δt/s 0.006 0.003 0.001 5 表 2 不同形状物体运动激发的内孤立波波幅和内孤立波数量
Table 2 The amplitude and number of internal solitary waves excited by the motion of objects with different shapes
参数 矩形 半椭圆形 三角形 z/h1 1.01 0.88 0.83 $ \sqrt{S /\left(2 h_1^2\right)}$ 1.00 0.89 0.71 内孤立波数量 5 3.5 3 -
[1] SCHOOLEY A H, STEWART R W. Experiments with a self-propelled body submerged in a fluid with a vertical density gradient[J]. Journal of fluid mechanics, 1963, 15(1): 83-96. doi: 10.1017/S0022112063000070 [2] ARNTSEN A. Disturbances, lift and drag forces due to the translation of a horizontal circular cylinder in stratified water[J]. Experiments in fluids, 1996, 21(5): 387-400. doi: 10.1007/BF00189060 [3] 马晖扬, 麻柏坤, 张人杰. 分层流体中物体运动尾迹的理论和实验研究[J]. 中国科学技术大学学报, 2000, 30(6): 677-684. https://www.cnki.com.cn/Article/CJFDTOTAL-ZKJD200006007.htm MA Huiyang, MA Baikun, ZHANG Renjie. Theoretical and experimental research on the wake of a moving body in stratified fluid[J]. Journal of University of Science and Technology of China, 2000, 30(6): 677-684. https://www.cnki.com.cn/Article/CJFDTOTAL-ZKJD200006007.htm [4] 李万鹏, 魏岗, 杜辉, 等. 分层流体中螺旋桨效应激发内波的实验分析[J]. 解放军理工大学学报(自然科学版), 2014, 15(6): 576-582. https://www.cnki.com.cn/Article/CJFDTOTAL-JFJL201406011.htm LI Wanpeng, WEI Gang, DU Hui, et al. Experimental study on internal wave generated by a propeller in a stratified fluid[J]. Journal of Army Engineering University of PLA, 2014, 15(6): 576-582. https://www.cnki.com.cn/Article/CJFDTOTAL-JFJL201406011.htm [5] 陈科, 王宏伟, 盛立, 等. 拖曳体激发内波时空特性实验及其理论模型[J]. 物理学报, 2018, 67(3): 158-174. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201803018.htm CHEN Ke, WANG Hongwei, SHENG Li, et al. Theoretical models and experiments for the time-space characteristics of internal waves generated by towed bodies[J]. Acta physica sinica, 2018, 67(3): 158-174. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201803018.htm [6] 高德宝, 张军, 周根水, 等. 分层流体中拖曳体内波尾迹水下/水面时空特征试验研究[C]//第三十一届全国水动力学研讨会论文集. 厦门, 2020: 577-587. GAO Debao, ZHANG Jun, ZHOU Genshui, et al. Experimental study on temporal-spatial characteristics of water surface flow and underwater flow for internal waves generated by towed body in stratified fluid[C]//Proceedings of the 31st National Conference on Hydrodynamics. Xiamen, 2020: 577-587. [7] 罗恒. 粘性分层流中水下航行体尾迹在随机海面中的表现特征研究[D]. 上海: 上海交通大学, 2007. LUO Heng. The surface wake generated by a submerged moving body in a stratified viscous fluid and its interaction with the stochastic ocean waves[D]. Shanghai: Shanghai Jiao Tong University, 2007. [8] 段菲. 分层流中潜体运动对内波及表层流场影响研究[D]. 哈尔滨: 哈尔滨工程大学, 2016. DUAN Fei. Numerical study of effects on internal waves and free surface flow field resulting from submerged body moving in the pycnocline[D]. Harbin: Harbin Engineering University, 2016. [9] 黄璐. 潜艇近水面航行尾流空间演化分析[D]. 哈尔滨: 哈尔滨工业大学, 2020. HUANG Lu. Spatial evolution analysis of wake of submarine sailing near water[D]. Harbin: Harbin Institute of Technology, 2020. [10] 黄凤来, 曹留帅, 万德成. 连续密度分层流中潜艇近水面航行时复杂流场数值模拟[C]//第三十一届全国水动力学研讨会论文集. 厦门, 2020: 857-870. HUANG Fenglai, CAO Liushuai, WAN Decheng. Numerical simulation of complex flow field of submarine sailing near water surface in linearly stratified fluid[C]//Proceedings of the 31st National Conference on Hydrodynamics. Xiamen, 2020: 857-870. [11] HUANG Fenglai, MENG Qingjie, CAO Liushuai, et al. Wakes and free surface signatures of a generic submarine in the homogeneous and linearly stratified fluid[J]. Ocean engineering, 2022, 250: 111062. doi: 10.1016/j.oceaneng.2022.111062 [12] 胡开业, 潘黎明, 于祥, 等. 含跃层的分层流中运动椭球尾流场数值模拟[C]//第三十一届全国水动力学研讨会论文集. 厦门, 2020: 402-411. HU Kaiye, PAN Liming, Yu Xiang, et al. Numerical simulation of wake field on moving ellipsoid in stratified fluid with a pycnocline[C]//Proceedings of the 31st National Conference on Hydrodynamics. Xiamen, 2020: 402-411. [13] 刘双, 何广华, 王威, 等. 密度分层流中浅航艇兴波尾迹分析[J]. 哈尔滨工业大学学报, 2021, 53(7): 52-59. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX202107006.htm LIU Shuang, HE Guanghua, WANG Wei, et al. Analysis on the wake of a shallow navigation submarine in the density-stratified fluid[J]. Journal of Harbin Institute of Technology, 2021, 53(7): 52-59. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX202107006.htm [14] 何广华, 刘双, 王威, 等. 密度分层对近水面航行潜体兴波阻力影响分析[J]. 哈尔滨工程大学学报, 2021, 42(8): 1125-1132. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=3659 HE Guanghua, LIU Shuang, WANG Wei, et al. Effect of density-stratified on wave-making resistance of submerged body navigating near free surface[J]. Journal of Harbin Engineering University, 2021, 42(8): 1125-1132. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=3659 [15] 何广华, 刘双, 张志刚, 等. 深水密度层航行潜艇兴波尾迹分析[J]. 哈尔滨工业大学学报, 2022, 54(1): 40-48. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX202201006.htm HE Guanghua, LIU Shuang, ZHANG Zhigang, et al. Analysis on the wake of submarine navigating in deeper density layer[J]. Journal of Harbin Institute of Technology, 2022, 54(1): 40-48. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX202201006.htm [16] 刘双, 何广华, 王威, 等. 深水密度层航行潜艇兴波阻力的影响分析[J]. 哈尔滨工程大学学报, 2021, 42(9): 1373-1379. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=3691 LIU Shuang, HE Guanghua, WANG Wei, et al. Effect of density stratification on wave-making resistance of submarine navigating in deep-water[J]. Journal of Harbin Engineering University, 2021, 42(9): 1373-1379. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=3691 [17] LIU Shuang, HE Guanghua, WANG Zhigang, et al. Resistance and flow field of a submarine in a density stratified fluid[J]. Ocean engineering, 2020, 217: 107934. [18] 刘双, 何广华, 王威, 等. 附体对分层流中潜艇水动力特性的影响[J]. 兵工学报, 2021, 42(1): 108-117. https://www.cnki.com.cn/Article/CJFDTOTAL-BIGO202101012.htm LIU Shuang, HE Guanghua, WANG Wei, et al. Effect of appendages on hydrodynamic characteristics of submarine in stratified fluid[J]. Acta armamentarii, 2021, 42(1): 108-117. https://www.cnki.com.cn/Article/CJFDTOTAL-BIGO202101012.htm [19] 于祥, 胡开业. 分层流中潜艇加减速对尾迹特征特性影响研究[J]. 中国舰船研究, 2022, 17(03): 67-77. https://www.cnki.com.cn/Article/CJFDTOTAL-JCZG202203005.htm YU Xiang, HU Kaiye. Influence of submarine's acceleration and deceleration on wake spectrum characteristics in stratified flow[J]. Chinese journal of ship research, 2022, 17(3): 67-77. https://www.cnki.com.cn/Article/CJFDTOTAL-JCZG202203005.htm [20] GRUE J, FRIIS H A, PALM E, et al. A method for computing unsteady fully nonlinear interfacial waves[J]. Journal of fluid mechanics, 1997, 351: 223-252. [21] DENNER F, WACHEM B. Compressive vof method with skewness correction to capture sharp interfaces on arbitrary meshes[J]. Journal of computational physics, 2014, 279: 127-144. [22] ZHAO Binbin, WANG Zhan, DUAN Wenyang, et al. Experimental and numerical studies on internal solitary waves with a free surface[J]. Journal of fluid mechanics, 2020, 899: A17.
