G-Function construction method based on iterative decomposition in adifferential frequency hopping system
-
摘要: 差分跳频是跳频技术中提高数据传输速率的一种有效方式，频率转移函数是差分跳频研究的重点，本文针对现有的频率转移函数所生成的跳频序列性质上的不足，提出了一种时变的频率转移算法，通过m序列，对频率对进行迭代分解，进而控制频率之间的对应关系，同时根据发端算法构造了解映射算法。对算法进行了理论分析和仿真验证，仿真验证表明：相比于基于m序列、RS码和混沌序列加扰的G函数算法，新的转移算法是时变的，产生的跳频序列的随机性、均匀性和安全性得到了改善，二维连续性符合卡方检验的理论值，在通信性能上也有了部分提升。Abstract: Differential frequency hopping is an effective way to improve data transmission rates in frequency hopping technology, and the frequency transfer function is the focus of differential frequency hopping research.Given the deficiency of the nature of the frequency hopping sequences generated by the exisiting frequency transfer function, this paper proposes a time-varying frequency shift algorithm, in which frequency pairs are iteratively decomposed through the m sequence. The corresponding relation between frequencies is therefore controled, and at the same time, an inverse algorithm is constructed in accordance with the original algorithm. Theoretical analysis and simulation show that compared with the G function algorithm based on the m sequence, the Reed-Solomon code, and chaotic sequence scrambling, the new transfer algorithm is time-varying with frequency hopping sequence randomness, uniformity, and improved safety. The two-dimensional continuity is in accordance with the theoretical value provided by the chi-square test. Communication performance has also been partially improved.
-
Keywords:
- differential frequency hopping /
- G-function /
- time-varying /
- 2-D continuity
-
差分跳频(differential frequency hopping, DFH)是近年来广受关注的一种高跳速、高效率的跳频技术，该跳频技术属于相关跳频，即相邻跳频率间的对应关系是通过传递的信息进行控制的[1-2]。1995年，美国Sanders公司开发了一种用差分跳频技术作为核心的扩展频谱电台，称为CHESS，跳频速率可以达到5 000跳/s，其中4 800跳用于信息的传输，每秒可以传输1~4 bit信息数据，数据传输速率可以达到9.6 kB/s。与传统跳频不同，相邻跳之间的频率转移关系不是由伪随机序列控制的，而是由当前跳跳频频率、前一跳跳频频率、数据符号和频率转移函数(G函数)共同控制的，因此，将调制、编码和跳频图案综合为一体设计的G函数就成为了差分跳频领域研究的重点[3-4]，而G函数的设计也就直接决定了差分跳频系统的抗截获性能和抗干扰性能。在这方面，目前较好的G函数，主要有基于m序列、RS(Reed-Solomon)码和混沌序列加扰系列的G函数[5-8]基于时变的TVG(time varying G function)G函数[9]等，但前者的G函数不是时变的, 安全性较差，后者的随机性、均匀性、二维连续性较差，且二者的通信性能相比传统G函数都没有提高，本文提出了一种基于迭代分解的频率转移函数TVID(time varying iterative decomposition)，在保证了G函数的时变性、提高了跳频序列性能的同时，设计了相应的解映射算法，提高了系统的通信性能。
1. 差分跳频系统模型
常规跳频(frequency hopping spread spectrum，FHSS)是通过伪随机序列生成跳频图案，在收发双方约定的情况下通过快速、随机的改变载波频率而进行抗干扰的一种通信方式。
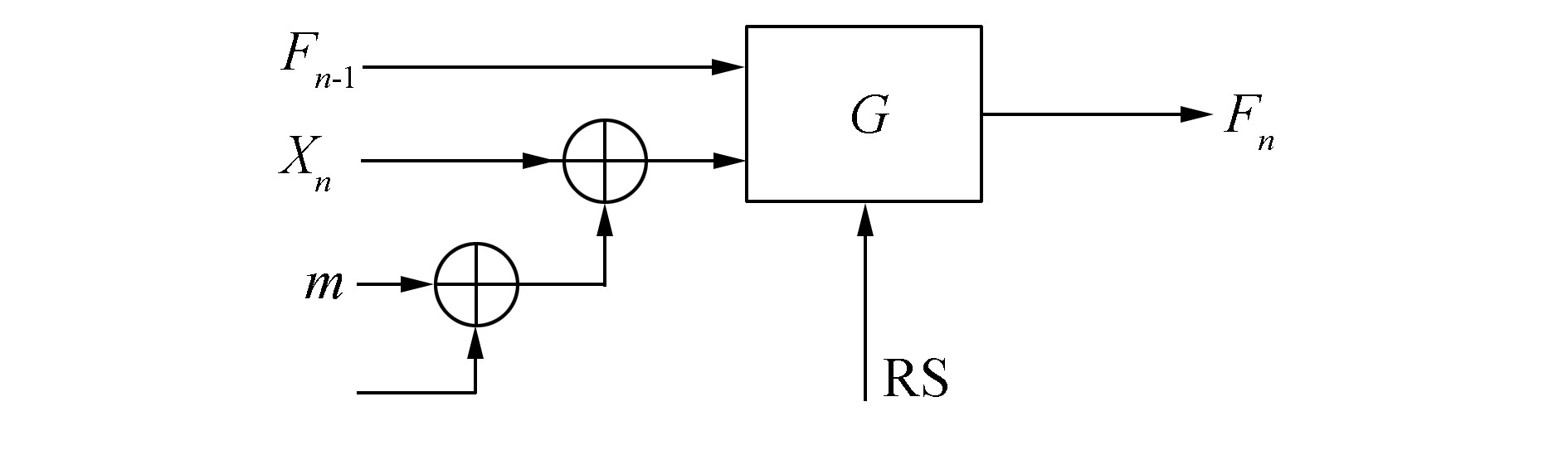
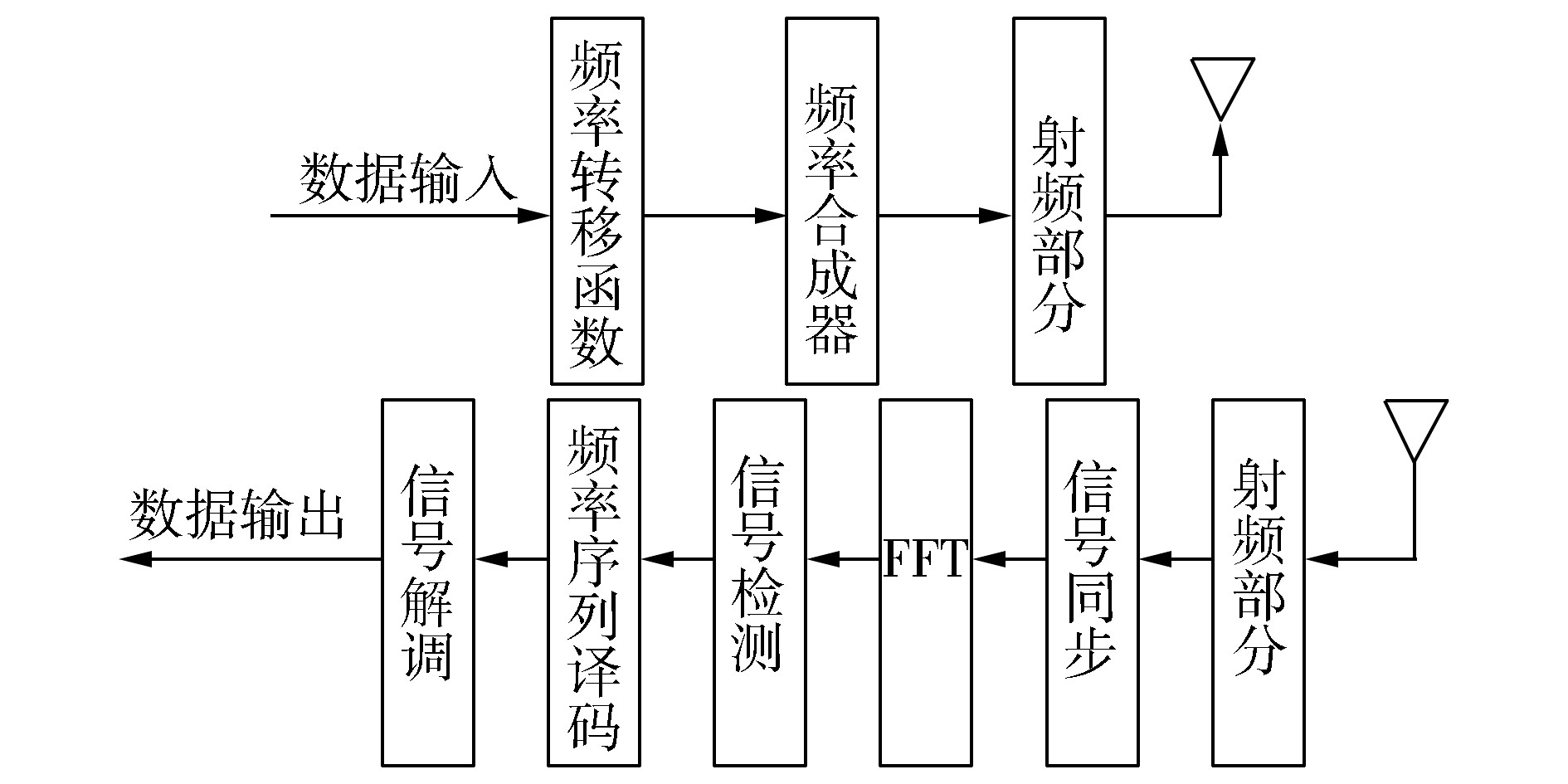
差分跳频(differential frequency hopping，DFH)系统中，将跳频、编码和调制当作一个统一的整体联合设计，通过宽带接收和序列纠错的方式对抗干扰，当前跳的频率Fn是由前一跳频率Fn-1和当前跳所携带的信息数据Xn经过G函数的转换决定的，记作Fn=G(Fn-1, Xn)，差分跳频通信系统原理模型如图 1所示[10-12]。
图 1 差分跳频原理模型Fig. 1 Differential frequency hopping system model
下载:
全尺寸图片
在接收方式上，由于接收方不知道跳频序列，首先要进行宽带接收，用FFT变换后的幅度值的平方作为接收的判决量，并将其作为频率检测的方法判定频率序列[10-13]，然后根据G函数的逆映射还原出原始信息序列，即Xn=G－1(Fn－1, Fn)。
基于m序列、RS(Reed-Solomon)码和混沌序列加扰系列等的G函数可以简单表示为Fn=G(Fn－1, Xn, Yn, m, RS)，其中Yn为混沌序列，该G函数通过m序列控制频率子集的选择，利用RS码控制跳频间隔，用混沌序列对原始信息数据进行加扰，使信息数据具有伪随机序列的性质，张月婷等[7-8]在此基础上用m序列控制映射关系进行加扰，加大了扇出系数，但该系列的G函数的缺点是传递函数时不变，安全性较低，G函数生成原理框图如图 2所示。
图 2 基于m序列、RS码和混沌序列的G函数生成原理框图Fig. 2 Block diagram of G function generation principle based on m sequence, RS code and chaotic sequence下载:
全尺寸图片
2. TVID G函数
本文提出一种改进的时变G函数TVID G函数，结合了传统时变G函数(TVG)和基于m序列、RS码和混沌序列G函数的优点，通过伪随机序列控制G函数的参数以向下迭代的方式进行频率对集合的分解，在接收端通过相应的解映射方式还原出原始信息序列。
2.1 TVIDG函数构造方法
G函数的映射关系可以表示为：
$$ F_n=G\left(F_{n-1}, X_n, Y_n, m, \mathrm{RS}, P_n\right) $$ (1) 定义频率转移函数具体的映射关系为：
$$ F_n=\mathit\Omega\left(\left(F_{n-1}+Z_n^2+2 Z_n-2 \mathrm{RS}+P_n\right) \bmod Q_n+p Q_n\right) $$ (2) 具体描述如下。
1) 将传输的信息序列进行编码，生成数据信息Xn。
2) 通过混沌映射式:
$$ y(n)=-(y(n-1))^2-|y(n-1)|+1 $$ (3) 设置门限值为0.5, 然后进行门限函数量化得到混沌序列Yn。
3) 根据系统要求选择控制频率子集选择的m序列和控制频点间隔的RS码。
4) 将用m序列与混沌序列异或后的序列对数据信息Xn加扰得到Zn。
5) 差分跳频系统的频点总数为N，分成的次级子块的频点数为Ni，k为分成的频率子集数，ki为次级分成的频率子块数，定义:
$$ Q_n=\frac{N_i}{k_i} $$ (4) $$ \text { 6) } p=m_1+2 m_2+\cdots+2^{h-1} m_h $$ (5) 式中：m1为所选择的h位m序列的最高位；m2为次高位；mh为最低位。
7) Pn为控制每个子块扇出系数的参数，f为频率对的关系映射函数，Ω定义为所有可能的频率对集合：
$$ \mathit\Omega=\mathit\Omega_1 \cup \mathit\Omega_2 \cup \cdots \cup \mathit\Omega_n $$ (6) 由m序列控制。
8) 通过频率间的映射关系式(2)得到当前跳的对应频率。
2.2 频率集合联合概率分析
一个具有良好二维连续性的差分跳频序列的频率联合概率密度应满足：
$$ P\left(f_i, f_j\right)=\frac{1}{N^2}, f_i, f_j \in \mathit\Omega_0 \leqslant i, j \leqslant N-1 $$ (7) 假定原频率转移函数的扇出系数为d, 由于信源数据信息是均匀分布的，各个频点的分布是等概的，即：
$$ P\left(f_i\right)=\frac{1}{N} $$ (8) 当前跳可能出现的频率集合:
$$ \mathit\Omega_i=G\left(f_i, x_n\right) $$ (9) 则
$$ P\left(f_j \mid f_i\right)=\left\{\begin{array}{l} \frac{1}{d}, f_j \in \mathit\Omega_i \\ 0, f_j \notin \mathit\Omega_i \end{array}\right. $$ (10) 根据贝叶斯公式得频率联合概率密度：
$$ P\left(f_i, f_j\right)=P\left(f_i\right) \cdot P\left(f_j \mid f_i\right)=\left\{\begin{array}{l} \frac{1}{N d}, f_j \in \mathit\Omega_i \\ 0, f_j \notin \mathit\Omega_i \end{array}\right. $$ (11) 因此，若d=N，则需要包含所有可能出现的频率对，即整个频率对集合Ω。
由伪随机序列控制字块的分解方式，令r1, r2, r3, …, rn为每级分成的子块，根据需求，用m序列中每2个比特来控制分成的子块，Pn则根据所分成的子块改变扇出系数，Ω′为新算法下的出现频率对集合，则：
$$ \left\{\begin{array}{l} \mathit\Omega^{\prime}= & \sum\limits_{i=1}^{r_1} \mathit\Omega_i-\left(\mathit\Omega_1 \cap \mathit\Omega_2+\mathit\Omega_1 \cap \mathit\Omega_3+\cdots+\right. \\ & \left.\mathit\Omega_{r_1-1} \cap \mathit\Omega_{r_1}\right)+\cdots+(-1) r_1-1 \cdot \\ & \left(\mathit\Omega_1 \cap \mathit\Omega_2 \cap \mathit\Omega_3 \cap \cdots \cap \mathit\Omega_{r_1}\right) \\ \mathit\Omega_i= & \sum\limits_{j=1}^{r_2} \mathit\Omega_{i j}-\left(\mathit\Omega_{i 1} \cap \mathit\Omega_{i 2}+\mathit\Omega_{i 1} \cap \mathit\Omega_{i 3}+\cdots+\right. \\ & \left.\mathit\Omega_{i r_2-1} \cap \mathit\Omega_{i r_2}\right)+\cdots+(-1) r_2-1 \cdot \\ & \left(\mathit\Omega_{i 1} \cap \mathit\Omega_{i 2} \cap \mathit\Omega_{i 3} \cap \cdots \cap \mathit\Omega_{i r_2}\right) \cdots \\ \mathit\Omega_{i j \cdots k}= & \sum\limits_{k=1}^{r_n} \mathit\Omega_{i j \cdots k}-\left(\mathit\Omega_{i j \cdots 1} \cap \mathit\Omega_{i j \cdots 2}+\mathit\Omega_{i j \cdots 1} \cap \mathit\Omega_{i j \cdots 3}+\right. \\ & \left.\cdots+\mathit\Omega_{i j \cdots r_n-1} \cap \mathit\Omega_{i r_n}\right)+\cdots+(-1) r_{n-1} \cdot \\ & \left(\mathit\Omega_{i j \cdots 1} \cap \mathit\Omega_{i j \cdots 2} \cap \mathit\Omega_{i j \cdots 3} \cap \cdots \cap \mathit\Omega_{i j \cdots r_n}\right) \end{array}\right. $$ (12) 由于字块之间互不相交，则:
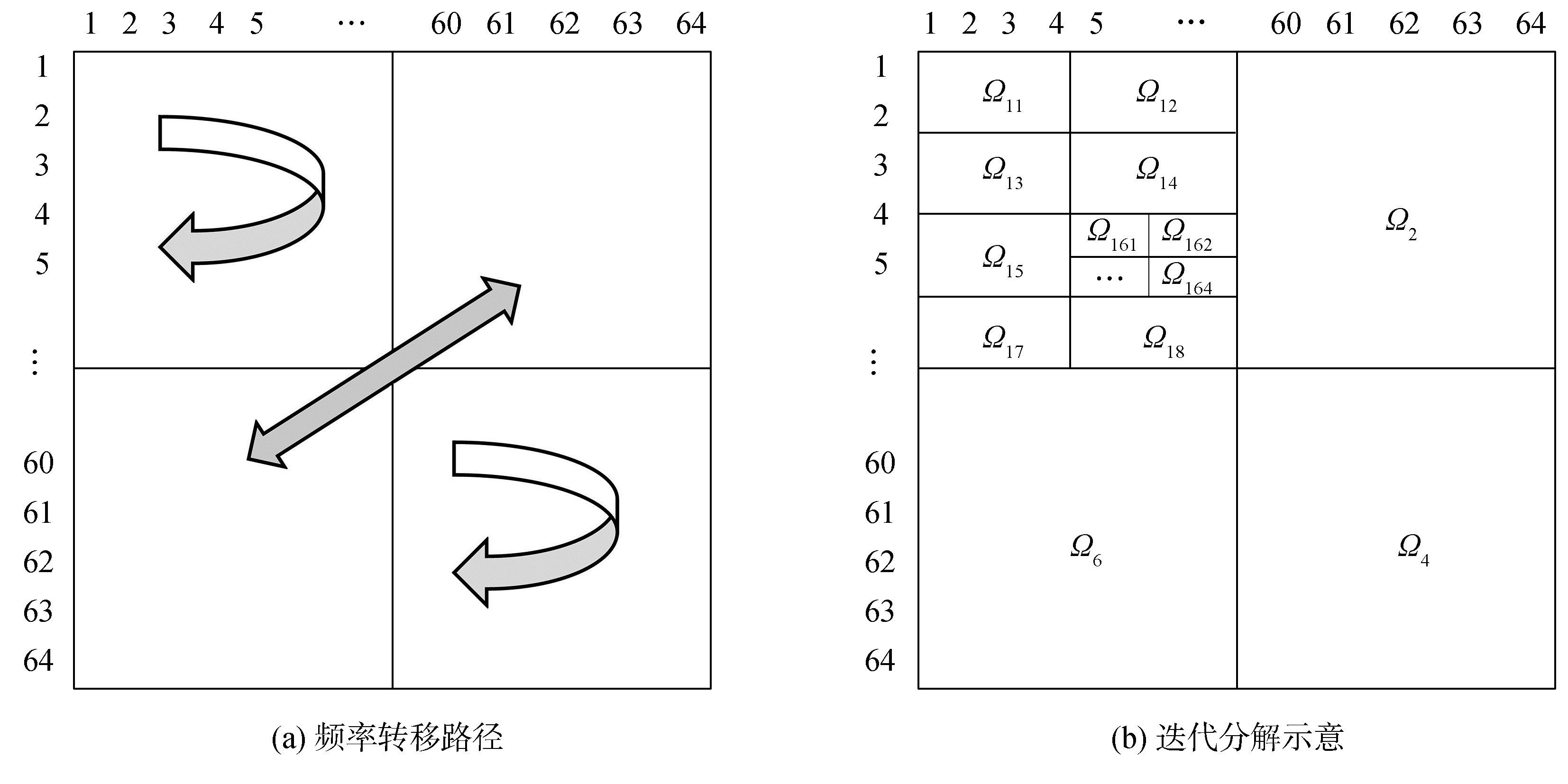
$$ \begin{gathered} \mathit\Omega^{\prime}=\sum\limits_{i=1}^{r_1} \mathit\Omega_i=\sum\limits_{i=1}^{r_1} \sum\limits_{j=1}^{r_2} \mathit\Omega_{i j}=\cdots= \\ \sum\limits_{i=1}^{r_1} \sum\limits_{j=1}^{r_2} \cdots \sum\limits_{k=1}^{r_n} \mathit\Omega_{i j \cdots k}=\mathit\Omega \end{gathered} $$ (13) N=64时，原理示意图如图 3所示，其中图(a)为频率转移示意图，图(b)为频率对迭代分解示意图。
图 3 TVID算法原理示意Fig. 3 Schematic diagram of TVID algorithm下载:
全尺寸图片
2.3 算法通信性能分析
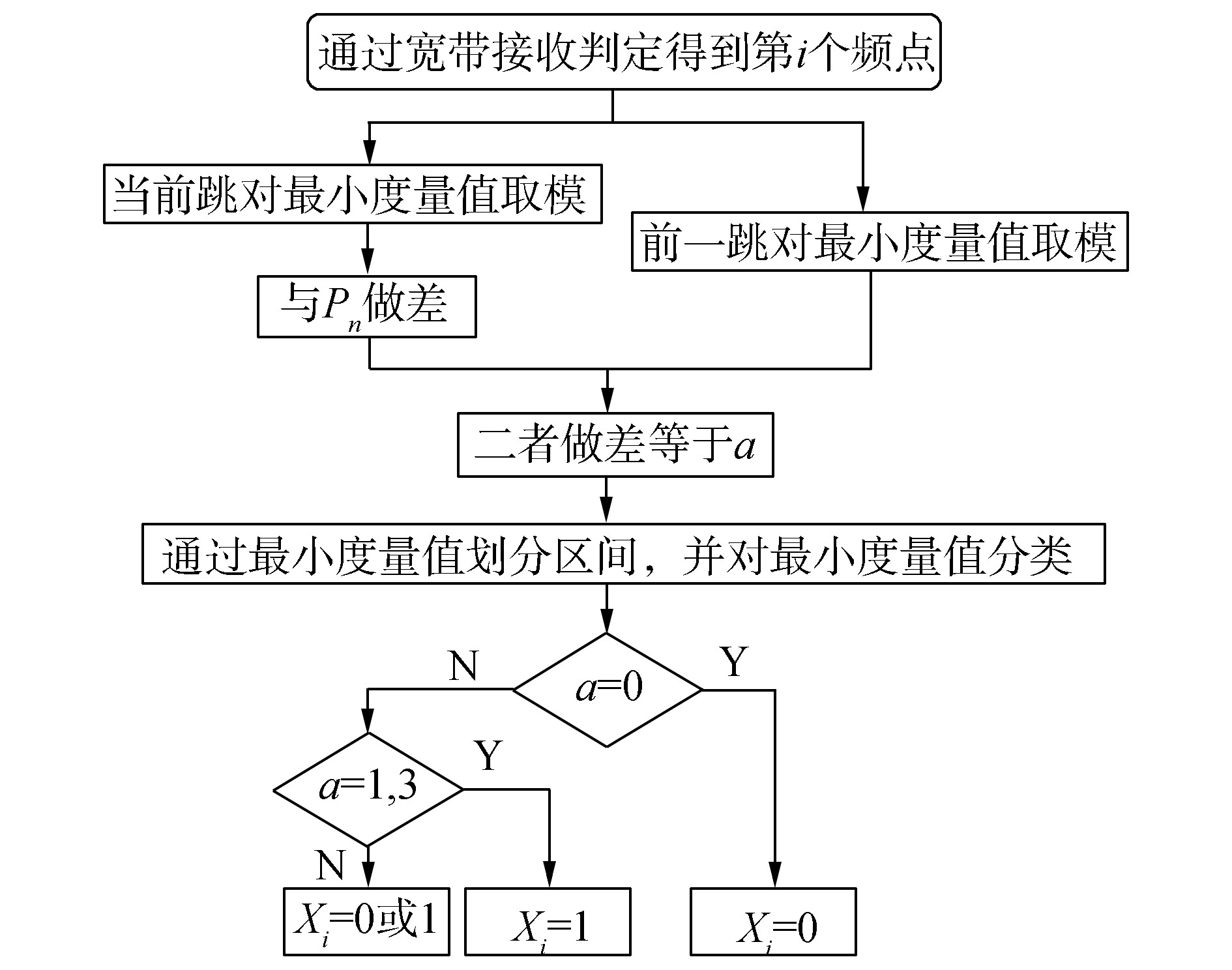
频率转移函数要求具有可逆性，即在收端接收频点正确的情况下可以完整逆映射为原始信息序列，根据频率转移函数设计逆映射算法，算法流程图如图 4所示。
图 4 解映射算法流程Fig. 4 Flow chart of demapping algorithm下载:
全尺寸图片
图中最小度量指的是根据m序列随机选择的最低阶的字块的扇出系数，且解映射的方法具有子类向父类的向上兼容性，Xi为经解映射判决后的信息序列。
差分跳频在AWGN，接收端采用逐符号检测接收机的情况[10-11]下，每一跳的频率被误判概率为：
$$ P_e=\sum\limits_{s=1}^{N-1}(-1)^{s+1} C_{N-1}^s \frac{1}{s+1} \mathrm{e}^{-\gamma_s /(s+1)} $$ (14) 式中γ=Es/N0，为符号信噪比，则符号的错误概率为：
$$ \begin{gathered} P_s \approx \frac{2(f-1)}{f} P_e=\frac{2(f-1)}{f} \sum\limits_{s=1}^{N-1}(-1)^{s+1} \\ C_{N-1}^s \frac{1}{s+1} \mathrm{e}^{-\gamma s /(s+1)} \end{gathered} $$ (15) 而本文根据发端G函数所设计的解映射算法的符号错误概率为：
$$ \begin{gathered} P_s^{\prime}=\sum\limits_{i=1}^n\left[\frac{r_i-1}{r_1 r_2 \cdots r_i} P_s\right] \approx \\ \sum\limits_{i=1}^n\left[\frac{2(f-1)\left(r_i-1\right)}{f r_1 r_2 \cdots r_i} \sum\limits_{s=1}^{N_i-1}(-1)^{s+1} \cdot\right. \\ \left.C_{N_i-1}^s \frac{1}{s+1} \mathrm{e}^{-\gamma_s /(s+1)}\right] \end{gathered} $$ (16) 3. 数值仿真结果
本文综合现有文献，通过随机性、均匀性、二维连续性、安全性来分析生成跳频序列的性能，仿真参数：伪随机序列选择m序列，反馈系数分别为100 003、133 663，跳频点数为64个频点，RS码为(31, 15)且生成多项式为f(x)=x5+x2+1，判别的跳频序列长度为10 000，方法1)G函数为基于m序列、RS码和混沌序列G函数[5-8]; 方法2)G函数为传统时变G函数TVG[9]; 方法3)G函数为基于状态网格图的G函数[12, 14]。
3.1 随机性检验与分析
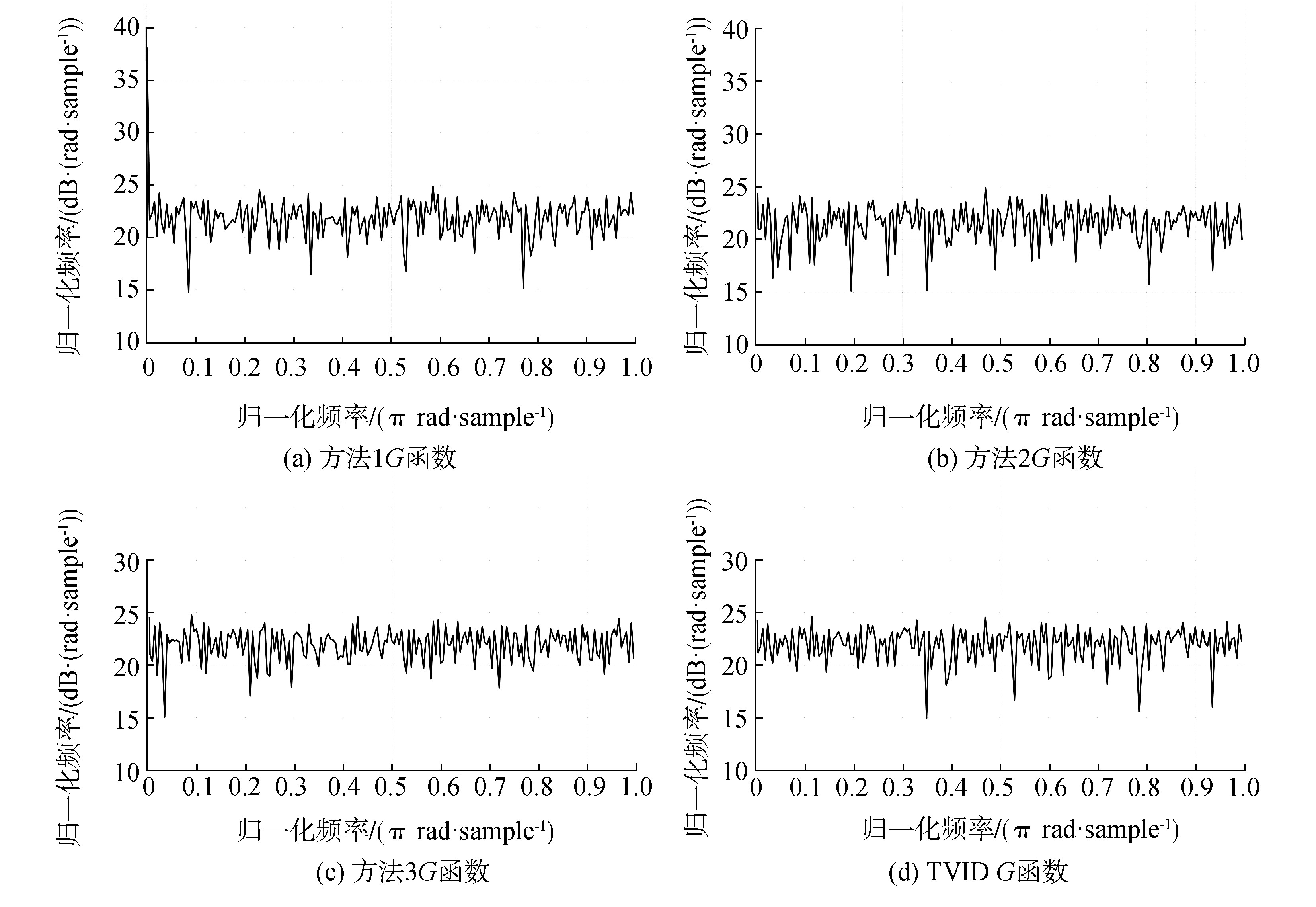
随机性指的是各个频点是否是随机出现的，也就是各个频点之间的独立性检验，序列的随机性越好，其冲激响应和相关函数越逼近，通常会采用序列的功率谱来检验序列的随机性好坏[5, 7-9]。方法1G函数、方法2G函数、方法3G函数和本文提出的TVID G函数的频率序列功率谱如图 5所示。
图 5 频率序列功率谱图Fig. 5 Frequency sequence power spectrum下载:
全尺寸图片
从图 5中可以看出，相较于方法1、方法2和方法3，本文提出的方法生成的G函数功率谱更平坦，随机性能最好，此外，结果中均出现了较大的直流分量，这是因为产生的跳频序列的均值不为零导致的，不会对差分跳频通信系统产生影响。
为了更加直观地对比4个方法频率序列功率谱数值，统计功率谱数值标准差STD，统计结果如表 1所示。
表 1 统计结果Table 1 The statistical results方法 标准差 方法1 2.031 方法2 2.186 方法3 2.006 TVID方法 1.946 从表 1中也可以直观地看出，本文提出的方法相较于其他方法的标准差最低，即频率序列功率谱更加平坦，随机性更好。
3.2 均匀性检验与分析
均匀性指的是每一个频率点出现的概率是服从均匀分布的，均匀性越好，即每个频点都能被等概率的被选取，系统的抗干扰性能更好[8, 10]。
均匀性的检测方法采用统计学中的χ2检验法。χ2检验法是一种基于计数资料的假设检验方法，通过理论样本量和实际样本量的拟合程度来进行判定。原理如表 2所示，其中，Ⅰ类错误是显著性错误，通常用α=0.05表示。
表 2 假设检验原理Table 2 Principle of hypothesis testing真实情况 结论 接受H0 接受H1 H0为真 正确 Ⅰ类错误 H1为真 Ⅱ类错误 正确 用ki表示表示跳频序列中频点出现的次数，M表示样本的总量，则频率均匀性的检验方程可以写为：
$$ \chi^2(N-1)=\sum\limits_{i=0}^{N-1} \frac{\left(k_i-M / N\right)^2}{M / N} $$ (17) 当实际的测量数据计算的χ2(N-1)的值小于理论值χα2(N-1)时，即可表征原假设成立，说明当前的频率序列具有良好的均匀性，当N=64时，理论值为82.244 7。
方法1G函数、方法2G函数、方法3G函数和本文提出的TVID G函数经过多次的检测均值结果如表 3所示。
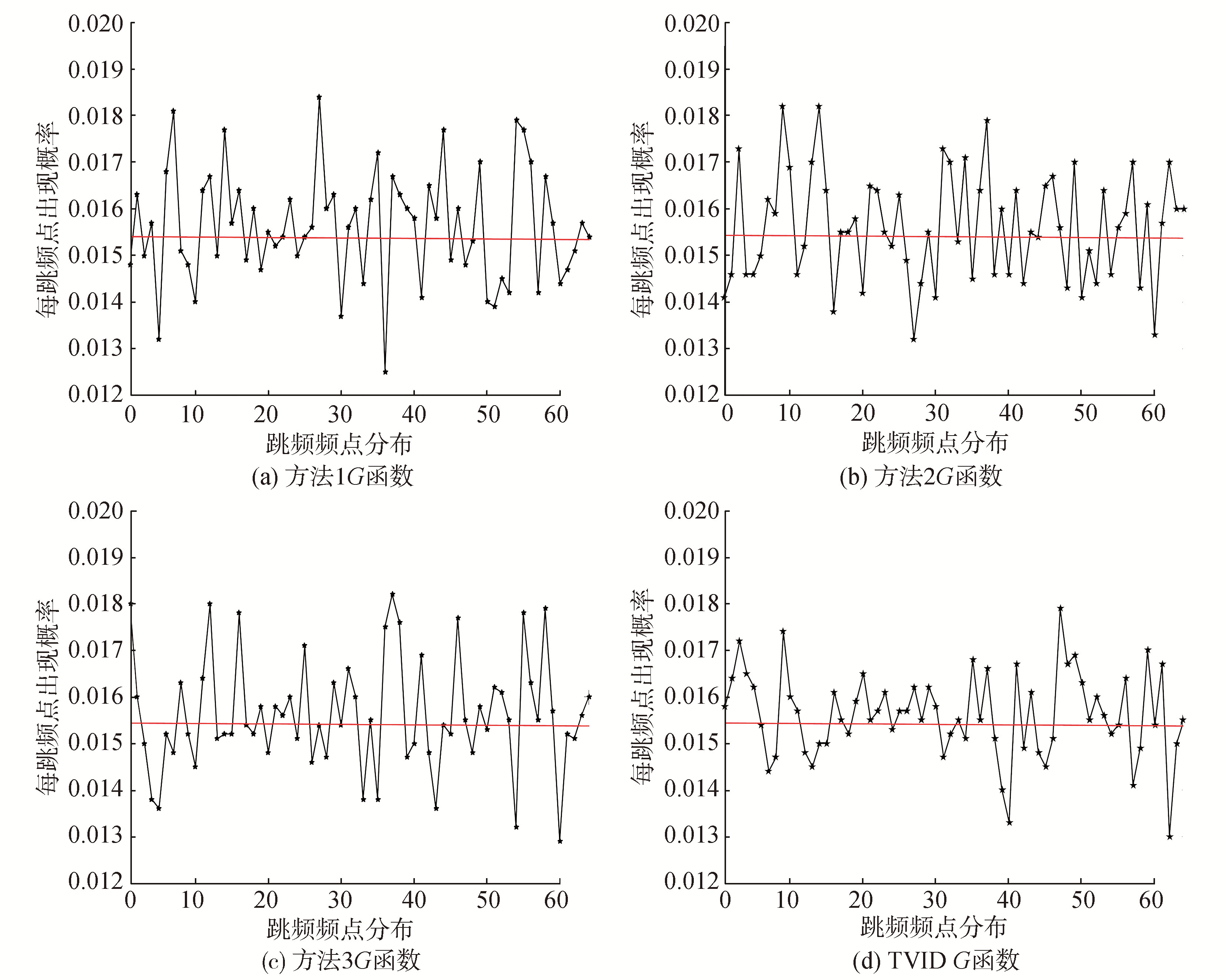
表 3 检测结果Table 3 Test results卡方检验临界值 方法1 方法2 方法3 TVID方法 82.244 7 59.555 2 55.462 4 59.968 0 43.859 2 从表中可以看出，4种G函数的χ2检验的结果均小于临界值，本文方法的仿真值最小，表明其均匀性最好，原因是本文提出的方法在迭代分解的过程中，频率的对应关系一直在发生改变，增大了扇出系数，为更加直观地表明频点分布的均匀情况，给出等分布检验的频率统计结果如图 6所示。
图 6 等分布检验的频率统计结果Fig. 6 Graph of the frequency statistics of the isometric distribution test下载:
全尺寸图片
从图 6中可以看出，本文提出的方法的概率的最大值与最小值相差最小，更接近均值0.015 625，分布的更加平均，即本文提出的方法均匀性更好。
3.3 二维连续性检验与分析
二维连续性是指连续频点出现的概率，是衡量连续频点随机性的一个特征，频率序列的二维连续性越好，差分跳频系统的抗截获性能越好[5-9]。二维连续性的检测方法采用统计学中的多维χ2检验法，当N=64时，二维χ2检验的理论值为4 277.714 2，当实际计算数据的结果小于理论值时，证明原假设成立。方法1、方法2、方法3和本文提出的方法的二维连续性的二维χ2检验结果如表 4所示。
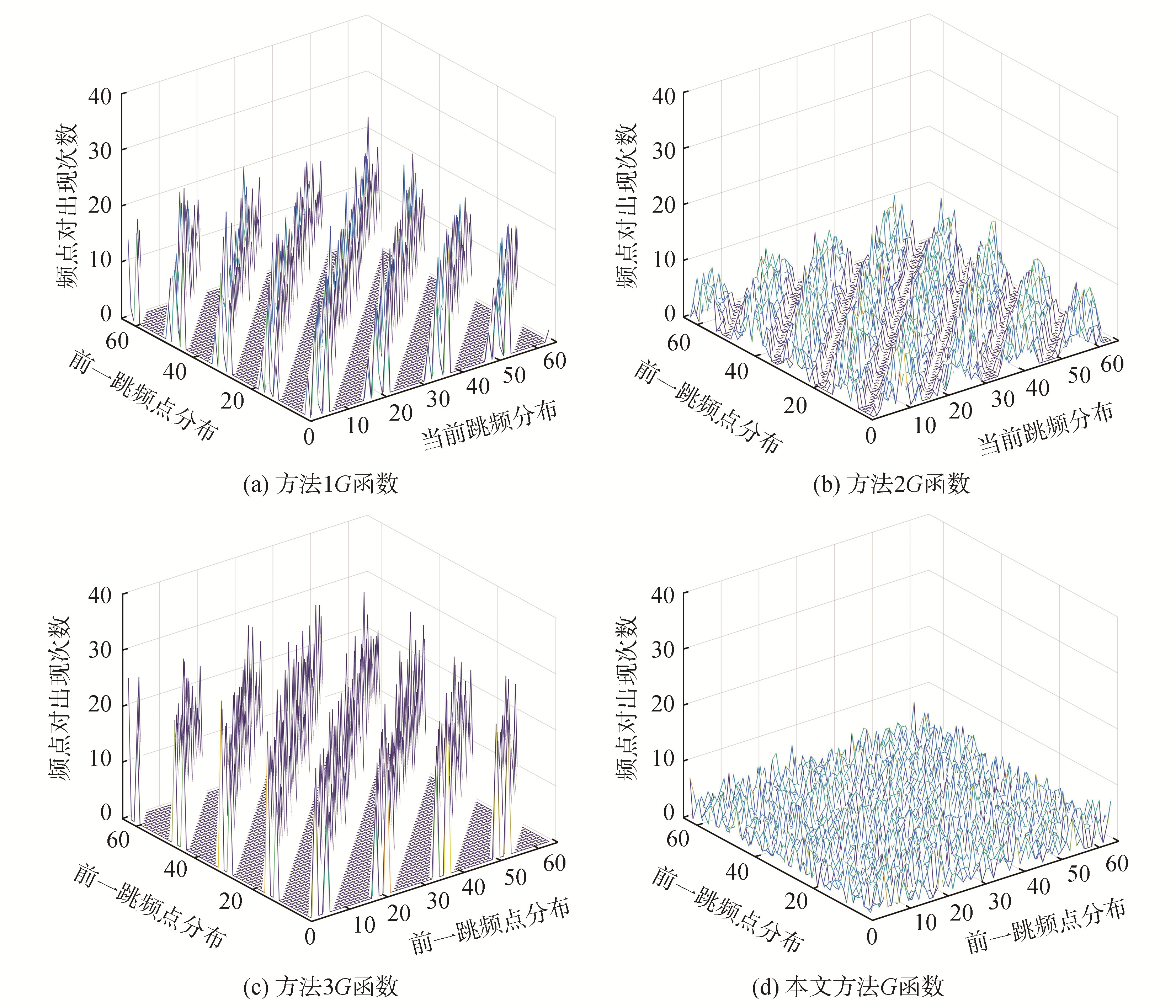
表 4 检验结果Table 4 Test results卡方检验临界值 方法1 方法2 方法3 TVID方法 4 277.714 2 43 542 9 295 74 412 4 036 从表 4的数值可知，本文提出的方法的检验结果小于临界值4 277.714 2，证明二维连续性检验的原假设成立，即每一种频率对的情况都被均匀的使用到，说明本文提出的方法有着更优越的抗截获性能。为了更直观地对比4种方法，现将DFH的频率序列二维连续性检验频率统计直方图引入，如图 7。
图 7 频率序列二维连续性检验频率统计直方图Fig. 7 Frequency series two-dimensional continuity test frequency statistical histogram下载:
全尺寸图片
由于引入了TVG的思想，使一个周期内的所有频率对都能被使用，且分解的方式和大小都是由m序列控制的，由于m序列具有良好的均匀特性和游程特性，使频率对的分布更加平均，由图 7可知，相比于其他3种方法，本文提出的方法产生的跳频点序列的二维连续性更好，每一个频率对都被使用且分布的更加平均，即本文提出的方法产生的跳频序列具有更好的抗截获性能。
3.4 安全性检验与分析
安全性指的是差分跳频的序列被破解的可能性，跳频序列越难以破解，则安全性越高。密码系统中，解密操作即为加密操作的逆过程，把解密同样长度的序列所需的时间可以作为衡量其安全性的重要指标，现有文献中均采用仿真序列解密所需要的时间衡量跳频序列的安全性[9-10, 15]。具体的参数为：方法2采用4个不同的G函数且包含所有可能出现的频率点集，本文方法分为4阶，每一个分集的子块数分别为32、16、8和4，采用的频率序列长度均为10 000，测试结果如表 5所示。
表 5 测试结果Table 5 Test results方法 t/s 方法1 0.005 61 方法2 0.012 34 TVID方法 0.015 61 从表 5中可以看出，相比于其他方法，本文提出的方法的解密所需时间最长，最难以破解，安全性最高，原因是由于本文设计的频率转移函数是随着迭代的过程而改变的，不同时刻的频率转移函数是不同的，因此，解密的时间也是最长的，安全性最高。
3.5 误码性能检验与分析
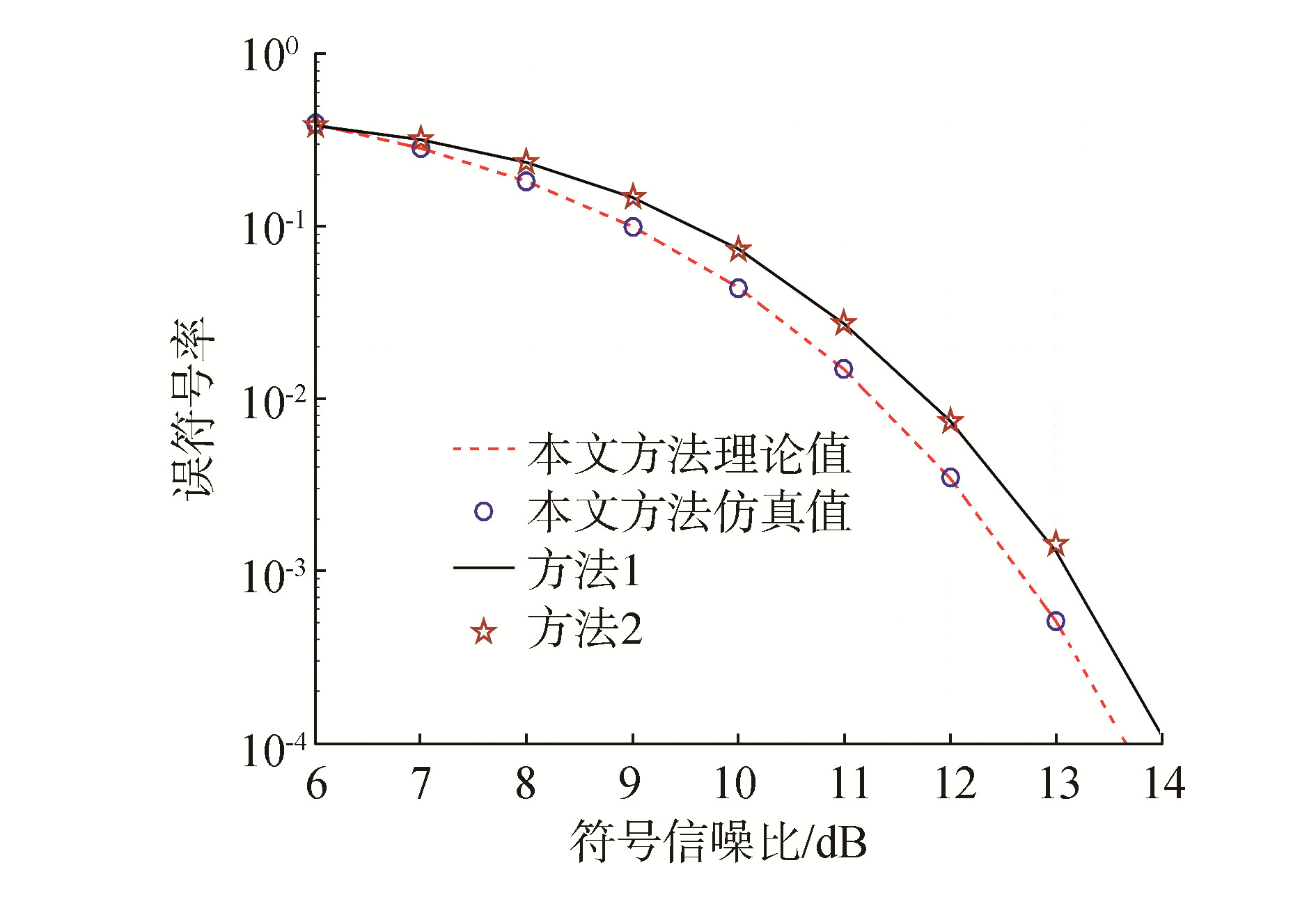
根据本文提出的频率转移函数及接收算法，对其接收端的译码性能进行仿真验证，本文方法中共分为4阶，每一个分集的子块数分别为32、16、8和4，仿真结果如图 8所示。
图 8 误码性能仿真对比Fig. 8 Error code performance simulation comparison diagram下载:
全尺寸图片
从图 8中可以看出，本文理论推导与实际仿真相吻合，且提出的频率转移函数在接收端经过FFT检测和解映射还原原始信息后的误码性能比其他方法更好，其增益主要来源于本文解映射的方法在接收端减少了判决的频率集，提升了正确判断接收频率的概率，而差分跳频还原原始数据的过程就是通过运算频率间的关系进行的，频点判断正确的越多，则还原原始数据越准确，因此，本文提出的方法在误码性能上会有提升。
4. 结论
1) 通过本文设计的G函数，可以产生安全性、随机性、均匀性更好的跳频序列，使非合作方更难以进行跳频信号的破译侦收，提高了差分跳频通信系统的抗截获性能和抗干扰性能。
2) 根据本文提出的G函数通过将频率区间分集的方式设计了相应的解映射算法，使接收端能够更准确的判决出跳频频点，还原解调出原始数据，从而提高了差分跳频通信系统的误码性能。
进一步，将继续分析迭代分解的子块数及分解的阶数对差分跳频通信系统的影响，以期在不同的信道环境下，找出最优的分解阶数及分解子块的方式。
-
图 1 差分跳频原理模型
Fig. 1 Differential frequency hopping system model
下载:
全尺寸图片
图 2 基于m序列、RS码和混沌序列的G函数生成原理框图
Fig. 2 Block diagram of G function generation principle based on m sequence, RS code and chaotic sequence
下载:
全尺寸图片
图 3 TVID算法原理示意
Fig. 3 Schematic diagram of TVID algorithm
下载:
全尺寸图片
图 4 解映射算法流程
Fig. 4 Flow chart of demapping algorithm
下载:
全尺寸图片
图 5 频率序列功率谱图
Fig. 5 Frequency sequence power spectrum
下载:
全尺寸图片
图 6 等分布检验的频率统计结果
Fig. 6 Graph of the frequency statistics of the isometric distribution test
下载:
全尺寸图片
图 7 频率序列二维连续性检验频率统计直方图
Fig. 7 Frequency series two-dimensional continuity test frequency statistical histogram
下载:
全尺寸图片
图 8 误码性能仿真对比
Fig. 8 Error code performance simulation comparison diagram
下载:
全尺寸图片
表 1 统计结果
Table 1 The statistical results
方法 标准差 方法1 2.031 方法2 2.186 方法3 2.006 TVID方法 1.946 表 2 假设检验原理
Table 2 Principle of hypothesis testing
真实情况 结论 接受H0 接受H1 H0为真 正确 Ⅰ类错误 H1为真 Ⅱ类错误 正确 表 3 检测结果
Table 3 Test results
卡方检验临界值 方法1 方法2 方法3 TVID方法 82.244 7 59.555 2 55.462 4 59.968 0 43.859 2 表 4 检验结果
Table 4 Test results
卡方检验临界值 方法1 方法2 方法3 TVID方法 4 277.714 2 43 542 9 295 74 412 4 036 表 5 测试结果
Table 5 Test results
方法 t/s 方法1 0.005 61 方法2 0.012 34 TVID方法 0.015 61 -
[1] BJÖRKLUND P, VÄRBRAND P, YUAN Di. Optimized planning of frequency hopping in cellular networks[J]. Computers & operations research, 2005, 32(1): 169-186. http://www.sciencedirect.com/science?_ob=ShoppingCartURL&_method=add&_eid=1-s2.0-S0305054803002107&originContentFamily=serial&_origin=article&_ts=1488513887&md5=4d8fe83070e8ca10084ed4a856076092 [2] KE Pinhui, ZHANG Shengyuan. Frequency hopping sequences based on d-form functions[J]. The journal of China universities of posts and telecommunications, 2010, 17(4): 58-62. doi: 10.1016/S1005-8885(09)60488-X [3] 李少谦, 董彬虹, 陈智. 差分跳频通信原理及应用[M]. 成都: 电子科技大学出版社, 2007: 26-131. LI Shaoqian, DONG Binhong, CHEN Zhi. Principle and application of differential frequency hopping[M]. Chengdu: University of Electronic Science and Technology Press, 2007: 26-131. [4] CHEN Zhi, LI Shaoqian, DONG Binhong. Synchronous multi-user performance analysis of differential frequency hopping system over Rayleigh-fading channels[C]//20066th International Conference on ITS Telecommunications. Piscataway, NJ: IEEE, 2006: 590-595. [5] 朱秀林, 胡用时, 于奇. 差分跳频系统的G函数算法研究[J]. 计算机与数字工程, 2005, 33(8): 46-48, 85. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSG200508008.htm ZHU Xiulin, HU Yongshi, YU Qi. Study of DFH system G function algorithm[J]. Computer & digital engineering, 2005, 33(8): 46-48, 85. https://www.cnki.com.cn/Article/CJFDTOTAL-JSSG200508008.htm [6] 朱秀林, 胡用时, 于奇. CHESS系统中一种改进的G函数算法[J]. 重庆邮电大学学报(自然科学版), 2005, 17(4): 444-446. https://www.cnki.com.cn/Article/CJFDTOTAL-CASH200504015.htm ZHU Xiulin, HU Yongshi, YU Qi. Improved G function algorithm of CHESS system[J]. Journal of Chongqing University of Posts and Telecommunications, 2005, 17(4): 444-446. https://www.cnki.com.cn/Article/CJFDTOTAL-CASH200504015.htm [7] 冯永新, 徐美荣, 钱博, 等. 一种差分跳频频率转移函数算法[J]. 航空学报, 2013, 34(3): 655-661. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201303022.htm FENG Yongxin, XU Meirong, QIAN Bo, et al. A frequency transform function algorithm for differential frequency hopping[J]. Acta aeronautica et astronauticasinica, 2013, 34(3): 655-661. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201303022.htm [8] 张月婷. 基于差分跳频抗截获抗干扰通信技术研究[D]. 西安: 西安电子科技大学, 2018. ZHANG Yueting. Research on anti-jamming and anti-interception communication technology based on diffe rential frequency hopping[D]. Xi'an: Xidian University, 2018. [9] QU Xiaoxu, WANG Shu, LI An, et al. A method to improve 2D continuity performance of differential frequency hopping sequence[C]//2008 4th International Conference on Wireless Communications, Networking and Mobile Computing. Piscataway, NJ: IEEE, 2008: 1-5. [10] 李潇. 基于频率转移函数的差分跳频抗干扰技术研究[D]. 西安: 西安电子科技大学, 2020. LI Xiao. Research on differential frequency hopping anti-interference technology based on frequency transfer function[D]. Xi'an: Xidian University, 2020. [11] 董彬虹, 李少谦, 陈智, 等. 差分跳频信号最佳接收机设计[J]. 电子科技大学学报, 2003, 32(5): 530-534. doi: 10.3969/j.issn.1001-0548.2003.05.014 DONG Binhong, LI Shaoqian, CHEN Zhi, et al. Design of optium receiver for DFH signal[J]. Journal of University of Electronic Science and Technology of China, 2003, 32(5): 530-534. doi: 10.3969/j.issn.1001-0548.2003.05.014 [12] 董彬虹, 唐诚, 李少谦. 基于状态网格图的差分跳频G函数构造方法研究[J]. 电子科技大学学报, 2011, 40(4): 497-500. https://www.cnki.com.cn/Article/CJFDTOTAL-DKDX201104005.htm DONG Binhong, TANG Cheng, LI Shaoqian. Research of G-function constructing method for DFH system based on state trellis diagram[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(4): 497-500. https://www.cnki.com.cn/Article/CJFDTOTAL-DKDX201104005.htm [13] 崔久冬. 基于FPGA的差分跳频信号频率检测技术研究[J]. 电子制作, 2020(23): 91-93. https://www.cnki.com.cn/Article/CJFDTOTAL-DZZZ202023030.htm CUI Jiudong. Research on frequency detection technology of differential frequency hopping signal based on FPGA[J]. Practical electronics, 2020(23): 91-93. https://www.cnki.com.cn/Article/CJFDTOTAL-DZZZ202023030.htm [14] 杨保峰, 沈越泓. 差分跳频的等效卷积码分析[J]. 吉林大学学报(信息科学版), 2006, 24(5): 495-500. https://www.cnki.com.cn/Article/CJFDTOTAL-CCYD200605007.htm YANG Baofeng, SHEN Yuehong. Study method of equivalent convolutional code structure for differential frequ ency hopping[J]. Journal of Jilin University (information science edition), 2006, 24(5): 495-500. https://www.cnki.com.cn/Article/CJFDTOTAL-CCYD200605007.htm [15] CHEN Rui, SHI Jia, YANG Lieliang, et al. High-security sequence design for differential frequency hopping systems[J]. IEEE systems journal, 2021, 15(4): 4895-4906. http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9198094
