Hydrodynamic performance of propeller in cavitating conditions under different ambient pressures
-
摘要: 为研究水面快速游艇、水面大型舰船和水下机器人的高负荷螺旋桨，本文采用MAU4-40小型桨，通过改变环境压力，基于两相流和空化模型预报了3种载体螺旋桨空泡初生的临界转速，空泡发展形状和空泡生成后的螺旋桨水动力性能曲线。并将水下机器人携带纵斜桨自航空泡问题进行研究。结果表明: 理论预报空泡发生的临界转速小于数值模拟的临界转速；3种工况对应不同的临界转速; 当空泡覆盖整个叶背区域，推力系数最大下降28.5%;纵斜能降低空泡发生，并使空泡位置移向随边; 水下机器人伴流对螺旋桨空泡略有影响。Abstract: To investigate the propeller cavitation of fast yachts, large ships and autonomous underwater vehicle (AUV) under heavy conditions, a MAU 4-40 model propeller is used to predict cavitation inception, cavitation development and hydrodynamic performance curve in cavitating conditions by changing the ambient pressure based on multiphase flow model and cavitation model. After that, the cavitation under non-uniform flow is studied for an AUV self-propulsion with a raked propeller. The numerical results showed that, the critical revolution for cavitation in theory is larger than that in numerical calculation; different critical revolution speeds for cavitation are found in three conditions; the maximum thrust coefficient decreased by 28.5% as the suction side is covered with cavitation; a raked propeller is helpful to decrease cavitation and to move the cavitation area into the trailing edge; The non-uniform inflow from the AUV will result in small cavitation variation.
-
高负荷螺旋桨容易产生空泡，空泡会带来振动、噪声、侵蚀的负面影响，还会降低螺旋桨的推进效率。工作于高负荷的螺旋桨通常包括3种载体：大负荷水面舰船、水面小型快速游艇和水下机器人。其中，大负荷水面舰船螺旋桨发生空泡现象十分常见[1-3]。通常采用空泡数相等方法，通过降低环境压强，在空泡水筒中进行模型试验或基于两相流和空化模型进行数值模拟。数值研究围绕捕捉空泡图的精度，开展螺旋桨网格生成方法、加密位置、湍流模型选择等研究内容。龚鹏[4]分别采用结构网格和非结构网格对其空泡性能进行验证；叶金铭等[5]用基于面元法，比较不同网格划分计算得到的空泡形状，讨论了网格疏密程度对空泡的影响; 朱志峰等[6]认为增加盘面到出口的距离和外流域使用结构网格可以提高片空化预报。胡健等[7]采用叶梢尖端螺旋加密方法捕捉叶梢空泡。Yilmaz等[8]采用自适应网格技术划分叶梢涡滑流区域，结合大涡模拟，研究了船、桨、舵之间耦合对螺旋桨梢涡发展的影响。对大负荷水面舰船船后非均匀伴流对螺旋桨空泡的发生、发展、溃灭的瞬态变化也有相关研究。刘恒等[1]和王超等[9]通过在入口处加载船艉非均匀伴流，研究螺旋桨处于不同强度伴流区域空泡性能，发现桨叶表面空泡范围和大小差异较大，进入高伴流区域空泡加剧，远离高伴流区域空泡减弱。对改善螺旋桨空泡的螺旋桨参数方面也开展了侧斜角、纵斜角、扭曲程度等方面的研究。赵旻晟等[10]采用OpenFOAM对E779A螺旋桨在斜流工况下的水动力特性及桨叶上的非定常空化进行模拟分析，结果表明，来流夹角增加会使桨叶吸力面空泡分布变得不均匀，对桨的水动力性能影响较大。相似结论在文献[11]中也表明，当纵倾向压力面弯曲时，空泡会向内半径延伸，而梢涡空泡减小。Hu等[12]对不同侧斜对梢涡空泡的影响进行了研究。
随着小型桨转速和进速提高，如水面小型快速游艇，水下高速AUV或近冰底航行AUV, 其螺旋桨负荷大大增加，空泡现象不可忽略。这种小型桨对应的临界转速和大负荷水面舰船螺旋桨有很大差别，需要进行预报，有利于避免空泡和提高安全操纵。本文对这3种载体可能发生的空化问题，理论分析了空泡初生转速[13]，结合汽液两相流和空化模型，研究了空泡形成和空泡发生后螺旋桨水动力性能曲线，探讨了纵斜角对改善空泡的作用，讨论了AUV携带螺旋桨自航的非均匀伴流场对空泡动态影响。
1. 数学模型
采用多相流模型中的均质混合流模型，求解螺旋桨发生空泡后的汽液两相均质混合流的连续方程：
$$ \frac{{\partial {\rho _m}}}{{\partial t}} + \frac{{\partial \left( {{\rho _m}{u_i}} \right)}}{{\partial {x_i}}} = 0 $$ (1) $$ {\rho _m} = {\rho _l}(1 - \alpha ) + {\rho _v}\alpha $$ (2) 式中：α为气相体积分数；ρm为混合相的密度。
动量方程为：
$$ \begin{array}{c} \frac{{\partial \left( {{\rho _m}{u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {{\rho _m}{u_i}{u_j}} \right)}}{{\partial {x_j}}} = \\ - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\left( {{\mu _m} + {\mu _{t, m}}} \right)\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right] \end{array} $$ (3) 式中: 下标l、v分别指液相和气相；μm为混合流的动力粘性系数，定义与混合密度类似；μt.m为湍流引起的涡粘性系数，需要对混合流采用湍流模型进行求解。本文采用RNG k-ε两方程模型求解涡粘系数。
关于蒸汽质量分数f的控制方程为：
$$ \frac{{\partial \left( {f{\rho _m}} \right)}}{{\partial t}} + \frac{{\partial \left( {f{\rho _m}{u_j}} \right)}}{{\partial {x_j}}} = {R_e} - {R_c} $$ (4) 式中：Re和Rc分别为由汽化和凝结引起的相变率，f为：
$$ f = \frac{{{\rho _v}}}{{{\rho _m}}}\alpha $$ (5) 空化模型采用Zwart-Gerber-Belamri模型：
当p≤pv时
$$ {R_e} = {C_e}\frac{{3{\alpha _{{\rm{nuc}}}}(1 - \alpha ){\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}\frac{{{\rho _v} - p}}{{{\rho _l}}}} $$ (6) 当p＞pv时
$$ {R_e} = {C_e}\frac{{3\alpha {\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}\frac{{p - {\rho _v}}}{{{\rho _l}}}} $$ (7) 式中：pv为水的饱和蒸气压，与温度相关；气核半径RB默认取值1 μm；αnuc为水中所含气核体积分数。
2. 物理模型
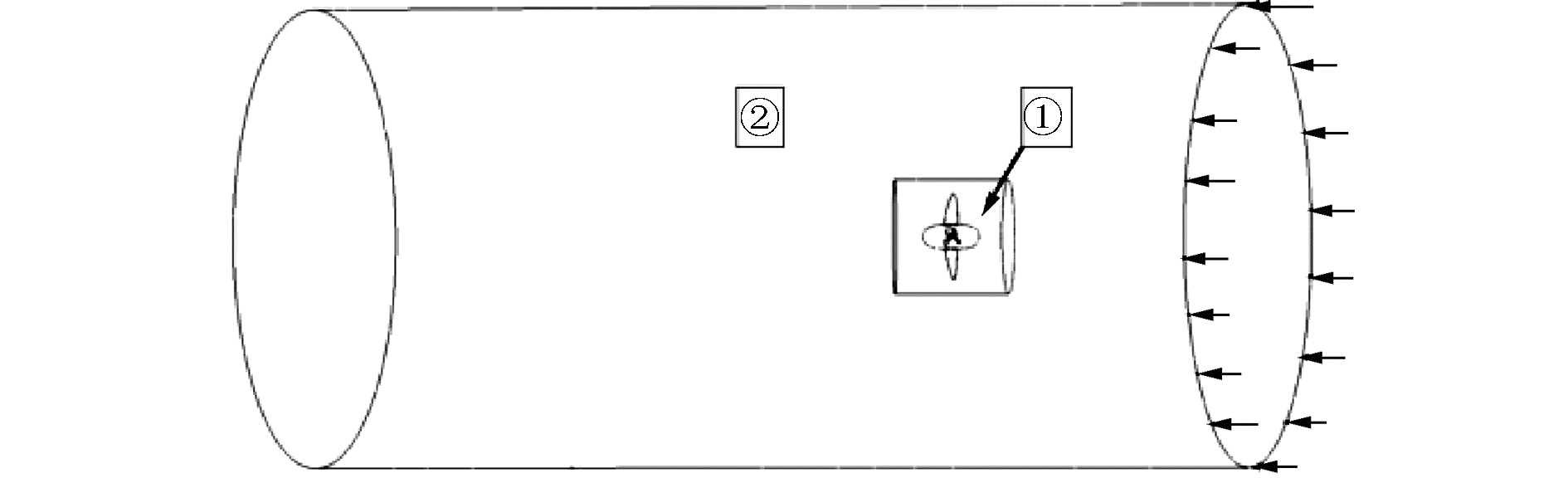
试验模型为MAU4-40标准桨，盘面比0.4，螺距比0.9，螺旋桨直径D=0.156 m，如图 1为螺旋桨网格正视图。计算流域为一圆柱形流域，入口距桨盘面3D，出口距桨盘面5D，外域直径为6D，如图 2所示。整个计算域包括旋转内流域①和静止外流域②，螺旋桨在旋转流域内，数值模拟时，螺旋桨和旋转内部流域一起旋转。内外流域之间用滑移界面连接，界面上的网格采用非一致连接。螺旋桨模型复杂，曲率变化较大，采用非结构网格进行划分，在桨毂和桨连接处、叶梢、导边和随边等处进行网格局部加密，以捕捉局部流场梯度变化，网格总数为1 046 147。
图 1 螺旋桨网格模型Fig. 1 Propeller mesh
下载:
全尺寸图片
图 2 螺旋桨空泡模拟的计算域Fig. 2 Computational domain of propeller cavitation下载:
全尺寸图片
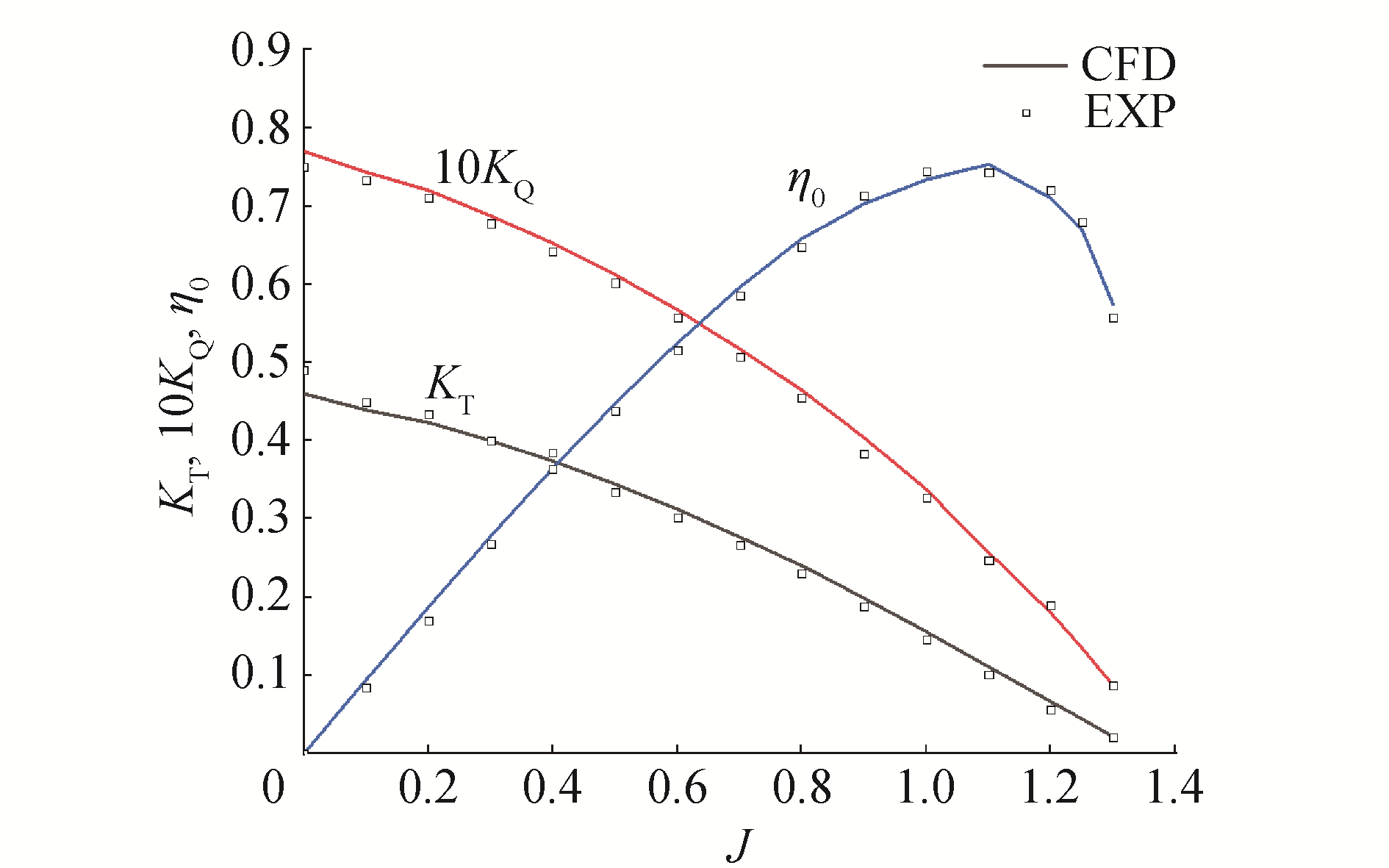
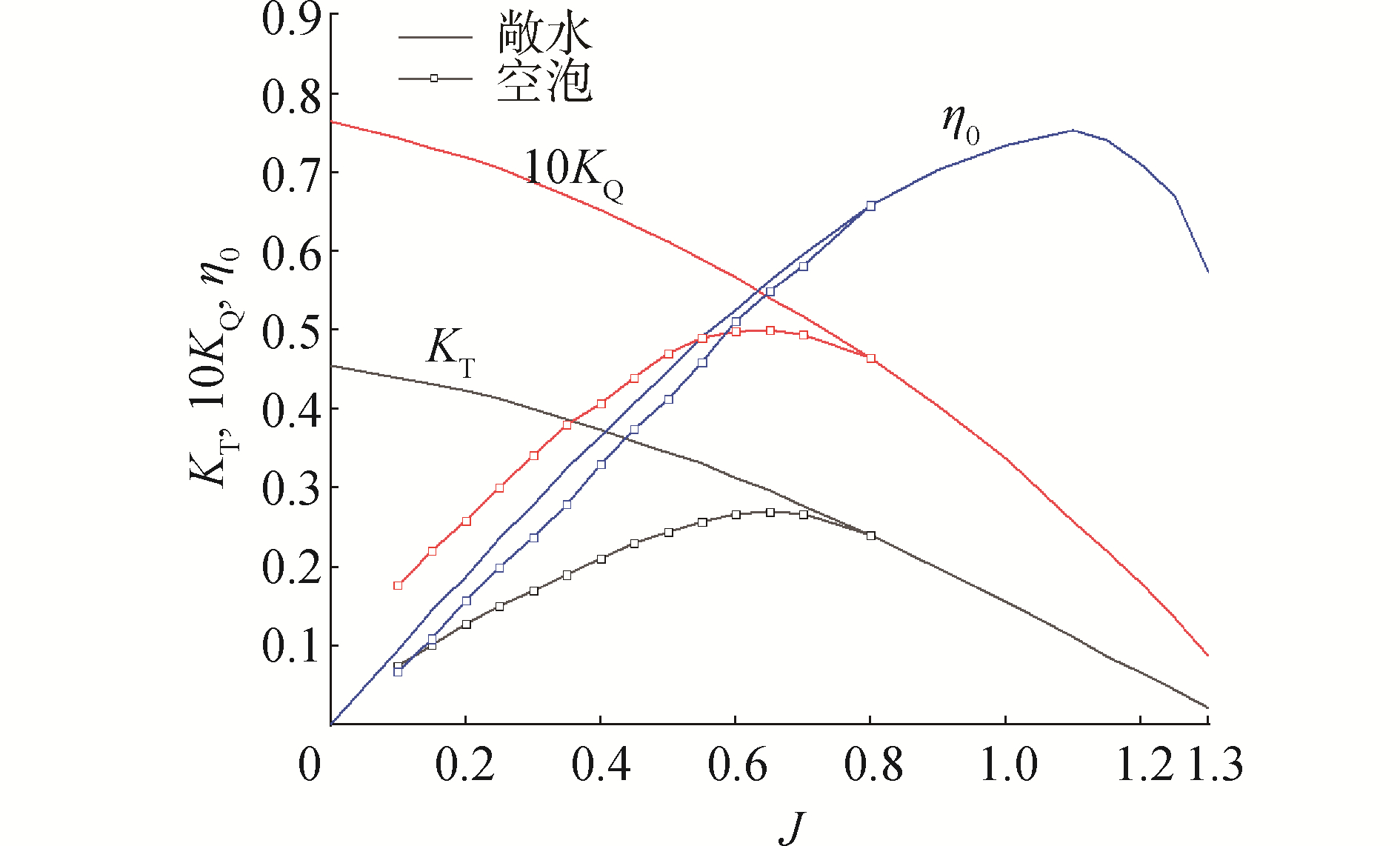
首先在无空泡的敞水工况下对MAU4-40进行螺旋桨水动力性能模拟。螺旋桨进速不变，通过改变转速，实现不同进速系数下的数值模拟，并与图谱试验值比较，如图 3所示[14]。J为进速系数；KT、KQ和η0分别为螺旋桨的推力系数、扭矩系数和敞水效率。数值计算(CFD)和试验结果(EXP)两者曲线基本一致，相对偏差均在较小误差范围内，各曲线均达到了较高的预报精度。
图 3 敞水性能曲线的试验结果与数值结果对比Fig. 3 Open water curve comparison between experimental and numerical results下载:
全尺寸图片
3. 空化预报
3.1 临界转速的理论预测
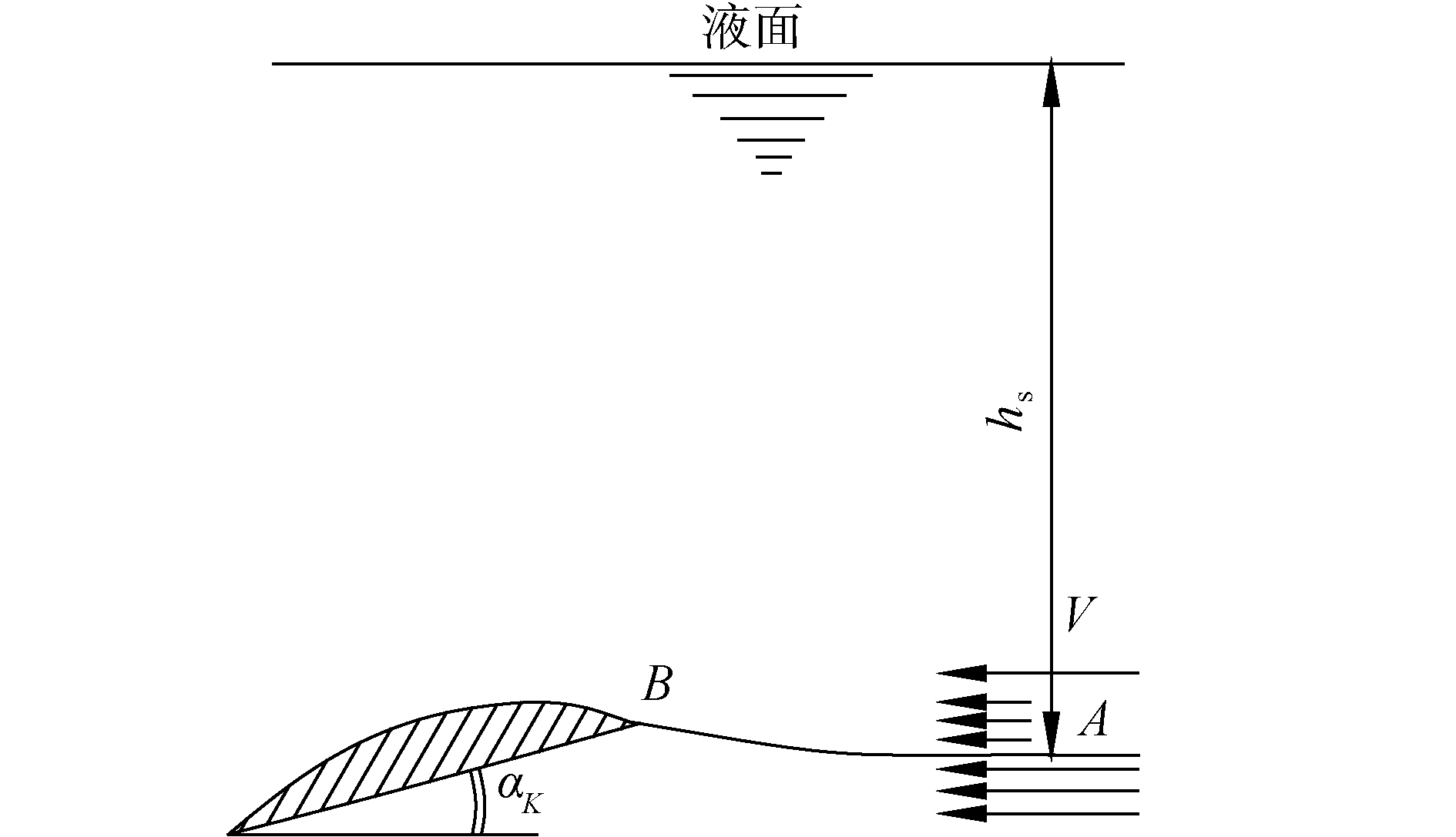
当螺旋桨叶片置于水下一定深度hs, 来流V经过叶剖面时，随着螺旋桨高速旋转，叶剖面速度Vb增加，叶剖面上的压强pb就会降低(如图 4所示)，列出叶背B点的伯努利方程，见式(8)。对应的最大减压系数ξ如式(9)。相应的最低压强达到该温度的气化压强pv，则对应无因次压强为空泡数σ。当最大减小系数ξ大于空泡数σ，空泡就能发生(p0为环境压强)。
$$ {p_b} + \frac{1}{2}\rho V_b^2 = {p_0} + \frac{1}{2}\rho {V^2} $$ (8) $$ \xi = \frac{{{p_0} - {p_b}}}{{\frac{1}{2}\rho {V^2}}} = {\left( {\frac{{{V_b}}}{V}} \right)^2} $$ (9) $$ \sigma = \frac{{{p_0} - {p_v}}}{{\frac{1}{2}\rho {V^2}}} $$ (10) $$ \xi \ge \sigma $$ (11) 
图 4 叶剖面来流Fig. 4 Inflow fluid to the section下载:
全尺寸图片
叶剖面的最大减压系数，就是叶剖面的最大压力系数Cpmin，可根据式(12)计算获得：
$$ {C_{p\min }} = - \left[ {2.28\frac{t}{c} + 0.56{C_{Li}} + {{(\alpha - 0.28)}^2}} \right] $$ (12) 假设海水温度10 ℃，螺旋桨叶剖面浸没深度hs＜1 m，则产生空泡的临界速度Vi为：
$$ {V_i} = \sqrt {\frac{{2(97.655 + 9.81h)}}{{\left| {{C_{p\min }}} \right|}}} $$ (13) 假设螺旋桨进速VA=6 m/s，则临界转速如式(14)所示，叶梢产生空泡的临界转速为n=3 537 r/min。随着进速提高，发生空泡的临界转速则降低，如表 1所示。因此水面高速游艇，常采用多对转桨分担推力，避免空泡发生。
$$ n = \frac{{\sqrt {V_i^2 - V_A^2} }}{{{\rm{ \mathsf{ π} }}D}} $$ (14) 表 1 近水面临界转速Table 1 Critical revolution speedV/(m·s-1) n/(r·min-1) 6 3 537 10 3 399 15 3 111 20 2 656 22.5 2 337 3.2 标准大气压下的空泡模型
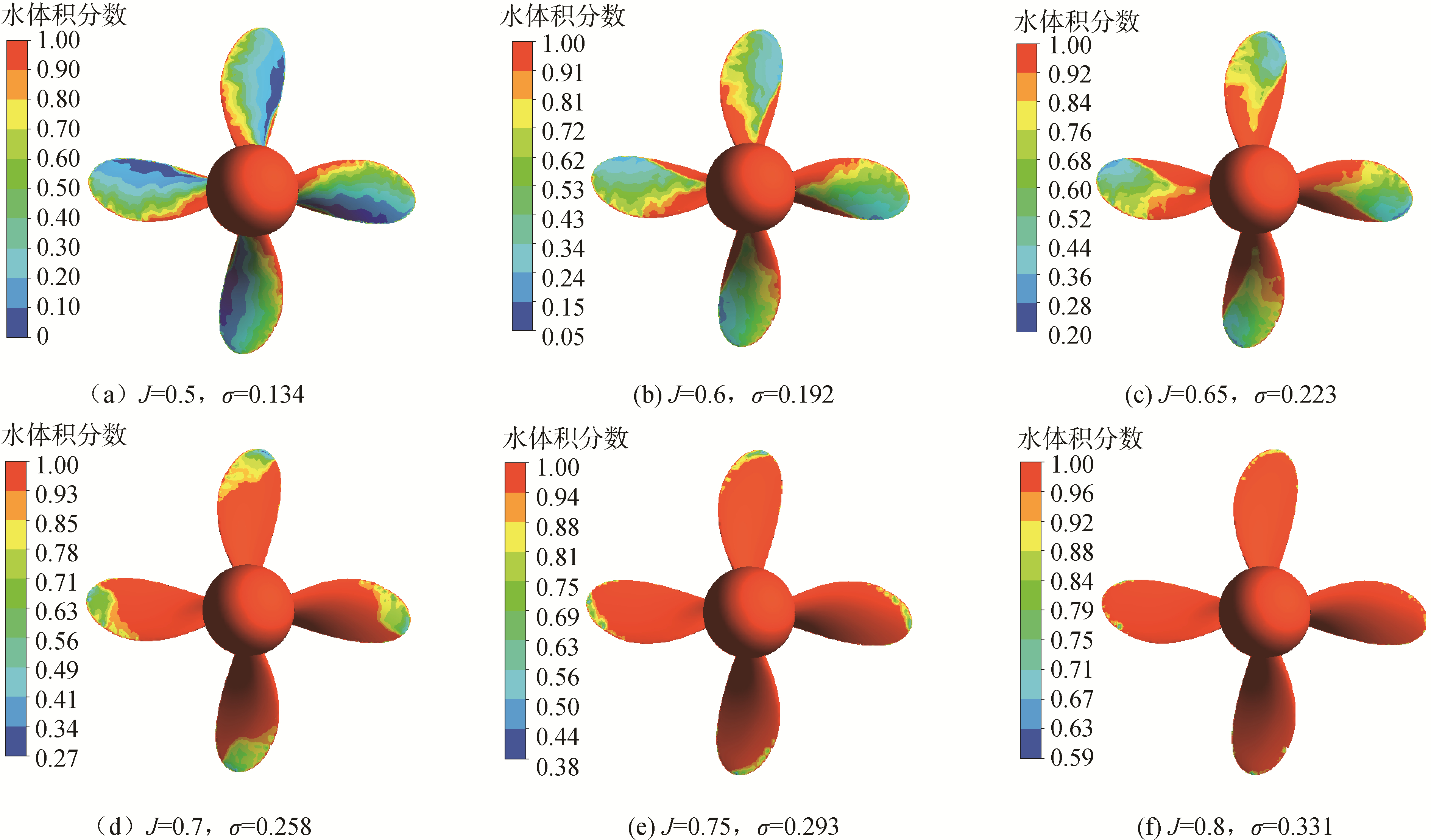
水面小型快速游艇的螺旋桨轴心压强为近似一个标准大气压。设环境压强为一个标准大气压，模拟MAU 4-40桨的空泡水动力性能。假定进速为6 m/s，调整转速，实现不同进速系数下的空泡模拟，其空泡在叶背面的发生形状随进速系数的变化如图 5所示。当进速系数为J=0.8，梢涡空泡初生(这与刘恒等[1]试验中梢涡空泡首先发生结论一致)，对应的临界转速为2 884 r·min-1，较理论预报值要小18%，主要因为螺旋桨各叶剖面连续作用于水，各剖面的耦合作用，使叶梢处合成速度增大，使空泡发生提前。随着螺旋桨转数的不断提高，空泡现象逐渐明显，主要位于导边至叶梢处(J=0.75, 0.7)，形成局部空泡，为空泡第1阶段。当转速进一步提高(J=0.65，0.6，0.5)，片状空泡几乎布满整个叶背，空泡开始延伸到随边外围，形成第2阶段空泡，叶背维持其汽化压力，叶背的压力不再随着转速的增加而降低，则螺旋桨的推力不再随着转速的提高而增加，因而其推力也将比没有汽化压力因素时要低，如图 6所示。当空泡完全布满叶背，计入空化影响的螺旋桨推力系数(J=0.5)相对无空泡情况降低28.5%。
图 5 不同进速系数下螺旋桨产生空泡情况Fig. 5 Cavitation situation of propellers at different advance ratios下载:
全尺寸图片
图 6 标准大气压下螺旋桨空泡后的水动力性能曲线Fig. 6 Propeller′s hydrodynamic performance curves in cavitating conditions at an atmospheric pressure下载:
全尺寸图片
3.3 不同真空度的空泡模拟
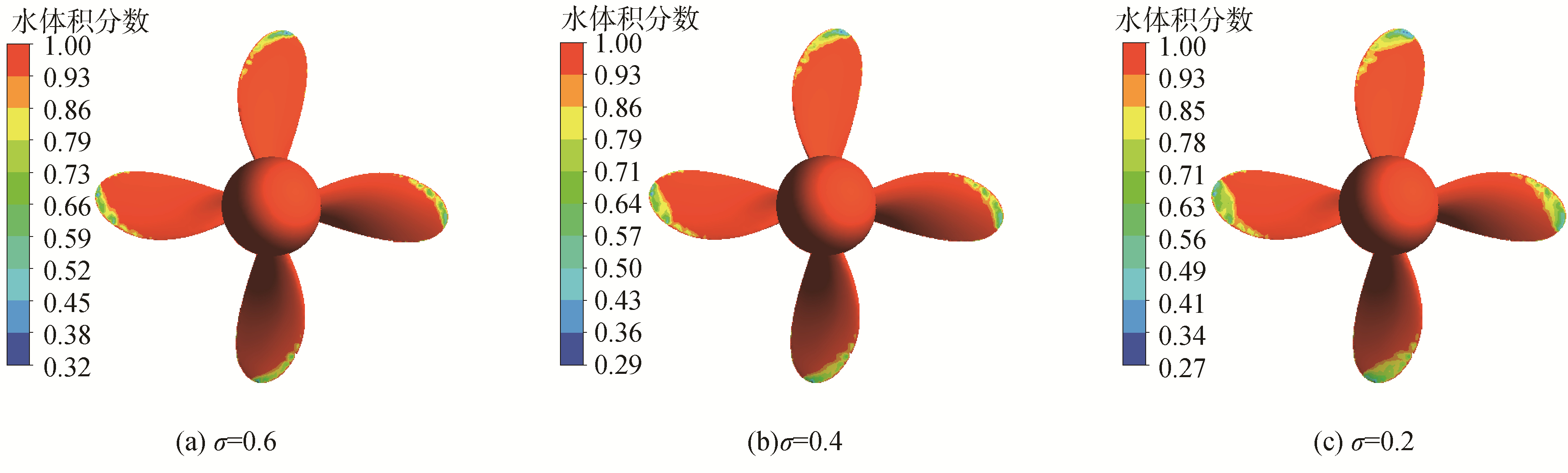
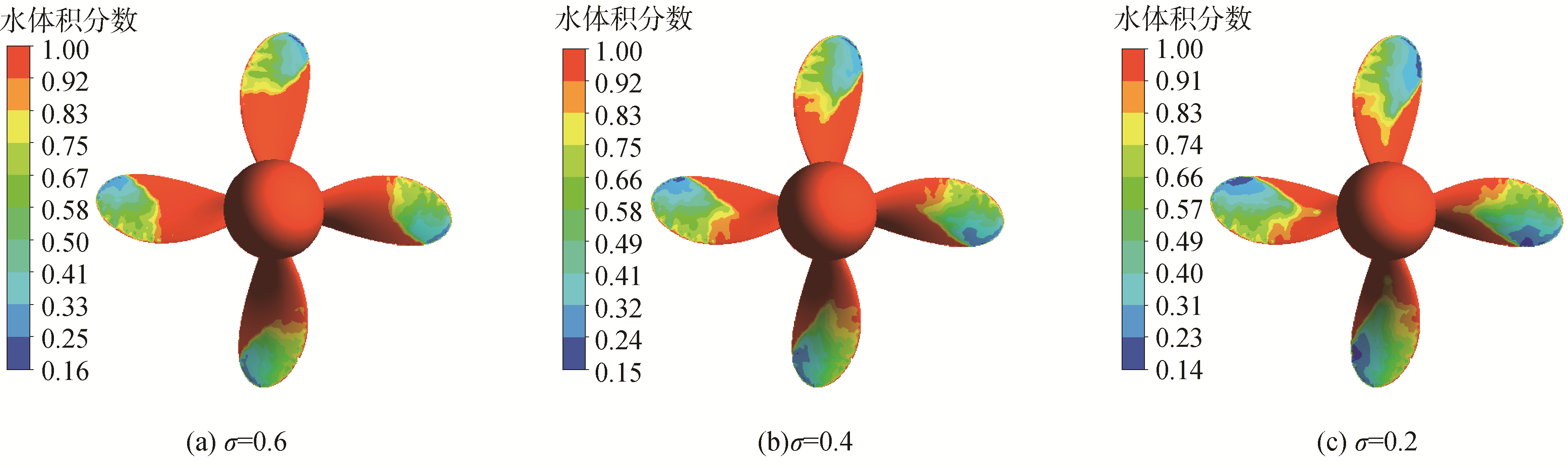
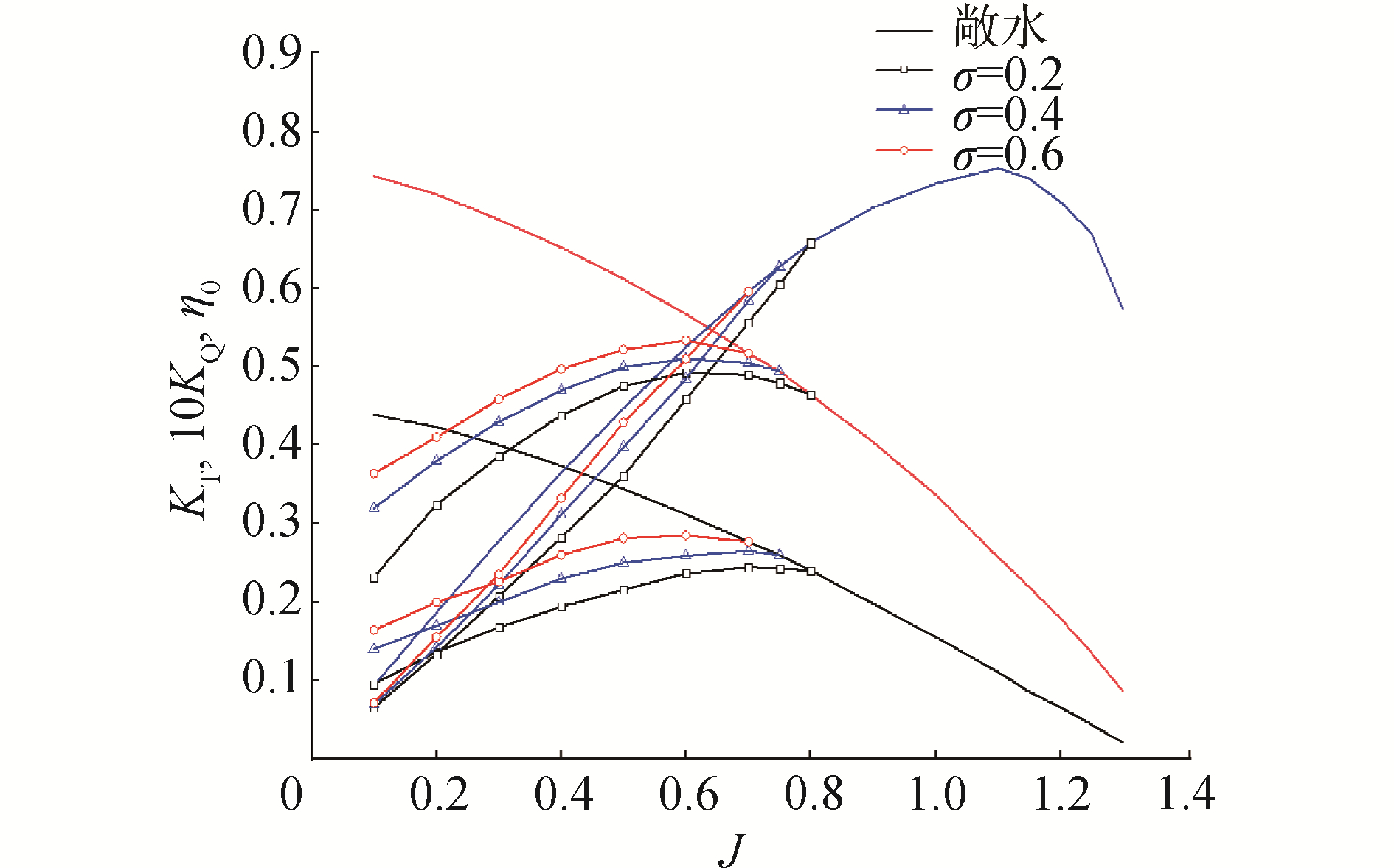
大负荷水面舰艇螺旋桨，其螺旋桨尺寸大，载体航速大，通常通过满足进速系数相等，空泡数相等，在减压空泡水筒中进行模型桨空泡数值模拟和试验。即通过降低环境压强，实现不同真空度下的空泡模拟，数值模拟条件和盛振邦[15]试验条件一致，获得了一致的空泡后螺旋桨性能曲线图。图 7~8分别为螺旋桨在进速系数J=0.7, 0.6，空泡数分别为0.6、0.4、0.2时的空泡云图。由图 7~8可见，相同进速系数下，空泡数越小，空泡越容易发生。空泡数一致时，螺旋桨载荷越大，空泡越严重，即螺旋桨合速度保持不变，提高转速，降低进速，则空泡更容易发生，表明载体螺旋桨高转速启动时，容易产生空泡。由图 9的空泡性能曲线可见，低空泡数对应的临界进速相对高空泡数的大些。低空泡数更容易产生空泡；相同进速下，低空泡数的空泡水动力性能下降更大。
图 7 J=0.7时不同空泡数下螺旋桨空泡图Fig. 7 Propeller cavitation contours in different cavitating indexes (J=0.7)下载:
全尺寸图片
图 8 J=0.6时不同空泡数下螺旋桨空泡图Fig. 8 Propeller cavitation contours in different cavitating indexes (J=0.6)下载:
全尺寸图片
图 9 不同空泡数下螺旋桨空泡性能曲线Fig. 9 Propeller′s hydrodynamic performance curves in cavitating conditions at different cavitation indexes下载:
全尺寸图片
3.4 正压下的空泡模拟
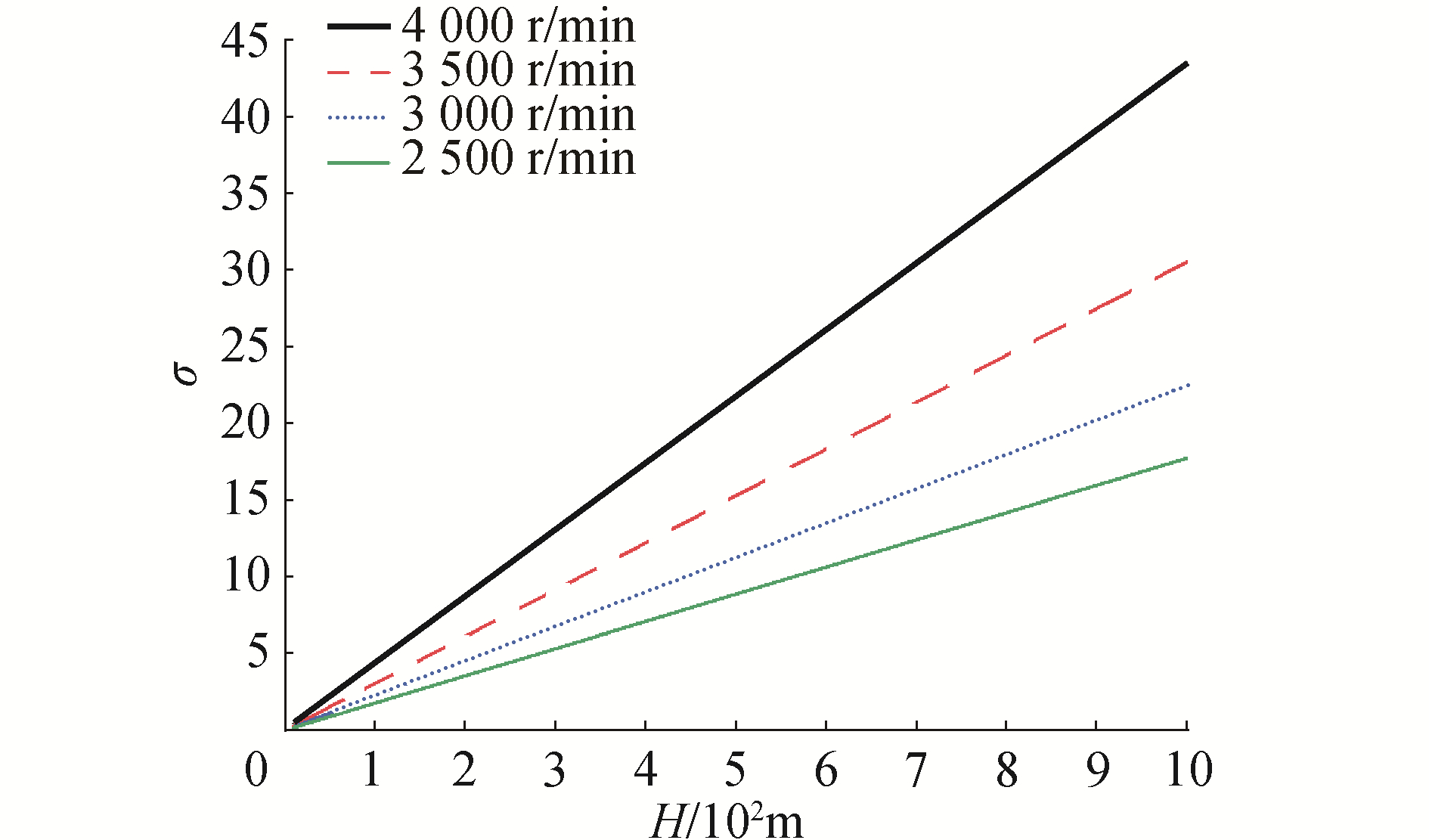
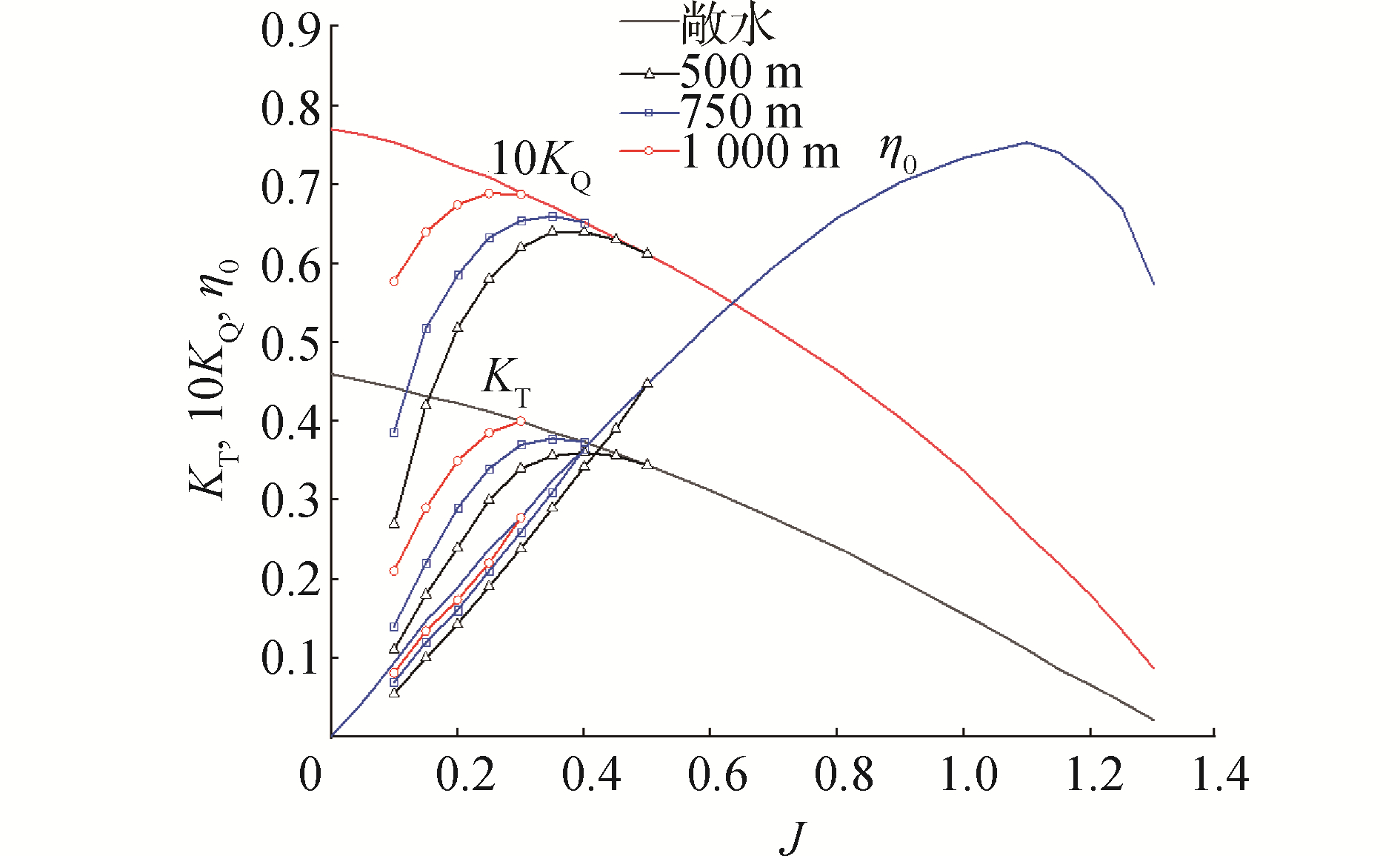
水下机器人工作深度从10~6 000 m变化, 螺旋桨直径较小。其最大电机转速也可以接近5 000 r/min, 遇到螺旋桨高负荷下，是否也会产生空泡，则需要对不同深度的环境压强下进行空泡模拟，即正压下的空泡模拟。如图 10所示，深度越大，空泡数越大(这是减压空泡水筒无法模拟的)，理论上越难产生空泡。如果产生了空泡，其空泡后的螺旋桨水动力性能如图 11所示。以深度500 m为例，临界空泡对应的进速系数J=0.5, 对应的转速n=4 614 r/min。
图 10 深度与空泡数曲线Fig. 10 Cavitation index variation with depth下载:
全尺寸图片
图 11 不同深度螺旋桨空泡性能曲线Fig. 11 Cavitation performance curves under different depths下载:
全尺寸图片
3.5 纵斜对螺旋桨空泡的性能的影响
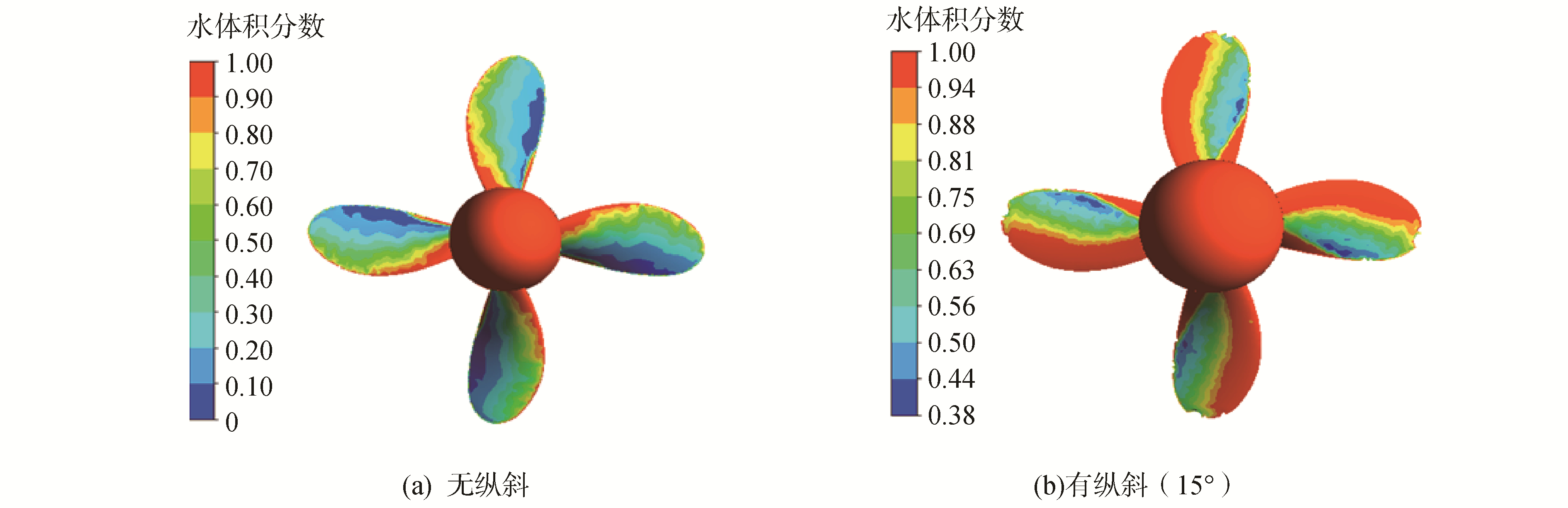
改变纵斜角对空泡的影响结果如图 12所示。在相同进速系数J=0.5时，在一个标准大气压下，采用无纵斜桨和纵斜桨(纵斜15°)，空泡图有了很大的改变，前者空泡较为严重，覆盖整个叶背；后者空泡范围减小，局限在中间到随边区域。可见，纵斜有利于改善空泡性能。这主要是因为纵斜可以减小不定常载荷通过轴系传递到载体的轴承力。
图 12 纵倾对螺旋桨空泡的影响Fig. 12 Effect of rake on the cavitation of suction side of the blade下载:
全尺寸图片
3.6 非均匀伴流影响
将螺旋桨安装在AUV后方，进行无空泡自航模拟[16]。当无空化计算稳定后，开启空泡模型，可以捕捉到载体非均匀尾迹(桨盘前非均匀伴流)对旋桨空泡影响，通过瞬态模拟，捕捉到0°~50°，每隔10°的螺旋桨叶背空泡图，如图 13所示，可见AUV伴流对螺旋桨空泡有一定的影响。
图 13 AUV非均匀伴流对螺旋桨空泡影响Fig. 13 Effect of non-uniform wake of AUV on the propeller cavitation下载:
全尺寸图片
4. 结论
1) 标准大气压下，理论预报发生空泡的临界转速比数值模拟偏大18%，数值模拟空泡发生提前，主要是螺旋桨叶片各剖面流场耦合所致。
2) 水面大型舰船螺旋桨更容易产生空泡。相等进速系数下，低空泡数的水动力性能下降更大。
3) 深度增加，空泡数增加。500 m水深，AUV螺旋桨发生空泡的临界转速高达4 614 r/min。小于这个转速，无需考虑AUV螺旋桨空化问题。
4) 纵斜有利于改善空泡性能，减少叶背空泡范围，但使空泡位置由导边向随边方向偏移。
5) AUV伴流对螺旋桨空泡的瞬态变化略有影响。
-
图 1 螺旋桨网格模型
Fig. 1 Propeller mesh
下载:
全尺寸图片
图 2 螺旋桨空泡模拟的计算域
Fig. 2 Computational domain of propeller cavitation
下载:
全尺寸图片
图 3 敞水性能曲线的试验结果与数值结果对比
Fig. 3 Open water curve comparison between experimental and numerical results
下载:
全尺寸图片
图 4 叶剖面来流
Fig. 4 Inflow fluid to the section
下载:
全尺寸图片
图 5 不同进速系数下螺旋桨产生空泡情况
Fig. 5 Cavitation situation of propellers at different advance ratios
下载:
全尺寸图片
图 6 标准大气压下螺旋桨空泡后的水动力性能曲线
Fig. 6 Propeller′s hydrodynamic performance curves in cavitating conditions at an atmospheric pressure
下载:
全尺寸图片
图 7 J=0.7时不同空泡数下螺旋桨空泡图
Fig. 7 Propeller cavitation contours in different cavitating indexes (J=0.7)
下载:
全尺寸图片
图 8 J=0.6时不同空泡数下螺旋桨空泡图
Fig. 8 Propeller cavitation contours in different cavitating indexes (J=0.6)
下载:
全尺寸图片
图 9 不同空泡数下螺旋桨空泡性能曲线
Fig. 9 Propeller′s hydrodynamic performance curves in cavitating conditions at different cavitation indexes
下载:
全尺寸图片
图 10 深度与空泡数曲线
Fig. 10 Cavitation index variation with depth
下载:
全尺寸图片
图 11 不同深度螺旋桨空泡性能曲线
Fig. 11 Cavitation performance curves under different depths
下载:
全尺寸图片
图 12 纵倾对螺旋桨空泡的影响
Fig. 12 Effect of rake on the cavitation of suction side of the blade
下载:
全尺寸图片
图 13 AUV非均匀伴流对螺旋桨空泡影响
Fig. 13 Effect of non-uniform wake of AUV on the propeller cavitation
下载:
全尺寸图片
表 1 近水面临界转速
Table 1 Critical revolution speed
V/(m·s-1) n/(r·min-1) 6 3 537 10 3 399 15 3 111 20 2 656 22.5 2 337 -
[1] 刘恒, 伍锐, 孙硕. 非均匀流场螺旋桨空泡数值模拟[J]. 上海交通大学学报, 2021, 55(8): 976-983. https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT202108009.htm LIU Heng, WU Rui, SUN Shuo. Numerical simulation of propeller cavitation in non-uniform flow[J]. Journal of Shanghai Jiao Tong University, 2021, 55(8): 976-983. https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT202108009.htm [2] 陆芳, 陆林章, 庞业珍, 等. 螺旋桨空泡与脉动压力及振动特性研究[J]. 船舶力学, 2019, 23(11): 1294-1299. doi: 10.3969/j.issn.1007-7294.2019.11.003 LU Fang, LU Linzhang, PANG Yezhen, et al. Investigation on tip vortex cavitation and pressure fluctuation of propeller[J]. Journal of ship mechanics, 2019, 23(11): 1294-1299. doi: 10.3969/j.issn.1007-7294.2019.11.003 [3] 王超, 韩康, 汪春辉, 等. 冰区航行船舶推进器特殊性分析[J]. 中国舰船研究, 2019, 14(2): 1-7. https://www.cnki.com.cn/Article/CJFDTOTAL-JCZG201902001.htm WANG Chao, HAN Kang, WANG Chunhui, et al. Analysis on the particularity of propulsor of ice-going ships[J]. Chinese journal of ship research, 2019, 14(2): 1-7. https://www.cnki.com.cn/Article/CJFDTOTAL-JCZG201902001.htm [4] 袭鹏, 熊鹰, 蒲汲君. 基于Fluent的E799A空泡性能数值计算网格对比[J]. 舰船科学技术, 2019, 41(7): 30-33. https://www.cnki.com.cn/Article/CJFDTOTAL-JCKX201907007.htm XI Peng, XIONG Ying, PU Jijun. Mesh comparison on E799A cavitation performance based on fluent[J]. Ship science and technology, 2019, 41(7): 30-33. https://www.cnki.com.cn/Article/CJFDTOTAL-JCKX201907007.htm [5] 叶金铭, 熊鹰. 螺旋桨非定常空泡数值预报中的几个问题[J]. 武汉理工大学学报(交通科学与工程版), 2006, 30(6): 961-964. doi: 10.3963/j.issn.2095-3844.2006.06.010 YE Jinming, XIONG Ying. Numerical and experimental research on pressure fluctuations induced by propeller cavitation[J]. Journal of Wuhan University of Technology (transportation science & engineering), 2006, 30(6): 961-964. doi: 10.3963/j.issn.2095-3844.2006.06.010 [6] 朱志峰, 方世良, 王晓燕. 船舶螺旋桨黏性空化流场数值方法[J]. 东南大学学报(自然科学版), 2010, 40(6): 1146-1151. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201006005.htm ZHU Zhifeng, FANG Shiliang, WANG Xiaoyan. Nnumerical method for viscous cavitating flow around ship propeller[J]. Journal of Southeast University (natural science edition), 2010, 40(6): 1146-1151. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201006005.htm [7] 胡健, 王雅楠, 王晴, 等. 基于螺旋加密网格的螺旋桨梢涡空化数值模拟[J]. 华中科技大学学报(自然科学版), 2020, 48(3): 30-34. https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG202003006.htm HU Jian, WANG Yanan, WANG Qing, et al. Numerical simulation of propeller tip vortex cavitation based on helical mesh encryption[J]. Journal of Huazhong University of Science and Technology (natural science edition), 2020, 48(3): 30-34. https://www.cnki.com.cn/Article/CJFDTOTAL-HZLG202003006.htm [8] YILMAZ N, ATLAR M, KHORASANCHI M. An improved Mesh Adaption and Refinement approach to Cavitation Simulation (MARCS) of propellers[J]. Ocean engineering, 2019, 171: 139-150. doi: 10.1016/j.oceaneng.2018.11.001 [9] 王超, 李亮, 叶礼裕, 等. 均匀流与非均匀流条件下螺旋桨空泡及噪声试验分析[J]. 船舶工程, 2016, 38(S2): 124-129, 134. https://www.cnki.com.cn/Article/CJFDTOTAL-CANB2016S2035.htm WANG Chao, LI Liang, YE Liyu, et al. Experimental analysis of propeller cavitation and noise in uniform and nonuniform flow[J]. Ship engineering, 2016, 38(S2): 124-129, 134. https://www.cnki.com.cn/Article/CJFDTOTAL-CANB2016S2035.htm [10] 赵旻晟, 赵伟文, 万德成. E779A螺旋桨斜流工况下的空泡数值模拟[J]. 中国造船, 2021, 62(3): 94-102. doi: 10.3969/j.issn.1000-4882.2021.03.008 ZHAO Minsheng, ZHAO Weiwen, WAN Decheng. Numerical simulation of cavitation on E779A propeller in oblique flow[J]. Shipbuilding of China, 2021, 62(3): 94-102. doi: 10.3969/j.issn.1000-4882.2021.03.008 [11] 温亮军, 唐登海, 辛公正, 等. 螺旋桨设计参数对桨叶片空泡性能的影响分析[J]. 船舶力学, 2016, 20(11): 1361-1368. https://www.cnki.com.cn/Article/CJFDTOTAL-CBLX201611002.htm WEN Liangjun, TANG Denghai, XIN Gongzheng, et al. Numerical study on the effect of the propeller design parameters on its sheet cavitation performance[J]. Journal of ship mechanics, 2016, 20(11): 1361-1368. https://www.cnki.com.cn/Article/CJFDTOTAL-CBLX201611002.htm [12] HU Jian, ZHANG Weipeng, WANG Chao, et al. Impact of skew on propeller tip vortex cavitation[J]. Ocean engineering, 2021, 220: 108479. doi: 10.1016/j.oceaneng.2020.108479 [13] 辛公正. 桨叶几何对梢涡空泡起始影响及其机理研究[D]. 北京: 中国舰船研究院, 2014. XIN Gongzheng. The investigation of the effect of blade geometry on tip vortex cavitation inception and its mechanism[D]. Beijing: China Ship Research and Development Academy, 2014. [14] WU Lihong, LI Yiping, LIU Kaizhou, et al. A physics-based simulation for AUV underwater docking using the MHDG method and a discretized propeller[J]. Ocean engineering, 2019, 187: 106081. doi: 10.1016/j.oceaneng.2019.05.063 [15] 盛振邦, 刘应中, 船舶原理[M]. 上海: 上海交通大学出版社, 2005. SHENG Zhenbang, LIU Yingzhong. Principles of shipping[M]. Shanghai: Shanghai Jiao Tong University Press, 2005. [16] 吴利红, 张爱锋, 李一平, 等. 水下机器人试航速度的类物理数值方法预报[J]. 哈尔滨工程大学学报, 2020, 41(2): 194-198. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=3257 WU Lihong, ZHANG Aifeng, LI Yiping, et al. Prediction of autonomous underwater vehicle cruising velocity using a physics-based numerical method[J]. Journal of Harbin Engineering University, 2020, 41(2): 194-198. http://heuxb.hrbeu.edu.cn/#/digest?ArticleID=3257
