高速飞行器是指飞行速度大于5 Ma的飞行器，具有飞行速度快，突防能力强等特点^[1]。近年，随着航天技术的发展，高速飞行器成为研究的热点，随着研究的深入和不断的实验验证，它在军事和民用上的作用变得越来越重要。

然而，由于高速飞行器模型具有高度非线性，严重耦合以及参数不确定等特点，有效合理地设计高速飞行器的控制器是非常困难的。除此之外，由于高速飞行器跨介质飞行，其飞行包线大，因此其气动参数呈现出强非线性特点以及明显的不确定性，采用一些传统的控制算法已经不能满足其控制指标的要求。现代控制方法经过几十年的蓬勃发展，已经形成一个完整的体系，将现代控制算法应用在高速飞行器上成为国内外许多学者研究的热点。

文献[2]对高速飞行器纵向模型设计了一种鲁棒自适应Backstepping控制器，将高度子系统分解成弹道倾角回路、攻角回路以及俯仰角速度回路。文中对这几个回路分别设计控制器，并且采用指令滤波方法防止微分爆炸，同时设计自适应律估计不确定参数。文献[3]针对高速飞行器纵向模型设计了一种反馈线性化方法。通过状态反馈，将飞行器高度子系统和速度子系统进行输入输出线性化，分别近似为四阶积分系统和三阶控制系统，最后在此基础上进行滑模控制器的设计。文献[4]针对高速飞行器具有外部扰动以及输入舵偏角饱和的特点，设计了一种基于滑模干扰观测器的抗饱和滑模控制器，对于系统中存在的扰动和不确定性，采用滑模干扰观测器对其进行估计并在滑模控制器中进行补偿。文献[5-7]采用自抗扰控制算法对高超声速飞行器进行控制，将飞行器的外部和内部扰动看作总扰动，设计扩张状态观测器对总扰动进行估计并进行补偿。文献[8]针对传统的扩张状态观测器连续但非光滑的特性，改进了扩张状态观测器，构造了连续光滑的qin函数，在此基础上设计高速飞行器姿态的自抗扰控制算法。由于高速飞行器具有模型阶数高的特点，以上的控制算法中均或多或少地包含了模型信息。由于建模不确定性，这些模型信息有时很难准确获得。

近年，随着人工智能的快速发展，智能控制在飞行器上的应用引起了学者们的广泛关注。由于神经网络具有逼近任意非线性连续函数的能力，因此具有很强的泛化能力。文献[9]将高速飞行器纵向模型转换为严格反馈形式，针对模型的不确定性设计了单隐藏层反馈神经网络对控制器进行学习，采用极限学习机对隐藏层的参数进行学习更新。文献[10]针对高速飞行器外部扰动以及参数不确定的特点，将纵向模型基于欧拉法转换为速度、高度、弹道倾角、俯仰角以及俯仰角速度这5个一阶离散子系统，并对每个子系统设计反馈控制器。由于反馈控制器中包含了模型信息，所以采用神经网络对其进行近似，最后构造李雅普诺夫函数证明系统的稳定性。文献[11]对高速飞行器纵向模型并考虑弹性模态进行连续神经网络控制器的设计。

强化学习作为机器学习的一个分支，由于其不同于以往监督学习的特点，智能体在与环境交互过程中，通过环境的奖励反馈来判断当前动作的品质，在这种与环境交互学习的过程中，控制策略收敛的方法不需要了解被控对象的内部模型信息，因而这种模拟人类学习过程的方法近几年被广泛关注。在强化学习控制中，由于因果性，普遍采用神经网络来近似性能指标以及控制策略。文献[12]对高速飞行器纵向模型进行强化学习与滑模结合控制，其中滑模控制器的作用是稳定系统，强化学习为辅助控制，用于在线估计扰动。文献[13]采用强化学习方法对高速飞行器纵向模型的建模不对定性进行估计，并采用鲁棒自适应控制进行系稳定以及对估计的建模不确定性进行补偿。

以上文献中提及高速的强化学习方法都是将强化学习作为辅助控制的，最核心的控制依然是现代控制。本文提出的基于强化学习的高速飞行器高度控制算法，不同于以上文献，本文将强化学习作为核心控制，并且以强化学习控制作为系统唯一的稳定控制算法。本文提出的算法不包含任何模型信息，只需要输入输出量及其相应导数即可。对于模型不确定问题，在仿真试验中，对气动参数进行正负极限拉偏，从而验证本方法对于模型不确定性依然有很好的控制效果。

1 高速飞行器高度纵向模型

高速飞行器高度纵向模型为：

$ \dot h = V\sin \theta $

(1)

$ \dot \theta = \frac{{L + T\sin \alpha }}{{mV}} - \frac{{\left( {\mu - {V^2}r} \right)\cos \theta }}{{{V^2}r}} $

(2)

$ \dot \alpha = {\omega _z} - \dot \theta $

(3)

$ {{\dot \omega }_z} = \frac{{{M_z}}}{{{J_z}}} $

(4)

式中：h为飞行高度；θ为弹道倾角；α为攻角；ω_z为俯仰角速度；V为飞行速度；L为升力；T为推力；m为飞行器质量；M_z为俯仰力矩；J_z为转动惯量。L、T、M_z、r、q计算表达式为：

$ L = qS{C_L} $

(5)

$ T = qS{C_T} $

(6)

$ {M_z} = qS_c^ - \left[ {{C_M}(\alpha )} \right.\left. { + {C_M}\left( {{\delta _e}} \right) + {C_M}\left( {{\omega _z}} \right)} \right] $

(7)

$ r = h + {R_e} $

(8)

$ q = \frac{1}{2}\rho {V^2} $

(9)

式中：q为动压；ρ为大气密度；C_L、C_T和C_M分别为升力系数、推力系数以及俯仰力矩系数；S为飞行器参考面积；r、R_e分别为地心距和地球半径。纵向气动参数为：

$ {C_L} = 0.6203\alpha $

(10)

$ {C_M}(\alpha ) = - 0.035{\alpha ^2} + 0.036617\alpha + 5.3261 \times {10^{ - 6}} $

(11)

$ {{C_M}\left( {{\delta _e}} \right) = {c_e}\left( {{\delta _e} - \alpha } \right)} $

(12)

$ {C_M}\left( {{\omega _z}} \right) = \left( {\frac{{\bar c}}{{2V}}} \right){\omega _z}\left( { - 6.79{\alpha ^2} + 0.3015\alpha - 0.2289} \right) $

(13)

由于高速飞行器采用的是超燃冲压发动机，在飞行过程中攻角要保持在一定小的范围内，因此式(2)中L+Tsin α≈L。在高速飞行器巡航飞行过程中，弹道倾角始终保持在较小值，即使做高度机动动作，变化的高度相对于飞行器所在高度仍然是可以忽略的，因此弹道倾角在飞行器做高度机动的过程中看做较小值也是合理的。因此式(1)可变为：

$ \dot h = V\sin \theta \approx V\theta $

(14)

假设在高速飞行器做高度机动的过程中，速度保持为定值。对式(14)求导并将式(2)代入式(14)可得：

$ \ddot h = \dot V\theta + V\dot \theta = \frac{L}{m} - \frac{{\left( {\mu - {V^2}r} \right)\cos \theta }}{{{r^2}}} $

(15)

令x₁=h，x₂=$\dot h$，那么式(15)可写成：

$ {{\dot x}_1} = {x_2} $

(16)

$ {\dot x_2} = {f_h} + {g_h}\vartheta $

(17)

式中ϑ为俯仰角。f_h与g_h表达式为：

$ {f_h} = - \frac{{qS \times 0.6203\theta }}{m} - \frac{{\left( {\mu - {V^2}r} \right)\cos \theta }}{{{r^2}}} $

(18)

$ {g_h} = \frac{{qS \times 0.6203}}{m} $

(19)

根据几何关系：ϑ=α+θ。令x₃=ϑ，x₄=ω_z, 则式(3)和(4)可写成：

$ {{\dot x}_3} = {x_4} $

(20)

$ {\dot x_4} = {f_\vartheta } + {g_\vartheta }{\delta _e}n $

(21)

f_ϑ与g_ϑ表达式为：

$ {f_\vartheta } = \frac{1}{{{J_z}}}qS\bar c\left[ {{C_M}(\alpha ) + {C_M}\left( {{\omega _z}} \right) - 0.0292\alpha } \right] $

(22)

$ {g_\vartheta } = \frac{{qS\bar c \times 0.0292}}{{{J_z}}} $

(23)

2 强化学习控制器设计 2.1 BP神经网络逼近

在强化学习控制器中，BP神经网络将被用于逼近控制策略和性能指标函数。BP神经网络理论上在节点足够多的情况下能够以任意精度逼近定义在紧集Ω⊆Rⁿ上的任何非线性连续函数。BP神经网络在输入量x=[x₁ x₂…x_n]^T∈Ω⊆Rⁿ与输出量y∈Rⁿ之间形成的映射定义为：

$ {\boldsymbol{y}} = {{\boldsymbol{\omega }}^{\rm{T}}}{\boldsymbol{\varphi }}\left( {{{\boldsymbol{v}}^{\rm{T}}}{\boldsymbol{x}}} \right) $

式中：ω∈R^N×1为隐藏层和输出层之间的权值; N为隐藏层节点数; φ(·)为隐藏层的激活函数通常取为φ(·)=tanh(·); v∈R^n×N为输入层和隐藏层之间的权值。对于一个未知连续非线性函数f(x)，存在理想权值ω^*∈R^N×1使得：f(x)=ω^*Tφ(v^Tx) + ε, |ε|≤ε_M。ε和ε_M分别为逼近误差和逼近误差的上界。

2.2 高度子系统强化学习控制器设计

高度子系统强化学习控制器设计的目的是使飞行器高度能够以一定精度并且稳定地跟踪期望高度指令h_d。高度子系统的输入是期望俯仰角ϑ_d。这里假设飞行器的高度、俯仰角能够通过传感器测量得到。

令x_1d=h_d，定义高度跟踪误差为：

$ {e_h} = h - {h_d} = {x_1} - {x_{1d}} $

(24)

定义滤波误差为：

$ {r_{dh}} = {\lambda _h}{e_h} + {\dot e_h} $

(25)

式中λ_h>0, λ_h∈ $\mathbb{R}$。

求导可得：

$ {\dot r_{dh}} = {f_h} + {g_h}{x_3} - {\ddot x_{1d}} + {\lambda _h}{\dot e_h} $

(26)

理想控制律可以设计为：

$ {x_{3d}} = \frac{1}{{{g_h}}}\left( { - {f_h} + {{\ddot x}_{1d}} - {\lambda _h}{{\dot e}_h} - {K_1}{r_{dh}}} \right) $

(27)

由于理想控制律中包含f_h、g_h等模型信息，因此在实际中不能应用。接下来，将采用强化学习来进行控制器设计，该控制器结构由动作网络和评价网络组成，评价网络的作用是根据飞行器当前状态来评价表现好坏，动作网络则是根据评价网络的评价输出来产生相应的控制量。

2.2.1 评价网络设计

定义性能指标函数为：

$ {J_h}(t) = \int_t^\infty {e_h^{ - \frac{{\tau - t}}{{{\gamma _h}}}}} {R_h}(\tau ){\rm{d}}\tau $

(28)

式中：γ_h为折扣因子；R_h(τ)为奖励函数；R_h(τ)=P_he_h², P_h>0。

由于性能指标是对当前时刻的后来时刻积分，这就产生了因果问题，所以不能直接计算出性能指标函数的值，因此需要对其进行估计，令性能指标函数的估计值为${\hat J_h}(t)$。则根据Bellman方程定义估计误差为：

$ {e_{ch}} = {R_h}(t) - \frac{1}{{{\gamma _h}}}{\hat J_h}(t) + {\dot {\hat J}_h}(t) $

(29)

评价网络的作用是通过当前飞行器的状态信息从而输出对性能指标函数的估计值。因此评价网络设计为：

$ {\hat J_h}(t) = \widehat {\boldsymbol{\omega }}_{ch}^{\rm{T}}{{\boldsymbol{\varphi }}_{ch}}\left( {{\boldsymbol{v}}_{ch}^{\rm{T}}{{\boldsymbol{c}}_{{\rm{inh}}}}} \right) $

(30)

式中：${\widehat {\boldsymbol{\omega }}_{ah}}$是理想权值ω_ch^*的估计；c_inh为评价网络的输入向量; ${{\boldsymbol{c}}_{{\rm{in}}h}} = {\left[ {\begin{array}{*{20}{l}} {{e_h}}&{{{\dot e}_h}} \end{array}} \right]^{\rm{T}}}$

2.2.2 动作网络设计

动作网络的作用是根据评价网络对性能指标函数的估计值来计算控制量。对于理想控制律(27)，可以采用动作网络来对其进行逼近。动作网络设计为：

$ {\widehat {\boldsymbol{x}}_3}(t) = \widehat {\boldsymbol{\omega }}_{ah}^{\rm{T}}{{\boldsymbol{\varphi }}_{ah}}\left( {{\boldsymbol{v}}_{ah}^{\rm{T}}{{\boldsymbol{a}}_{{\rm{inh}}}}} \right) $

(31)

式中：${\widehat {\boldsymbol{\omega }}_{ah}}$是理想权值ω_ah^*的估计；a_inh为动作网络的输入向量，且

$ {{\boldsymbol{a}}_{{\rm{in}}h}} = {\left[ {\begin{array}{*{20}{l}} {{x_1}}&{{{\dot x}_1}}&{{r_{dh}}}&{{e_h}}&{{{\dot e}_h}}&{{{\ddot x}_{1d}}} \end{array}} \right]^{\rm{T}}} $

那么理想控制律(27)可表示为：

$ {x_{3d}} = {\boldsymbol{\omega }}_{ah}^{*{\rm{T}}}{{\boldsymbol{\varphi }}_{ah}}\left( {{\boldsymbol{v}}_{ah}^{\rm{T}}{{\boldsymbol{a}}_{{\rm{in}}h}}} \right) + {{\boldsymbol{\varepsilon }}_{ah}} $

(32)

2.2.3 评价网络权值更新

对于评价网络，其权值更新的目标是最小化估计误差e_ch。因此定义评价网络的目标函数为：

$ {E_{ch}} = \frac{1}{2}e_{ch}^2 $

(33)

根据梯度下降法，评价网络更新律为：

$ {{\boldsymbol{\dot {\hat \omega }}}_{ch}} = - {\sigma _{ch}}\frac{{\partial {E_{ch}}}}{{\partial {{\widehat {\boldsymbol{\omega }}}_{ch}}}} $

(34)

式中σ_ch为评价网络的学习率, 0＜σ_ch＜1。

对式(34)进一步推导:

$ {{\boldsymbol{\dot {\hat \omega }}}_{ch}}= - {\sigma _{ch}}\frac{{\partial {E_{ch}}}}{{\partial {{\widehat {\boldsymbol{\omega }}}_{ch}}}} = - {\sigma _{ch}}\left( {{R_h}(t) + \mathop {{\boldsymbol{\omega }}_{ch}^{\rm{T}}}\limits^. {{\mathit{\pmb{\Gamma }}}_h}} \right){{\mathit{\pmb{\Gamma }}}_h} $

(35)

式中${{\mathit{\pmb{\Gamma }}}_h} = - \frac{{{{\boldsymbol{\varphi }}_{ch}}}}{{{R_h}}} + \nabla {{\boldsymbol{\varphi }}_{ch}}{\mathop {\boldsymbol{c}}\limits^. _{{\rm{inh}}h}}$，▽代表梯度。

2.2.4 动作网络权值更新

动作网络的逼近误差为：

$ {e_{ah}} = \sqrt {{g_h}} {\xi _{ah}} + \frac{1}{{\sqrt {{g_h}} }}\left( {{{\hat J}_h} - {J_{dh}}} \right) $

(36)

式中${\xi _{ah}} = \widetilde {\boldsymbol{\omega }}_{ah}^{\rm{T}}{{\boldsymbol{\varphi }}_{ah}}\left( {{\boldsymbol{v}}_{ah}^{\rm{T}}{{\boldsymbol{a}}_{{\rm{in}}h}}} \right)$。

J_dh为理想性能指标函数的值，由式(28)性能指标函数可以看到，最后是使得性能指标为0，从而跟踪误差为0，动作网络的学习目标之一就是让性能指标的估计值为0，因此J_dh取0，代表最理想的情况。ξ_ah代表动作估计权值与理想权值之间的差，理想权值产生的控制策略能对飞行器进行理想的控制，那么当估计权值无限逼近与理想权值的时候，就可以对飞行器进行理想的控制。由于g_h的值存在不确定性，因此在动作网络权值更新律中不应该含有g_h项，因此在动作网络的逼近误差表达式中引入g_h有关项使得在动作网络权值更新律中不存在g_h有关项，由于动作网络的学习目标是使得ξ_ah和$\left( {{{\hat J}_h} - {J_{dh}}} \right)$2项最终为0，因此逼近误差表达式中引入g_h不影响最终结果。动作网络的目标函数定义为：

$ {E_{ah}} = \frac{1}{2}e_{ah}^2 $

(37)

动作网络权值更新的目标就是最小化目标函数。因此根据梯度下降法，评价网络更新律为：

$ {{\boldsymbol{\dot {\hat \omega} }}_{ah}} = - {\sigma _{ah}}\frac{{\partial {E_{ch}}}}{{\partial {{\widehat {\boldsymbol{\omega }}}_{ah}}}} $

(38)

式中σ_ah为动作网络的学习率，0＜σ_ah＜1。

对式(38)进一步推导：

$ \begin{array}{l} \;\;\;\;{{\boldsymbol{\dot {\hat \omega }}}_{ah}} = - {\sigma _{ah}}\frac{{\partial {E_{ah}}}}{{\partial {{\widehat {\boldsymbol{\omega }}}_{ah}}}} = - {\sigma _{ah}}{e_{ah}}\frac{{\partial {e_{ah}}}}{{\partial {{\widehat {\boldsymbol{\omega }}}_{ah}}}} = \\ - {\sigma _{ah}}{e_{ah}}\frac{{\partial {e_{ah}}}}{{\partial {\xi _{ah}}}}\frac{{\partial {\xi _{ah}}}}{{\partial {{\widehat {\boldsymbol{\omega }}}_{ah}}}} = - {\sigma _{ah}}\left( {{g_h}{\xi _{ah}} + {{\hat J}_h}} \right){{\boldsymbol{\varphi }}_{ah}} \end{array} $

(39)

由于在动作网络权值更新律表达式中存在ξ_ah项。因此无法将其获得。接下来，根据滤波误差表达式来将其求出。

由式(26)可得：

$ \begin{array}{l} \;\;\;\;\;\;{{\dot r}_{dh}} = {f_h} + {g_h}{x_3} - {{\ddot x}_{1d}} + \lambda {{\dot e}_h} = \\ {f_h} + {g_h}\left( {{{\hat x}_3} - {x_{3d}}} \right) - {{\ddot x}_{1d}} + \lambda {{\dot e}_h} + {g_h}{x_{3d}} \end{array} $

(40)

将式(31)和(32)代入式(40)可得：

$ \begin{array}{l} {{\dot r}_{dh}} = {f_h} + {g_h}\left( {{{\hat x}_3} - {x_{3d}}} \right) - {{\ddot x}_{1d}} + \lambda {{\dot e}_h} + {g_h}{x_{3d}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{g_h}\left( {{\xi _{ah}} - {\varepsilon _{ah}}} \right) - {K_1}{r_{dh}} \end{array} $

(41)

因为ε_ah很小可忽略，所以可以求得：

$ {\xi _{ah}} = \frac{1}{{{g_h}}}\left( {{{\dot r}_{dh}} + {K_1}{r_{dh}}} \right) $

(42)

将式(41)代入式(39)可得：

$ {{\boldsymbol{\dot {\hat \omega }}}_{ah}} = - {\sigma _{ah}}\left( {{{\dot r}_{dh}} + {K_1}{r_{dh}} + {{\hat J}_h}} \right){{\boldsymbol{\varphi }}_{ah}} $

(43)

因此，经过一系列推导之后得出的动作网络权值更新律中的所有项均可获得，而且不包含任何模型信息。

2.3 姿态子系统强化学习控制器设计

姿态子系统强化学习控制器的设计目的是使飞行器的俯仰角能以一定精度并且稳定地跟踪由高度子系统产生的期望角指令ϑ_d。姿态子系统的输入是升降舵偏角δ_e。由于姿态子系统数学模型的形式与高度子系统一致，所以姿态子系统强化学习控制器设计步骤也与高度子系统相同。

令x_3d=ϑ_d，定义俯仰角跟踪误差为：

$ {e_\vartheta } = \vartheta - {\vartheta _d} = {x_3} - {x_{3d}} $

(44)

定义滤波误差为：

$ {r_{d\vartheta }} = {\lambda _\vartheta }{e_\vartheta } + {\dot e_\vartheta } $

(45)

式中λ_ϑ>0, λ_ϑ∈R。

对滤波误差求导可得：

$ \dot{r}_{d \vartheta}=f_{\vartheta}+g_{\vartheta} \delta_{e}-\ddot{x}_{3 d}+\lambda_{\vartheta} \dot{e}_{\vartheta} $

(46)

理想控制律可以设计为：

$ {\delta _{ed}} = \frac{1}{{{g_\vartheta }}}\left( { - {f_\vartheta } + {{\ddot x}_{3d}} - {\lambda _\vartheta }{{\dot e}_\vartheta } - {K_2}{r_{d\vartheta }}} \right) $

(47)

2.3.1 评价网络设计

定义性能指标函数为：

$ {J_\vartheta }(t) = \int_t^\infty {{\rm{e}}_\vartheta ^{ - \frac{{\tau - t}}{{{\gamma _\vartheta }}}}} {R_\vartheta }(\tau ){\rm{d}}\tau $

式中：γ_ϑ为折扣因子；R_ϑ(τ)为奖励函数，R_ϑ(τ)=P_ϑe_ϑ², P_ϑ>0。

令性能指标函数的估计值为${\hat J_\vartheta }(t)$。则估计误差为：

$ {e_{c\vartheta }} = {R_\vartheta }(t) - \frac{1}{{{\gamma _\vartheta }}}{\hat J_\vartheta }(t) + {\dot {\hat J}_\vartheta }(t) $

(48)

评价网络设计为：

$ {\hat J_\vartheta }(t) = {\dot {\hat {\boldsymbol{\omega }}}}_{c\vartheta }^{\rm{T}}{{\boldsymbol{\varphi }}_{c\vartheta }}\left( {{\boldsymbol{v}}_{c\vartheta }^{\rm{T}}{{\boldsymbol{c}}_{{\rm{in}}\vartheta }}} \right) $

(49)

式中：${\dot {\hat \omega} _{c\vartheta }}$是理想权值ω_cϑ^*的估计；c_inϑ为评价网络的输入向量，${{\boldsymbol{c}}_{{\rm{in}}\vartheta }} = {\left[ {\begin{array}{*{20}{l}} {{e_\vartheta }}&{{{\dot e}_\vartheta }} \end{array}} \right]^{\rm{T}}}$。

2.3.2 动作网络设计

动作网络设计为：

$ {\delta _e} = \widehat {\boldsymbol{\omega }}_{a\vartheta }^{\rm{T}}{{\boldsymbol{\varphi }}_{a\vartheta }}\left( {{\boldsymbol{v}}_{a\vartheta }^{\rm{T}}{{\boldsymbol{a}}_{{\rm{in}}\vartheta }}} \right) $

(50)

式中：${\widehat {\boldsymbol{\omega }}_{a\vartheta }}$是理想权值ω_aϑ^*的估计；a_inϑ为动作网络的输入向量，且${{\boldsymbol{a}}_{{\rm{in}}\vartheta }} = \left[ {\begin{array}{*{20}{l}} {{x_3}}&{{{\dot x}_3}}&{{r_{d\vartheta }}}&{{e_\vartheta }}&{{{\dot e}_\vartheta }} \end{array}} \right]$。

那么理想控制律(47)可表示为：

$ {\delta _{ed}} = {\boldsymbol{\omega }}_{a\vartheta }^{*\;{\rm{T}}}{{\boldsymbol{\varphi }}_{a\vartheta }}\left( {{\boldsymbol{v}}_{a\vartheta }^{\rm{T}}{{\boldsymbol{a}}_{{\rm{in}}\vartheta }}} \right) + {\varepsilon _{a\vartheta }} $

2.3.3 评价网络权值更新

定义评价网络的目标函数为：${E_{c\vartheta }} = \frac{1}{2}e_{c\vartheta }^2$。根据梯度下降法，评价网络更新律为：

$ {{\boldsymbol{\dot \omega }}_{c\vartheta }} = - {\sigma _{c\vartheta }}\frac{{\partial {E_{c\vartheta }}}}{{\partial {{\widehat {\boldsymbol{\omega }}}_{c\vartheta }}}} $

(51)

式中σ_cϑ为评价网络的学习率，0＜σ_cϑ＜1。

对式(51)进一步推导:

$ {{\boldsymbol{\dot {\hat \omega }}}_{c\vartheta }} = - {\sigma _{c\vartheta }}\left( {{R_\vartheta }(t) + \widehat {\boldsymbol{\omega }}_{c\vartheta }^{\rm{T}}{\mathit{\pmb{\Gamma }}_\vartheta }} \right){\mathit{\pmb{\Gamma }}_\vartheta } $

(52)

式中：${{\mathit{\pmb{\Gamma }}}_\vartheta } = - \frac{{{{\boldsymbol{\varphi }}_{c\vartheta }}}}{{{R_\vartheta }}} + \nabla {{\boldsymbol{\varphi }}_{c\vartheta }}{\mathop {\boldsymbol{c}}\limits^. _{{\rm{in}}\vartheta }}$，▽代表梯度。

2.3.4 动作网络权值更新

动作网络的逼近误差为：

$ {e_{a\vartheta }} = \sqrt {{g_\vartheta }} {\xi _{a\vartheta }} + \frac{1}{{\sqrt {{g_\vartheta }} }}\left( {{{\hat J}_\vartheta } - {J_{d\vartheta }}} \right) $

(53)

式中：$\xi_{a \vartheta}=\hat{\boldsymbol{\omega}}_{c \vartheta}^{\mathrm{T}} \boldsymbol{\varphi}_{c \vartheta}\left(\boldsymbol{v}_{c \vartheta}^{\mathrm{T}} \boldsymbol{c}_{\mathrm{in\vartheta}}\right)-\hat{\boldsymbol{\omega}}_{a \vartheta}^{* \mathrm{~T}} \boldsymbol{\varphi}_{a \vartheta}\left(\boldsymbol{v}_{a \vartheta}^{\mathrm{T}} \boldsymbol{a}_{\mathrm{in} \vartheta}\right)$；J_dϑ为理想性能指标函数的值，这里取0；动作网络的目标函数定义为${E_{a\vartheta }} = \frac{1}{2}e_{a\vartheta }^2$。

姿态子系统动作网络权值更新律的推导步骤与高度子系统完全相同，这里直接给出动作网络权值更新律表达式：

$ {{\boldsymbol{\dot {\hat \omega }}}_{a\vartheta }} = - {\sigma _{a\vartheta }}\left( {{{\dot r}_{d\vartheta }} + {K_2}{r_{d\vartheta }} + {{\hat J}_\vartheta }} \right){{\boldsymbol{\varphi }}_{a\vartheta }} $

(54)

2.4 高速飞行器纵向高度强化学习控制算法结构图

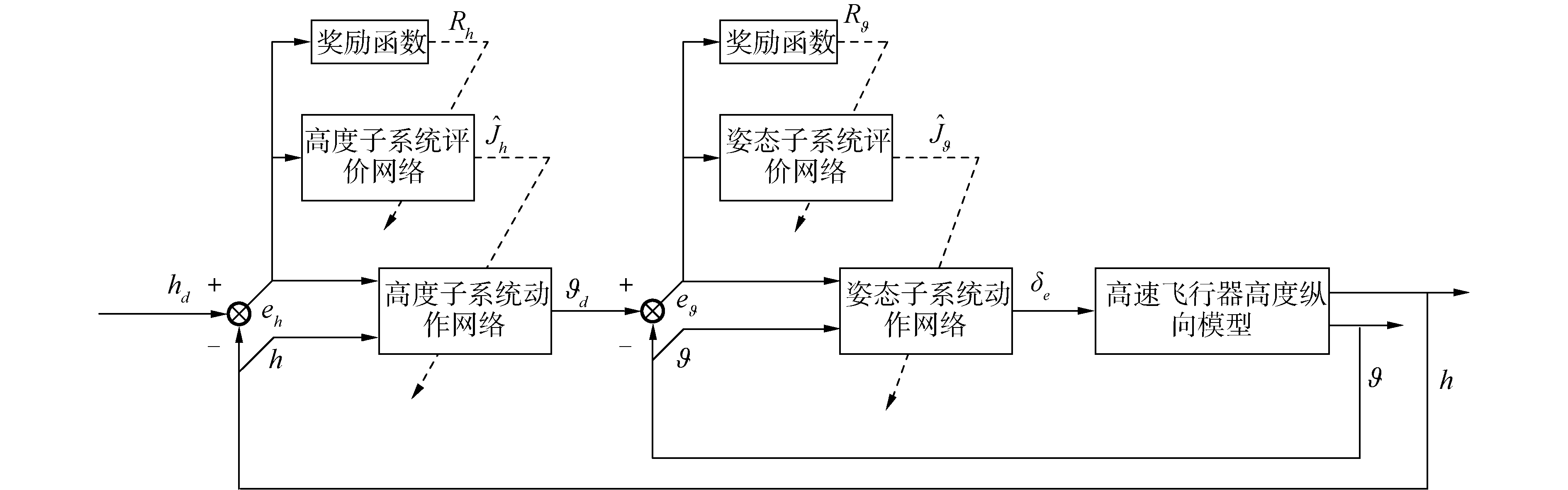
综合前2部分的推导，基于强化学习的高速飞行器高度控制算法结构图如图 1所示。

3 仿真分析

本文采用数值仿真来验证所设计的强化学习高度控制算法的有效性。飞行器的模型采用的是式(1)~(4)的非线性模型进行的数值仿真。飞行器的初始状态为：V=4 590.3 m/s，h(0)=33 528 m，θ(0)=0°，α(0)=0°，ω_z(0)=0°/s。机动后高度为h(∞)=34 028 m，机动爬升高度为500 m。期望高度变化参考模型为：

$ \frac{{{h_d}}}{{{h_c}}} = \frac{{{\omega _1}\omega _2^2}}{{\left( {s + {\omega _1}} \right)\left( {{s^2} + 2\zeta {\omega _2}s + \omega _2^2} \right)}} $

式中：h_d为高度参考指令；h_c为机动后高度；ω₁=0.2，ω₂=0.1，ζ=0.7。

飞行器相关参数为：m=136 820 kg，J_z=9 490 740 kg ·m²，S=334.73 m²，c =24.384 m，ρ=0.012 537 kg/m³。

强化学习控制器参数为：高度子系统与姿态子系统的动作网络和评价网络的隐藏层节点数均为20，即N_ch=N_ah=N_cϑ=N_aϑ=20。

v_ch、v_ah、v_cϑ、v_aϑ取(0, 1)的随机数并且保持不变。w_ch、w_ah、w_cϑ、w_aϑ初始值均为0。学习率σ_ch=0.2，σ_ah=0.2，σ_cϑ=0.2，σ_aϑ=0.2。λ_h=300，λ_ϑ=300，P_h=50，P_ϑ=50，K₁=5，K₂=15。

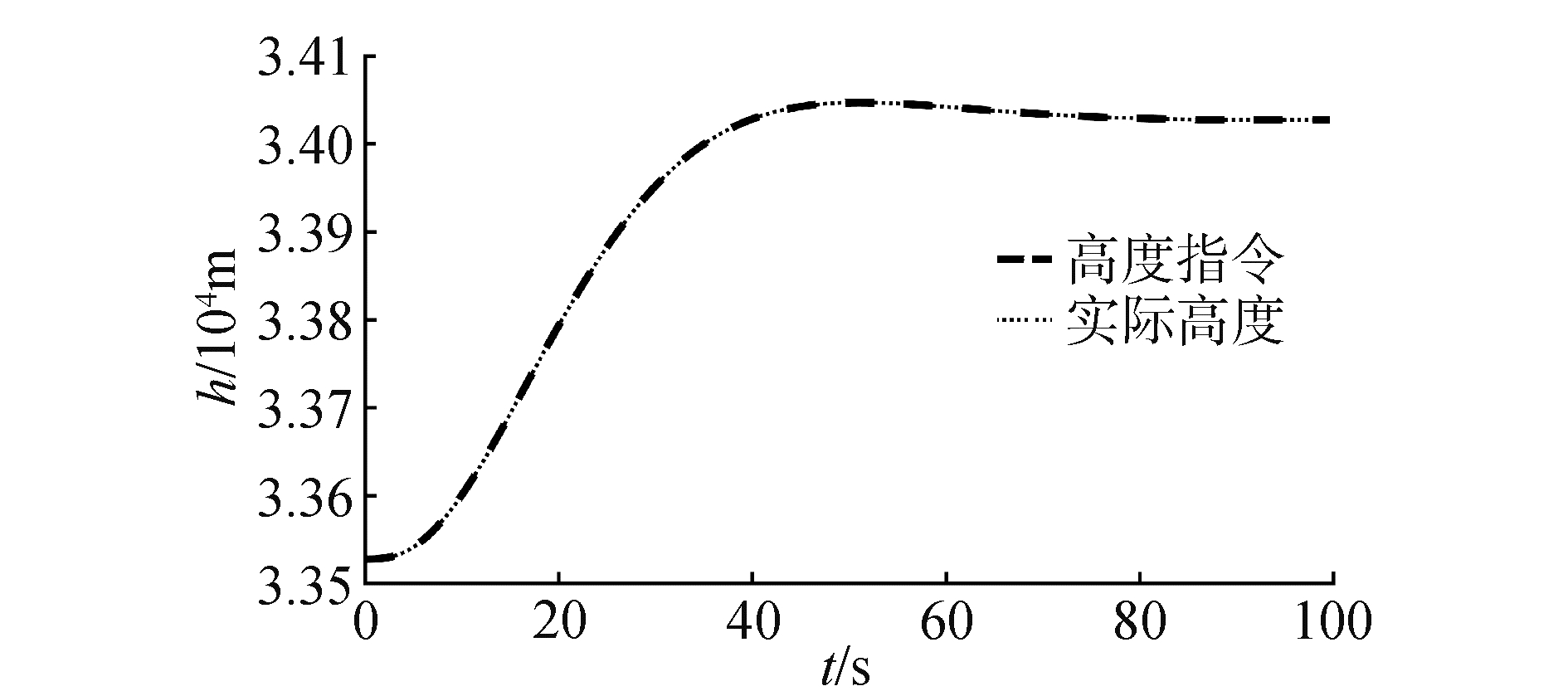
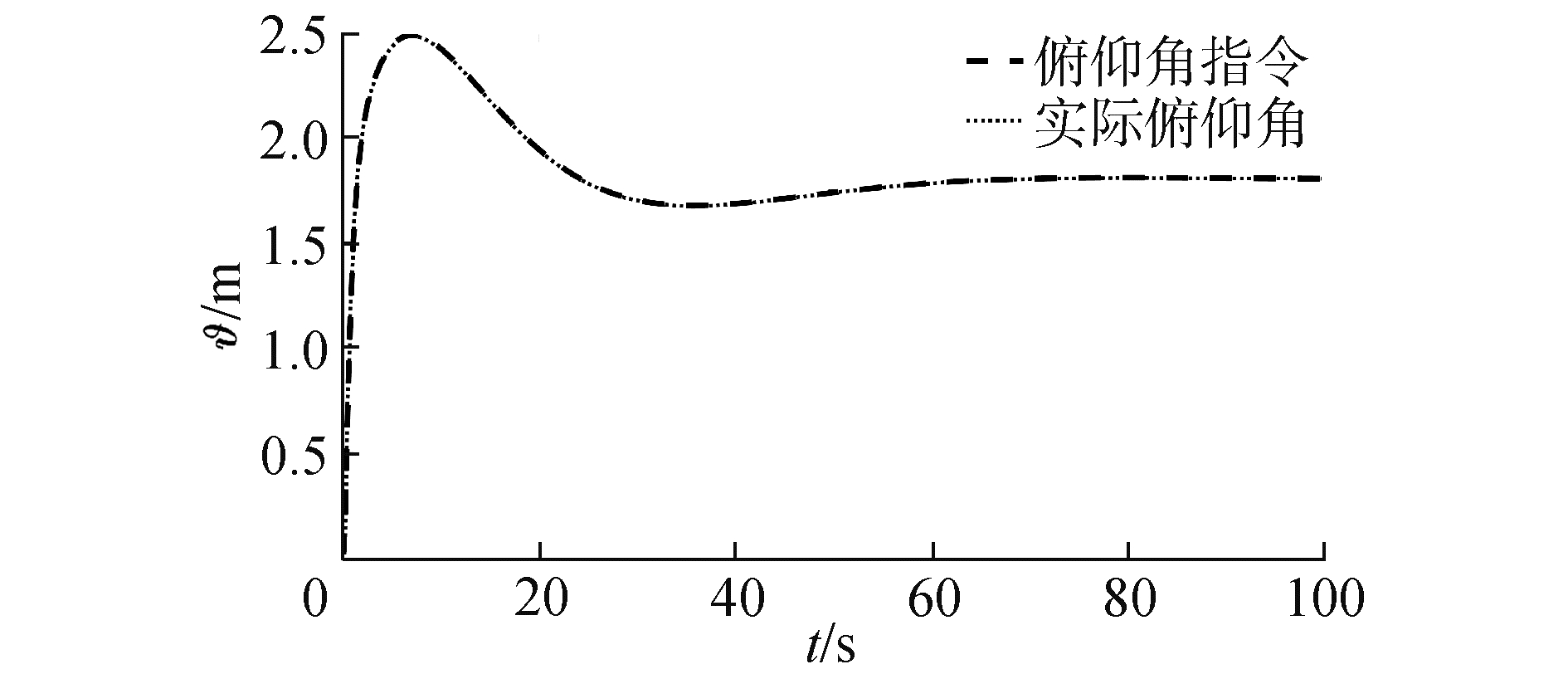
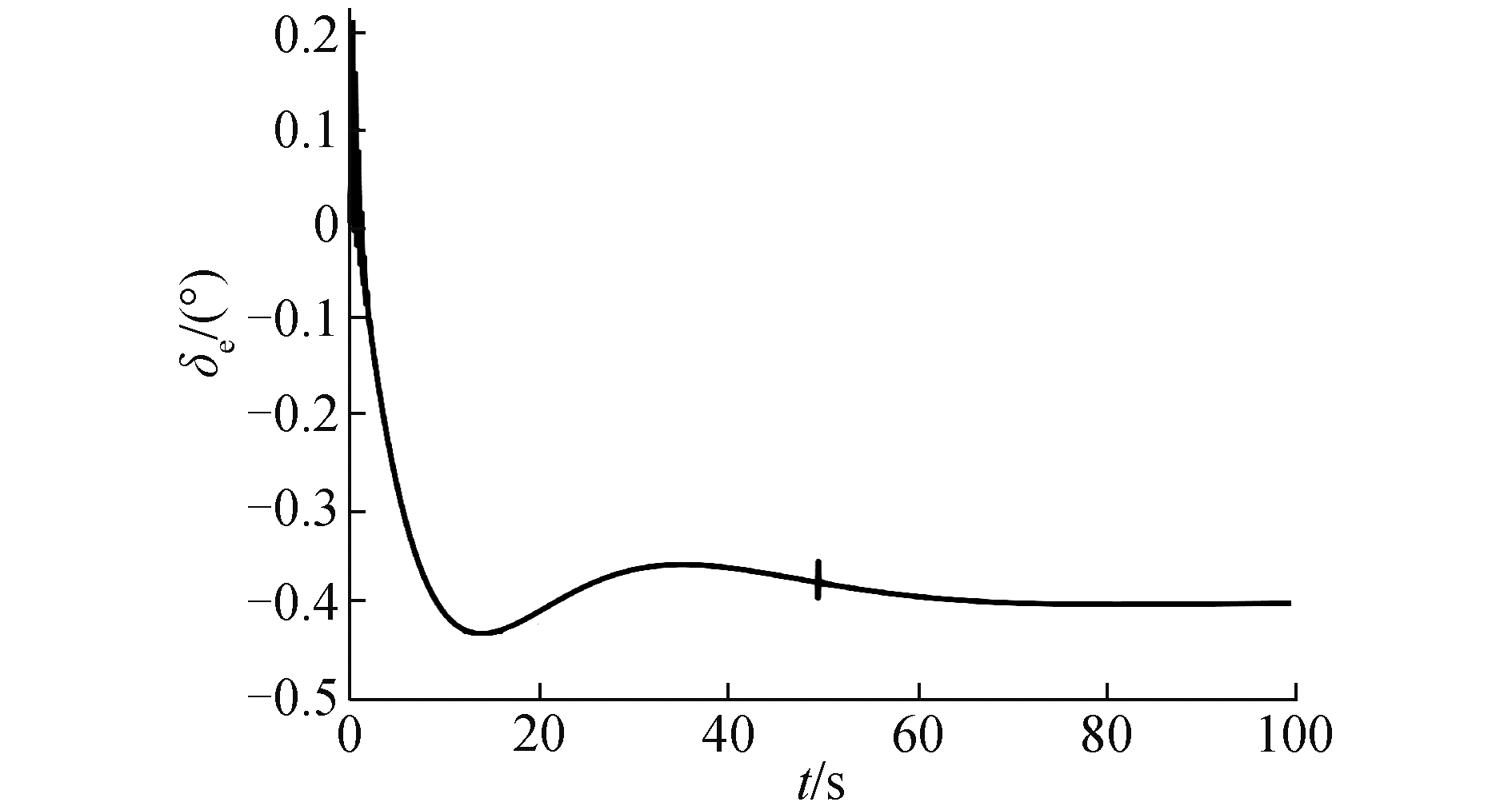
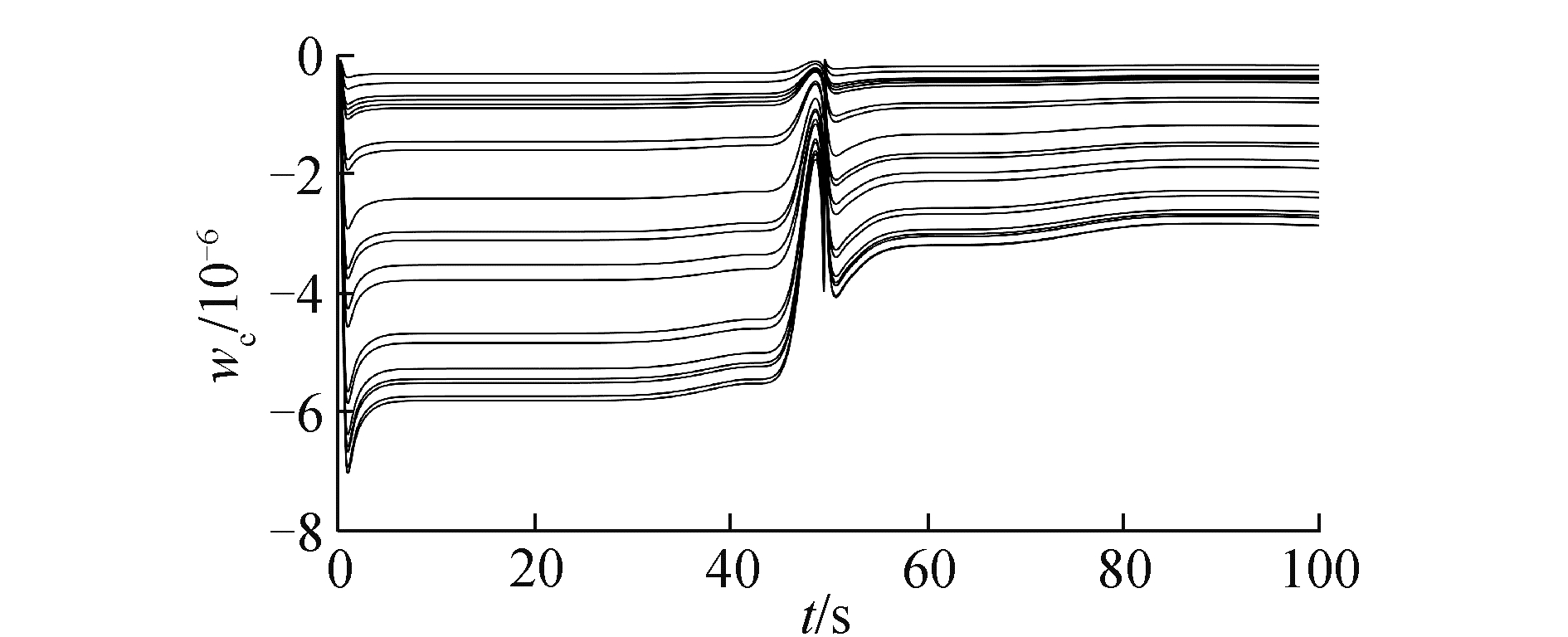
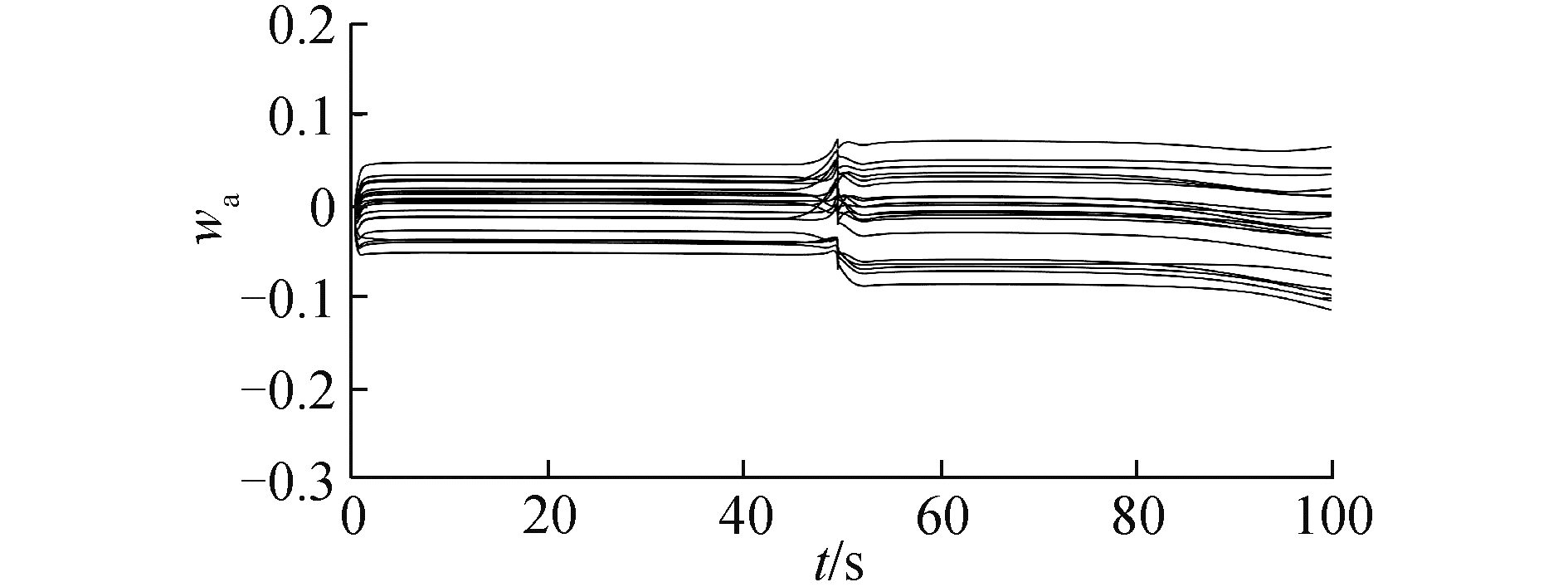
3.1 标称状态下仿真分析

在气动参数无拉偏条件下仿真结果如图 2~6所示。由图 2可以看出，对于高度子系统来说，所设计的强化学习控制器能够快速稳定地跟踪高度参考指令。姿态子系统跟踪曲线如图 3所示，俯仰角同样能够快速稳定地跟踪高度子系统的俯仰角指令。图 4为升降舵偏角变化曲线，从图 4中可以看出，舵偏角始终保持在合理范围内。图 5和图 6分别为评价网络权值变化曲线和动作网络的权值变化曲线，可以看出评价网络的变化曲线逐渐趋于收敛且稳定，动作网络权值曲线变化逐渐趋于平稳并收敛，因此控制策略也随之收敛。

3.2 极限拉偏状态下仿真分析

在建模具有参数不确定性时，通过仿真验证所设计的强化学习控制器的控制性能。采用正反极限拉偏来验证所设计的控制器的控制能力，拉偏条件Ⅰ为：C_L拉偏+10%，C_M拉偏+30%，m拉偏+5%，J_z拉偏+5%，ρ拉偏+5%。拉偏条件Ⅱ为：C_L拉偏-10%，C_M拉偏-30%，m拉偏-5%，J_z拉偏-5%，ρ拉偏-5%。

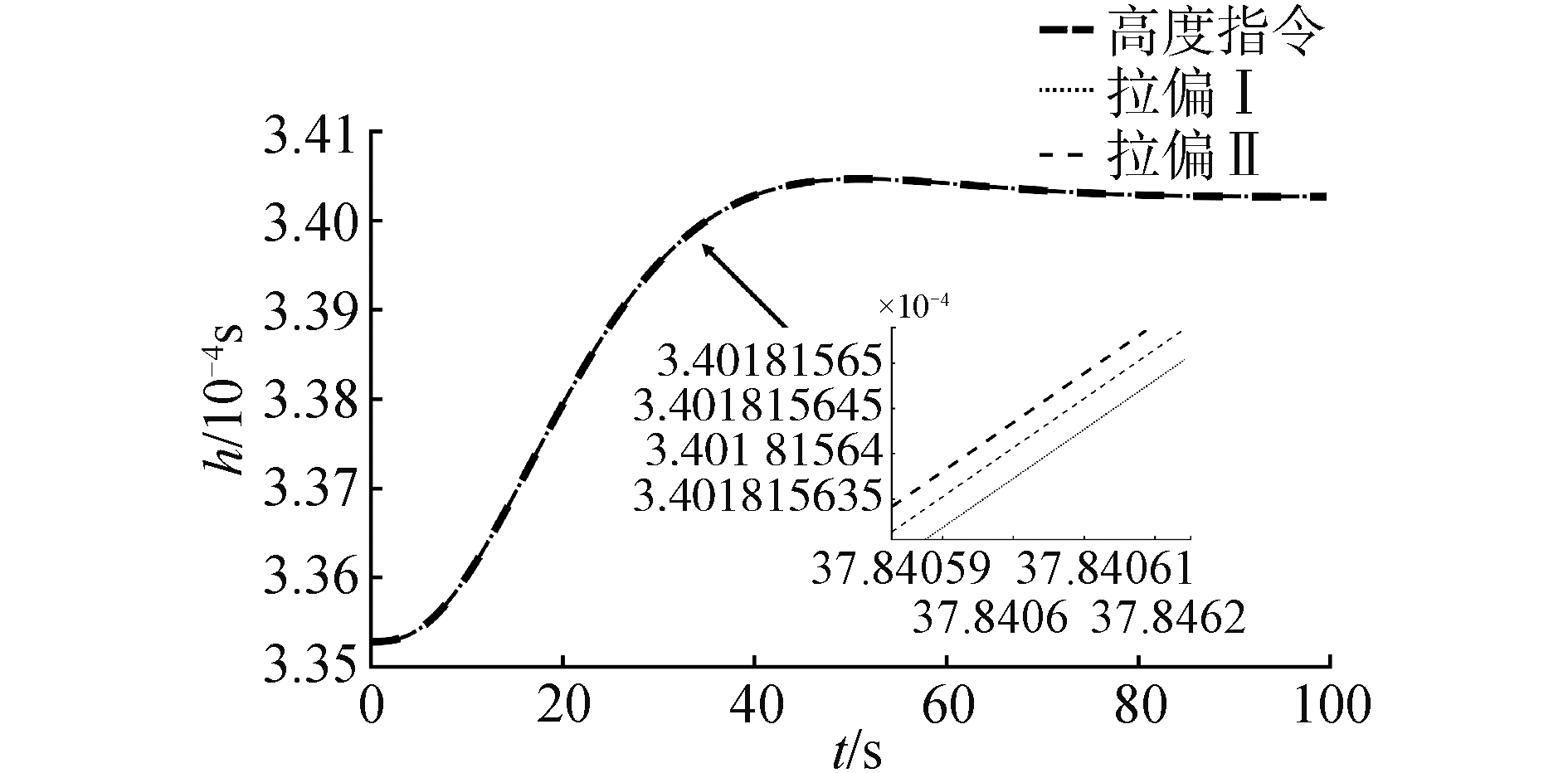
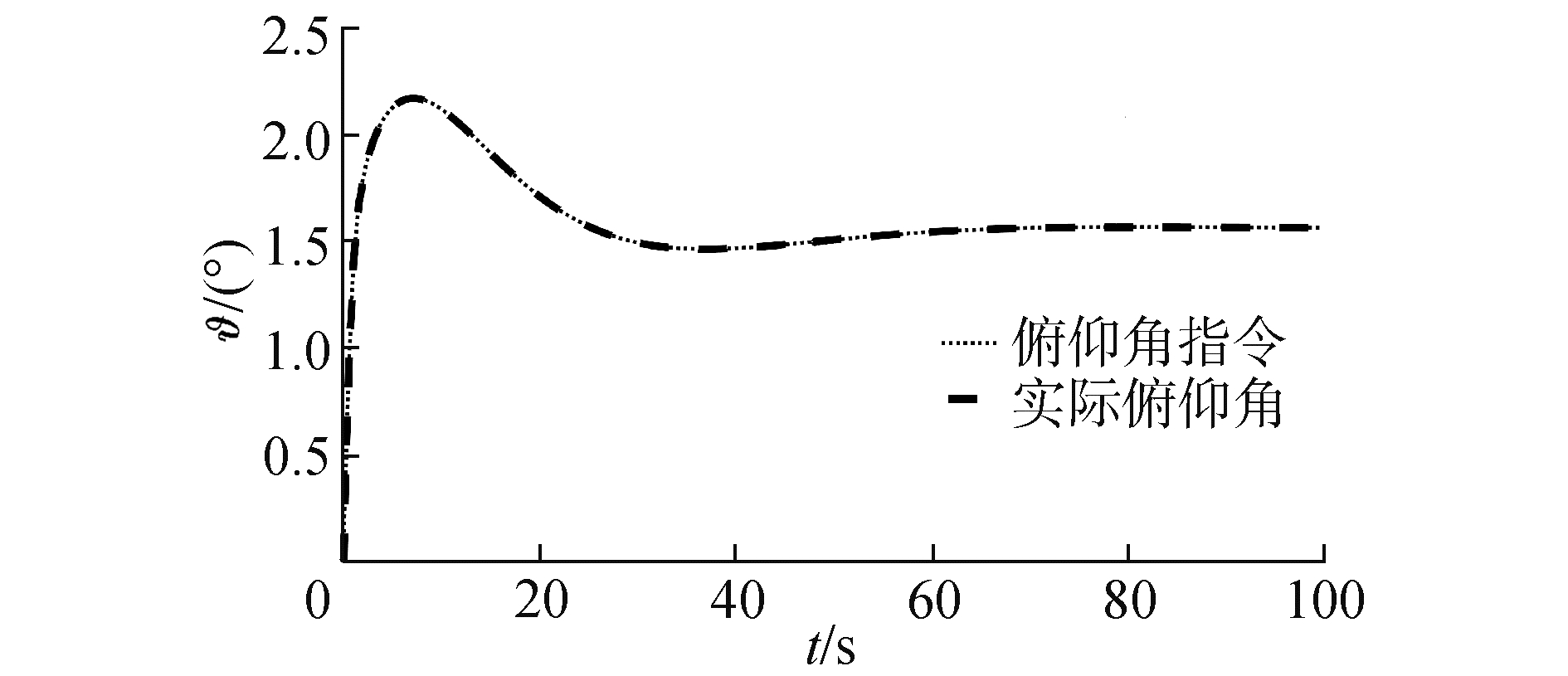
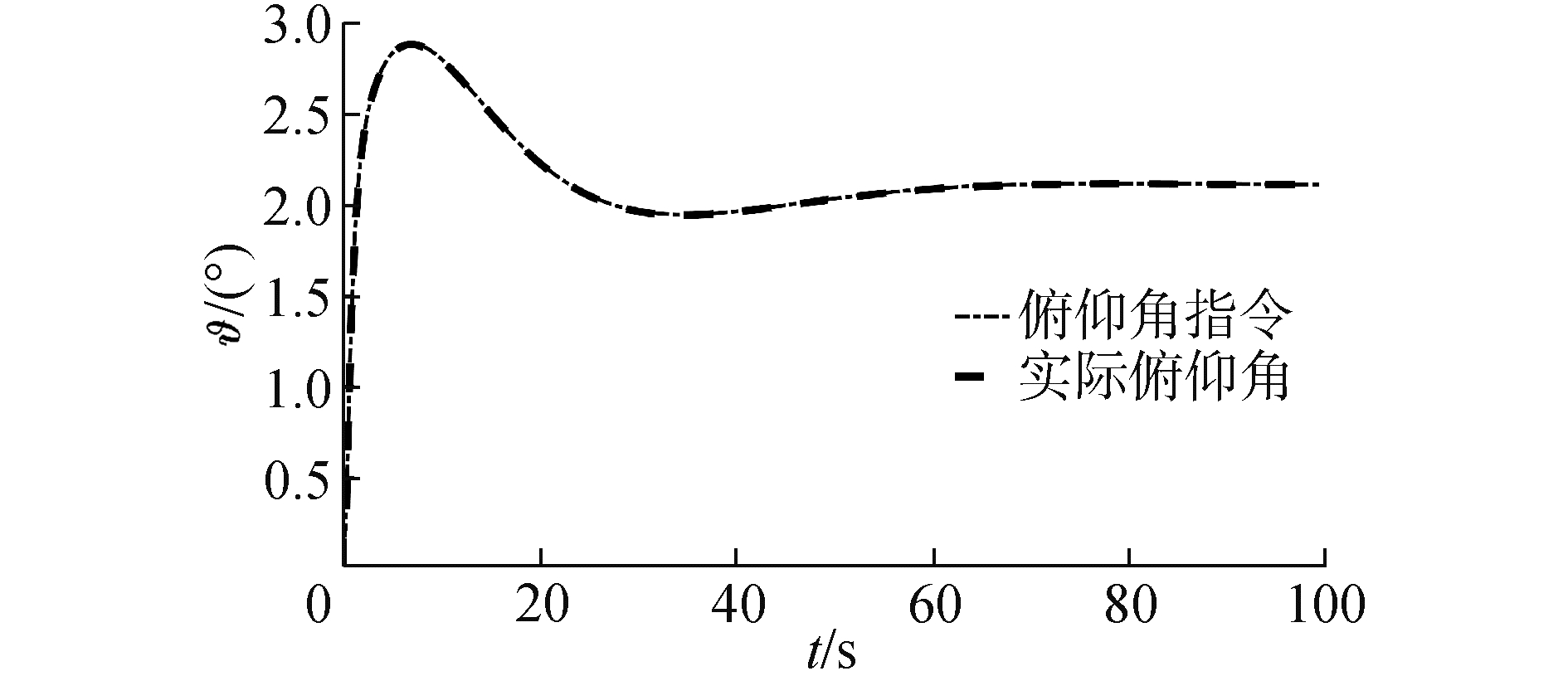
在气动参数拉偏条件下仿真结果如图 7~10所示。在极限拉偏Ⅰ和极限拉偏Ⅱ条件下，所设计的强化学习控制算法依然能够使高度快速、稳定地跟踪高度参考指令。说明设计的强化学习控制算法对模型参数不确定依然具有很好的控制效果。

3.3 与PID控制算法相对比

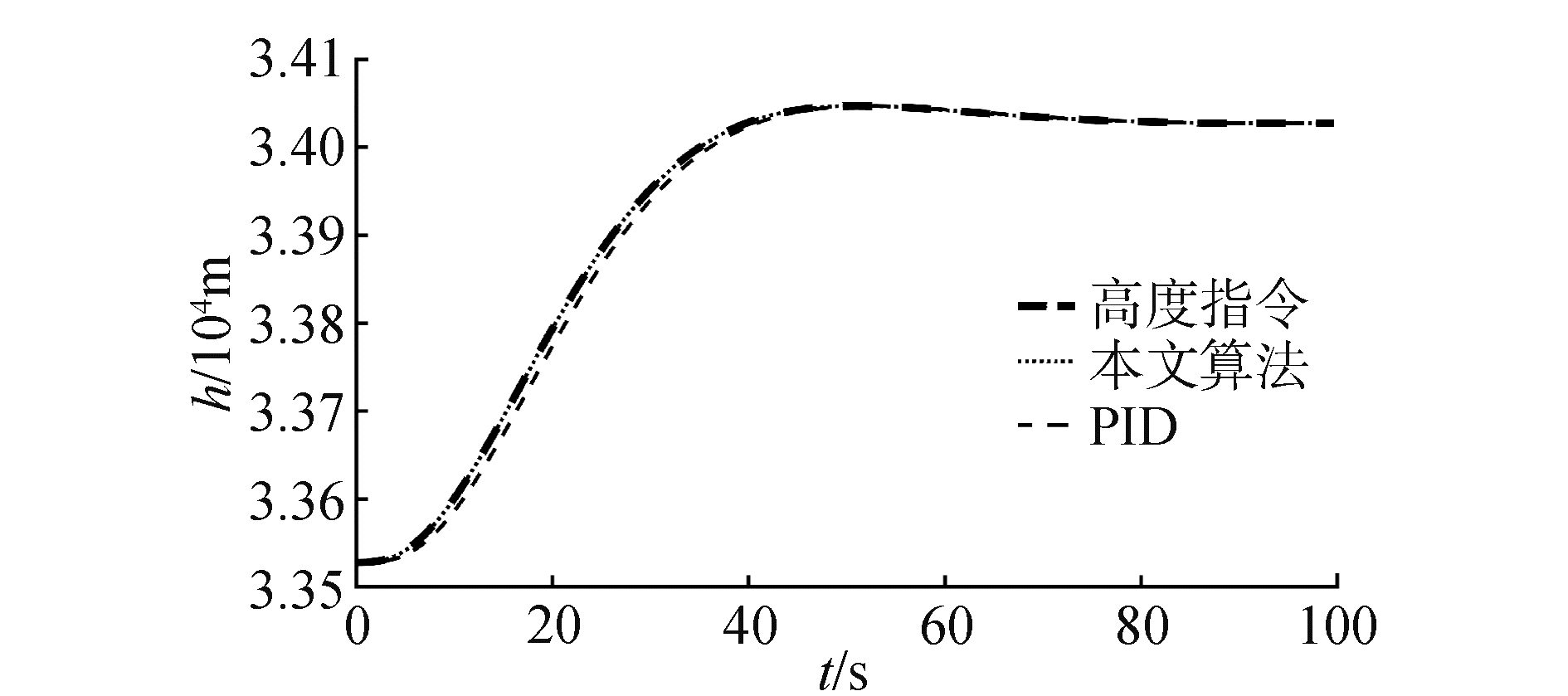
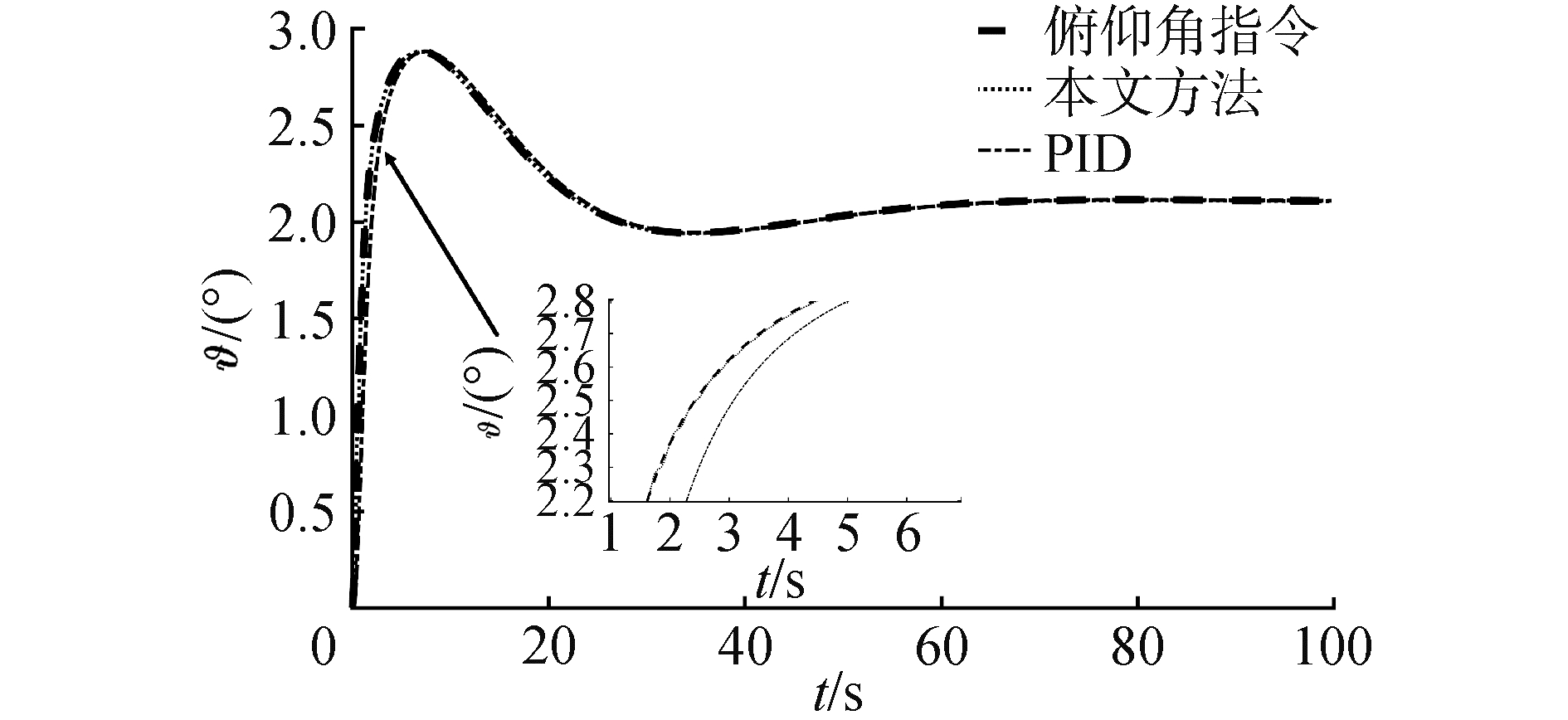
将本文提出的算法与传统PID相对比，姿态子系统分别采用内环俯仰角速度反馈的阻尼回路，外环采用PI控制，高度子系统采用PI控制。2种算法的对比结果如图 11、图 12所示。从图中可以看出，对于稳态阶段，2种控制算法的稳态误差都在可接受范围内，误差大小没有实质上的区别。但是在动态过程，PID控制算法响应要慢于本文提出的控制算法，本文提出的算法能快速跟踪期望轨迹，但是PID控制算法要稍滞后于期望轨迹。从而验证了本文提出的算法的有效性。

4 结论

1) 对飞行器参数标称情况以及极限拉偏情况下均做了仿真试验，同时将本文提出的算法与传统PID控制算法进行对比，验证了其有效性。仿真结果表明，本文提出的方法对高速飞行器参数不确定的情况下有很好地控制效果。

2) 本文提出的控制器不需要精确了解飞行器的模型信息，因此减少了对模型的依赖，为高速飞行器高度控制系统设计提供了一种新的思路。