2. 哈尔滨工程大学 航天与建筑工程学院, 黑龙江 哈尔滨 150001
2. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China
火箭发动机中的不稳定燃烧现象自得到观测起便引起了学者们的广泛关注,周期性的压力振荡是不稳定燃烧现象的重要表现。即使在发动机正常工作时,燃烧室内仍会存在压力振荡,而大振幅压力振荡很有可能引起严重的结构损坏和灾难性的发动机故障[1]。因此不稳定燃烧一直以来都是火箭发动机领域最具挑战性的问题之一[2]。不稳定燃烧按照其压力振荡频率与燃烧室声频的关系可以分为声不稳定和非声不稳定。我国在对大长径比翼柱装药固体火箭发动机的研制中出现了声不稳定现象[3]。美国末段高空防御系统(terminal high altitude area defense,THAAD)反导固体发动机采用了一种特殊的环向开槽型装药[4]结构,并且未见有关其不稳定燃烧的报道。对以上2种典型装药结构展开对比研究,或可从装药结构角度为我国战术火箭发动机不稳定燃烧问题找到解决途径。
发动机燃烧室常作为声腔进行分析,通过有限元技术可以获得燃烧室的声模态[5],也有学者通过扬声器激励测量燃烧室内的声学响应特性[5-6]。在美国海军与空军共同开发的声不稳定性预估软件SSP[7-9]中,也包含发动机的声学特性分析。我国学者也在燃烧不稳定性的声学问题上取得了一定成果:樊晓波[10]研究了声抑制装置对燃烧不稳定的抑制机理;杨向明等[11]对翼柱型固体发动机燃烧室声场进行分析,得出了喷管潜入段空腔的阻尼作用;张峤等[12]对H型声腔的固有频率进行了计算,得到了该类型声腔纵向声频的变化规律,并且在对发动机头部空腔的研究中,使用了有限元手段与CFD仿真结果进行了相互验证[13];苏万兴[14]在对大长径比固体火箭发动机的涡-声耦合研究中,将燃烧室声频与涡脱落频率进行了对比,表明某翼柱型发动机燃烧末段的燃烧不稳定不是由涡-声耦合所导致的。
对通过声模态分析可迅速获得确定声压波形和频率[1-2],但所得声振幅是相对值,不能得到发动机燃烧室在激励下的声学响应特性。推进剂的压力耦合响应、速度耦合响应[15]以及发动机结构振动[16-17]会使燃速发生变化,漩涡脱落[18]与内流道微小弹性形变[19]也会导致燃烧室压力的变化,最终影响燃烧室声腔响应。Wang等[20]通过声学有限元方法对燃烧室的响应声场进行了研究,获得了声压在时间-空间的分布规律。
为解决在大长径比翼柱装药发动机研制过程中出现的不稳定燃烧问题,对燃烧室在特定激励下的声学响应展开研究是迫切需要的。本文从声学角度出发,对比分析了典型翼柱型和环向开槽型装药发动机在燃面退移过程中燃烧室声频和声学响应特性变化规律,并给出了装药结构设计的一些建议。
1 声学有限元方法理论方法计算声场的固有频率和声振型一般只应用于简单的声腔形状,发动机燃烧室声腔形状多为较复杂的结构,解析法求解三维波动方程极为复杂,不同结构需采用不同的修正系数,准确性也不能保证,而低维的求解不能表征其物理特性[21]。本文采用有限元方法,对不同内流道形状声腔进行模拟。该方法的优点是可以求解复杂几何形状声腔的固有频率和声振型,且可以模拟燃烧室中不同位置在频域的响应特性。
1.1 控制方程根据质量守恒可以得到流体的连续性方程:
| $ \frac{\partial \rho}{\partial t}=-\nabla \cdot(\rho \boldsymbol{v})+\boldsymbol{Q} $ | (1) |
式中:v是速度向量;ρ是密度;Q是质量源项。
根据动量守恒,纳维-斯托克斯方程为:
| $ \rho \frac{\mathrm{d} \boldsymbol{v}}{\mathrm{d} t}=-\nabla \cdot \boldsymbol{p}+\nabla \cdot \boldsymbol{S}+\rho \boldsymbol{b} $ | (2) |
式中:b是体积力;S是粘性应力张量;p是压力。
使用下列假设可以将方程化简并得到声波方程:1)流体是可压缩的(密度是压力的函数);2)流体是无旋的;3)无体积力;4)流体的压力扰动很小;5)在流体中没有平均流动;6)流体为理想气体,绝热并且可逆。
线性化的连续性方程为:
| $ \nabla \cdot \boldsymbol{v_{a}}=-\frac{1}{\rho_{0} c^{2}} \frac{\partial \boldsymbol{p_{a}}}{\partial t}+\frac{\boldsymbol{Q}}{\rho_{0}} $ | (3) |
线性化的纳维-斯托克斯方程为:
| $ \frac{\partial \boldsymbol{v_{a}}}{\partial t}=-\frac{1}{\rho_{0}} \nabla \cdot \boldsymbol{p_{a}}+\frac{4 \mu}{3 \rho_{0}} \nabla \cdot\left(-\frac{1}{\rho_{0} c^{2}} \frac{\partial \boldsymbol{p_{a}}}{\partial t}+\frac{\boldsymbol{Q}}{\rho_{0}}\right) $ | (4) |
式中:va是声学速度;pa是声压;ρ0是流体的平均密度。
声波在流体中的有损传播方程可以表示为:
| $ \begin{gathered} \nabla \cdot\left(\frac{1}{\rho_{0}} \nabla \cdot \boldsymbol{p}\right)-\frac{1}{\rho_{0} c^{2}} \frac{\partial^{2} \boldsymbol{p}}{\partial t^{2}}+\nabla \cdot \\ {\left[\frac{4 \mu}{3 \rho_{0}} \nabla \cdot\left(\frac{1}{\rho_{0} c^{2}} \frac{\partial \boldsymbol{p}}{\partial t}\right)\right]=-\frac{\partial}{\partial t}\left(\frac{\boldsymbol{Q}}{\rho_{0}}\right)+\nabla \cdot\left[\frac{4 \mu}{3 \rho_{0}} \nabla \cdot\left(\frac{\boldsymbol{Q}}{\rho_{0}}\right)\right]} \end{gathered} $ | (5) |
式中:c是声速可表示为
使用伽辽金法对式(5)进行处理,与测试函数w相乘并且在体积上积分可以获得[22]:
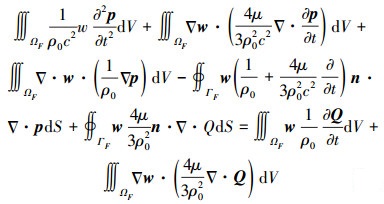
|
(6) |
式中:dV是声学域ΩF的微分体积;dS是声学域边界ΓF的微分面积;n是声学域边界ΓF的单位外法向量。
从动量守恒方程可以得到声学域边界的法向速度:
| $ \begin{gathered} \frac{\partial \boldsymbol{v_{n, F}}}{\partial t}=\boldsymbol{n} \cdot \frac{\partial \boldsymbol{v}}{\partial t}=-\left(\frac{1}{\rho_{0}}+\frac{4 \mu}{3 \rho_{0}^{2} c^{2}} \frac{\partial}{\partial t}\right) \boldsymbol{n} \cdot \nabla \cdot \boldsymbol{p}+ \\ \frac{4 \mu}{3 \rho_{0}^{2}} \boldsymbol{n} \cdot \nabla \cdot \boldsymbol{Q} \end{gathered} $ | (7) |
将流体的法向加速度使用位移表示,可得:
| $ \frac{\partial \boldsymbol{v_{n, F}}}{\partial t}=\boldsymbol{n} \cdot \frac{\partial^{2} \boldsymbol{u}_{\boldsymbol{F}}}{\partial t^{2}} $ | (8) |
将式(7)、(8)代入到式(6)中可以得到式(5)的弱形式:
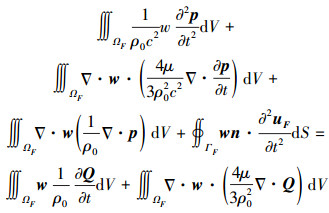
|
(9) |
式中:流体压力p和位移uF作为待求解量。
使用有限元近似得到压力和位移的形函数为:
| $ \boldsymbol{p} =\boldsymbol{N}^{\mathrm{T}} \boldsymbol{p}_{\boldsymbol{e}} $ | (10) |
| $ \boldsymbol{u} =\boldsymbol{N}^{\prime \mathrm{T}} \boldsymbol{u}_{\boldsymbol{e}} $ | (11) |
式中:N是压力的单元形函数;N′是位移的单元形函数;pe是节点压力向量;ue是节点位移向量。
根据式(10)、(11)待求解量对时间的二阶导数以及压力的变化为:
| $ \frac{\partial^{2}}{\partial t^{2}} \boldsymbol{p}=\boldsymbol{N}^{\mathrm{T}} \ddot{\boldsymbol{p}}_{e} $ | (12) |
| $ \frac{\partial^{2}}{\partial t^{2}} \boldsymbol{u}=\boldsymbol{N}^{\prime \mathrm{T}} \ddot{\boldsymbol{u}}_{e} $ | (13) |
| $ \delta \boldsymbol{p}=\boldsymbol{N}^{\mathrm{T}} \delta \boldsymbol{p}_{\boldsymbol{e}} $ | (14) |
将式(10)、(11)代入到式(9)中可以得到有限元形式的声波方程:
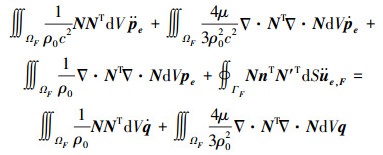
|
(15) |
式中:n是流体边界的外法向量;q是节点质量源向量。
将式(15)两边同时乘以ρ02,写成矩阵形式可得:
| $ \boldsymbol{M_{F}} \ddot{\boldsymbol{p}_{e}}+\boldsymbol{C}_{\boldsymbol{F}} \dot{\boldsymbol{p}}_{\boldsymbol{e}}+\boldsymbol{K_{F}} \boldsymbol{p_{e}}+\rho_{0} \boldsymbol{R}^{\mathrm{T}} \ddot{u}_{\boldsymbol{e, F}}=\boldsymbol{f}_{\boldsymbol{F}} $ | (16) |
式中:MF是声质量矩阵;CF是声流体阻尼矩阵;KF是声流体刚度矩阵;RT是声流体边界矩阵;fF是声流体载荷向量。
1.2 几何模型及网格划分文中的研究对象是2种典型装药的固体火箭发动机内流场。根据燃面的平行退移假设分别建立了2种内流道结构从初始时刻到结束工作时刻共计22个几何模型。为方便后文讨论,将发动机的工作时刻做归一化处理:
| $ T_{n}=t_{a} / t_{d} $ | (17) |
式中:Tn为归一化工作时刻;ta为目前工作时刻;td为设计工作时长。
Tn=0时的内流道几何模型如图 1所示,喉部直径L0=78 mm。由于发动机工作时喉部为声速,喉部下游的声学振荡不会传递回燃烧室,采用文献[20]对模型的处理方法移除了喷管扩张段。并且由于发动机头部位置和后封盖位置在多种轴向振型下始终为声压波腹[20],位置对声不稳定下的压力振荡更为敏感,定义位于发动机头部附近(0.013, 0.04, 0 m)为监测点P1;P2位于发动机后封盖附近(3.238, 0.125, 0 m)为监测点P2。

|
Download:
|
| 图 1 Tn=0时内流道几何模型 Fig. 1 Geometric model of internal flow-field when Tn=0 | |
计算中声流体使用根据典型复合推进剂热力计算所得的燃气物性参数,见表 1。燃烧室最左侧端面为质量声源激励端面,用以表征推进剂燃速变化或者结构振动对燃烧室内声流体的扰动。质量振幅
| 表 1 典型燃气物性参数 Table 1 Gas property parameters |
为验证本文方法,对冯卡门流体力学研究所(Von Karman institute for fluid dynamics,VKI)采用的P230发动机缩比模型[23-24]进行了有限元仿真,并与结果进行了对比。为与文献保持一致,验证中使用温度为285 K的空气作为声流体。模型喉部截面定义为声辐射阻抗边界,其余外表面定义为刚性壁面,所有表面无位移[20]。如图 2所示,模型燃烧室2 000 Hz以下共有4阶声模态,并且都为轴向声模态。模型燃烧室头部位置与潜入式喷管空前尾端始终是轴向声模态声压的波腹。验证工况结果与文献[20]中的声压振型进行了理论计算声压分布规律一致。如表 2所示,验证工况的声频计算结果与对比组[23-24]结果的一致性良好。前4阶声频的数值验证结果与实验值依次相差1.9%、3.9%、1.0%和2.5%,现有模型计算结果是合理并且有效的。因此,文中使用的声学有限元方法能够对燃烧室声场进行合理且有效地预测。

|
Download:
|
| 图 2 模态相位角φ=0°时,模型燃烧室的前4阶声模态振型 Fig. 2 First four acoustic mode shapes of the computational model, when modal phase angle φ=0° | |
| 表 2 模型燃烧室前4阶声模态频率与文献对比 Table 2 Comparison of the calculated frequencies of first four acoustic modes with data obtained from the literatures |
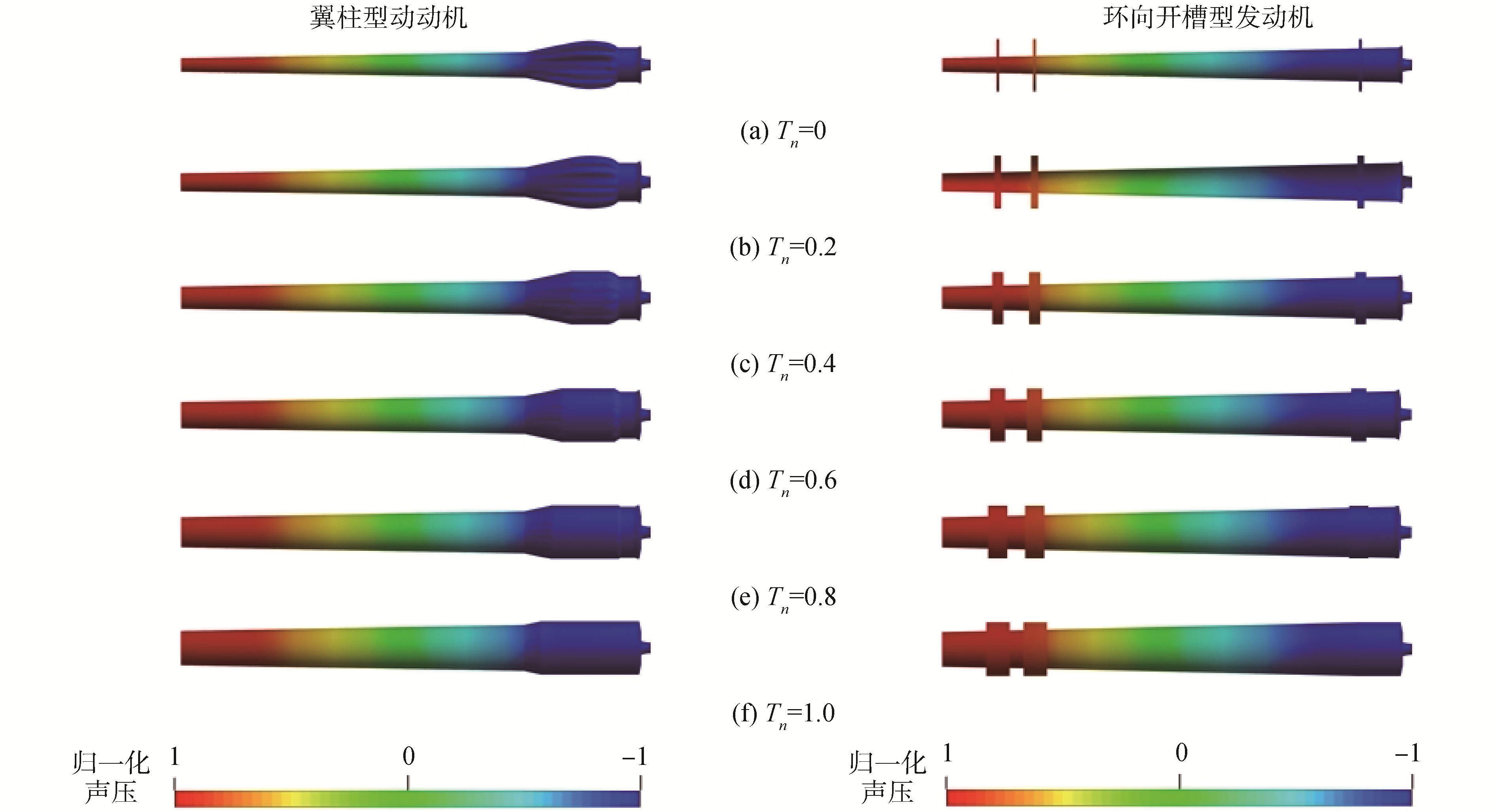
对2种结构发动机不同时刻下的燃烧室做声模态分析,如图 3所示。工作时间内翼柱型发动机与环向开槽型发动机前5阶声模态均为轴向模态。对于一定幅值不同频率的扰动对燃烧室的激励,当扰动频率接近燃烧室声频时燃烧室内压力振幅显著增大[20]。因此,在工程设计角度上,燃烧室声频变化范围不应太大。小的声频变化范围更有助于通过结构设计避免声频与结构频率接近所引起的共振现象。因此,本节重点讨论2种结构发动机随工作时间的声频变化。
|
Download:
|
| 图 3 相位角φ=0°时,翼柱装药发动机声模态基振型随工作时间变化 Fig. 3 First order acoustic mode shape of finocyl motor over time when phase angle φ=0° | |
图 3中显示了翼柱型发动机和环向开槽型发动机随工作时间的第1阶声模态振型。翼柱型发动机随工作时间翼结构不断变宽加深,并形成一个整体突扩腔,并且腔的容积逐渐增大。环向开槽型发动机槽的深度逐渐变浅,宽度逐渐变大。处在尾部的槽结构在工作中期已经变得不明显,并逐渐消失。燃烧室内尾端的扩张结构会使得发动机的声学稳定性变差[25]。而环槽装药发动机中,环槽特征结构在工作中期的逐渐退化可能有声学稳定性的考量。
对2种结构发动机不同时刻下的燃烧室做声模态分析可以得到其随时间变化的前5阶声频,如图 4。本文中计算得到的2种发动机各时刻前5阶声模态均为轴向模态,文中所讨论的所有声频均为轴向声模态频率。

|
Download:
|
| 图 4 声频随归一化工作时刻的变化 Fig. 4 Acoustic frequency variation with normalized operating time | |
如图 4,随着工作过程燃面退移,翼柱型发动机的前2阶声频先降低再升高,声频最低值出现在Tn=0.3时刻。翼柱型发动机的第3~5阶声频均存在着随工作时间先升高再降低的规律,声频最高值出现在Tn=0.3附近。环向开槽型发动机的前5阶声频均具有随工作时间先降低再升高的变化规律,声基频最低值均出现在Tn=0.3,第2~5阶声频最低值出现在Tn=0.4时刻附近。2种装药发动机由于特征结构不同,导致其高阶声频的变化规律也不一致。2种装药发动机的前2阶声频最低值均出现在工作时间的中前段。图 4中,翼柱型发动机的声频高于环向开槽型发动机。2种发动机声频在相同阶数下均有差别,前5阶声频依次相差7.9、18.3、36.1、76.4、79.3 Hz。该结果表明,在相同长度不同特征结构的燃烧室中,特征结构对声频有影响。此外,声频相差的最大值都出现在工作时间的中前段。这是由于在燃烧室燃面退移的过程中,如翼、环槽的特征结构先逐步加深、扩大,而后随着装药燃尽逐渐消失。翼型结构在发动机工作中前期已不明显,而槽型结构依旧显著。较大的特征结构差别导致了较大的声频差别。如图 4所示,翼柱型发动机声基频在179.2~186.8 Hz变化;第4阶声频在759.3~789.1 Hz变化,随工作时间改变最显著。环向开槽型发动机声基频在171.5~183.3 Hz变化;第4阶声频在712.4~754.4 Hz变化,随工作时间变化范围最大。
综上,特征结构不同将导致主尺寸相同的燃烧室声频变化规律具有明显差异。相比于环向开槽型发动机翼柱型发动机随工作时间声频变换范围更小。虽然较小的声频变化范围更有利于通过结构设计避免结构与声腔的共振,但是对于学者们广泛重视的声基频变化范围两型发动机差别不明显。
2.2 声学响应特性随燃面退移分析最大响应幅值实际上出现在声模态频率处,而由于在谐响应分析中,频率间隔的设定导致了最大响应幅值的频率出现在实际声频的附近。为方便讨论将最大响应幅值的频率直接称为声频。
如图 5(a)所示,P1在翼柱型发动机中最大声振幅为2 823.5 Pa,其出现在Tn=0.8的模型中,为第2阶声频下的振荡。在翼柱型发动机中,P1前5阶声频下的最大振幅依次为1 992.6、2 823.5、2 660.7、1 465.9、1 566.1 Pa。前3阶声频下的最大响应幅值依次出现在Tn=0.5, 0.8, 0.6时刻模型中;第4阶和第5阶声频下的最大响应幅值出现在Tn=1时刻的模型中。将第5阶声频下的压力振荡幅值选做基准,第1~4阶声频下的振荡幅值在同一时刻下依次为第5阶声频下振荡幅值284%、452%、364%、221%。而且P1点在大部分工作时间内,第1到3阶声频下的振荡比第4、第5阶声频下的振荡更为明显。如图 5(a)所示,P1在翼柱型发动机中的主要振荡频率为第1~3阶声频下的振荡。

|
Download:
|
| 图 5 P1与P2处声压时-频幅值 Fig. 5 Acoustic pressure amplitude at P1 and P2 in time and frequency domain | |
如图 5(b)所示,P1在环向开槽发动机中,最大声振幅为2 946.2 Pa,其出现在Tn=1的模型中,为第4阶声频下的振荡。在环向开槽型发动机中,P1前5阶声频下的最大振幅依次为1 418.0、854.1、1 430.0、2 946.2、1 749.1 Pa。第1阶和第4阶声频下的最大响应幅值出现在Tn=1时刻的模型中;第2阶和第3阶声频下的最大响应幅值出现在Tn=0.8时刻的模型中;第5阶声频下的最大响应幅值出现在Tn=0.7时刻的模型中。将第2阶声频下的压力振荡幅值选做基准,第1、3、4、5阶声频下的振荡幅值在同一时刻下依次为第2阶声频下振荡幅值224%、200%、381%、302%。而且P1点在大部分工作时间内,第4、第5阶声频下的振荡比第1到第3阶声频下的振荡更为明显。如图 5(b)所示,P1在环向开槽型发动机中的主要振荡频率为第4、第5阶声频下的振荡。
如图 5(c)所示,P2在翼柱型发动机中最大声振幅为1 378.1 Pa,其出现在Tn=0.9时刻,为第2阶声频下的振荡。在翼柱型发动机中,P2前5阶声频下的最大振幅依次为1 243.4、1 378.1、1 094.1、698.3、889.2 Pa。第1、第2和第4阶声频下的最大响应幅值出现在Tn=0.9时刻的模型中;第3阶声频下的最大响应幅值出现在Tn=0.6时刻的模型中;第5阶声频下的最大响应幅值出现在Tn=0.8时刻的模型中。将第5阶声频下的压力振荡幅值选做基准,第1到第4阶声频下的振荡幅值在同一时刻下依次为第5阶声频下振荡幅值159%、203%、185%、148%。而且P2点在大部分工作时间内,第1到3阶声频下的振荡比第4、第5阶声频下的振荡更为明显。如图 5(c)所示,P2在翼柱型发动机中的主要振荡频率为第1~3阶声频下的振荡。
如图 5(d)所示,P2在环向开槽发动机中,最大声振幅为1 515.8 Pa,其出现在Tn=1时刻,为第4阶声频下的振荡。在环向开槽型发动机中P2前5阶声频下的最大振幅依次为1 032.0 Pa、700.2 Pa、914.8 Pa、1 515.8 Pa、976.6 Pa。第1、第4和第5阶声频下的最大响应幅值出现在Tn=1时刻的模型中;第2阶和第3阶声频下的最大响应幅值出现在Tn=0.8时刻的模型中。将第2阶声频下的压力振荡幅值选做基准,第1和第3~5阶声频下的振荡幅值在同一时刻下依次为第2阶声频下振荡幅值189%、147%、277%、198%。而且P2点在大部分工作时间内,第3~5阶声频下的振荡比第1和第2阶声频下的振荡更为明显。如图 5(d)所示,P2在环向开槽型发动机中的主要振荡频率为第3~5阶声频下的振荡。
图 5中,2种发动机声频随工作时间有不同程度的变化,翼柱型发动机第1和第2阶声频随工作时间先降低再升高,第3~5阶声频先升高再下降。环槽型发动机的声频随工作时间按先降低再升高。声频随工作时间的变化规律与声模态分析中得到的结果一致。2种发动机随着工作时间响应幅值在各阶声频下都有变大趋势,也就是说2种发动机的声学稳定性都会随着工作时间逐渐变差。
由于2种类型发动机声压响应幅值随时间不断变化,为了比较2种发动机的主要声振型,将2个发动机的声压响应幅值在工作时间内做加权平均如表 3所示。翼柱发动机中,发动机头部P1处响应幅值最大的3阶声频,由大幅值到小幅值依次为第2、3、1阶声频。发动机尾部P2处响应幅值最大的3阶声频,按大幅值到小幅值依次为第2、1、3阶声频。可以得出,翼柱型发动机的主要响应频率为前3阶声频,第2阶声频处的响应能力最强。环槽型发动机中,发动机头部P1与发动机尾部P2处响应幅值最大的3阶声频,由大幅值到小幅值依次为第4、5、3阶声频。环槽型发动机的主要响应频率为第3~5阶声频,第4阶声频处的响应能力最强。翼柱型2个发动机在监测点处的响应幅值均大于环槽型发动机,因此环槽发动机在前3阶声频下更稳定。
| 表 3 时间加权平均响应幅值 Table 3 Time-weighted average response amplitude |
在某一阶声频响应能力强,则说明受到该声频激励情况下压力振幅大。因此,翼柱燃烧室声场在受到第1~3阶声频激励下,振幅放大最为明显。在翼柱型发动机的稳定性设计中,需要着重考虑避免外界激励频率与燃烧室第1~3阶声频相接近。同理,环槽型发动机应着重避免激励频率与第3~5阶声频接近。
近年来,固体发动机中多发的不稳定燃烧为轴向一阶不稳定。因此,对于声基频处的响应能力是工程上最应关注的。如表 3,环槽发动机P1处在第1阶声频的响应幅值是翼柱发动机的54.8%,环槽发动机P2处在第1阶声频的响应幅值是翼柱发动机的75.4%。环向开槽型发动机在工作时间内声基频下的响应幅值显著低于翼柱型发动机。
尤其在发动机工作中期,Tn=0.5时,环向开槽型发动机在P1与P2处的一阶声振幅依次为翼柱型发动机的34.5%与48.2%,如图 5。环槽型发动机在一阶声频下的声学稳定性优势最为显著,即便发生一阶声频下的压力振荡,环槽发动机也比翼柱发动机产生的压力振幅更小。
综上,特征结构不同将导致主尺寸相同的燃烧室声学响应特性具有明显差异。1 000 Hz以内,翼柱型发动机的主要声振频率为第1~3阶声频;环向开槽型发动机的主要声振荡频率为第4、第5阶声频。环槽发动机P1处在一阶声频的时间加权平均响应幅值是翼柱发动机的54.8%,环槽发动机P2处在一阶声频的时间加权平均响应幅值是翼柱发动机的75.4%。在大部分工作时间中,环向开槽型发动机在一阶声频下的声压响应幅值低于翼柱型装药发动机。特别是在发动机工作中段,环向开槽型燃烧室的稳定性优势最为显著,环向开槽型发动机P1和P2处的一阶声振幅分别是翼柱型发动机的34.5%和48.2%。
3 结论1) 特征结构不同,导致2种等长度发动机的声频特性有显著差异。随着发动机工作,燃烧室的各阶声频随在一定范围内变化,低阶声频变化范围小,高阶声频变化范围大。
2) 2种典型发动机在相同激励下,声学响应随着工作过程整体呈增大趋势。
3) 低阶声频下,尤其在声基频下,环向开槽型发动机相比翼柱型发动机声学稳定性更强。可以通过更改特征结构,增强发动机声学稳定性。
| [1] |
ZHAO Dan, LI X Y. A review of acoustic dampers applied to combustion chambers in aerospace industry[J]. Progress in aerospace sciences, 2015, 74: 114-130. DOI:10.1016/j.paerosci.2014.12.003 (  0) 0)
|
| [2] |
ZHAO Dan, LU Zhengli, ZHAO He, et al. A review of active control approaches in stabilizing combustion systems in aerospace industry[J]. Progress in aerospace sciences, 2018, 97: 35-60. DOI:10.1016/j.paerosci.2018.01.002 (  0) 0)
|
| [3] |
刘佩进, 金秉宁, 李强. 战术导弹固体发动机燃烧不稳定研究概述[J]. 固体火箭技术, 2012, 35(4): 446-449, 456. LIU Peijin, JIN Bingning, Li Qiang. A survey of combustion instability in tactical SRM[J]. Journal of solid rocket technology, 2012, 35(04): 446-449, 456. (  0) 0)
|
| [4] |
ZELLER B. Solid rocket propulsion technology[M]. New York: Pergamon Press, 1993: 606.
(  0) 0)
|
| [5] |
BROWNING S C, KRASHIN M, THACHER J H. Application of combustion instability technology to solid-propellant rocket motor problems[J]. Journal of spacecraft and rockets, 1972, 9(5): 293-294. DOI:10.2514/3.61675 (  0) 0)
|
| [6] |
MATHES H B, PRICE E W. Methods for determining characteristics of acoustic waves in rocket motors[J]. Journal of spacecraft and rockets, 1975, 12(1): 39-43. DOI:10.2514/3.56949 (  0) 0)
|
| [7] |
FRENCH J. Non-linear combustion stability prediction of SRMs using SPP/SSP[C]//39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Huntsville, Alabama: AIAA, 2003: 4668.
(  0) 0)
|
| [8] |
FRENCH J, FLANDRO G, MAJDALANI J. Improvements to the linear standard stability prediction program (SSP)[C]//40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Fort Lauderdale, Florida: AIAA, 2004: 4181.
(  0) 0)
|
| [9] |
FLANDRO G, FRENCH J, MAJDALANI J. Incorporation of nonlinear capabilities in the standard stability prediction program[C]//40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Fort Lauderdale, Florida: AIAA, 2004: 4182.
(  0) 0)
|
| [10] |
樊晓波. 燃烧室的声学特性分析及声抑制装置的研究[D]. 西安: 西北工业大学, 2007. FAN Xiaobo. Study of acoustic characteristic and suppression device of the combustion chamber[D]. Xi'an: Northwestern Polytechnical University, 2007. (  0) 0)
|
| [11] |
杨向明, 刘佩进, 陈晓龙. 翼柱型装药固体火箭发动机燃烧室声场分析[J]. 宇航学报, 2008, 29(5): 1593-1597. YANG Xiangming, LIU Peijin, CHEN Xiaolong. Analyse of acoustic property with complicated grain shape in combustion chamber of solid rocket motor[J]. Journal of astronautics, 2008, 29(5): 1593-1597. DOI:10.3873/j.issn.1000-1328.2008.05.024 (  0) 0)
|
| [12] |
张峤, 李军伟, 王宁飞. 突变截面燃烧室声腔纵向振荡频率规律分析[J]. 航空动力学报, 2010, 25(7): 1653-1658. ZHANG Qiao, LI Junwei, WANG Ningfei. Analysis on acoustic longitudinal oscillation frequency in combustion chamber with sudden change sections[J]. Journal of aerospace power, 2010, 25(7): 1653-1658. (  0) 0)
|
| [13] |
ZHANG Qiao, LI Junwei, SU Wanxing, et al. Studies on effect of head cavity on resonance damping characteristics in solid rocket motors[C]//48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Atlanta, Georgia: AIAA, 2012: 3729.
(  0) 0)
|
| [14] |
苏万兴. 大长径比固体火箭发动机不稳定燃烧预示及抑制方法研究[D]. 北京: 北京理工大学, 2015. SU Wanxing. Prediction and suppression methods of combustion instability in large aspect ratio solid rocket motors[D]Beijing: Beijing Institute of Technology, 2015. (  0) 0)
|
| [15] |
BLOMSHIELD F. Lessons learned in solid rocket combustion instability[C]//43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Cincinnati, OH: AIAA, 2007: 5803.
(  0) 0)
|
| [16] |
GREATRIX D R. Assessing the influence of orientation angle on acceleration-augmented burning in solid rockets[C]//2018 Joint Propulsion Conference. Cincinnati, Ohio: AIAA, 2018: 4691.
(  0) 0)
|
| [17] |
GREATRIX D R. Powered Flight: the engineering of aerospace propulsion[M]. London: Springer, 2012.
(  0) 0)
|
| [18] |
王健儒, 何国强, 李强, 等. 分段式固体火箭发动机内部流动不稳定性数值分析[J]. 推进技术, 2013, 34(1): 95-100. WANG Jianru, HE Guoqiang, LI Qiang, et al. Numerical analysis of flow instability in segmented SRM[J]. Journal of propulsion technology, 2013, 34(1): 95-100. (  0) 0)
|
| [19] |
KLINE H L, PALACIOS F, ALONSO J J. Sensitivity of the performance of a 3-dimensional hypersonic inlet to shape deformations[C]//19th AIAA International Space Planes and Hypersonic Systems and Technologies Conference. Atlanta, GA: AIAA, 2014: 3228.
(  0) 0)
|
| [20] |
WANG Dapeng, YANG Yuzhuo, FAN Weipeng, et al. Simulation of pressure oscillations in a combustion chamber under periodic inlet disturbances[J]. Acta astronautica, 2018, 152: 859-871. DOI:10.1016/j.actaastro.2018.07.033 (  0) 0)
|
| [21] |
刘联鋆. 内燃机进、排气系统声学分析的三维时域脉冲法[D]. 杭州: 浙江大学, 2013. LIU Lianyun. Acoustic analysis of ICE intake and exhaust systems by a 3D time-domain pulse method[D]. Zhejiang University, 2013. (  0) 0)
|
| [22] |
BATHE K J. Finite element procedures[M]. New Jersey: Prentice Hall, 2006.
(  0) 0)
|
| [23] |
ANTHOINE J, BUCHLIN J M, GUERY J F. Effect of nozzle cavity on resonance in large SRM: numerical simulations[J]. Journal of propulsion and power, 2003, 19(3): 374-384. DOI:10.2514/2.6141 (  0) 0)
|
| [24] |
SU Wanxing, LI Shipeng, ZHANG Qiao, et al. Influence of thermal inhibitor position and temperature on vortex-shedding-driven pressure oscillations[J]. Chinese journal of aeronautics, 2013, 26(3): 544-553. DOI:10.1016/j.cja.2013.04.021 (  0) 0)
|
| [25] |
刘佩进, 何国强. 固体火箭发动机燃烧不稳定及控制技术[M]. 西安: 西北工业大学出版社, 2014. LIU Peijin, HE Guoqiang. SRM combustion instability and control technology[M]. Xi'an: Northwestern Polytechnical University Press Co.Ltd., 2014. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


