在目前的航天器相对运动框架中,动力学模型呈多样化趋势,具体取决于两星的距离、运行轨道的扁率、运动递推的运算复杂度等因素,难以用单一标准来明确某个动力学模型更加适合或更加有效[1]。相对运动描述方法分为相对轨道要素描述法和直角坐标描述法2类[2]。本文主要针对相对导航制导设计应用场景,如二阶段滤波、非线性预测估计等滤波方法需要明确的干扰误差特性,基于此,对直角坐标系描述方法进行分析。
多年来,研究人员在CW方程[3]的基础上,从近圆和近距离等理想化假设条件下出发,向保留高阶项、考虑轨道摄动、椭圆轨道等几方面进行了扩展研究。文献[4-5]分别研究了圆轨道假设下二阶、三阶项对相对运动的影响。Lawden[6]以真近点角为参变量,给出了椭圆轨道下的相对动力学解析描述,称为Lawden方程,已经广泛应用于椭圆轨道的相对运动控制领域。文献[7-8]采用逐次逼近的QV(Quadratic-Volterra solution)方法研究了椭圆轨道下考虑高阶项的分析模型。
轨道环境摄动,如地球非球形引力摄动、大气阻力摄动、太阳光压摄动等均会导致期望轨迹产生偏差,是影响编队飞行的关键因素。基于CW方程,文献[9-10]提出了一种地球非球形引力摄动的补偿模型,提升了相对运动精度。文献[11]将变化幅度较小的地心距及轨道倾角平均化,推导了考虑J2项摄动干扰的近地轨道相对运动解析方程。文献[12]采用分析法研究了三体引力对卫星相对运动的影响,三体引力主要对对轨道面内运动产生长周期作用。太阳光压是高轨卫星的主要摄动元素之一,对于高面质比(high area-to-mass ratio, HAMR)目标其影响甚至占主导地位。太阳光压摄动一般考虑为非保守力,但在全轨道考虑时会呈现一些近似保守力的影响特性,如平均轨道半长轴不变、轨道偏心率或倾角以年或年的倍数周期进行波动[13-14]。
目前对CW方程的各误差要素的影响分析成果较多,但缺少地球静止轨道小倾角、小偏心率等特性下针对相对导航制导应用场景的分析,本文结合地球静止轨道的特点,推导CW方程的建模误差,并对其主要误差项进行分析,以得到误差的规律和量化特性。
1 高轨环境分析与建模卫星在轨道上始终受到各种摄动力的作用,主要包括:地球非球形摄动,高层大气的气动力摄动,太阳、月亮的引力摄动,太阳光辐射压力摄动等。在摄动力的作用下,卫星轨道偏心率e、周期、升交点赤经Ω和轨道倾角i等不断演化,呈现周期或非周期特性。虽然摄动力量级通常较小,但其长期影响不容忽视,需对各摄动的特性进行详细数值分析。
由于大气阻力随轨道高度的增加而急剧减小,地球静止轨道摄动主要考虑地球非球形引力摄动、日月引力摄动(也称三体引力摄动)、太阳光压摄动,其量级特性见表 1[15]。
| 表 1 地球静止轨道各摄动力与理想地球引力比值 Table 1 The power of the geostationary orbit is proportional to the ideal gravity |
下面以柯氏定理为基础对相对运动模型进行推导。惯性系下的矢量在转动坐标系下求导为:
| $ \dot{\boldsymbol{H}}_{i}^{o}=\dot{\boldsymbol{H}}_{o}^{o}+\boldsymbol{\omega}_{o i}^{o} \times \boldsymbol{H}_{i}^{o} $ | (1) |
式中:o表示转动坐标系;i表示惯性坐标系;Hio为惯性系下的矢量;ωoio为坐标系旋转角速度;Hoo为转动坐标系下的矢量。
目标星(target)和追踪星(chaser)的绝对动力学方程分别为:
| $ \left\{\begin{array}{l} \ddot{\boldsymbol{r}}_{t}=-\frac{m}{r_{t}^{3}} \boldsymbol{r}_{t}+\boldsymbol{a}_{t} \\ \ddot{\boldsymbol{r}}_{c}=-\frac{\mu}{r_{t}^{3}} \boldsymbol{r}_{c}+\boldsymbol{a}_{c} \end{array}\right. $ | (2) |
式中:rt、rc分别为目标星和追踪星在惯性坐标系下的位置矢量;at、ac分别为目标星和追踪星的环境摄动加速度。
|
Download:
|
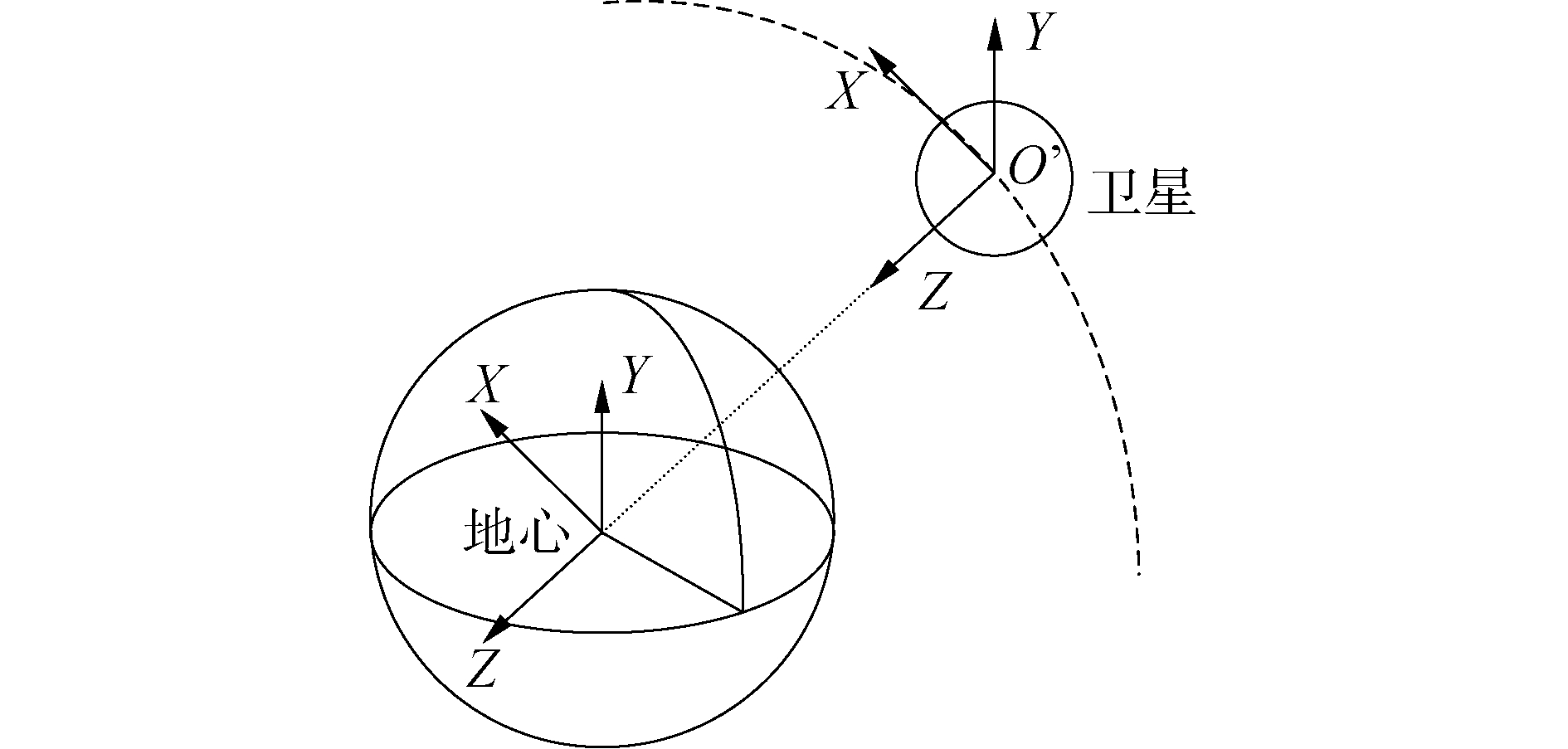
| 图 1 地心轨道坐标系 Fig. 1 Geocentric coordinate system | |
相对运动通常在卫星轨道坐标系下研究,轨道坐标系采用VVLH坐标系,定义为OoXoYoZo。
轨道坐标系OoXoYoZo不是惯性系,因此在轨道坐标系下推导相对运动方程需考虑OoXoYoZo的转动信息。为了便于研究其转动特性,建立地心轨道系OXYZ,原点在地心,相当于轨道坐标系平移到地球球心。因此地心轨道系OXYZ和星体轨道系OoXoYoZo有同样的转动特性。
假设瞬时轨道角速度各方向均存在分量,令ωico=[ωx, ωy, ωz]T,在地心轨道系下,卫星惯性速度矢量
| $ \dot{\boldsymbol{r}}_{c}^{o}=\left[\begin{array}{c} v_{i x}^{o} \\ 0 \\ v_{i z}^{o} \end{array}\right]=\left[\begin{array}{c} 0 \\ 0 \\ v_{o z}^{o} \end{array}\right]+\left[\begin{array}{c} -\omega_{y} r \\ \omega_{x} r \\ 0 \end{array}\right] $ | (3) |
显然,ωx=0,即轨道坐标系不存在X轴方向的转动分量。
根据柯氏定理求二阶导:
| $ \left[\begin{array}{c} F_{x} \\ F_{y} \\ F_{z} \end{array}\right]=\left[\begin{array}{c} 0 \\ 0 \\ \dot{v}_{o z}^{o} \end{array}\right]+\left[\begin{array}{c} -\dot{\omega}_{y} r \\ 0 \\ 0 \end{array}\right]+\left[\begin{array}{c} 2 \omega_{y} v_{o z}^{o} \\ 0 \\ 0 \end{array}\right]+\left[\begin{array}{c} 0 \\ -\omega_{y} \omega_{z} r \\ \omega_{y}^{2} r \end{array}\right] $ | (4) |
式中(Fx, Fy, Fz) 为轨道摄动加速度。解式(4),并结合两体运动轨道动力学可得瞬时轨道根数表示的瞬时轨道角速度和角加速度:
| $ \left\{\begin{array}{l} \omega_{z}=-\frac{F_{y}}{r \omega_{y}} \\ \omega_{y}=\sqrt{\frac{\mu}{a^{3}\left(1-e_{c}^{2}\right)^{3}}}\left(1+e_{c} \cos f\right)^{2}=\sqrt{\frac{\mu}{r^{3}}\left(1+e_{c} \cos f\right)} \\ \omega_{y}^{2}=\frac{\mu}{r^{3}}\left(1+e_{c} \cos f\right) \\ \dot{\omega}_{y}=\frac{2 \omega_{y} v_{z}}{r}-\frac{F_{x}}{r}=-\frac{2 \mu}{r_{c}^{3}} e_{c} \sin f-\frac{F_{x}}{r} \end{array}\right. $ | (5) |
式中:a为轨道半长轴;ec为偏心率;f为纬度幅角;Fx/r是轨道摄动力所带来的。
在追踪星轨道坐标系中,ρoo=[x y z]T,ωico=[0 ωy ωz]T,rc=[0 0 -rc]T,rt=[x y z-rc]T,
根据苛氏定理,在追踪星轨道坐标系下的两星相对运动方程表示为:
| $ \begin{aligned} \ddot{\boldsymbol{\rho}}_{i}^{o}=&\left[\begin{array}{l} x \\ y \\ z \end{array}\right]+\left[\begin{array}{c} 2 \omega_{y} \dot{z} \\ 0 \\ -2 \omega_{y} \dot{x} \end{array}\right]+\left[\begin{array}{c} -2 \omega_{z} \dot{y} \\ 2 \omega_{z} \dot{x} \\ 0 \end{array}\right]+\left[\begin{array}{c} -\omega_{y}^{2} x \\ 0 \\ -\omega_{y}^{2} z \end{array}\right]+\\ &\left[\begin{array}{c} -\omega_{z}^{2} x \\ \omega_{y} \omega_{z} z-\omega_{z}^{2} y \\ \omega_{y} \omega_{z} y \end{array}\right]+\left[\begin{array}{c} \dot{\omega}_{y} z \\ 0 \\ -\dot{\omega}_{y} x \end{array}\right]=\\ &-\frac{\mu}{r_{t}^{3}} \boldsymbol{r}_{t}+\frac{\mu}{r_{c}^{3}} \boldsymbol{r}_{c}+\boldsymbol{a}_{t}-\boldsymbol{a}_{c} \end{aligned} $ | (6) |
式中:
| $ \begin{array}{c} -\frac{\mu}{r_{t}^{3}} \boldsymbol{r}_{t}+\frac{\mu}{r_{c}^{3}} \boldsymbol{r}_{c}+\boldsymbol{a}_{t}-\boldsymbol{a}_{c}=\left[\begin{array}{c} -\omega_{y}^{2} x \\ -\omega_{y}^{2} y \\ 2 \omega_{y}^{2} z \end{array}\right]-\left[\begin{array}{c} -\omega_{y}^{2} x \\ -\omega_{y}^{2} y \\ 2 \omega_{y}^{2} z \end{array}\right] \cdot \\ e_{c} \cos u+\boldsymbol{O}\left(\boldsymbol{n}^{2}\right)+\Delta \boldsymbol{a}_{t c} \end{array} $ | (7) |
式中:O(n2) 为地球球形引力场的2阶以上高阶项引力差;Δatc为轨道环境摄动力差。式(7)可改写为:
| $ \begin{array}{c} \left[ {\begin{array}{*{20}{c}} {\ddot x}\\ {\ddot y}\\ {\ddot z} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {2{\omega _y}\dot z}\\ 0\\ { - 2{\omega _y}\dot x} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {\omega _y^2y}\\ { - 3\omega _y^2z} \end{array}} \right] = \\ - \left[ {\begin{array}{*{20}{c}} { - \omega _y^2x}\\ { - \omega _y^2y}\\ {2\omega _y^2z} \end{array}} \right]{e_c}\cos u - \left[ {\begin{array}{*{20}{c}} { - 2{\omega _z}\dot y}\\ {2{\omega _z}\dot x}\\ 0 \end{array}} \right] - \\ \left[ {\begin{array}{*{20}{c}} { - \omega _z^2x}\\ {{\omega _y}{\omega _z}z - \omega _z^2y}\\ {{\omega _y}{\omega _z}y} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{\dot \omega }_y}z}\\ 0\\ { - {{\dot \omega }_y}x} \end{array}} \right] + \mathit{\boldsymbol{O}}\left( {{\mathit{\boldsymbol{n}}^2}} \right) + \Delta {\mathit{\boldsymbol{a}}_{tc}} \end{array} $ | (8) |
若忽略ΔF的影响,上述方程是线性方程,即著名的Hill方程或CW方程,该方程被广泛用于交会对接动力学分析与控制问题中。为了得到CW方程误差的量化特性,有必要对ΔF的各组成部分进行详细研究。
2 相对运动模型误差推导分析可知,CW方程是近似方程,其误差体现在加速度项ΔF。将ΔF分解为2部分:一部分是地球球形引力场的高阶项和环境摄动力差等未建模作用力ΔF1;另一部分是圆轨道假设下,由于实际偏心率的存在等带来CW方程的未建模作用力ΔF2。
2.1 圆轨道假设下的建模误差首先,对地球球形引力场高阶项和环境摄动力差等未建模作用力ΔF1进行量化分析,该部分误差可改写为:
| $ \Delta \boldsymbol{F}_{1}=\boldsymbol{O}\left(\boldsymbol{n}^{2}\right)+\Delta \boldsymbol{a}_{t c} $ | (9) |
式中:Δatc表示空间环境中各摄动力的综合作用;O(n2) 表示地球球形引力场两星作用力差的二阶及其高阶项,若只考虑二阶项,有:
| $ \begin{array}{l} \boldsymbol{O}\left(\boldsymbol{n}^{2}\right)=\left[\begin{array}{c} \frac{-3 \omega_{k}^{2} x z}{r} \\ \frac{-3 \omega_{k}^{2} y z}{r} \\ \frac{3 \omega_{k}^{2}\left(2 y^{2}-x^{2}-z^{2}\right)}{2 r} \end{array}\right]= \\ {\left[\begin{array}{c} \frac{-3 \mu x z}{r^{4}} \\ \frac{-3 \mu y z}{r^{4}} \\ \frac{3 \mu\left(2 y^{2}-x^{2}-z^{2}\right)}{2 r^{4}} \end{array}\right]=\boldsymbol{O}\left(\frac{3 \mu}{r^{4}} \boldsymbol{\rho}^{2}\right)} \end{array} $ | (10) |
其次,对于日月引力对相对运动的作用力参见式(2)。日月引力对两星作用力的差消去共同部分,作用形式与地球球形引力场对两星作用力的形式相同。同相对动力学中地球球形引力场的一阶近似过程(7),在太阳或月球中心惯性坐标系下,对两星的日月引力差取一阶形式为:
| $ \left\{\begin{array}{c} \left.\left|\Delta \boldsymbol{f}_{\mathrm{sun}}\right|=\left|-\frac{\mu_{\mathrm{sun}}}{s_{t}^{3}} \boldsymbol{s}_{t}+\frac{\mu_{\mathrm{sun}}}{s_{c}^{3}} \boldsymbol{s}_{c}\right)\right|=\left|-\frac{\mu_{\mathrm{sun}}}{s_{t}^{3}}\left[\begin{array}{c} s_{x} \\ s_{y} \\ -2 s_{z} \end{array}\right]\right| \leqslant \\ \frac{\mu_{\mathrm{sun}}}{s_{t}^{3}} \boldsymbol{\rho}=\boldsymbol{O}\left(5 \boldsymbol{\rho} \times 10^{-14}\right) \\ \left.\left|\Delta \boldsymbol{f}_{\mathrm{moon}}\right|=\left|-\frac{\mu_{\mathrm{moon}}}{m_{t}^{3}} \boldsymbol{m}_{t}+\frac{\mu_{\mathrm{moon}}}{m_{c}^{3}} \boldsymbol{m}_{c}\right)\right|=\left|-\frac{\mu_{\mathrm{moon}}}{s_{t}^{3}}\left[\begin{array}{c} m_{x} \\ m_{y} \\ -2 m_{z} \end{array}\right] \right| \leqslant \\ \frac{\mu_{\mathrm{sun}}}{m_{t}^{3}} \boldsymbol{\rho}=\boldsymbol{O}\left(\boldsymbol{\rho} \times 10^{-13}\right) \end{array}\right. $ | (11) |
式中:mt、mc表示在月球中心惯性坐标系下目标星和追踪星的位置矢量;st、sc表示在太阳中心惯性坐标系下目标星和追踪星位置矢量;sx、sy、sz表示卫星在太阳轨道系下的相对位置坐标;mx、my、mz表示卫星在月球轨道系下的相对位置坐标。
进一步的,由表 1可见,地球非球形引力摄动中,各摄动项形式相似,带谐项J2项引力势能作用力最大,较其他项高约3个数量级。在地心惯性系下,J2摄动作用力表示为:
| $ \left\{\begin{array}{l} f_{x}=\mu \frac{1}{2} J_{2} R_{E}{}^{2}\left(15 \frac{x z^{2}}{r^{7}}-3 \frac{x}{r^{5}}\right) \\ f_{y}=\mu \frac{1}{2} J_{2} R_{E}{}^{2}\left(15 \frac{y z^{2}}{r^{7}}-3 \frac{y}{r^{5}}\right) \\ f_{z}=-\frac{\mu z}{r^{3}}\left[\frac{3}{2} J_{2} \frac{R_{E}{}^{2}}{r^{2}}\left(3-5 \frac{z^{2}}{r^{2}}\right)\right. \end{array}\right. $ | (12) |
略去r-7以上高阶项,式(12)可改写为:
| $ \begin{array}{c} {\left[\begin{array}{c} f_{x} \\ f_{y} \\ f_{z} \end{array}\right]=\left[\begin{array}{c} -\mu \frac{3}{2} J_{2} R_{E}{}^{2}\left(\frac{x}{r^{5}}\right) \\ -\mu \frac{3}{2} J_{2} R_{E}{}^{2}\left(\frac{y}{r^{5}}\right) \\ -\mu \frac{3}{2} J_{2} R_{E}{}^{2} \frac{z}{r^{5}} \end{array}\right]+\left[\begin{array}{c} 0 \\ 0 \\ -\mu \frac{6}{2} J_{2} R_{E}{}^{2} \frac{z}{r^{5}} \end{array}\right]=} \\ -\frac{\mu \frac{3}{2} J_{2} R_{E}{}^{2}}{r^{5}} \boldsymbol{r}+\left[\begin{array}{c} 0 \\ 0 \\ -\mu \frac{6}{2} J_{2} R_{E}{}^{2} \frac{z}{r^{5}} \end{array}\right] \end{array} $ | (13) |
式中:
| $ \begin{array}{c} -\mu \frac{3}{2} J_{2} R_{E}{}^{2}\left[\begin{array}{l} x \\ y \\ z \end{array}\right]_{t}+\mu \frac{3}{2} J_{2} R_{E}{}^{2}\left[\begin{array}{l} x \\ y \\ z \end{array}\right]_{c}= \\ \mu \frac{3}{2 r^{5}} J_{2} R_{E}{}^{2}\left[\begin{array}{c} -x \\ -y \\ 4 z \end{array}\right]-\mu \frac{6}{2} J_{2} R_{E}{}^{2} \frac{z_{t}}{r^{5}}+\mu \frac{6}{2} J_{2} R_{E}{}^{2} \frac{z_{c}}{r^{5}}= \\ \quad-\mu \frac{6}{2} J_{2} R_{E}{}^{2} \frac{z_{t}-z_{c}}{r^{5}} \end{array} $ | (14) |
为了便于分析,希望采用相对位置坐标的形式表示各摄动项,需要进一步推导式(14)中
倾角i对于地球静止轨道卫星正常情况下是小量,小于0.1°,进行一阶展开得:
| $ \begin{aligned} y=&-\sin i \sin \varOmega\left(x_{t}-x_{c}\right)-\sin i \cos \varOmega\left(y_{t}-y_{c}\right) \\ &-\cos i\left(z_{t}-z_{c}\right) \approx-\left(z_{t}-z_{c}\right) \end{aligned} $ | (15) |
将式(15)代入式(14),J2项的摄动差在追踪星轨道坐标系可表示为:
| $ \mu \frac{3}{2 r^{5}} J_{2} R_{E}{}^{2}\left[\begin{array}{c} -x \\ -y \\ 4 z \end{array}\right]+\left[\begin{array}{c} 0 \\ \mu \frac{6}{2 r^{5}} J_{2} R_{E}{}^{2} y \\ 0 \end{array}\right]=\mu \frac{3}{2 r^{5}} J_{2} R_{E}{}^{2}\left[\begin{array}{c} -x \\ y \\ 4 z \end{array}\right] $ | (16) |
综上所述,地球球形引力场的高阶项和环境摄动力差等未建模作用力ΔF1可统一表示为:
| $ \begin{array}{c} \Delta \boldsymbol{F}_{1}=\left[\begin{array}{c} \frac{-3 \mu x z}{r^{4}} \\ \frac{-3 \mu y z}{r^{4}} \\ \frac{3 \mu\left(2 y^{2}-x^{2}-z^{2}\right)}{2 r^{4}} \end{array}\right]-\frac{\mu_{\mathrm{sun}}}{s_{t}^{3}}\left[\begin{array}{c} s_{x} \\ s_{y} \\ -2 s_{z} \end{array}\right]- \\ \frac{\mu_{\mathrm{moon}}}{s_{t}^{3}}\left[\begin{array}{c} m_{x} \\ m_{y} \\ -2 m_{z} \end{array}\right]+\mu \frac{3}{2 r^{5}} J_{2} R_{E}{}^{2}\left[\begin{array}{c} -x \\ y \\ 4 z \end{array}\right] \end{array} $ | (17) |
由圆轨道假设等带来CW方程的未建模误差ΔF2表达式:
| $ \begin{array}{c} \Delta {\mathit{\boldsymbol{F}}_2} = - \left[ {\begin{array}{*{20}{c}} { - \omega _y^2x}\\ { - \omega _y^2y}\\ {2\omega _y^2z} \end{array}} \right]{e_c}\cos f - \left[ {\begin{array}{*{20}{c}} { - 2{\omega _z}\dot y}\\ {2{\omega _z}\dot x}\\ 0 \end{array}} \right] - \\ \left[ {\begin{array}{*{20}{c}} { - \omega _z^2x}\\ {{\omega _y}{\omega _z}z - \omega _z^2y}\\ {{\omega _y}{\omega _z}y} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{\dot \omega }_y}z}\\ 0\\ { - {{\dot \omega }_y}x} \end{array}} \right] \end{array} $ | (18) |
其中:
| $ \left[\begin{array}{c} \dot{\omega}_{y} z \\ 0 \\ -\dot{\omega}_{y} x \end{array}\right]=\frac{2 \mu}{r_{c}^{3}} e_{c} \sin f\left[\begin{array}{c} z \\ 0 \\ -x \end{array}\right] $ | (19) |
| $ \left[\begin{array}{c} -\omega_{y}^{2} x \\ -\omega_{y}^{2} y \\ 2 \omega_{y}^{2} z \end{array}\right] e_{c} \cos f=\omega_{y}^{2} e_{c} \cos f\left[\begin{array}{c} -x \\ -y \\ 2 z \end{array}\right] $ | (20) |
其中,用瞬时轨道根数表示的瞬时轨道角速度和角加速度见式(5)。在卫星轨道角加速度的两部分中,
ΔF2表达式中有相对速度项,为了获得相对位置表示的统一表达式。将速度项用相对位置表示。
在追踪星轨道系下,目标星相对运动的一阶闭环形式,那么垂直于轨道平面运动,即轨道法向运动可以表示为:
| $ \left\{\begin{array}{l} y=\sqrt{y_{0}{}^{2}+\left(\dot{y}_{0} / \omega\right)^{2}} \sin \left(\omega t+a_{1}\right) \\ \dot{y}=\omega \sqrt{y_{0}{ }^{2}+\left(\dot{y}_{0} / \omega\right)^{2}} \cos \left(\omega t+a_{1}\right)=\omega y(t+T / 4) \end{array}\right. $ | (21) |
易见,该方向运动为正弦周期振荡,振荡角速度为追踪星瞬时轨道角速度。轨道面内是椭圆运动,可表示为:
| $ \left\{\begin{array}{l} x=2 A \sin \left(\omega t+a_{2}\right)+x_{0}+\frac{2 \dot{z}_{0}}{\omega}-\left(3 \dot{x}_{0}-6 \omega z_{0}\right) t \\ z=A \cos \left(\omega t+a_{2}\right)+4 z_{0}-\frac{2 \dot{x}_{0}}{\omega} \end{array}\right. $ | (22) |
令Δl为一轨时间内两星距离变化量,zc为椭圆运动Z轴的中心坐标,表示为:
| $ \begin{array}{*{20}{l}} {\Delta l = \left( {3{{\dot x}_0} - 6\omega {z_0}} \right)\frac{{2{\rm{ \mathsf{ π} }}}}{\omega }}\\ {{z_c} = 4{z_0} - \frac{{2{{\dot x}_0}}}{\omega } = - \frac{{\Delta l}}{{3{\rm{ \mathsf{ π} }}}}} \end{array} $ | (23) |
因此,X轴相对速度可表示为:
| $ \dot x = 2\omega \left( {z - {z_c}} \right) - \left( {3{{\dot x}_0} - 6\omega {z_0}} \right) = 2\omega z + \frac{{\Delta l\omega }}{{6{\rm{ \mathsf{ π} }}}} $ | (24) |
将式(5)、(21)、(24)代入ΔF2中,忽略两阶小量得轨道面法向力摄动为:
| $ \begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{F}}_2} = - \left[ {\begin{array}{*{20}{c}} { - 2{\omega _z}\dot y}\\ {2{\omega _z}\dot x}\\ 0 \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} { - \omega _z^2x}\\ {{\omega _y}{\omega _z}z - \omega _z^2y}\\ {{\omega _y}{\omega _z}y} \end{array}} \right] = }\\ { - \left[ {\begin{array}{*{20}{c}} { - 2\frac{{{F_y}}}{r}y(t + T/4)}\\ {\frac{{{F_y}}}{r}\left( {5z + \frac{{\Delta l}}{{{\rm{3 \mathsf{ π} }}}}} \right)}\\ {\frac{{{F_y}}}{r}y} \end{array}} \right]} \end{array} $ | (25) |
统计各误差的作用效果如表 2,包含CW方程推导过程中引入的主要误差源。地球球形引力场线性化中二次项误差与卫星高度的四次方成反比,与两星的距离平方成正比;地球田谐项摄动可以忽略;带谐项摄动中J2项误差与卫星高度五次方成反比,与两星的距离成正比;日月引力的摄动作用与卫星高度相关性弱,与两星的距离成正比;圆轨道假设中轨道偏心率相关误差与卫星高度的三次方成反比,与两星的距离成正比;轨道面法向力摄动通过影响轨道坐标系的角速度耦合相对运动引入误差,与卫星高度的一次方成反比,与两星的距离和一轨漂移量成正比。
| 表 2 轨道摄动力带来的误差 Table 2 The error of the orbital perturbation force |
综上所述,CW方程的误差一方面与卫星高度有关,会随卫星高度的增加急速变小;另一方面与两星的距离有关,包含线性相关和平方相关项。
3 地球静止轨道相对运动模型误差特性分析本节对地球静止轨道相对运动模型误差进行特性分析,得到其误差的量级以及与运动构型的关系,为后面章节的相对导航设计提供依据。
前节分析可得:日月引力摄动、轨道面法向力摄动、J2摄动量级相同,且都与两星的距离成正比;地球球形引力场二次项在两星距离小于1 km时与J2等摄动同阶,在两星距离大于1 km时摄动力随距离平方增加;偏心率相关摄动大小与轨道偏心率成正比,在卫星轨道偏心率小于1×10-5时摄动力与J2等摄动同阶。CW方程在高轨误差的作用形式变得复杂,相关因素较多,没有明确的主要误差,不易补偿。
但对于典型的在轨飞行轨道,通常地球静止轨道卫星轨道偏心率小于0.001,两星相对距离大于1 km,因此地球球形引力场的二次项和偏心率相关摄动可以作为CW方程的主要误差源,用以分析CW方程误差的量级和作用形式。
利用轨道仿真软件STK的HPOP轨道输出,对主要摄动和总摄动的特性进行数值分析。主要摄动项包括地球引力二次项和偏心率相关摄动,总摄动在动力学模型中按式(8)右端引出。
分析条件为:追踪星偏心率0.001,两星相距10 km,伴飞椭圆1 km。主要摄动项的量化特性见图 2,总摄动项的量化特性见图 3。
|
Download:
|
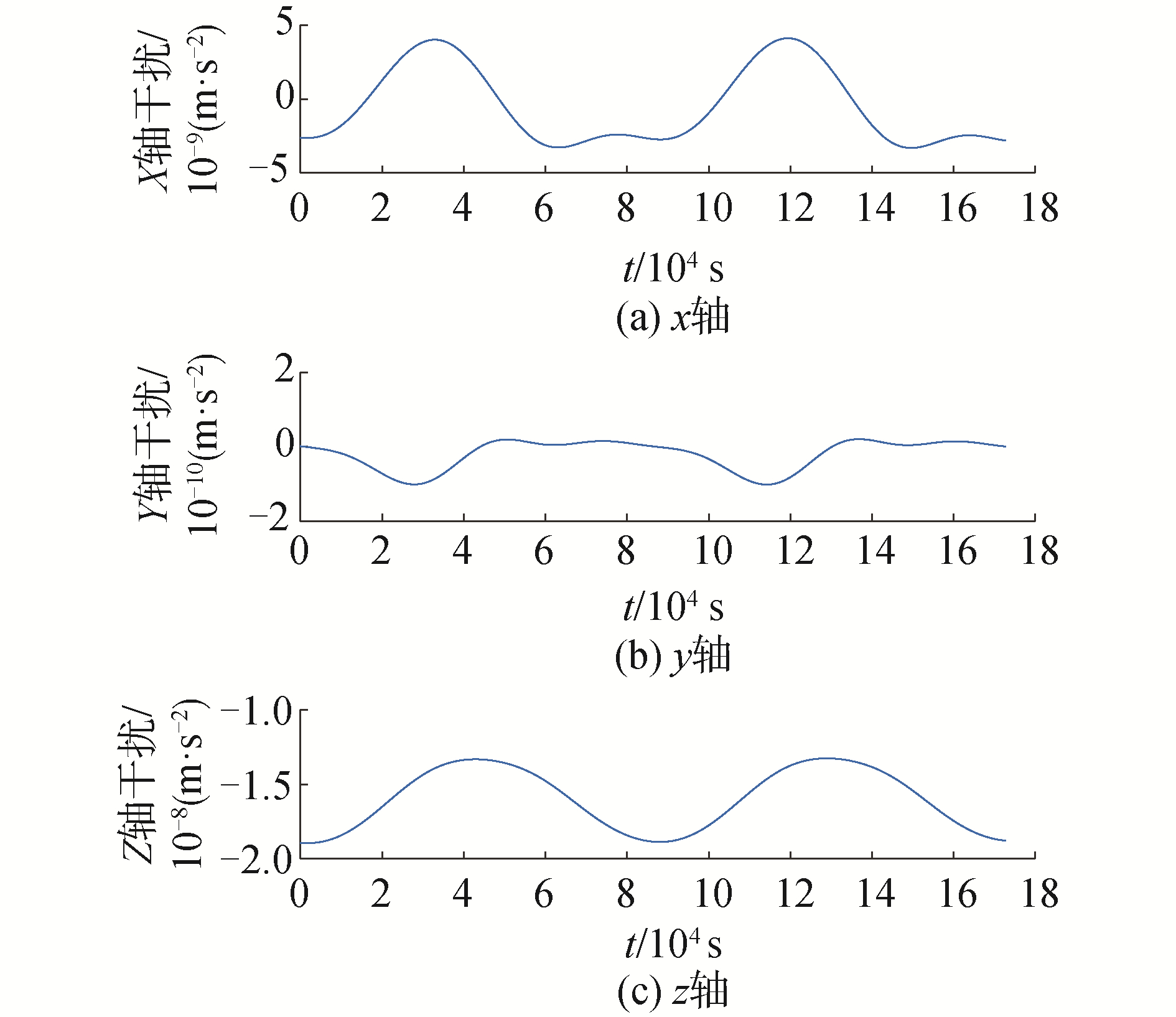
| 图 2 地球静止轨道主要摄动累加 Fig. 2 The main perturbation of the geostationary orbit | |

|
Download:
|
| 图 3 地球静止轨道CW方程各轴总摄动 Fig. 3 The total perturbation of each axis of the CW equation of geostationary orbit | |
仿真可见,上述主要摄动项在各类误差中占主要部分,与总误差量级相同,且振荡和常偏特性类似,能够反映地球静止轨道相对运动模型CW方程的误差特性。图 3中的波动部分是目标进出阴影过程中的太阳光压摄动差。
下面对地球引力二次项和偏心率相关摄动项的量化特性进行独立分析。图 4是对表 2中,地球球形引力二阶项在两星10 km稳定伴飞工况下各轴作用力的量化特性。相对运动椭圆和轨道面外振荡控制的比较小,此时地球球形引力场二阶项在轨道面法向Y轴作用力很小,该项与两星的相对距离没有关系;地球球形引力场的二阶项对X轴和Z轴的摄动作用与两星相对距离和伴飞椭圆尺寸均相关,由于相对运动在Z轴为周期运动,X轴摄动项表现出周期振荡;Z轴的摄动作用主要特点是常偏,在稳定伴飞期间,由于Y轴振荡小,Z项的摄动表现为跟两星距离平方成正比的常偏和一个与伴飞椭圆相关的小幅振荡的综合。

|
Download:
|
| 图 4 地球球形引力场二阶项摄动各轴分量 Fig. 4 Second order perturbation of the earth′s spherical gravitational field perturbs each axial component | |
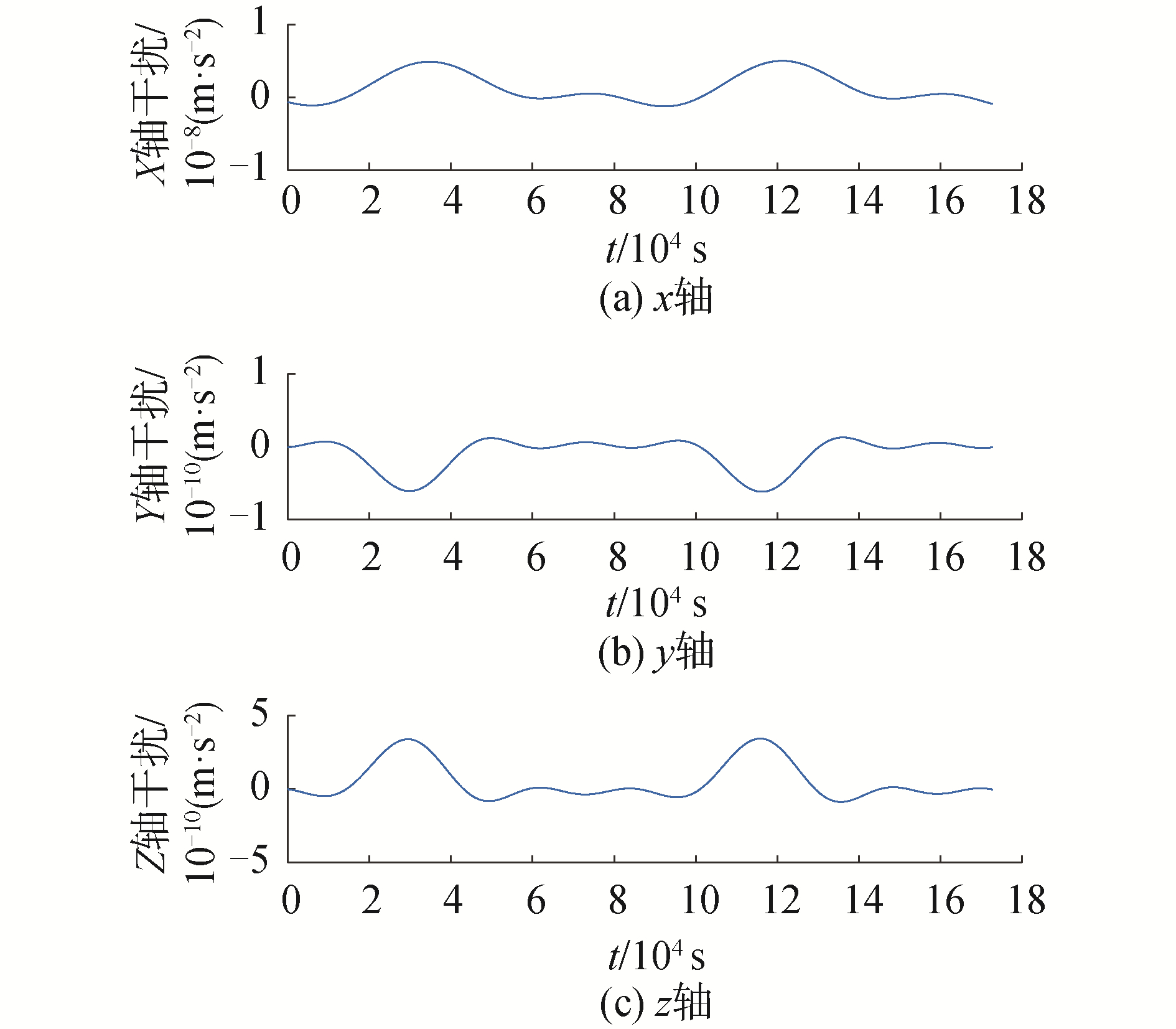
图 5是对表 2中偏心率相关项在两星10 km稳定伴飞工况下各轴作用力的仿真输出,呈现周期性的振荡特性。从相对运动方程CW方程的稳态解析式(22)可得,各轴相对位置呈现周期性变化,偏心率相关项各轴摄动耦合因素多,偏心率和相对运动椭圆尺寸联合影响振荡的幅值,相对运动的当前位置和当前轨道幅角等综合影响振荡的相位。
|
Download:
|
| 图 5 偏心率相关摄动各轴分量 Fig. 5 Eccentricity correlative perturbation of each axis component | |
综合分析表明,地球球形引力二次项和偏心率相关摄动项反映了CW方程在地球静止轨道的主要误差特性,可以在相对导航滤波设计中用以定量分析状态方程的误差情况,或设计干扰估计模型。地球球形引力场二次项的误差在各轴呈现周期振荡特性,并随两星距离变大,在Z轴产生常值偏差分量;偏心率相关摄动与两星相对构型线性相关,各轴均呈现为周期振荡特性。
5 结论1) 考虑地球球形引力场高阶项、地球非球形引力摄动、三体引力摄动和太阳光压摄动,分析了地球静止轨道环境中各摄动力的对相对运动的作用量级,对两星相对运动方程进行了建模分析,得到了完整的误差要素。
2) 为研究CW方程的误差特性,对加速度项进行深入分析,给出了各误差源的近似表达式、作用量级和影响因素,分析表明,CW方程的误差随卫星高度的增加急速变小,并且与相对距离存在线性和平方复合的相关特性。
3) 对典型的相对运动型态进行了数值仿真,结果表明地球球形引力二次项、偏心率相关项以及J2项相关误差为CW方程的主要误差来源,在轨道系坐标系各轴向具体呈现为常值偏差和轨道周期振荡组合的分布特性。
| [1] |
SULLIVAN J, GRIMBERG S, D'AMICO S. Comprehensive survey and assessment of spacecraft relative motion dynamics models[J]. Journal of guidance, control, and dynamics, 2017, 40(8): 1837-1859. DOI:10.2514/1.G002309 (  0) 0)
|
| [2] |
李俊峰, 雪丹. 编队卫星相对运动描述方法综述[J]. 宇航学报, 2008, 29(6): 1689-1694. LI Junfeng, XUE Dan. Review of relative motion description methods for satellite formation flying[J]. Journal of astronautics, 2008, 29(6): 1689-1694. (  0) 0)
|
| [3] |
CLOHESSY W H, WILTSHIRE R S. Terminal guidance system for satellite rendezvous[J]. Journal of the aerospace sciences, 1960, 27(9): 653-658. DOI:10.2514/8.8704 (  0) 0)
|
| [4] |
LONDON H S. Second approximation to the solution of the rendezvous equations[J]. AIAA journal, 1963, 1(7): 1691-1693. DOI:10.2514/3.1896 (  0) 0)
|
| [5] |
RICHARDSON D L, MITCHELL J W. A third-order analytical solution for relative motion with a circular reference orbit[J]. The journal of the astronautical sciences, 2003, 51(1): 1-12. DOI:10.1007/BF03546312 (  0) 0)
|
| [6] |
LAWDEN D F. Optimal trajectories for space navigation[M]. London: Butterworths, 1963.
(  0) 0)
|
| [7] |
BUTCHER E A, LOVELL T A, HARRIS A. Third order Cartesian relative motion perturbation solutions for slightly eccentric chief orbits[C]//Proceedings of the 26th AAS/AIAA Space Flight Mechanics Meeting. Napa, CA, 2016.
(  0) 0)
|
| [8] |
WILLIS M, LOVELL A, D'AMICO S. Second order analytical solution for relative motion on arbitrarily eccentric orbits[C]//Proceedings of 2019 AAS/AIAA Astrodynamics Specialist Conference. Ka'anapali, Maui, 2019.
(  0) 0)
|
| [9] |
GISA G S, KRISHNAN Y, BHARATH R K. A study on the effect of J2 perturbation on optimum delta-v for collision avoidance maneuver[J]. International journal of engineering and technical research, 2020, 9(10): 485-490. (  0) 0)
|
| [10] |
CAO Lu, MISRA A K. Linearized J2 and atmospheric drag model for satellite relative motion with small eccentricity[J]. Proceedings of the institution of mechanical engineers, part G: journal of aerospace engineering, 2015, 229(4): 2718-2736. (  0) 0)
|
| [11] |
WU Baolin, XU Guangyan, CAO Xibin. Relative dynamics and control for satellite formation: accommodating J2 perturbation[J]. Journal of aerospace engineering, 2016, 29(4): 04016011. DOI:10.1061/(ASCE)AS.1943-5525.0000600 (  0) 0)
|
| [12] |
周敬, 郑建华, 李明涛. J2摄动下卫星相对运动解析方程研究[J]. 航天控制, 2017, 35(2): 44-50. ZHOU Jing, ZHENG Jianhua, LI Mingtao. Analytical solutions for satellite relative motion under J2 perturbation[J]. Aerospace control, 2017, 35(2): 44-50. (  0) 0)
|
| [13] |
徐光延, 谌颖, 罗健夫, 等. 第三体引力摄动的近地轨道卫星相对运动方程[J]. 宇航学报, 2015, 36(1): 25-32. XU Guangyan, CHEN Ying, LUO Jianfu, et al. Satellite relative equations in low earth orbits under third-body perturbation[J]. Journal of astronautics, 2015, 36(1): 25-32. (  0) 0)
|
| [14] |
BRACK D N, GURFIL P. In-orbit tracking of high area-to-mass ratio space objects[J]. Journal of guidance, control, and dynamics, 2017, 40(8): 2030-2041. DOI:10.2514/1.G002501 (  0) 0)
|
| [15] |
杨嘉墀. 航天器轨道动力学与控制[M]. 北京: 宇航出版社, 2001.
(  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


