将毛细管电泳小型化为平面微流控芯片具有分析时间短、样品量减少和电导率提高等多种优势,芯片上电泳的一个缺点是微通道的深度较小,约为10 μm,导致检测路径更短。与常规电泳相比,会降低片上电泳的检测灵敏度。通过将电泳分离与在线样品预富集方法[1]结合使用,可以大大提高检测灵敏度,如场效应放大的样品堆叠(FASS)[2-5]、离子浓度差极化(ICP)[6-9]和pH梯度聚焦[10]。在各种样品预富集方法中,FASS由于其简单性和易于实施性而最受欢迎。在FASS中,通过创建高浓度和低浓度电解质的相邻区域来建立背景电解质的电导率梯度。首先将样品分析物混入低电导率的背景电解质中。施加电场后,分析物会从低电导率区域迁移到高电导率区域,从而在整个电导率梯度上迁移。电导率梯度会在本地电场中建立一个梯度,与低电导率区域相比,这会导致分析物在高电导率区域(由于较低的局部电场)而缓慢迁移。电迁移速度的这种差异会导致分析物堆积在高电导率区域中。通常,在FASS中,堆积前后的分析物浓度明显小于背景电解质种类的浓度,因此,分析物不会影响电导率梯度。因此,如果pH和离子强度[11]对电解液的电泳迁移率的影响是,理想的浓度增加等于高电导率电解质和低电导率样品的电导率之比。实验证明,FASS可使片上电泳的检测灵敏度提高1 000倍[12]。在理论上,如果没有分子扩散和不均匀的流体流动,则FASS中的样品分析物迁移到高电导率区域后会立即达到其最大允许浓度。此后,堆积的分析物区的前导前沿进一步迁移到高电导率区,而初始电导率梯度保持稳定。实际上,FASS中的分析物需要有限的时间才能达到最大浓度。这是因为初始的电导率梯度和堆积的样品区分别由于背景电解质种类和分析物的扩散而变宽,这限制了堆积的分析物达到其最大允许浓度的速率。本文基于理论比例分析,数值模拟了芯片上样品堆叠实验,阐明了FASS中的富集现象。根据轴向扩散还是对流扩散主导峰展宽,确定了2种不同的样品叠加方案。首先在FASS中介绍相关的时长和时标,然后使用这些特征长度和时间标度以无量纲形式表示峰浓度和宽度的依赖性。接下来,在存在EOF的情况下,使用芯片上FASS的多维数值模拟验证了理论富集分析。再Comsol中进行有限元求解,得到了芯片上的电流、电导率、富集倍数等结果并进行分析。
1 场放大样品堆叠理论仿真 1.1 问题描述考虑在湿法蚀刻的具有D形横截面的玻璃微通道中的单个阴离子分析物的FASS。微通道的宽度和中心线深度分别为w和d,假设微通道较浅(d
|
Download:
|
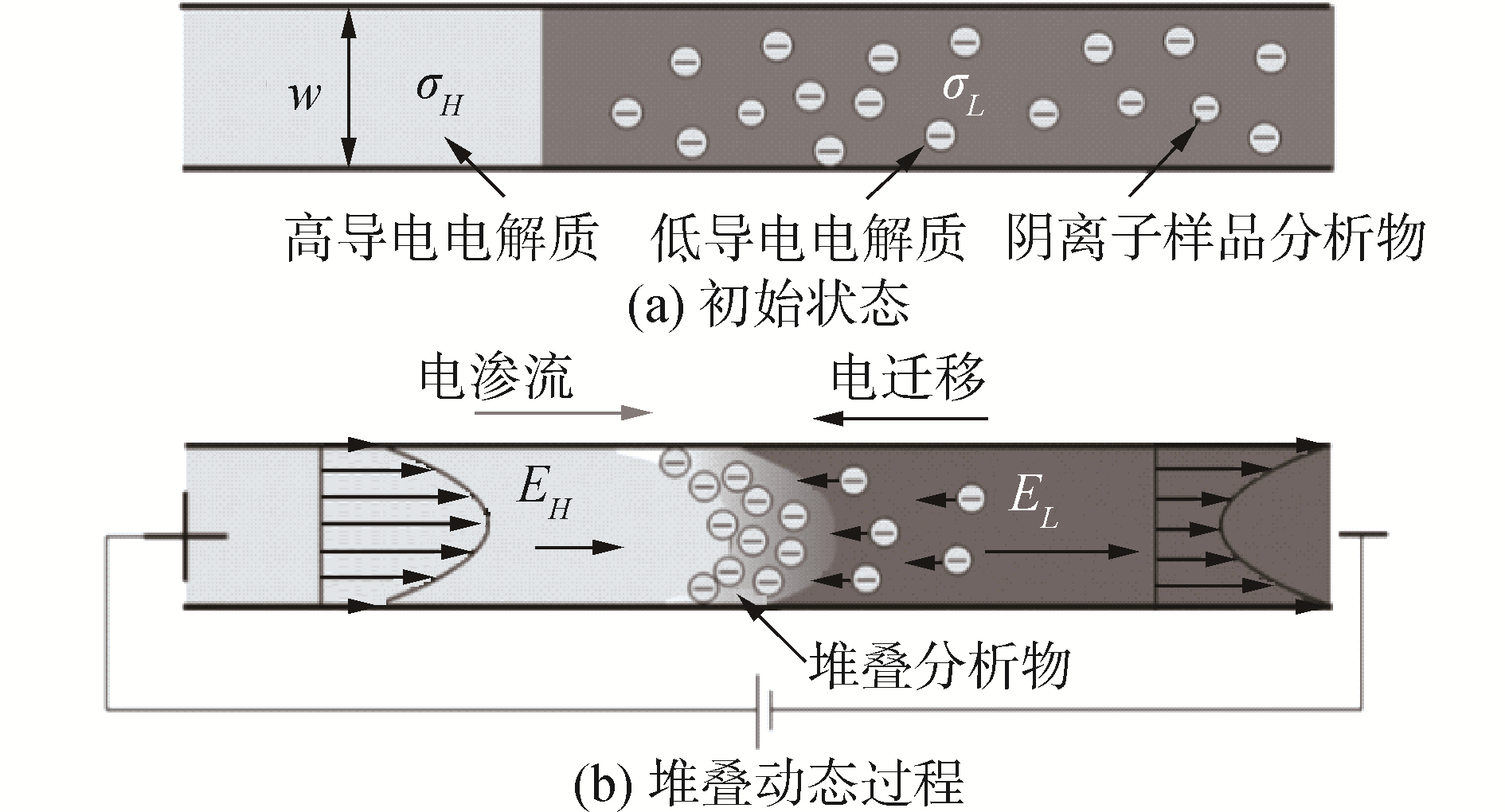
| 图 1 存在EOF时在单个通道中的FASS Fig. 1 Schematic showing FASS in a single channel in the presence of EOF | |
从理论上描述FASS过程动力学的一种方法是使用3-D对流-电迁移-扩散方程式以及适当的初始条件和边界条件。除了这些守恒定律外,还需要用酸碱平衡和离子强度校正方程来模拟pH和离子强度对离子种类的有效迁移率和扩散率的影响。为了专注于FASS的基本物理学,而不必深入研究电解质化学,在理论分析中,认为离子物种的迁移率和扩散率是恒定的。当物质被完全电离或电解质得到良好缓冲时,这是一个合理的假设。
首先,在FASS过程中查看相关的长度和时间尺度,如图 1所示。在当前问题中,通道宽度ω和深度d是2个明显的长度尺度。因为假设深度明显小于宽度,所以由于在短时间范围d2/D内分子的快速扩散,沿深度的物种浓度的任何变化都会迅速减小,其中D表示分析物的扩散率。因此,深度d不会影响样品堆积的动力学,此后在尺寸分析中就不会考虑深度。在当前问题中,轴向上没有外部长度尺度,因为初始界面将高和低电导率的半无限区域分开很尖锐。但是,存在一个固有的轴向长度标度与样品堆积现象有关,这是由于电迁移和扩散通量之间的平衡引起的:
| $ \mu \frac{\partial }{{\partial x}}(cE) \sim D\frac{{{\partial ^2}c}}{{\partial {x^2}}} $ | (1) |
式中:c表示分析物浓度;E是电场;x是轴向坐标;μ和D分别为去注意分析物的电泳迁移率和扩散率。由于分析物迁移高到电导率区域,等式(1)中电场的相关标度是高导电区,用EH表示。如果与高导电区的长度相比,低导电率的样品区的长度是显著变大,则在样品区EL的电场几乎等于在通道施加的平均电场,即ES≈E。在这种情况下,由于电流的连续性决定EH≈/γ,因此高导电区中的电场可以近似为σHEH=σLEL。σH和σL是高和低电导率区的电导率,γ=σH/σL。接下来,使用式(1)可以得到固有长度尺度δ:
| $ \frac{{\mu E}}{{\delta \gamma }} \sim \frac{D}{{{\delta ^2}}},\delta \equiv \frac{{\gamma D}}{{\mu E}} $ | (2) |
式中:扩散率与能谱性的关系是通过能斯特-爱因斯坦方程D=μkT/(ze)建立,其中z是化合价数,kT/e=25.7 mV是温度T=298 K时的热电压。因此,长度标尺δ可以替代地解释为高导电区中热电压与局部电场的比值。样品堆叠的固有时间标度τs可以用长度δ表示为:
| $ {\tau _s} \equiv \frac{{{\delta ^2}}}{D} = \frac{{{\gamma ^2}D}}{{{\mu ^2}{E^2}}} $ | (3) |
该时间尺度可以解释为分析物在长度δ上扩散的时间尺度。由于电迁移和扩散通量的平衡,τs也对应于在整个长度δ上进行电迁移所需的时间。分析物在通道宽度上扩散的时间标度为τd=ω2/D, 通过电迁移使距离ω移动的时间为τem=μEOFE。除了τd,还有另一个扩散时间尺度τbg=ω2/Dσ, 对应于电导率场的扩散。对于二元电解质,有效扩散系数为Dσ=D+D-(z+-z-)/(z+D+-z-D-),其中z±和D±表示阴离子和阳离子的化合价和扩散率。通常分析物和背景电解质种类的扩散度处于相同的数量级,τd和τbg的也是如此。为了获得对应于非均匀EOF的时间尺度,定义通道中的平均EOF速度为μEOFE,EOF是通道表面的电渗运动,E是平均电场。高电导率区域(μEOFE(γ-1))驱动强烈的压力驱动流,从而导致样品分散。因此,由于不均匀的EOF而导致对流扩散的时间尺度可作为τEOF=ωγ/E(γ-1)。可以注意到,电场和电导率梯度的耦合会导致电粘性流,这具有相关的电粘性时间标度。在这里忽略电粘性时间标度,基于各种长度和时间尺度,现在在2个极限中描述FASS的动力学:当轴向扩散主导对流扩散时和当对流扩散主导轴向扩散时。
1.3 扩散主导型扩散和对流的相对重要性可以用Peclet数Pe来描述,其定义为扩散和对流时间尺度的比率Pe≡τd/τEOF=(γ-1)μEOFEω/(γD)。从泰勒色散分析中得知,对流扩散仅出现在10以上的Peclet数之上, 因此在低Peclet数下,可以忽略EOF对峰浓度和峰宽的影响。在这种以扩散为主的体系中,EOF的唯一作用是对流下游的堆叠的分析物区域。当可以忽略对流扩散时,沿着通道轴线的堆叠过程可以被认为是基本上一维的。因此,FASS的动力学仅取决于固有长度尺度(由式(2)定义),而不取决于通道宽度ω。类似地,依赖于ω的时间尺度在以扩散为主的体系中是不相关的,并且唯一相关的时间尺度是τs,峰值浓度用cmax和FWHM表示为:
| $ \frac{c_{\max }}{c_{0}}=f\left(\frac{t}{\tau_{s}}, \gamma, \frac{D_{\sigma}}{D}\right), \quad \frac{l}{\delta}=g\left(\frac{t}{\tau_{s}}, \gamma, \frac{D_{\sigma}}{D}\right) $ | (4) |
式中:c0是初始分析物浓度。在这些无量纲关系中,通过选择电解质化学性质和样品分析物来固定参数Dσ/D。
无量纲峰浓度和宽度的确切函数依赖性只能通过数值模拟或实验来确定。可以进一步简化式(4),对于给定的Dσ/D,峰值浓度和宽度的时间增长率主要由时间标度τs决定,电导率的唯一其他影响是γ,可以简化式(4)中Dσ/D为固定的值:
| $ \frac{c_{\max } / c_{0}-1}{\gamma-1}=f\left(t / \tau_{s}\right), \frac{l}{\delta}=g\left(t / \tau_{s}\right) $ | (5) |
在实际试验中,由于有限的通道长度可用于在微流体装置上进行预浓缩,因此重要的是要考虑峰浓度和峰宽作为堆积峰x轴向位置的函数。堆叠峰主要是由于EOFx≈μEOFEt迁移,即t/τs=xμ2E/(μEOFγ2D)。由于高迁移率区域中被分析物的电泳速度小,因此忽略了由于电迁移导致的峰最大值迁移。所以式(5)可以用峰位置x表示为:
| $ \frac{c_{\mathrm{max}} / c_{0}-1}{\gamma-1}=f\left(\frac{\mu^{2} E}{\mu_{\mathrm{EOF} } \gamma^{2} D} x\right), l=\frac{\gamma D}{\mu E} g\left(\frac{\mu^{2} E}{\mu_{\mathrm{EOF} } \gamma^{2} D} x\right) $ | (6) |
由于f是单调递增函数,因此该方程式表明,在给定的轴向峰值位置x处,较高电场下的预浓缩效率较高。另一方面,在给定位置x处的峰宽l对电场的依赖性很弱,如式(6)表明,在高E处函数g的较高值被1/E取反。因此,以扩散为主的状态中增加电场会在固定的通道位置处产生更高的集中度,而峰宽没有任何显着变化。
1.4 对流主导型在高电场下,不均匀的EOF导致堆叠峰的严重对流扩散。这种情况对应于的大Peclet数
在对流占优的情况下,由于强的横向浓度梯度,相关的长度尺度为通道宽度ω。在这种情况下,重要的时间尺度是
| $ \frac{c_{\max }}{c_{0}}=f\left(\frac{t}{\tau_{\text {EOF }}}, \frac{\tau_{d}}{\tau_{\text {EOF }}}, \frac{\tau_{d}}{\tau_{\text {bg }}}, \frac{\tau_{\text {EOF }}}{\tau_{\text {em }}}, \gamma\right)=f\left(\frac{t}{\tau_{\text {EOF }}}, P_{e}, \frac{D_{\sigma}}{D}, \frac{\mu}{\mu_{\text {EOF }}}, \gamma\right) $ | (7) |
式中:cmax是堆积峰的最大面积平均浓度, 面积平均浓度的FWHM可以用无量纲形式描述为:
| $ \frac{l}{\omega}=g\left(\frac{t}{\tau_{\mathrm{EOF}}}, P_{e}, \frac{D_{\sigma}}{D}, \frac{\mu}{\mu_{\mathrm{EOF}}}, \gamma\right) $ | (8) |
同样,在这些方程式中,Dσ/D由背景电解质和分析物的选择决定。在实验过程中,电泳迁移率与电渗迁移率的比率μ/μEOF不能改变,因为它取决于背景电解质和微通道底物的选择。此外,可以忽略式(7)和(8)中Peclet数Pe的依赖性。在实际实验情况下,Pe
| $ \frac{{{c_{\max }}}}{{{c_0}}} = f\left( {\frac{t}{{{\tau _{{\rm{EOF}}}}}}} \right),\quad \frac{l}{\omega } = g\left( {\frac{t}{{{\tau _{{\rm{EOF}}}}}}} \right) $ | (9) |
本节描述了用于模拟单个分析物在微通道高、低电导区界面处样品堆积的控制方程。使用这些控制方程在COMSOL中进行数值模拟。带电分析物的浓度c由平流电迁移扩散方程模拟:
| $ \frac{\partial_{c}}{\partial_{t}}+\nabla \cdot(u c+\mu E c)=\nabla \cdot(D \nabla c) $ | (10) |
式中: D表示扩散系数; 电泳迁移率; E表示电场; u表示流体速度。电泳迁移率μ和扩散率D与能斯特-爱因斯坦方程D=μkT/ze有关,其中k是玻尔兹曼常数; z是离子价; e是质子电荷; T是温度。背景电解液假定为二元电解液。在FASS中,分析物的浓度明显小于背景电解质离子的浓度。因此,二元电解液的电导率可以模拟为:
| $ \frac{\partial_{c}}{\partial_{t}}+\nabla \cdot(u \sigma)=\nabla \cdot\left(D_{\sigma} \nabla \sigma\right) $ | (11) |
式中:σ表示电解液的局部电导率。对于二元电解液,有效扩散系数由(Dσ=D+D-(z+-z-)/(z+D+-z-D-)来给出,其中z±和D±分别表示背景电解液的阴离子和阳离子的价和扩散系数。电场E是准静态的,因此可以引入电势
| $ E=-\nabla \phi $ | (12) |
根据欧姆定律,局部电场依赖于局部电导率σ:
| $ \nabla \cdot(\sigma E)=0 $ | (13) |
在这里假设扩散电流与欧姆电流相比可以忽略不计。不可压缩流体流动由连续性方程控制为:
| $ \nabla \cdot u=0 $ | (14) |
以及Navier-Stokes方程:
| $ \rho \frac{\partial_{u}}{\partial_{t}}+\rho u \cdot \nabla u=-\nabla p+\eta \nabla^{2} u $ | (15) |
式中:ρ表示流体的密度;p表示压力;η表示流体的动态粘度。
2.2 几何模型模拟区域是一个二维条形通道,如图 2所示,由5 mm长的左侧通道和35 mm长的右侧通道组成。通道的宽度为50 μm。最初,右侧通道充满低导电性电解液,右侧通道充满高导电性电解液。在接合处的高导电区和低导电区之间存在明显的梯度,样品分析物在低电导率电解质中混合。低电导区的分析物浓度为1 μM,在两侧施加电压,将右通道出口电位设为零,施加电场。

|
Download:
|
| 图 2 几何模型图 Fig. 2 Geometric model diagram | |
使用商业模拟软件包COMSOL Multiphysics(版本5.4)进行了二维数值模拟。使用COMSOL内置的电场、流体场、分析物浓度场和偏微分方程(PDE)构建的电导率场,在COMSOL中实现了耦合仿真。通过设定边界条件,利用式(11)和“稀释物种迁移”模块对电导率场进行了建模。方程((13)连同方程(12))和方程(10)使用“系数形式PDE”模块求解。模拟流体流动使用方程式。式(14)和(15)用COMSOL的“层流”模块求解。采用多前额大规模并行稀疏直接解算器(MUMPS),每个模拟有1 066 058个自由度。模拟时间为10 s,每0.5 s保存一次数据。为了处理样品堆积过程中出现的浓度梯度,绝对公差降低到10-5,在样本堆积区域使用高分辨率(Δx=Δy=0.002 mm)的Mapped(矩形)网格单元。
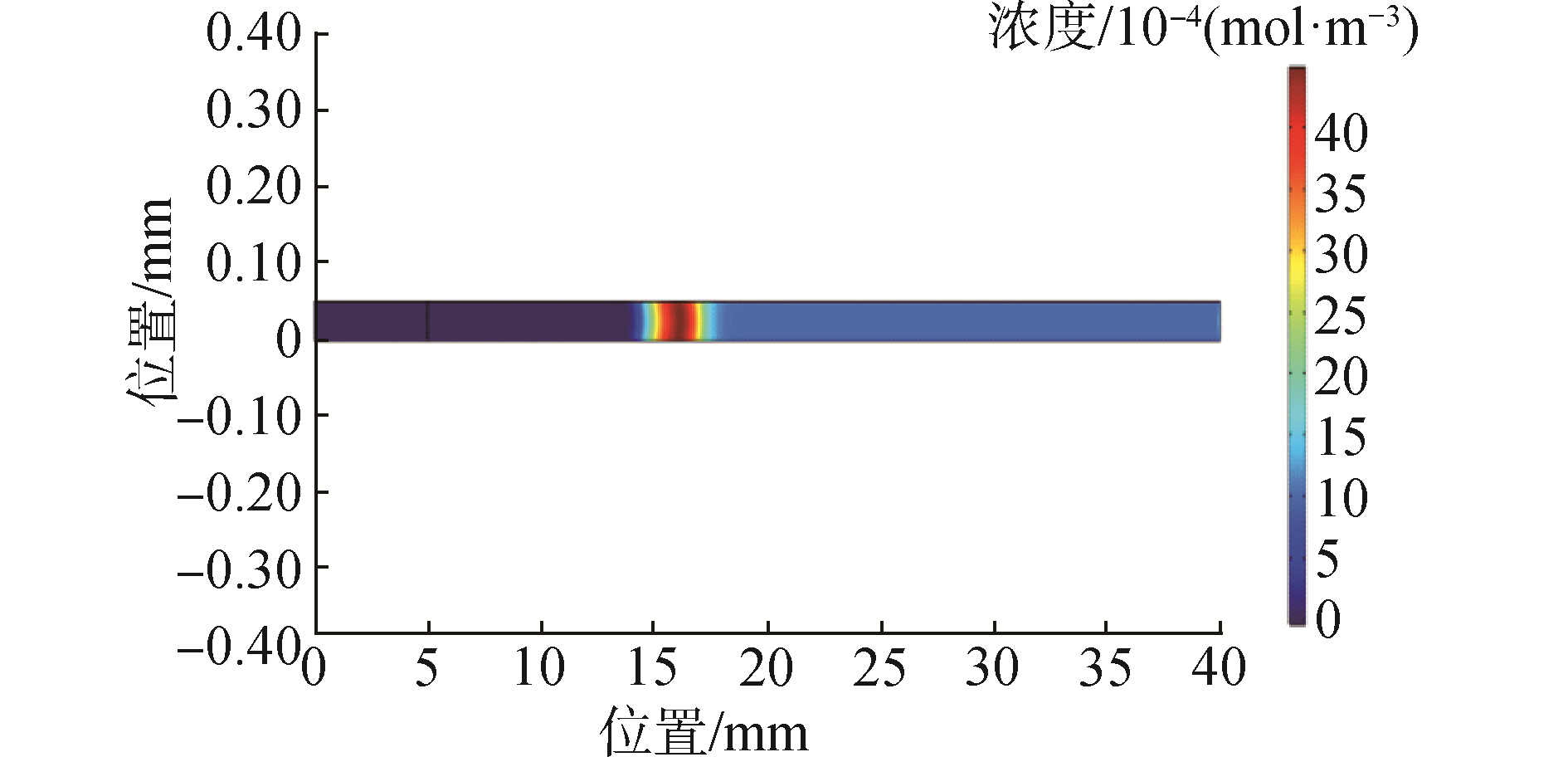
3.2 仿真结果经Comsol软件有限元求解后,得到下图结果,可以看到在芯片上渐渐形成了一块高浓度的样品富集区域,随着时间变化富集区域渐渐向右侧推进,且富集带逐渐变宽,富集的样品逐渐增多。
|
Download:
|
| 图 3 仿真结果 Fig. 3 Simulation result | |
|
Download:
|
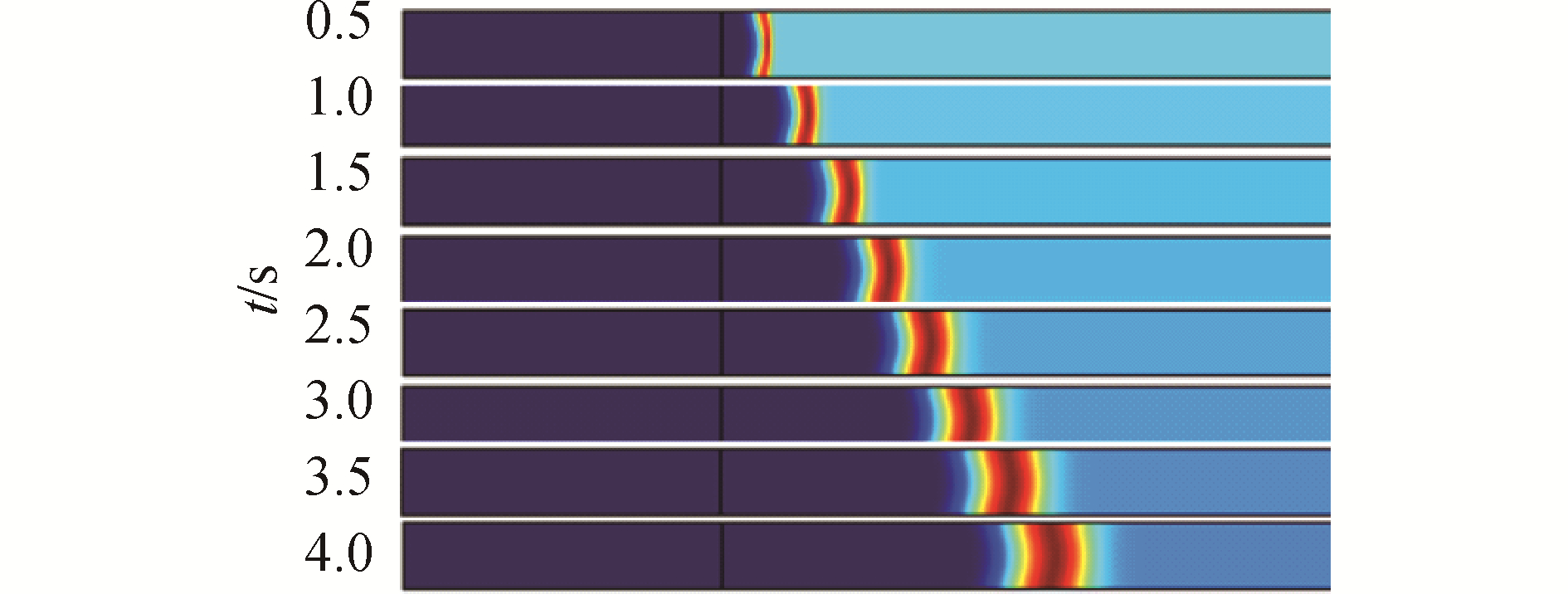
| 图 4 仿真过程中的动态截图 Fig. 4 Dynamic screenshot during simulation | |
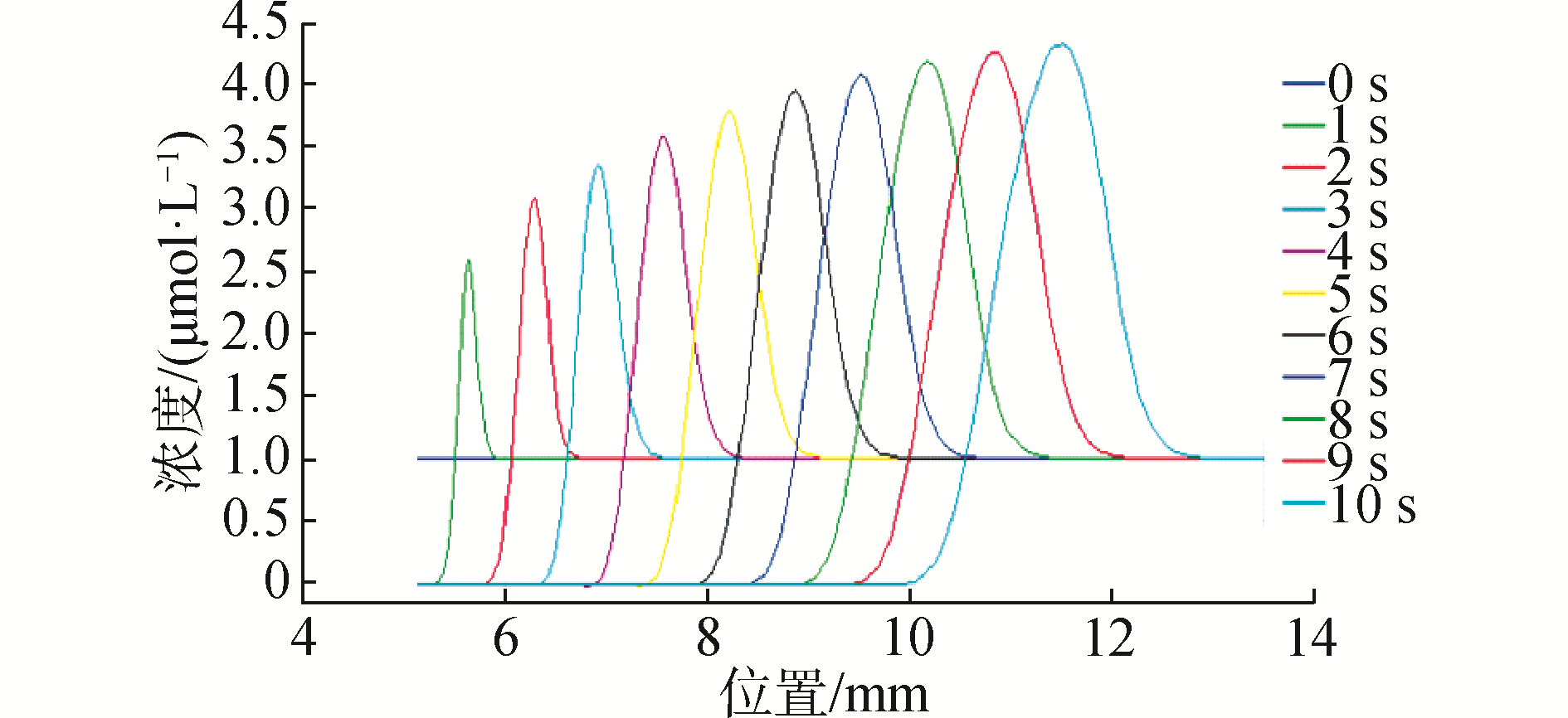
同时对应得到不同时刻芯片不同位置上样品浓度随时间变化的曲线,可以看到随时间变化芯片上不同位置的样品浓度(每时刻y=1上方的积分)逐渐增加,在10 s时达到最大。
|
Download:
|
| 图 5 样品浓度在芯片不同位置的浓度变化 Fig. 5 Concentration change of sample concentration at different positions of the chip | |
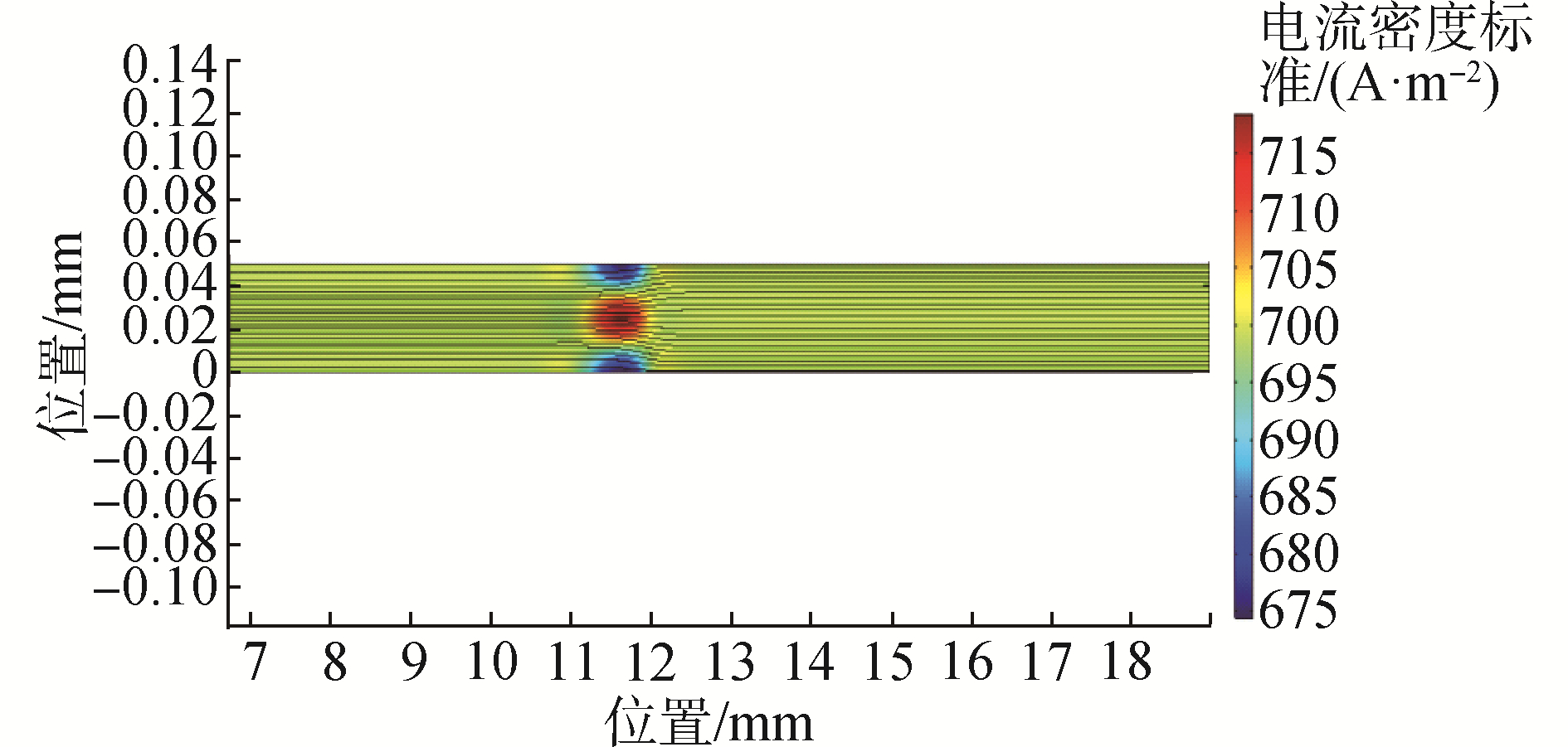
得到芯片上电流分布图,可以看到电流在片上某一段会有很大通量,这个结果可以很好地解释实际试验时通电时间长造成的芯片某段被灼烧的现象产生原因。
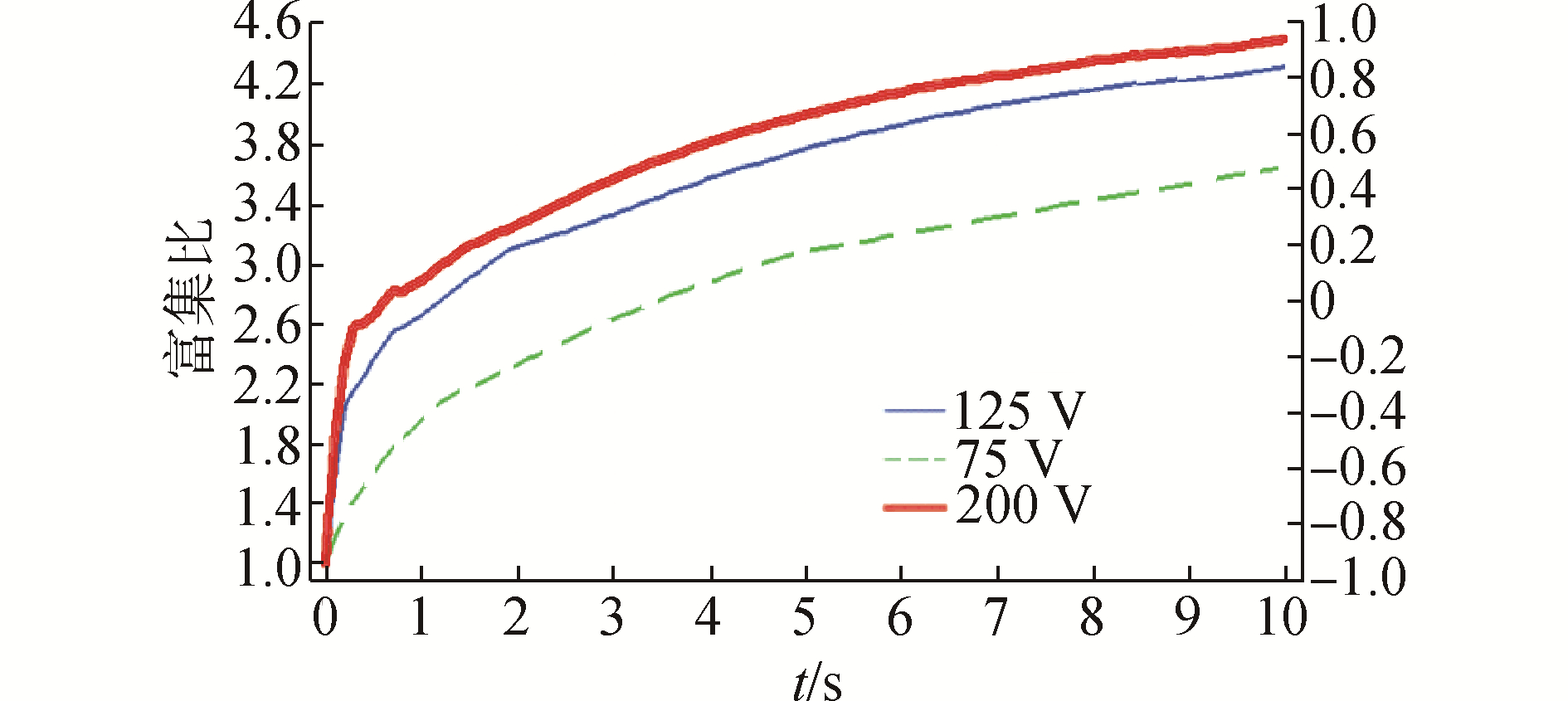
3.3 扩散与对流主导在低Pe值情况下,控制其他条件不变,只改变施加在两侧的电压强度,得到了图 7的结果。表明在扩散占主导地位的系统中,电场的增加产生会导致浓度增强。当不受抑制时,高、低电导率区的局部电致滑移速度的匹配导致不均匀流动,从而导致堆积分析物不必要的对流扩散。在预浓缩时间通常较短的芯片上FASS中,缓慢的分子扩散不能减小非均匀流动产生的横向浓度梯度。对流占优的情况下,叠加的动力学完全由非均匀EOF的时间尺度控制
|
Download:
|
| 图 6 芯片上电流分布图 Fig. 6 Current distribution on the chip | |
|
Download:
|
| 图 7 不同电压条件下的富集倍数曲线 Fig. 7 Curves of enrichment multiples under different voltage conditions | |
1) 自主构建了耦合多物理场(电势场、电导率场、流体场、分析物浓度场)的FASS物理模型,并在COMSOL Multiphysics软件上进行了仿真。
2) 为了提高计算效率提出了跨数量级疏密空间与时间定标分析的仿真计算策略。
3) 探索了FASS优化的条件,仿真结果表明可通过优化微纳通道长度与富集时间,来控制分子扩散和对流扩散的影响,并获得了较好分析物富集结果,富集倍比与电压值呈正相关。
本研究可以为在微纳通道中富集带电分析物提供理论基础。动电堆叠现象在实际的样品预富集处理中往往应用于多孔纤维素膜中。受限于该材质中毛细通道的复杂性,在接下来的研究中可以进一步复杂化仿真模型,以求解更趋于应用中的富集现象。
| [1] |
OSBOURN D M, WEISS D J, LUNTE C E. Online preconcentration methods for capillary electrophoresis[J]. Electrophoresis, 2015, 21(14): 2768-2779. (  0) 0)
|
| [2] |
ZHANG Chanxuan, THORMANN W. Head-column field-amplified sample stacking in binary system capillary electrophoresis: a robust approach providing over 1000-fold sensitivity enhancement[J]. Analytical chemistry, 1996, 68(15): 2523-2532. DOI:10.1021/ac951250e (  0) 0)
|
| [3] |
CHIEN R L, BURGI D S. Field amplified sample injection in high-performance capillary electrophoresis[J]. Journal of chromatography A, 1991, 559(1/2): 141-152. (  0) 0)
|
| [4] |
CHIEN R L, BURGI D S. On-column sample concentration using field amplification in CZE[J]. Analytical chemistry, 1992, 64(8): 489A-496A. DOI:10.1021/ac00032a721 (  0) 0)
|
| [5] |
GONG Maojum, WEHMEYER K R, LIMBACH P A, et al. On-line sample preconcentration using field-amplified stacking injection in microchip capillary electrophoresis[J]. Analytical chemistry, 2006, 78(11): 3730-3737. DOI:10.1021/ac0521798 (  0) 0)
|
| [6] |
GOPMANDAL P P, BHATTACHARYYA S. Numerical study on isotachophoretic separation of ionic samples in microfluidics[M]//BASU S K, KUMAR N. Modelling and Simulation of Diffusive Processes. Cham: Springer, 2014: 97-117.
(  0) 0)
|
| [7] |
GOPMANDAL P P, BHATTACHARYYA S. Effects of convection on isotachophoresis of electrolytes[J]. Journal of fluids engineering, 2015, 137(8): 081202. DOI:10.1115/1.4029888 (  0) 0)
|
| [8] |
BAHGA S S, SANTIAGO J G. Coupling isotachophoresis and capillary electrophoresis: a review and comparison of methods[J]. Analyst, 2013, 138(3): 735-754. DOI:10.1039/C2AN36150G (  0) 0)
|
| [9] |
KITAGAWA F, KAWAI T, OTSUKA K. On-line sample preconcentration by large-volume sample stacking with an electroosmotic flow pump (LVSEP) in microscale electrophoresis[J]. Analytical sciences, 2013, 29(12): 1129-1139. DOI:10.2116/analsci.29.1129 (  0) 0)
|
| [10] |
BRITZ-MCKIBBIN P, CHEN D D Y. Selective focusing of catecholamines and weakly acidic compounds by capillary electrophoresis using a dynamic pH junction[J]. Analytical chemistry, 2000, 72(6): 1242-1252. DOI:10.1021/ac990898e (  0) 0)
|
| [11] |
BAHGA S S, BERCOVICI M, SANTIAGO J G. Robust and high-resolution simulations of nonlinear electrokinetic processes in variable cross-section channels[J]. Electrophoresis, 2012, 33(19/20): 3036-3051. (  0) 0)
|
| [12] |
JUNG B, BHARADWAJ R, SANTIAGO J G. Thousandfold signal increase using field-amplified sample stacking for on-chip electrophoresis[J]. Electrophoresis, 2003, 24(19/20): 3476-3483. (  0) 0)
|
| [13] |
BAHGA S S, MOZA R, KHICHAR M. Theory of multi-species electrophoresis in the presence of surface conduction[J]. Proceedings of the royal society A: Mathematical, Physical and Engineering Sciences, 2016, 472(2186): 20150661. DOI:10.1098/rspa.2015.0661 (  0) 0)
|
| [14] |
MANI A, BAZANT M Z. Deionization shocks in microstructures[J]. Physical review E, 2011, 84(6 Pt 1): 061504. (  0) 0)
|
| [15] |
PORADA S, BORCHARDT L, OSCHATZ M, et al. Direct prediction of the desalination performance of porous carbon electrodes for capacitive deionization[J]. Energy & environmental science, 2013, 6(12): 3700-3712. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


