扩频通信是一种发射信号占用带宽远远大于发送信息所需带宽最大值的传输方式,由于其具有抗干扰能力强、隐蔽性好、易于实现码分多址等诸多优点被广泛应用于定位、通信、测距等领域。线性调频信号扩频(chirp spread spectrum, CSS)作为多种扩频技术的一种,在一定的符号间隔内,Chirp信号频率扫过一定的范围,因此占用的频带宽度比信息带宽大得多,实现了对信息的频谱扩展,因此可将其视为一种扩频信号[1]。
Tsai等[2]在匹配滤波相干解调基础上进一步分析了在Rayleigh和Rician衰落信道下采用Chirp信号抗多径干扰的优势。基于Chirp信号的多用户通信、混合扩频通信等的提出,进一步提升通信系统容量和性能[3-5]。基于Chirp信号的Rake接收的提出,进一步提升系统的抗多径性能[6]。近年来,多种技术与扩频通信技术相结合也逐渐成为研究热点。分数域傅里叶变换(fractional Fourier transform, FrFT)作为傅里叶变换的推广,其以Chirp信号为基函数,因此Chirp信号在适当的分数域出现聚敛现象[7-8]。在文献[9-10]中,利用了Chirp信号分数域特性进行参数估计;在文献[11]中提出将Chirp信号用作OFDM系统的同步信号;在文献[12]中提出了一种基于FrFT的Chirp信号扩频调制算法,以二进制数字调制解调为例,探讨了基于分数域傅里叶变换的Chirp非相干解调的相关理论问题。通过与匹配滤波解调法的比较可知,FrFT非相干解调的优势是不受到相位误差的影响[11],且在对抗多普勒频移和码同步误差的影响时与时域相干解调是相同的[12];分数域非相干解调的性能劣势是没有利用到相位信息导致的。
为了保留FrFT非相干解调对抗相位偏差的优势,并且提升对抗多普勒频移和码同步误差的能力,本文在FrFT非相干解调的基础上进行了改进,提出了峰值搜索-FrFT非相干解调,与传统方法进行了对比分析,证明了该方法在频偏条件下具有更好的误码率性能。
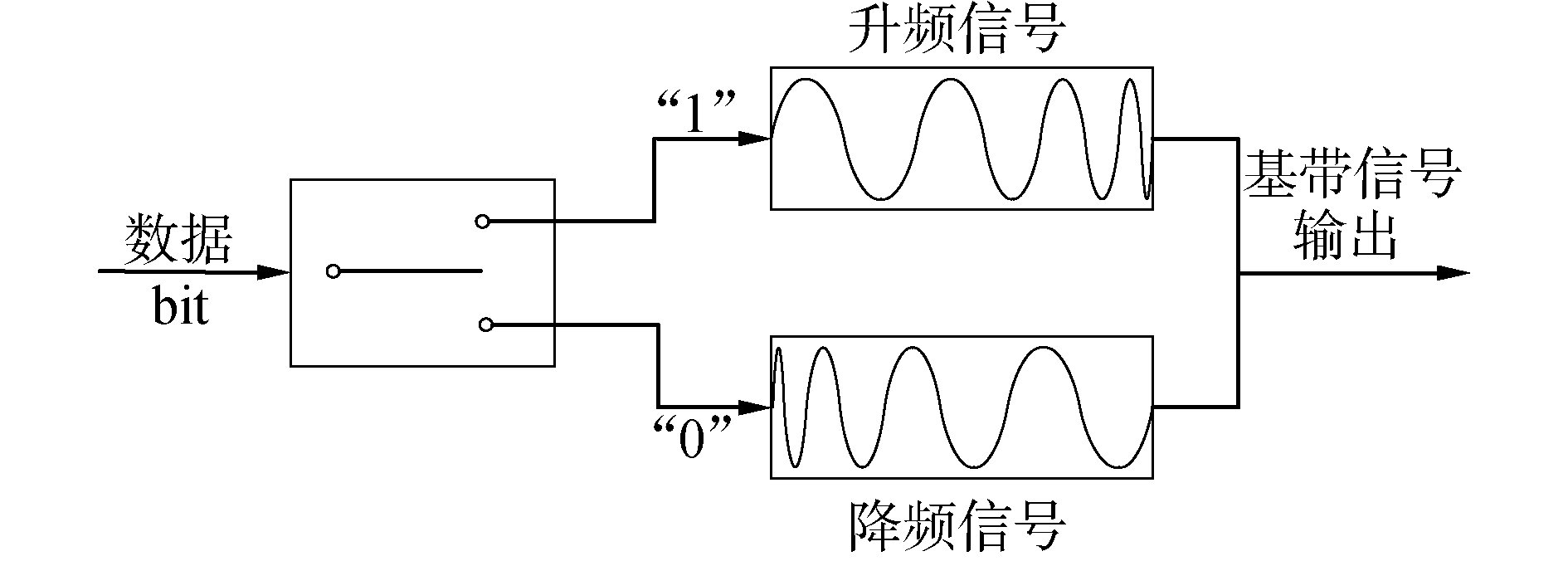
1 Chirp-BOK调制解调 1.1 Chirp-BOK调制方案基于二进制正交键控(binary orthogonal keying,BOK),提出了Chirp-BOK调制方式。它利用了Chirp信号的扫频特性,对Chirp信号的正、反调频率进行信息携带处理,达到信号调制解调的目的,这种方式具有结构简单、低复杂度、低功耗等特点,是Chirp信号的常用调制方式[13-14]。设k为正整数,本文使用调频率为k的升频信号(Up-Chirp)表示"1",使用调频率为-k的降频信号(Down-Chirp)表示"0"。Chirp信号表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{c_{{\rm{up}}}}(t) = A\cos \left( {2{\rm{ \mathsf{ π} }}{f_0}t + {\rm{ \mathsf{ π} }}k{t^2}} \right)}\\ {{c_{{\rm{down}}}}(t) = A\cos \left( {2{\rm{ \mathsf{ π} }}{f_0}t - {\rm{ \mathsf{ π} }}k{t^2}} \right)} \end{array}} \right. $ | (1) |
Chirp-BOK调制框图如图 1所示。
|
Download:
|
| 图 1 Chirp-BOK调制 Fig. 1 The bock diagram of Chirp-BOK modulation | |
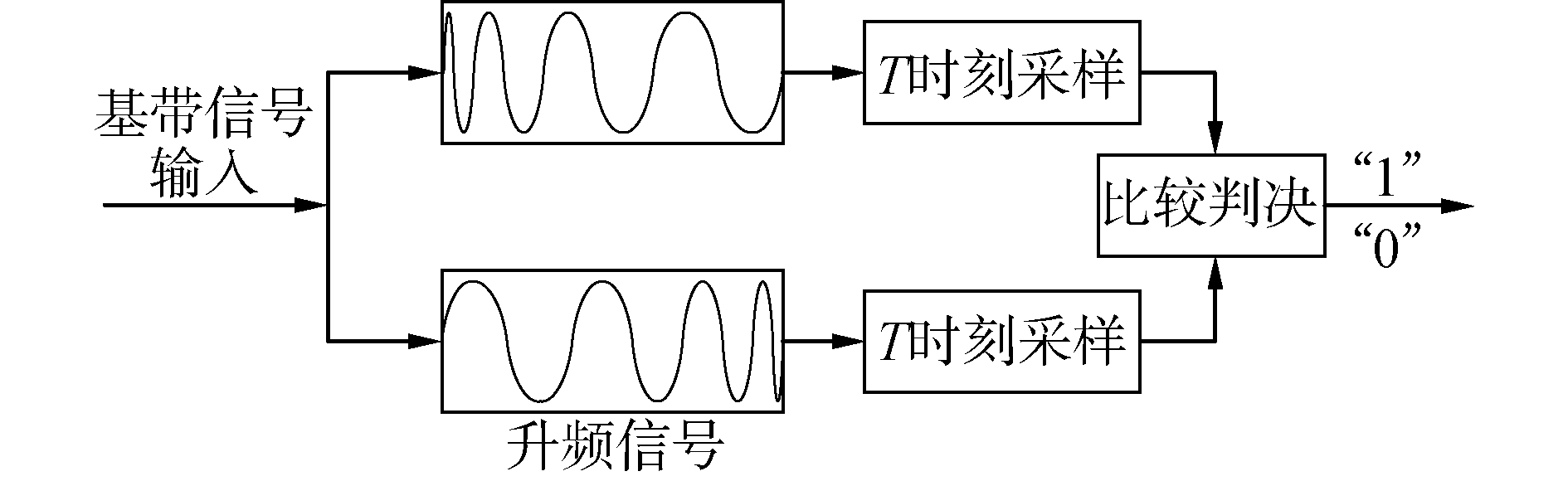
Up-Chirp与调频率相反的Down-Chirp信号互为匹配滤波函数[11],因此接收端解调框图如图 2所示。
|
Download:
|
| 图 2 匹配滤波解调 Fig. 2 The bock diagram of MF demodulation | |
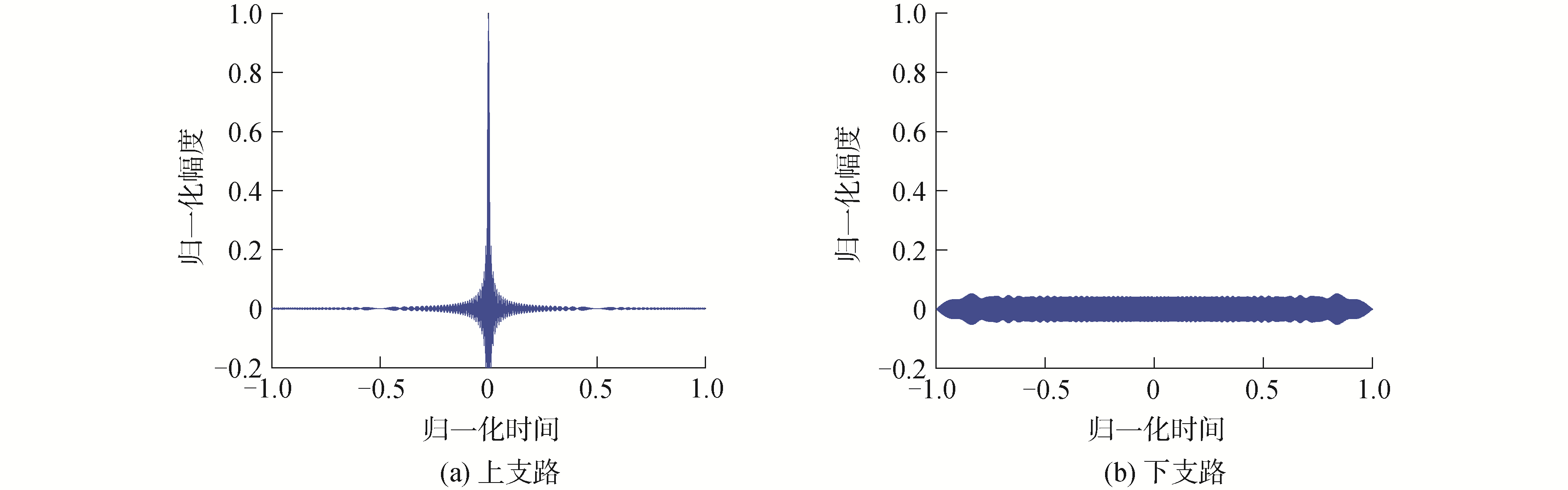
以升频信号为例,匹配滤波输出如图 3(a)所示,非匹配滤波输出如图 3(b)所示。
|
Download:
|
| 图 3 滤波器输出波形 Fig. 3 Output waveform of filter | |
分数域傅里叶变换可以看作是传统傅里叶变换的一种推广。正余弦函数是傅里叶变换的基函数,而Chirp函数正是其调频率对应阶次的分数域傅里叶变换的基函数[15]。分数域傅里叶变换是公认的适合处理Chirp信号的工具,分数域傅里叶变换的定义式[16]为:
| $ F_{p}(u)=\int_{-\infty}^{+\infty} f(t) K(\alpha ; u, t) \mathrm{d} t $ | (2) |
式中:下标p为分数域傅里叶变换的阶次;α=pπ/2;u为分数域坐标;t为时域坐标;算子核K(α; u, t)定义为:
| $ \begin{array}{*{20}{c}} {K(\alpha ;u,t) = \sqrt {1 - {\rm{j}}\cot \alpha } \cdot \exp \left[ {{\rm{j \mathsf{ π} }}\left( {{u^2}\cot \alpha - } \right.} \right.}\\ {\left. {\left. {2ut\csc \alpha + {t^2}\cot \alpha } \right)} \right]} \end{array} $ | (3) |
当p=1时,有F1(u)=∫-∞+∞f(t)exp(-j2πut)dt,就是普通的傅里叶变换。
调频率为k的Chirp信号经过p=-2arccot(k/π) 阶FrFT后出现聚敛峰值,该阶次p被称为Chirp信号的最优阶次[7];由高斯分布线性变换不变性,高斯白噪声经过p阶分数域傅里叶变换后仍然是高斯白噪声。
根据欧拉公式可以将调频率为k的实Chirp信号拆分为2个调频互为相反数的复Chirp信号:
| $ \begin{array}{*{20}{c}} {{c_{{\rm{up}}}}(t) = c_{{\rm{up}}}^1(t) + c_{{\rm{up}}}^2(t) = \frac{1}{2}\exp \left[ {{\rm{j}}\left( {2{\rm{ \mathsf{ π} }}{f_0}t + {\rm{ \mathsf{ π} }}k{t^2}} \right)} \right] + }\\ {\frac{1}{2}\exp \left[ { - {\rm{j}}\left( {2{\rm{ \mathsf{ π} }}{f_0}t + {\rm{ \mathsf{ π} }}k{t^2}} \right)} \right]} \end{array} $ | (4) |
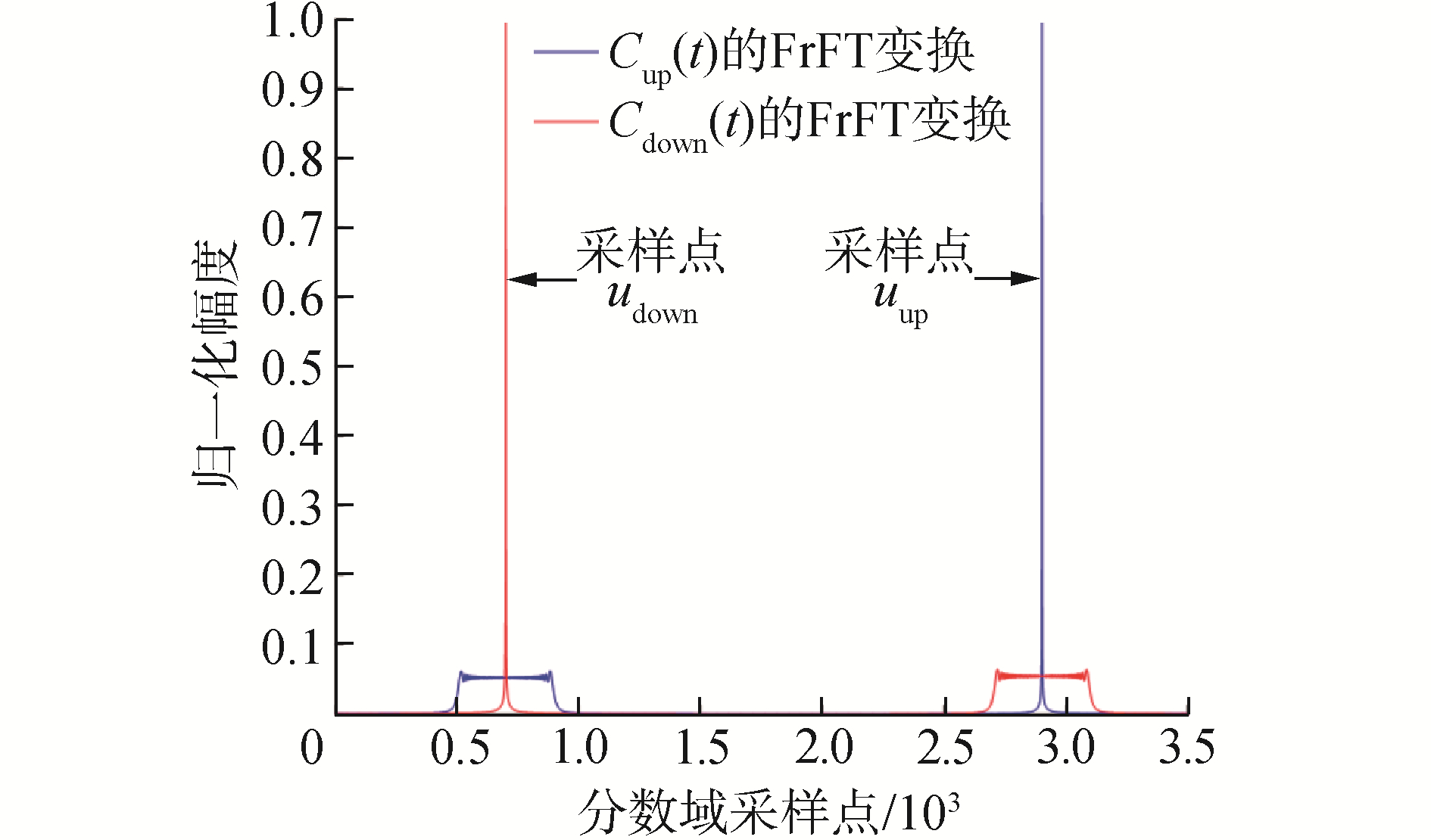
式中:cup1(t)的调频率为k,初始频率为f0,其最优阶次为p=-2arccot(k/π),因此cup1(t)经过p阶FrFT后,在分数域上出现冲击函数,峰值点出现在uup=f0sinα处;而cup2(t)的调频率为-k,其在p阶分数域上不会产生聚敛现象,能量分布均匀。
同理,调频率为-k的实Chirp信号拆分为2个调频互为相反数的复Chirp信号:
| $ \begin{array}{*{20}{c}} {{c_{{\rm{down }}}}(t) = c_{{\rm{down }}}^1(t) + c_{{\rm{down }}}^2(t) = \frac{1}{2}\exp \left[ {{\rm{j}}\left( {2{\rm{ \mathsf{ π} }}{f_0}t - } \right.} \right.}\\ {\left. {\left. {\pi k{t^2}} \right)} \right] + \frac{1}{2}\exp \left[ { - {\rm{j}}\left( {2{\rm{ \mathsf{ π} }}{f_0}t - {\rm{ \mathsf{ π} }}k{t^2}} \right)} \right]} \end{array} $ | (5) |
式中:cdown2(t)的调频率为k;初始频率为-f0,其最优阶次仍为p=-2arccot(k/π),分数域峰值点出现在udown=-f0sinα处,与uup在分数域互为对称点。Chirp信号的分数域幅度谱如图 4所示。
|
Download:
|
| 图 4 p阶分数域谱 Fig. 4 Impact of p order fractional domains | |
1) 定点采样解调。
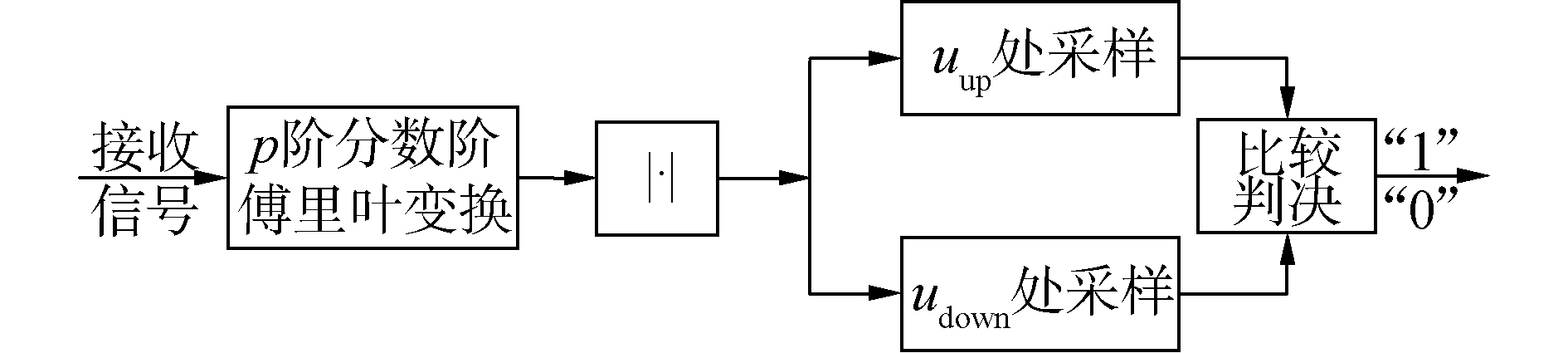
根据Chirp信号的分数域性质,对接收到的Chirp信号进行分数域傅里叶变换,然后采样判决[17-18]。FrFT非相干解调框图如图 5所示。因为该方法是在固定频点进行采样,为了与本文提出的方法进行区分,称之为定点采样-FrFT非相干解调。
|
Download:
|
| 图 5 定点采样-FrFT非相干解调框图 Fig. 5 The bock diagram of Fixed point sampling-FrFT non-coherent demodulation | |
2) 峰值搜索解调。
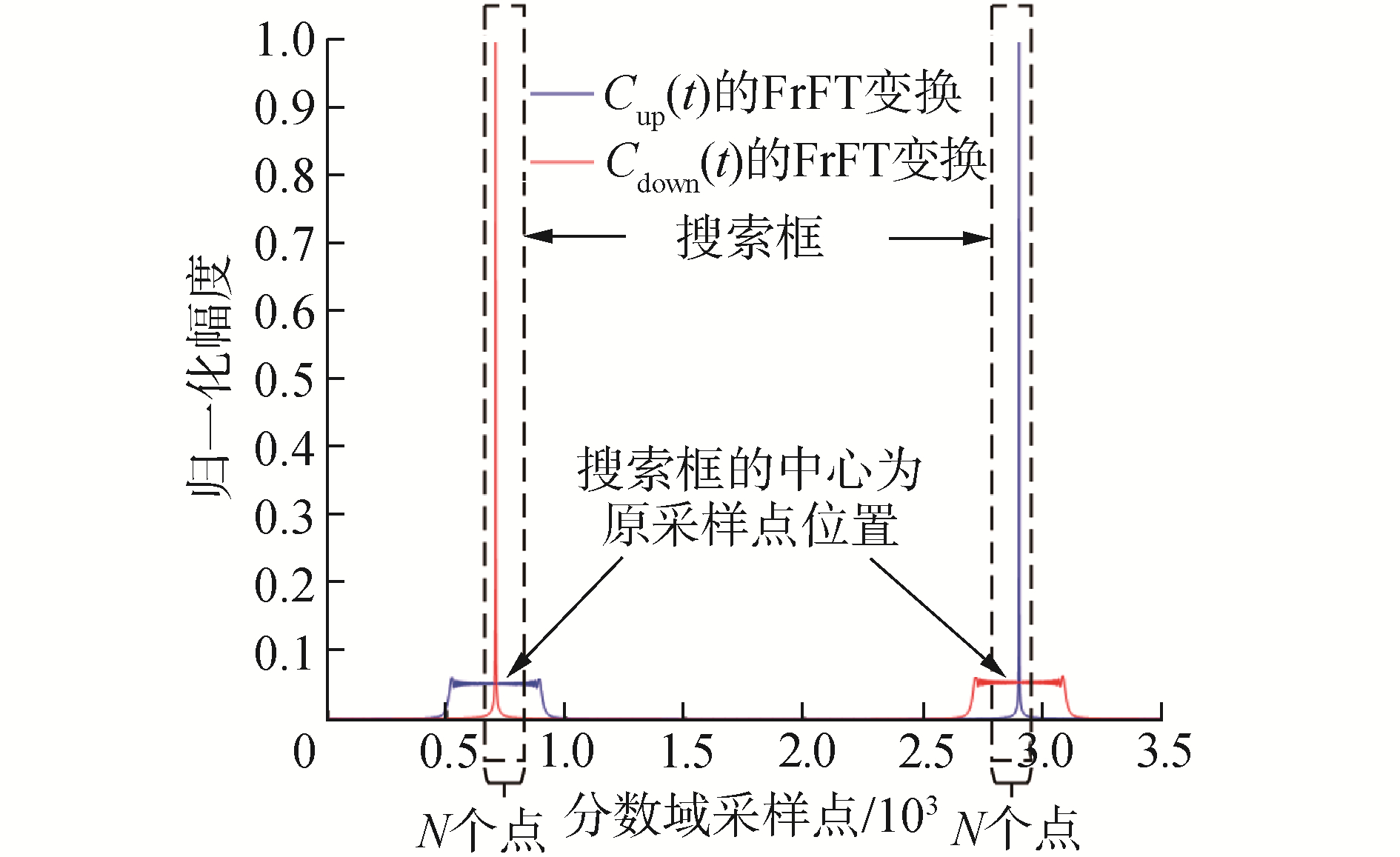
针对存在多普勒频移和码同步误差时定点采样法性能下降严重的问题,本文提出了峰值搜索-FrFT非相干解调。峰值搜索示意图如图 6所示,图中N为奇数。当分数域峰值位置存在偏移,如果还在原来的位置进行采样判决,系统的性能将严重下降,甚至无法解调。但是峰值位置的大致区域是可以确定的,如果将定点采样扩展为区域峰值采样,只要该区域的范围超过最大偏移的范围,即可以保证峰值一定能落在该区域内。然后在采样得到的2N个值中搜索峰值,由峰值所在区域得到判决结果。
|
Download:
|
| 图 6 分数域峰值搜索示意 Fig. 6 Impact of peak search | |
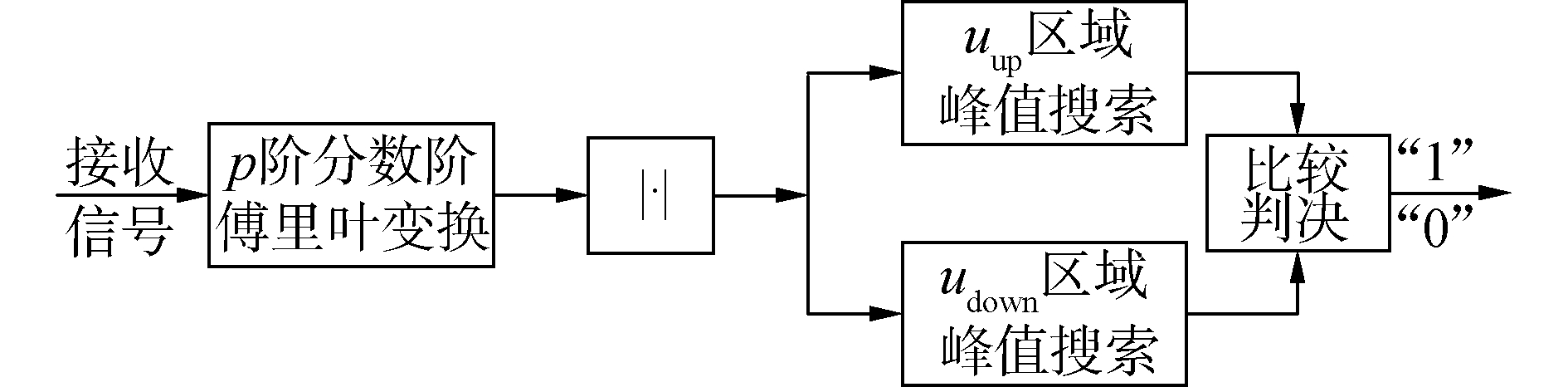
峰值搜索法的解调框图如图 7所示。基带信号先经过p阶FrFT,取模值后得到Chirp信号的分数域谱,以cup(t)和cdown(t)对应位置uup和udown为参考点将定点采样扩展为区域峰值搜索。
|
Download:
|
| 图 7 峰值搜索-FrFT非相干解调框图 Fig. 7 The bock diagram of peak search-FrFT non-coherent demodulation | |
2.1.1匹配滤波法的性能分析
对于匹配滤波相干解调,根据二进制最佳接收公式可以得出其误码率公式:
| $ P_{\mathrm{el}}=\frac{1}{2} \operatorname{erfc}\left(-\frac{E_{b}}{2 n_{0}}(1-\rho)\right) $ | (6) |
式中:ρ为升频信号和降频信号的相关系数;Eb为码元能量;n0为带限高斯白噪声的单边功率谱密度。
2.1.2 定点采样法的性能分析以调频率为k的Chirp信号为例,经过AWGN信道后接收到的信号为:
| $ r(t) = {\rm{A}}{{\rm{e}}^{2{\rm{ \mathsf{ π} }}{f_0}t + {\rm{ \mathsf{ π} }}k{t^2}}} + n(t){{\rm{e}}^{{\rm{j}}\theta }} $ | (7) |
式中:n(t)是复窄带高斯白噪声,其均值为0,方差为σn2。
接收信号r(t)经过p阶FrFT后,在u1处采样可以得到:
| $ R_{p}\left(u_{\mathrm{up}}\right)=A \mathrm{e}^{\mathrm{j} \theta_{0}}+n\left(u_{\mathrm{up}}\right) \mathrm{e}^{\mathrm{j} \theta_{1}} $ | (8) |
而在u2处采样可以得到:
| $ R_{p}\left(u_{\text {down }}\right)=\xi A \mathrm{e}^{\mathrm{j} \theta_{0}}+n\left(u_{\text {down }}\right) \mathrm{e}^{\mathrm{j} \theta_{2}} $ | (9) |
式中:A为经过最优阶次变换的分数域采样值;ξA是经过非最优阶次变换的分数域采样值,ξ和θ0是与Chirp信号具体参数有关的值;θ1和θ2是由噪声引入的随机相位。
调整相位可以得到:
| $ \left\{\begin{array}{l} R_{p}\left(u_{\mathrm{up}}\right)=A+n\left(u_{\mathrm{up}}\right) \mathrm{e}^{\mathrm{j}\left(\theta_{1}-\theta_{0}\right)} \\ R_{p}\left(u_{\mathrm{down}}\right)=\xi A+n\left(u_{\mathrm{down}}\right) \mathrm{e}^{\mathrm{j}\left(\theta_{2}-\theta_{0}\right)} \end{array}\right. $ | (10) |
两路信号取模值可以得到:
| $ \left\{\begin{array}{l} \operatorname{abs}\left(R_{p}\left(u_{\mathrm{up}}\right)\right)=\sqrt{\left(A+n_{1 c}(u)\right)^{2}+n_{1 s}{}^{2}(u)} \\ \operatorname{abs}\left(R_{p}\left(u_{\mathrm{down}}\right)\right)=\sqrt{\left(\xi A+n_{2 c}(u)\right)^{2}+n_{2 s}{}^{2}(u)} \end{array}\right. $ | (11) |
式中abs(·)表示取模值。
由随机信号分析可知,abs(Rp(uup))的抽样值Rup和abs(Rp(udown))的抽样值Rdown服从莱斯分布。它们的概率密度分布分别为:
| $ \left\{\begin{array}{l} f\left(R_{\mathrm{up}}\right)=\frac{R_{\mathrm{up}}}{\sigma_{n}^{2}} \mathrm{I}_{0}\left(\frac{A R_{\mathrm{up}}}{\sigma_{n}^{2}}\right) \exp \left(\frac{-\left(R_{\mathrm{up}}^{2}+A^{2}\right)}{2 \sigma_{n}^{2}}\right) \\ f\left(R_{\mathrm{down}}\right)=\frac{R_{\mathrm{down}}}{\sigma_{n}^{2}} \mathrm{I}_{0}\left(\frac{\xi A R_{\mathrm{down}}}{\sigma_{n}^{2}}\right) \exp \left(\frac{-\left(R_{\mathrm{down}}^{2}+\xi^{2} A^{2}\right)}{2 \sigma_{n}^{2}}\right) \end{array}\right. $ | (12) |
式中I0(·)为第1类零阶修正贝塞尔函数。
以升频信号为例,定点采样法判决正确的概率为:
| $ \begin{array}{c} P_{\mathrm{up}}=\int_{0}^{\infty} P\left(R_{\mathrm{up}}>R_{\mathrm{down}} \mid R_{\mathrm{up}}\right) f\left(R_{\mathrm{up}}\right) \mathrm{d}\left(R_{\mathrm{up}}\right)= \\ 2 \int_{0}^{\infty} t I_{0}(2 t \sqrt{r}) \exp \left(-\left(t^{2}+\xi^{2} r\right)\right)\left(1-Q_{1}(\sqrt{2 \xi r}, \sqrt{2} t)\right) \mathrm{d} t \end{array} $ | (13) |
式中:Q1(·)为Marcum Q函数;
当发送信号为降频信号时,判决正确的概率Pdown=Pup。
当发送升频信号和降频信号的概率相等时,定点采样-FrFT非相干解调的误码率为:
| $ P_{\mathrm{e} 2}=1-\left(P_{\mathrm{up}} / 2+P_{\mathrm{down}} / 2\right)=1-P_{\mathrm{up}}=1-2 \int_{0}^{\infty} t \mathrm{I}_{0}\left(2 t \sqrt{\frac{E_{b}}{n_{0}}}\right) \exp \left(-\left(t^{2}+\xi^{2} \frac{E_{b}}{n_{0}}\right)\right)\left(1-Q_{1}\left(\sqrt{\frac{2 \xi E_{b}}{n_{0}}}, \sqrt{2} t\right)\right) \mathrm{d} t $ | (14) |
对于峰值搜索法,由2点比较判决扩展为2N个点互相比较判决。首先对存在峰值区域的N个点进行搜索,寻找最大值。在AWGN信道且同步准确的情况下,第(N+1)/2个点即峰值所在位置。然后对不存在峰值区域的N个点进行搜索,寻找最大值。将这2N个点记为x1, x2, …, xi, …, x2N,xi的采样值为:
| $ x_{i}=\xi_{i} A+n_{i} \mathrm{e}^{\mathrm{j} \theta_{i}} $ | (15) |
式中:ξiA为每个采样点的幅值,ξi和θi是与Chirp信号具体参数有关的值,0<ξi≤1。abs(xi)服从莱斯分布,它们的概率密度函数为:
| $ f\left(x_{i}\right)=\frac{x_{i}}{\sigma_{n}^{2}} \mathrm{I}_{0}\left(\frac{\xi_{i} A x_{i}}{\sigma_{n}^{2}}\right) \exp \left(-\frac{1}{2 \sigma_{n}^{2}}\left(x_{i}^{2}+\xi_{i}^{2} A^{2}\right)\right) $ | (16) |
当xi, i=1, 2, …, N为最大值时可以正确解调,则峰值搜索法判决正确的概率为:
| $ \begin{aligned} P=& \sum\limits_{i=1}^{N} \int_{0}^{\infty} P\left(x_{i}>x_{1}, x_{i}>x_{2}, \cdots,\right.\\ &\left.x_{i}>x_{2 N} \mid x_{i}\right) f\left(x_{i}\right) \mathrm{d}\left(x_{i}\right) \end{aligned} $ | (17) |
式中2N个采样点之间相互独立,互不影响,式(17)可以化简为:
| $ P=\sum\limits_{i=1}^{N} \int_{0}^{\infty} \prod\limits_{j=1, j \neq i}^{2 N} P\left(x_{i}>x_{j} \mid x_{i}\right) f\left(x_{i}\right) \mathrm{d} x_{i} $ | (18) |
式中:
| $ \begin{array}{*{20}{c}} {\prod\limits_{j = 1,j \ne i}^{2N} P \left( {{x_i} > {x_j}\mid {x_i}} \right) = }\\ {\int_0^{{x_i}} {\frac{{{x_j}}}{{\sigma _n^2}}} {{\rm{I}}_0}\left( {\frac{{{\xi _j}A{x_j}}}{{\sigma _n^2}}} \right)\exp \left[ { - \frac{1}{{2\sigma _n^2}}\left( {x_j^2 + \xi _j^2{A^2}} \right)} \right]} \end{array} $ | (19) |
经过化简,可得峰值搜索法误码率为:
| $ {P_{{\rm{e}}3}} = 1 - P = 1 - 2\sum\limits_{i = 1}^N {\int_0^\infty t } {{\rm{I}}_0}\left( {2{\xi _i}t\sqrt {\frac{{{E_b}}}{{{n_0}}}} } \right)\exp \left[ { - \left( {{t^2} + \frac{{{\xi _i}^2{E_b}}}{{{n_0}}}} \right)} \right]\prod\limits_{j = 1,j \ne i}^{2N} {\left[ {1 - {Q_1}\left( {{\xi _j}\sqrt {\frac{{2{E_b}}}{{{n_0}}}} ,\sqrt 2 t} \right)} \right]} {\rm{d}}t $ | (20) |
以调频率为k的Chirp信号为例,分析频率偏移对Chirp信号FrFT非相干解调的影响,以证明将定点采样改进为区域峰值搜索的必要性和优越性。
首先,频偏主要来源于位同步误差、多普勒频移和收发端接收机参数差异。当存在同步误差时,本地同步时间与信号实际到达时间存在时刻τ的延时或超前,信号表达式为:
| $ c(t) = \cos \left( {2{\rm{ \mathsf{ π} }}{f_0}(t + \tau ) + {\rm{ \mathsf{ π} }}k{{(t + \tau )}^2}} \right) $ | (21) |
把τ看做定值,则上式可以化简为:
| $ c(t) = \cos \left( {{\rm{ \mathsf{ π} }}{f_m}t + {\rm{ \mathsf{ π} }}k{t^2} + \mathit{\Delta }} \right) $ | (22) |
式中:fm=f0+kτ/2,Δθ=2πf0τ+πkτ2。可以看到,Chirp信号的时间τ的同步误差可以转化为频率的频移kτ/2和相位的偏移Δθ;同时,由于存在时间偏差,因此只有部分信号被利用到,造成了能量的损失。
当存在多普频移时,Chirp信号中心频率发生偏移,因为入射角的不同多普勒频移的值将会出现变化,取最大值时Chirp信号表达式为:
| $ c(t) = \cos \left( {2{\rm{ \mathsf{ π} }}\left( {{f_0} + {f_d}} \right)t + {\rm{ \mathsf{ π} }}k{t^2} + \varphi } \right) $ | (23) |
可以看到,多普勒频移造成的影响首先是中心频率偏移fd,与同步误差造成的影响是类似的。
下面分析频偏对采样点的具体影响。首先将同步误差和多普勒频移造成的频偏统一记为fd。根据1.2.2节中的分析,以升频信号为例,在p阶分数域的峰值聚敛位置为uup=f0sinα,能量集中在|u-uup|<sinα/T。当存在频偏时,初始频率由f0变为fm=f0+fd,Chirp信号表达式变为:
| $ c(t) = \cos (2{\rm{ \mathsf{ π} }}{f_m}t + {\rm{ \mathsf{ π} }}k{t^2}) $ | (24) |
新的峰值聚敛位置为um=(f0+fd)sinα,偏移距离fdsinα。当频偏较大时,能量聚敛位置甚至会完全偏离该区域,如果仍以uup为采样点,则无法正确解调出信息。
当采样点移动的区域仍在|u-uup|<sinα/T之间时,以uup为采样点得到的采样值会变小。下文分析采样值的变化情况。为了便于推导,将式(24)的实Chirp信号改写为复Chirp信号为:
| $ c(t) = {\rm{exp}}({\rm{j}}2{\rm{ \mathsf{ π} }}{f_m}t + {\rm{j \mathsf{ π} }}k{t^2}) $ | (25) |
将c(t)代入分数域变换公式得:
| $ \begin{array}{*{20}{c}} {{C_p}(u) = \frac{1}{{\sqrt {\sin \alpha } }}\exp \left( {{\rm{j}}\left( {\frac{\alpha }{2} + \frac{{3{\rm{ \mathsf{ π} }}}}{4} + {\rm{ \mathsf{ π} }}{u^2}\cot \alpha } \right)} \right) \cdot }\\ {\int_{ - T/2}^{T/2} {\exp } \left( {{\rm{j \mathsf{ π} }}{t^2}(\cot \alpha + k) + {\rm{j}}2{\rm{ \mathsf{ π} }}t\left( {{f_m} - u\csc \alpha } \right)} \right){\rm{d}}t} \end{array} $ | (26) |
当k=-cotα,u=f0sinα时,可得:
| $ \begin{array}{c} {C_p}(u) = \frac{1}{{\sqrt {\sin \alpha } }}\exp \left( {{\rm{j}}\frac{\alpha }{2} + {\rm{j}}\frac{{3{\rm{ \mathsf{ π} }}}}{4} + {\rm{j \mathsf{ π} }}\left( {{u^2}\cot \alpha } \right)} \right) \cdot \\ \int_{ - T/2}^{T/2} {\exp } \left( {{\rm{j}}2{\rm{ \mathsf{ π} }}{f_d}t} \right){\rm{d}}t \end{array} $ | (27) |
化简得:
| $ {C_p}(u) = \frac{{\sin \left( {{\rm{ \mathsf{ π} }}{f_d}T} \right)}}{{{\rm{ \mathsf{ π} }}{f_d}\sqrt {\sin \alpha } }}\exp \left( {{\rm{j}}\frac{\alpha }{2} + {\rm{j}}\frac{{3{\rm{ \mathsf{ π} }}}}{4} + {\rm{j \mathsf{ π} }}\left( {{u^2}\cot \alpha } \right)} \right) $ | (28) |
取包络得:
| $ {\mathop{\rm abs}\nolimits} \left( {{C_p}(u)} \right) = \frac{{\sin \left( {{\rm{ \mathsf{ π} }}{f_d}T} \right)}}{{{\rm{ \mathsf{ π} }}{f_d}\sqrt {\sin \alpha } }} $ | (29) |
可以看出abs(Cp(u))的值与T和fd有关,当T固定时,fd越大,采样值越小。
综上,同步误差、多普勒频移和接收机收发端参数差异可以统一转换为中心频率的偏移和能量的损失。映射到分数域,对应着峰值位置的偏移和采样值的降低,严重影响了定点采样-FrFT非相干解调的性能。因此本文提出了峰值搜索-FrFT非相干解调来改善频偏下的性能。
引入频率偏移后,峰值搜索-FrFT非相干解调仍然为2N个点互相比较判决,只是峰值所在位置可能不再是第(N+1)/2个点。推导过程与AWGN信道下相同,故误码公式也与式(20)相同。系数ξi与引入频偏的Chirp信号分数域采样值有关。
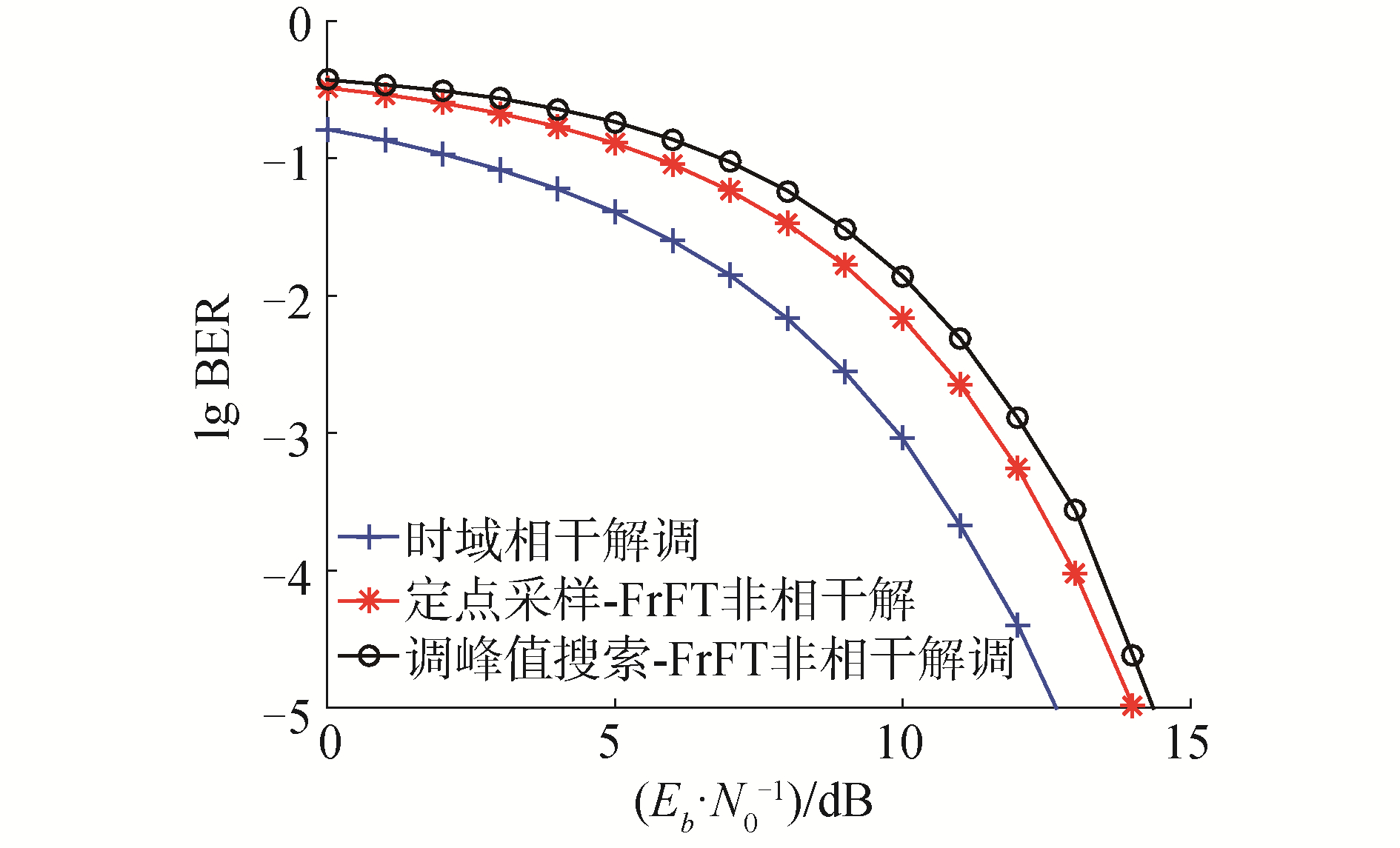
3 仿真验证 3.1 AWGN信道下性能仿真图 8对比了Chirp-BOK调制的3种解调方式在AWGN信道下的误码率曲线。仿真参数:带宽20 MHz、码长10 μs、搜索点数为3个采样点。从图 8中可以看出相干解调的性能最好;而峰值搜索-FrFT方法的性能相比于定点采样-FrFT性能下降不超过0.5 dB。
|
Download:
|
| 图 8 AWGN信道下3种解调方式性能对比 Fig. 8 Performance comparison of three demodulation methods in AWGN channel | |
图 9给出了AWGN信道下峰值搜索-FrFT的理论曲线和仿真曲线。搜索区域长度分别设置为3、21个采样点。从图 9中可以看出,当搜索区域的长度越小时,本方法在AWGN信道下的性能越好。因此搜索区域范围的设置要根据频偏动态地调整,使得搜索范围尽可能小。

|
Download:
|
| 图 9 不同长度搜索区域的误码率曲线 Fig. 9 Performance comparison of different length search ranges | |
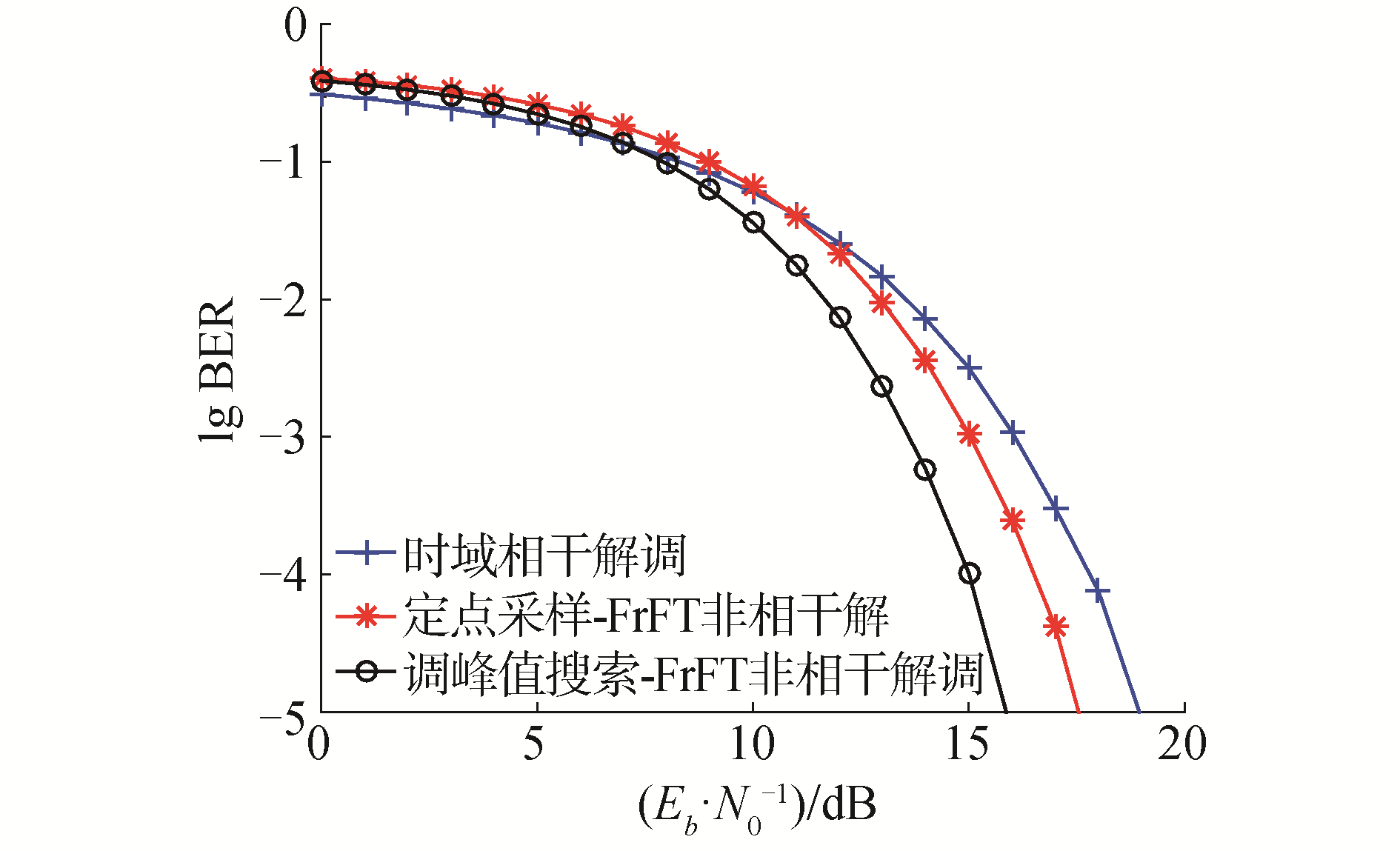
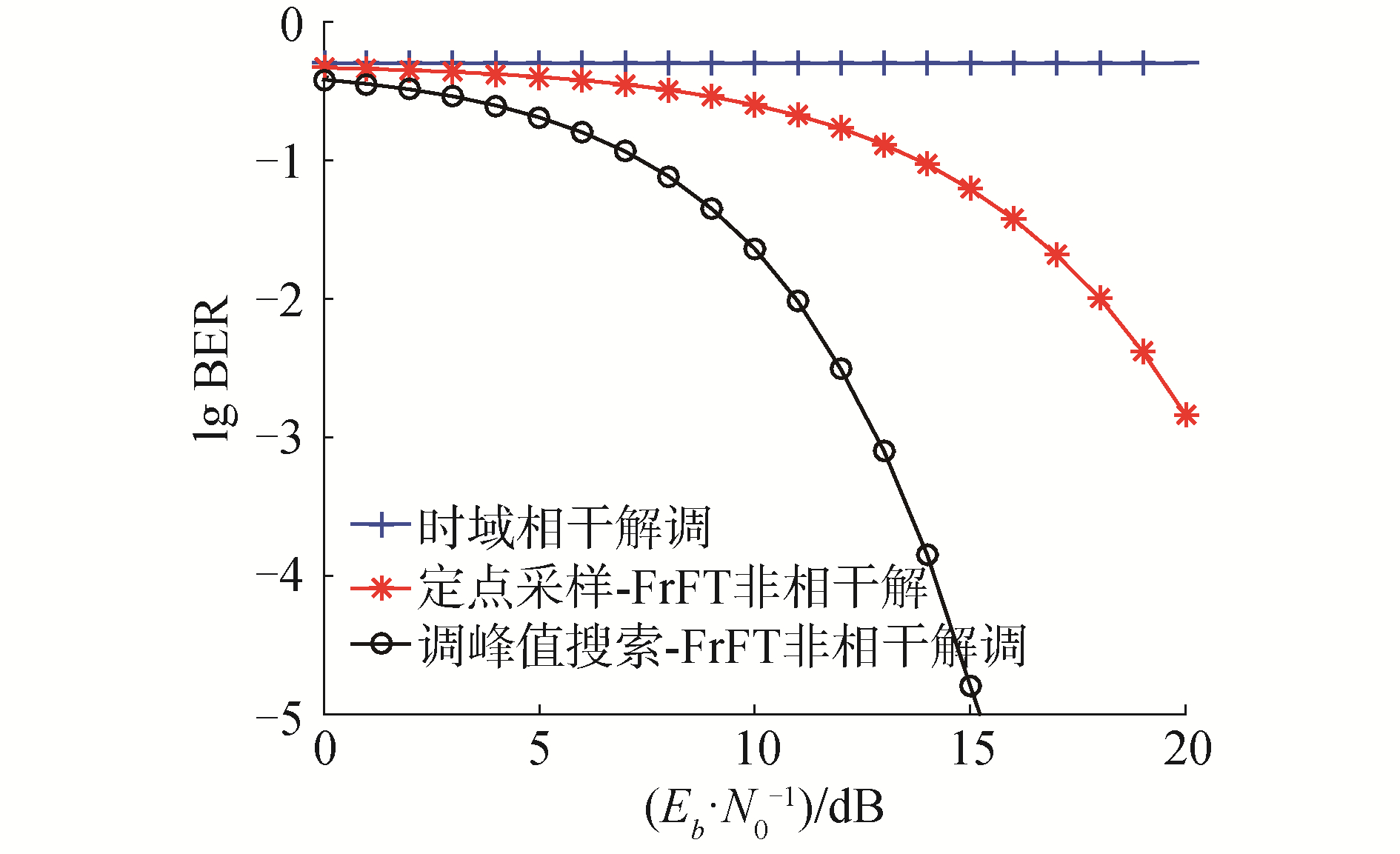
图 10和图 11给出了存在频偏时3种解调方式的性能对比。通过仿真可以看出,当归一化频偏比为0.001 5时,峰值搜索-FrFT的误码率性能优于定点采样-FrFT与相干解调。当频偏比增大至0.002 5时,定点采样-FrFT与相干解调的性能迅速下降,但是峰值搜索-FrFT的性能却几乎不受影响。
|
Download:
|
| 图 10 归一化频偏0.001 5时3种解调方式性能对比 Fig. 10 Performance comparison of three demodulation methods under normalized frequency offset 0.001 5 | |
|
Download:
|
| 图 11 归一化频偏0.002 5时3种解调方式性能对比 Fig. 11 Performance comparison of three demodulation methods under normalized frequency offset 0.002 5 | |
1) 该方法将传统的定点采样改进为采样点周围区域的峰值搜索,以提升对位同步误差、多普勒频移和收发端参数差异导致的信号频率偏移的容忍度。
2) 推导了该解调方法下AWGN信道的误码率公式,在AWGN信道下的性能主要受搜索长度的影响,当搜索长度越短时,性能越接近定点采样-FrFT;当存在频偏时,峰值搜索-FrFT可以对峰值位置进行搜索,只要满足搜索范围大于偏移范围,则可以极大程度地改善误码率性能,而匹配滤波相干解调和定点采样-FrFT的性能严重恶化。
| [1] |
FEI Yuan, QIAN Wei, EN Cheng. Joint virtual time reversal communications with an orthogonal chirp spread spectrum over underwater acoustic channel[J]. Applied acoustics, 2017, 117: 122-131. DOI:10.1016/j.apacoust.2016.11.005 (  0) 0)
|
| [2] |
TSAI Y R, CHANG Jinfu. The feasibility of combating multipath interference by chirp spread spectrum techniques over Rayleigh and Rician fading channels[C]//Proceedings of IEEE 3rd International Symposium on Spread Spectrum Techniques and Applications. Oulu, Finland: IEEE, 1994: 282-286, DOI: 10.1109/ISSSTA.1994.379577.
(  0) 0)
|
| [3] |
JU Y, BARKAT B. A new efficient chirp modulation technique for multi-user access communications systems[C]//Proceedings of 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing. Montreal, QC, Canada: IEEE, 2004: 937-940, DOI: 10.1109/ICASSP.2004.1326982.
(  0) 0)
|
| [4] |
郭俊杰, 禹健, 席小霞. 基于Chirp组合信号调制的多址技术[J]. 科学技术与工程, 2015, 15(34): 205-209. GUO Junjie, YU Jian, XI Xiaoxia. Multiple access technology based on chirp composite signal modulation[J]. Science technology and engineering, 2015, 15(34): 205-209. DOI:10.3969/j.issn.1671-1815.2015.34.036 (  0) 0)
|
| [5] |
陈善学, 杨翼豪, 李方伟. 基于扩频通信的伪随机码时间反演多址通信[J]. 重庆邮电大学学报(自然科学版), 2020, 32(02): 248-254. CHEN Shanxue, YANG Yihao, LI Fangwei. Pseudo-noise code time-reversal division multiple access communication based on spread spectrum communication[J]. Journal of Chongqing University of Posts and Telecommunications(natural science edition), 2020, 32(02): 248-254. (  0) 0)
|
| [6] |
OTHMAN M A B, BELZ J, FARHANG-BOROUJENY B. Performance analysis of matched filter bank for detection of linear frequency modulated chirp signals[J]. IEEE transactions on aerospace and electronic systems, 2017, 53(1): 41-54. DOI:10.1109/TAES.2017.2649162 (  0) 0)
|
| [7] |
陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009. TAO Ran, DENG Bing, WANG Yue. Fractional Fourier transform and its applications[M]. Beijing: Tsinghua University Press, 2009. (  0) 0)
|
| [8] |
OZAKTAS H M, ZALEVSKY Z, KUTAY M A. The fractional Fourier transform with applications in optics and signal processing[M]. New York: John Wiley & Sons, 2000.
(  0) 0)
|
| [9] |
TAO Ran, LI Bingzhao, WANG Yue. Spectral analysis and reconstruction for periodic nonuniformly sampled signals in fractional Fourier domain[J]. IEEE transactions on signal processing, 2007, 55(7): 3541-3547. DOI:10.1109/TSP.2007.893931 (  0) 0)
|
| [10] |
LIU Xuelian, HAN Jun, WANG Chunyang, et al. Parameters estimation for chirp signal based on QPF-FRFT[J]. Optik, 2019, 182: 529-537. DOI:10.1016/j.ijleo.2019.01.063 (  0) 0)
|
| [11] |
LOU Qi, HU Bo. A fast joint frame synchronization and frequency offset acquisition algorithm for OFDM systems[C]//Proceedings of 2018 IEEE Wireless Communications and Networking Conference. Las Vegas, NV, USA: IEEE, 2008, DOI: 10.1109/WCNC.2008.228.
(  0) 0)
|
| [12] |
沙学军, 郭佩, 徐玉滨. 一种分数傅里叶变换域的切普信号扩频通信方式[J]. 哈尔滨工程大学学报, 2009, 30(8): 944-947, 951. SHA Xuejun, GUO Pei, XU Yubin. A new spread spectrum scheme combined with a chirp signal in a fractional Fourier transform domain[J]. Journal of Harbin Engineering University, 2009, 30(8): 944-947, 951. DOI:10.3969/j.issn.1006-7043.2009.08.018 (  0) 0)
|
| [13] |
贺鹏飞, 吕英华, 张洪欣, 等. 基于Chirp-BOK调制的超宽带无线通信系统研究[J]. 南京邮电大学学报: 自然科学版, 2006, 26(02): 21-25. HE Pengfei, LYU Yinghua, ZHANG Hongxin, et al. Study of ultra-wideband wireless communication system based on Chirp-BOK modulation[J]. Journal of Nan jing University of Posts and Telecommunications: natural science, 2006, 26(02): 21-25. (  0) 0)
|
| [14] |
王晓炜, 李昕, 费敏锐. Chirp扩频通信系统抗噪声性能研究[J]. 通信技术, 2009, 42(03): 36-37+50. WANG Xiaowei, LI Xin, FEI Minrui. Anti-noise Performance of Chirp Spread Spectrum System[J]. Communications technology, 2009, 42(03): 36-37+50. (  0) 0)
|
| [15] |
QI Lin, TAO Ran, ZHOU Siyong, et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J]. Science in China series F: information sciences, 2004, 47(2): 184-198. DOI:10.1360/02yf0456 (  0) 0)
|
| [16] |
MCBRIDE A C, KERR F H. On namias's fractional Fourier transforms[J]. IMA journal of applied mathematics, 1987, 39(2): 159-175. DOI:10.1093/imamat/39.2.159 (  0) 0)
|
| [17] |
邓兵, 陶然, 平殿发. 基于分数阶Fourier变换的chirp-rate调制解调方法研究[J]. 电子学报, 2008, 36(6): 1078-1083. DENG Bing, TAO Ran, PING Dianfa. Study on chirp-rate modulation and demodulation based on fractional Fourier transform[J]. Acta electronica sinica, 2008, 36(6): 1078-1083. DOI:10.3321/j.issn:0372-2112.2008.06.008 (  0) 0)
|
| [18] |
孙志国, 王欣, 宁晓燕. SNCK通信系统解调方案及性能分析[J]. 沈阳工业大学学报, 2015, 37(4): 410-416. SUN Zhiguo, WANG Xin, NING Xiaoyan. Demodulation scheme and performance analysis for SNCK communication system[J]. Journal of Shenyang University of Technology, 2015, 37(4): 410-416. DOI:10.7688/j.issn.1000-1646.2015.04.10 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


