2. 南京航空航天大学 中小型无人机先进技术工业和信息化部重点实验室, 江苏 南京 210016;
3. 南京航空航天大学 航天学院, 江苏 南京 210016
2. Key Laboratory of Advanced Technology for Small and Medium-sized UAV, Ministry of Industry and Information Technology, Nanjing University of Aeronautics and Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
3. College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
通过在传统固定翼无人机上加装旋翼,混合翼垂直起降无人机结合了旋翼和固定翼无人机的优点,不仅能够同多旋翼无人机一样垂直起降,还可以实现固定翼无人机一样的高航时远航程[1]。因此,该类飞行器在军事、民用领域均具有广泛的应用前景,其关键技术的研究引起了国内外学者的广泛关注。
目前,垂直起降无人机可分为3类:倾转旋翼无人机、混合翼无人机和尾座式无人机[2-4]。其中,倾转旋翼无人机旋翼与机翼之间存在很强的气动耦合,且倾转机构设计困难,导致其安全性难以保证[5-6]。尾座式垂直起降无人机动力学模型耦合强、欧拉角奇异,导致其控制器设计非常困难[7-10]。相比之下,混合翼垂直起降无人机无需复杂的倾转结构,还能在起降中实现无人机姿态的稳定,消除了欧拉角奇异问题,所以将旋翼与固定翼复合而成的垂直起降方案是目前工程实现难度最低、实用性及可靠性最强的方案[11]。
混合翼垂直起降无人机在垂直起飞状态和前飞状态的气动模型存在巨大的差别,因此其过渡过程的稳定控制对整个飞行任务起着决定性作用。文献[12]分别对混合式垂直起降无人机的垂起模式、过渡模式和平飞模式3种模式进行了六自由度的建模,并使用积分滑模控制器实现了垂起模式下高度和航向的控制。文献[13]根据混合翼无人机存在的固定翼巡航模式时不活动的旋翼将会增加空气阻力的问题,提出了形态盒方法将其结合到一致的降阻系统的设计概念。文献[14]通过传统的三回路PID控制器实现了混合翼垂直起降无人机的控制,保证了不同模式间控制信号的平滑切换。文献[15]针对副翼卡住等多种特殊情况,基于线性自抗扰技术设计了无人机过渡过程的容错控制器。
Saydy等[16]提出了保护映射理论,用来分析处理参数化矩阵族和多项式的广义稳定性,可以更加方便地分析带参数系统的稳定性。文献[17]通过一个二阶线性模型验证了保护映射理论用于解决带参数线性系统的鲁棒广义稳定性问题的有效性。肖地波等[18]将保护映射理论用于高超声速飞行器大包线控制律的设计,实现了飞行控制参数的自适应整定。
本文提出了一种基于保护映射理论的混合翼垂直起降无人机过渡过程自适应切换控制律设计方法。首先推导了无人机过渡过程的非线性动力学模型,并基于雅可比线性化方法,获得了过渡过程中飞行器线性变参数模型;给出了自适应切换控制律设计的具体步骤;通过数值仿真验证了所提方法的有效性。
1 垂直起降无人机建模本文研究的混合翼垂直起降无人机如图 1所示。将4个用以提供垂直起降时所需升力的旋翼,安装在机翼两侧,与水平面保持平行。为了减少旋翼与固定翼之间力和力矩的相互影响,应将4个旋翼的机械中心放到固定翼的气动中心,从而提高4个旋翼的工作效率。

|
Download:
|
| 图 1 混合翼垂直起降无人机 Fig. 1 Hybrid wing vertical take-off and landing UAV | |
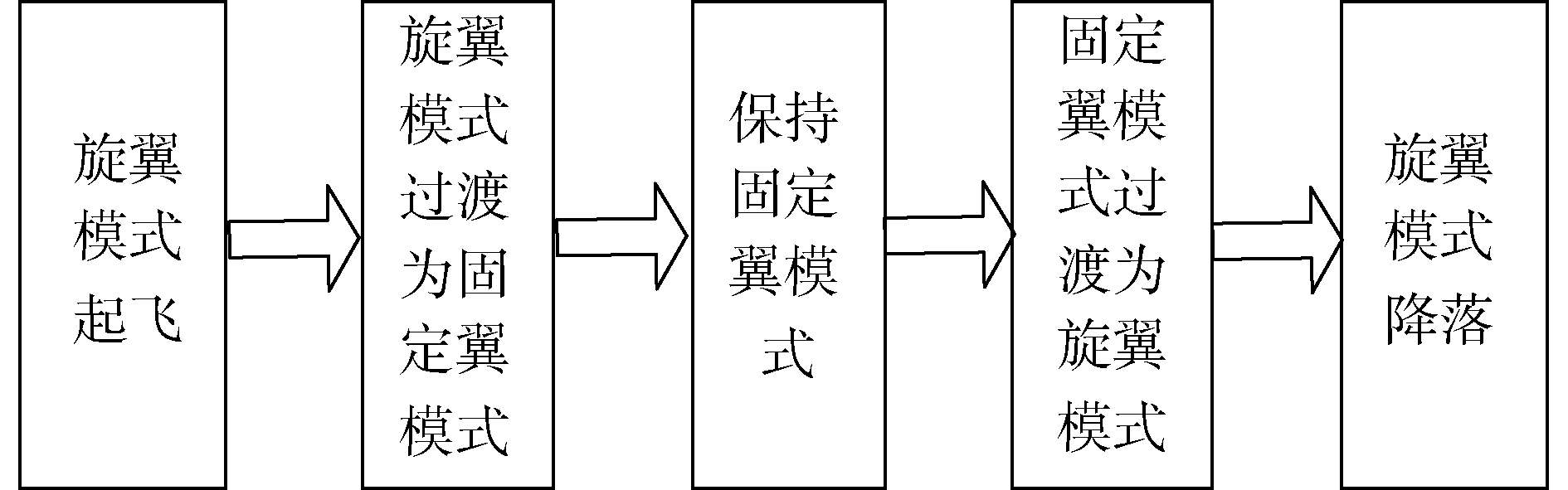
旋翼模式、固定翼模式和过渡模式是混合翼垂直起降无人机的3种飞行模式。飞行过程如图 2所示。在旋翼模式下依靠4个旋翼工作,过渡模式需要旋翼与固定翼同时工作,固定翼模式动下仅有固定翼工作。
|
Download:
|
| 图 2 混合翼垂直起降无人机模态转换过程 Fig. 2 Transition process of hybrid wing UAV | |
传统的旋翼或固定翼无人机的建模方法已经比较成熟,而混合式垂直起降无人机在过渡过程中旋翼部分和固定翼部分的控制面和系统输入均对飞行器整体施加作用,旋翼部分和固定翼部分的控制面和系统输入又不尽相同。但归根结底两部分施加的力和力矩都可分解到三维坐标X、Y、Z轴上。这样即可对混合翼垂直起降无人机进行非线性六自由度建模。
对于无人机平动有:
| $ m\left( {\frac{{{\rm{d}}{\mathit{\boldsymbol{V}}_b}}}{{{\rm{d}}t}} + \mathit{\boldsymbol{\omega }} \times {\mathit{\boldsymbol{V}}_b}} \right) = {\mathit{\boldsymbol{f}}_b} $ | (1) |
式中:m为无人机质量;Vb为无人机在机体坐标系下的速度;ω为无人机机体坐标系相对于惯性系的角速度;fb为无人机在机体坐标系下的受力[5]。
将式(1)展开得:
| $ \left[ {\begin{array}{*{20}{c}} {\dot u}\\ {\dot v}\\ {\dot w} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {rv - qw}\\ {pw - ru}\\ {qu - pv} \end{array}} \right] + \frac{1}{m}\left[ {\begin{array}{*{20}{c}} {{F_x}}\\ {{F_y}}\\ {{F_z}} \end{array}} \right] $ | (2) |
式中:Fx、Fy、Fz为无人机在机体坐标系下沿机体轴方向受力的分量;u、v、w为沿机体坐标轴方向上的速度分量;p、q、r为沿机体坐标轴各方向上的角度分量。Fx、Fy、Fz为:
| $ \left[ {\begin{array}{*{20}{c}} {{F_x}}\\ {{F_y}}\\ {{F_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{F_{fx}}}\\ {{F_{fy}}}\\ {{F_{fz}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{F_{rx}}}\\ {{F_{ry}}}\\ {{F_{rz}}} \end{array}} \right] $ | (3) |
式中:Ffx、Ffy、Ffz为固定翼在机体轴3个方向上的分力;Fxz、Fyz、Frz为旋翼在机体轴3个方向上产生的升力。
对于无人机绕质心的运动有:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot \omega }} = {\mathit{\boldsymbol{J}}^{ - 1}}\left[ { - \mathit{\boldsymbol{\omega }} \times (\mathit{\boldsymbol{J\omega }}) + {\mathit{\boldsymbol{m}}_b}} \right]}\\ {{\mathit{\boldsymbol{m}}_b} = {{\left[ {\begin{array}{*{20}{l}} L&M&N \end{array}} \right]}^{\rm{T}}}} \end{array}} \right. $ | (4) |
式中:L、M、N为无人机受力矩在机体坐标轴上的投影;J为惯性矩阵:
| $ \left[ {\begin{array}{*{20}{l}} L\\ M\\ N \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{l_f}}\\ {{m_f}}\\ {{n_f}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{l_r}}\\ {{m_r}}\\ {{n_r}} \end{array}} \right] $ | (5) |
式中:lf、mf、nf为固定翼产生的滚转、俯仰、偏航力矩;lr、mr、nr为旋翼产生的滚转、俯仰、偏航力矩。
现假设过渡过程中飞行器水平无侧滑飞行,则过渡过程纵向运动方程组为:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot V = \frac{{T\cos \alpha - D}}{m} - g\sin (\theta - \alpha )}\\ {\dot \alpha = - \frac{{T\sin \alpha + {F_z}}}{{mV}} + q + \frac{g}{V}\cos (\theta - \alpha )}\\ {\dot q = \frac{M}{{{J_y}}}}\\ {\dot h = V\sin (\theta - \alpha )}\\ {\dot \theta = q} \end{array}} \right. $ | (6) |
式中:T为固定翼推力;D为无人机所受阻力;α为迎角;θ为俯仰角;V为前飞速度。
1.2 混合翼垂直起降无人机过渡过程LPV建模过渡过程最重要特征参数是混合翼垂直起降无人机的前飞速度,在无人机过渡过程中前飞速度由从0开始加速,直到固定翼起飞速度,即18 m/s,前飞速度的增加同时导致固定翼提供的升力也在不断增加,此时需要调整旋翼油门,从而保持合理的飞行姿态。将纵向运动方程组在速度V=[0, 18] m/s范围内进行配平,并对配平状态进行线性化,线性拟合得到关于前飞速度V的表达式:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{A}}(V)\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{B}}(V)\mathit{\boldsymbol{u}}}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{C}}(V)\mathit{\boldsymbol{x}}} \end{array}} \right. $ | (7) |
式中:系统状态x=[V α q h θ]; 输入u=[δt δe T1 T2]; δt为固定翼油门;δe为升降舵输入;T1、T2分别为前边一对和后边一对的旋翼油门。
2 保护映射理论 2.1 保护映射的定义与构造保护映射是一种将N阶实矩阵集映射到复平面某一区域上的标量映射。定义映射ν将Rn×n实矩阵的集合映射到整个复平面C,Ω为复平面上某一已知区域。定义矩阵集合S:
| $ \mathit{\boldsymbol{S}}(\varOmega ) = \left\{ {\mathit{\boldsymbol{A}} \in {{\bf{R}}^{n \times n}}:\lambda (\mathit{\boldsymbol{A}}) \subset \varOmega } \right\} $ | (8) |
式中λ(A)为矩阵A的所有特征值的集合。定义S (Ω)为矩阵集S(Ω)的边界矩阵集合,当且仅当A∈S (Ω)时, ν(A)=0。即:
| $ \nu (\mathit{\boldsymbol{A}}) = 0 \Leftrightarrow \mathit{\boldsymbol{A}} \in \mathit{\boldsymbol{\bar S}}(\varOmega ) $ | (9) |
此时称ν为S(Ω)的保护映射。
3种典型凸区域的保护映射定义如下:
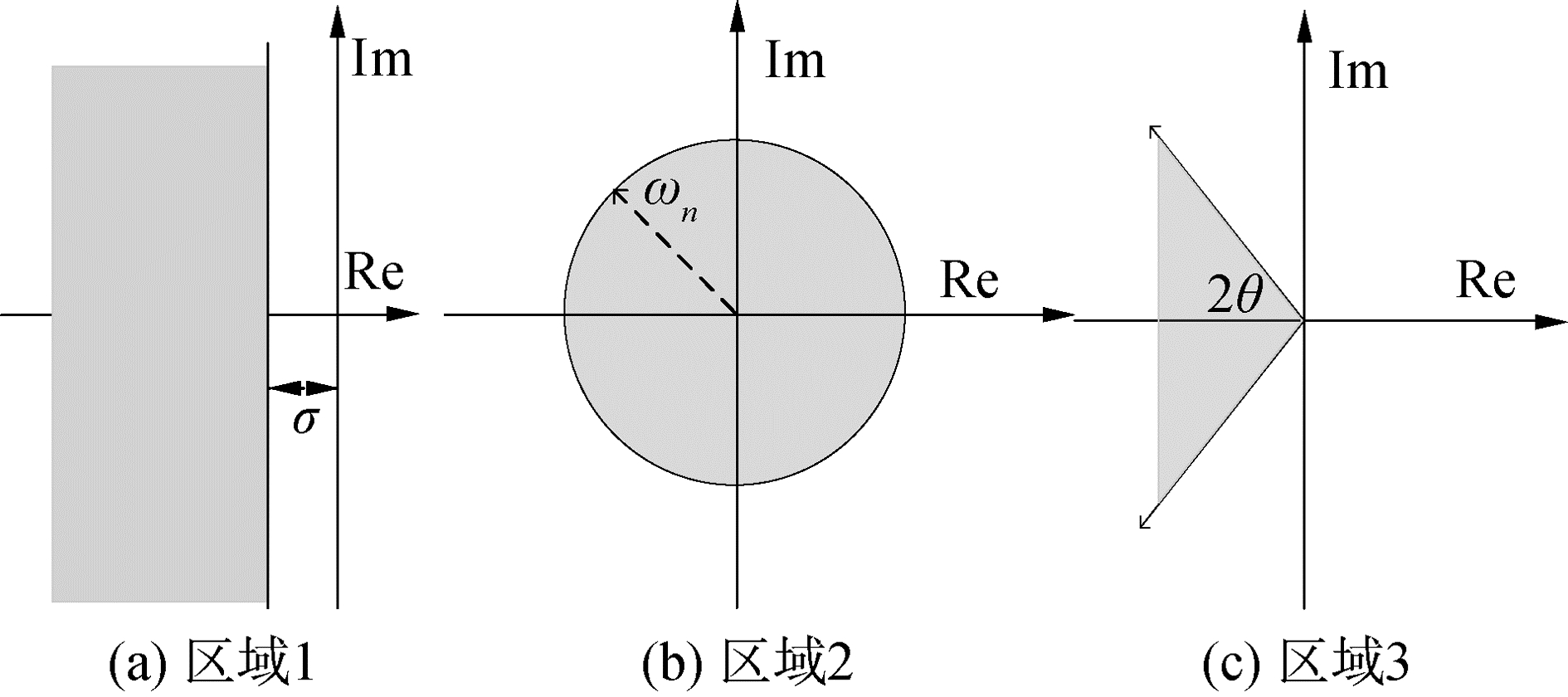
1) 图 3(a)为虚轴向左平移σ的左半平面,其对应的保护映射为:
| $ {\nu _\sigma }\left( {{\mathit{\boldsymbol{A}}_s}} \right) = \det \left( {{\mathit{\boldsymbol{A}}_s} \otimes \mathit{\boldsymbol{I}} - \sigma \mathit{\boldsymbol{I}} \otimes \mathit{\boldsymbol{I}}} \right)\det \left( {{\mathit{\boldsymbol{A}}_s} - \sigma \mathit{\boldsymbol{I}}} \right) $ | (10) |
|
Download:
|
| 图 3 3种典型区域 Fig. 3 Three typical regions | |
式中运算符号⊗为Bialternate积。
2) 图 3(b)为以复平面原点为圆心半径为ωn的圆盘,其保护映射:
| $ {\nu _{{\omega _n}}} = \det \left( {{\mathit{\boldsymbol{A}}_s} \otimes {\mathit{\boldsymbol{A}}_s} - \omega _n^2\mathit{\boldsymbol{I}} \otimes \mathit{\boldsymbol{I}}} \right)\det \left( {\mathit{\boldsymbol{A}}_s^2 - \omega _n^2\mathit{\boldsymbol{I}}} \right) $ | (11) |
3) 图 3(c)所示的内角为2θ的圆锥面,即阻尼比大于ξ=cosθ区域,相应的保护映射为:
| $ {\nu _\xi }\left( {{\mathit{\boldsymbol{A}}_s}} \right) = \det \left[ {\mathit{\boldsymbol{A}}_s^2 \otimes \mathit{\boldsymbol{I}} + \left( {1 - 2{\xi ^2}} \right){\mathit{\boldsymbol{A}}_s} \otimes {\mathit{\boldsymbol{A}}_s}} \right]\det \left( {{\mathit{\boldsymbol{A}}_s}} \right) $ | (12) |
通过上述3种典型凸区域的保护映射组成飞行控制系统稳定区域的保护映射:
| $ \nu \left( {{\mathit{\boldsymbol{A}}_s}} \right) = {\nu _\sigma }\left( {{\mathit{\boldsymbol{A}}_s}} \right){\nu _{{\omega _n}}}\left( {{\mathit{\boldsymbol{A}}_s}} \right){\nu _\xi }\left( {{\mathit{\boldsymbol{A}}_s}} \right) $ | (13) |
保护映射理论描述了特征值在复平面上特定区域内的矩阵集与复平面上的点之间的映射关系,而矩阵集可以用来表示需要稳定性分析的系统,矩阵集所有特征值的位置可以用来表示系统的极点位置。因此通过使用保护映射理论分析矩阵集的稳定性,就能够判断系统的稳定性。
设系统可以用连续参数r∈ Rn决定的实数方阵集A(r)表示,并且已知参数r边界,那么矩阵集A(r)的稳定性就可以根据如下引理进行判断:
引理1[19] 如果νΩ是n维矩阵集关于区域Ω的保护映射,要使矩阵集{A(r), r∈ Rn}稳定则需满足的充要条件是:在参数r的上下界范围内存在某一个值r0使得A(r0)特征值在区域Ω中,并且对于任意参数r,都有νΩ[A(r0)]νΩ[A(r)]>0。
可由上述引理得出推论1 [19]:由条件νΩ[A(r)]=0将参数r∈ Rn空间分成的若干子空间中的任意一个参数rp使得A(rp)稳定,则这个子空间的所有参数r确定的矩阵都关于复平面区域Ω稳定。
根据引理1,若想要判断矩阵集的稳定性,首先寻找参数r0使得矩阵A(r0)关于区域Ω稳定,且νΩ[A(r0)]。由于νΩ[A(r0)]νΩ[A(r)]是一个关于参数r有关的函数,则可以通过判断νΩ[A(r0)]νΩ[A(r)]的正负来判断νΩ[A(r0)]与νΩ[A(r)]是否同号,若同号, 则说明参数r使得矩阵A(r)关于区域Ω稳定。同时当νΩ[A(r)]=0时, 即可判定矩阵稳定是的参数r的范围。
3 控制器设计 3.1 控制器结构为使飞行器能够从旋翼单独工作的悬停状态转换到固定翼单独工作的状态,需要飞行器在过渡过程中达到足够的前飞速度,使固定翼机翼和机身产生足够与重力平衡的升力。采用LQR理论设计最优跟踪控制,使飞行器前飞速度由0逐渐加速到起飞速度,并在过渡过程中保证平稳。
对于飞行器小扰动线性化之后的平衡点线性系统为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot x}}}_0} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_0} + \mathit{\boldsymbol{Bu}}}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}_0}} \end{array}} \right. $ | (14) |
跟踪输入信号为z=[v(t) h(t)]T,跟踪输出信号为y=Cx0,输入与输出误差定义为:
| $ {{\mathit{\boldsymbol{e}}_1} = \mathit{\boldsymbol{z}} - \mathit{\boldsymbol{y}}} $ | (15) |
令误差积分:
| $ {{\mathit{\boldsymbol{x}}_1} = \int_0^t {{\mathit{\boldsymbol{e}}_1}} (\tau ){\rm{d}}\tau } $ | (16) |
代入到系统进行扩维:
| $ \left[ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot x}}}_0}}\\ {{{\mathit{\boldsymbol{\dot x}}}_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&{\bf{0}}\\ { - \mathit{\boldsymbol{C}}}&{\bf{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_0}}\\ {{\mathit{\boldsymbol{x}}_1}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{B}}\\ {\bf{0}} \end{array}} \right]\mathit{\boldsymbol{u}} + \left[ {\begin{array}{*{20}{l}} {\bf{0}}\\ \mathit{\boldsymbol{I}} \end{array}} \right]\mathit{\boldsymbol{z}} $ | (17) |
令x2=[x0 x1]T,扩维后的系统写为:
| $ {\mathit{\boldsymbol{\dot x}}_2} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}} + \mathit{\boldsymbol{Gz}} $ | (18) |
得到关于系统误差的状态方程:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{e}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{z}} - \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{x}}_0}}\\ {{\mathit{\boldsymbol{x}}_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{I}}\\ {\bf{0}} \end{array}} \right]\mathit{\boldsymbol{z}} + \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{C}}}&{\bf{0}}\\ {\bf{0}}&\mathit{\boldsymbol{I}} \end{array}} \right]{x_2} = }\\ {\mathit{\boldsymbol{Mz}} + {\mathit{\boldsymbol{C}}_z}{\mathit{\boldsymbol{x}}_2}} \end{array} $ | (19) |
取二次性能指标为:
| $ J = \frac{1}{2}\int_0^\infty {\left( {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{Qe}} + {\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{Ru}}} \right)} {\rm{d}}t $ | (20) |
式中:Q为半正定矩阵;R为正定矩阵。标函数的意义为使用较小的输入量使得系统的状态量的误差尽可能地小,所以当取得能量函数J最小时,目标成立:
| $ \begin{array}{*{20}{c}} {J = \frac{1}{2}\int_0^\infty {\left( {\mathit{\boldsymbol{x}}_2^{\rm{T}}{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{QC}}{\mathit{\boldsymbol{x}}_2} + 2{\mathit{\boldsymbol{z}}^{\rm{T}}}{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{QC}}{\mathit{\boldsymbol{x}}_2} + } \right.} }\\ {\left. {{\mathit{\boldsymbol{z}}^{\rm{T}}}{\mathit{\boldsymbol{M}}^{\rm{T}}}\mathit{\boldsymbol{QMz}} + {\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{Ru}}} \right){\rm{d}}t} \end{array} $ | (21) |
为使性能指标的值最小,利用标准解法求得Riccati方程和伴随向量方程。
若(A, B)可控,(A,
| $ \mathit{\boldsymbol{u}} = - {\mathit{\boldsymbol{K}}_x}\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{K}}_z}\mathit{\boldsymbol{z}} $ | (22) |
式中:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_x} = {\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}}\\ {{\mathit{\boldsymbol{K}}_z} = {{\left( {\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}} - {\mathit{\boldsymbol{A}}^{\rm{T}}}} \right)}^{ - 1}}\left( {{\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{QM}} + \mathit{\boldsymbol{PG}}} \right)} \end{array} $ |
首先选择合适的控制器结构,在过渡过程起始点计算控制器参数K0,并应用保护映射理论计算控制器参数K0使得系统关于已知区域Ω稳定的调度参数范围。接下来取调度参数边界值重新计算新的控制器参数K1及其对应的稳定范围,直至控制器参数Kn使得系统稳定的调度参数范围涵盖整个过渡过程。
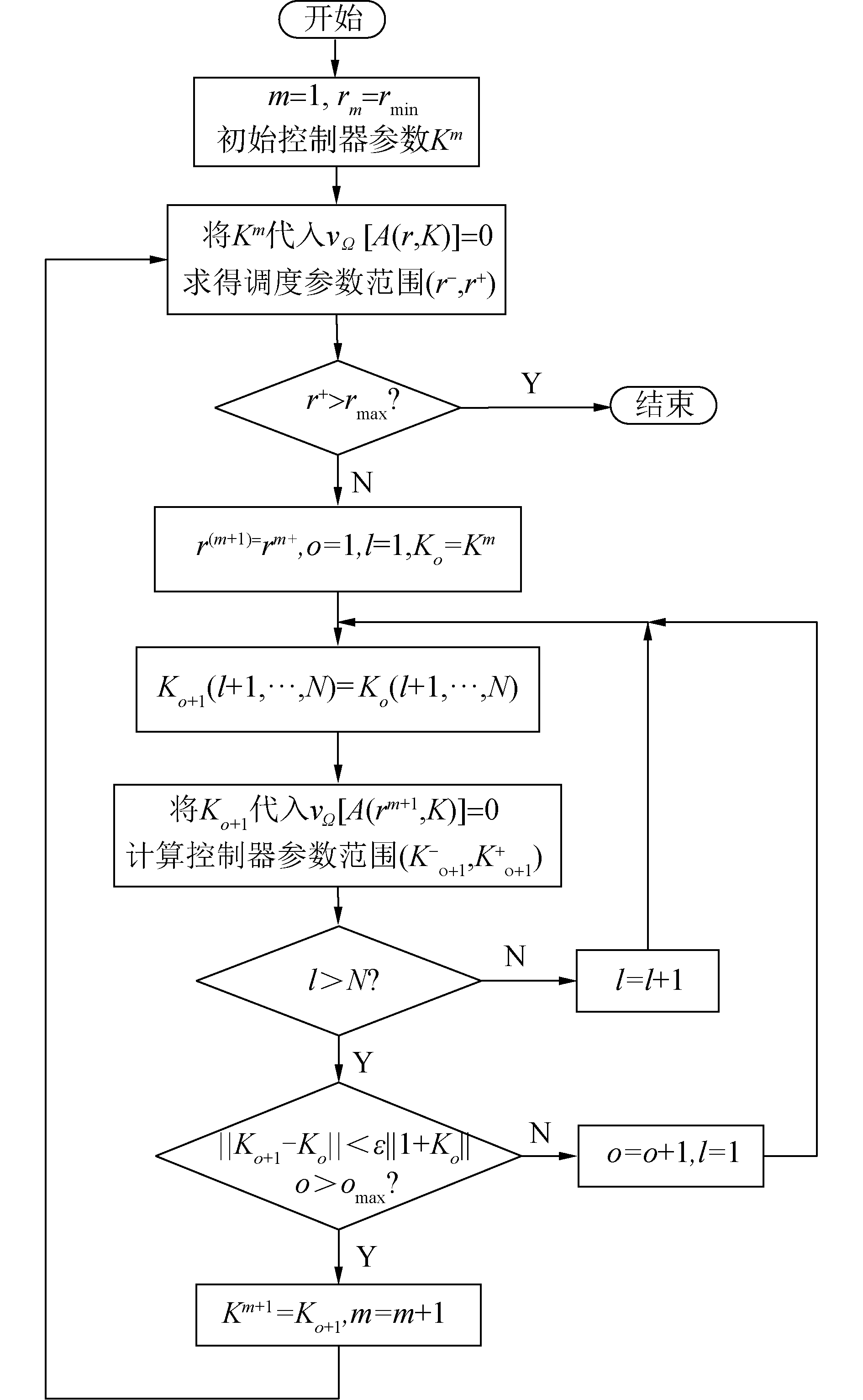
在该算法中,只需要选定控制架构及初始控制参数,后续控制参数可由自动迭代获得,不必在每个点计算控制参数。算法步骤如图 4所示。
|
Download:
|
| 图 4 单变量系统控制参数自适应整定算法流程 Fig. 4 Flow chart controller searching for one-parameter varying system | |
只要给出控制结构和初始得到控制参数,可以通过该算法得出数组控制律和每组控制律使得系统稳定的调度参数范围。所得的多组控制律根据其对应的调度参数范围进行自适应切换,从而对研究对象进行控制。
基于保护映射进行参数整定是一种离线调参方法,通过判定闭环系统极点是否满足在性能指标对应的目标区域Ω内来调整控制参数。本文所采用的目标区域定义为2.1节中式(13),其中包括了闭环极点位于复平面左半平面的约束,因此最终获得的控制参数能够保证系统的稳定性。
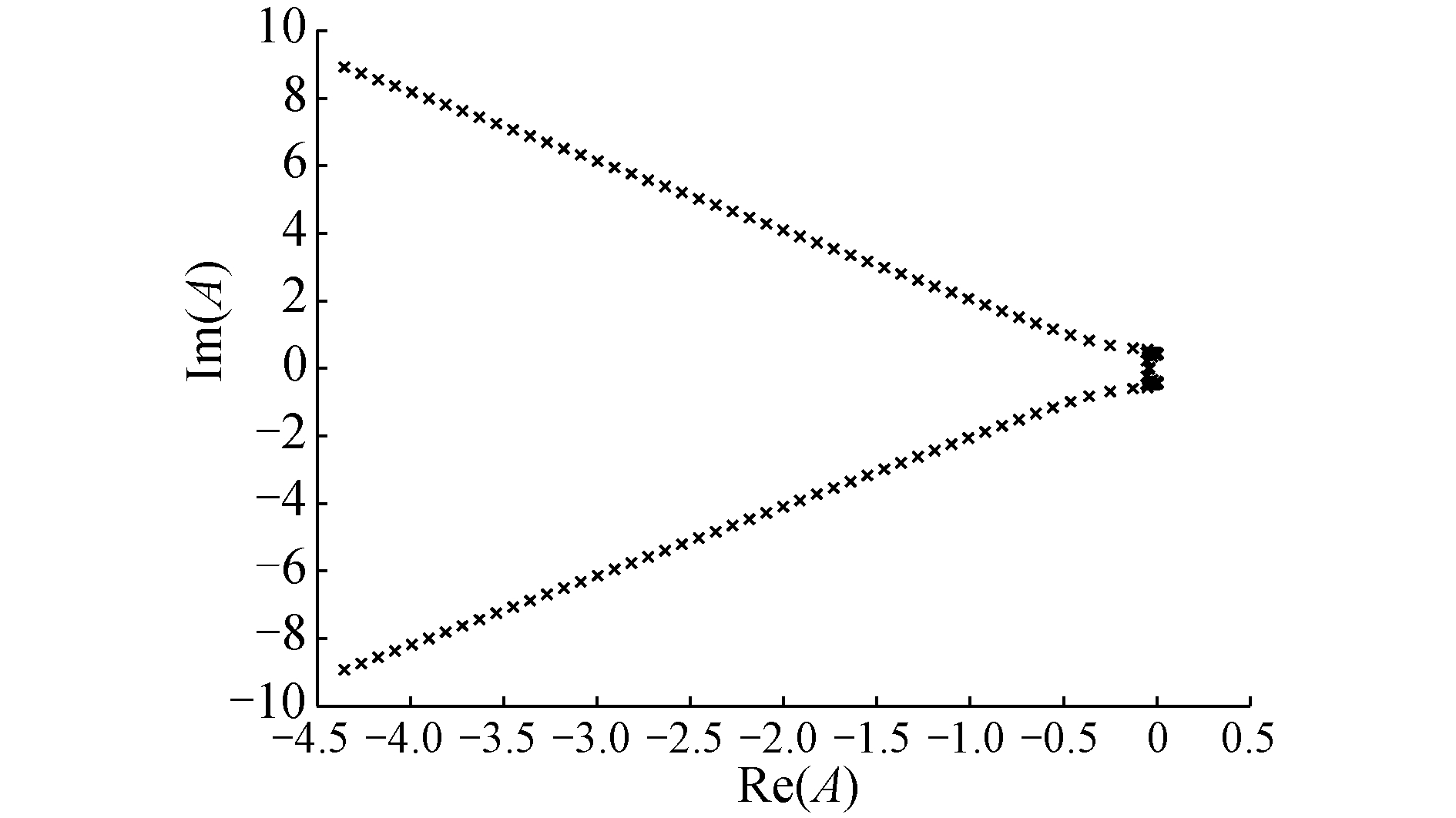
4 仿真结果 4.1 LPV模型验证本文研究的混合翼垂直起降无人机过渡过程的前飞速度范围是V=[0, 18] m/s,假设飞行高度保持100 m,在不同前飞速度下对飞行器进行配平,各配平点特征值分布如图 5所示,对应的控制输入如图 6所示。
|
Download:
|
| 图 5 不同飞行速度下系统特征根分布 Fig. 5 Eigenvalues under different velocities | |
|
Download:
|
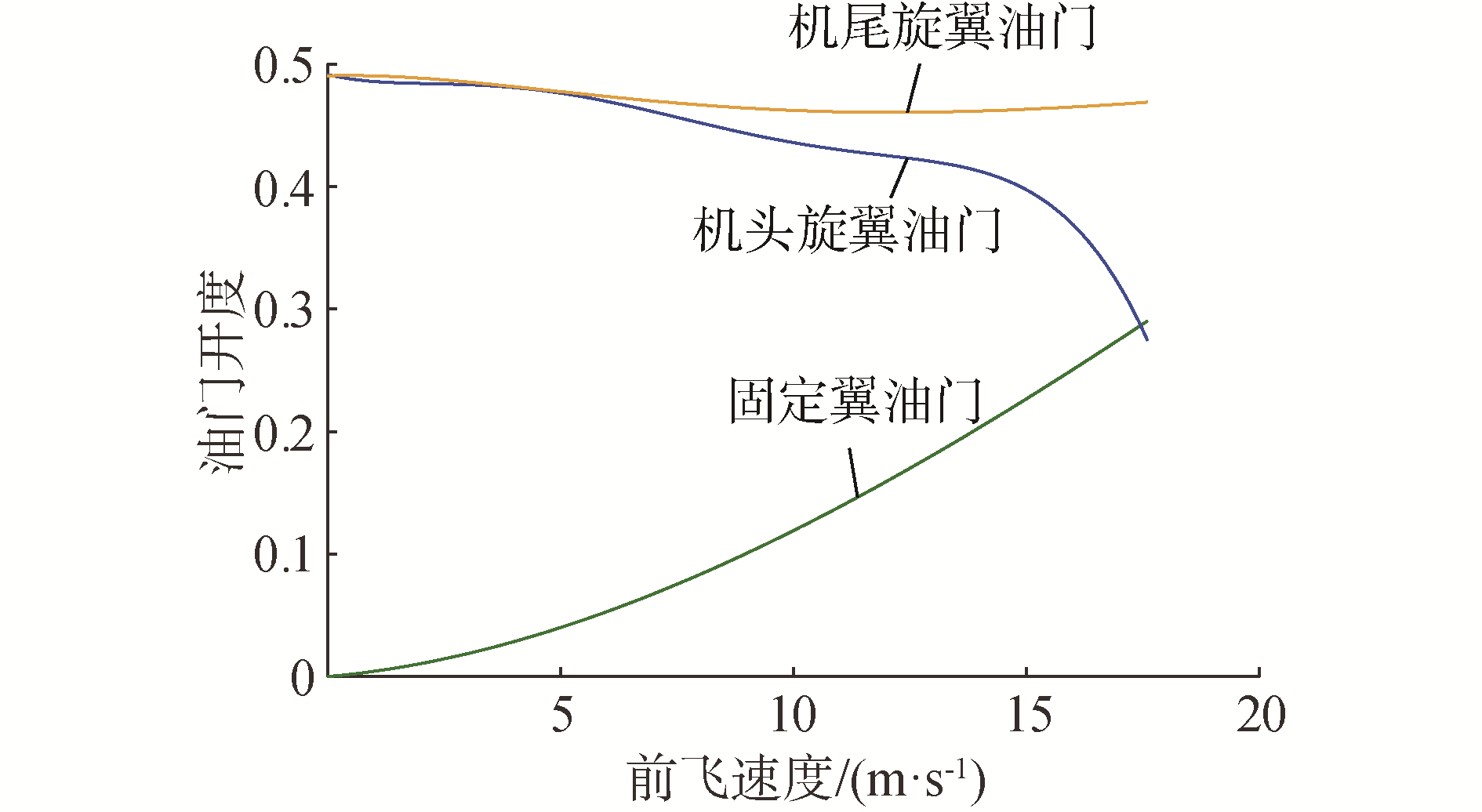
| 图 6 不同前飞速度对应的控制输入 Fig. 6 Control inputs under different velocities | |
由图 5可以得出,在前飞速度V=[0, 18] m/s,系统中存在实部大于0的特征根,在速度变化过程中会出现不稳定状态。在过渡过程中,短周期模态特征值受前飞速度影响产生的变化较大,长周期模态特征值影响产生的变化相对较小,特征值在前飞速度增大时会逐渐向左半平面移动,因此过渡过程中,随着前飞速度的不断增加,无人机的稳定性会变得越来越好。当前飞速度较低时,力和力矩的施加主要依靠旋翼,此时无人机的飞行特性与普通四旋翼无人机更相似,然而普通四旋翼无人机是不稳定系统,这也就解释了前飞速度较低时系统稳定性差的原因。伴随着前飞速度增加,机翼以及各舵面所产生的力和力矩也会不断增加,旋翼部分施加的力和力矩协同降低,此时无人机的飞行特性更类似于固定翼无人机,固定翼无人机是稳定系统,所以当前飞速度增大后,混合翼垂直起降无人机稳定性也不断增强。
与速度相比,过渡过程中高度对模型影响可以忽略,所以在飞行包线内根据前飞速度来选取设计点,最后把变参数进行归一化:
| $ \bar V = \frac{{V - {V_{\min }}}}{{{V_{\max }} - {V_{\min }}}} $ | (23) |
基于线性化得到的5个LTI模型,获得无人机的LPV系统模型:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot x}}}_0} = \mathit{\boldsymbol{A(}}V){\mathit{\boldsymbol{x}}_0} + \mathit{\boldsymbol{B}}(V)\mathit{\boldsymbol{u}}}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{C}}(V){\mathit{\boldsymbol{x}}_0}} \end{array}} \right. $ | (24) |
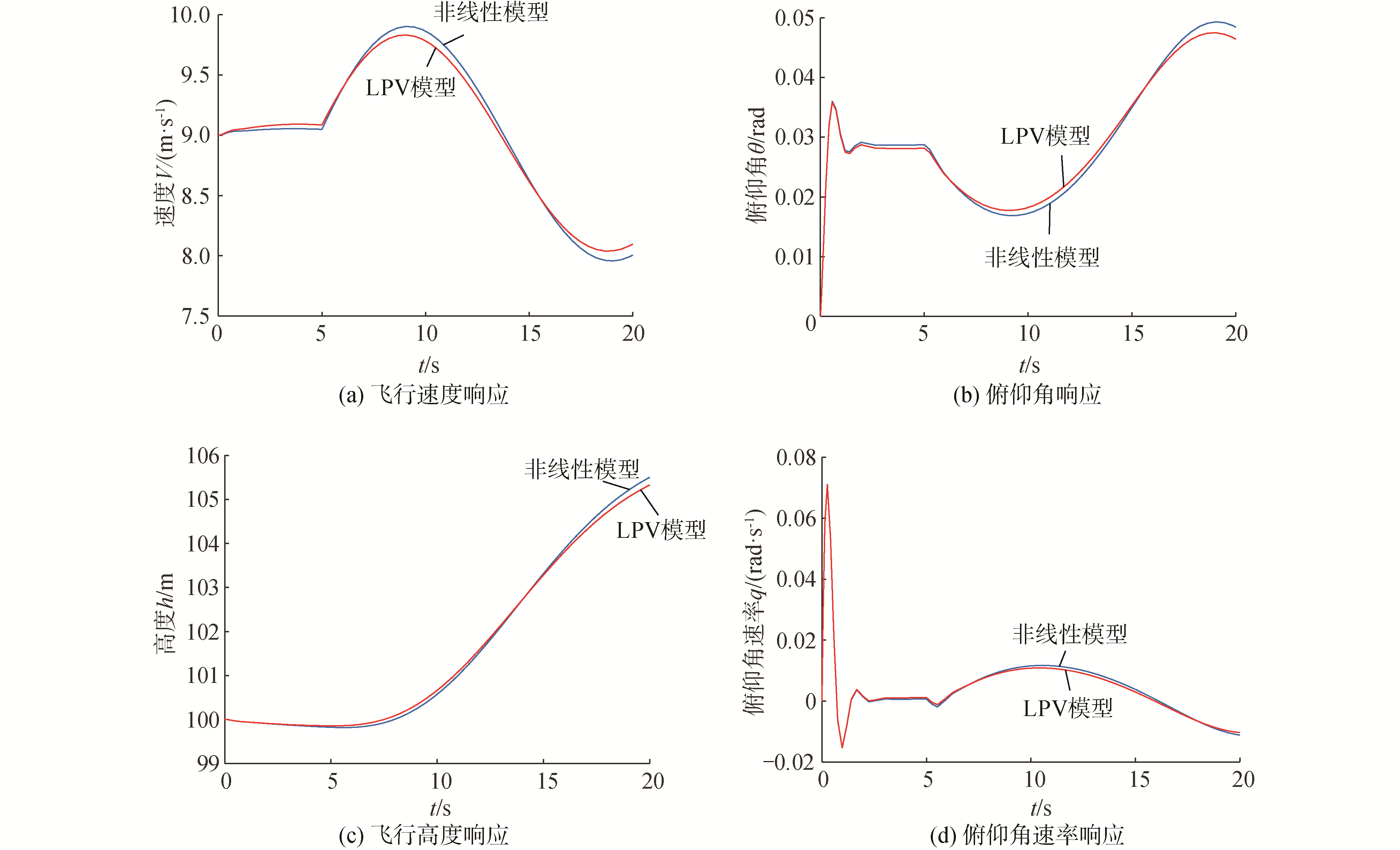
对所建立的LPV模型进行验证,通过将建立的模型与无人机非线性模型两者进行对比,从而判断模型是否正确。首先,初始状态设定为前飞速度为9 m/s,高度为100 m时的配平状态,固定翼油门开度为10%,经过5 s的仿真后,固定翼油门开度调整为20%,整个过程2个模型响应如图 7所示。
|
Download:
|
| 图 7 LPV模型与非线性模型各状态响应对比 Fig. 7 Response of nonlinear and LPV systems | |
从LPV模型和非线性模型的响应对比图可以得出,2种模型结果十分接近,所以通过雅克比线性化得到的LPV模型能够很好地替代已有的混合翼垂直起降无人机非线性模型。
4.2 控制器设计仿真首先确定V =0时的初始控制器参数为:
| $ {\mathit{\boldsymbol{K}}_0} = \left[ {\begin{array}{*{20}{c}} { - 0.308{\kern 1pt} {\kern 1pt} {\kern 1pt} 0}&{ - 0.062{\kern 1pt} {\kern 1pt} 2}&{0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 1}&{ - 4.402{\kern 1pt} {\kern 1pt} {\kern 1pt} 1}&{0.062{\kern 1pt} {\kern 1pt} 2}&{}\\ 0&0&0&0&0&{}\\ {0.333{\kern 1pt} {\kern 1pt} {\kern 1pt} 2}&{0.161{\kern 1pt} {\kern 1pt} {\kern 1pt} 9}&{ - 0.001{\kern 1pt} {\kern 1pt} {\kern 1pt} 0}&{ - 0.114{\kern 1pt} {\kern 1pt} {\kern 1pt} 1}&{ - 0.162{\kern 1pt} {\kern 1pt} {\kern 1pt} 0}&{}\\ {0.332{\kern 1pt} {\kern 1pt} {\kern 1pt} 6}&{0.161{\kern 1pt} {\kern 1pt} {\kern 1pt} 7}&{0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 7}&{ - 0.177{\kern 1pt} {\kern 1pt} 0}&{ - 0.161{\kern 1pt} {\kern 1pt} {\kern 1pt} 7}&{} \end{array}} \right] $ |
根据保护映射理论求出使控制器满足条件的稳定范围上边界为0.413 9 m/s, 以此上边界计算相应的控制律矩阵。以此类推,得到的随前飞速度变化控制器序列及稳定区域的上边界分别为:0.413 9、1.822 9、20.564 1 m/s。至此, 3个控制器能够使闭环系统极点稳定在期望的复平面区域。将各个控制器控制律参数的插值拟合,避免在各个稳定邻域边界处的控制器参数突变。
采用上述计算的控制器参数在飞行包线V=[0, 18] m/s,对混合式垂直起降无人机非线性模型进行仿真分析。在h=100 m给定高度下,针对初始前飞速度V=[0, 12] m/s, 每隔1 m/s取初始状态,给定跟踪速度跟踪偏差信号为2 m/s进行速度跟踪控制,其速度及高度响应曲线如图 8。

|
Download:
|
| 图 8 不同初始速度下指令跟踪效果 Fig. 8 Tracking performance under different initial velocities | |
由图 8可以看出,在各个初始速度下均能快速对速度进行较好的跟踪,同时飞行高度也能保证在合理的范围变化之内,并最终稳定在初始给定值。
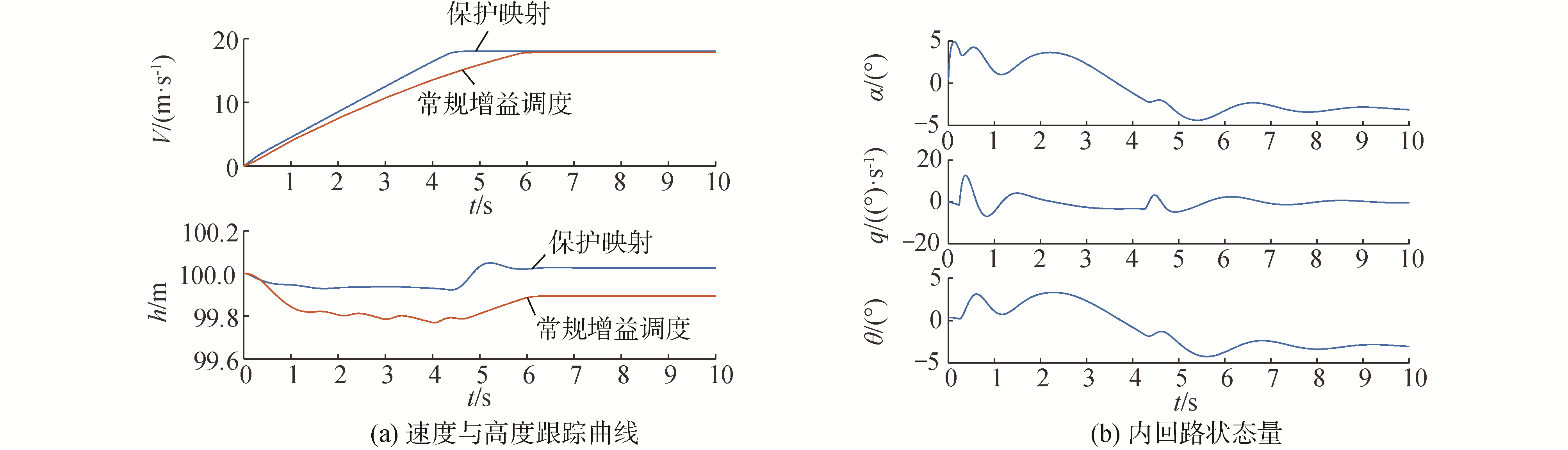
在给定高度h=100 m,前飞速度V=0的初始条件下。给定斜坡信号,并使斜坡信号达到18 m/s后进行保持,在飞行器非线性模型中进行仿真分析得到速度V、高度h、迎角、俯仰角θ和俯仰角速率q随时间的变化曲线,如图 9所示。其中图 9(a)中对比了本文基于保护映射的控制参数整定方法与文献[20]中常规分段增益调度方法的速度和高度跟踪效果。
|
Download:
|
| 图 9 过渡过程状态量变化曲线 Fig. 9 States tracking during the transition process | |
由图 9可知,基于保护映射的切换控制相比常规增益调度切换控制具有更快的速度跟踪和更稳定的高度保持效果。同时,无人机前飞速度能够良好地跟踪斜坡信号并逐渐增加到给定输入值,在前飞速度跟踪过程中飞行高度有0.1 m的掉高,达到前飞速度设定值后高度保持在给定高度。该过渡过程对应的控制输入如图 10所示。由图 10可知升降舵在跟踪过程中偏转角在合理范围之内。基于保护映射的控制参数整定方法相较与常规的增益调度算法在整定效率上存在明显优势,只需给定期望性能指标对应的稳定区域及起始状态点,即可自动获取满足全包线范围内的所有控制参数。
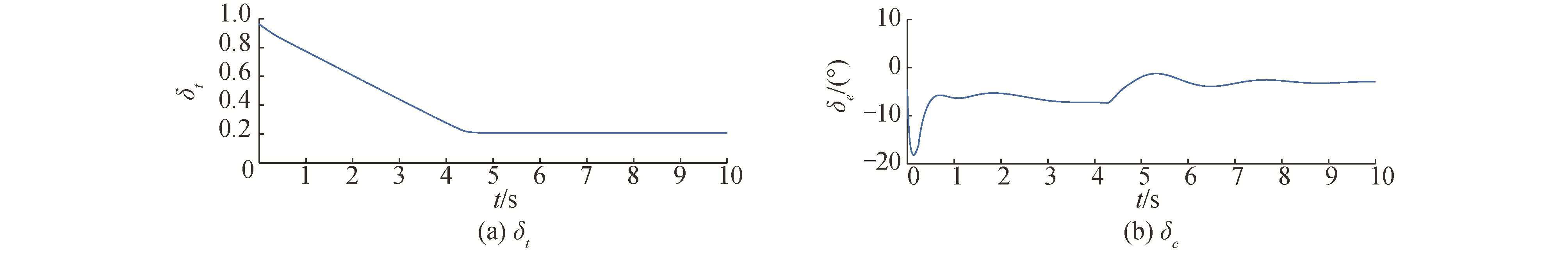
|
Download:
|
| 图 10 过渡过程控制输入 Fig. 10 Control inputs during the transition process | |
1) 通过对混合翼垂直起降无人机垂平过渡过程中旋翼和固定翼动力学进行一体化建模,推导出了混合翼垂直起降无人机纵向非线性动力学方程组。
2) 基于雅可比线性化方法建立了过渡过程的纵向LPV模型,通过对LPV模型及原非线性模型输出响应进行对比,验证了所得LPV模型的准确性。
3) 通过使用增益调度方法设计了以线性二次型调节器为基础的速度和高度跟踪控制器,结合保护映射理论设计了控制律参数自适应整定算法。仿真结果表明,所设计的自适应控制律能够实现满足混合翼垂直起降无人机过渡过程的设计要求,实现了定高加速过程中的稳定控制。
| [1] |
汪文凯.可垂直起降固定翼飞行器概念设计研究[D].长沙: 国防科学技术大学, 2014. WANG Wenkai. Research on conceptual design of VFW aircraft[D]. Changsha: National University of Defense Technology, 2014. (  0) 0)
|
| [2] |
于进勇, 王超. 垂直起降无人机技术发展现状与展望[J]. 飞航导弹, 2017(5): 37-42. YU Jinyong, WANG Chao. Development status and prospect of VTOL UAV technology[J]. Aerodynamic missile journal, 2017(5): 37-42. (  0) 0)
|
| [3] |
何小九, 李彦彬, 朱枫, 等. 国外垂直起降无人机发展现状及设计制造关键技术[J]. 飞航导弹, 2016(6): 22-27. HE Xiaojiu, LI Yanbin, ZHU Feng, et al. Development status of foreign VTOL UAVs and key technologies of design and manufacture[J]. Aerodynamic missile journal, 2016(6): 22-27. (  0) 0)
|
| [4] |
王冠林, 武哲. 垂直起降无人机总体方案分析及控制策略综合研究[J]. 飞机设计, 2006(3): 25-30. WANG Guanlin, WU Zhe. Configurations and control strategy for VTOL UAVs[J]. Aircraft design, 2006(3): 25-30. DOI:10.3969/j.issn.1673-4599.2006.03.006 (  0) 0)
|
| [5] |
ANSARI A A, ZHANG Ningyuan, BERNSTEIN D. Retrospective cost adaptive PID control of quadcopter/fixed-wing mode transition in a VTOL aircraft[C]//Proceedings of 2018 AIAA Guidance, Navigation, and Control Conference. Kissimmee, Florida, 2018: 1838.
(  0) 0)
|
| [6] |
樊鹏辉, 王新华, 蔡开元. 可垂直起降、高速前飞的飞行器设计与控制[J]. 控制理论与应用, 2010, 27(9): 1171-1177. FAN Penghui, WANG Xinyuan, CAI Kaiyuan. Design and control of aircraft of vertical take-off-and-landing and high-speed forward flight[J]. Control theory & applications, 2010, 27(9): 1171-1177. (  0) 0)
|
| [7] |
JUNG Y, SHIM D H. Development and application of controller for transition flight of Tail-Sitter UAV[J]. Journal of intelligent & robotic systems, 2012, 65(1/2/3/4): 137-152. DOI:10.1007/s10846-011-9585-1 (  0) 0)
|
| [8] |
KITA K, KONNO A, UCHIYAMA M. Transition between level flight and hovering of a Tail-Sitter vertical takeoff and landing aerial robot[J]. Advanced robotics, 2010, 24(5/6): 763-781. (  0) 0)
|
| [9] |
KUBO D, SUZUKI S. Tail-sitter vertical takeoff and landing unmanned aerial vehicle:transitional flight analysis[J]. Journal of aircraft, 2008, 45(1): 292-297. (  0) 0)
|
| [10] |
刘玉焘.尾座式无人机的飞行控制器设计[D].哈尔滨: 哈尔滨工业大学, 2014. LIU Yutao. Design of flight controller for a Tail-sitter UAV[D]. Harbin: Harbin Institute of Technology, 2014. (  0) 0)
|
| [11] |
杨传广, 马铁林, 甘文彪, 等.垂直起降固定翼无人机技术特点浅析[C]//2017年(第三届)中国航空科学技术大会论文集(下册).北京, 2017: 56-61. YANG Chuanguang, MA Tielin, GAN Wenbiao, et al. Analysis on technical characteristics of vertical takeoff and landing fixed-Wing UAV[C]//2017(Third Session) Proceedings of China Aviation Science and Technology Conference (Part Ⅱ). Beijing, 2017: 56-61. (  0) 0)
|
| [12] |
PARTOVI A R, WANG Xinhua, LUM K Y, et al. Modeling and control of a small-scale hybrid aircraft[J]. IFAC proceedings volumes, 2011, 44(1): 10385-10390. DOI:10.3182/20110828-6-IT-1002.03784 (  0) 0)
|
| [13] |
STAHL P, RÖßLER C, HORNUNG M. Benefit analysis and system design considerations for drag reduction of inactive hover rotors on electric fixed-wing VTOL vehicles[C]//Proceedings of 2018 Aviation Technology, Integration, and Operations Conference. Atlanta, Georgia, 2018: 4150.
(  0) 0)
|
| [14] |
AKICI F, LEBLEBICIOLU M K. Control system design of a vertical take-off and landing fixed-Wing UAV[J]. IFAC-papersonline, 2016, 49(3): 267-272. DOI:10.1016/j.ifacol.2016.07.045 (  0) 0)
|
| [15] |
GUCLU A, KURTULUS D F, ARIKAN K B. Attitude and altitude stabilization of fixed wing VTOL unmanned air vehicle[C]//AIAA Modeling and Simulation Technologies Conference. Washington, DC, 2016: 3378.
(  0) 0)
|
| [16] |
SAYDY L, TITS A L, ABED E H. Guardian maps and the generalized stability of parametrized families of matrices and polynomials[J]. Mathematics of control, signals and systems, 1990, 3(4): 345-371. DOI:10.1007/BF02551375 (  0) 0)
|
| [17] |
SAUSSIÉ D, SAYDY L, AKHRIF O, et al. Gain scheduling with guardian maps for longitudinal flight control[J]. Journal of guidance, control, and dynamics, 2011, 34(4): 1045-1059. (  0) 0)
|
| [18] |
肖地波, 陆宇平, 刘燕斌, 等. 应用保护映射理论的高超声速飞行器自适应控制律设计[J]. 航空学报, 2015, 36(10): 3327-3337. XIAO Dibo, LU Yuping, LIU Yanbin, et al. Adaptive control law design using guardian maps theory for hypersonic vehicles[J]. Acta aeronautica et astronautica sinica, 2015, 36(10): 3327-3337. (  0) 0)
|
| [19] |
SAUSSIÉ D, SAYDY L, Akhrif O, et al. Gain scheduling with guardian maps for longitudinal flight control[J]. Journal of guidance, control, and dynamics, 2011, 34(4): 1045-1059. (  0) 0)
|
| [20] |
王博豪, 张勇, 徐伟程, 等. 小型混合翼无人机过渡过程一体化建模与控制[J]. 宇航计测技术, 2019, 39(2): 27-31. WANG Bohao, ZHANG Yong, XU Weicheng, et al. Integrated modeling and control of small hybrid wing UAV transient process[J]. Journal of astronautic metrology and measurement, 2019, 39(2): 27-31. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


