纵倾平衡系统由水舱、阀门、直管和高压空气系统等构成,是控制水下航行器保持纵向位置平衡的管路系统。在船体发生纵倾不平衡时,纵倾平衡系统会利用高压空气将设置在水下航行器一端水舱的水调至另一端的空水舱,以水舱间的重力不平衡来抵消航行过程中船体受到外力影响产生的不平衡。
由于纵倾平衡系统运行时管压高、流速快、流量大,且结束调水时,阀门闭合突然,极易发生水锤现象。水锤会引发严重的瞬态噪声,对水下航行器的隐蔽性产生负面影响,且水锤产生的压力脉动亦会损伤管路系统,缩短阀门等部件的寿命。因此,研究水锤规律极其控制措施,具有重要的理论和工程实际意义。
采用包含弹性结构的装置吸收压力脉动是常见的水锤控制手段,如水锤消除罐等。一般的水锤抑制研究普遍针对长距离输水管路,不必考虑空间成本问题。与此不同,水下航行器管路系统布置通常极为紧凑,空间狭小,因此对水锤的控制必须考虑空间尺寸问题,不具备使用大型水锤消除罐的条件。环状气囊消声器[1]作为一种能够有效抑制压力脉动的装置,具有结构紧凑、外形尺寸小的特点。本文将通过仿真和实验探究其对水锤现象的控制效果。
对于简单管路管内压力脉动的模拟,一维模型已经满足一般的工程需求。一般采用特征线方程的有限差分法(finite difference method,FDM),其算法简单,可以最大程度节约计算成本。但对消声器这样的复杂结构,使用FDM很难描述其复杂结构的特性,模型与真实情况有较大差距,故一般采用有限元法或有限体积法,用三维模型进行仿真计算。
参考文献[2]介绍了通过OpenFOAM和fluent进行模型耦合的方法,即利用前者进行简单管路一维模型部分的仿真,利用后者的FVM来计算复杂结构部分的湍流物理场。
本文采用多物理场仿真软件COMSOL进行模型耦合的方法对安装有环状气囊消声器的纵倾平衡管路系统进行仿真,实现对该结构特点管路的瞬变流压力脉动仿真计算。
1 仿真模型建立 1.1 1D-3D建模发生以下2种情况时[2],一维模型的计算结果将产生较大误差,需要采用耦合模型建模:
1) 径向尺寸相对于管线长度较大,其径向流携带的能量无法忽略,断面上流速和压强的分布不均匀,无法忽略;
2) 结构复杂的管路部件,用简化的一维模型无法对其能量、流量特性进行模拟。
本文中环状气囊消声器抑制水锤压力脉动的仿真计算中,消声器结构复杂,属于上述第2种情况。
瞬变流研究涉及液体中压力波的传播,因此需要考虑流体的可压缩性。
采用的连续方程和动量方程为[3]:
| $ {\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot (\rho \mathit{\boldsymbol{U}}) = 0} $ | (1) |
| $ {\frac{{\partial \rho \mathit{\boldsymbol{U}}}}{{\partial t}} + \nabla (\rho \mathit{\boldsymbol{UU}}) - \nabla \cdot \mu \nabla \mathit{\boldsymbol{U}} = - \nabla p} $ | (2) |
式中:U为液体速度矢量;μ为液体黏度;ρ为液体密度;p为液压。
液体的可压缩性通过压力和流体密度的线性关系实现,即:
| $ \frac{\partial \rho}{\partial p}=\frac{\rho}{K}=\varphi $ | (3) |
式中:K为体积弹性模量;φ为反映其线性关系的系数。
利用参考压力和参考密度可以得到压力和密度的关系为:
| $ \rho=\rho_{0}+\varphi\left(p-p_{0}\right) $ | (4) |
波速则通过Newton-Laplace方程得到,即:
| $ a=\sqrt{\frac{K}{\rho}}=\sqrt{\frac{1}{\varphi}} $ | (5) |
在耦合模型中采用的湍流模型为Realizable k-ε模型,与标准k-ε模型相比,其采用了黏度计算公式并根据二次平均的涡量输运方程推导了耗散率公式。
其湍动能k及耗散率ε的输运方程为:
| $ \rho \frac{\mathrm{d} k}{\mathrm{d} t}=\frac{\partial}{\partial x_{i}}\left[\left(\mu+\frac{\mu_{t}}{\sigma_{k}}\right) \frac{\partial k}{\partial x_{i}}\right]+G_{k}+G_{b}-\rho \varepsilon-Y_{M} $ | (6) |
| $ \begin{array}{c} \rho \frac{\mathrm{d} \varepsilon}{\mathrm{d} t}=\frac{\partial}{\partial x_{i}}\left[\left(\mu+\frac{\mu_{t}}{\sigma_{\varepsilon}}\right) \frac{\partial \varepsilon}{\partial x_{i}}\right]+\rho C_{1} S \varepsilon- \\ \rho C_{2} \frac{\varepsilon^{2}}{k+\sqrt{v \varepsilon}}+C_{1 \varepsilon} \frac{\varepsilon}{k} C_{3 \varepsilon} G_{b} \end{array} $ | (7) |
式中:
相关湍流系数与标准k-ε模型是一致的。
对于耦合的边界,由于Realizable k-ε湍流模型描述的是充分发展的湍流,而边界层内的流动雷诺数低,湍流发展不充分,需要引入壁函数对边壁加以特殊处理,即:
| $ \frac{u_{p} u^{*}}{\frac{\tau_{\omega}}{\rho}}=\frac{1}{\aleph} \ln \left(E \frac{\rho u^{*} y_{p}}{\mu}\right)-\Delta B $ | (8) |
式中:u*=Cμ1/4kp1/2;
COMSOL提供了几种不同的耦合算子来对不同维度的边界进行耦合。软件提供广义拉伸算子、线性拉伸算子、积分算子等组件耦合算子,这几种算子可以将高维度边界的值通过平均等方式赋给低维度边界,也可以通过拉伸将低维度边界的值赋给高维度[4]。若使用这几种耦合算子,在配置求解器时,求解步骤的设定将较为复杂。
为了解决一维管路和三维流场的耦合问题,COMSOL 5.4版本中新增了一个多物理场接口“管接头”。该接口可以将一维的管道流模块的边界(点)同三维流场模块边界(面)耦合,自动编译解析耦合边界条件方程,实现简单管路和复杂部件的多尺度模型耦合仿真。管接头边界条件设置方便快捷,但会导致仿真的初始条件设定出现一些问题,对计算的收敛性也有较大影响。
采用二维轴对称几何建模符合环形消声器结构特点,且可以简化网格,降低计算成本,避免受到计算机性能的限制。耦合算子的拉伸维度也从由点到面的拉伸简化为由点到线的线性拉伸。
本文采用线性拉伸耦合算子进行多维度耦合计算。
1.2.2 环状气囊消声器及管路的物理场
|
Download:
|
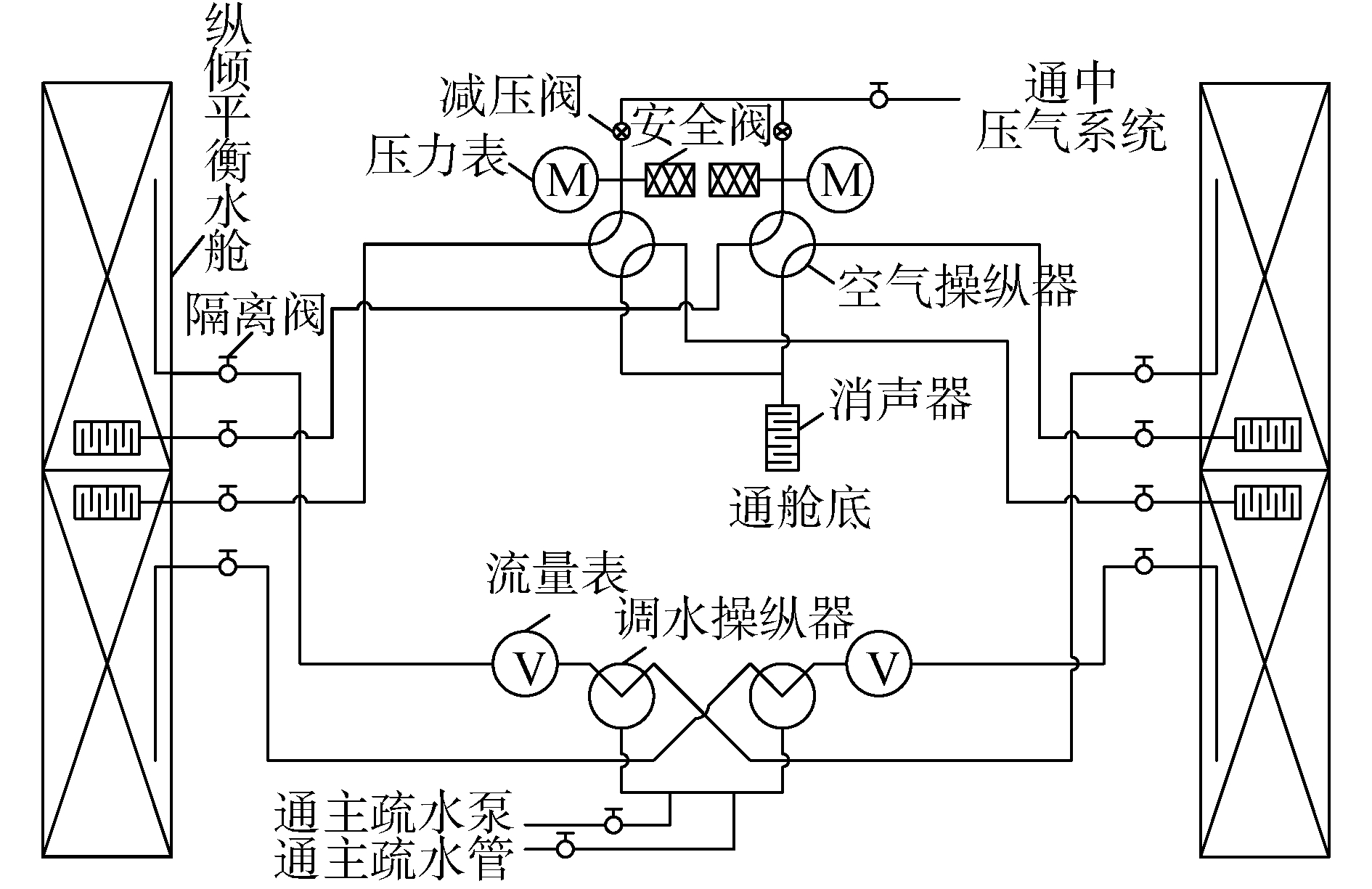
| 图 1 纵倾平衡系统管系示意 Fig. 1 Schematic diagram of trim balance pipeling system | |
图 1中的管路系统较为复杂,包含多种结构,在探究其水锤规律的仿真计算中,根据其工作特性,无需考虑预先开启的机械截止阀、疏水管路等装置,而图中所示的调水操纵器一般为电液球阀,阀门特性视作线性。
高压空气系统在调水过程中保持常压,故可直接设定为常数值的压力边界条件。
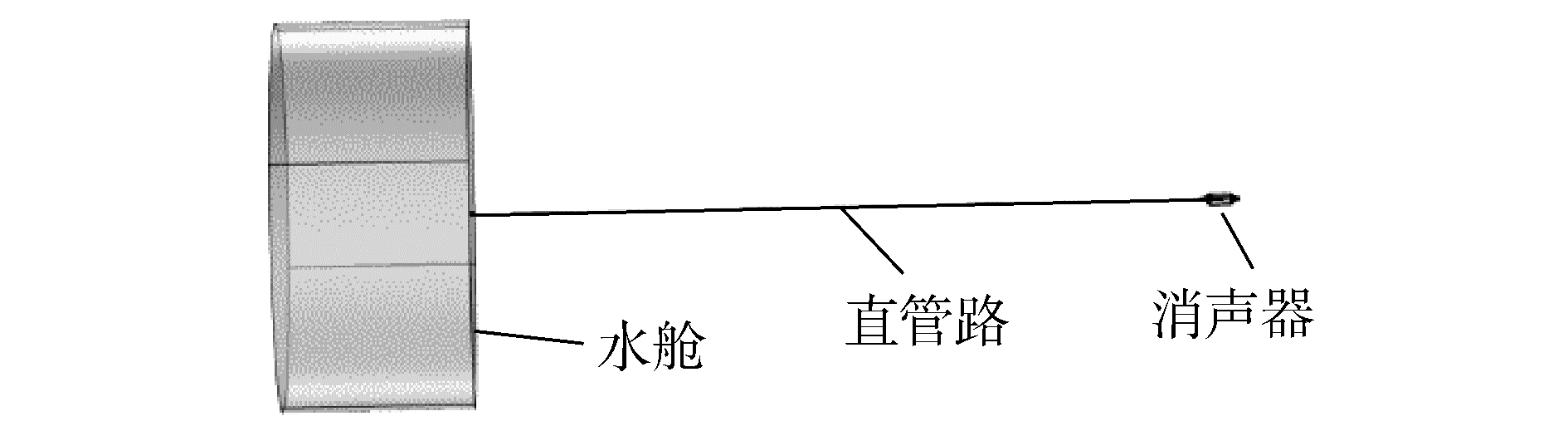
环状气囊消声器的流场计算应考虑流固耦合,再耦合上管道流物理场,实际是一个管道流-湍流-固体力学耦合计算。借助COMSOL的多物理场计算能力可以实现这样的计算仿真,整个三维模型如图 2所示。左端圆柱为水舱,右端为消声器结构,中间部分连接线为直管路。阀门设定在消声器右端边界面上,通过边界条件控制,故没有具体的阀门结构。其阀门流量特点为线性,关阀时间由边界条件中控制函数调整。瞬时关阀采用阶跃函数控制,其他关阀时间采用斜坡函数控制。
|
Download:
|
| 图 2 仿真模型三维示意 Fig. 2 3D schematic diagram of the simulation model | |
管路系统相关参数设置如表 1,管道的材料按不锈钢管设定。同时需要设定橡胶材料和气囊中的气体压力[6-7]。
| 表 1 设定参数及意义 Table 1 Setting parameters and meaning |
水下航行器内部空间极为紧凑,管系及相关设备的布置均受到严格限制。水锤消除罐等装置难以得到足够的安装空间,无法发挥其设计性能。环状气囊消声器对流噪声具有广谱消减效果,且具备结构尺寸小的优势。
2.1 傅里叶变换及频域解由压力波频谱结果可以了解到水锤压力波频率特点,这在选用压力脉动抑制装置时具有指导作用。本文使用origin的数据处理模块对已有的水锤压力波时域结果[1]进行傅里叶变换,以得到可作为对照的频域信号。
2.2 消声器的传递损失传递损失是仿真预测消声器声学性能的常用指标,环状气囊消声器的传递损失计算除考虑压力声学部分外,还应考虑声固耦合的影响,这不仅可以更好地反映气囊吸收压力脉动的能力,也考虑到了外壳的透声情况,更符合实际的状态。
COMSOL作为具备多物理场耦合能力的仿真软件,可以调用声固耦合模块进行传递损失计算,其包含了压力声学和固体力学2个部分物理场,并具备自动编译耦合边界方程的功能。
流体部分设定压力声学物理场,固体部分设定固体力学物理场,并设置多物理场耦合边界为“声-结构耦合边界”。从材料库可调用需要的流体、固体材料参数,需要设定的材料包括气囊内空气、外壳不锈钢、气囊橡胶和模型其他部分的水。值得一提的是,气囊材料作为非常用橡胶材料,不能从软件材料库中直接调用,可以直接在固体力学物理场的设定中定义线弹性材料的杨氏模量、泊松比和密度,并确定其材料模型为各向同性。
在结果处理中,利用积分算子对进出口边界的声压值求和,并依照传递损失定义进行公式输入,得到传递损失计算结果。
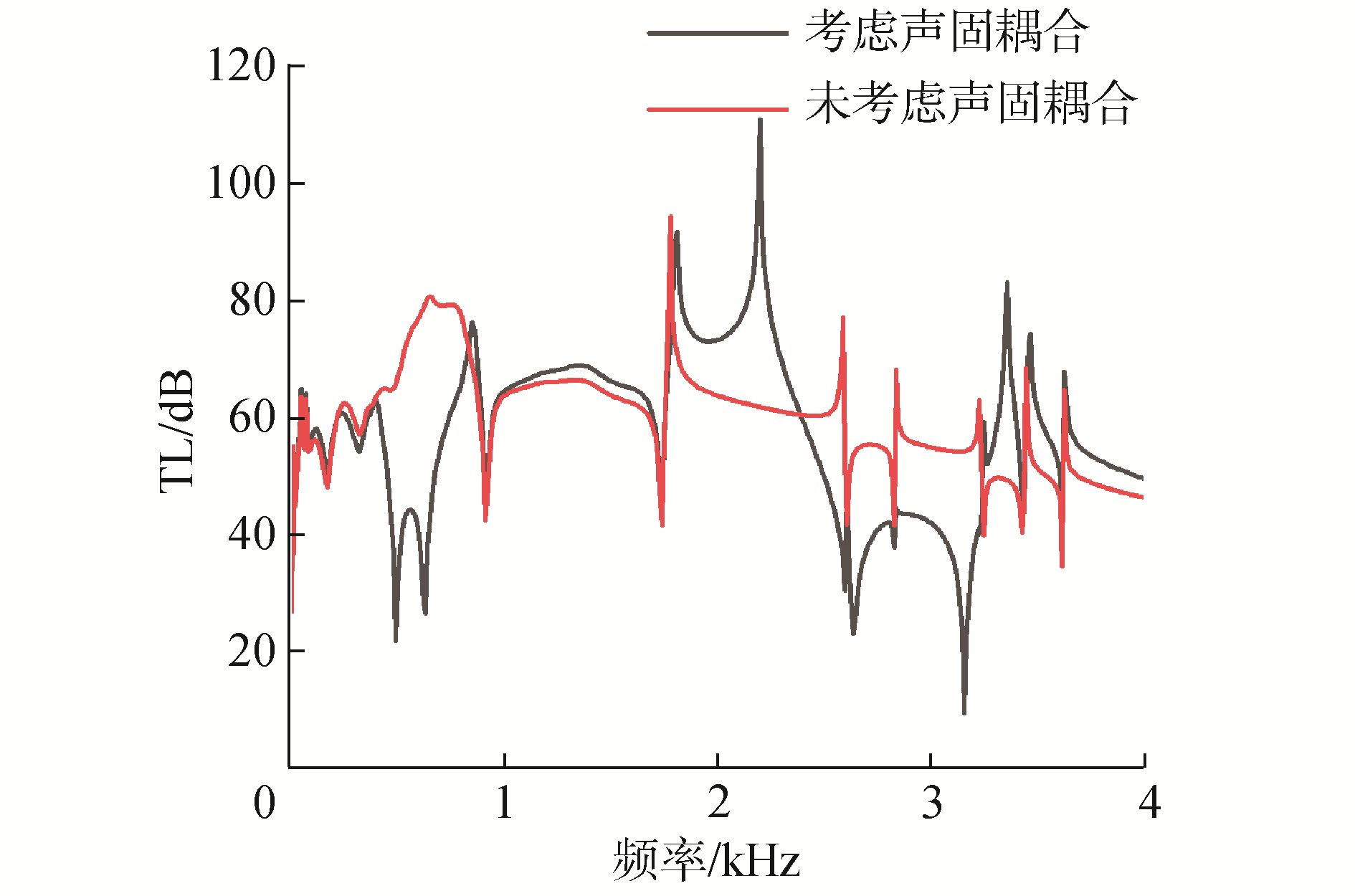
图 3为COMSOL声固耦合模块计算所得环状气囊消声器的传递损失曲线。环状气囊消声器对低、中、高压力脉动的抑制效果都很优秀。考虑声固耦合后,外壳结构不再全反射声波造成计算结果中部分频率声学性能有所下降,但低频和高频的声学性能依然表现良好。
|
Download:
|
| 图 3 消声器4 kHz内传递损失 Fig. 3 Transmission loss of muffler within 4 kHz | |
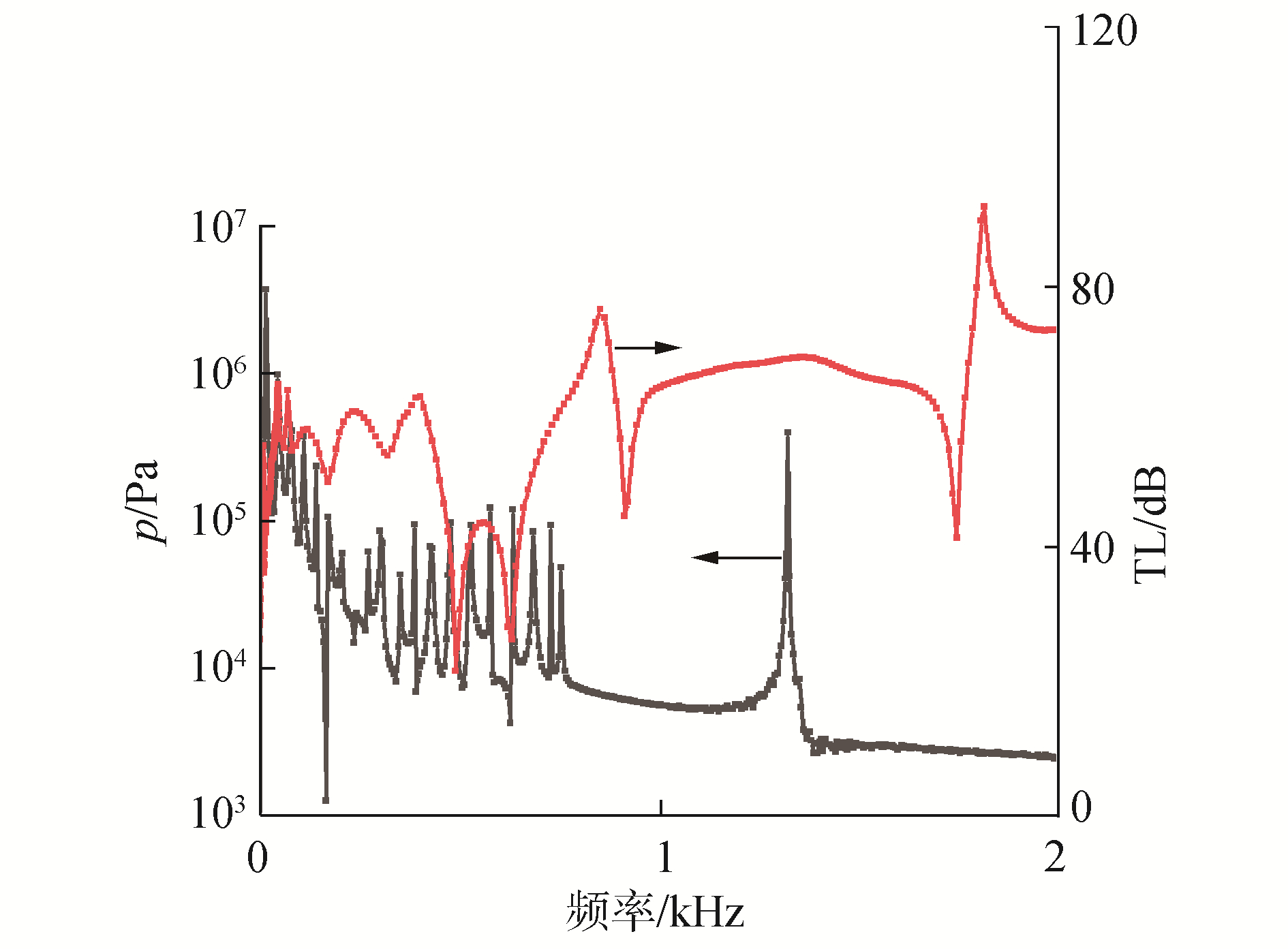
对水锤波进行频域分析并结合传递损失曲线得到图 4结果,由于2 kHz后压力幅值相对很小,故只截取2 kHz前的数据。可以观察到在峰值频率处消声器传递损失对应性良好,这从声学特性适配的仿真预测角度说明了环状气囊消声器对水锤压力波的良好抑制效果。
|
Download:
|
| 图 4 水锤波频域分析及消声器传递损失曲线 Fig. 4 Comparison of water hammer wave frequency domain analysis and muffler transmission loss curve | |
工程中常使用插入损失评价消声器的实际声学性能。本文所采用的环状气囊消声器,在设计研发过程中已获得大量试验数据证明其在各类工况下对流噪声具有广谱消减效果。本文依据与纵倾平衡系统调水工况相近的原则,仅选取了与管路静压0.7 MPa的实验结果作为对照。
2.4.1 试验设备及系统实验利用哈尔滨工程大学传播冷却水循环管路陆上模拟试验台架进行。试验台架由耐压储水罐、离心泵、连接管路和测试段等构成。测试部分由消声器/替换管、B & K8103水听器,匹配适应高输出阻抗的B & K2692型四通道通用电荷放大器,B & K3160多通道数据采集分析仪和IFM4 080 K电磁流量计等组成。
2.4.2 试验步骤1) 储水罐充满水后,通过高压水泵向储水罐内打水,使管路静压力达到0.7 MPa;
2) 测量实验管路背景噪声;
3) 通过调频使离心泵转速达到额定转速2 930 r/min;
4) 调整循环水管路非测试段阀门开度,使流量随之变化,然后测量消声器在100、130、160和190 m3/h 4种管路流量条件下环状气囊消声器下游测点处的声压信号;
5) 将消声器替换成等长的DN125直管,并重复1次步骤1)~步骤4)。
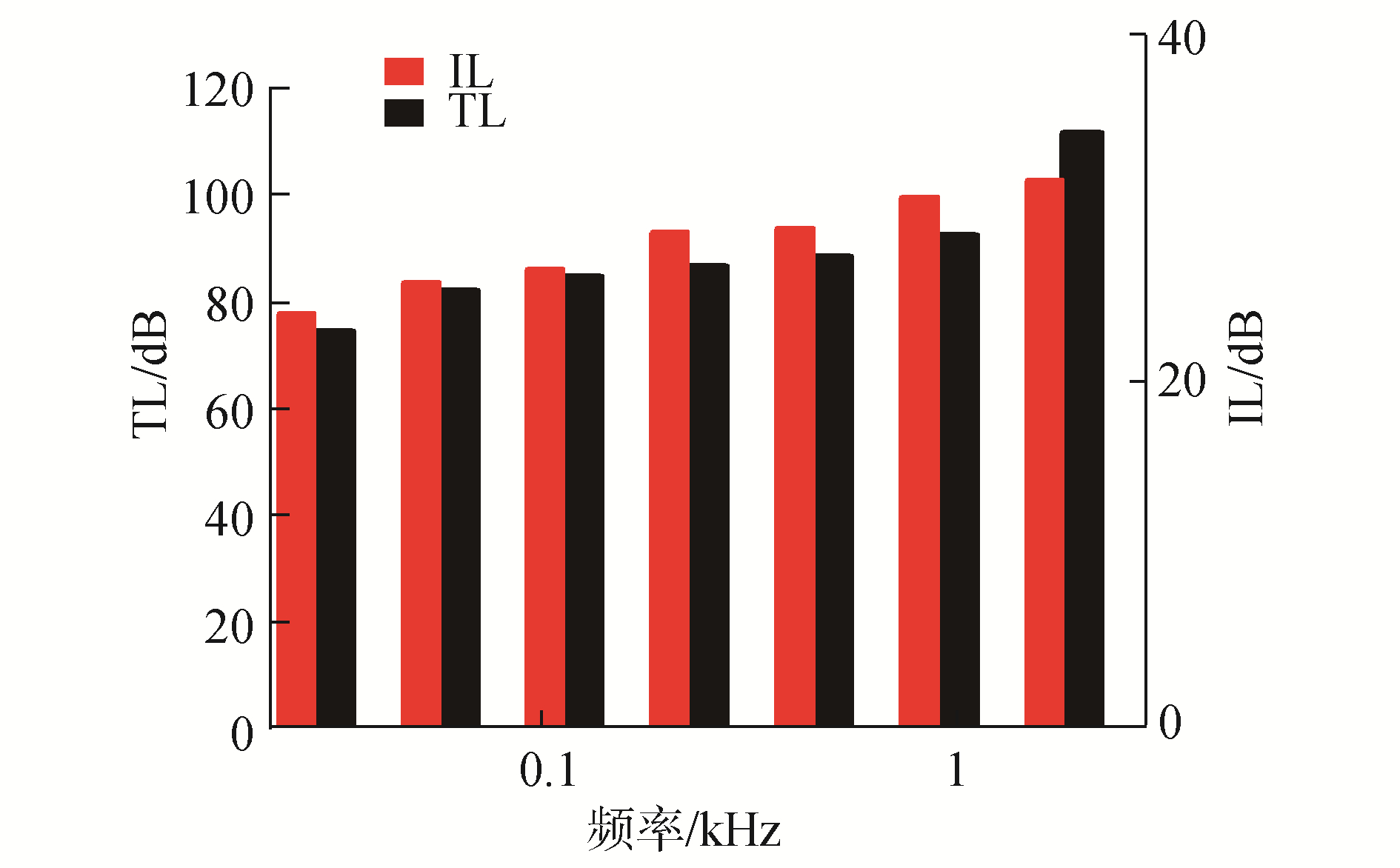
2.4.3 试验数据及分析选取的试验工况下,插入损失的1/3倍频程分析处理结果如表 2所示。初步观察,插入损失频谱特点与传递损失规律较为相符,在验证了环状气囊消声器对广谱流噪声有良好抑制效果的同时,也证明声固耦合计算得到的传递损失更贴近实际情况。由于插入损失在不同流量下频域特点类似,故仅选取190 m3/h的工况,采用倍频程处理数据,其对比情况如图 5所示。
| 表 2 环状气囊消声器插入损失 Table 2 IL of annular airbag muffler |
|
Download:
|
| 图 5 传递损失与插入损失对比 Fig. 5 Comparison of TL and IL | |
通过表 2、图 5可以看出,循环管路中安装消声器可以大幅度抑制管路流噪声,取得了良好的管路流体压力脉动抑制效果。由于计算公式和概念差异,插入损失和传递损失的数值并不能直接对照,因而采用了双Y轴图比对两者的频率特征。
整体来看,其频率特点趋势基本一致,反映出声固耦合计算和测试实验中对消声器声学性能评估的一致性。因此可以得出结论:消声器广谱流噪声消减能力非常优秀。
在一些频率上,传递损失和插入损失的趋势并不能完全对应,一方面是因为实验测试和有限元法数值解都存在难以避免的误差,另一方面,试验的循环水管路结构复杂,由于存在离心泵、储水罐以及大量的管路接头,在运行过程中会产生规律复杂的驻波,对测试的影响无法忽略。
3 计算结果对比 3.1 仿真结果 3.1.1 水锤模型计算结果在COMSOL软件中使用水锤模块直接计算压力脉动,基于水锤基本理论中考虑管路系统流固耦合的相关理论,并引入了区别管路两端锚固方式的不同波速修正系数[2],其计算结果如图 6所示。
|
Download:
|
| 图 6 水锤模块压力脉动三维曲面 Fig. 6 3D surface picture of water hammer module pressure pulsation | |
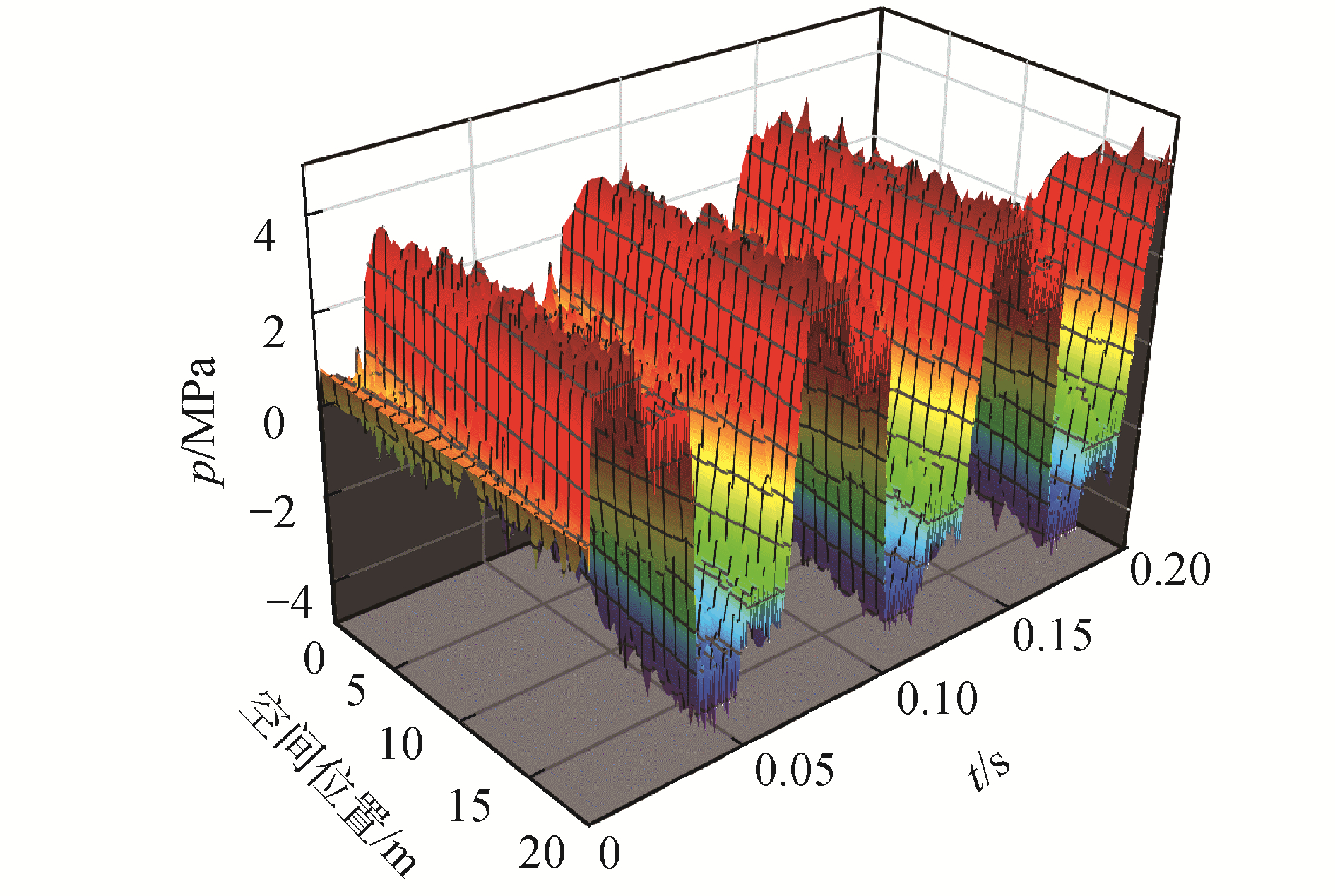
图 6为使用水锤物理场计算的整个系统轴向的压力变化曲线,其中空间位置坐标以水舱为零点,阀门坐标为20。越靠近阀门处,峰值宽度越大。在时间轴上也可以观察到压力波从阀门处传递到了水舱接口位置,压力脉动由于摩擦耗散有所衰减。而在安装消声器后,压力变化特点如图 7所示。

|
Download:
|
| 图 7 水锤模块消声器-管路水锤波三维曲面 Fig. 7 3D surface picture of 1D model muffler-pipeline water hammer module wave | |
图 7中数据为通过水锤模块计算得到的数据,模型设定为两端闭合管路中的压力波状态,并且由于计算周期短,直管摩擦有限,故水锤波的能量耗散几乎可以忽略不计,虽然在计算中考虑到了相关参数的设定,但对于最终结果影响很小。
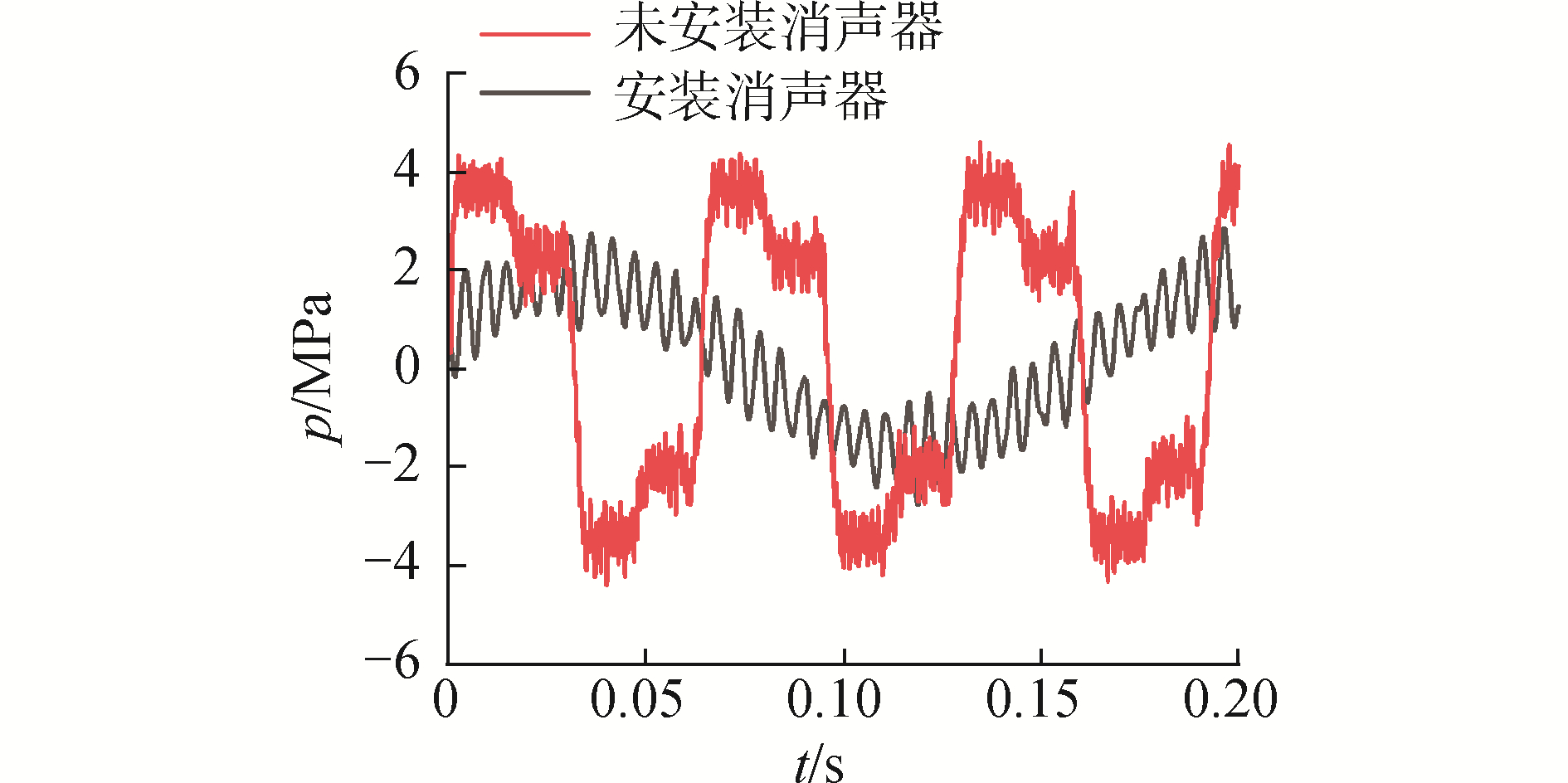
选取消声器出口处的压力脉动数据,比较安装消声器前后的压力脉动变化情况。考虑到水锤波以阀门作为压力源的假设,这个位置也能较好地反映消声器对压力波的抑制效果。对比情况如图 8所示。
|
Download:
|
| 图 8 时域水锤压力抑制对比 Fig. 8 Comparison picture of water hammer pressure suppression by time domain | |
在安装消声器结构后,水锤波的幅值明显下降,并且极大地减少了峰值的数量。对比结果如表 3所示。
| 表 3 消声器压力抑制效果对比 Table 3 Comparison of water hammer pressure suppression by muffler |
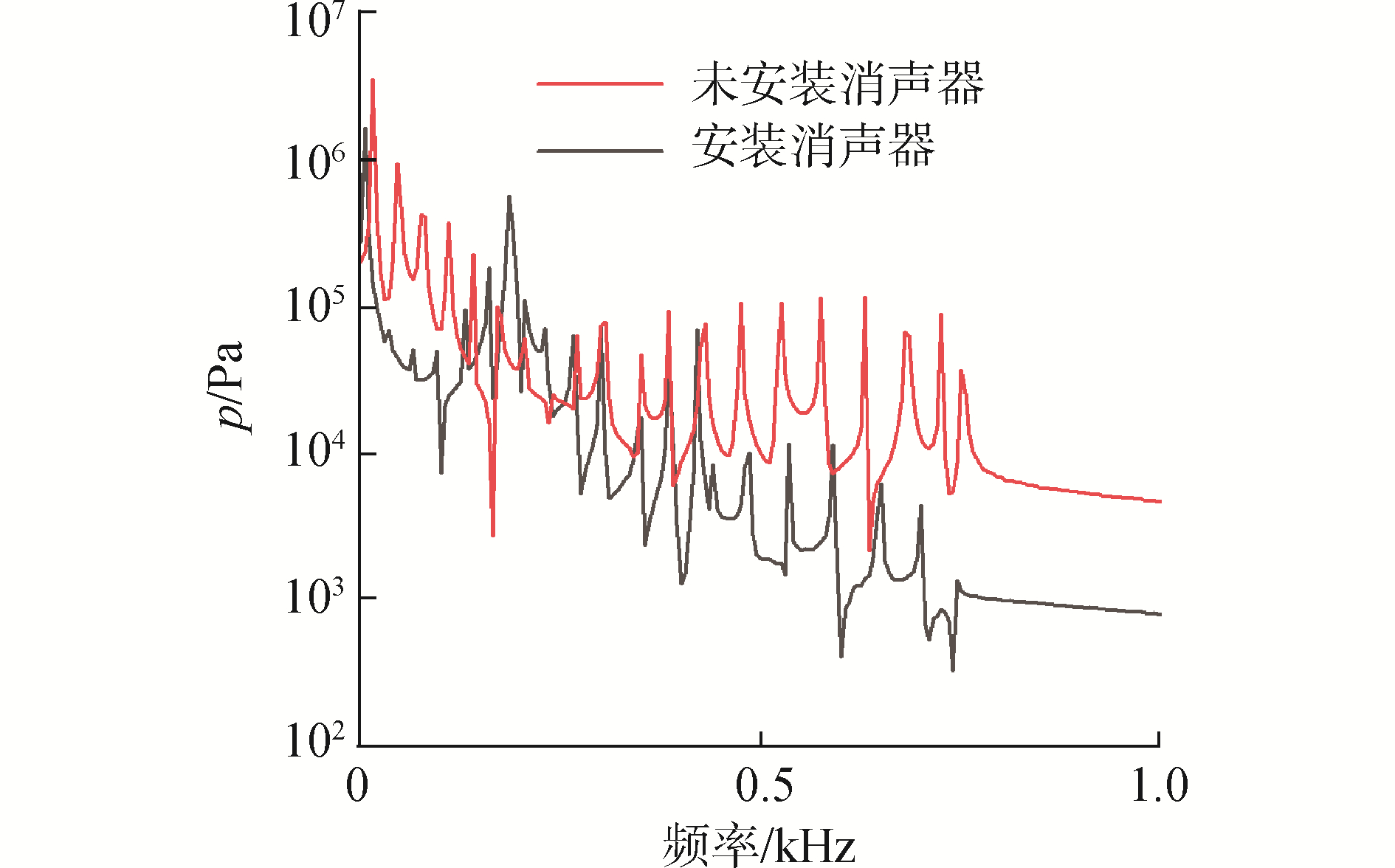
对消声器出口位置产生的压力波进行频域分析,分析结果如图 9所示。
|
Download:
|
| 图 9 频域水锤压力抑制对比 Fig. 9 Comparison chart of water hammer pressure suppression by frequency domain | |
低频处峰的个数明显减少,且峰值也有所下降。可以看出低频及中高频的压力波都得到了良好的抑制效果。但在185 Hz附近产生了新的峰值。说明消声器在降低了压力幅值的同时,在闭合管路中形成了新的峰值。压力波抑制情况与消声器的传递损失特性也有较好的对应。在实际的系统中,由于管路中还包含体积极大的水舱,可以避免压力波往复传递,实际的抑制效果应较图中更理想。
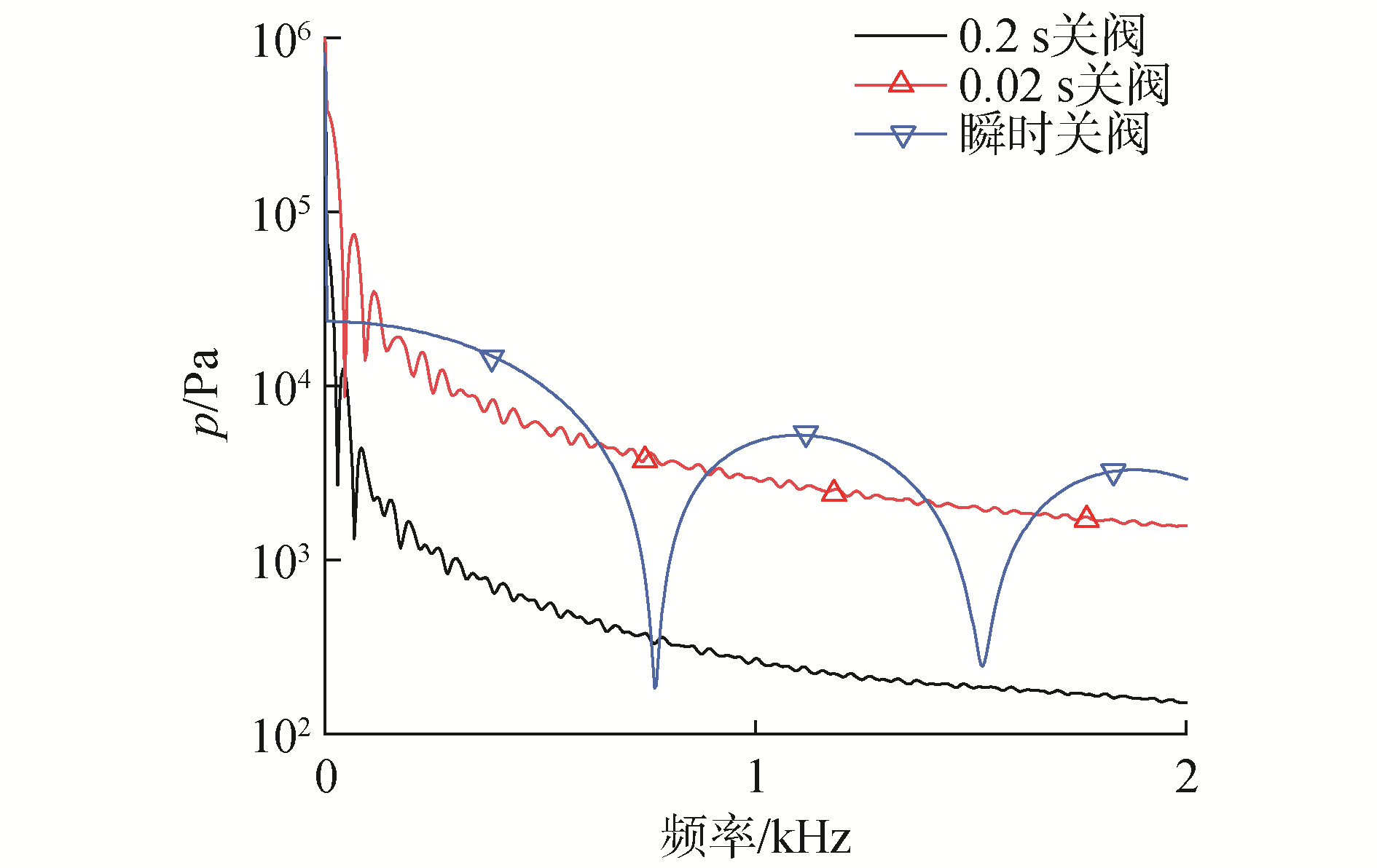
3.1.2 耦合模型计算结果利用阶跃函数和斜坡函数对关阀时间进行控制。傅里叶变换后如图 10所示。
|
Download:
|
| 图 10 耦合模型计算结果 Fig. 10 Calculation results of coupling model | |
将耦合模型计算结果与一维模型计算结果进行时域上压力峰值的对比,如表 4所示。
| 表 4 仿真时域结果对比 Table 4 Comparison of simulation result by time domain |
水锤模块计算的结果在未安装消声器的直管路中与耦合模型结果保持一致,说明了2种方法的对照性良好。
可以观察到压力峰值的规律与一维模型仿真的结果基本吻合,但在流场的模型中,由于入口边界的设置问题,压力波在阀门处产生后并没有在管路中来回传播,故没有形成周期性的压力波,且三维模型中消声器的结构完整,理应有更好的压力波抑制效果。
3.2 环状气囊消声器的效果及验证试验思路无论时域计算结果还是频域对比都表现出环状气囊消声器在压力脉动抑制上的良好效果,而不同计算方法的结果也都支持这一点。从仿真的角度基本可以证明其对水锤产生的压力波抑制效果良好。
进一步的研究应当从实验验证的角度开展,稳态工况下,该消声器的声学性能已有如上文所述的大量实验数据作为参考,可以确定其消减压力脉动的能力。但环状气囊消声器对于瞬态压力波的实际抑制效果还需要专门的实验进行验证。与验证声学性能的插入损失试验相比,由于压力脉动的特点不同,实验方案在方法步骤和测试传感器选用上都应做出较大调整。测试指标应主要关注消声器出口压力,阀门及消声器法兰位置振动以及空气噪声。通过上述指标在安装消声器前后的测试结果对比,判断安装环状气囊消声器的措施对水锤压力波直接抑制效果、水锤危害管路的治理效果以及船上人员舒适性改善情况。
4 结论1) 环状气囊消声器发挥抑制压力脉动的作用可以对水锤波产生良好的抑制效果,其计算结果表明,在实际中存在良好的应用可能。
2) 环状气囊消声器的压力脉动抑制能力经过大量实验验证,在与纵倾平衡系统相近的高管压工况中依然能够表现出良好的性能。
3) 与常用的广义特征线法相比,多维度耦合模型计算瞬变流更适用于纵倾平衡系统调水管路的结构特点。
4) 相对于一维模型,耦合建模更接近实际结构,也会提高计算成本和建模难度。COMSOL中“管接头”接口可以实现管道流的一维模型与单相流的三维模型之间的耦合,易于实现建模;而几类耦合算子设定较为复杂,但在求解中具有更好的收敛性;2种设定方式都可以实现多维度模型耦合,选用时应根据具体情况判断。
纵倾平衡系统模型耦合的计算结果与相关研究人员描述的现象相符,但仍需在下一步的试验工作中得到更多的数据,以验证该方法的可行性、精确性。若需深入探究纵倾平衡系统水锤的危害,则需要通过流固耦合计算管路振动等方法。与之相关的可靠性研究,也有较高的研究价值。
| [1] |
沈位, 柳贡民, 李俊益.纵倾平衡系统噪声及控制分析[C]//第十七届船舶水下噪声学术讨论会论文集.衢州, 2019: 1-7. SHEN Wei, LIU Gongmin, LI Junyi. Trim balance system noise and control analysis[C]// Academic Papers Collection of The Chinese Society of Naval Architects And Marine Engineers.Quzhou, 2019: 1-7. (  0) 0)
|
| [2] |
杨建东. 实用流体瞬变流[M]. 北京: 科学出版社, 2018.
(  0) 0)
|
| [3] |
苏尔皇. 管道动态分析及液流数值计算方法[M]. 哈尔滨: 哈尔滨工业大学出版社, 1985: 24-65.
(  0) 0)
|
| [4] |
孙培德, 杨东全, 陈奕柏. 多物理场耦合模型及数值模拟导论[M]. 北京: 中国科学技术出版社, 2001: 216-220. SUN Peide, YANG Dongquan, CHEN Yibai. Introduction to coupling models for multiphysics and numerical simulations[M]. Beijing: China Science and Technology Press, 2001: 216-220. (  0) 0)
|
| [5] |
张希贤, 唐荣庆. 潜艇装置及系统[M]. 上海: 上海交通大学出版社, 1996: 260-271.
(  0) 0)
|
| [6] |
国防科学技术工业委员会. GJB 38.45-87, 常规动力潜艇系泊、航行试验规程-纵倾平衡系统设计方法[S].北京: 国防科学技术工业委员会, 1987. COSTIND. GJB 38.45-87, Regulations for dock trials and sea trials of conventionally-powered submarines submarine trim system[S]. Beijing: COSTIND, 1987. (  0) 0)
|
| [7] |
国防科学技术工业委员会. GJB 272-87, 潜艇纵倾平衡系统设计方法[S].北京: 国防科学技术工业委员会, 1987. COSTIND. GJB 272-87, Design method for submarine trim system[S]. Beijing: COSTIND, 1987. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


