2. 中国地震局地震工程与工程震动重点实验室, 黑龙江 哈尔滨 150080
2. Key Laboratory of Earthquake Engineering and Engineering Vibration of China Earthquake Administration, Harbin 150080, China
地震动输入是结构进行动力分析的前提,对结构如何有效进行抗震设计具有重要的意义。一般在对结构进行动力分析时采用一致地震动输入,这种输入条件对于尺寸较小的结构来说其影响可以忽略不计,但对于超长、大跨结构,例如跨海大桥、机场、体育馆、输电塔等而言,由于地震波所引起的地面运动在本质上是一种随时间和空间而变化的现象。若仍采用一致输入必然会影响最终结构,不利于抗震设计。且多位学者已经证明地震动的空间性对大跨结构具有较大的影响[1-2]。理想状态下,应用同一次地震所触发的台阵中不同台站的地震记录来对结构进行分析是最为所接受的,但全球范围内,台阵数量稀少且台阵中的不同台站的间距及方位并不一定满足结构的尺寸。因此,如何形成一套较为合理的空间相关多点地震动的合成方法对于抗震设计领域来说是至关重要的。
针对如何有效进行空间相关多点地震动的合成,近几年来国内外众多学者进行了相关研究。Hao[3]提出了空间地震动的合成方法,该法认为所合成的每个点与之前生成的每个点相关;Deodatis[4]提出了一种在概念上与Hao类似的方法,主要针对功率谱密度函数(PSDF)进行了迭代升级;而后屈铁军[5-6]对其方法进行相应的改变,认为每个点不仅仅与其后所生成的各个点相关,而与所生成其余各点均相关。部分专家[7-9]通过引入小波函数来生成频谱兼容的人工地震记录。基于非均匀场地,引入了场地转化函数来实现不同场地类型下的空间地震动合成[10-12]。在实现频谱虽然众多学者已经对合成空间相关地震动的方法做了很大的改进,合成方法也日趋成熟。但绝大部分的方法合成方法并未涉及实际地震的因素,仅仅是通过规范中的目标设计谱或功率谱模型,这就使得所合成的地震动记录缺乏实际地震记录的特性;更重要的是,抗震规范中仅给出了包络函数2个时间点的大小[13],却并未给出其与地震动的持时的关系。这就很容易导致地震动的尾波过长或过短,很明显不符合实际地震动的波形。因此,本文通过引入实际地震记录的波形来解决该缺陷。
针对该不足,本文通过引入实测记录将目标设计谱分解为实测地震动加速度反应谱及两者之间的校正项。由于所选记录对最终模拟结果影响较大,因此需严格按照选波流程进行地震动的选取,然后基于所选记录进行空间地震动模拟。而本文工作重心为方法的实施,为简化流程略过选波流程,随机选取日本K-net网站中某一记录,通过一算例,分别合成距其50 m、100 m 2点的地震动时程。然后基于该法,分别研究了不相干效应、行波效应对合成空间地震动的影响程度。
1 空间相关多点非平稳地震动合成 1.1 基于随机振动理论的功率谱合成地震动的空间合成由加速度功率谱密度函数PSD计算。而《规范》给出的是反应谱并非功率谱,为了与《规范》对应,采用迭代求解方法,由规范反应谱生成功率谱[14]。具体步骤如下:
1) 近似地选择输入PSD初始值,Si0(ωk),k=0, 1, …, n,其中n表示在有效频域内描述PSD曲线的离散频率个数。为了减少迭代次数,功率谱与反应谱的近似公式作为输入功率谱的初始值:
| $ S\left( {{\omega _k}} \right) = - \frac{\xi }{{{\rm{ \mathsf{ π} }}{\omega _k}}}{\rm{RS}}{{\rm{A}}^2}\left( {{\omega _k}} \right)/\ln \left( { - \frac{{\rm{ \mathsf{ π} }}}{{{\omega _k}T}}\ln q} \right) $ | (1) |
式中:ξ为阻尼比;RSA为记录的加速度反应谱;T为地震动持时;q为概率系数,通常q≥0.85,本文取其值为0.85。
2) 对于阻尼比为ξ、圆频率为ωk的单自由度体系,其绝对加速度峰值:
| $ {A_m}({\omega _k}) = p{\sigma _0}({\omega _k}) $ | (2) |
式中:p、σ0为绝对加速度过程的峰值因子及均方根。
3) 通过引入拟合优度指数Fg来判定其与目标设计谱之间的吻合度,各圆频率下Fg取值:
| $ {\rm{Fg}}\left( {{\omega _k}} \right) = 10{\rm{exp}}\left\{ { - {{\left[ {\frac{{({\rm{RSA}}\left( {{\omega _k}} \right) - {A_m}\left( {{\omega _k}} \right)}}{{\min \left[ {{\rm{RSA}}\left( {{\omega _k}} \right),{A_m}\left( {{\omega _k}} \right)} \right]}}} \;\;\right]}^2}} \right\} $ | (3) |
并以各圆频率下Fg的均值作为最终结果,当其大于9.9时即可输出结果S(ω),否则继续进行迭代,直到满足条件为止:
| $ S_i^{\left( {k + 1} \right)}\left( {{\omega _k}} \right) = S_i^{\left( k \right)}\left( {{\omega _k}} \right) \cdot {\left( {\frac{{{\rm{RSA}}\left( {{\omega _k}} \right)}}{{{A_m}\left( {{\omega _k}} \right)}}} \right)^2} $ | (4) |
以上为基于随机振动理论求解目标功率谱的迭代过程。在Rosenblueth提出的“平方和的平方根SRSS阵型组合的基础上,将目标设计谱分解为2种因素的叠加,分别是已知地震动记录的加速度反应谱RSAR(ω,ξ)和为匹配功率谱密度函数的一个校正项RSAS(ω,ξ)。其中α为记录地震的放缩系数,其目的是在不超过目标设计谱的前提下,使所生成的空间地震动含有实际地震动记录的程度达到最大化,分解过程:
| $ {\rm{RSA}}\left( {\omega ,\xi } \right) = \sqrt {{\alpha ^2}{\rm{RS}}{{\rm{A}}^R}{{\left( {\omega ,\xi } \right)}^2} + {\rm{RS}}{{\rm{A}}^S}{{\left( {\omega ,\xi } \right)}^2}} $ | (5) |
因此,最终合成的加速度时程可表示为2种因素的叠加:
| $ u\left( {\rm{t}} \right) = \alpha {u^R}\left( t \right) + {u^S}\left( t \right) $ | (6) |
式中uR(t)、uS(t)分别为记录项与校正项。
1.2 空间相关多点平稳地震动的合成公式基于1.1节所生成的目标功率谱S(ω),由于本文所用到的空间尺寸是一定的,各点间的自功率谱密度函数相差不大,这里可以假设每个测点都有相同的加速度功率谱密度函数,即S(ω)。因此,所要合成的各点地震动的自功率谱及各点之间的互功率谱可用功率谱矩阵来表示。所组成的多点地震动功率谱矩阵:
| $ S({\rm{i}}{\omega _k}) = \left[ {\begin{array}{*{20}{c}} {{S_1}({\omega _k})}&{{S_{12}}({\rm{i}}{\omega _k})}& \cdots &{{S_{1n}}({\rm{i}}{\omega _k})}\\ {{S_{21}}({\rm{i}}{\omega _k})}&{{S_2}({\omega _k})}& \cdots &{{S_{2n}}({\rm{i}}{\omega _k})}\\ \vdots & \vdots & \vdots & \vdots \\ {{S_{n1}}({\rm{i}}{\omega _k})}&{{S_{n2}}({\rm{i}}{\omega _k})}& \cdots &{{S_n}({\omega _k})} \end{array}} \right] $ | (7) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {S_{nm}}({\rm{i}}{\omega _k}) = \sqrt {{S_n} \times {S_m}} \cdot {\gamma _{nm}}({\rm{i}}{\omega _k}) = \\ \sqrt {{S_n} \times {S_m}} \times \left| {{\gamma _{nm}}({\rm{i}}{\omega _k})} \right| \cdot \exp \left( { - {\rm{i}}\omega \frac{{{d_{nm}}}}{{{v_{app}}}}} \right) \end{array} $ | (8) |
式中:γnm(iωk)为所选择的相干函数模型;|γnm(iωk)|为迟滞相干函数,用来表征2点地震动的相关性;ωdnm/vapp为2点地震动的相位角,用来表征其行波效应;dnm表示2点间沿波传播方向的投影的距离;vapp为视波速。由于该矩阵为Hermite矩阵,可对其进行cholesky分解,将其分解为下三角矩阵L(iωk)和上三角矩阵LH(iωk)。
每个测点的平稳地震动合成公式为:
| $ \begin{array}{l} {u_i}\left( t \right) = \mathop \sum \limits_{m = 1}^i \mathop \sum \limits_{k = 1}^N {A_{im}}\left( {{\omega _k}} \right){\rm{cos}}\left[ {{\omega _k}t + {\theta _{im}}\left( {{\omega _k}} \right) + {\varphi _k}} \right]\\ {A_{nm}} = \sqrt {4\Delta \omega } \left| {{l_{nm}}\left( {i{\omega _k}} \right)} \right|,\;{\theta _{nm}} = {\rm{arctan}}\frac{{{\rm{Im}}\left[ {{l_{nm}}\left( {{\rm{i}}{\omega _k}} \right)} \right]}}{{{\rm{Re}}\left[ {{l_{nm}}\left( {{\rm{i}}{\omega _k}} \right)} \right]}} \end{array} $ | (9) |
式中:Aim(ωk)、θim(ωk)表示第m点与第i点相关的第k个频率分量的幅值和相位角;φk表示随机相位角,在(0, 2π)区间上均匀分布。
1.3 空间地震动的非平稳化实际地震记录是非平稳的,工程中通常引入规范中的包络函数φ(t)与上述所求的平稳过程相乘以实现地震动的非平稳性,包络函数表示为:
| $ \varphi (t) = \left\{ \begin{array}{l} {\left( {t/{t_1}} \right)^2},t < {t_1}\\ 1,{t_1} \le t < {t_2}\\ {\rm{exp}}[ - \beta (t - {t_2})]\;,t \ge {t_2} \end{array} \right. $ | (10) |
式中:t1、t2以所选记录的Husid函数在5%和95%时所对应的时刻代替规范中的固定值。
理论上,通过目标功率谱生成的地震动加速度反应谱与目标反应谱存在的差异并不大,满足式(4)大于等于9.9。如果结果不满意,可继续通过上述迭代公式继续进行一次迭代,一般情况下,迭代一次后的结果可以很好的符合目标反应谱。
2 合成实例选择7度多遇地震、2类场地、第1组地震分组,其对应反应谱的水平地震影响系数最大值αmax=0.08,特征周期Tg=0.25 s,结构阻尼比ξ=0.05。根据第1.1节中所描述的分解目标设计谱原理引入一实测地震动。以日本K-net网站中2016-04-15(UTC)日本熊本县发生的地震为例,并选取该次地震中EHM016台站所记录的EW分量。该记录时程及其Husid函数、空间各点的位置关系如图 1所示,其中点1为地震波首次传播到达的位置。由于地震波是从震源向四周传播,因此可近似认为场地上的某点与震中的连线即为地震波的传播方向。即由点1向点2、3传播的方向即为视波速的方向;通过Husid函数所求的t1、t2、β分别为15.61、40.96、0.153 9 s。考虑到行波效应和不相干效应,令视波速vapp=400 m/s,相干函数模型采用Abrahamson模型[15],该模型表达为:
| $ \begin{array}{l} {\rm{arctanh}}\left| {\gamma \left( {f,d} \right)} \right| = \left( {{a_1} + {a_2} \cdot d} \right) \cdot \\ {\rm{\{ exp}}\left[ {({b_1} + {b_2} \cdot d} \right)f{\rm{]}} + 1/3{f^c}\} + k \end{array} $ | (11) |

|
Download:
|
| 图 1 实测记录及其Husid函数 Fig. 1 The calculation process of synthetic spatial correlation ground motion | |
式中:f为频率,d为2台站间的距离;a1、a2、b1、b2、c、k为拟合参数,Abrahamson[15]已求出各参数取值分别为2.54、-0.012、-0.115、-0.000 84、-0.878、0.35。
模拟过程中首先将目标设计谱分为由实测记录的加速度反应谱RSAR(ω,ξ)及校正项的加速度反应谱RSAS(ω,ξ)。由式(7)求得α=3.63,将记录加速度反应谱放缩后,通过式(5)求得校正项反应谱,其表达形式如图 2(a)所示,将校正项的反应谱作为临时目标谱进行功率谱迭代,迭代结果如图 2(b)所示。其Fg为9.19不满足输出条件,黑色点划线为通过随机振动理论迭代1次后的结果,此时Fg为9.92, 满足最终的输出条件;图 2(c)为迭代最终结果所代表的临时目标功率谱。由图 2(b)所示迭代过程可知,由近似公式所求结果与目标值较为接近,但仍存在一定误差,进而通过迭代满足条件后所求结果几乎与目标值吻合。

|
Download:
|
| 图 2 目标谱迭代过程及所生成的目标功率谱 Fig. 2 The iterative process of target spectrum and the generated target power spectrum | |
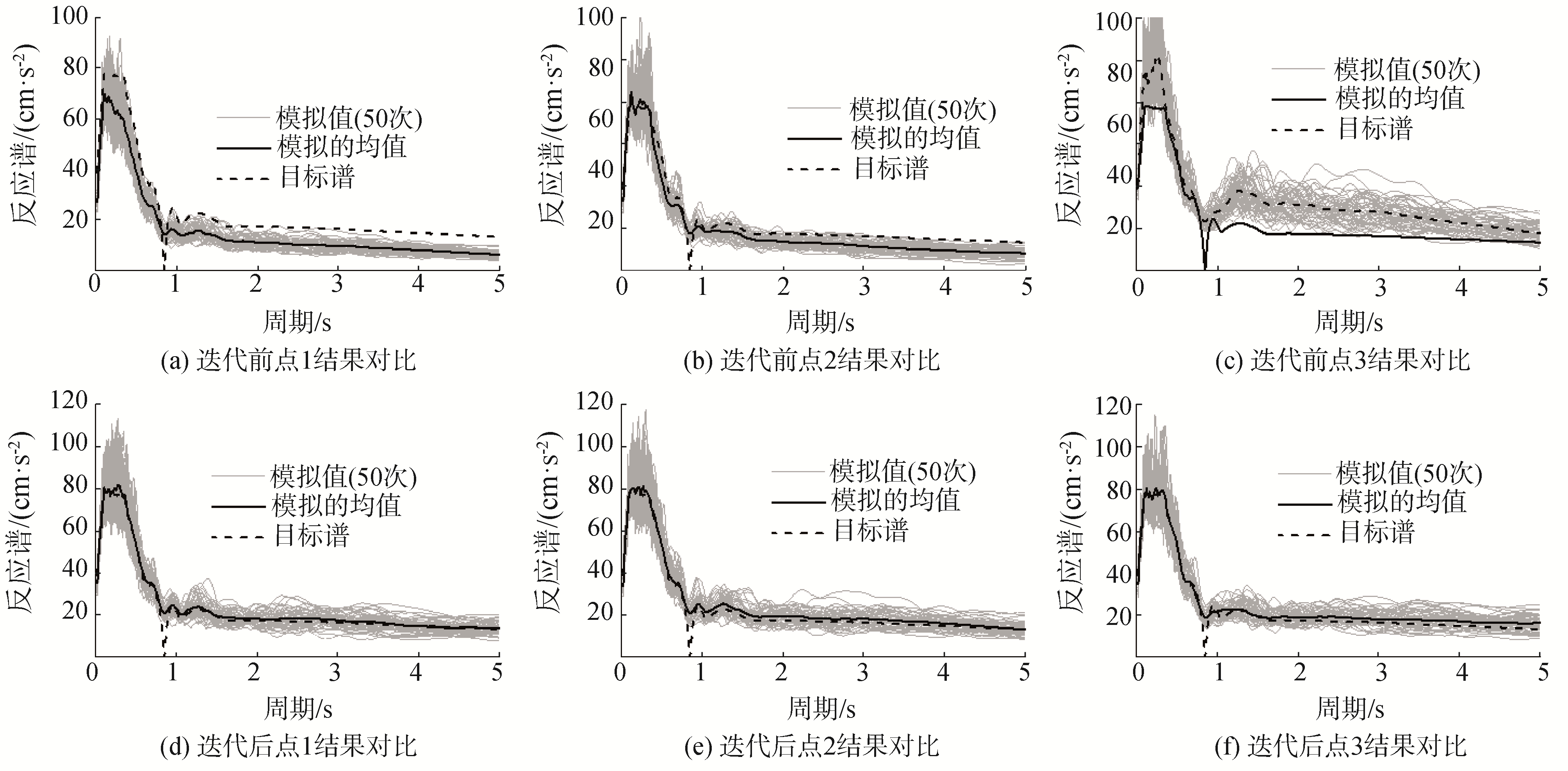
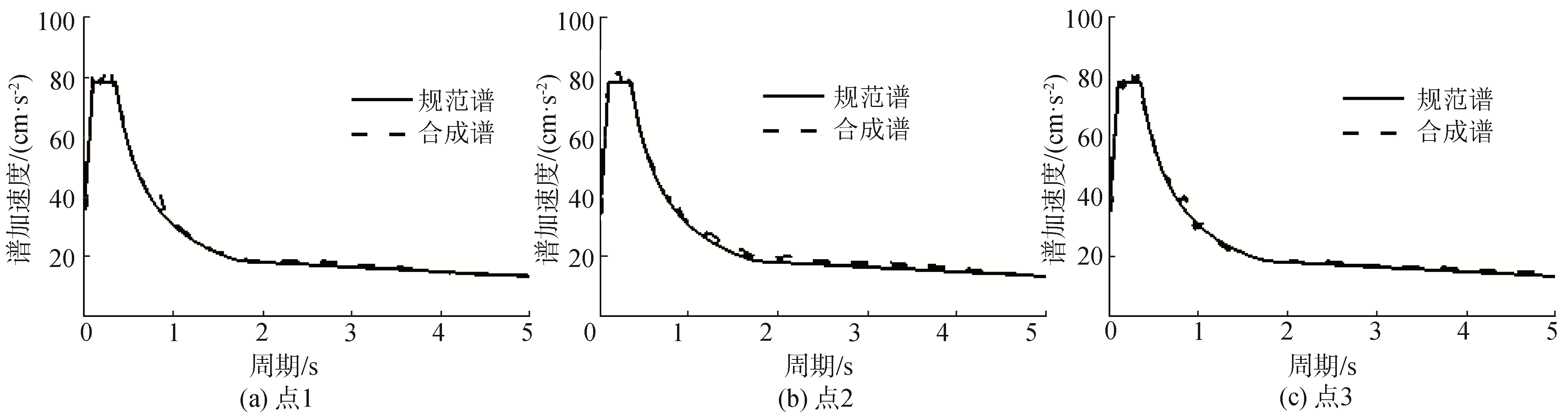
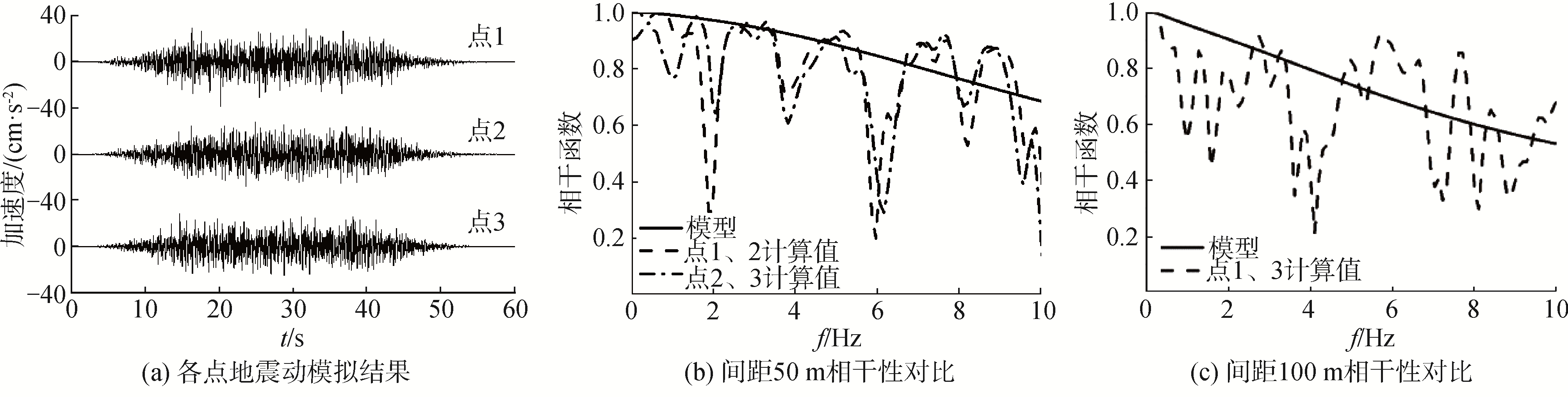
在所求临时目标功率谱基础上,通过第1.2节所述进行空间地震动模拟,所模拟各点的反应谱与目标谱的对比情况如图 3所示,图 3(a)~(c)为通过临时目标设计谱生成的空间地震动时程反应谱,可以发现点1、2与目标谱相比较低、点3较高,分别各进行一次迭代后,匹配情况分别如图 3(d)~(f)所示,可以发现迭代一次后的反应谱可以很好的符合临时目标谱。将临时目标谱与实测反应谱叠加后,最终与规范设计谱的对比情况如图 4所示,合成的加速度时程及其各点相干函数与目标值对比如图 5所示,从图中可以看出,不同地震动之间的相干函数计算值与目标值吻合较好。
|
Download:
|
| 图 3 合成地震动反应谱与校正项反应谱对比 Fig. 3 Compare synthetic ground motion response spectrum with correction term spectrum | |
|
Download:
|
| 图 4 规范设计谱的最终对比情况 Fig. 4 Final comparison of specification design spectrum | |
|
Download:
|
| 图 5 合成的加速度时程及相干函数对比 Fig. 5 The synthetic acceleration time history and the comparision of coherence funciton | |
在多点地震动合成过程中,导致地震动空间变化的重要因素大致分为以下3类:1)场地效应,主要由于不同场地的地质条件不同引起地震波的振幅和频率变化;2)不相干效应,主要由于地震波在不同土层介质中传播的散射和反射所引发;3)行波效应,主要由于同所致。这3种因素分别与功率谱函数S(ω)、迟滞相干函数|γnm(iωk)|、视波速vapp有关。其中迟滞相干函数主要采用现有的相干函数模型;视波速可通过实测获得,对于大部分无法进行实测的场地,可以近似通过规范中各场地类型下的剪切波速范围来代替视波速。
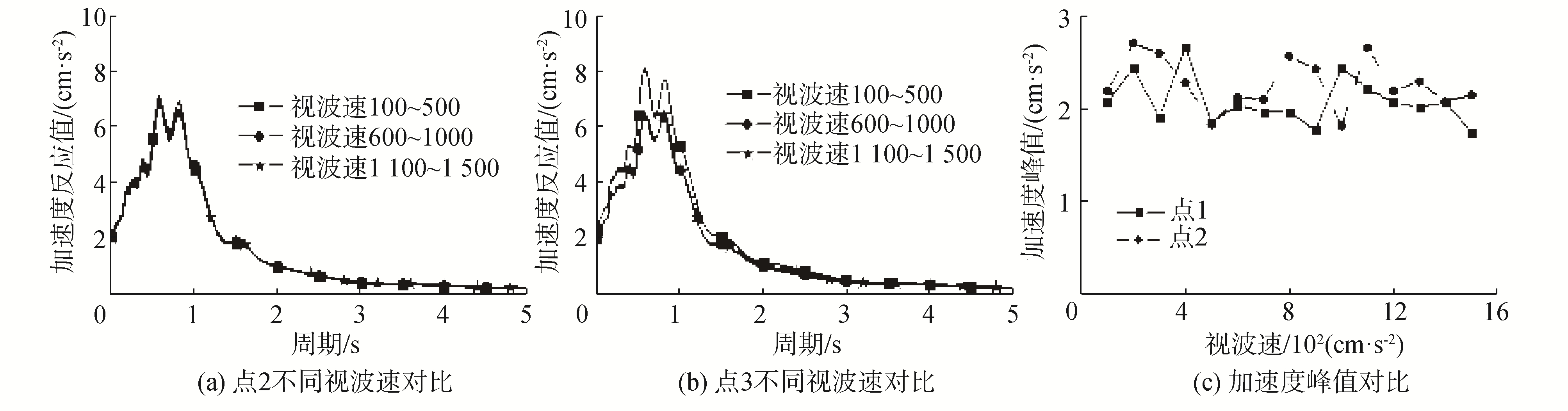
由于本文中局部区域所用各点的自功率谱相同,因此忽略了场地效应对结果的印象。为进一步研究视波速、所选取相干函数模型对空间地震动合成的影响,基于本文所应用的空间地震动合成方法,分别选用不同大小的视波速或不同相干函数模型同时进行合成实例中3点的空间地震动合成。由于在合成过程中,由式(9)可以看出点1并没有考虑不相干效应和行波效应,仅仅通过该点的目标功率谱合成。因此,只通过对比点2、点3在不同参数下的结果来验证视波速及相干函数模型的影响。其中,视波速的大小选用100~1 500 m/s以100为步长的15组,其中,点2、3在不同视波速下的对比如图 6所示;同时除本文合成实例中选取Abrahamson模型外,又选取了4种比较常用的相干函数模型,表达式如下表 1所示,其中,d表示两侧点间距,ω为圆频率,为统一变量,视波速统一设为400 m/s,点2、3在不同相干函数模型下的对比如图 7所示。
|
Download:
|
| 图 6 不同视波速下所合成的空间地震动 Fig. 6 The spatial ground motion synthesized under different apparent wave velocities | |
| 表 1 所选取模型及其表达形式 Table 1 The selected model and its expression form |

|
Download:
|
| 图 7 不同相干函数模型下所合成的空间地震动 Fig. 7 Spatial seismic motions synthesized under different coherent function models | |
由图 6可以看出,点2在不同视波速下所合成的加速度反应谱除少数情况下存在一定偏差,在整体上并无明显变化趋势;点3在100~500 m/s内所合成的加速度反应谱在中短周期上要略大于其他范围,且在超过500 m/s后,视波速的增大对加速度影响减弱;所合成的加速度峰值仅在一定范围内波动,无明显变化趋势。造成行波效应对空间地震动合成无明显影响的原因可能是由于局部区域内各合成点的距离有限,地震波到达不同点的时间差异并不明显,且随着视波速增大,这种差异趋向于零。由图 7可以看出,点2在采用不同相干函数模型下所合成的加速度反应谱在中短周期内存在微弱的局部性差异,在长周期范围内无明显影响;点3在采用不同相干函数模型下所合成的加速度反应谱在中短周期内存在明显差异,且这种差异明显强于当视波速较大情况下下所造成的差异,在长周期范围内差异相对较弱;同时,点2、3所合成的加速度峰值在采用不同相干函数模型下也是不同的。
另一方面,点3对参数改变的敏感性要强于点2,这可能是由于在进行空间地震动合成时,在生成第n个点的时候,只考虑其与已生成的前n-1个点的地震动相关性,因此在合成过程中,随着生成个数的增加,参数改变所造成的影响也呈现叠加的趋势。
综上分析,可以得出,在合成空间地震动的过程中,不相干效应发生变化时对结果的影响要强于行波效应发生变化时对结果的影响。
4 结论1) 通过引入实测记录,将目标设计谱分解为实测记录反应谱及两者之间校正项,并以所选记录的Husid函数确定地震动非平稳化的时间参数代替包络函数中固定的时间参数。以此所模拟地震动在波形上能良好保持实测记录的特性,同时不同点地震动之间满足空间相关性要求。而选用不同记录对结果影响较大,后续工作需与选波工作对接以选取合理记录。
2) 通过设置一系列不同视波速及相干函数模型,对比发现不相干效应发生变化时对结果的影响要强于行波效应发生变化时对结果的影响;而且在依次合成各点的过程中,由于每点与前面已合成各点相互关联,因此各效应的影响呈现递增趋势。
| [1] |
BILICI Y, BAYRAKTAR A, SOYLUK K, et al. Stochastic dynamic response of dam-reservoir-foundation systems to spatially varying earthquake ground motions[J]. Soil dynamics and earthquake engineering, 2009, 29(3): 444-458. DOI:10.1016/j.soildyn.2008.05.001 (  0) 0)
|
| [2] |
ZHANG Y H, LI Q S, LIN J H, et al. Random vibration analysis of long-span structures subjected to spatially varying ground motions[J]. Soil dynamics and earthquake engineering, 2009, 29(4): 620-629. DOI:10.1016/j.soildyn.2008.06.007 (  0) 0)
|
| [3] |
HAO H, OLIVEIRA C S, PENZIEN J. Multiple-station ground motion processing and simulation based on SMART-1 array data[J]. Nuclear engineering and design, 1989, 111(3): 293-310. DOI:10.1016/0029-5493(89)90241-0 (  0) 0)
|
| [4] |
DEODATIS G. Non-stationary stochastic vector processes: seismic ground motion applications[J]. Probabilistic engineering mechanics, 1996, 11(3): 149-167. DOI:10.1016/0266-8920(96)00007-0 (  0) 0)
|
| [5] |
屈铁军, 王前信. 空间相关的多点地震动合成(I)基本公式[J]. 地震工程与工程振动, 1998, 18(1): 8-15. QU Tiejun, WANG Qianxin. Simulation of spatial correlative time histories of multi-point ground motion, Part I: fundamental formulas[J]. Earthquake engineering and engineering vibration, 1998, 18(1): 8-15. DOI:10.3969/j.issn.1000-1301.1998.01.002 (  0) 0)
|
| [6] |
屈铁军, 王前信. 空间相关的多点地震动合成(Ⅱ)合成实例[J]. 地震工程与工程振动, 1998, 18(2): 25-32. QU Tiejun, WANG Qianxin. Simulation of spatial correlative time histories of multi-point ground motion, Part Ⅱ: application of fundamental formulas[J]. Earthquake engineering and engineering vibration, 1998, 18(2): 25-32. DOI:10.3969/j.issn.1000-1301.1998.02.004 (  0) 0)
|
| [7] |
MUKHERJEE S, GUPTA V K. Wavelet-based generation of spectrum-compatible time-histories[J]. Soil dynamics and earthquake engineering, 2002, 22(9/12): 799-804. (  0) 0)
|
| [8] |
CECINI D, PALMERI A. Spectrum-compatible accelerograms with harmonic wavelets[J]. Computers & structures, 2015, 147: 26-35. (  0) 0)
|
| [9] |
SARKAR K, GUPTA V K, GEORGE R C. Wavelet-based generation of spatially correlated accelerograms[J]. Soil dynamics and earthquake engineering, 2016, 87: 116-124. DOI:10.1016/j.soildyn.2016.05.005 (  0) 0)
|
| [10] |
BI Kaiming, HAO Hong. Influence of irregular topography and random soil properties on coherency loss of spatial seismic ground motions[J]. Earthquake engineering and structural dynamics, 2011, 40(9): 1045-1061. DOI:10.1002/eqe.1077 (  0) 0)
|
| [11] |
BI Kaiming, HAO Hong. Modelling and simulation of spatially varying earthquake ground motions at sites with varying conditions[J]. Probabilistic engineering mechanics, 2012, 29: 92-104. DOI:10.1016/j.probengmech.2011.09.002 (  0) 0)
|
| [12] |
WU Yongxin, GAO Yufeng, ZHANG Ning, et al. Simulation of spatially varying ground motions in v-shaped symmetric canyons[J]. Journal of earthquake engineering, 2016, 20(6): 992-1010. DOI:10.1080/13632469.2015.1010049 (  0) 0)
|
| [13] |
薛素铎, 王雪生, 曹资. 基于新抗震规范的地震动随机模型参数研究[J]. 土木工程学报, 2003, 36(5): 5-10. XUE Suduo, WANG Xuesheng, CAO Zi. Parameters study on seismic random model based on the new seismic code[J]. China civil engineering journal, 2003, 36(5): 5-10. DOI:10.3321/j.issn:1000-131X.2003.05.002 (  0) 0)
|
| [14] |
LIN J H, ZHANG Y H, LI Q S, et al. Seismic spatial effects for long-span bridges, using the pseudo excitation method[J]. Engineering structures, 2004, 26(9): 1207-1216. DOI:10.1016/j.engstruct.2004.03.019 (  0) 0)
|
| [15] |
ABRAHAMSON N A, SCHNEIDER J F, STEPP J C. Empirical spatial coherency functions for application to soil-structure interaction analyses[J]. Earthquake spectra, 1991, 7(1): 1-27. DOI:10.1193/1.1585610 (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


