2. 沈阳工业大学 机械工程学院, 辽宁 沈阳 110870
2. School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870, China
在针对换热器[1]、空调系统[2]、电子设备冷却[3]等众多工程设计和能源问题的研究中,被分析流体往往受到外力和温度的共同影响,多以混合对流形式存在。合理设计和布置设备结构不仅可以有效加大能源利用率,还能够减少重要零件的损耗。利用方腔模型可以分析多种复杂场内流体的运动特性和传热规律[4]。在针对混合对流的研究中,也多采用具有内部加热元件的开口方腔模型进行模拟。Radhakrishnan等[5]通过实验证明了模型的可靠性,并指出采用数值模拟方法有利于优化热流表现。孙猛等[6]在不同的格拉晓夫数、瑞利数以及纵横比的条件下,研究了外界来流对方腔内混合对流换热的影响。Karimi等[7-8]建立了具有多个加热单元的复杂混合对流模型,并对热源的大小和位置进行了讨论。Chamkha等[9-10]借助于方腔模型对多种结构因素进行分析,研究结果表明,进、出流口的位置对混合对流的影响很大,在改善换热效率方面起着关键作用。
随着流体流动和换热机理研究的深入,新的数值计算方法也在不断涌现。格子Boltzmann方法(LBM)作为介观模拟算法的代表,在近几十年里发展迅速。与传统计算方法相比,LBM使用简化的动力学模型来处理微观过程,这使其在具有出色并行计算能力的同时能够更直观地表现粒子间的相互作用[11]。多参数弛豫时间(MRT)的引入也进一步提高了LBM的计算精度和稳定性[12]。目前,LBM主要通过多速度法[13]、多分布法[14]和混合法[15]对多场问题进行模拟,并在混合对流、辐射传热、双扩散对流等问题上得到了验证。
综上可以发现,在分析腔内热源对混合对流的影响时,研究工作主要集中在热元件的布置方式和尺寸上,而对热元件的形状特征很少提及。此外,内热源结构和外部方腔的开口位置共同变化下的流体和换热表现也很少被讨论。因此,本文采用结合MRT-LBM与有限差分法(FDM)的耦合算法[15],通过模拟流函数线图、等温线图和努赛尔数,探讨了不同进、出流口位置下热源形状变化对方腔内混合对流的流动、温度及换热特性的影响。
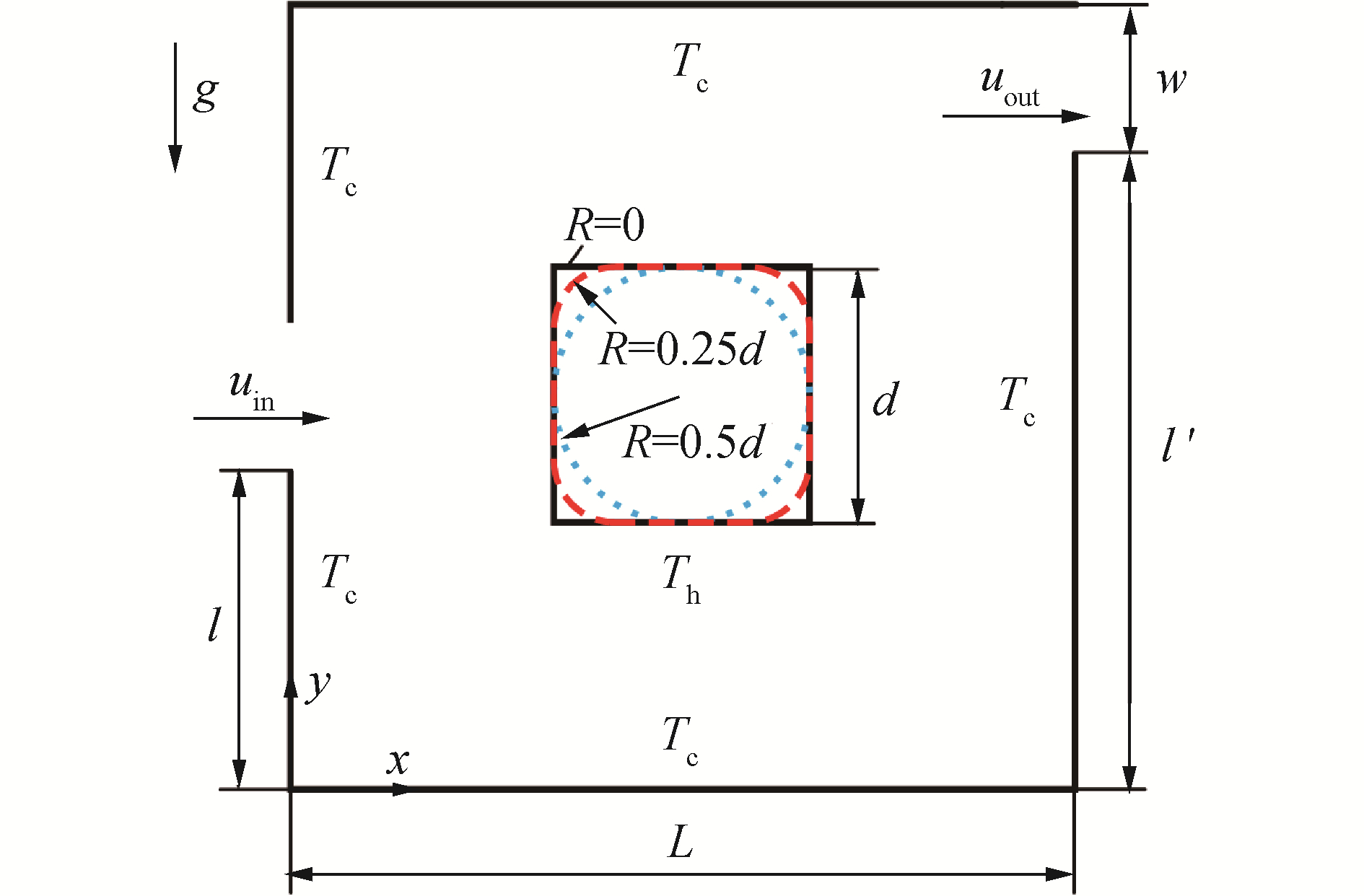
1 方腔内混合对流模型的建立 1.1 问题描述本文研究的含内热源的开口方腔结构如图 1所示。计算基于笛卡尔坐标系(x, y),坐标原点位于计算域的左下角。正方形腔体与等长宽中心加热元件的尺寸分别定义为L和d=0.3L。方腔内壁为具有温度Tc的恒温壁面,热源外表面的温度为Th(Th>Tc)。
|
Download:
|
| 图 1 物理模型 Fig. 1 Schematic of physical configuration | |
具有速度uin和温度Tin=Tc的流体通过左腔壁上尺寸为w=0.2L的进流口流入,最终从对侧壁面上相同尺寸的出流口以速度uout和温度Tout流出,流动过程中所受重力加速度为g。以进、出流口下边缘高度l和l′来定义开口位置,并分别在底部、中部和顶部开口下进行讨论。同时,引入圆角半径R来讨论加热元件的形状变化,R的值取为0、0.25d和0.5d。由图 1中可见,R=0和R=0.5d分别表示热源具有正方形截面和圆形截面。
1.2 计算模型本文采用普朗特数Pr为0.71的空气作为工作流体,认为它是满足Boussinesq近似的牛顿流体,并以稳态、层流运动。因此,可以得到混合对流的无量纲控制方程为:
| $ \frac{{\partial U}}{{\partial X}} + \frac{{\partial V}}{{\partial Y}} = 0 $ | (1) |
| $ \frac{{\partial U}}{{\partial \tau }} + U\frac{{\partial U}}{{\partial X}} + V\frac{{\partial U}}{{\partial Y}} = - \frac{{\partial P}}{{\partial X}} + \frac{1}{{Re}}\left( {\frac{{{\partial ^2}U}}{{\partial {X^2}}} + \frac{{{\partial ^2}U}}{{\partial {Y^2}}}} \right) $ | (2) |
| $ \frac{{\partial V}}{{\partial \tau }} + U\frac{{\partial V}}{{\partial X}} + V\frac{{\partial V}}{{\partial Y}} = - \frac{{\partial P}}{{\partial Y}} + \frac{1}{{Re}}\left( {\frac{{{\partial ^2}V}}{{\partial {X^2}}} + \frac{{{\partial ^2}V}}{{\partial {Y^2}}}} \right) + Ri\theta $ | (3) |
| $ \frac{{\partial \theta }}{{\partial \tau }} + U\frac{{\partial \theta }}{{\partial X}} + V\frac{{\partial \theta }}{{\partial Y}} = \frac{1}{{RePr}}\left( {\frac{{{\partial ^2}\theta }}{{\partial {X^2}}} + \frac{{{\partial ^2}\theta }}{{\partial {Y^2}}}} \right) $ | (4) |
式中:U=u/uin、V=v/uin、X=x/L、Y=y/L、θ=(T-Tc)/(Th-Tc)、P=p/ρuin2、τ=tuin/L、Re=uinL/υ、Ri=gβ(Th-Tc)L3/(Re2υ2)。u、v为沿x、y方向的速度分量;ρ为密度;p为压力;t为时间变量;T为温度;υ为运动粘度;β为热膨胀系数。
引入努赛尔数来表征热源表面的对流换热强度。由局部温度梯度可求得的局部努赛尔数Nu和平均努赛尔数Nuav分别为:
| $ Nu = - \frac{{\partial \theta }}{{\partial \mathit{\boldsymbol{n}}}} $ | (5) |
| $ N{u_{{\rm{av}}}} = \frac{1}{A}\int_A {Nu} {\rm{d}}A $ | (6) |
式中:n为沿热表面外法线方向的矢量;A为热源廓线周长。
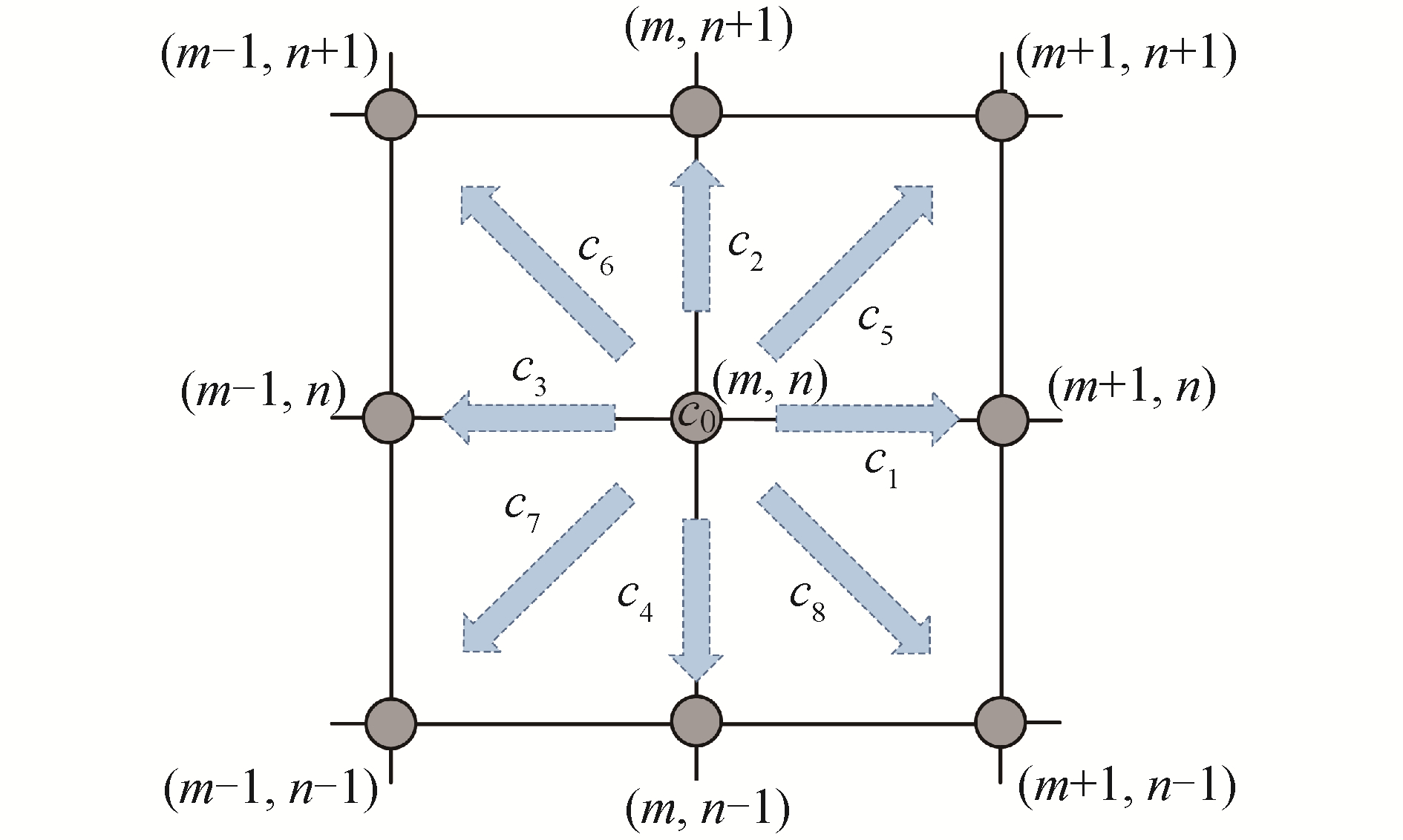
用于求解速度场的MRT-LBM采用如图 2所示的9速度模型(D2Q9),其演化方程为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{f}}(r + {c_i}\delta t,t + \delta t) - \mathit{\boldsymbol{f}}(r,t) = \\ - {\mathit{\boldsymbol{M}}^{ - 1}}\mathit{\boldsymbol{S}}(\mathit{\boldsymbol{m}}(\mathit{\boldsymbol{r}},t) - {\mathit{\boldsymbol{m}}^{{\rm{(eq)}}}}(\mathit{\boldsymbol{r}},t)) + \mathit{\boldsymbol{F}} \end{array} $ | (7) |
|
Download:
|
| 图 2 D2Q9模型 Fig. 2 Model of D2Q9 | |
式中:f(r, t)=(f0, f1, …, f8)T为位置r处的速度分布函数矢量;m(r, t)、m(eq)(r, t) 为矩和矩对应的平衡态;M为正交转换矩阵,并满足m=Mf;S为驰豫系数矩阵;δt、δx为单位长度的离散时间步长和格子间距;c=δx/δt为格子速率。
各个速度方向上的粒子速度集c,权重系数集ω和体积力F分别定义为:
| $ {c_i} = \left\{ {\begin{array}{*{20}{l}} {(0,0),}& \ \ \ \ {i{\rm{ = 0}}}\\ {c(\cos[(i - 1){\rm{ \mathsf{ π} }}/2],\sin[(i - 1){\rm{ \mathsf{ π} }}/2]),}&{{\rm{1}} \le {\rm{ }}i \le 4}\\ {\sqrt 2 c(\cos\frac{{(2i - 9){\rm{ \mathsf{ π} }}}}{4},\cos\frac{{(2i - 9){\rm{ \mathsf{ π} }}}}{4}),}&{{\rm{5}} \le {\rm{ }}i \le 8} \end{array}} \right. $ | (8) |
| $ \omega = \left( {\frac{{\rm{4}}}{{\rm{9}}}{\rm{, }}\frac{{\rm{1}}}{{\rm{9}}}{\rm{, }}\frac{{\rm{1}}}{{\rm{9}}}{\rm{, }}\frac{{\rm{1}}}{{\rm{9}}}{\rm{, }}\frac{{\rm{1}}}{{\rm{9}}}{\rm{, }}\frac{{\rm{1}}}{{{\rm{36}}}}{\rm{, }}\frac{{\rm{1}}}{{{\rm{36}}}}{\rm{, }}\frac{{\rm{1}}}{{{\rm{36}}}}{\rm{, }}\frac{{\rm{1}}}{{{\rm{36}}}}} \right) $ | (9) |
| $ \begin{array}{*{20}{c}} {{F_i} = 3{\omega _i}{\rho _0}\alpha (T - {T_0})g\frac{{{\mathit{\boldsymbol{c}}_i}\mathit{\boldsymbol{\bar y}}}}{{{c^2}}}}&{i{\rm{ = 0}},{\rm{ 1}},{\rm{ }} \cdots ,{\rm{ 8}}} \end{array} $ | (10) |
在LBM中,宏观物理量被视为分布函数的平均特性,因此流体密度ρ和速度u可以表示为:
| $ \rho = \sum\limits_{i = 0}^8 {{f_i}} $ | (11) |
| $ \rho \mathit{\boldsymbol{u}} = \sum\limits_{i = 0}^8 {{f_i}} {c_i} + \delta t\mathit{\boldsymbol{F}} $ | (12) |
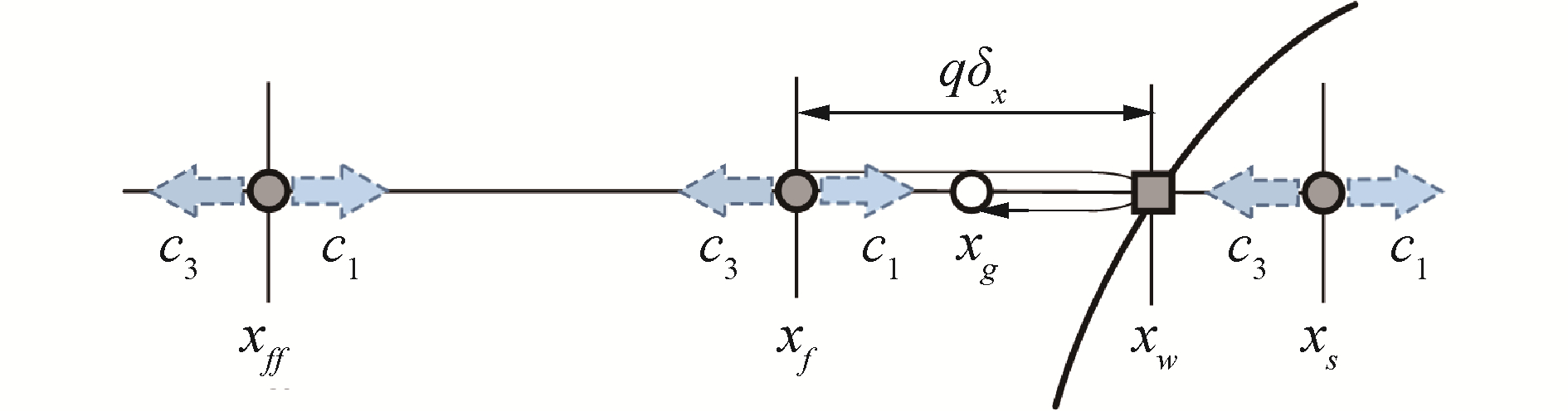
在MRT-LBM的算式中,方腔内壁面和进、出流口位置采用非平衡态外推边界条件[16]。对于曲线边界与网格不完全一致的热源表面,有些粒子在被壁面反弹后会脱离节点,落到间隙位置(图 3中的xg位置),则采用线性插值边界条件[17]。如图 3所示,该方法首先假设分布函数f1(xf, t)可以穿过边界节点xw到达实体节点xs,由线性插值得到:
| $ {f_1}({x_w},t + \delta t) = (1 - q){f_1}({x_f},t + \delta t) + q{f_1}({x_s},t + \delta t) $ | (13) |
|
Download:
|
| 图 3 曲面插值边界条件 Fig. 3 Interpolation boundary condition for curved wall | |
式中q为流体节点到边界间的距离与网格长度之比,q=|xf-xw|/|xf-xs|。再根据动量守恒和固体边界的无滑移条件,最终得到在实体节点xs处的分布函数为:
| $ \begin{array}{l} {f_3}({x_s},t) = \frac{1}{{1 + q}}[q{f_3}({x_f},t) + q{f_1}({x_f},t) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (1 - q){f_1}({x_{ff}},t)] \end{array} $ | (14) |
式(14)具有二阶精度,并可以避免按q≤1/2和q>1/2划分时所引起的数值振荡。
在计算温度场时,采用有限差分方法在与MRT-LBM相同的网格上对方程(4)进行求解[18]。这里采用一阶向前和二阶中心差分方法来分别求解时间和空间的偏微分方程,即有:
| $ \frac{{\partial \theta }}{{\partial t}} = {\theta ^{n + 1}}(m,n) - {\theta ^n}(m,n) $ | (15) |
| $ \left\{ \begin{array}{l} \frac{{\partial \theta }}{{\partial x}} = \frac{{\theta (m + 1,n) - \theta (m - 1,n)}}{2}\\ \frac{{\partial \theta }}{{\partial y}} = \frac{{\theta (m,n + 1) - \theta (m,n - 1)}}{2} \end{array} \right. $ | (16) |
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}\theta }}{{\partial {x^2}}} = \theta (m + 1,n) - 2\theta (m,n) + \theta (m - 1,n)\\ \frac{{{\partial ^2}\theta }}{{\partial {y^2}}} = \theta (m,n + 1) - 2\theta (m,n) + \theta (m,n - 1) \end{array} \right. $ | (17) |
不同位置的无量纲热边界条件定义为:在方腔内壁面和进流口位置,θ=0;在热源表面,θ=1;在出流口位置,∂θ/∂X=0。
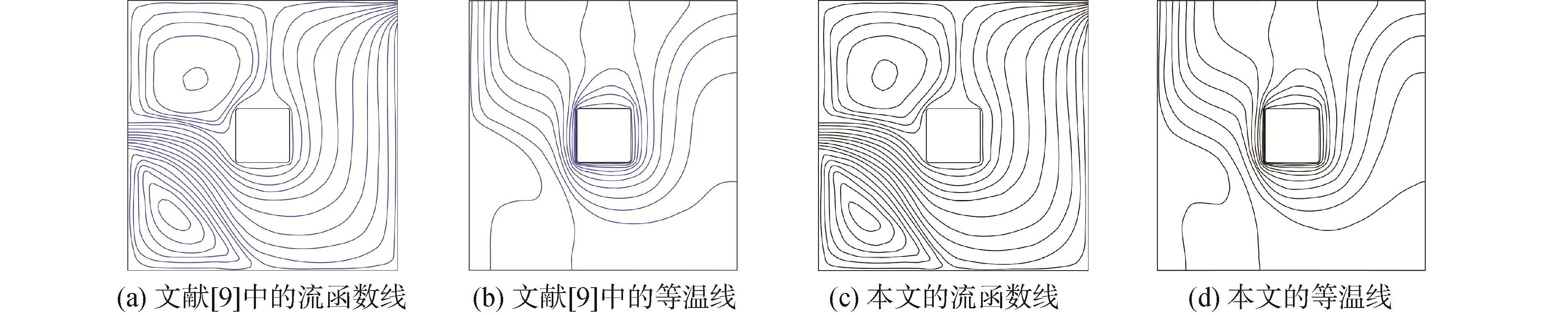
1.3 模型验证为确认所采用算法的可靠性和准确性,以文献[9]中所描述的具有中部进流口、顶部出流口以及方形截面内热源的方腔混合对流模型作为算例进行验证。通过对比图 4中给出的流场和温度场分布(Re=200,Ri=1)可以看出,采用本文方法所得到的模拟结果与文献中的结果具有很好的一致性。同时,表 1中的对比表明,当Ri变化时,2种计算的Nuav具有相同的趋势,最大百分比差异为3.52%,说明本文的计算方法是具有足够精度的。
|
Download:
|
| 图 4 本文和文献[9]的流场和温度场的算例验证 Fig. 4 Comparison of streamlines and isotherms between the present work and that of ref.[9] | |
| 表 1 模拟结果对比 Table 1 Comparison of simulation results |
考虑到算法对网格的敏感性,分别采用100×100、150×150、200×200和250×250的网格分布对本文的混合对流模型进行计算。当网格超过200×200时,继续加密网格对模拟结果的改进很小,因此在下述分析中均采用200×200的网格。
2 对流换热的计算结果与分析为保证混合对流换热中始终存在强制对流和自然对流,且方腔内的流体为层流状态,本文在Re=200,Ri=1的工况下对参数进行讨论。不同形状的加热元件在不同进、出流口位置下的流场、温度场分布如图 5~7所示。

|
Download:
|
| 图 5 进流口位于底部时,R和出流口位置对流函数线和等温线的影响 Fig. 5 Effects of R and outlet location on the streamlines and isotherms for cavity with bottom inlet | |

|
Download:
|
| 图 6 进流口位于中部时,R和出流口位置对流函数线和等温线的影响 Fig. 6 Effects of R and outlet location on the streamlines and isotherms for cavity with middle inlet | |
|
Download:
|
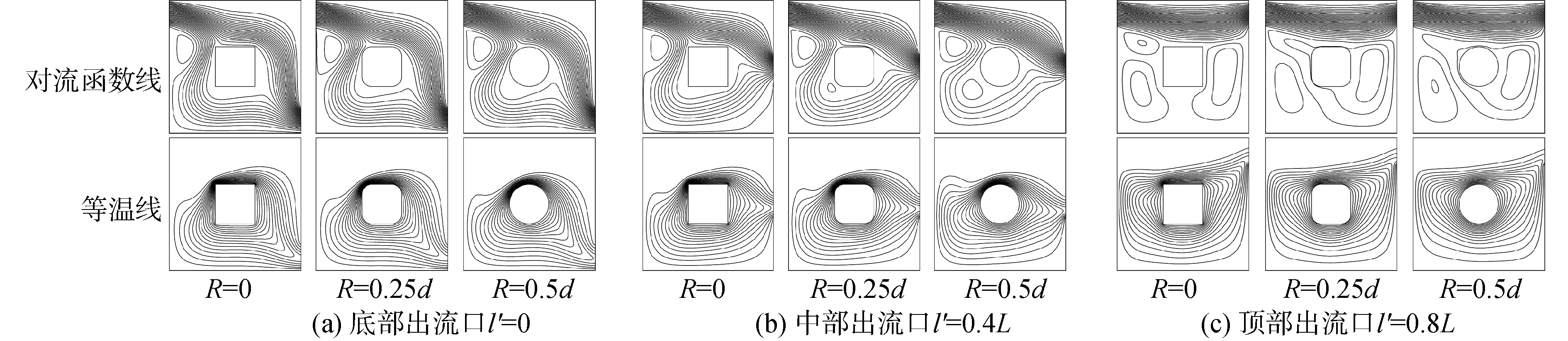
| 图 7 进流口位于顶部时,R和出流口位置对流函数线和等温线的影响 Fig. 7 Effects of R and outlet location on the streamlines and isotherms for cavity with top inlet | |
图 5给出了当进流口位于底部(l=0)时腔内混合对流的流函数线图和等温线图。在图 5(a)中,当出流口也位于底部(l′=0)时,流体从方腔底部直接流过,惯性力使加热元件被逆时针环流包围。由于强迫对流和自然对流的共同作用,在加热元件左侧和方腔右上角还会出现2个涡流。R的增大会使环流增强,涡流被挤压。当l′=0.4L时(图 5(b)),冷来流与加热元件的右下角发生直接接触,腔内右部的流动发生变化。由于进流口附近的流体受到出流口位置的影响较小,所以热源左侧与腔壁间仍存在涡流。当R=0时,有小部分来流会从左侧绕经热源后再流至腔外,但随着R的增大,腔内逐渐出现与图 5(a)中相似的环流结构。当l′=0.8L时(图 5(c)),热源被整个包含在来流中,R的增大会减少上部绕流,但也为涡流的流动提供了更大的空间。在出流口位置由l′=0升高到l′=0.8L的过程中,冷来流的上移使腔内右部的等温线向上收缩,热源底部的等温线也变得越来越密集,这说明该位置的具有较大的温差。R的增大会使热源附近的等温线发生变化,但对整体温度场的影响不大。
图 6给出的是当进流口位于中部(l=0.4L)时腔内混合对流的流函数线图和等温线图。此时,加热元件正对进流口,在进行热交换的同时也阻碍了流体运动。流入的流体会在进流口两侧产生上大下小的两个低温角涡,并从热源上下两侧流过,最终在出流口处汇合。等温线图表明,腔体左侧温度主要由来流决定,而当流体流至右侧时热源的作用开始变得明显起来。随着出流口位置l′的升高,右侧腔体内的流函数线和等温线受到较大影响,但腔内流体的整体流动模式变化很小。R的增大会使涡流的运动区域变大,并使对应位置的等温线向右倾斜。
进流口位于顶部(l=0.8L)时腔内混合对流的流函数线和等温线如图 7所示。在图 7(a)和(b)中(l′=0和l′=0.4L),腔内的绕流虽然占主导地位,但它们难以覆盖进流口下方的空间,因而产生了顺时针涡流。等温线聚集在热源上表面,可以看出上部绕流对温度场的影响要大于下部绕流。随着R的增大,流体更多地从腔体上部流过,下部绕流减少,并逐渐脱离热源表面。当进流口和出流口都位于图 7(c)顶部(l=l′=0.8L)时,流体不再受加热元件阻碍,几乎水平地流过腔体顶部。在冷来流未经过的区域内,温度也分布得较为均匀。R的增大会改变腔内其他位置的流体运动,使部分涡流开始向环流转变。由于重力的存在,腔体内的流函数线和等温线分布与图 5(a)并不对称。
从上面的讨论可以看出,进、出流口位置选择对腔内流场的影响要大于加热元件的形状变化,R的变化对温度场的影响并不明显。实际上,热源形状的特征主要反映在加热表面的对流换热上。
图 8给出了9种不同方腔结构下的热源表面局部努赛尔数Nu,图中以热源上表面与其中心线的交点为横坐标零点,沿逆时针方向绘制了Nu曲线,R为0、0.25d和0.5d时所对应的热表面的无量纲长度分别为1.2、1.07和0.94。当R=0时,在热源的4个直角位置会出现尖锐的峰值,这表明该位置的温度梯度很大,在相应的温度场中也会出现了密集的等温线。随着R的增大,4个峰值开始下降并变得平缓,至热源截面变为圆(R=0.5d)时,Nu曲线中只剩下一个明显的主峰值。更改进、出流口的位置可以改变峰值的大小和位置分布,相比而言,进流口的影响要大于出流口。

|
Download:
|
| 图 8 不同腔体结构下,R对局部努赛尔数Nu的影响 Fig. 8 Effect of R on local Nusselt number in different cavity structures | |
图 9中给出了不同方腔结构下热源表面的平均努赛尔数Nuav,图中的大写字母B、M和T分别表示底部、中部和顶部进流口;B′、M′和T′分别表示底部、中部和顶部出流口。与局部努赛尔数的最大值出现在R=0时相反,平均努赛尔数是随着R的增大而增大的,这说明虽然一些特殊位置的局部对流换热能力有所下降,但整体表面的换热却是增强的,且Nuav的值并不与换热表面的面积大小成正比。另外可以看出,当方腔的进、出流口在同一位置时,冷流体直接从顶部或底部通道流出腔体,Nuav较小;而当方腔具有中部进流口和顶部出流口时,热源与来流正面接触,换热充分,Nuav取得最大值。

|
Download:
|
| 图 9 不同腔体结构下,R对平均努赛尔数Nuav的影响 Fig. 9 Effect of R on average Nusselt number in different cavity structures | |
1) 流场和温度场分布与热源形状关系不大,而主要受进、出流口位置影响。当进流口位于腔体底部或顶部时,随着出流口位置与进流口位置之间距离的增大,热源周围的环流被挤压,并逐渐被外部来流所取代;而当进流口位于中部时,外部来流始终流经热源的上、下表面,出流口位置不改变腔内流体的流动模式。在温度场中,由于受到外部强制对流的影响,等温线会向进流口附近的热源表面以及出流口位置聚集。
2) 当热源截面为圆形时(R=0.5d),热源表面的局部努赛尔数Nu曲线具有平缓变化的单峰值;随着R的减小,Nu曲线上会逐渐出现多个尖锐峰值。Nu的最大值出现在热源表面靠近进流口位置的一侧,而出流口位置对Nu的影响不大。当进、出流口分别位于顶部和底部时,可在正方形热源截面(R=0)的左上角获得最佳局部对流换热位置。
3) 当进、出流口位置固定时,热源表面的平均努赛尔数Nuav随着R的增大而增大。当R不改变时,Nuav的最大值在方腔具有中部进流口和顶部出流口时出现。因此,在进、出流口分别位于中部和顶部时,采用圆形截面的热源(R=0.5d)可以使热源整体表面的对流换热最强。
| [1] |
ANDRZEJCZYK R, MUSZYNSKI T. An experimental investigation on the effect of new continuous core-baffle geometry on the mixed convection heat transfer in shell and coil heat exchanger[J]. Applied thermal engineering, 2018, 136: 237-251. DOI:10.1016/j.applthermaleng.2018.03.003 (  0) 0)
|
| [2] |
PIÑA-ORTIZ A, HINOJOSA J F, NAVARRO J M A, et al. Experimental and numerical study of turbulent mixed convection in a cavity with an internal heat source[J]. Journal of building physics, 2018, 42(2): 142-172. DOI:10.1177/1744259117735451 (  0) 0)
|
| [3] |
NOSONOV I I, SHEREMET M A. Conjugate mixed convection in a rectangular cavity with a local heater[J]. International journal of mechanical sciences, 2018, 136: 243-251. DOI:10.1016/j.ijmecsci.2017.12.049 (  0) 0)
|
| [4] |
李培生, 孙金丛, 张莹, 等. 内置高温体倾斜多孔腔体中自然对流的LBM模拟[J]. 哈尔滨工程大学学报, 2018, 39(6): 1073-1080. LI Peisheng, SUN Jincong, ZHANG Ying, et al. Lattice Boltzmann simulation of natural convection in an inclined porous cavity with a hot square obstacle[J]. Journal of Harbin Engineering University, 2018, 39(6): 1073-1080. (  0) 0)
|
| [5] |
RADHAKRISHNAN T V, VERMA A K, BALAJI C, et al. An experimental and numerical investigation of mixed convection from a heat generating element in a ventilated cavity[J]. Experimental thermal and fluid science, 2007, 32(2): 502-520. DOI:10.1016/j.expthermflusci.2007.06.001 (  0) 0)
|
| [6] |
孙猛, 雷兢, 刘靖, 等. 开口方腔内混合对流换热的数值模拟[J]. 热科学与技术, 2006, 5(4): 295-300. SUN Meng, LEI Jing, LIU Jing, et al. Numerical simulation of mixed convective heat transfer in open-ended cavity[J]. Journal of thermal science and technology, 2006, 5(4): 295-300. DOI:10.3969/j.issn.1671-8097.2006.04.003 (  0) 0)
|
| [7] |
KARIMI F, XU Hongtao, WANG Zhiyun, et al. Numerical simulation of steady mixed convection around two heated circular cylinders in a square enclosure[J]. Heat transfer engineering, 2016, 37(1): 64-75. DOI:10.1080/01457632.2015.1042343 (  0) 0)
|
| [8] |
GAROOSI F, HOSEININEJAD F. Numerical study of natural and mixed convection heat transfer between differentially heated cylinders in an adiabatic enclosure filled with nanofluid[J]. Journal of molecular liquids, 2016, 215: 1-17. DOI:10.1016/j.molliq.2015.12.016 (  0) 0)
|
| [9] |
CHAMKHA A J, HUSSAIN S H, ABD-AMER Q R. Mixed convection heat transfer of air inside a square vented cavity with a heated horizontal square cylinder[J]. Numerical heat transfer, part A: applications, 2011, 59(1): 58-79. DOI:10.1080/10407782.2011.541216 (  0) 0)
|
| [10] |
张翠珍, 杨茉, 单彦广, 等. 方腔内竖直板混合对流换热的数值模拟[J]. 工程热物理学报, 2009, 30(2): 309-311. ZHANG Cuizhen, YANG Mo, SHAN Yanguang, et al. Numerical simulation of mixed convection heat transfer in an enclosure with vertical isothermal plate[J]. Journal of engineering thermophysics, 2009, 30(2): 309-311. DOI:10.3321/j.issn:0253-231X.2009.02.037 (  0) 0)
|
| [11] |
郭照立, 郑楚光. 格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2009. GUO Zhaoli, ZHENG Chuguang. Theory and applications of lattice Boltzmann method[M]. Beijing: Science Press, 2009. (  0) 0)
|
| [12] |
王猛, 朱卫兵. 基于孔隙尺度的方腔内多孔介质融化模拟研究[J]. 哈尔滨工程大学学报, 2015, 36(6): 774-778. WANG Meng, ZHU Weibing. Simulation study for melting of porous media in a square cavity based on the pore scale[J]. Journal of Harbin Engineering University, 2015, 36(6): 774-778. (  0) 0)
|
| [13] |
FRAPOLLI N, CHIKATAMARLA S S, KARLIN I. Simulations of heated bluff-bodies with the multi-speed entropic lattice Boltzmann method[J]. Journal of statistical physics, 2015, 161(6): 1434-1452. DOI:10.1007/s10955-015-1373-z (  0) 0)
|
| [14] |
孙涛, 孙建刚, 昂雪野, 等. 基于格子Boltzmann方法的微通道传热特性数值研究[J]. 太阳能学报, 2016, 37(9): 2344-2349. SUN Tao, SUN Jiangang, ANG Xueye, et al. A numerical investigation on heat transfer characteristic of micro-channel strutures by lattice Boltzmann method[J]. Acta energiae solaris sinica, 2016, 37(9): 2344-2349. DOI:10.3969/j.issn.0254-0096.2016.09.026 (  0) 0)
|
| [15] |
BETTAIBI S, KUZNIK F, SEDIKI E. Hybrid LBM-MRT model coupled with finite difference method for double-diffusive mixed convection in rectangular enclosure with insulated moving lid[J]. Physica A: statistical mechanics and its applications, 2016, 444: 311-326. DOI:10.1016/j.physa.2015.10.029 (  0) 0)
|
| [16] |
何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用[M]. 北京: 科学出版社, 2009. HE Yaling, WANG Yong, LI Qing. Lattice Boltzmann method: theory and applications[M]. Beijing: Science Press, 2009. (  0) 0)
|
| [17] |
YU Dazhi, MEI Renwei, LUO Lishi, et al. Viscous flow computations with the method of lattice Boltzmann equation[J]. Progress in aerospace sciences, 2003, 39(5): 329-367. DOI:10.1016/S0376-0421(03)00003-4 (  0) 0)
|
| [18] |
MEZRHAB A, BOUZIDI M H, LALLEMAND P. Hybrid lattice-Boltzmann finite-difference simulation of convective flows[J]. Computers & fluids, 2004, 33(4): 623-641. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


