当前,航空航天、生物医疗、信息通信等领域对高质量小型零件的需求日益递增。介观尺度铣削加工作为一种高效的加工方法,可以实现复杂三维结构的加工。对于介观尺度(或中间尺度)的定义,在机械加工领域一般指介乎于宏观尺度和微观尺度之间,几何特征尺寸范围为0.01~1mm的尺度范围[1]。刀具偏心对于介观尺度铣削影响极大,可能导致在相同轴向位置,不同切削齿实际切削半径不相等,极大几率出现单齿切削现象;在不同轴向位置,偏心角沿刀具螺旋线改变,导致相同切削齿的实际切削半径不同,甚至可能导致单齿切削和两齿切削分别出现在不同轴向位置。相对于常规尺度铣削加工,介观尺度铣削刀具偏心将极大地影响铣削力、铣削表面形貌及刀具寿命等[2],刀具的偏心参数识别对于介观尺度铣削极为重要。
在常规尺度铣削刀具偏心参数识别方面,国内外已开展过大量研究。Tai等[3]采用直接测量方法测量了刀具偏心参数。Attanasio等[4]提出了一种基于粒子群优化策略的方法,用于校准包括刀具跳动在内的铣削力解析模型系数。Nakkiew等[5]采用端铣刀加工出一系列特定形状的标志,通过对这些标志的测量间接获得了刀具偏心参数。文献[6-8]分别建立了切削力模型,将刀具偏心参数作为切削力模型中的未知量,采用递归算法求解了刀具偏心参数。刘璨等[9]基于三角级数对切削合力进行展开,提出一种用切削合力频谱估算刀具偏心参数的方法。相对于常规尺度铣削,介观尺度铣削刀具偏心参数受尺寸限制更加难以识别,相关研究较少。李成锋等[10]采用轴向进给的方式加工圆孔,通过显微镜测量孔径识别了介观尺度铣削刀具的偏心量。Jing等[11]建立了耦合刀具偏心参数的刀具轨迹解析模型,通过位移测量求解了以刀具偏心参数为未知量的非线性方程。Zhang等[12]建立了考虑到单齿切削现象和间断性切屑形成的介观尺度铣削力模型,通过迭代算法求解了模型中的刀具偏心参数。上述方法大多基于切削力模型,需要大量的切削力实验数据,刀具偏心参数识别算法复杂,效率较低。
针对于此,本文首先分析刀具偏心参数对实际切削刃半径的影响,建立了刀具偏心参数解析识别模型,通过激光位移传感器分别测量刀柄和切削齿轮廓位移,采用迭代算法实现了基于位移测量的介观尺度铣削刀具偏心参数在位识别。
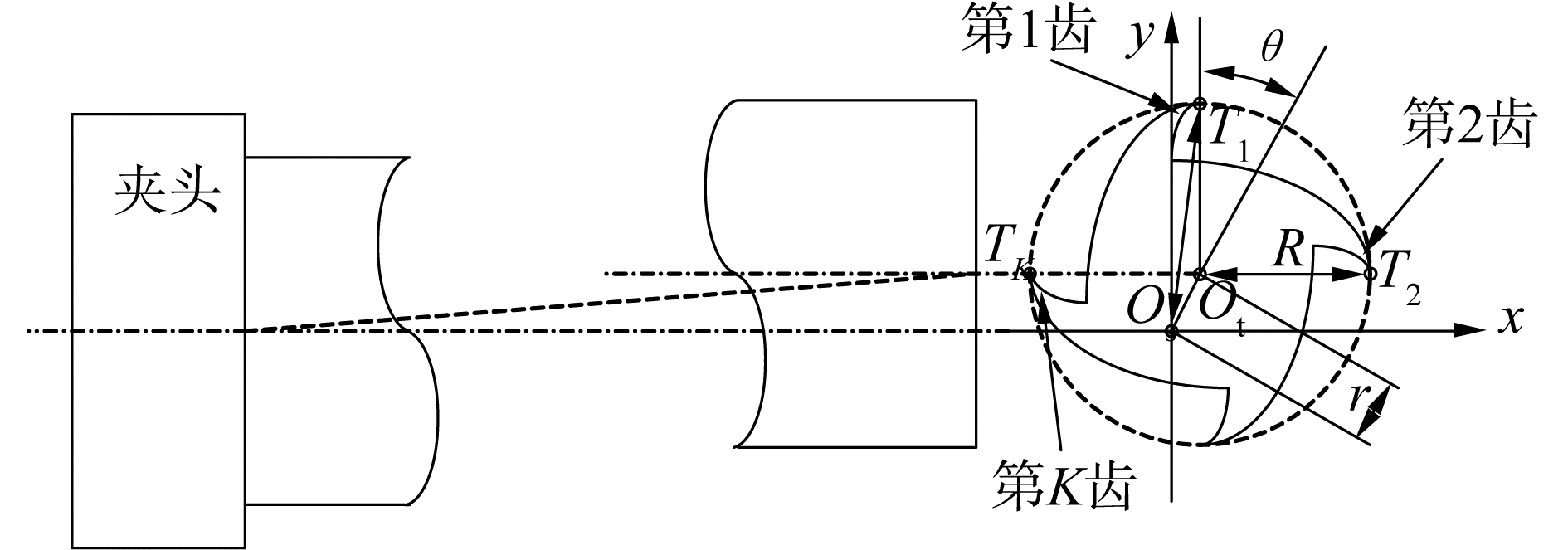
1 刀具偏心参数定义及影响铣削刀具由制造误差和装夹误差所引起的偏心如图 1所示,图中点Ot为刀具中心,Os为主轴回转中心。对于具有K个切削齿的刀具,首先固定刀具的一个切削齿为第1齿,其余切削齿按顺时针分别为第2齿~第K齿。本文将刀具偏心量r定义为刀具中心与主轴回转中心的距离;刀具偏心角θ定义为当第1齿齿尖与刀具中心的连线与Y轴正方向一致时,刀具中心与主轴回转中心连线与Y轴正方向的逆时针夹角。
|
Download:
|
| 图 1 刀具偏心参数定义 Fig. 1 Definitions of tool runout parameters | |
由图 1可推得第1齿齿尖绕主轴回转中心旋转而成的实际切削半径R1为:
| $ {R_1} = \overline {{O_{\rm{s}}}{T_{\rm{1}}}} = \sqrt {{{(R + r\cos \theta )}^2} + {r^2}{{\sin }^2}\theta } $ | (1) |
进一步可推导出第k齿的实际切削半径Rk(k=1, 2, ..., K):
| $ {R_k} = \overline {{O_{\rm{s}}}{T_k}} = \sqrt {{R^2} + {r^2} + 2Rr\cos [2{\rm{ \mathsf{ π} }}(k - 1)/K - \theta ]} $ | (2) |
以介观尺度铣削常用的两齿和四齿铣刀为例,刀具1为两齿铣刀,半径为250μm;刀具2为四齿铣刀,半径为500μm。分别计算两种刀具各切削齿的实际切削半径,如图 2、图 3所示。当刀具偏心角固定为80°时,刀具1各切削齿的实际切削半径随刀具偏心量变化如图 2(a)所示。随着刀具偏心量增大,两切削齿实际切削半径之差变大。当刀具偏心量固定为5μm时,刀具1两切削齿的实际切削半径随刀具偏心角变化如图 2(b)所示。当刀具偏心角分别为90°和270°时,两切削齿实际切削半径相等;当刀具偏心角分别为0°和180°时,两切削齿实际切削半径之差最大,且等于2倍的刀具偏心量。同时考虑刀具偏心量和偏心角的变化,由图 2(c)、图 2(d)可见,两切削齿实际切削半径以刀具半径尺寸为中线对称分布,刀具偏心量越大,两切削齿实际切削半径相差越大。

|
Download:
|
| 图 2 刀具1各切削齿实际切削半径 Fig. 2 The actual radius of each cutting edge of the first cutter | |
当刀具偏心角固定为80°时,刀具2各切削齿的实际切削半径如图 3(a)所示。4个切削齿的实际切削半径均随着刀具偏心量线性变化。随着刀具偏心量增大,切削齿之间实际切削半径之差增大。当刀具偏心量固定为5μm时,各切削齿的实际切削半径如图 3(b)所示。4个切削齿的实际切削半径均随着刀具偏心角周期性变化,相位相差90°。只要刀具偏心量不为零,无论刀具偏心角为何值,四切削齿实际切削半径都不相等。由图 3(c)~(f)可见,第1齿与第3齿、第2齿与第4齿的实际切削半径分别以刀具半径为中线呈对称分布,且实际切削半径之和分别与刀具直径相等,与刀具偏心量和偏心角无关。刀具偏心量越大,各切削齿之间实际切削半径差别越大。

|
Download:
|
| 图 3 刀具2各切削齿实际切削半径 Fig. 3 The actual radius of each cutting edge of the second cutter | |
刀具实际切削半径难以直接测量,因此需对式(2)做出变形:
| $ \left\{ \begin{array}{l} \Delta {R_k} = {R_k} - {R_{k + 1}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{R^2} + {r^2} + 2Rr\cos [2{\rm{ \mathsf{ π} }}(k - 1)/K - \theta ]} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{R^2} + {r^2} + 2Rr\cos (2{\rm{ \mathsf{ π} }} k/K - \theta )} \\ \Delta {R_K} = {R_K} - {R_1} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{R^2} + {r^2} + 2Rr\cos (2{\rm{ \mathsf{ π} }} /K + \theta )} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{R^2} + {r^2} + 2Rr\cos \theta } \end{array} \right. $ | (3) |
式中:ΔRk为第k个切削齿与第k+1个切削齿实际切削半径之差;Rk为第k个切削齿实际切削半径;r为刀具偏心量;θ为刀具偏心角。对于介观尺度铣削最常用的两齿铣刀:
| $ \begin{array}{l} \Delta {R_1} = - \Delta {R_2} = {R_1} - {R_2} = \sqrt {{R^2} + {r^2} + 2Rr\cos \theta } - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {{R^2} + {r^2} - 2Rr\cos \theta } \end{array} $ | (4) |
该式包含r和θ两个未知量,无法通过一个方程求解。由于刀具偏心角θ难以测量,因此必须先通过间接测量方法获得刀具偏心量r。
2.2 刀具偏心量测量本文采用激光位移传感器测量刀具偏心量。首先校准光束对准主轴回转中心:将激光位移传感器固定在Y轴上,调整光束照射在刀柄的圆柱部分。反复沿X轴方向平移刀柄,找到使位移传感器示数最小位置,记录横坐标为x1。将刀具旋转180°,重复上述步骤,记录横坐标为x2。沿X轴方向将刀具平移至(x1+x2)/2处,完成激光光束校准。
位移传感器光束校准后,以刀具端面与主轴回转中心线交点为坐标原点,将刀具端面Z向位置记录为z=0。沿Z轴移动刀具至z1,使光束聚焦于刀柄圆柱部分,如图 4所示。旋转刀具记录示数最大、最小的位移值L(z1)max和L(z1)min,则刀具轴向高度z1处偏心量r(z1)可表示为:
| $ \Delta r({z_1}) = \Delta L({z_1})/2 = [L{({z_1})_{\max }} - L{({z_1})_{\min }}]/2 $ | (5) |

|
Download:
|
| 图 4 识别模型参数测量 Fig. 4 Measurement of tool runout model | |
重复上述过程,测量刀柄圆柱部分的一系列偏心量r(z1)、r(z2)、…、r(zn),刀具偏心量r可通过刀柄偏心量最小二乘法线性拟合获得:
| $ \begin{array}{l} r = \bar r(z) - \bar z\sum\limits_{i = 1}^n {{{[r({z_i}) - \bar r(z)]}^2}} /\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^n {[r({z_i}) - \bar r(z)]({z_i} - \bar z)} \end{array} $ | (6) |
| $ \bar r(z) = \sum\limits_{i = 1}^n {r({z_i})} /n,\bar z = \sum\limits_{i = 1}^n {{z_i}} /n $ | (7) |
继续沿Z轴向上平移刀具,微调刀具轴向高度使位移传感器刚好测量刀尖处位移值。旋转刀具测量切削齿的回转轮廓曲线,将第k齿的轮廓曲线峰值记录为Pk,则刀具各切削齿实际切削半径差ΔRk可表示为:
| $ \left\{ \begin{array}{l} \Delta {R_k} = {R_k} - {R_{k + 1}} = {P_k} - {P_{k{\rm{ + }}1}}\\ \Delta {R_K} = {R_K} - {R_1} = {P_K} - {P_1} \end{array} \right. $ | (8) |
由上述测量方法可知,本方法的测量误差主要为测量轴线与基准轴线不在同一直线上所产生的阿贝误差,如图 5所示。激光位移传感器漫反射测量的参考距离为150mm;α为测量轴线与基准轴线夹角;ΔL为实际位移;ΔL’为实测位移,则位移测量的阿贝误差δ为:
| $ \delta = \Delta L - \Delta L' = \Delta L(1 - {\rm{sec}}\alpha ) $ | (9) |

|
Download:
|
| 图 5 测量误差分析 Fig. 5 Measurement error analysis | |
由于α很小,sec α近似为1,所引起的测量误差极小,可以忽略。
3 参数识别实验采用基恩士激光位移传感器LK-G150(分辨率0.1μm,重复测量精度0.5μm)测量刀具偏心量和实际切削半径差;采用介观尺度铣削中最常用的两齿铣刀作为被测铣刀,其参数如表 1所示。
| 表 1 被测铣刀参数 Table 1 Cutter parameters |
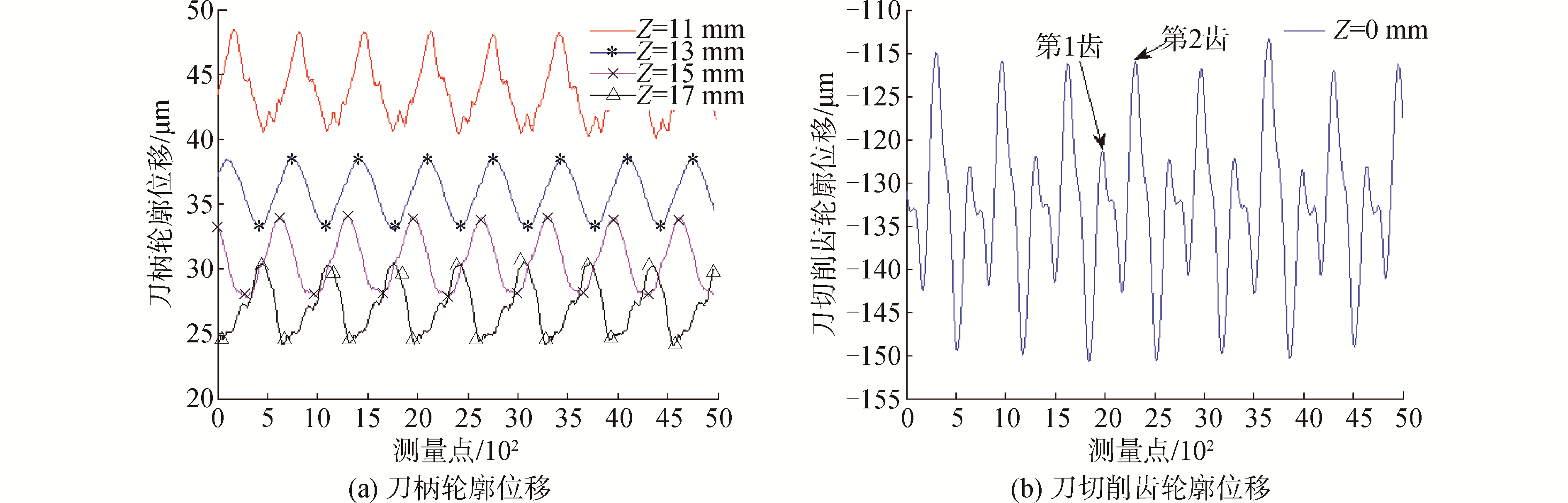
刀具的刀柄旋转轮廓位移和切削齿旋转轮廓位移测量结果分别如图 6(a)和6(b)所示。为减小测量误差,每个Z向位置的最大、最小位移分别取几个旋转周期刀柄旋转轮廓位移曲线的波峰、波谷平均值。由图 6(a)可见,沿着Z轴正方向,偏心量逐渐减小且与Z向位置近似呈线性关系,与前文偏心量分析结果一致。切削齿旋转轮廓曲线的峰值同样取多个旋转周期的平均值。由图 6(b)可见切削齿间的旋转轮廓曲线峰值差别较大。在介观尺度铣削加工中,为保证加工质量、延长铣削刀具寿命,每齿进给量通常较小,图 6(b)所示切削齿轮廓曲线势必出现只有一个切削齿参与切削的单齿切削现象。
|
Download:
|
| 图 6 刀具位移参数测量结果 Fig. 6 Displacement measurement results of the cutter | |
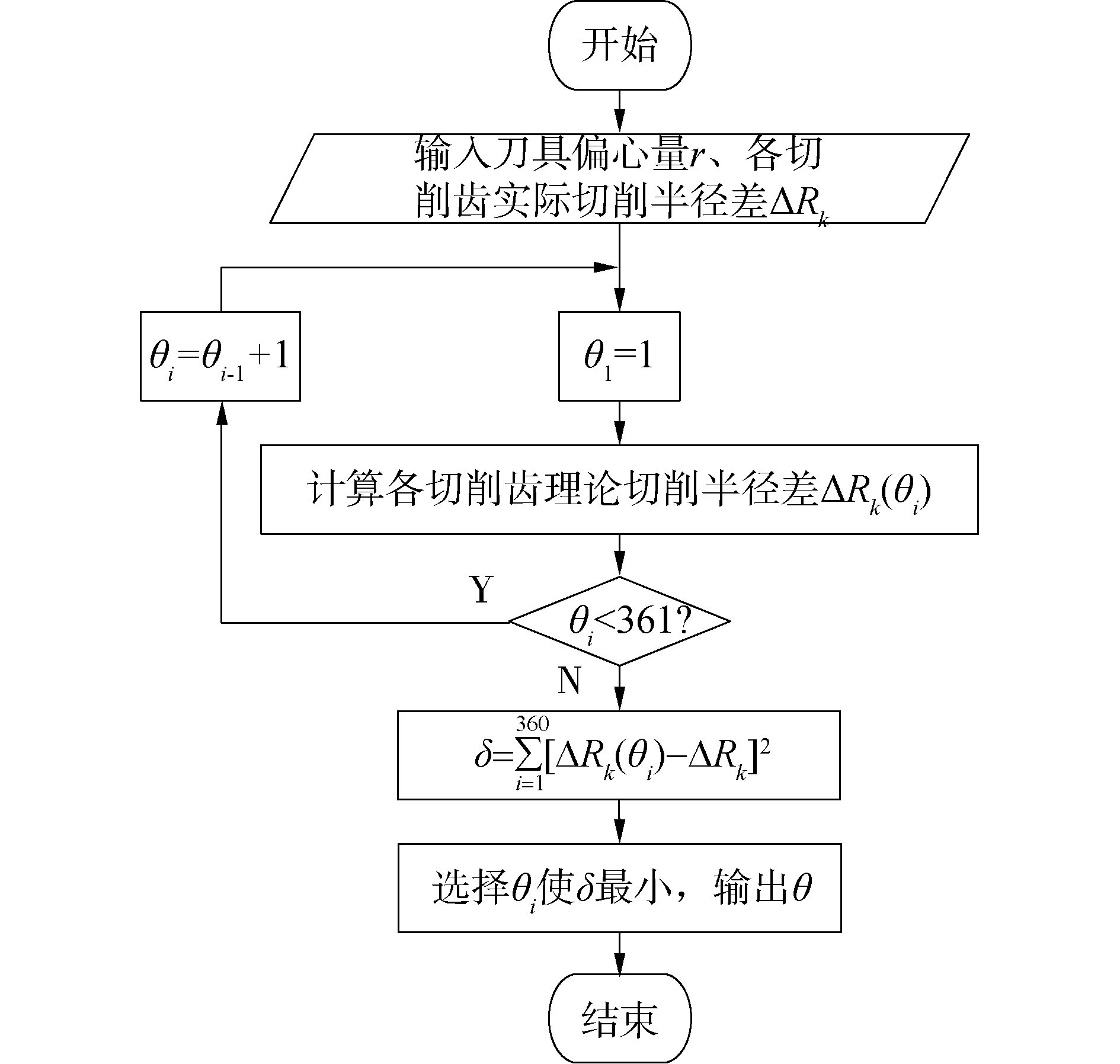
采用流程如图 7所示的迭代算法求解刀具偏心角θ(迭代范围为1°~360°,以1°递增)。
|
Download:
|
| 图 7 刀具偏心参数迭代识别流程 Fig. 7 Iterative identification process for tool runout parameters | |
将刀具偏心量r和各切削齿实际切削半径差ΔRk,分别带入式(3)和式(4)中计算各切削齿理论切削半径差ΔRk(θi),采用迭代算法求解并输出使各切削齿理论和实际切削半径差的标准偏差平方和最小时的刀具偏心角。实际切削半径差和刀具偏心参数识别结果如表 2所示。
| 表 2 实际切削半径差及刀具偏心参数识别结果 Table 2 Actual cutting radius difference and tool runout parameter recognition result |
将表 2中的介观尺度铣削刀具偏心参数识别结果带入式(2)可得两切削齿的实际切削半径,分别为494.90μm和505.13μm。在机床上采用轴向进刀方式加工一系列圆孔,采用基恩士数码显微镜VHX-1000在100倍放大倍率下,以三点法实测圆孔直径,如图 8所示。

|
Download:
|
| 图 8 铣削圆孔直径测量 Fig. 8 Milled hole diameter measurement | |
圆孔直径实测分别为1009.78、1011.31、1011.08、1010.80、1011.15μm,与理论上圆孔直径1010.26μm(2倍于较大实际切削半径)之间误差分别为-0.48、1.04、0.82、0.54、0.89μm,验证了本文提出介观尺度铣削刀具偏心参数识别方法的准确性。与基于切削力的刀具偏心参数识别方法相比,本文所提出的介观尺度铣削刀具偏心参数识别方法在所需实验次数少,迭代分辨率及迭代识别时间等方面均有明显的优势。
4 结论(1)刀具偏心导致铣削刀具各切削齿实际切削半径差别较大,且刀具偏心量越大,两切削齿实际切削半径相差越大。
(2)建立了刀具偏心参数识别模型,通过高精度激光位移传感器对模型中参数进行了精确测量,分析了测量误差。
(3)通过铣孔实验验证了本文提出的刀具偏心参数识别方法,该方法操作简便,识别效率优于基于切削力的识别算法。
(4)本文提出的刀具偏心参数识别方法可应用于常规尺度铣削刀具偏心参数的识别。
| [1] |
孙雅洲, 梁迎春, 程凯. 微米和中间尺度机械制造[J]. 机械工程学报, 2004, 40(5): 1-6. SUN Yazhou, LIANG Yingchun, CHENG Kai. Micro-scale and meso-scale mechanical manufacturing[J]. Chinese journal of mechanical engineering, 2004, 40(5): 1-6. (  0) 0)
|
| [2] |
HAN Zhenyu, ZHANG Xiang, SUN Yazhou, et al. Single edge cutting phenomenon and instantaneous uncut chip thickness model of micro-ball-end milling[J]. Advanced science letters, 2011, 4(4/5): 1387-1393. (  0) 0)
|
| [3] |
TAI C C, FUH K H. A predictive force model in ball-end milling including eccentricity effects[J]. International journal of machine tools and manufacture, 1994, 34(7): 959-979. DOI:10.1016/0890-6955(94)90028-0 (  0) 0)
|
| [4] |
ATTANASIO A, GARBELLINI A, CERETTI E, et al. Force modelling in micromilling of channels[J]. International journal of nanomanufacturing, 2015, 11(5/6): 275-296. DOI:10.1504/IJNM.2015.075238 (  0) 0)
|
| [5] |
NAKKIEW W, LIN Chiwei, TU J F. A new method to quantify radial error of a motorized end-milling cutter/spindle system at very high speed rotations[J]. International journal of machine tools and manufacture, 2006, 46(7/8): 877-889. (  0) 0)
|
| [6] |
ZHANG Dongliang, MO Rong, CHANG Zhingyong, et al. A study of computing accuracy of calibrating cutting force coefficients and run-out parameters in flat-end milling[J]. The international journal of advanced manufacturing technology, 2016, 84(1/2/3/4): 621-630. (  0) 0)
|
| [7] |
LI Kexuan, ZHU Kunpeng, MEI Tao. A generic instantaneous undeformed chip thickness model for the cutting force modeling in micromilling[J]. International journal of machine tools and manufacture, 2016, 105: 23-31. DOI:10.1016/j.ijmachtools.2016.03.002 (  0) 0)
|
| [8] |
张臣, 周儒荣, 庄海军, 等. 确定铣削力模型中刀具偏心参数的一种算法[J]. 机械科学与技术, 2006, 25(5): 509-512. ZHANG Chen, ZHOU Rurong, ZHUANG Haijun, et al. An algorithm for determining cutters' eccentricity paramers during modeling their milling force[J]. Mechanical science and technology, 2006, 25(5): 509-512. DOI:10.3321/j.issn:1003-8728.2006.05.002 (  0) 0)
|
| [9] |
刘璨, 吴敬权, 刘焕牢, 等. 基于三角级数展开的铣削合力频谱推导及刀具偏心估算[J]. 中国机械工程, 2016, 27(2): 246-250, 272. LIU Can, WU Jingquan, LIU Huanlao, et al. Spectral derivation of resultant milling force and eccentric estimation of tool based on trigonometric series expansion[J]. China mechanical engineering, 2016, 27(2): 246-250, 272. (  0) 0)
|
| [10] |
李成锋. 介观尺度铣削力与表面形貌建模及工艺优化研究[D]. 上海: 上海交通大学, 2008. LI Chengfeng. Study on force and surface topography modeling and process optimization of meso-scale end-milling[D]. Shanghai: Shanghai Jiao Tong University, 2008. (  0) 0)
|
| [11] |
JING Xiubing, TIAN Yanling, YUAN Yanjie, et al. A runout measuring method using modeling and simulation cutting force in micro end-milling[J]. The international journal of advanced manufacturing technology, 2017, 91(9/10/11/12): 4191-4201. DOI:10.1007/s00170-017-0076-9 (  0) 0)
|
| [12] |
ZHANG Xiang, HAN Zhenyu, FU Hongya, et al. Identification of spindle runout parameters in micro-ball-end milling[J]. Advanced science letters, 2011, 4(4/5): 1776-1781. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42



