2. 燕山大学 机械工程学院, 河北 秦皇岛 066004
2. School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China
工程中的承载结构在工作中常由于载荷或几何形状不连续而产生应力集中,甚至会在局部出现塑性变形。此时,对于受循环载荷作用的结构件则可能出现棘轮效应、包申格效应、循环软/硬化等变形行为,从而影响结构性能。因此,深入了解材料在循环载荷作用下的力学相应特性对于结构设计及安全评定具有十分重要的意义。棘轮应变会随着循环次数的增加而增加,会严重恶化部件的性能[1]。棘轮应变的累积取决于载荷中平均应力和应力幅值的组合[2-3]。在恒平均应力时,无论应力速率如何变化,随应力幅值的增加,棘轮寿命都会下降,棘轮应变累积率增加[4-6]。这些研究使人们对金属材料棘轮效应的基本特性有了较为深入的了解。
包申格效应是指金属材料在经历了一定量的单向拉伸或压缩塑性变形之后再反向加载,其屈服应力会低于连续正向变形的屈服应力,这是造成金属材料力学方向性的重要原因之一[7-9]。盛光敏等[10]通过对AZ31进行拉压和压拉循环试验,得出其包申格效应比反包申格效应明显;文献[11-12]分析了不同应变历史、预应变量、应变速率和循环周次对铝合金7A04和高强钢10CrNi5MoV包申格效应的影响;文献[13-14]对Q345、Q460和Q235进行循环加载试验,指出3种钢材均存在包申格效应。
当外加循环载荷使得材料进入塑性变形后,反复变形会令金属的塑性流动特性发生变化,造成材料抵抗变形的能力增强或减弱,这种现象称为循环硬化或循环软化。文献[15]探讨了不同加载条件下不锈钢316L的循环软硬化行为;文献[16-18]指出低碳钢S355循环硬/化行为随塑性应变范围的增大而增大,循环软化行为随塑性应变范围的减小而减小;文献[19-21]研究发现Q235钢在不同应变幅值和平均应变组合下表现为循环硬化,循环硬化指数随平均应变水平的增加而增大。
学者们对不同材料在不同条件下的循环变形特性进行了深入探讨,但对于焊接结构件最为常用的Q235钢在非对称应力控制下产生棘轮效应、包申格效应及循环软硬化特性的系统研究却鲜见报道。本文以Q235钢为研究对象,进行了多种条件下的循环加载试验,运用数据分析的方法,并结合唯象理论,对试验结果进行系统分析,深入研究了此材料的力学响应特性。
1 应力循环加载试验方案试验所用原材料为20 mm厚Q235钢板,测得其弹性模量为210 GPa,上、下屈服极限分别为310 MPa和243 MPa。沿轧制方向取样,按照GB/T 3075-2008《金属材料疲劳试验轴向力控制方法》加工成圆形截面循环加载试样,其平行段直径9 mm,平行段长度27 mm,过渡圆弧半径25 mm。在精度为0.2 kN的Instron8801型电液伺服疲劳试验机上进行循环加载试验,并通过精度为0.1 μm,标距为25 mm的接触式引伸计采集轴向应变。试验加载波形如图 1所示,加载应力率为40 MPa/s,循环周次为30周,具体试验方案如表 1所示。
| 表 1 应力循环试验加载工况 Table 1 Loading conditions of stress cycle test |
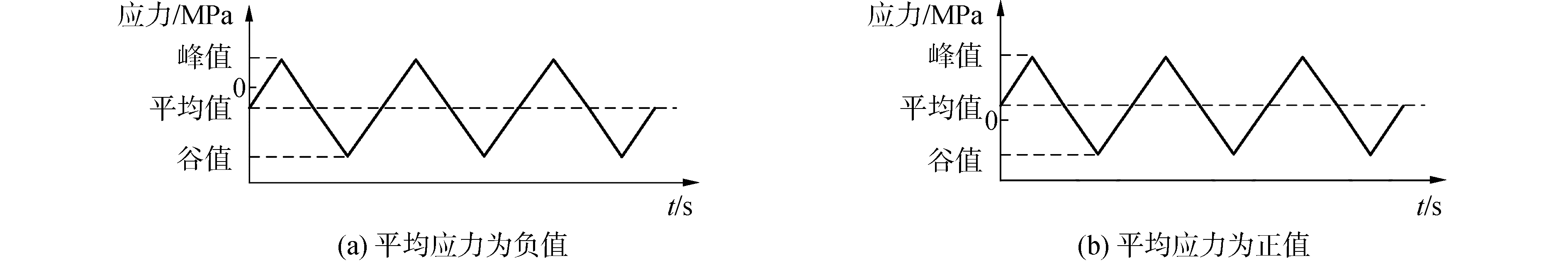
|
Download:
|
| 图 1 应力循环加载曲线 Fig. 1 Single stage stress cyclic loading curves | |
本文材料在非对称应力循环载荷作用下产生的棘轮应变εr为:
| $ {\varepsilon _{\rm{r}}} = (\varepsilon _{{\rm{max}}}^{\rm{T}} + \varepsilon _{{\rm{min}}}^{\rm{T}})/2 $ | (1) |
式中εmaxT、εminT分别表示某一个循环周次的最大真应变和最小真应变。如无特殊说明,本文所涉及应变均为真应变。
由于Q235钢存在屈服平台,使得第1周的应变值较大,棘轮应变的计算均从第2周开始。将相邻2个循环周次内棘轮应变的变化量定义为棘轮应变率Δεr,其反映了循环加载过程中棘轮应变累积的快慢程度。
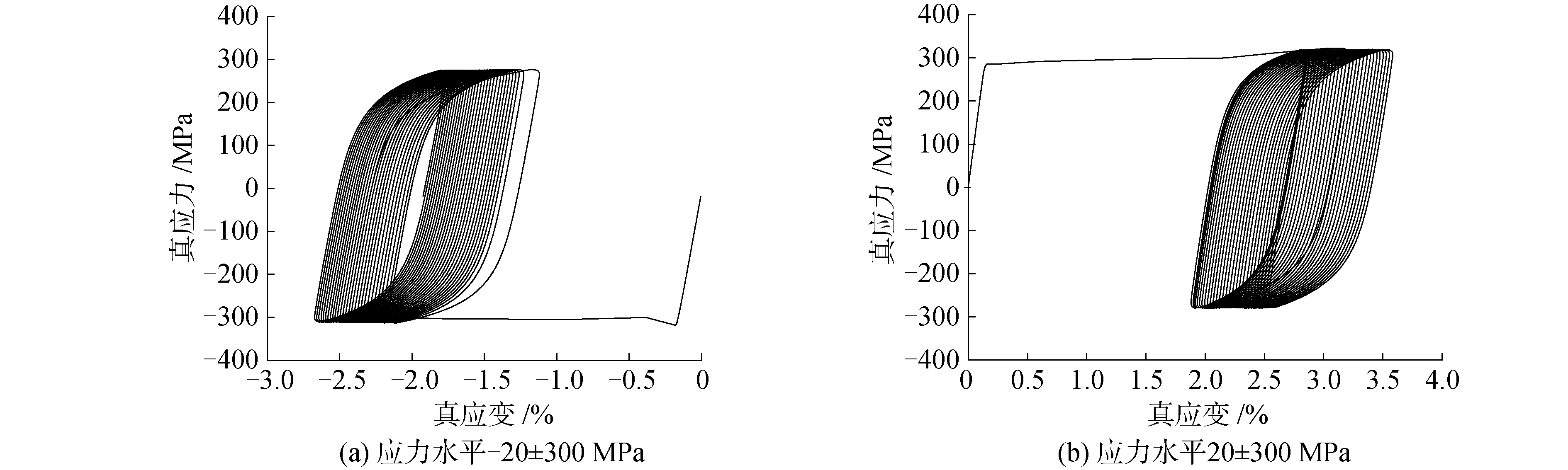
应力幅值为300 MPa,平均应力分别为-20 MPa和20 MPa时,循环加载过程中Q235钢的应力应变曲线如图 2所示。可以看出,正、负平均应力时均产生了棘轮效应。当平均应力为负值时,随循环周次的增加,滞回曲线向负应变方向移动;当平均应力为正值时,滞回曲线则向正应变方向移动。
|
Download:
|
| 图 2 循环应力应变曲线 Fig. 2 Cyclic stress-strain curve | |
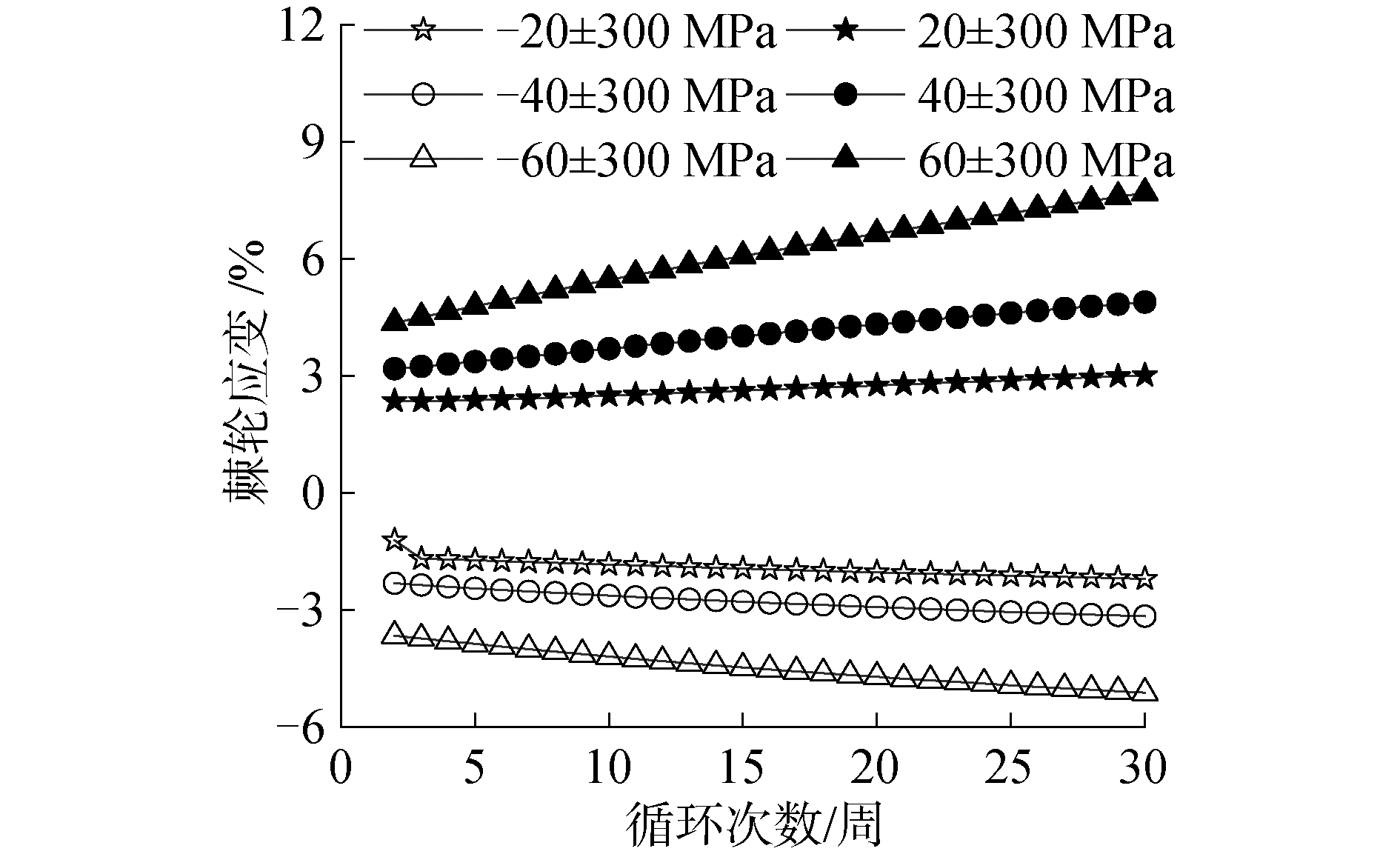
应力幅值为300 MPa,不同平均应力条件下棘轮应变随循环周次的变化如图 3所示。由图可知,平均应力为正值时棘轮应变为正值,平均应力为负值时棘轮应变为负值,棘轮应变的绝对值均随循环周次增加而增大。不同正负平均应力条件下棘轮应变的变化趋势不同,且棘轮应变率也不相同,但棘轮应变率均在第20周后趋于稳定。
|
Download:
|
| 图 3 应力幅值为300 MPa时的棘轮应变 Fig. 3 Ratcheting strain at stress amplitude 300 MPa | |
平均应力为正值时,棘轮应变率为正值,平均应力越大,棘轮应变率越高;平均应力为负值时,棘轮应变率为负值,平均应力绝对值越大,棘轮应变率也越高。应力幅值为300 MPa时,棘轮应变率稳定值与平均应力之间的关系曲线如图 4所示,两者之间呈指数函数关系。

|
Download:
|
| 图 4 应力幅值为300 MPa时不同平均应力下的棘轮应变率 Fig. 4 Ratcheting strain rate under different mean stress at stress amplitude 300 MPa | |
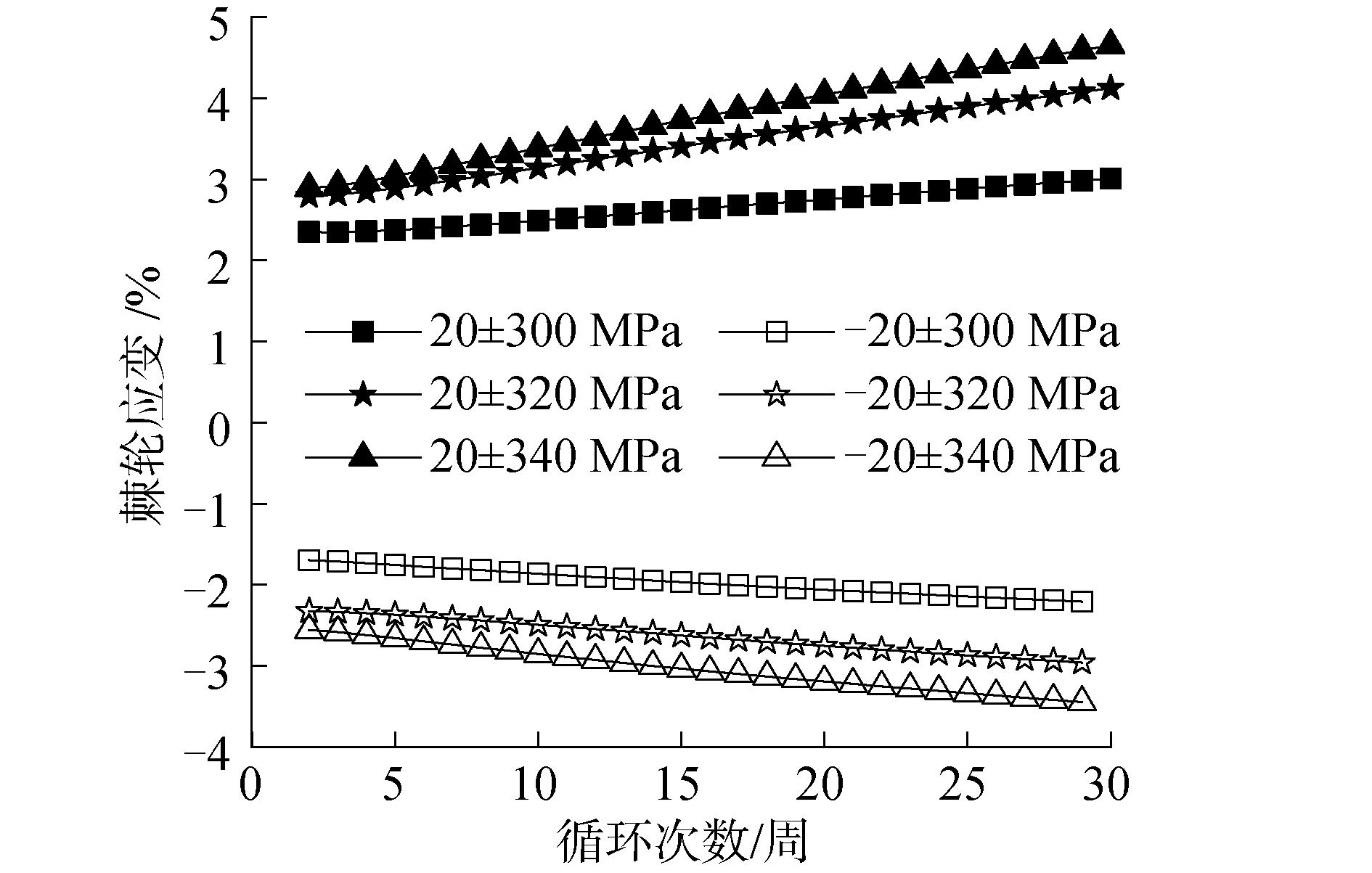
图 5所示为不同应力幅值下Q235钢的棘轮应变曲线。无论平均应力为正值还是负值,棘轮应变及棘轮应变速率均随应力幅值的增加而增大。
|
Download:
|
| 图 5 不同应力幅值条件下的棘轮应变 Fig. 5 Ratcheting strain at different stress amplitude | |
由上述分析可知,Q235钢在循环过程中产生的棘轮应变与平均应力、应力幅值和循环周次有关,根据唯象理论得出棘轮应变的预测模型:
| $ \varepsilon_{\mathrm{r}}=\left\{\begin{array}{ll} \frac{10^{-4} \lambda \eta \sigma_{\mathrm{m}}}{\sigma_{\mathrm{s} 0}^{\prime}-\sigma_{\mathrm{s} 0}} \exp (\eta) N+\frac{\varepsilon^{\prime}}{\eta}, & \sigma_{\mathrm{m}}>0 \\ \frac{10^{-4} \lambda \sigma_{\mathrm{m}}}{\left(\sigma_{\mathrm{s} 0}^{\prime}-\sigma_{\mathrm{s} 0}\right) \eta} \exp (\eta) N-\frac{\varepsilon^{\prime}}{\eta}, & \sigma_{\mathrm{m}}<0 \end{array}\right. $ | (2) |
式中:λ为材料参数,可通过试验数据获取,此处取λ=3.5;N为循环周次;σm为平均应力;σa为应力幅值;σ′s0、σs0分别为单向拉伸时的上、下屈服极限;η=σa/σs;ε′为循环加载试验时应力峰值在单向拉伸试验曲线中所对应的应变值。
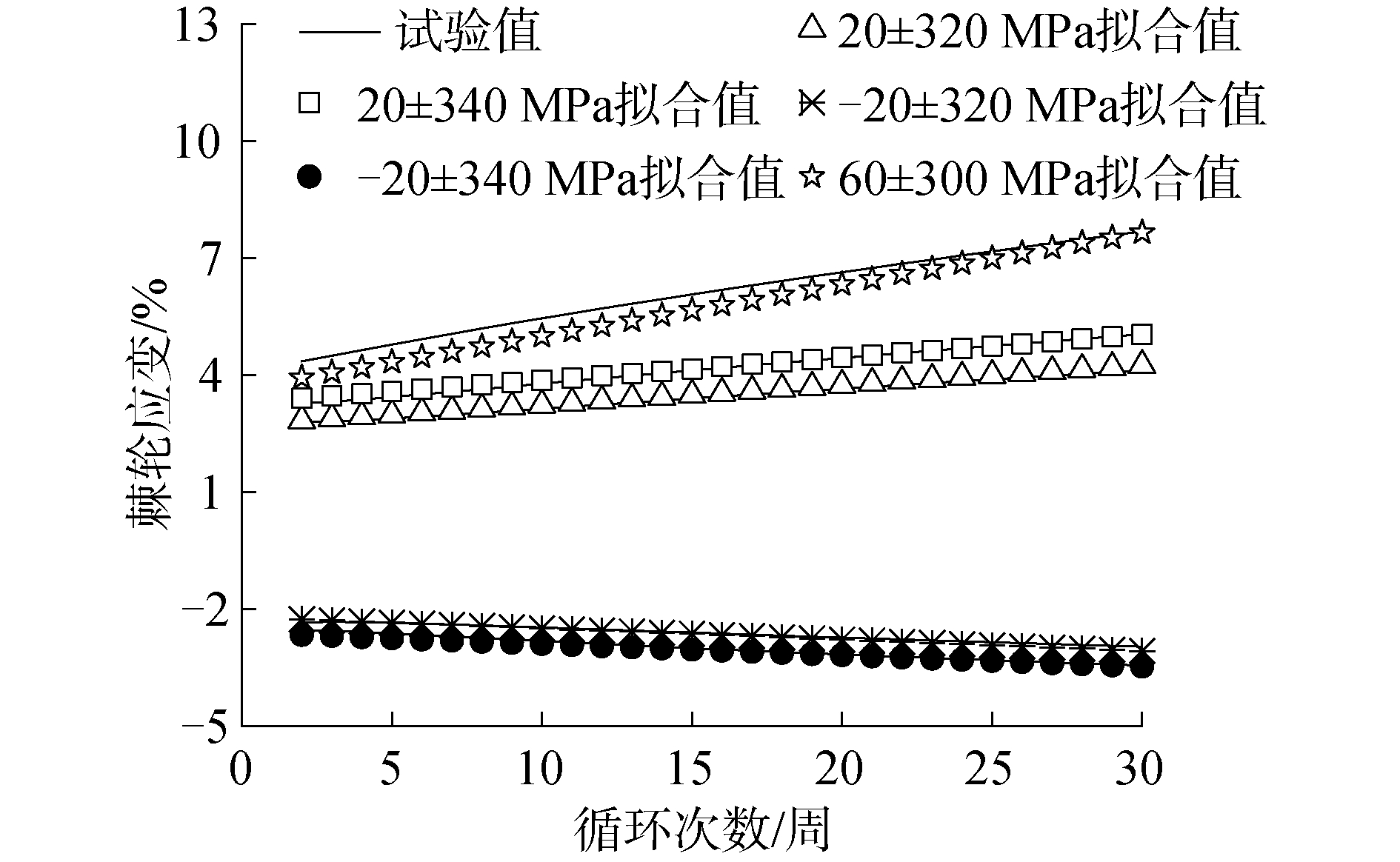
如图 6所示,将计算得到的棘轮应变与试验数据进行对比,两者吻合良好,说明该公式可以在非对称应力控制的循环加载试验中,较好的表征Q235钢的棘轮效应。
|
Download:
|
| 图 6 棘轮应变试验值与拟合值比较 Fig. 6 Comparison of test and fitting data of ratcheting stress | |
包申格效应在金属材料构件中一般扮演着负面的角色,会影响到材料的抗疲劳性能,造成工件不能满足正常的服役条件。试验发现,Q235钢在循环加载过程中产生了明显的包申格效应。为使计算结果更有可比性,在循环第1周取屈服平台的值作为屈服应力,其他不产生屈服平台且无明显屈服点的循环周次,取相应周次发生0.2%相对塑性变形时对应的应力值,即取该周应力应变曲线起始部分的斜率,然后偏移0.2%应变量对应得到的应力值。
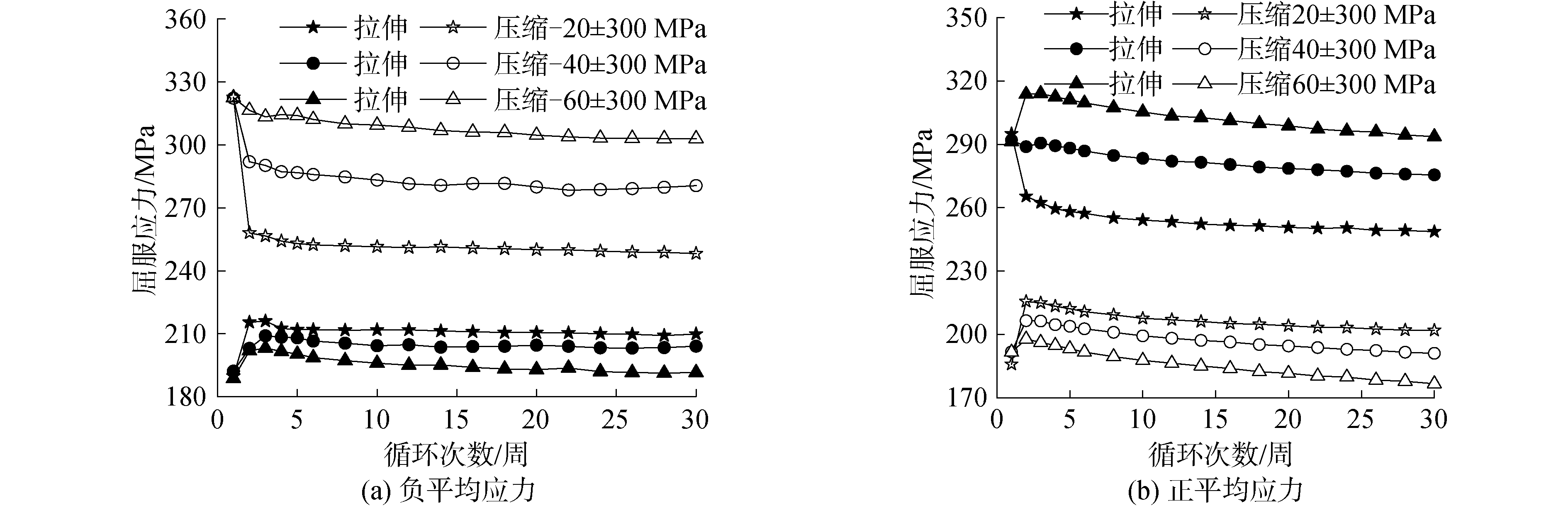
图 7给出了应力幅值为300 MPa,不同平均应力条件下的屈服应力随循环周次的变化曲线。图中显示,当平均应力为负值时,压缩屈服应力大于拉伸屈服应力,平均应力绝对值越大,拉伸屈服应力越小,压缩屈服应力越大;而当平均应力为正值时,拉伸屈服应力大于压缩屈服应力,平均应力越大,拉伸屈服应力越大,压缩屈服应力越小。且随循环周次的增加无论平均应力为正值还是负值,拉伸和压缩方向的屈服应力均呈现下降趋势。
|
Download:
|
| 图 7 不同平均应力条件下屈服应力随循环周次变化曲线 Fig. 7 Changing curves of yield stress with cycle numbers at different mean stresses | |
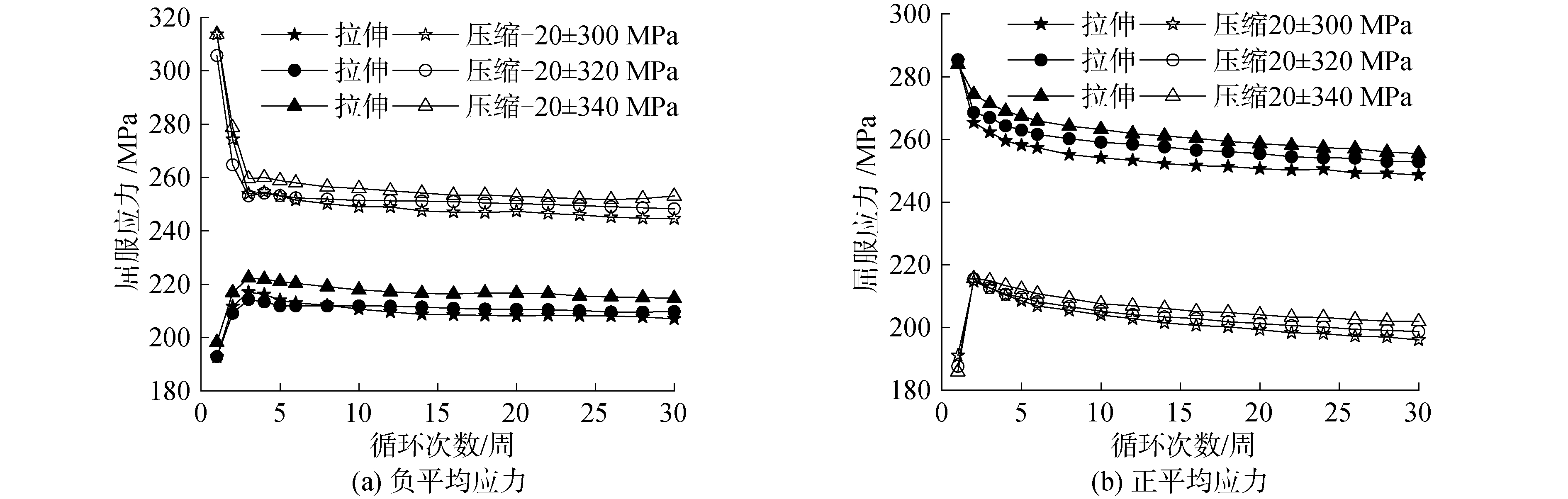
图 8为相同平均应力不同幅值条件下各循环周次的屈服应力。结合图 7的结论,可以得出,在应力载荷控制下,在拉伸和压缩2个方向哪个方向载荷大,对应方向的屈服应力相对较高。平均应力一定时,随应力幅值的增大,拉伸屈服应力和压缩屈服应力均略有增大,在循环到第30周时相邻载荷条件下的屈服应力相对变化量不超过2%。对比图 7和图 8,可以看出,平均应力和应力幅值分别增大所得到的屈服应力变化规律并不一致,相同峰值条件下,平均应力比应力幅值对屈服应力的影响更为明显。这是因为,平均应力为负值时,平均应力增大,应力峰值减小,应力谷值绝对值增大;平均应力为正值时,平均应力增大,应力峰值增大,应力谷值绝对值减小;而应力幅值增大,正负平均应力下的应力峰值和应力谷值的绝对值均增大。
|
Download:
|
| 图 8 不同应力幅值下的屈服应力变化曲线 Fig. 8 Changing curve of yield stress at different stress amplitude and same mean stresses | |
从上述对屈服应力的数据分析可以得出,屈服应力是关于循环周次、平均应力和应力幅值的函数。当外加载荷大于上屈服极限时,屈服应力σs随循环周次的演化规律为:
| $ \sigma_{s}=\left\{\begin{array}{ll} \sigma_{i}, & N=1 \\ \left(\mu+\lambda_{i}\right) \sigma_{i} \eta^{\frac{M_{i}}{\sqrt{N}}}, & N>1 \end{array}\right. $ | (3) |
式中:i=1, 2分别代表拉伸和压缩;σi为第1周屈服应力值,平均应力为正值时,拉伸屈服应力为289 MPa,压缩屈服应力为189 MPa;平均应力为负值时,拉伸屈服应力为191 MPa,压缩屈服应力为320 MPa;λi为材料参数,通过试验获取,平均应力为正值时,λ1取0.78,λ2取1.10;平均应力为负值时,λ1取0.87,λ2取1.15;

|
Download:
|
| 图 9 屈服应力试验值与拟合值比较 Fig. 9 Comparison of test data and fitting data about yield stress | |
包申格系数B与循环载荷作用下预拉伸/压缩变形后屈服应力的变化直接相关,可对包申格效应进行定量表征和描述,其表达式为:
| $ B=\left\{\begin{array}{ll} \frac{\sigma_{0.2}^{-}-\sigma_{0.2}^{+}}{\sigma_{0.2}^{-}}, & \sigma_{\mathrm{m}}<0 \\ \frac{\sigma_{0.2}^{+}-\sigma_{0.2}^{-}}{\sigma_{0.2}^{+}}, & \sigma_{\mathrm{m}}>0 \end{array}\right. $ | (4) |
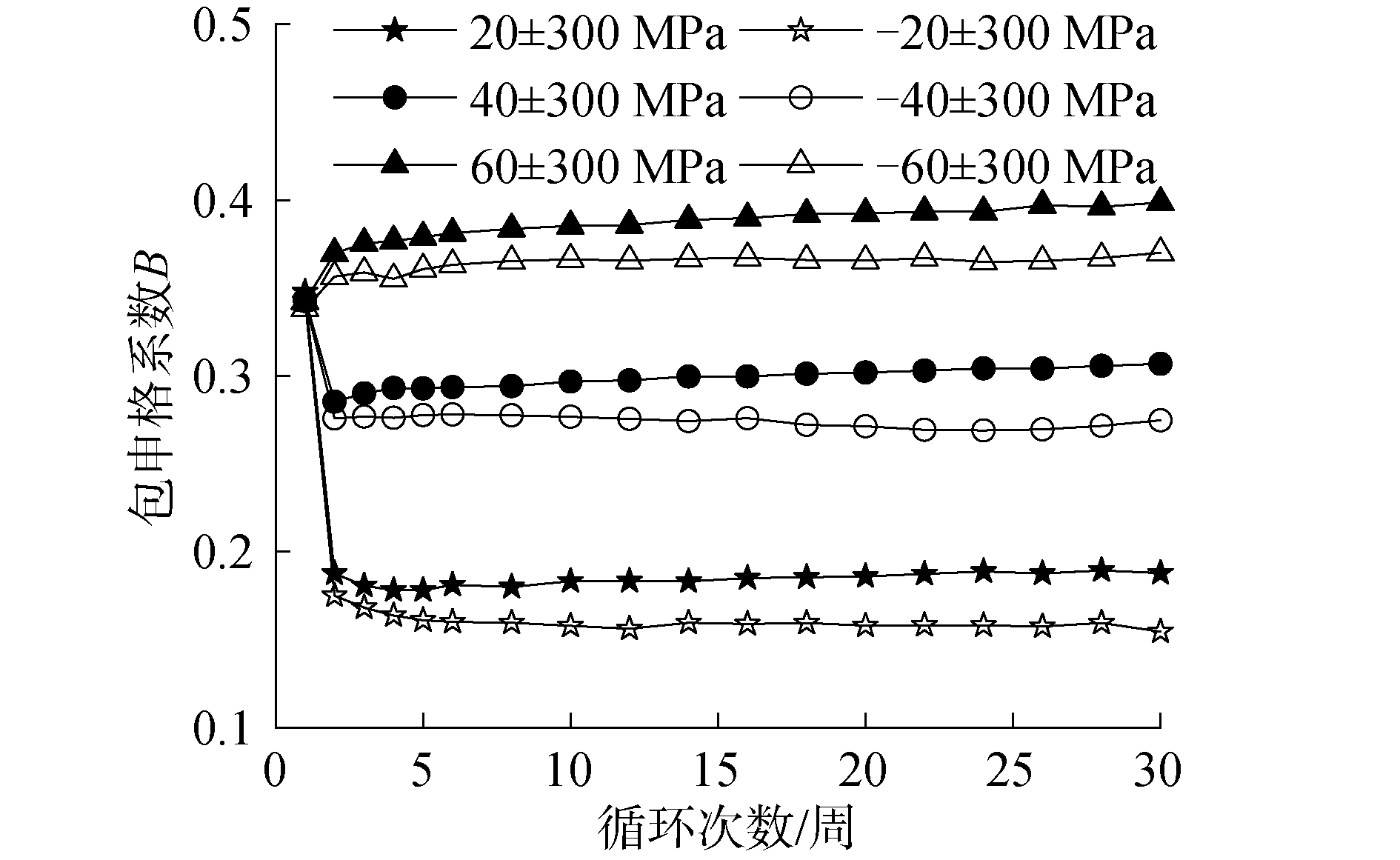
式中:σ0.2+、σ0.2-分别为材料的拉伸和压缩屈服应力。屈服应力下降越大,包申格系数越高,包申格效应越明显。Q235钢在幅值为300 MPa,不同平均应力下包申格系数的变化如图 10所示。
|
Download:
|
| 图 10 应力幅值为300 MPa时包申格系数随循环周次的变化 Fig. 10 The variation of Bauschinger coefficient with cycle numbers at stress amplitude 300 MPa | |
可以看出,不同应力状态第1周时的包申格系数基本相同,约为0.346,说明Q235在经历一定的预拉伸/压缩变形后再反向压缩/拉伸时均表现出明显的包申格效应。从第2周开始,包申格系数随平均应力的变化表现出较大差异,但相同应力条件下则变化很小。因此,可以用第2周的包申格系数来描述材料的包申格效应。平均应力绝对值越大,包申格效应越显著。平均应力绝对值相同时,Q235钢在正平均应力条件下表现出的包申格效应更明显。
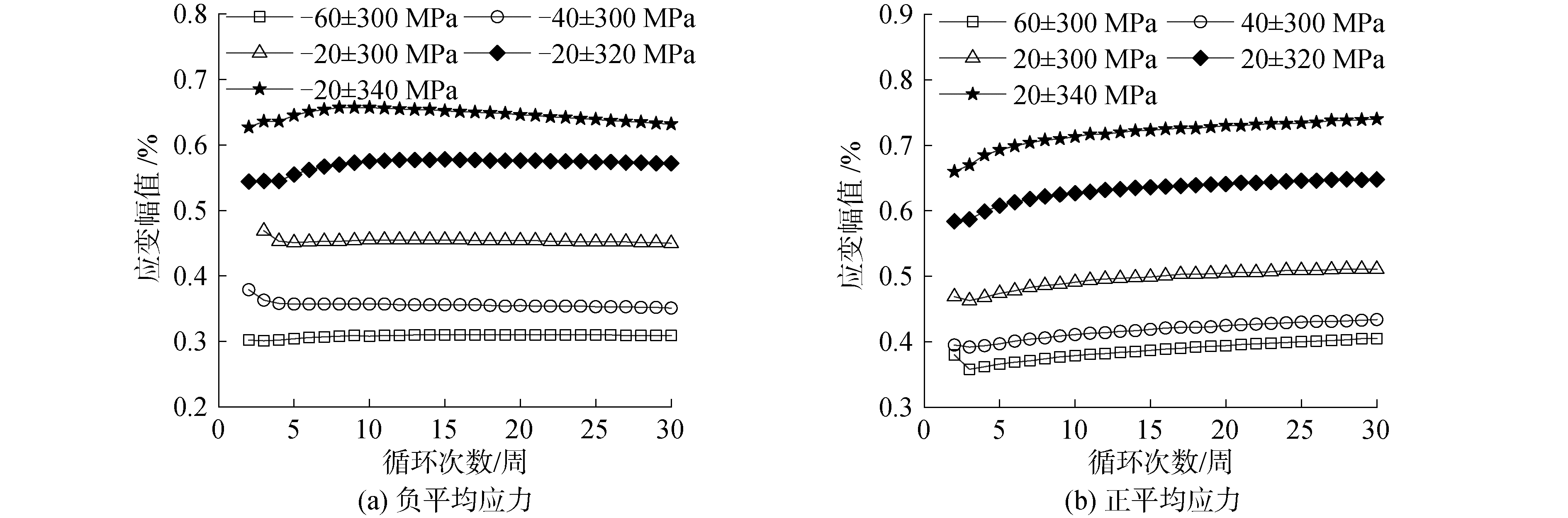
4 循环软/硬化特性分析Q235钢在不同应力组合条件下表现出不同的循环软/硬化行为。不同平均应力和应力幅值条件下的响应应变幅值随着循环周次的变化曲线如图 11所示。可以看出,当平均应力为负值时,表现出轻微的硬化特性;当平均应力为正值时,则表现出明显的软化特性,但2种工况下,应力幅值越大应变幅值越大,而平均应力绝对值越大应变幅值却越小。随循环周次的增加,Q235钢循环软/硬化速率在第20周之后趋于稳定。将不同应力条件下的循环软/硬化速率稳定值列于表 2,负值表示循环硬化,正值表示循环软化。
|
Download:
|
| 图 11 不同条件下的应变幅值变化曲线 Fig. 11 Changing curve of strain amplitude at different conditions | |
| 表 2 不同条件下的循环软/硬化速率 Table 2 Cyclic softening/hardening rate at different conditions |
比较发现,负平均应力时,循环硬化速率随平均应力绝对值的增大逐渐减小,即硬化程度减弱;正平均应力时,循环软化速率随平均应力的增大呈增长趋势,即软化程度增强;应力幅值增大使循环软硬化速率均增加,软硬化程度更显著。
5 结论1) 在非对称应力循环载荷作用下,负平均应力产生负棘轮应变,正平均应力产生正棘轮应变。
2) 外加载荷平均应力相同,应力幅值增大,或外加载荷应力幅值相同,平均应力绝对值增大,均会造成棘轮应变绝对值增大,棘轮应变率升高。
3) 在非对称应力循环载荷作用下,Q235钢表现出明显的包申格效应。当平均应力为负值时,压缩屈服应力大于拉伸屈服应力;当平均应力为正值时,拉伸屈服应力大于压缩屈服应力。在循环的第1周屈服应力值基本相同,可以用第2周的包申格系数来表征材料的包申格效应。
4) 当外加载荷平均应力为负值时,Q235钢表现出循环硬化特性,平均应力绝对值越小或应力幅值越大,循环硬化现象越明显;当外加载荷平均应力为正值时,Q235钢表现出循环软化特性,平均应力或应力幅值越大,循环软化现象越明显。
| [1] |
陈旭, 焦荣, 田涛. 棘轮效应预测及其循环本构模型研究进展[J]. 力学进展, 2003, 33(4): 461-470. CHEN Xu, JIAO Rong, TIAN Tao. Research advances of ratcheting effects and cyclic constitutive models[J]. Advances in mechanics, 2003, 33(4): 461-470. (  0) 0)
|
| [2] |
LIN Y C, LIU Zhenghua, CHEN Xiaomin, et al. Uniaxial ratcheting and fatigue failure behaviors of hot-rolled AZ31B magnesium alloy under asymmetrical cyclic stress-controlled loadings[J]. Materials science and engineering: A, 2013, 573: 234-244. DOI:10.1016/j.msea.2013.03.004 (  0) 0)
|
| [3] |
赵路远, 黄俊, 陈涛, 等. 7075铝合金的单轴棘轮行为[J]. 机械工程材料, 2018, 42(9): 21-25. ZHAO Luyuan, HUANG Jun, CHEN Tao, et al. Uniaxial ratcheting behavior of 7075 aluminum alloy[J]. Materials for mechanical engineering, 2018, 42(9): 21-25. (  0) 0)
|
| [4] |
PAUL S K, SIVAPRASAD S, DHAR S, et al. Key issues in cyclic plastic deformation: experimentation[J]. Mechanics of materials, 2011, 43(11): 705-720. DOI:10.1016/j.mechmat.2011.07.011 (  0) 0)
|
| [5] |
PAUL S K, SIVAPRASAD S, DHAR S, et al. Cyclic plastic deformation behavior in SA333 Gr. 6 C-Mn steel[J]. Materials science and engineering: A, 2011, 528(24): 7341-7349. DOI:10.1016/j.msea.2011.06.009 (  0) 0)
|
| [6] |
PAUL S K, SIVAPRASAD S, DHAR S, et al. Cyclic plastic deformation and damage in 304LN stainless steel[J]. Materials science and engineering: A, 2011, 528(15): 4873-4882. DOI:10.1016/j.msea.2011.03.048 (  0) 0)
|
| [7] |
XIANG Yang, VLASSAK J J. Bauschinger effect in thin metal films[J]. Scripta materialia, 2005, 53(2): 177-182. DOI:10.1016/j.scriptamat.2005.03.048 (  0) 0)
|
| [8] |
CHAWLA N, JESTER B, VONK D T. Bauschinger effect in porous sintered steels[J]. Materials science and engineering: A, 2003, 346(1/2): 266-272. (  0) 0)
|
| [9] |
张功庭, 盛光敏, 黄利. 金属包申格效应的表征、影响因素与机理研究进展[J]. 材料导报, 2008, 22(S3): 135-138. (  0) 0)
|
| [10] |
盛光敏, 张功庭, 阎春. AZ31镁合金包辛格效应研究[J]. 稀有金属材料与工程, 2011, 40(4): 615-619. SHENG Guangmin, ZHANG Gongting, YAN Chu. Research of bauschinger effect of AZ31 magnesium alloy[J]. Rare metal materials and engineering, 2011, 40(4): 615-619. (  0) 0)
|
| [11] |
BAIRSTOW L. The elastic limits of iron and steel under cyclical variations of stress[J]. Proceedings of the royal society A: mathematical, physical and engineering sciences, 1909, 82(557): 483-485. (  0) 0)
|
| [12] |
LIN Y C, LIU Zhenghua, CHEN Xiaomin, et al. Uniaxial ratcheting and fatigue failure behaviors of hot-rolled AZ31B magnesium alloy under asymmetrical cyclic stress-controlled loadings[J]. Materials science and engineering: A, 2013, 573: 234-244. DOI:10.1016/j.msea.2013.03.004 (  0) 0)
|
| [13] |
DUTTA K, SIVAPRASAD S, TARAFDER S, et al. Influence of Asymmetric cyclic loading on substructure formation and ratcheting fatigue behaviour of AISI 304LN stainless steel[J]. Materials science and engineering: A, 2010, 527(29/30): 7571-7579. (  0) 0)
|
| [14] |
DUTTA K, RAY K K. Ratcheting strain in interstitial free steel[J]. Materials science and engineering: A, 2013, 575: 127-135. DOI:10.1016/j.msea.2013.02.052 (  0) 0)
|
| [15] |
XIE Xuefang, JIANG Wenchun, CHEN Jingkai, et al. Cyclic hardening/softening behavior of 316L stainless steel at elevated temperature including strain-rate and strain-range dependence: experimental and damage-coupled constitutive modeling[J]. International journal of plasticity, 2019, 114: 196-214. DOI:10.1016/j.ijplas.2018.11.001 (  0) 0)
|
| [16] |
WANG Chen, FAN Jiansheng, XU Liyan, et al. Cyclic hardening and softening behavior of the low yield point steel: implementation and validation[J]. Engineering structures, 2020, 210: 110220. DOI:10.1016/j.engstruct.2020.110220 (  0) 0)
|
| [17] |
GUO Yibin, HO H C, CHUNG K F, et al. Cyclic deformation characteristics of S355 and S690 steels under different loading protocols[J]. Engineering structures, 2020, 221: 111093. DOI:10.1016/j.engstruct.2020.111093 (  0) 0)
|
| [18] |
KROLO P, GRANDIĆ D, SMOLČIĆ Ž. Experimental and numerical study of mild steel behaviour under cyclic loading with variable strain ranges[J]. Advances in materials science and engineering, 2016, 2016: 7863010. (  0) 0)
|
| [19] |
GUO Yi, LUO Yunrong, WANG Qingyuan. Mean strain effect on the cyclic stress-strain behavior of steel structure materials Q235[J]. Advanced materials research, 2012, 602-604: 430-434. DOI:10.4028/www.scientific.net/AMR.602-604.430 (  0) 0)
|
| [20] |
WANG J G, JIA Weiping, JU Dongying. Cyclic deformation behavior and fatigue crack propagation of low carbon steel prestrained in tension[J]. Advances in materials science and engineering, 2009, 2009: 657284. (  0) 0)
|
| [21] |
高柳. 不同拉压循环下Q235钢单轴拉伸力学性质研究[D]. 南宁: 广西大学, 2016: 32-50. GAO Liu. Effect of fatigue damage on the dynamic tensile behavior of Q235 abstract[D]. Nanning: Guangxi University, 2016: 32-50. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


