2. 南京理工大学 能源与动力工程学院, 江苏 南京 210094
2. School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China
发射药包括单基发射药、双基发射药和三基发射药,是枪炮的重要能源来源。以硝化棉(nitrocotton, NC)和硝化甘油(nitroglycerine, NG)为基本能量体系的简称为双基药,具有结构均匀、能量高及性能稳定等优点[1],但在低温下力学性能较差,撞击条件下极易发生破碎,引发安全事故。以硝化棉(NC)和硝化三乙二醇(triethyleneglycol dinitrate, TEGDN)体系的火药简称太根药,TEGDN增塑剂感度低、热安定性较NG好,毒性及挥发性较低。在发射药中进行添加TEGDN提高发射药的力学性能[2],TEGDN质量分数越高,抗拉强度越大,材料的延伸率逐渐增加。赵凤起等[3]利用高压DSC研究了TEGDN的热分解性能,提出了有压力条件下TEGDN的反应机理,并研究了不同TEGDN含量[4-7]的太根药的分解机理及热安全性。何卫东等[8]利用DSC方法和密闭爆发器试验,研究了加入黑索金和聚醚聚氨酯体材料改性的太根发射药,研究发现RDX颗粒的大小对改性材料对NC、NG和TEGDN的影响较大。太根发射药的燃烧性能是发射药重要的性能,通过对其燃烧研究可以为发射药的应用提供基础。火药燃烧模型主要分为3类[9]:1)只考虑凝聚相和气相质量能量方程,不考虑化学反应的简单的模型;2)基于简单化学反应的总包模型;3)考虑基元反应的详细化学反应的模型。在双基药的简单模型中,Bechstead[10]改进了BDP模型并应用到双基药,能够通过初始的温度,火药能量得到一个与压强有关的燃烧速度公式,且与实验拟合较好。Brewster等[11]将WSB燃烧模型应用到双基药,该模型考虑了双基药的辐射传热,并对温度曲线,振荡燃烧过程进行了预测。由于简单模型中没有考虑物质之间的化学反应过程,无法对燃烧波进行预测,总包反应能够对能量项和组分输运过程进行模拟。Cohen等[12]建立了HMX凝聚相和气相的化学反应过程,并且计算值与实验值吻合较好。Bizot等[13]建立了考虑凝聚相三组分的化学反应和气相4个化学反应的模型,计算得到的燃烧速度、表面温度分布和暗区厚度与试验结果较好。Yang等[14]在Beckstead[13]模型基础上提出了包含2步凝聚相反应和5步气相反应的燃烧模型,模拟结果与试验测试的燃烧速度、温度及组分分布和暗区厚度非常吻合,并应用该模型研究了固体火箭发动机的振荡燃烧,李腾等[15]利用该模型计算了微尺度推进器的内流场过程。本文为了研究太根药的气相燃烧过程,建立考虑气相总包化学反应的燃烧模型,并对该模型进行数值求解,为太根药的应用提供理论基础和指导。
1 火药燃烧模型建立太根发射药的主要成分是NC([C6H7O2(ONO2)a(OH)3-a]n)、NG(C3H5N3O9)及TEGDN(C6H12N2O8),其中a为酯化度,n为聚合度,分解过程分别为:
NC[16]:C6H7N3O11→3NO2+3CH2O+CHO+CO+C
NG[16]:C3H5N3O9→3NO2+2CH2O+HCO
TEGDN[4]:C6H12N2O8→2NO2+4CH2O+C2H4
双基药的质量分数不同,不同组分的双基药(DBP)的分解后各组分质量分数也是不同的,质量分数52%NC、43%NG和5%其他组分的双基药[15]的2个凝聚相反应为:
反应1:
| $ \begin{array}{l} \mathrm{DBP} \rightarrow 2.49 \mathrm{NO}_{2}+2.36 \mathrm{CH}_{2} \mathrm{O}+ \\ 1.26(\mathrm{CHO})_{2}+0.17 \mathrm{CO}+0.3 \mathrm{C} \end{array} $ |
反应2:
| $ \begin{array}{c} \mathrm{NO}_{2}+0.56 \mathrm{CH}_{2} \mathrm{O}+0.16(\mathrm{CHO})_{2} \rightarrow \\ \mathrm{NO}+0.38 \mathrm{CO}+0.5 \mathrm{CO}_{2}+0.5 \mathrm{H}_{2} \mathrm{O}+0.22 \mathrm{H}_{2} \end{array} $ |
| $ \frac{\partial}{\partial t}(\rho \phi)+\operatorname{div}(\rho U \phi)=\operatorname{div}(\Gamma \operatorname{grad} \phi)+S_{\phi} $ | (1) |
式中:ρ为流体密度;U为广义流体速度;Γ为广义扩散系数;Sϕ为广义源项;ϕ为通用变量。燃气为纯气相可压理想气体,气体粘度采用Sutherland方程描述。
气相反应区域控制方程及化学反应速率方程为:
反应3:
| $ \begin{array}{c} \mathrm{NO}_{2}+0.56 \mathrm{CH}_{2} \mathrm{O}+0.16(\mathrm{CHO})_{2} \rightarrow \\ \mathrm{NO}+0.38 \mathrm{CO}+0.5 \mathrm{CO}_{2}+0.5 \mathrm{H}_{2} \mathrm{O}+0.22 \mathrm{H}_{2} \end{array} $ |
反应4:
| $ \mathrm{CH}_{2} \mathrm{O}+\mathrm{CH}_{2} \mathrm{O} \rightarrow \mathrm{CO}+0.5 \mathrm{C}_{2} \mathrm{H}_{4}+0.5 \mathrm{H}_{2} \mathrm{O} $ |
反应5:
| $ (\mathrm{CHO})_{2}+(\mathrm{CHO})_{2} \rightarrow 4 \mathrm{CO}+2 \mathrm{H}_{2} $ |
反应6:
| $ \begin{array}{c} \mathrm{NO}+0.16 \mathrm{CO}+0.12 \mathrm{C}_{2} \mathrm{H}_{4}+0.12 \mathrm{H}_{2} \rightarrow \\ 0.5 \mathrm{~N}_{2}+0.40 \mathrm{CO}_{2}+0.36 \mathrm{H}_{2} \mathrm{O} \end{array} $ |
反应7:
| $ \mathrm{C}+\mathrm{NO} \rightarrow 4 \mathrm{CO}+0.5 \mathrm{~N}_{2} $ |
反应3的反应速率:
| $\dot{\omega}_{\mathrm{NO}_{2}}=-A_{\mathrm{NO}_{2}} p^{0.39} \exp \left(\frac{-E_{\mathrm{NO}_{2}}}{R_{u} T}\right) \rho_{g} Y_{\mathrm{NO}_{2}} $ | (2) |
反应4的反应速率:
| $ \begin{aligned} \dot{\omega}_{\mathrm{CH}_{2} \mathrm{O}}=&-0.56 \frac{W_{\mathrm{CH}_{2} \mathrm{O}}}{W_{\mathrm{NO}_{2}}} \dot{\omega}_{\mathrm{NO}_{2}}-\\ & A_{\mathrm{CH}_{2} \mathrm{O}} \exp \left(\frac{-E_{\mathrm{CH}_{2} \mathrm{O}}}{R_{u} T}\right) \rho_{\mathrm{g}}^{2} Y_{\mathrm{CH}_{2} \mathrm{O}}^{2} \end{aligned} $ | (3) |
反应5的反应速率:
| $ \begin{aligned} \dot{\omega}_{(\mathrm{CHO})_{2}}= -0.16 \frac{W_{(\mathrm{CH} \mathrm{O})_{2}}}{W_{\mathrm{NO}_{2}}} \dot{\omega}_{\mathrm{NO}_{2}}-\\ A_{(\mathrm{CH} \mathrm{O})_{2}} \exp \left(\frac{-E_{(\mathrm{CHO})_{2}}}{R_{u} T}\right) \rho_{g}^{2} Y_{(\mathrm{CHO} )_{2}} \end{aligned} $ | (4) |
反应6的反应速率:
| $ \begin{array}{c} \dot{\omega}_{\mathrm{NO}}=\frac{W_{\mathrm{No}}}{W_{\mathrm{NO}_{2}}} \dot{\omega}_{\mathrm{NO}_{2}}-\frac{W_{\mathrm{No}}}{W_{\text {carb }}} \dot{\omega}_{\text {carb }}- \\ A_{\mathrm{N} 0} \exp \left(\frac{-E_{\mathrm{NO}}}{R_{u} T}\right) \rho_{g}^{2} Y_{\mathrm{NO}}^{2} \end{array} $ | (5) |
反应7的反应速率:
| $ \dot{\omega}_{\text {carb }}=-A_{\text {carh }} p \tilde{W} \exp \left(\frac{-E_{\text {carb }}}{R_{u} T}\right) \rho_{g} Y_{\text {carb }} Y_{\mathrm{NO}} $ | (6) |
能量源项:
| $ \dot{q}_{c}=\sum\limits_{j=3}^{7} \omega_{j} Q_{j} $ | (7) |
式中:
火药气体的主要物性参数及化学动力学参数[14]如表 1所示。
| 表 1 火药气体化学动力学参数 Table 1 Propellant gas thermal chemical parameters |
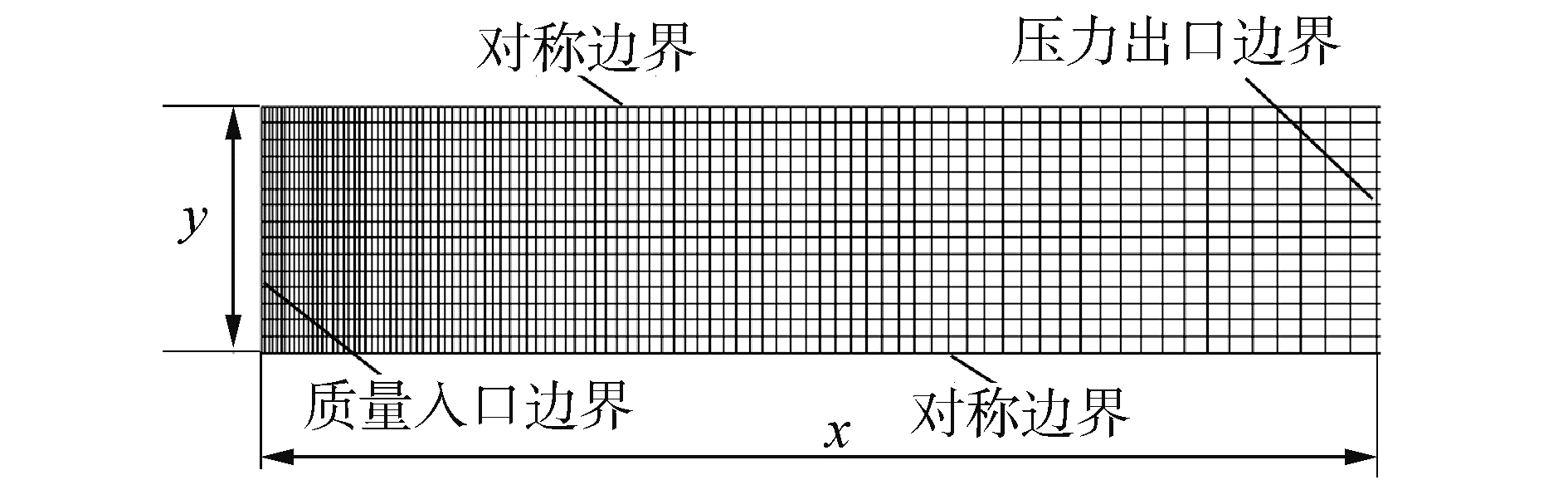
计算区域为火药气相区域,由于靠近凝聚相表面的化学反应层比较薄且反应区域主要在这一薄层内完成,对表层网格进行加密处理。计算区域尺寸为x=5 mm、y=0.1 mm,网格示意如图 1所示。
|
Download:
|
| 图 1 气相燃烧区域网格示意 Fig. 1 Calculation mesh of propellant surface | |
火药燃烧气相燃面边界条件为质量入口边界,质量入口流率边界条件:
| $ \dot{m}=\rho_{p} r_{b} $ | (8) |
式中:
气相区域求解采用Fluent软件进行求解,气相区域的各个化学反应速率、化学反应源项及组分项的对流扩散方程用UDF编写进行求解。流场的计算采用隐式稳态求解器,压力速度耦合方法为SIMPLEC算法,当质量、速度残差小于10-3,能量项小于10-6认为计算例收敛。
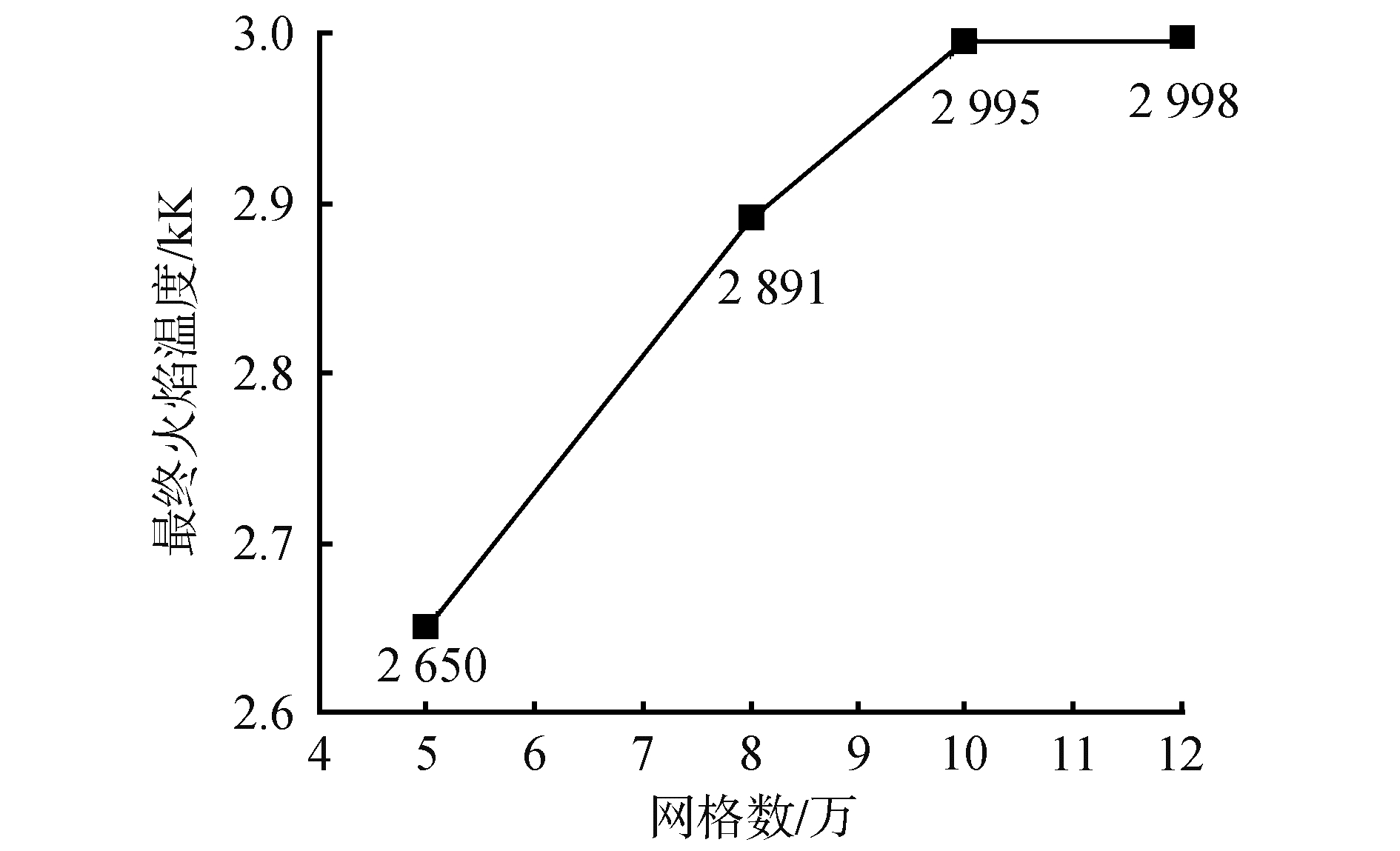
1.3 网格无关性验证网格尺寸对计算结果有显著影响,为了找到既满足计算结果准确性又节省计算资源的网格划分方法。计算区域进行5万、8万、10万和12万网格进行数值计算。由于最终火焰温度是计算结果的重要参考,故选其进行网格无关性验证具有一定的代表性。不同网格数量计算得到的最终火焰温度如图 2所示,从图 2可以看出当网格数为5万和8万时,火焰最终温度分别为2 650 K和2 891 K;网格数目为10万和12万时,火焰最终温度为2 995 K和2 998 K;在网格数小于10万时,随着网格数目的增加最终火焰温度明显增加;当网格数大于10万时,最终火焰温度基本不变,可以认为计算结果与网格数无关。本研究选取的网格数为10万,火药表面网格最薄层为1×10-8 m。
|
Download:
|
| 图 2 不同网格数计算得到的最终火焰温度 Fig. 2 End flame zone temperature distribution in different calculation meshes | |
环境压力p=1.01 MPa,气相区域质量入口边界初始温度T0=650 K,计算得到气相火焰区域的温度分及CO质量分数分布云图如图 3所示。气相最终火焰温度为2 995 K与文献[14]结果3 006 K吻合较好。从图 3可以看出,NO质量分数先增加后减小,这主要是在嘶嘶区的NO2、CH2O及(CHO)2之间进行的化学反应3生成较多NO;随着温度升高,在发光区内,NO与C的化学反应7进行反应,NO反应至结束,火焰温度升高达到最终火焰温度。

|
Download:
|
| 图 3 气相区域温度和NO质量分数分布云图 Fig. 3 Temperature and NO mass fraction distribution in the gas phase | |
暗区及最终火焰区的各个物质质量分数如表 2所示。本文计算的结果与文献[14, 16]计算得到的嘶嘶区及最终火焰区的质量分数对比吻合较好,说明本文计算方法及模型建立准确,能够较好地描述火药的燃烧过程。
| 表 2 暗区及最终火焰的质量分数比较 Table 2 Comparison of the mass fraction in dark zone and end flame zon |
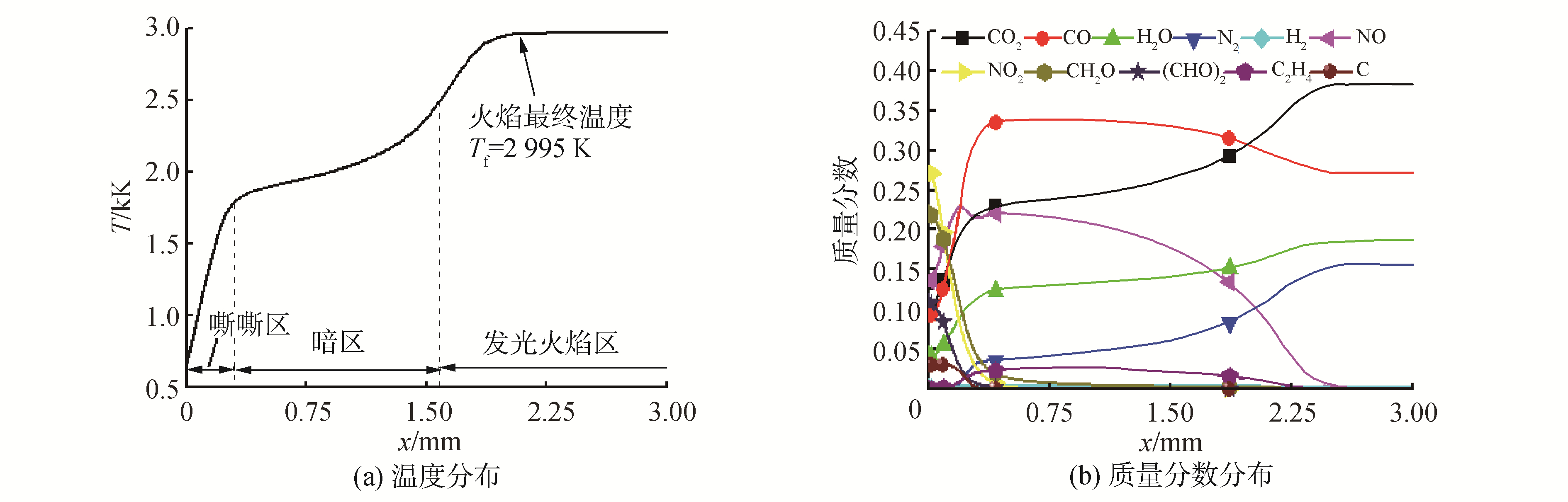
气相火焰区域温度及各种物质质量分数的分布曲线如图 4所示。由图 4可见,在x < 0.25 mm的嘶嘶区温度较低,由于反应3的反应活化能低,该反应速率较快,NO2、CH2O及(CHO)2质量分数减小,同时生成NO、CO2、CO和H2O等物质质量分数明显增加。在暗区,气体温度约为2 000 K,活化能较高的反应4和反应5反应开始反应,CH2O和(CHO)2被消耗,质量分数逐渐减小,同时生成CO2、N2和H2O等质量分数逐渐增加;由于反应4和反应5分别是放热和吸热反应且反应放热不明显,导致暗区整体温度升高不明显。在发光区,气体温度大于2 500 K,活化能最高的反应6和反应7开始反应,NO、CO、C2H4和H2等物质逐渐反应,质量分数降低;同时生成N2、CO2和H2O,CO2和H2O,质量分数增加;由于反应6和反应7是明显的放热反应,释放出大量的热量使气体温度升高到最终火焰温度Tf=2 995 K。
|
Download:
|
| 图 4 气相区域温度及质量分数分布 Fig. 4 Temperature and mass fraction in gas phase | |
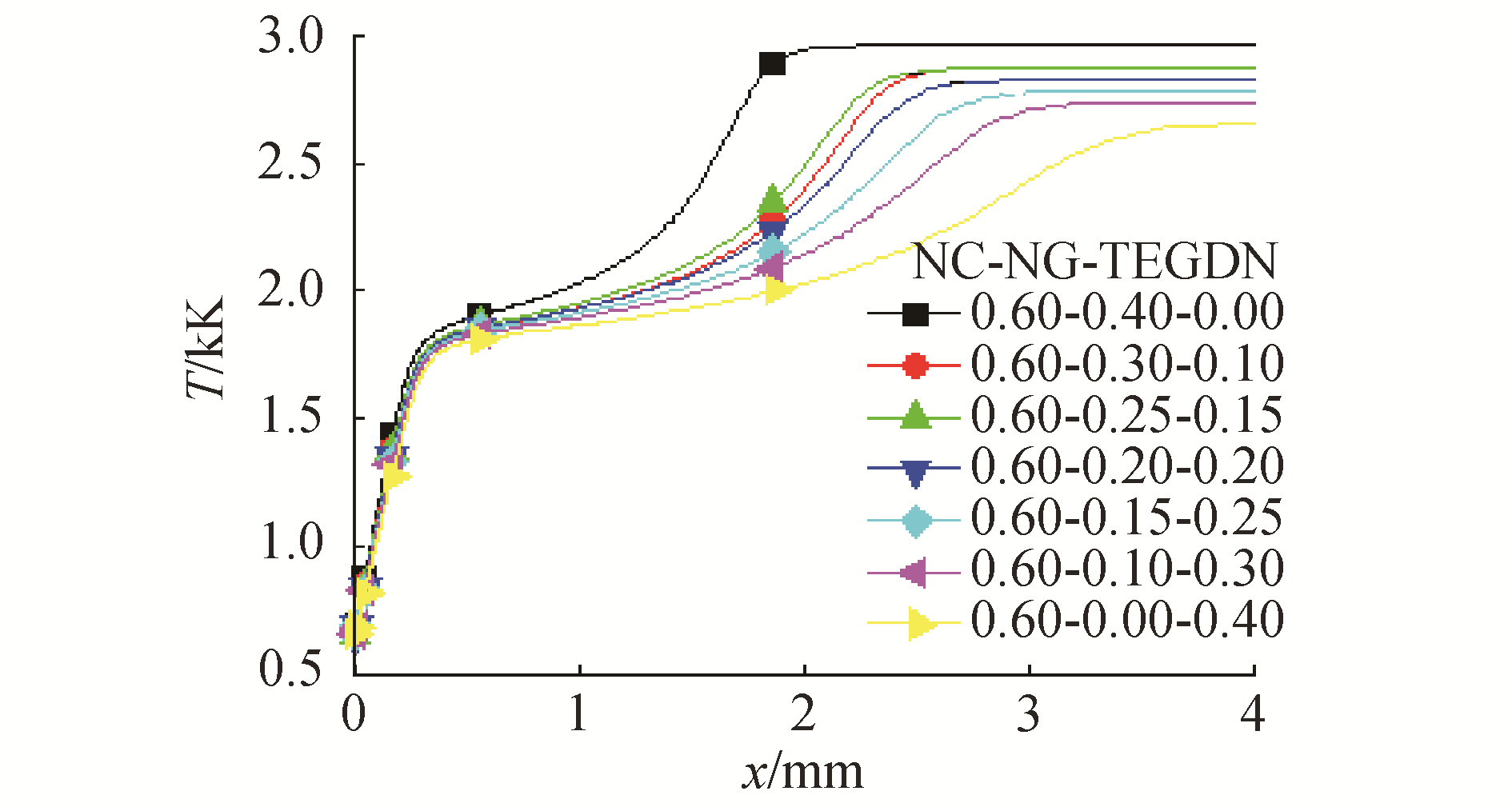
太根药是由NC、NG和TEGDN为主要成分的火药。NC质量分数为60%,不同NG与TEGDN质量分数的太根药的温度曲线如图 5所示,随着TEGDN质量分数由0.10增加到0.40,火焰最终的温度由2 887 K降低到2 654 K。火药力f为:
| $ f=R T $ | (9) |
|
Download:
|
| 图 5 不同TEGDN含量温度的分布 Fig. 5 Temperature distributions in different TEGDN mass fractions | |
式中:R为气体常数;T为火焰最终温度。
火药力将随着TEGDN含量增加而减小。NG与TEGDN的含量对暗区厚度影响不大,随着TEGDN含量增加,最终火焰厚度由2.68 mm增加到3.63 mm,火焰发光区变厚。
不同TEGDN含量的嘶嘶区内NO2、(CHO)2和CH2O质量分数如图 6。嘶嘶区厚度小于0.40 mm,随着TGEDN含量增加,NO2和(CHO)2的质量分数分别由0.33减小到0.27和0.12减小到0.07,CH2O质量分数由0.21增加到0.31。
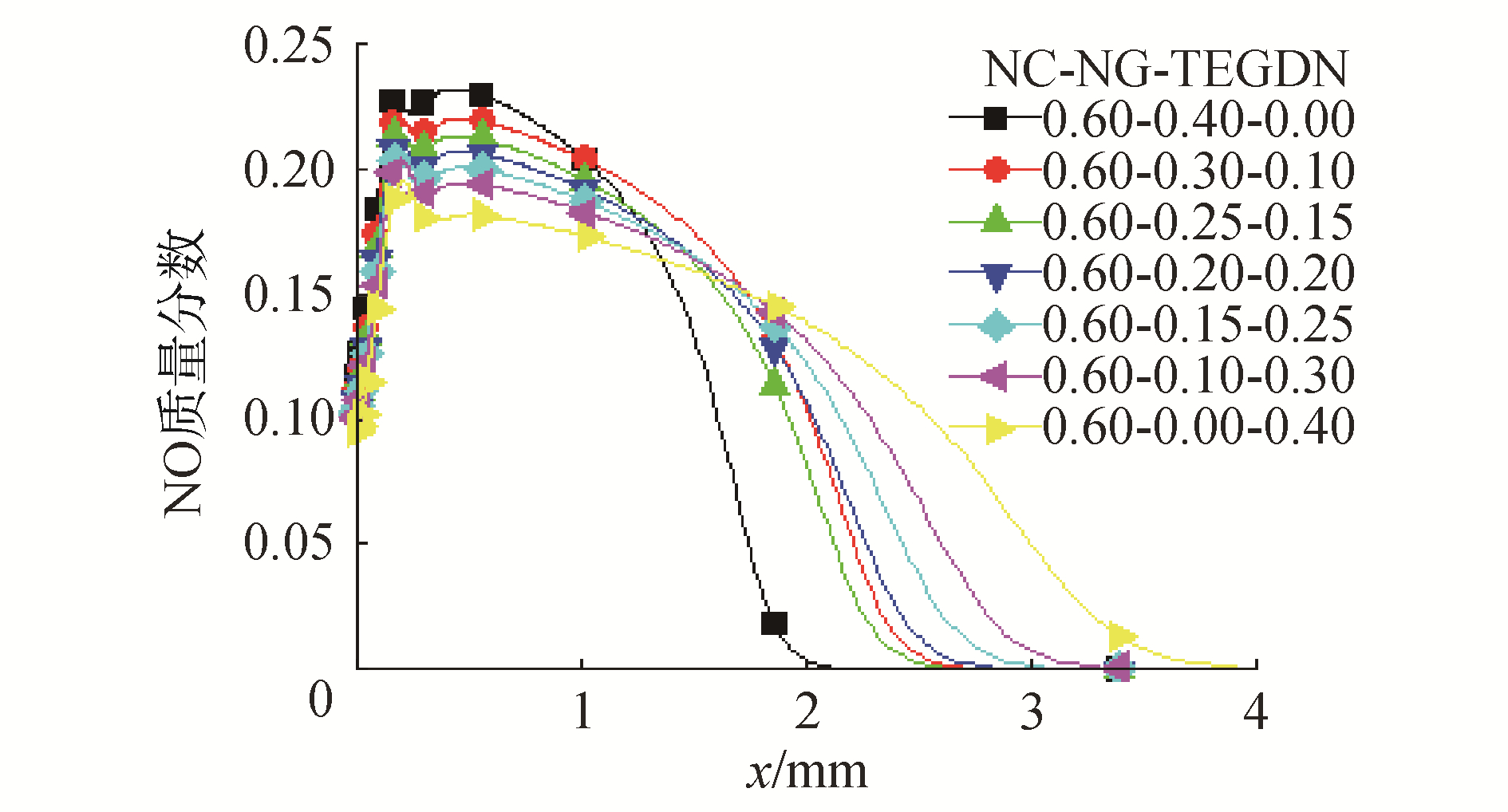
气相火焰区域NO的质量分数如图 7所示。在火焰的嘶嘶区,NO的质量分数增加,且随着TEGDN含量的增加,火焰厚度增加,NO的质量分数的最大值由0.23降低到0.18。

|
Download:
|
| 图 6 不同TEGDN含量嘶嘶区主要物质质量分布 Fig. 6 Main spices distributions in fizz zone of different TEGDN mass fractions | |
|
Download:
|
| 图 7 不同TEGDN含量的NO质量分数分布 Fig. 7 NO distributions in different TEGDN mass fractions | |
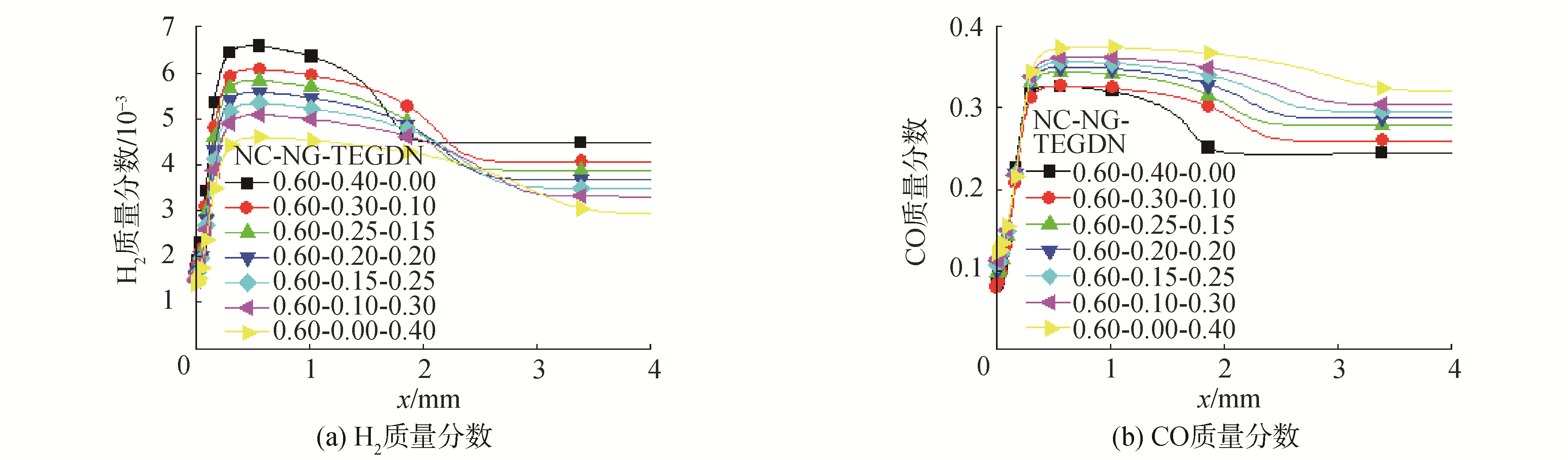
不同TEGDN含量太根药火焰区域H2和CO的质量分数变化如图 8所示。随着TEGDN由0增加到0.40,最终火焰区域,H2的质量分数由0.004 7下降到0.003 3,CO的质量分数由0.25增加到0.35。TEGDN的含量增加后,CO的质量分数增加明显且具有可燃性,因此膛口二次焰的强度将会增强。
|
Download:
|
| 图 8 不同TEGDN含量的H2和CO气体质量分布 Fig. 8 H2 and CO mass fraction distributions in different TEGDN mass fractions | |
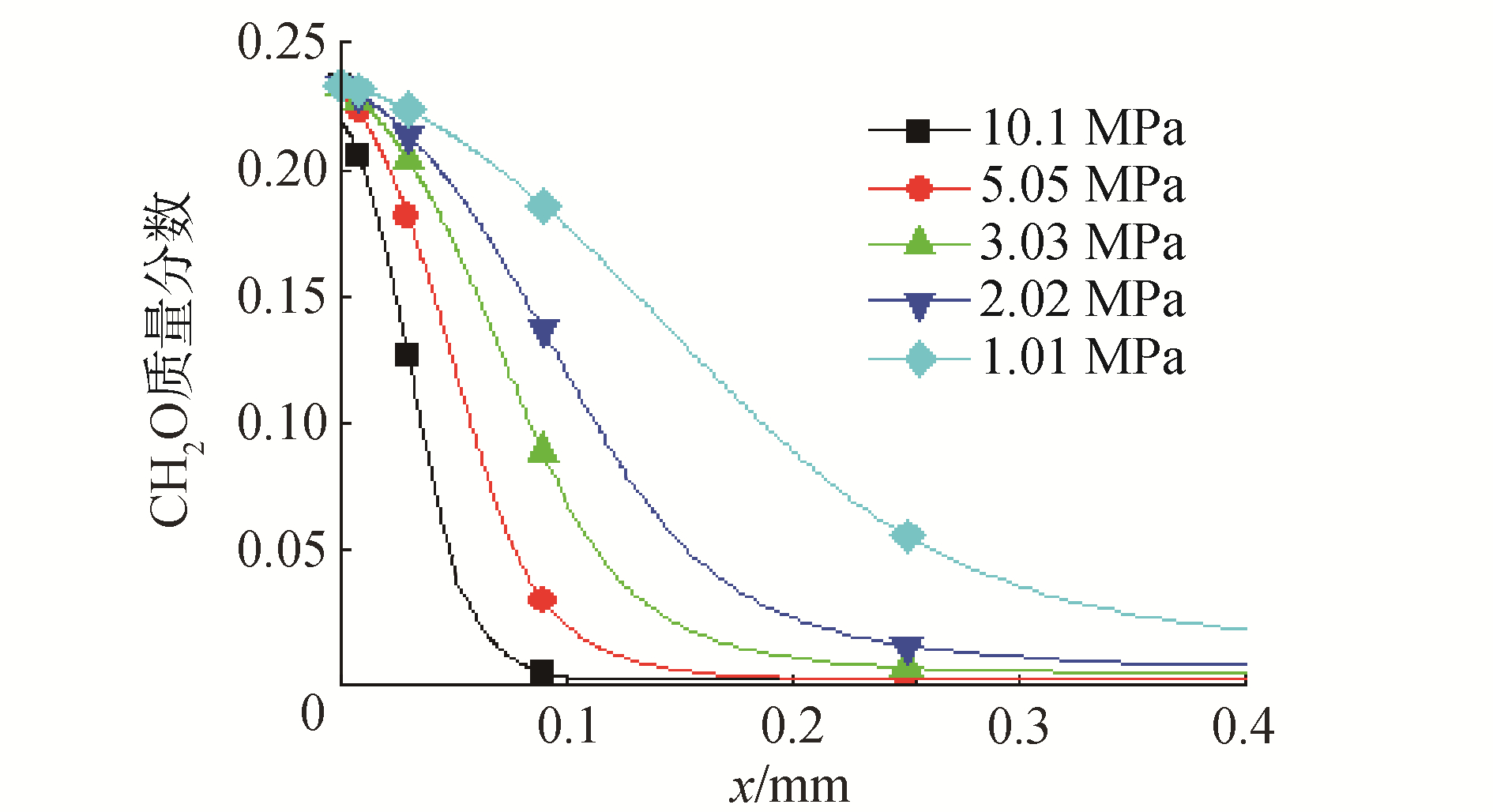
不同压力火药表面CH2O含量的分布如图 9所示,随着压力由1.01 MPa增加到10.1 MPa,CH2O质量分数下降速度增加,气相火焰区域被压缩变薄,嘶嘶区内的反应速率加快,嘶嘶区厚度由0.40 mm减小到0.09 mm。
|
Download:
|
| 图 9 不同压力下嘶嘶区CH2O质量分数分布 Fig. 9 CH2O mass fraction of fizz zone in different pressure | |
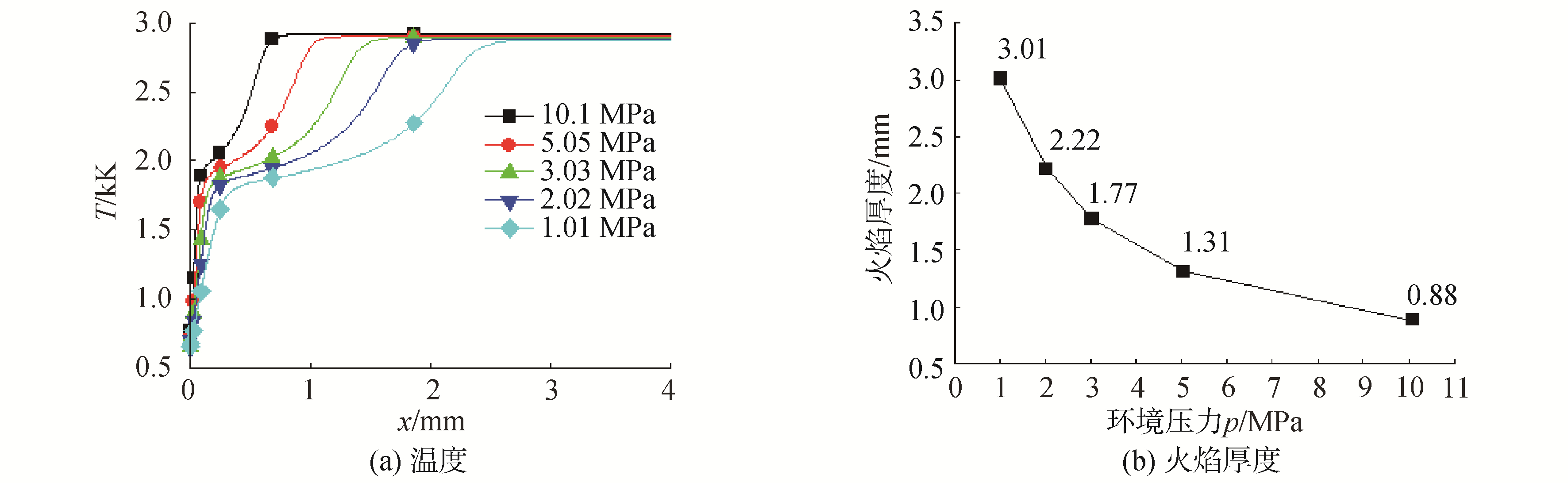
不同压力条件下火焰区域温度分布如图 10所示。由图 10可见,不同压力下,火焰最终温度相基本相同;当压力p由1.01 MPa增加到10.1 MPa时,火焰厚度由3.01 mm减小到0.88 mm,火焰厚度变薄,这主要是由于在高压力条件下,化学反应被压缩在1个更薄层内,化学反应速度更快。
|
Download:
|
| 图 10 不同压力温度的分布及火焰厚度变化情况 Fig. 10 Temperature distribution and combustion thickness in different pressures | |
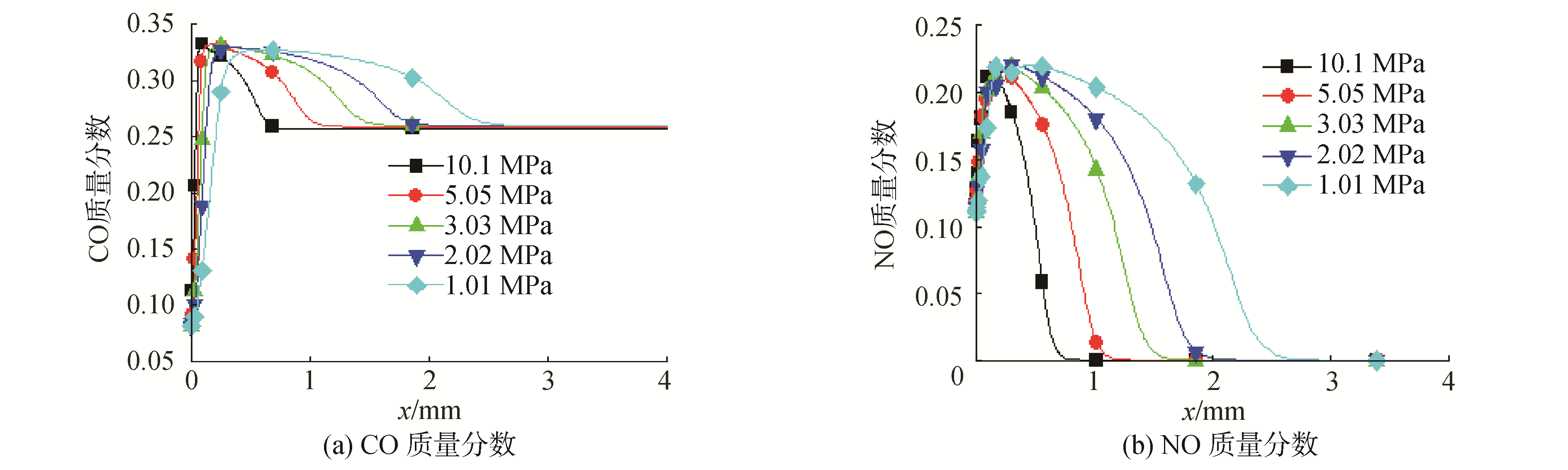
不同压力条件下火焰区域CO和NO的质量分数如图 11所示。由图 11可见,嘶嘶区末端的CO和NO的质量分数最大,分别为0.327和0.219,最终火焰区质量分数分别为0.256和0。不同压力下最终火焰区的CO和NO的质量分数几乎相同,由此可见压力对最终火焰的质量分数几乎没有影响。
|
Download:
|
| 图 11 不同压力条件下CO和NO的质量分数分布 Fig. 11 CO and NO mass fraction distribution in different pressures | |
由图 9~11可以看出,随着压力增加,火药气体温度升高变快,嘶嘶区和整体火焰区的厚度均明显变薄。这是由于随着环境压力增加,火药气体密度增大,在嘶嘶区,反应3的反应速度随压力增加明显加快,放热速率增加,温度升高迅速;当温度达到2 000 K左右,活化能较高的反应4和反应5随即开始反应,暗区的反应速度增加,火焰暗区厚度也随之变薄。当温度达到反应6和反应7所需的反应温度后开始进行反应最终燃烧完成达到最终火焰温度。
3 结论1) 本文建立的火药气相化学反应模型能够较好的描述火药气相区域嘶嘶区、暗区及发光区的燃烧过程,计算得到的火焰温度及各物质质量分数与文献数据吻合度很高,验证了该模型及计算方法的准确性。
2) NC质量分数为0.60的太根火药中,TEGDN由0增加到0.40情况下,最终火焰温度由2 965 K降低到2 654 K,火药力降低;火药嘶嘶区厚度几乎不变,嘶嘶区末端的NO2和(CHO)2的含量降低、CH2O含量增加;最终火焰区可燃气体CO的浓度由较大的增加,容易引起炮口二次焰。
3) 燃烧压力p由1.01 MPa增加到10.1 MPa,嘶嘶区厚度由0.40 mm减小到0.09 mm,火焰厚度由3.01 mm减小到0.88 mm,嘶嘶区及火焰厚度明显减小;压力变化对火药的温度和最终产物影响不大。
| [1] |
吴银秀. 双基发射药及其组分的结构与性能研究[D]. 南京: 南京理工大学, 2013. WU Xiuyin. Study on components and structure of double base propellant[D]. Nanjing: Nanjing University of Science and Technology, 2013. (  0) 0)
|
| [2] |
赵本波, 刘强, 李伟, 等. TEGDN含量和NC含氮量对TEGDN/NG混合酯双基推进剂力学性能的影响[J]. 火炸药学报, 2017, 40(4): 92-96. ZHAO Benbo, LIU Qiang, LI Wei, et al. Effect of TEGDN content and NC nitrogen content on mechanical properties of double-base propellant[J]. Chinese journal of explosives & propellants, 2017, 40(4): 92-96. (  0) 0)
|
| [3] |
陈沛, 赵凤起, 李上文, 等. 二缩三乙二醇二硝酸酯的热分解性能[J]. 火工品(火工品与烟火), 1999(3): 5-10. CHEN Pei, ZHAO Fenqi, LI Shangwen, et al. Thermal Decomposition characteristics of triethylene glycol dinitrate[J]. Initiators & pyrotechnics, 1999(3): 5-10. (  0) 0)
|
| [4] |
YI Jianhua, ZHAO Fengqi, XU Siyu, et al. Effects of pressure and TEGDN content on decomposition reaction mechanism and kinetics of DB gun propellant containing the mixed ester of TEGDN and NG[J]. Journal of hazardous materials, 2009, 165(1/2/3): 853-859. (  0) 0)
|
| [5] |
YI Jianhua, ZHAO Fengqi, GAO Hongxu, et al. Thermal behavior, nonisothermal decomposition reaction kinetics of mixed ester double-base gun propellants[J]. Chemical research in Chinese universities, 2008, 24(5): 608-614. DOI:10.1016/S1005-9040(08)60128-2 (  0) 0)
|
| [6] |
YI J H, ZHAO F Q, HU R Z, et al. Thermal safety study on TEGDN/NG/NC gun propellant[J]. Journal of energetic materials, 2010, 28(4): 285-298. DOI:10.1080/07370651003785695 (  0) 0)
|
| [7] |
仪建华, 徐司雨, 马晓东, 等. 太根发射药的非等温热分解反应动力学[J]. 火炸药学报, 2007, 30(4): 76-80. YI Jianhua, XU Siyu, MA Xiaodong, et al. Non-isothermal thermal decomposition reaction kinetics of TEGDN gun propellant[J]. Chinese journal of explosives & propellants, 2007, 30(4): 76-80. DOI:10.3969/j.issn.1007-7812.2007.04.020 (  0) 0)
|
| [8] |
薛欢, 何卫东, 徐汉涛. 改性高能太根发射药热分解与燃烧性能研究[J]. 含能材料, 2015, 23(8): 791-795. XUE Huan, HE Weidong, XU Hantao. Thermal decomposition and combustion performance of modified high-energy TEGN propellant[J]. Chinese journal of energetic materials, 2015, 23(8): 791-795. (  0) 0)
|
| [9] |
BECKSTEAD M W, PUDUPPAKKAM K, THAKRE P, et al. Modeling of combustion and ignition of solid-propellant ingredients[J]. Progress in energy and combustion science, 2007, 33(6): 497-551. DOI:10.1016/j.pecs.2007.02.003 (  0) 0)
|
| [10] |
BECKSTEAD M W. Model for double-base propellant combustion[J]. AIAA journal, 1980, 18(8): 980-985. DOI:10.2514/3.7701 (  0) 0)
|
| [11] |
BREWSTER M Q, WARD M J, SON S F. Simplified combustion modeling of double base propellant: gas phase chain reaction vs. thermal decomposition[J]. Combustion science and technology, 2000, 154(1): 2-30. DOI:10.1080/00102200008947270 (  0) 0)
|
| [12] |
COHEN N S, LO G A, CROWLEY J C. Model and chemistry of HMX combustion[J]. AIAA journal, 1985, 23(2): 276-282. DOI:10.2514/3.8906 (  0) 0)
|
| [13] |
BIZOT A, BECKSTEAD M W. A Model for double base propellant combustion[J]. Symposium (international) on combustion, 1989, 22(1): 1827-1834. DOI:10.1016/S0082-0784(89)80196-1 (  0) 0)
|
| [14] |
ROH T S, TSENG I S, YANG V. Effects of acoustic oscillations on flame dynamics of homogeneous propellants in rocket motors[J]. Journal of propulsion and power, 1995, 11(4): 640-650. DOI:10.2514/3.23889 (  0) 0)
|
| [15] |
李腾, 方蜀州, 刘旭辉, 等. 固体推进剂二维绝热微尺度燃烧模型的数值研究[J]. 推进技术, 2016, 37(12): 2385-2393. LI Teng, FANG Shuzhou, LIU Xuhui, et al. Numerical study on two dimensional adiabatic microscale combustion model for solid propellant[J]. Journal of propulsion technology, 2016, 37(12): 2385-2393. (  0) 0)
|
| [16] |
COHEN N S, LO G A. Combustion chemistry of nitrate ester-based propellants[C]//AIAA/SAE/ASME 19th Joint Propulsion Conference. Seattle, USA: AIAA, 1983.
(  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


