两相界面流动现象随处可见。在实际工程计算中，海洋平台受力分析、波浪水池、气泡上升及毛细管中气泡流动问题，都需要借助于精确实用的两相流模拟技术才能有效解决问题^[1-2]。众多学者提出并发展了一系列成熟的可用于商业计算的两相界面捕捉方法，其中体积分数类方法(volume of fluid，VOF)因其严格的质量守恒特性得到了广泛应用。Xiao等^[3]提出了采用双曲正切函数重构网格内自由界面(tangent of hyperbola interface capturing method，THINC)方法，该方法看作是几何重构/代数混合型的体积分数方法，通过确定单元内表征两相分布的双曲正切函数显式确定网格单元内自由界面位置，通过对双曲正切函数在网格间界面上积分平均得到数值流通量，其间并没有复杂的几何重构。通过参数β，THINC格式能够很好的控制自由界面的厚度在2、3层网格，而不会带来很强的数值扩散。Xiao等^[4]将该方法从一维扩展至多维，由结构化网格到非结构化网格，网格内自由界面的形状也由一开始的倾斜线段(平面)发展到THINC/QQ中考虑界面曲率的曲线(曲面)，已发展成一种适用于多种网格类型的能精确模拟两相界面的成熟的界面捕捉方法^[5-9]。

本文基于守恒形式不可压同位网格有限体积法离散N-S方程，采用THINC/QQ格式捕捉两相间自由界面，对互不相溶两相自由面问题进行数值模拟。利用有限体积法框架下的方程离散和求解，通过典型算例验证数值方法在不同类型网格下的实施精度并得出结论。

1 两相流数学模型 1.1 控制方程

假定两相流体为不可压、互不相溶的粘性流体，两相之间的交界面被认为是物性参数的间断，界面单元中两相流体共用速度和压力。连续性方程、动量方程以及体积分数方程可表示为：

$ \left\{ \begin{array}{l} \nabla \cdot \mathit{\boldsymbol{u}} = 0\\ \frac{{\partial \rho \mathit{\boldsymbol{u}}}}{{\partial t}} + \nabla \cdot {\rm{ }}(\mathit{\boldsymbol{u}} \otimes \mathit{\boldsymbol{u}}) - \nabla \cdot {\rm{ }}[\mu (\nabla \otimes \mathit{\boldsymbol{u}} + {(\nabla \otimes \mathit{\boldsymbol{u}})^{\rm{T}}})] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {\rm{ }}\nabla p + {\rm{ }}\rho \mathit{\boldsymbol{g}} + {\mathit{\boldsymbol{F}}_\sigma }\\ \frac{{\partial \phi }}{{\partial t}} + \nabla \cdot {\rm{ }}(\mathit{\boldsymbol{u}}\phi ) = 0 \end{array} \right. $

(1)

式中：u 和p分别是速度和压力；t为时间；g 为重力加速度；F_σ表示两相流体间表面张力；ρ和μ分别是密度和动力粘性系数：

$ \left\{ {\begin{array}{*{20}{l}} {\rho = \phi {\rho _1} + (1 - \phi ){\rho _2}}\\ {\mu = \phi {\mu _1} + (1 - \phi ){\mu _2}} \end{array}} \right. $

(2)

式中：下标1和2分别指代2种流体；ϕ为单元中流体1所占的体积分数。

根据连续表面力模型，两相流体间表面张力为：

$ {\mathit{\boldsymbol{F}}_\sigma } = {\rm{ }}\sigma \kappa \nabla \phi $

(3)

式中：σ为表面张力系数；κ为两相界面曲率，可表示为：

$ \kappa = {\rm{ - }}\nabla \cdot \left( {\frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}} \right) $

(4)

采用守恒形式有限体积法在非结构同位网格上对方程(1)进行离散，采用一阶欧拉隐格式处理时间项，采用二阶迎风格式离散对流项，对扩散项采用中心差分格式离散，对连续性方程和动量方程中的压力速度耦合问题，采用SIMPLE算法进行处理。采用THINC/QQ格式对体积分数方程进行求解。

1.2 THINC/QQ格式的数值实施方案

THINC格式借助于双曲正切函数H(x)表征两相分布，对于多维情况，界面单元中的分段双曲正切函数可表示为：

$ {H_i}(x) = \frac{1}{2}(1 + {\rm{tanh}}(\beta ({P_i}(x,y,z) + {\rm{ }}{d_i}))) $

(5)

式中：β是控制界面厚度的参数；${P_i}\left( {x, y, z} \right) + {d_i} = 0 $表示网格单元中界面位置方程。网格单元的体积分数是H函数在整个控制单元内的积分平均：

$ {\phi _i} = \frac{1}{{\left| {{\varOmega _i}} \right|}}\int\limits_{{\varOmega _i}(x)} {H(x){\rm{d}}x} $

(6)

为了计算简化，将整个界面重构过程映射到等参坐标系$ (\xi , {\rm{ }}\eta , {\rm{ }}\zeta )$下进行计算。表征单元中两相界面位置的表达式$ {P_i}(\xi , {\rm{ }}\eta , {\rm{ }}\zeta )$采用二次多项式表示：

$ \begin{array}{l} {P_i}(\xi ,\eta ,\zeta ) = {\rm{ }}{a_{200}}{\xi ^2} + {\rm{ }}{a_{020}}{\eta ^2} + {\rm{ }}{a_{002}}{\zeta ^2} + {\rm{ }}{a_{110}}\xi \eta {\rm{ }} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {a_{011}}\eta \zeta {\rm{ }} + {\rm{ }}{a_{101}}\xi \zeta {\rm{ }} + {\rm{ }}{a_{100}}\xi {\rm{ }} + {\rm{ }}{a_{010}}\eta {\rm{ }} + {\rm{ }}{a_{001}}\zeta \end{array} $

(7)

式中：$ {a_{str}}(s, {\rm{ }}t, {\rm{ }}r = 0, 1, 2s + t + r < = 2)$是确定界面形状的参数，可以通过界面法线、曲率显示表示。在确定a_str后，可以通过求解以下方程计算得到d_i：

$ \frac{1}{{\left| {{\varOmega _i}(\xi )} \right|}}\int\limits_{{\varOmega _i}(\xi )} {{{\tilde H}_i}(\xi ,\eta ,\zeta ){\rm{d}}\xi {\rm{d}}\eta {\rm{d}}\zeta } {\rm{ }} = {\rm{ }}{\bar \phi _i} $

(8)

假定在第i个单元中设置G个高斯积分点，每个点对应坐标为$ {\xi _{ig}} = ({\xi _{ig}},{\eta _{ig}},{\zeta _{ig}})$，则等式(8)可以转换为：

$ \sum\limits_{g = 1}^G {{\omega _{ig}}} \left( {\frac{1}{2}(1 + {\rm{tanh}}(\beta ({P_i}({\xi _{ig}}) + {\rm{ }}{d_i})))} \right) = {\rm{ }}{\bar \phi _i} $

(9)

式中ω_ig为第g个高斯积分点占的权重，且满足：

$ \sum\limits_{g = 1}^G {{\omega _{ig}}} = 1 $

(10)

根据正切函数恒等变形公式，得到：

$ \begin{array}{l} {\rm{tanh}}(\beta ({P_i}({\xi _{ig}}) + {\rm{ }}{d_i})) = \\ \frac{{{\rm{tanh}}(\beta {P_i}({\xi _{ig}})) + {\rm{tanh}}(\beta {d_i})}}{{1 + {\rm{tanh}}(\beta {P_i}({\xi _{ig}}))\cdot{\rm{ tanh}}(\beta {d_i})}} \end{array} $

(11)

将式(10)和(11)代入到方程(9)中，可以得到：

$ \sum\limits_{g = 1}^G {{\omega _{ig}}} \cdot \frac{{{\rm{tanh}}(\beta {P_i}({\xi _{ig}})) + {\rm{tanh}}(\beta {d_i})}}{{1 + {\rm{tanh}}(\beta {P_i}({\xi _{ig}})) \cdot {\rm{tanh}}(\beta {d_i})}} = {\bar \phi _i} - 1 $

(12)

方程(12)可以看作关于未知数${\rm{tanh(}}\beta {d_i}) $的一元非线性方程，可以采用牛顿-拉夫逊法迭代求解，进而得到d_i的值。

结合式(6)，体积分数方程(1)可离散为：

$ \frac{{\partial {{\bar \phi }_i}(t)}}{{\partial t}} = {\rm{ }} - \frac{1}{{\left| {{\varOmega _i}} \right|}}\sum\limits_{j = 1}^J {({v_{{n_{ij}}}}\int\limits_{{\varGamma _{ij}}} {H{{(x,t)}_{i{\rm{up}}}}} {\rm{d}}\varGamma )} $

(13)

式中：$ \mathit{\boldsymbol{v}}{\mathit{\boldsymbol{}}_{{n_{ij}}}} = \mathit{\boldsymbol{ v}}{\rm{ }}\cdot{\rm{ }}\mathit{\boldsymbol{n}}{_{ij}}$是面Γ_ij的法向速度；下标iup表示Γ_ij的上游迎风单元，考虑到流动的方向性，采用上游迎风单元中的体积分数分布确定通过单元界面上的体积流量。一般建议采用三阶龙格-库塔方法(total variation diminishing，TVD)对方程(13)进行显示迭代更新。式(13)中右端的积分项用高斯积分进行计算：

$ \int\limits_{{\varGamma _{ij}}} {H{{(\mathit{\boldsymbol{x}},t)}_{i{\rm{up}}}}{\rm{d}}\varGamma } = \left| {{\varGamma _{ij}}} \right|\sum\limits_{c = 1}^G {{\omega _g}{{\tilde H}_{i{\rm{up}}}}({\xi _g},{\eta _g},{\zeta _g})} $

(14)

式中：G是高斯点数目；ω_g是权重系数；$({\xi _g}, {\rm{ }}{\eta _g}, {\rm{ }}{\zeta _g}) $是局部坐标系下Γ_ij上的高斯点坐标。

2 数值结果及分析

本节通过3个典型的自由面流动算例测试有限体积法框架下THINC/QQ格式的性能。给定剪切流场，测试两相界面在剪切流场中发生大变形时，当前算法捕捉界面的精度。分别对重力、表面张力作用下的二维和三维气泡上浮问题进行数值模拟，说明当前数值算法的适用性。

2.1 二维剪切流动

考虑半径0.15的圆在[0, 1]×[0, 1]计算域中发生剪切变形，初始圆心坐标为(0.5, 0.75)，速度场为：

$ \left\{ \begin{array}{l} u{\rm{ }} = {\rm{sin}}(2{\rm{ \mathsf{ π} }}y)\cdot{\rm{ si}}{{\rm{n}}^2}({\rm{ \mathsf{ π} }}x)\cdot{\rm{ cos}}({\rm{ \mathsf{ π} }}t{\rm{ }}/{\rm{ }}T)\\ v{\rm{ }} = - {\rm{sin}}(2{\rm{ \mathsf{ π} }}x)\cdot{\rm{ si}}{{\rm{n}}^2}({\rm{ \mathsf{ π} }}y)\cdot{\rm{ cos}}({\rm{ \mathsf{ π} }}t{\rm{ }}/{\rm{ }}T) \end{array} \right. $

(15)

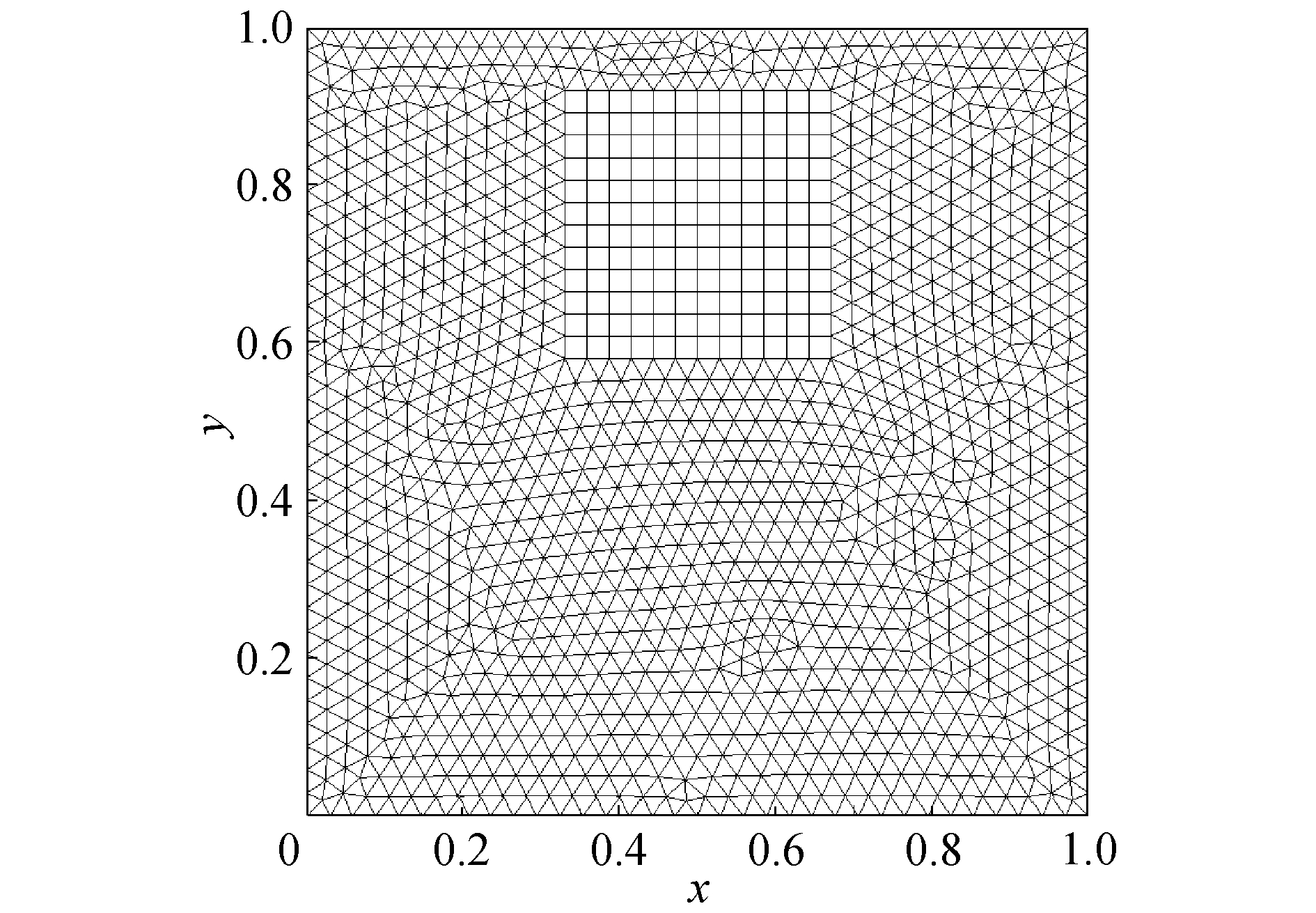
计算周期T为8.0 s。界面在剪切速度场变形为螺旋状，在T/2时刻变形最大，在T时刻回到初始位置。采用非结构化混合网格对当前问题进行测试，如图 1所示，网格数分别为2 564、10 025、40 217。

采用当前THINC/QQ格式对该问题进行数值模拟，取界面厚度控制参数β=3.6，计算时间步长5.0×10^-4 s。得到不同网格数下数值误差，如表 1所示。其中数值误差定义为：

$ {E_{rr}}\frac{{\sum\limits_{i = 1}^N {(\left| {{{\bar \phi }_{ni}} - {{\bar \phi }_{ei}}} \right| \cdot \left| {{\varOmega _i}} \right|)} }}{{\sum\limits_{i = 1}^N {({{\bar \phi }_{ei}} \cdot \left| {{\varOmega _i}} \right|)} }} $

(16)

式中：${\overline \phi _{ni}} $和${\overline \phi _{ei}} $分别为体积分数数值解和解析解；N为单元个数；丨Ω_i丨为第i个单元体积。

从表 1可以看出，随着网格加密，计算误差显著降低，计算结果更加精确。

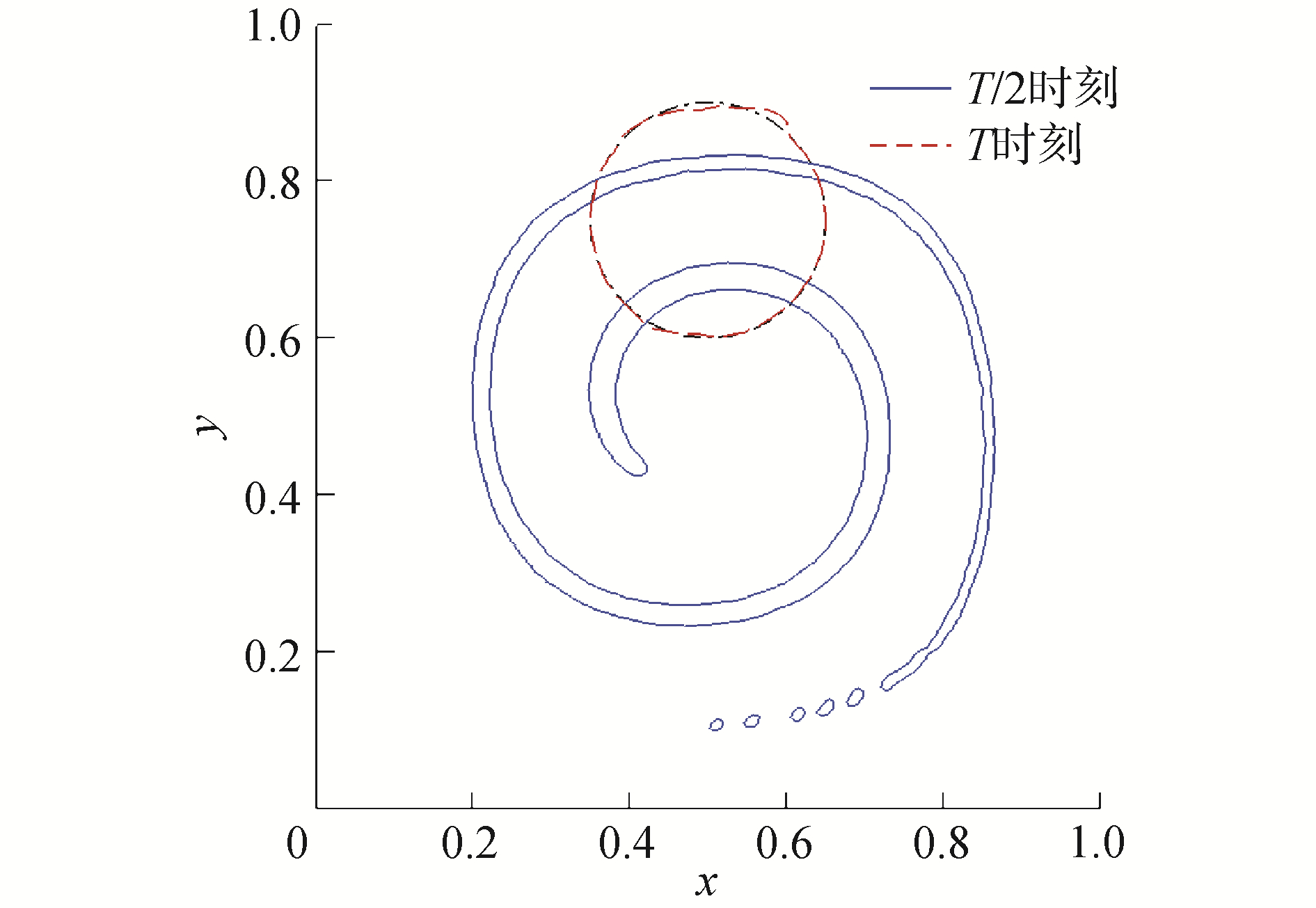
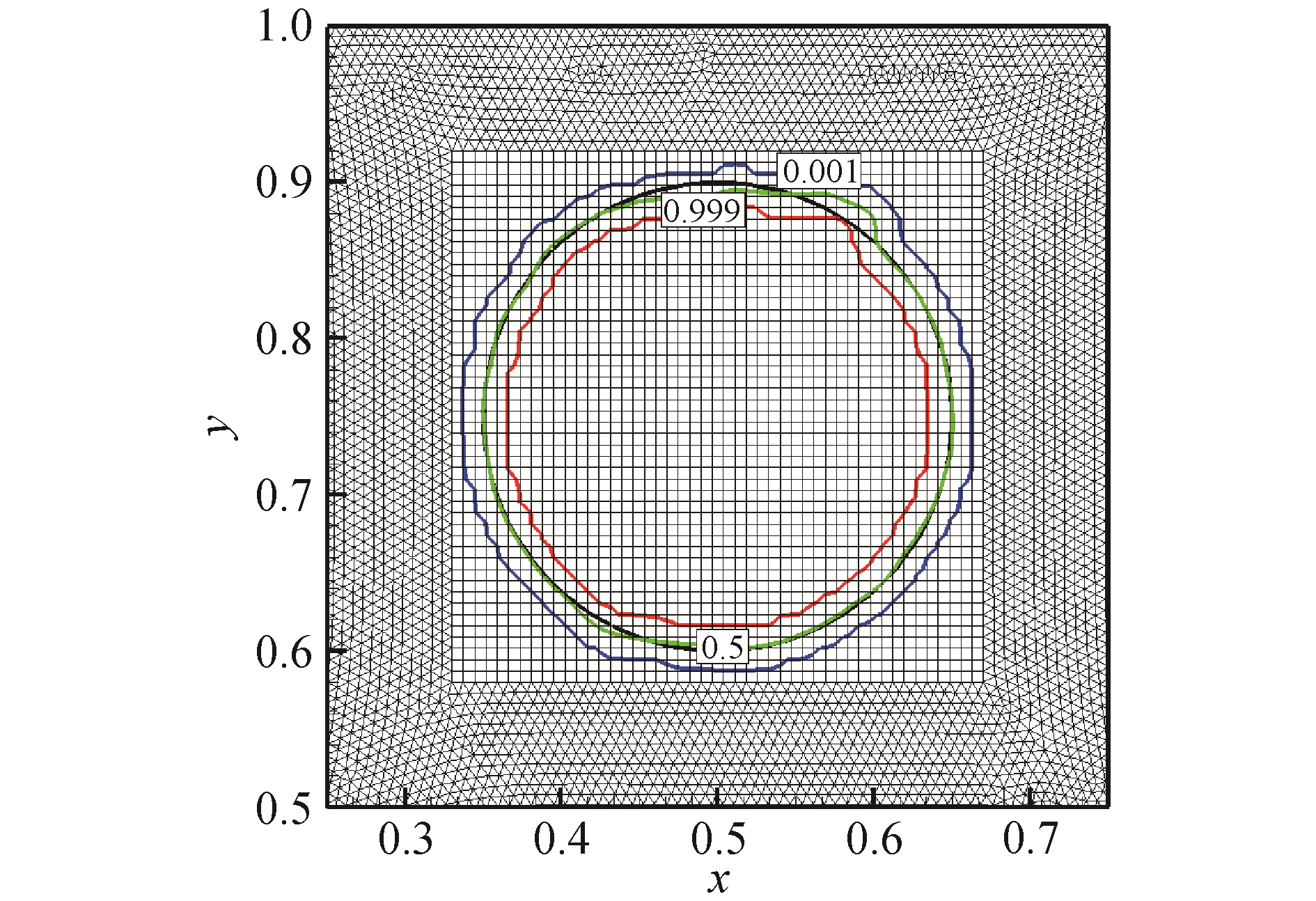
图 2给出了40 217网格下T/2时刻和T时刻的两相界面形状，可以看到，在T/2时刻，界面变成螺旋形，尾部有破碎的小液滴，这是因为网格尺度较尾部界面厚度尺寸过大。此外尽管经过了很大变形，T时刻两相界面仍能够回复到最初圆形，数值解和解析解吻合良好。图 3为T时刻的体积分数等值线放大云图，图中选取体积分数为0.001、0.5和0.999的等值线，可以看到界面厚度均匀分布，长时间计算后THINC/QQ格式仍能够控制界面厚度在3到4层网格之间。

2.2 二维气泡上浮

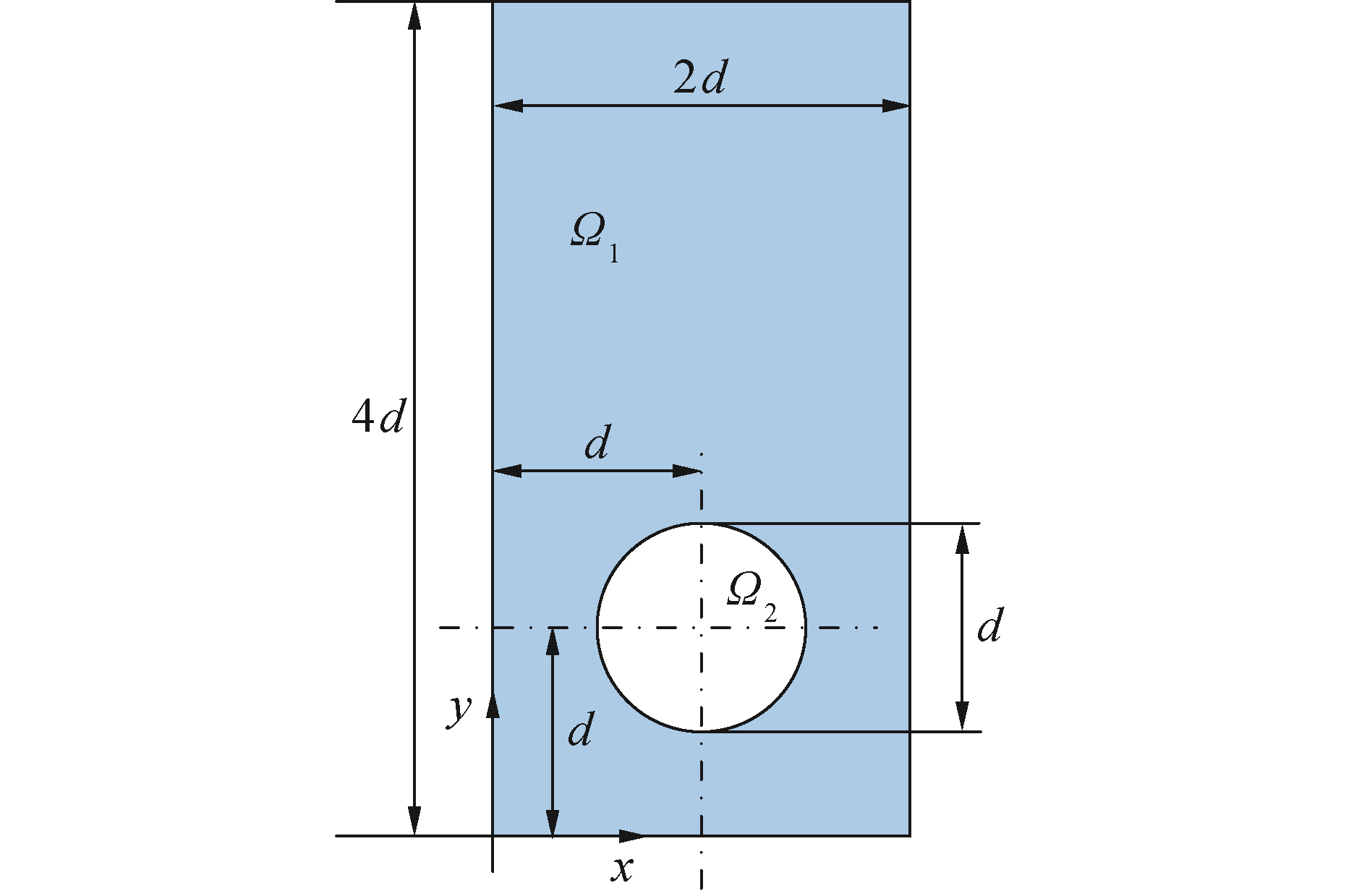
本节考虑在重力以及表面张力作用下的二维气泡上浮问题，验证当前数值算法的计算精度和鲁棒性。Hysing等^[10]对2个典型二维气泡上升算例采用3种不同数值算法进行了定量计算分析，得到了典型时刻气泡形状、气泡上浮位置以及气泡上浮速度的时间变化曲线。其数值结果被广泛用于程序验证。计算模型示意图如图 4所示。

直径d=0.5的气泡位于[0, 1]×[0, 2]的矩形计算域中，上下边界设置为不可滑移固壁，左右边界为可滑移固壁。2个算例的物性参数设置如表 2所示。在计算域内划分三角形网格，网格数为44 760。

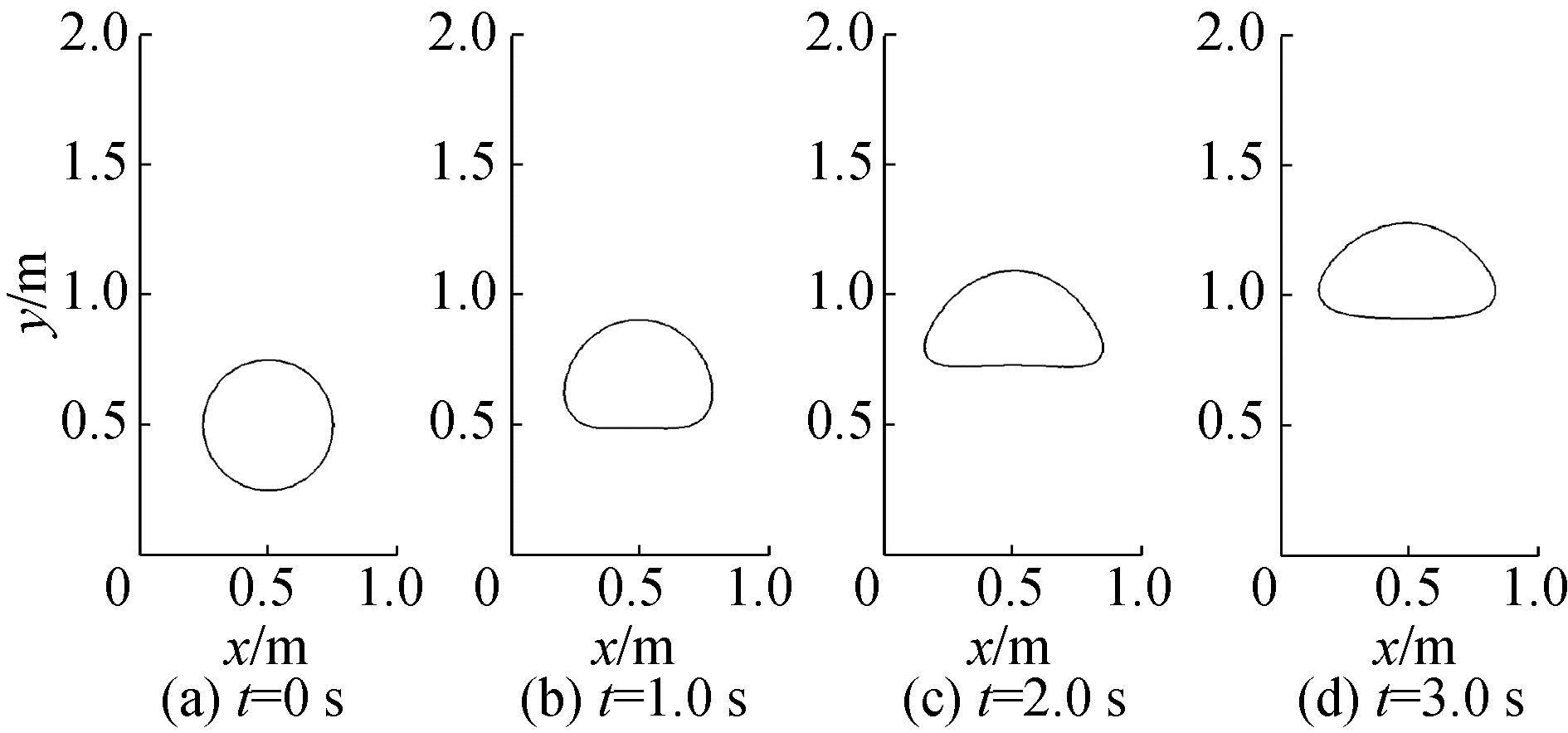
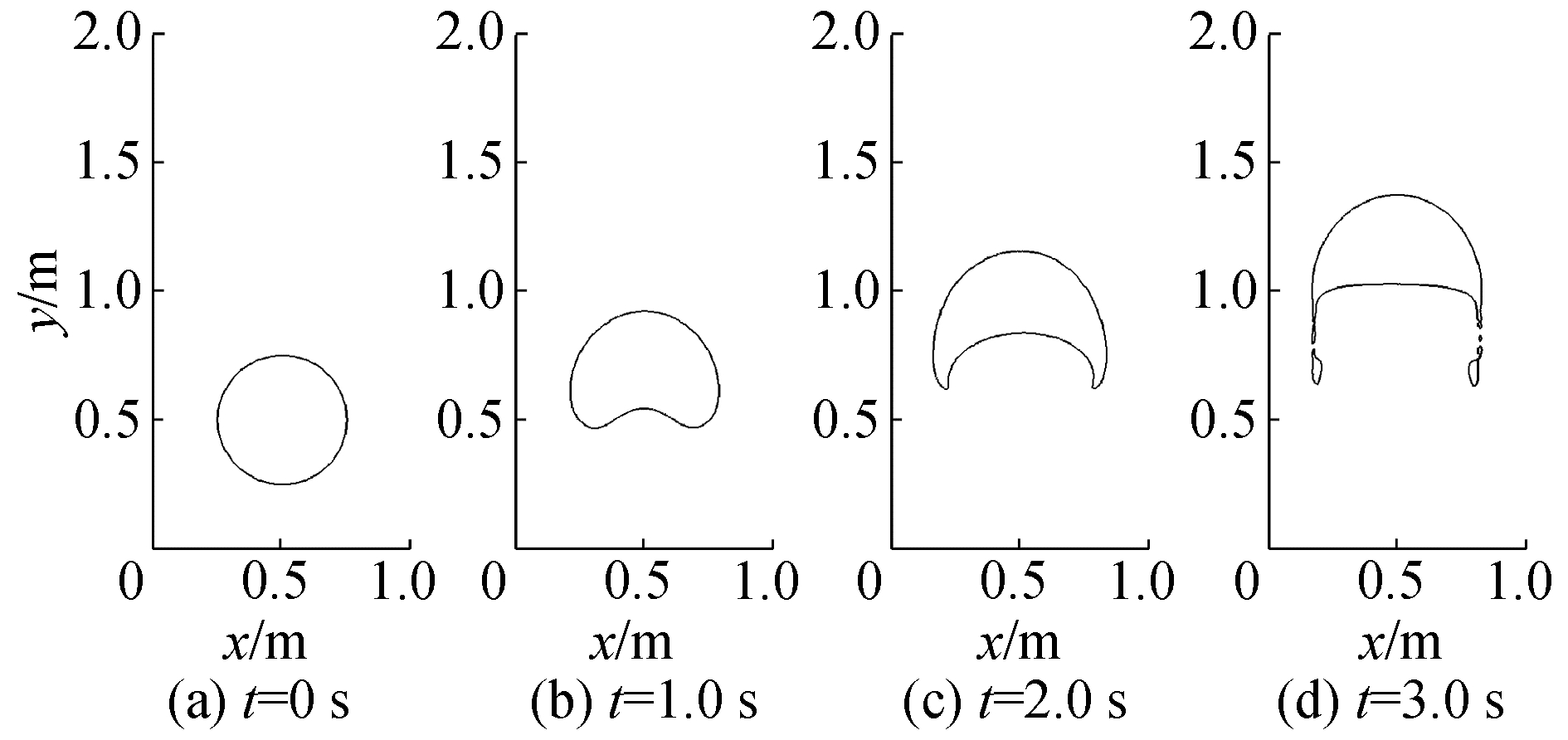
图 5和图 6分别给出了t=0.0, 1.0, 2.0, 3.0 s时刻2种物性参数设置下上浮气泡的形状，可以看到气泡在重力和表面张力作用下发生变形，在算例2中两相密度比和粘性系数比更大，而且两相间表面张力系数更小，导致气泡在上浮过程中逐渐变化为凹形，且逐步拉长拉细，并最终破碎成小气泡。

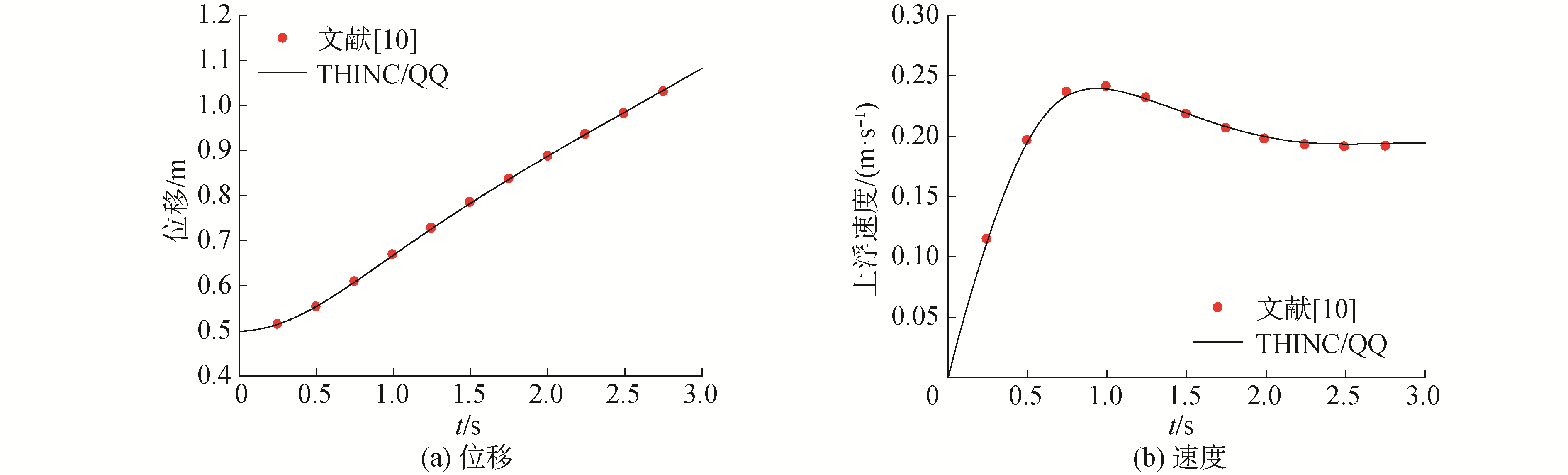
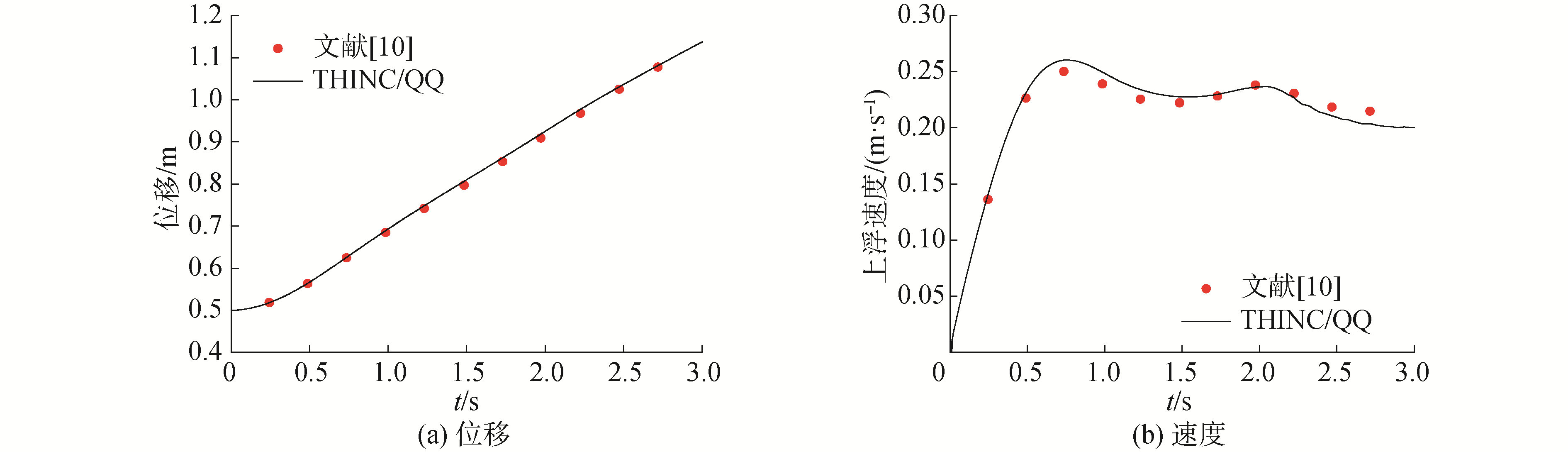
图 7和图 8分别给出了2个算例气泡上浮位移和速度随时间的变化曲线，并与Hysing等^[10]的数值结果进行比较。可以看到当前数值算法在三角形网格下得到的气泡位移和上浮速度时历曲线与文献[10]在结构化网格得到的计算结果吻合良好。

2.3 三维气泡融合

本节考虑三维情况下2个气泡在表面张力作用下发生融合。所用到的无量纲参数埃奥特沃斯数Eo、莫顿数Mo以及雷诺数Re分别定义为：

$ Eo = \frac{{g{d^2}\Delta \rho }}{\sigma };Mo = \frac{{g\mu _1^4\Delta \rho }}{{p_1^2{\sigma ^3}}};Re = \frac{{{\rho _1}Ud}}{{{\mu _1}}} $

(17)

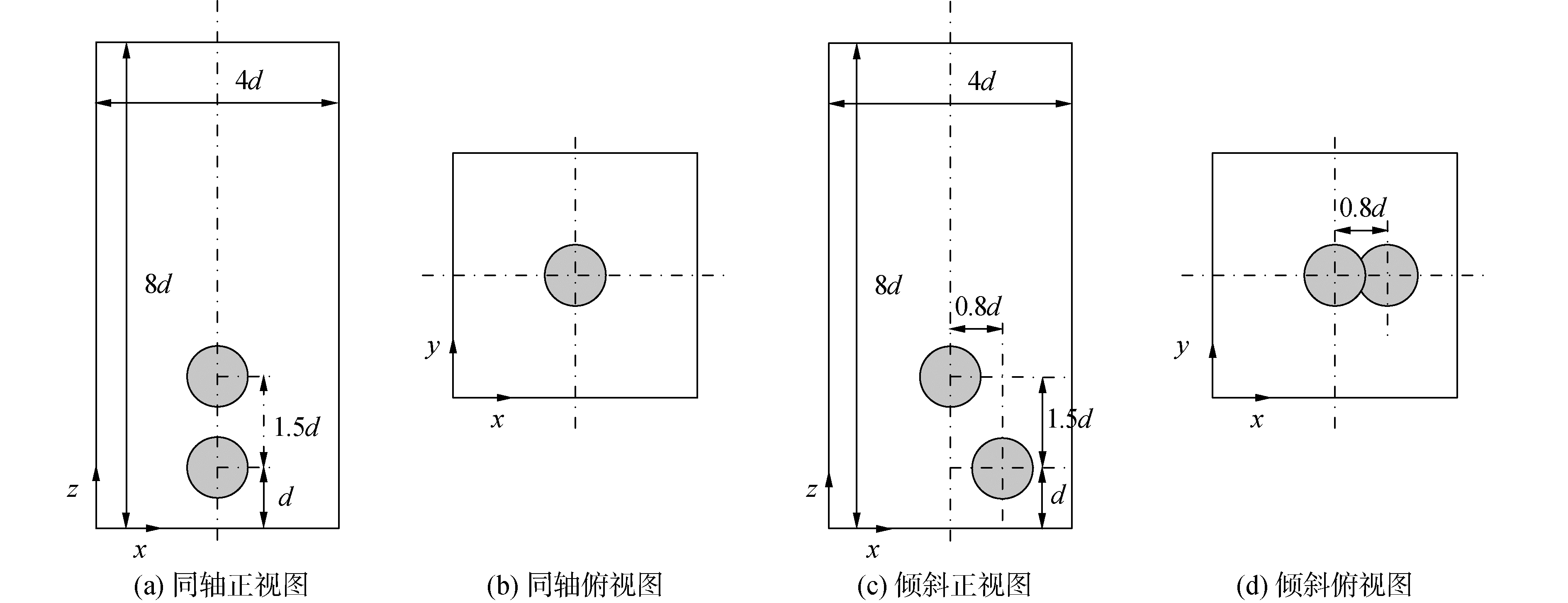
式中：U为气泡上浮速度；考虑直径为d、球心垂直方向相距1.5d的2个同轴气泡，底部气泡距离计算域底部为d，分别考虑2个同轴气泡和2个水平方向相距0.8d的气泡的上浮融合情况。计算模型示意图如图 9所示。计算域大小为4d×4d×8d，采用规整的六面体网格，网格尺寸为h=1/20d。上下边界(z=0，z=8d)采用无滑移固壁边界，四周为滑移固壁边界，初始时刻气泡和周围流体均处于静止状态。两相流体物性参数满足Eo=16，Mo=2.0×10^-4，两相密度比和动力粘度比均为100。计算过程中时间步长满足库朗数小于0.25。

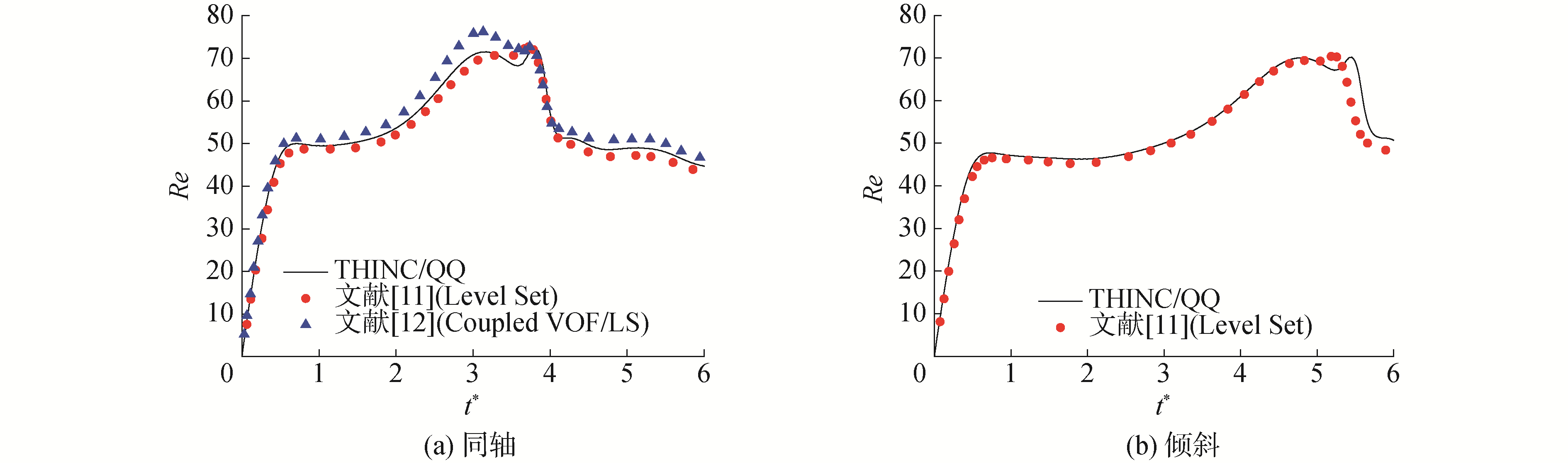
图 10给出了同轴2个气泡和水平方向相距0.8d的两倾斜气泡上浮过程中的雷诺数时历曲线，计算结果与Balcázar等^[11-12]采用Level Set方法和耦合VOF/LS方法得到的数值结果进行了对比，可以看到不管两气泡初始相对位置如何，本文采用的THINC/QQ格式能够准确捕捉两气泡上浮过程的速度特性。

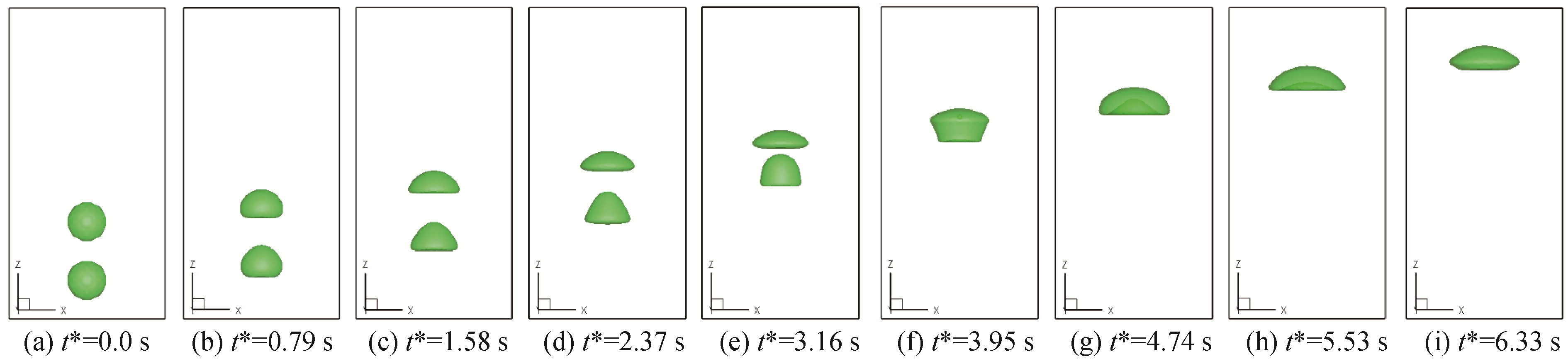
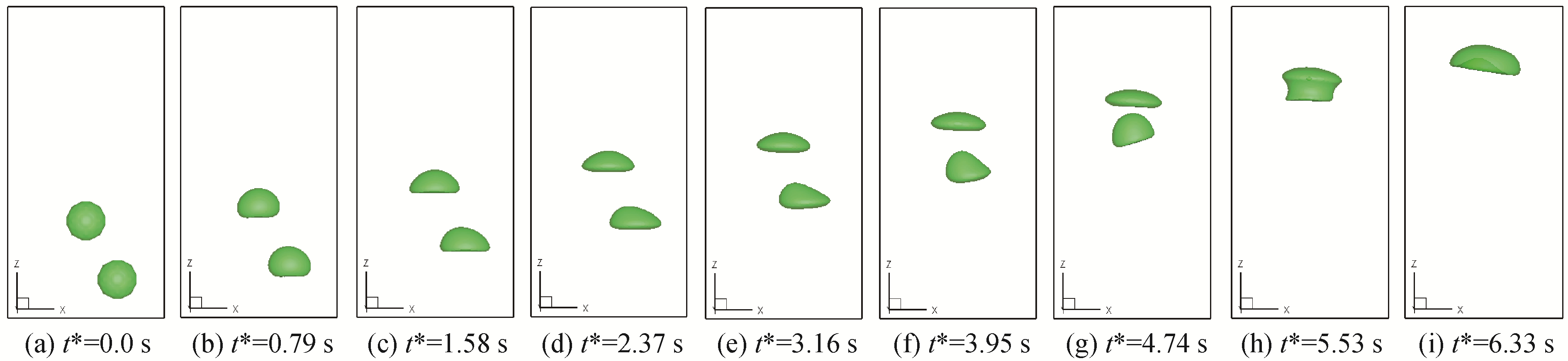
图 11和12给出了2同轴气泡和水平方向相距0.8d的2倾斜气泡的融合过程，结合图 10所示的雷诺数时历曲线，可以看到气泡上升初期，气泡上升速度迅速增大，两气泡形状变化相近，随着时间推移，顶部气泡逐渐趋向于扁平状，底部气泡进入顶部气泡的尾流区，导致底部气泡逐渐变成子弹形状，底部气泡速度增大，追上顶部气泡并与之融合，随后融合气泡继续上浮，但上浮速度在减小。对初始时刻相对倾斜的两上浮气泡，其流场分布也不是对称的，最终融合的大气泡的主轴方向与z轴方向存在夹角。

3 结论

1) 当前算法能准确模拟非结构化网格下两相界面的变形、分离以及融合，数值结果与相应的解析解和文献中数值解吻合良好，说明当前两相流模拟程序的准确性。

2) 气相物性参数和表面张力系数直接影响上浮过程中气泡形状，减小气相密度、粘性系数及表面张力系数更容易发生气泡破碎。

在一定条件下，两垂直方向存在指定间距的气泡会发生融合，对影响气泡融合的参数有待进一步研究。