2. 广东省能源高效清洁利用重点实验室, 广东 广州 510640
2. Guangdong Provincial Key Laboratory of Efficient and Clean Energy Utilization, Guangzhou 510640, China
生物柴油是指由长链烷基酯组成的基于植物油或动物脂肪的柴油燃料,通常通过使脂质(例如植物油、大豆油、动物脂肪)与产醇脂肪酸酯进行化学反应来制备[1]。生物柴油既能单独使用,也能与柴油混合使用,具有污染小,可再生的特点。目前,各国学者常用热动力学来对燃料的热解及燃烧特性进行分析[2-4],所研究的“动力学三因子”(活化能、指前因子、机理函数)为燃料燃烧过程的优化及燃烧器的设计提供指导。因此研究生物柴油的热解与燃烧特性并求解“动力学三因子”对于生物柴油的高效利用具有重要的研究意义和应用价值。
采用热重分析技术获得燃料的失重曲线,并与傅里叶红外分析仪(FTIR)联用以获得气体产物成分,结合动力学特征参数与产物特性有助于综合性地进行动力学分析,能够深入掌握样品整个热解与燃烧过程的特性与规律。霍梦佳等[5]采用TG-FTIR联用对生物柴油的热解进行了研究,通过非预置模型法的Vyazovkin算法和Avrami理论计算了生物柴油热解的活化能和反应级数;孙财等[6]利用TG-FTIR联用对生物柴油热裂解进行研究,将热解过程分为3个阶段,并利用Coats-Redfern积分法计算了活化能。Slopiecka等[7]利用Kissinger法[8]、KAS法、OWF法计算了杨木热解的活化能和指前因子,并分析了无模式函数法的差异,但未对其机理函数进行分析。尽管上述研究都对动力学三因子进行求解,并依据TG曲线将其划分阶段,但在分析机理函数的过程中,利用多元非线性回归法[9]对生物柴油求解动力学参数及机理函数,将拟合机理函数所得的失重曲线与实验曲线进行对比,直观反应出所拟合的准确性,并以F-检验进行验证其回归良好的工作较少。
本文通过热重-傅里叶红外分析仪联用对生物柴油进行实验,采用多元非线性回归法来计算生物柴油热解和燃烧的活化能,指前因子及机理函数。首先分析热重数据与红外光谱图来比较生物柴油热解和燃烧过程中的差异,其次采用Kissinger法来初步计算生物柴油热解和燃烧的活化能与指前因子,利用Starink[10]的无模式函数法计算不同转化率下的活化能来为Kissinger法的计算值作支撑,同时根据活化能随转化率的变化对其反应步数作出假设,再以无模式函数法所求的活化能与指前因子作为初值,采用多元非线性回归法求取活化能与指前因子,以获得回归良好的机理函数。
1 实验材料和方法 1.1 材料实验中采用广州市某公司所生产的生物柴油,原料油为棕榈油,其密度为0.868 g/cm3,碘值为68 cg/g,酸值为0.712 mgKOH/g,其水分、C14、C16、C18质量百分含量分别为0.03%、1.18%、21%、76%。
1.2 分析测试装置及实验工况生物柴油的热解与燃烧均在Mettler Toledo TGA热分析天平(精度0.1 μg)上完成,升温范围为30~800 ℃。初始质量控制在8.5±0.3 mg,经过多组实验,其实验工况如表 1所示。热解和燃烧过程中产生的气态产物通过传输线进入NicoletTM iSTM 10型傅里叶变换红外光谱仪的气室中进行分析,其检测波数为4000~400 cm-1。实验前将气室和输气管线加热至225 ℃以防止气体冷凝,确保实验准确。
| 表 1 实验工况 Table 1 Experimental condition |
生物柴油的热解过程发生在氮气气氛下,燃烧过程发生在空气气氛下。图 1所示为生物柴油在不同升温速率下热解的TG-DTG曲线。在温度达到365 K之前,生物柴油的TG曲线并未下降。随着温度升高,生物柴油缓慢分解,直到升温速率为5、10、20 K/min的TG曲线的温度分别达到425、467、485 K时,生物柴油中的各种脂肪酸甲酯开始迅速分解[1],失重速率不断提高,当温度分别达到500、545、590 K时,热解反应基本完成,最终残余质量均约为1%。

|
Download:
|
| 图 1 生物柴油在不同升温速率热解的TG-DTG曲线 Fig. 1 TG-DTG curves of biodiesel pyrolysis at different heating rates | |
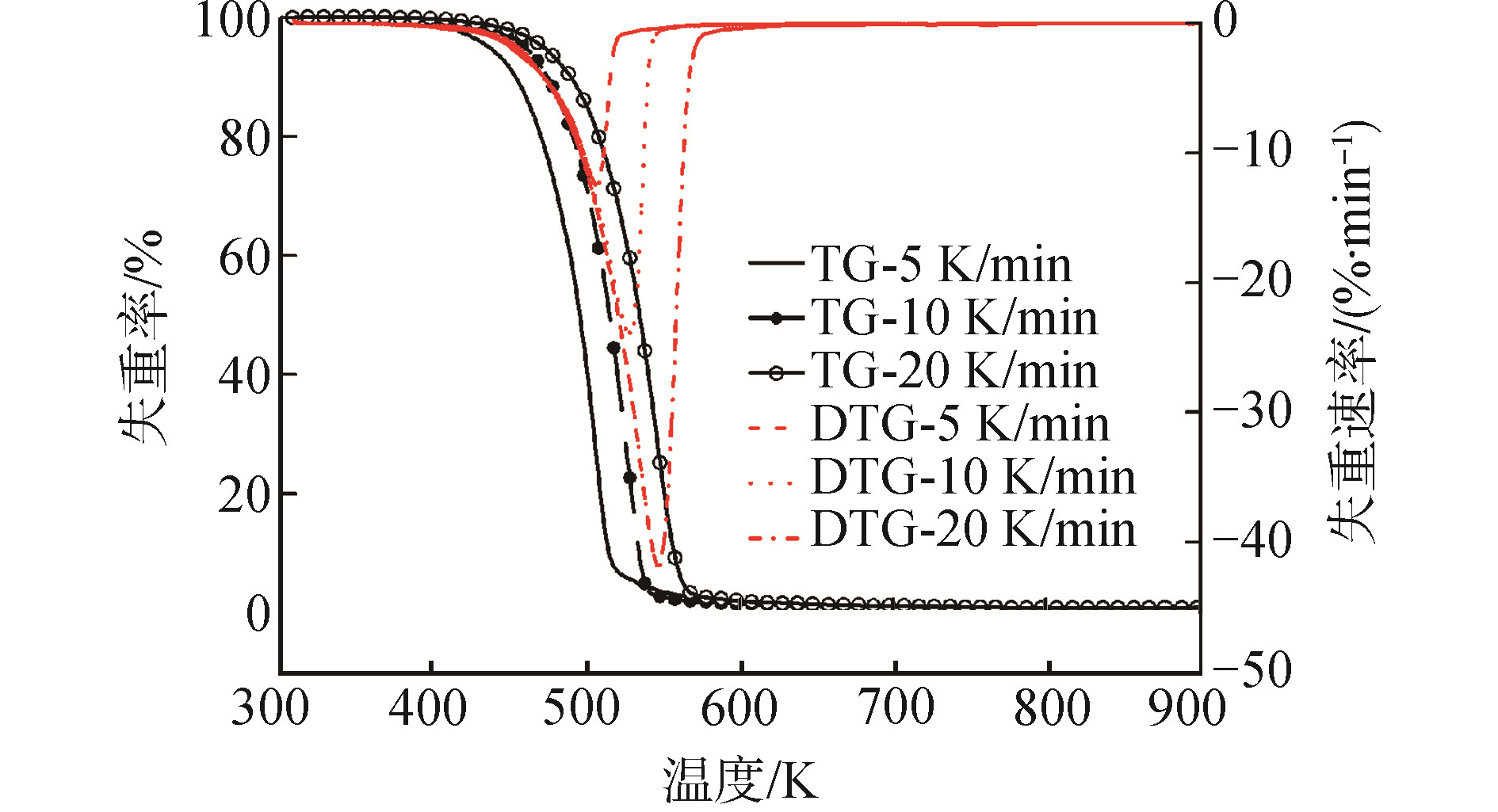
图 2所示为生物柴油在不同升温速率下燃烧的TG-DTG曲线。在温度达到365 K之前,生物柴油的TG曲线并未下降,随着温度升高,生物柴油缓慢分解,直到升温速率为5、10、20 K/min的TG曲线的温度分别达到453、473、488 K时,生物柴油中的各种脂肪酸甲酯开始迅速分解,失重速率不断提高,当温度分别达到520、542、572 K时,燃烧反应基本完成,残余质量均约为1%。
|
Download:
|
| 图 2 生物柴油在不同升温速率燃烧的TG-DTG曲线 Fig. 2 TG-DTG curves of biodiesel combustion at different heating rates | |
由图 1、2分析可得,生物柴油在热解与燃烧过程中,其TG-DTG曲线的变化趋势一致,缓慢分解与快速分解的区间以及残余质量基本相同。DTG为TG曲线的微分,其峰顶处为最大失重速率,所对应的温度Tp如表 2所示,在相同升温速率不同气氛下,所对应的最大失重点基本相同;而在相同气氛不同升温速率时,其峰值点温度及最大失重速率随着升温速率的提高而提高。
| 表 2 不同升温速率及气氛下的最大失重点 Table 2 The point of maximum mass loss rate at different heating rates and atmosphere |
通过采用FTIR分析生物柴油热解和燃烧过程所释放出气态产物的类型,升温速率为10 K/min时,不同温度下的红外光谱图如图 3所示。在波数3 700~3 500 cm-1处,未出现由O—H的伸缩振动引起较为明显的吸收峰[5]。这是由于该生物柴油中水分较少,而生物柴油中各类甲酯的含氧基团酯基(RC=OOR)仅分解为C=O—与C—O—,而不形成羟基(OH)[11]。在2 930 cm-1和2 860 cm-1处为烷烃基团H—C—H的伸缩振动带,随着C—C键断裂,烷烃逐渐形成,根据Lambert-Bee定律[12],由于吸光度最高,烷烃基团是放出的气态产物中的最大浓度,其气态产物可能对应CH4等烷烃类物质[13]。在1 440 cm-1处为C—H弯曲振动带,2 350 cm-1附近为羰基C=O的伸缩振动带,对应着CO2的生成;酯基C=OOR的短链经脱氧反应生成醛和醚,在1 760 cm-1和670 cm-1处为醛基弯曲振动带,1 170 cm-1处为C—O—C醚基伸缩振动带。以上基团及产物均为燃烧和热解过程中共同存在,而由醚键和羰基键断裂产生的一氧化碳(CO)的特征峰[14]仅在燃烧过程中波数为2 250~2 000 cm-1处检测到,在热解过程中未检测到。由图 3并结合图 1、2分析可知,生物柴油热解和燃烧过程释放气态产物的吸收强度变化规律与热重实验的结果一致,随着温度的升高,于470 K附近开始有气体析出,对应生物柴油开始分解;温度为530 K附近为最大失重速率,气态产物的吸光度增大,对应气体的快速析出;560 K附近气体析出减少,气态产物的吸光度逐渐减少,对应生物柴油分解反应即将完成。

|
Download:
|
| 图 3 生物柴油热解和燃烧的红外光谱图(升温速率为10 K/min) Fig. 3 Infrared spectrum of pyrolysis and combustion of biodiesel (heating rate 10 K/min) | |
为了更清楚地表达不同升温速率对失重的影响,现引入转化率α:
| $ \alpha = ({M_0} - {M_{\rm{t}}})/({M_0} - {M_{\rm{f}}}) $ | (1) |
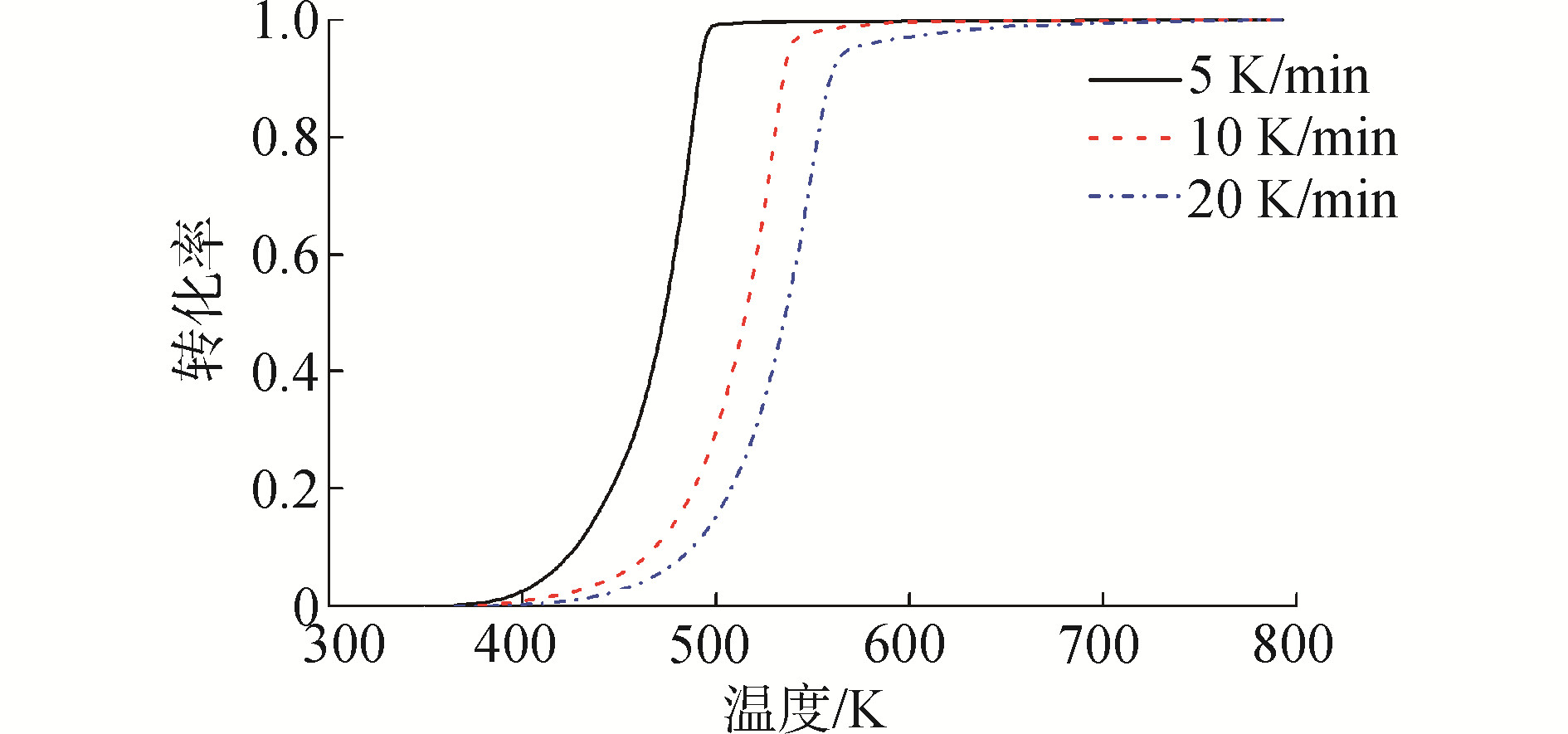
式中:M0和Mf分别为反应初始和最终样品质量;Mt为反应t时刻样品质量。不同气氛下,生物柴油转化率的曲线分别如图 4、5所示。在不同气氛下,生物柴油的转化规律表现一致,随着升温速率的提高,生物柴油的转化率曲线向高温区方向移动。这是因为随着升温速率的提高,生物柴油在相同温度内接受热量的时间减少,产气扩散困难,导致热滞后现象严重,使得整个曲线向高温区移动。
|
Download:
|
| 图 4 生物柴油在不同升温速率热解的转化率曲线 Fig. 4 Conversion curves of biodiesel pyrolysis at different heating rates | |

|
Download:
|
| 图 5 生物柴油在不同升温速率燃烧的转化率曲线 Fig. 5 Conversion curves of biodiesel pyrolysis at different heating rates | |
目前动力学分析中所采用的非等温、非均相反应的动力学方程为:
| $ \frac{{{\rm{d}}a}}{{{\rm{d}}T}} = \frac{1}{\beta }k\left( T \right)f\left( \alpha \right) $ | (2) |
式中:β为升温速率,在本实验中,β=dT/dt,为常数;T为热力学温度;k(T)为速率常数;f(α)为机理函数。
在各类速率常数的经验式中,Arrhenius提出的速率常数-温度关系式最为常用:
| $ k = A{\rm{exp}}\left( { - \frac{E}{{RT}}} \right) $ | (3) |
式中:A为指前因子;E为活化能;R摩尔气体常量。
将式(3)代入式(2),得到非均相体系在非等温条件下的动力方程:
| $ \frac{{{\rm{d}}a}}{{{\rm{d}}T}} = \left( {\frac{A}{\beta }} \right){\rm{exp}}\left( { - \frac{E}{{RT}}} \right)f\left( \alpha \right) $ | (4) |
动力学分析的主要目的在于求出上述方程中的“动力三因子”E、A和f(α)。采取多个升温速率进行实验,可以提高计算Arrhenius参数的精度,因为基础数据正是动力学信息的重要来源。本文分别采取Kissinger法与Starink法求取活化能E与指前因子A。
2.2.1 Kissinger方法Kissinger方法主要用于利用多组TG数据来求取动力学参数,是一种方便简单的求解方法。但它是基于假设DTA(差热分析法)或者DSC(示差扫描量热法)曲线峰顶数值为最大反应速率发生的温度进行求解,即dα2/dt2=0。实际上,最大反应速率不一定发生在DTA或者DSC曲线峰顶处,会随着升温速率β的变化而改变。故动力学分析过程中,由于最大失重速率发生在DTG的峰顶处,一般利用DTG的峰顶温度Tp来进行替代修正。Kissinger方程为:
| $ {\rm{ln}}(\beta /T_{\rm{p}}^2) = {\rm{ln}}\left( {AR/E} \right) - (E/R{T_{\rm{p}}}) $ | (5) |
由式(5)可知,通过取得不同升温速率下的DTG曲线的峰顶温度Tp,以1/Tp为横坐标,ln(β/Tp2)为纵坐标,通过线性拟合,即可利用其斜率和截距求出活化能E与指前因子A。所求动力参数如表 3所示。
| 表 3 Kissinger方法所求的动力学参数 Table 3 Kinetic parameters sought by the Kissinger method |
KAS法[15]和OFW法[16]是一种无模式函数法,OFW法求解活化能的不准确性已经被多次讨论[17],而Starink方法是基于对KAS法和OFW法的研究,通过对式子中常数的调节,所得出的一种比KAS法和OFW法求取活化能Eα更准确的无模式函数法。其表达式为:
| $ {\rm{ln}}\left( {\frac{\beta }{{T_\alpha ^{\rm{B}}}}} \right) = C - D\left( {\frac{{{E_\alpha }}}{{R{T_\alpha }}}} \right) $ | (6) |
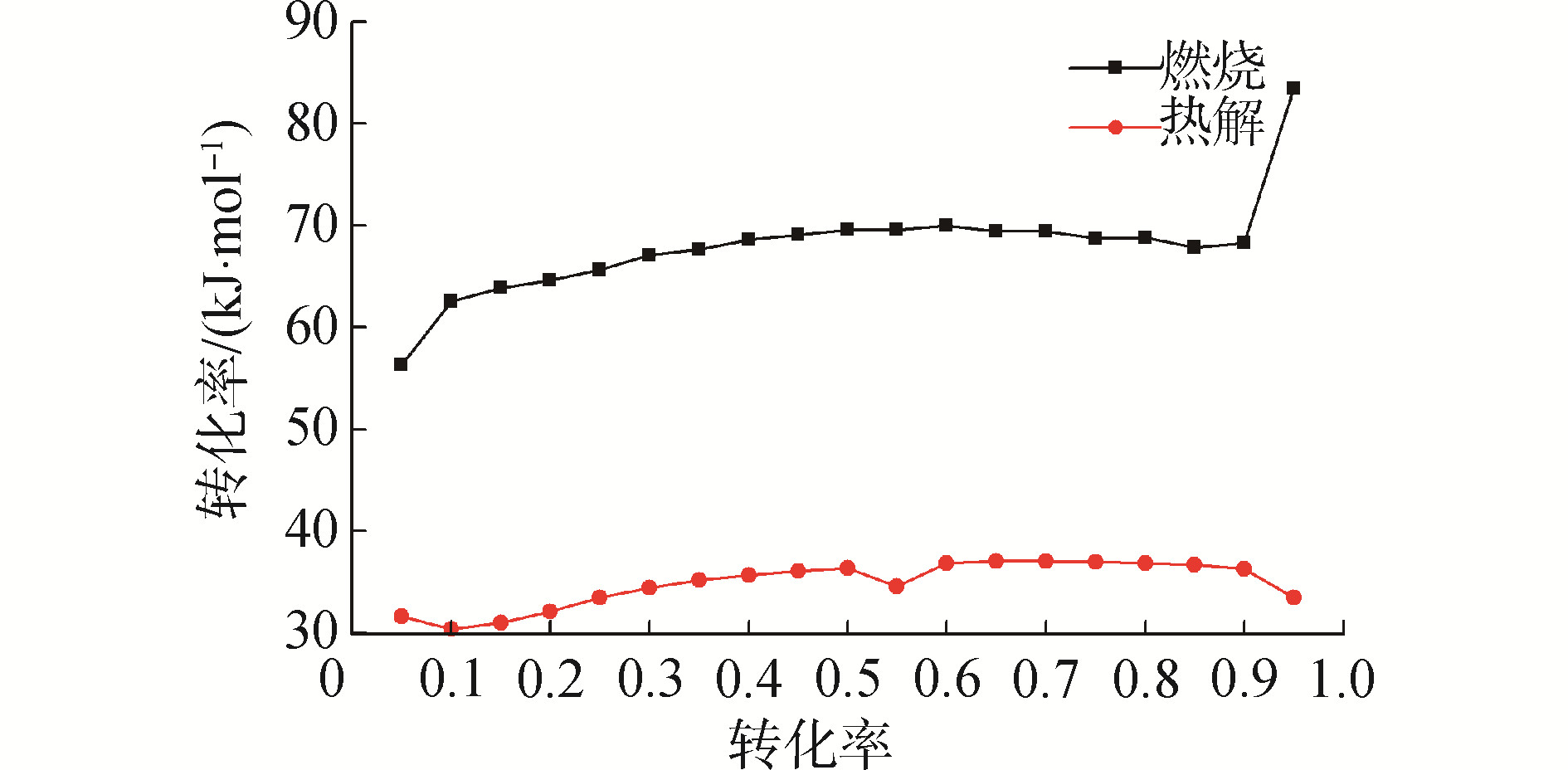
式中:Tα为不同转化率下的热力学温度,当B=1.92,D=1.000 8时,所求取的活化能较准确[9]。在本文中,生物柴油转化率的区间取为0.05~0.95,在不同升温速率下,选取处于相同转化率的温度值,对ln(β/T2)与1/T线性拟合,通过所得斜率即可求出不同转化率所对应的活化能。活化能会随着温度以及转化率α的改变而引起复杂的波动[18],所求出的生物柴油燃烧和热解的活化能E与转化率α曲线如图 6所示。
|
Download:
|
| 图 6 活化能E与转化率α的关系曲线 Fig. 6 Relationship between activation energy E and conversion rate α | |
在生物柴油热解过程中,其活化能随转化率的变化较小,在35.00 kJ/mol附近波动,求得平均值为34.83 kJ/mol;在生物柴油的燃烧过程中,其活化能随转化率增加而不断升高,当转化率大于0.40后,活化能稳定在69.50 kJ/mol, 平均活化能为68.00 kJ/mol, 但当转化率达到0.95时,活化能达到了83.50 kJ/mol。这意味着生物柴油在热解过程可以简化为单步动力学反应,即反应过程由一个主要的机理函数所控制。而生物柴油在燃烧过程中活化能E随转化率α波动较大,故而简化为两步连续动力学反应,在本研究中假定由2个连续的机理函数所控制。
2.3 动力学机理函数的确定由2.2节分析可知,生物柴油的热解过程简化为单步动力学反应,燃烧过程简化为两步连续动力学反应。由Starink法所求取的活化能E对动力学参数有良好的预测性[19],故将所求活化能E作为多元非线性拟合方法的初值,以便更准确地确定相应的动力学机理函数及其余动力学参数。由Arrhenius方程式(3)的假设前提:活化能E与指前因子A不随温度的变化而变化。故应由式(4)对不同升温速率下转化率α与热力学温度T的多条关系曲线进行非线性回归,来确定相符的动力学机理函数,以此获得更准确的拟合结果。利用Matlab编写程序对已知的多种机理函数[20]拟合,并选出相关系数较高的机理函数进行分析。
生物柴油热解过程的多元非线性拟合结果如表 5所示。在筛选出相关系数R2较高的机理函数后,由于其相关系数R2以及所求解的活化能E较为接近,难以选出最优的机理函数,因此利用F-检验方法[21]来确定最优的机理函数。由表 4中可知,Fexp均小于Fcrit,表明其机理函数的拟合均有良好的回归性,其中A2机理函数的Fexp值最小,且R2最大,活化能E及指前因子A均符合上文中利用无模式函数法所求得的活化能,故而A2机理函数为生物柴油热解的机理函数。
| 表 5 生物柴油燃烧的多元非线性拟合结果 Table 5 Multivariate nonlinear fitting results of biodiesel combustion |
| 表 4 生物柴油热解的多元非线性拟合结果 Table 4 Multivariate nonlinear fitting results of biodiesel pyrolysis |
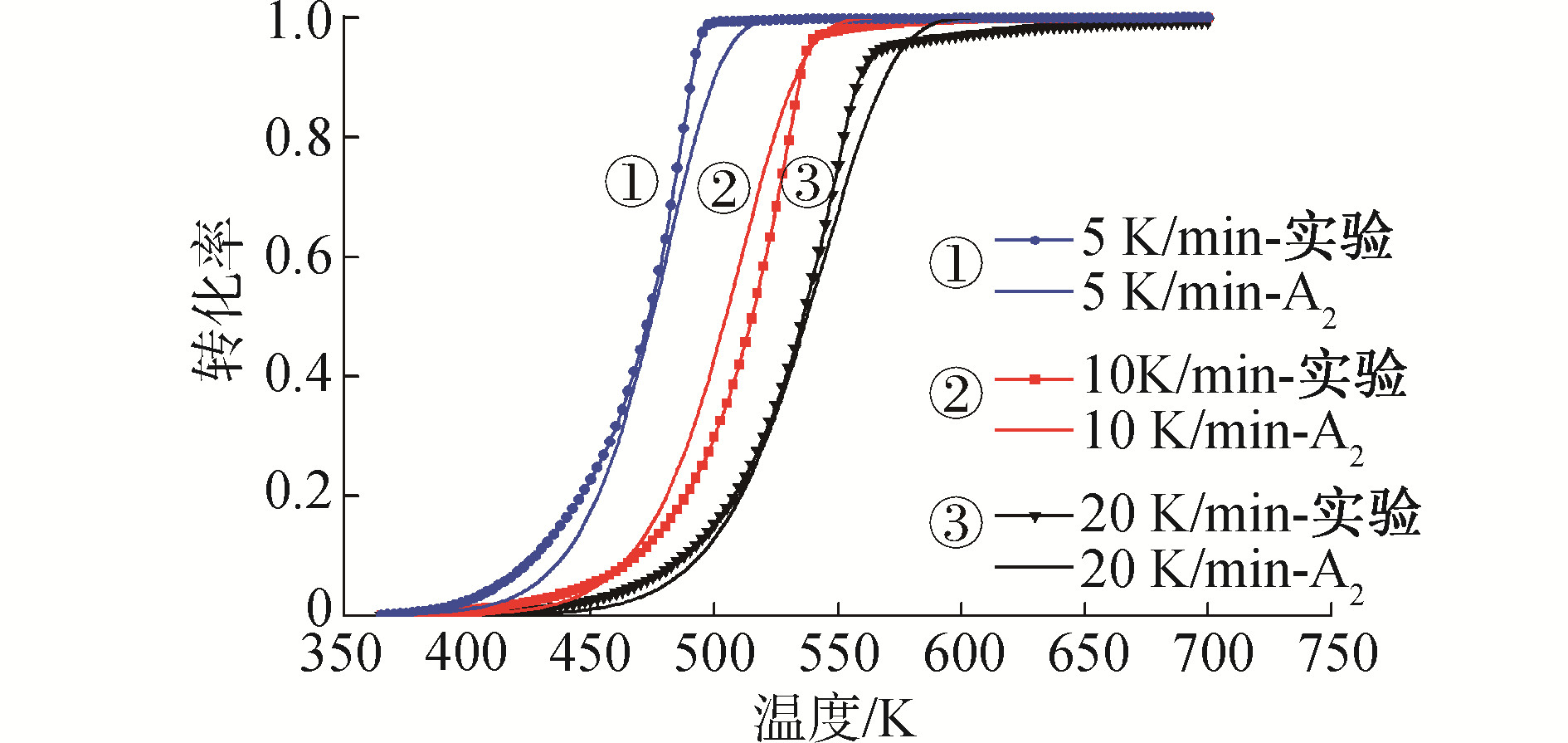
其拟合曲线如图 7所示,Am机理函数的微分形式为:
| $ f\left( \alpha \right) = m\left( {1 - \alpha } \right){[ - {\rm{lg}}\left( {1 - \alpha } \right)]^{1 - 1/m}} $ | (7) |
|
Download:
|
| 图 7 热解过程中机理函数A2的拟合曲线 Fig. 7 Fitting curve of kinetic function A2 in pyrolysis process | |
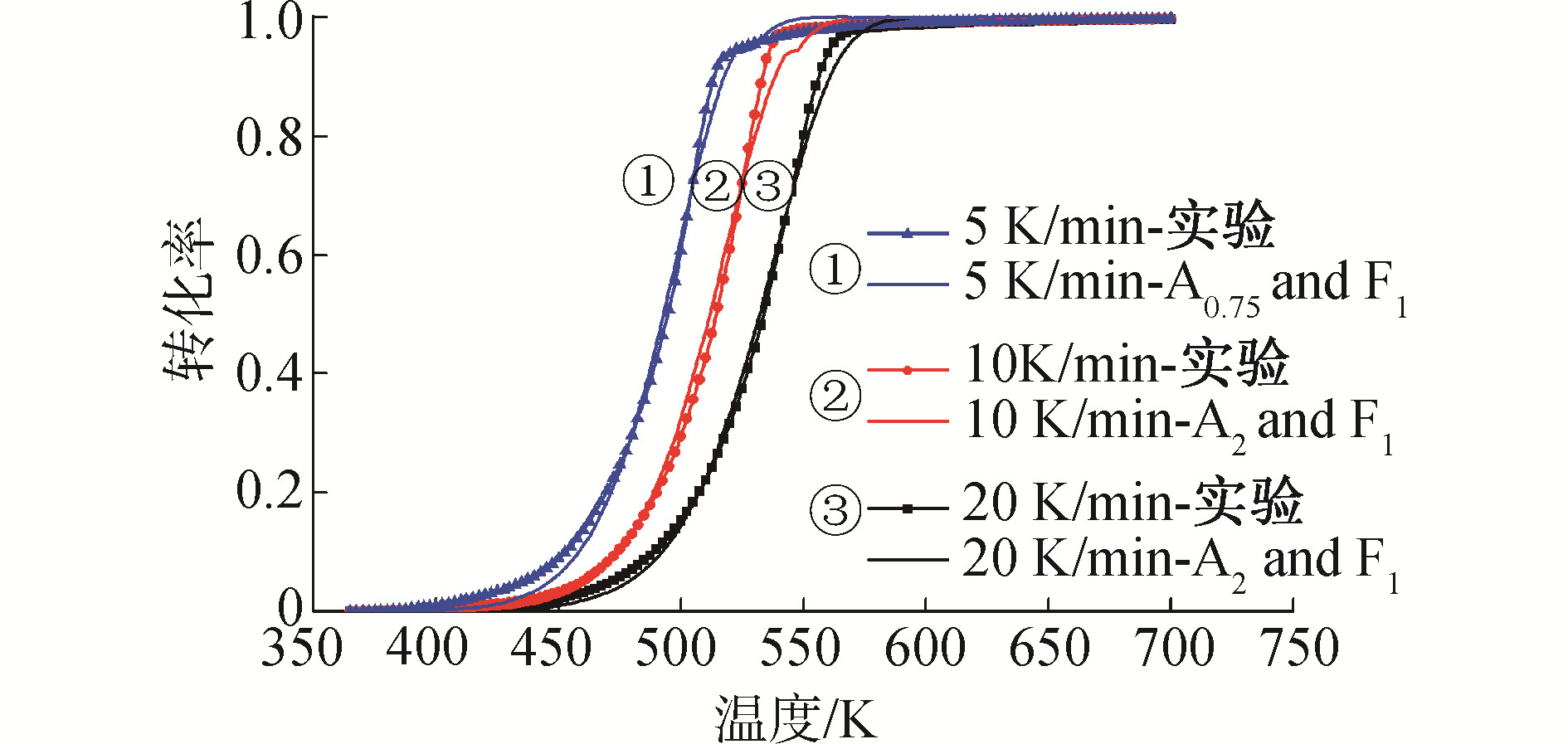
2.2节中假定生物柴油的燃烧过程为2步反应机理,在对多种机理函数进行单个拟合后,根据所求得的活化能E来分别筛选出2个机理函数,再进行拟合分析,拟合结果如表 5所示。综合考虑无模式函数法所计算出的活化能E以及拟合所得的相关系数R2,并采用F-检验进行判定,选取A4/3为第1步反应机理函数;再根据图 6中E0.95=83.00 kJ/mol,可选定F1为第2步反应机理函数。通过拟合这2种机理函数可发现,其R2与Fexp为最优,故而本文对生物柴油热解过程由2个连续的机理函数所控制的假定正确。拟合曲线图如图 8所示,A4/3和F1机理函数的微分形式为:
| $ \begin{array}{l} {A_{4/3}}:\\ \;\;\;\;f\left( \alpha \right) = 4/3\left( {1 - \alpha } \right){( - {\rm{lg}}\left( {1 - \alpha } \right))^{1/4}} \end{array} $ | (8) |
| $ \begin{array}{l} {F_1}:\\ \;\;\;\;f\left( \alpha \right) = 1 - \alpha \end{array} $ | (9) |
如图 8所示,该拟合具有良好的回归性,并且活化能接近于无模式函数法所求出的活化能E。由于主要的反应过程由A4/3机理函数所控制,F1机理函数所控制的阶段仅占整个质量损失过程的5.63% (不同升温速率下转化率为0.95~1时的平均失重量),因此对整个过程影响并不明显。
|
Download:
|
| 图 8 燃烧过程中2步连续反应机理函数的拟合曲线 Fig. 8 Fitting curves of two-step consecutive kinetics in combustion process | |
1) 生物柴油在不同升温速率下燃烧和热解的TG-DTG曲线变化规律一致,且随升温速率增加,由热滞后现象导致TG-DTG曲线均向高温区移动; 其热解和燃烧过程的气态产物均含CO2、CH4、烷烃类等有机化合物,仅在燃烧过程中于波数2 250~2 000 cm-1处检测到有CO的特征峰。
2) 利用Kissinger法求解出生物柴油热解和燃烧的活化能分别为39.31和70.00 kJ/mol。利用Starink法求解出生物柴油热解和燃烧的平均活化能分别为34.80和68.00 kJ/mol。2种方法所求出的活化能接近,且燃烧时的活化能远大于热解时的活化能,这是因为燃烧需要进行更为复杂的反应过程。由E-α曲线图预测热解过程为单步动力学反应,燃烧过程为2步连续动力学反应。
3) 结合无模式函数法取得的活化能和指前因子,利用多元非线性回归法得出该生物柴油的热解过程符合A2机理函数,活化能为39.00 kJ/mol;燃烧过程为2步连续反应动力学,即符合A4/3→F1机理函数,第1步活化能为68.00 kJ/mol,第2步活化能为82.00 kJ/mol;且所求活化能接近无模式函数法所求得的活化能,并利用F-检验方法与相关系数R2验证了所求取的机理函数的可靠性,符合对热解过程与燃烧过程动力学机理的预测。
| [1] |
SINGH D, SHARMA D, SONI S L, et al. Chemical compositions, properties, and standards for different generation biodiesels:a review[J]. Fuel, 2019, 253: 60-71. (  0) 0)
|
| [2] |
陈梅倩, 胡德豪, 黄友旺. 基于热重分析法的生物质变温热解特性实验研究[J]. 华北电力大学学报, 2019, 46(6): 99-104. CHEN Meiqian, HU Dehao, HUANG Youwang. Experimental study on pyrolysis characteristics of biomass based on thermogravimetric analysis[J]. Journal of North China Electric Power University, 2019, 46(6): 99-104. (  0) 0)
|
| [3] |
UBANDO A T, CHEN W H, ONG H C. Iron oxide reduction by graphite and torrefied biomass analyzed by TG-FTIR for mitigating CO2 emissions[J]. Energy, 2019, 180: 968-977. (  0) 0)
|
| [4] |
FERREIRA E N, ARRUDA T B M, RODRIGUES F E A, et al. Investigation of the thermal degradation of the biolubricant through TG-FTIR and characterization of the biodiesel-Pequi (Caryocar brasiliensis) as energetic raw material[J]. Fuel, 2019, 245: 398-405. (  0) 0)
|
| [5] |
霍梦佳, 牛胜利, 路春美, 等. 生物柴油热解的TG-FTIR联用研究及动力学参数计算[J]. 化工进展, 2014, 33(6): 1435-1439. HUO Mengjia, NIU Shengli, LU Chunmei, et al. TG-FTIR investigation on the biodiesel pyrolysis with kinetic calculation[J]. Chemical industry and engineering progress, 2014, 33(6): 1435-1439. (  0) 0)
|
| [6] |
孙财, 李博, 王华, 等. 地沟油生物柴油热裂解特性及动力学机理[J]. 太阳能学报, 2017, 38(8): 2033-2039. SUN Cai, LI Bo, WANG Hua, et al. Pyrolysis characteristics and kinetics mechanism of biodiesel from waste oil[J]. Acta energiae solaris sinica, 2017, 38(8): 2033-2039. (  0) 0)
|
| [7] |
SLOPIECKA K, BARTOCCI P, FANTOZZI F. Thermogravimetric analysis and kinetic study of poplar wood pyrolysis[J]. Applied energy, 2012, 97: 491-497. (  0) 0)
|
| [8] |
KISSINGER H E. Reaction kinetics in differential thermal analysis[J]. Analytical chemistry, 1957, 29(11): 1702-1706. (  0) 0)
|
| [9] |
OPFERMANN J. Kinetic analysis using multivariate non-linear regression. Ⅰ. Basic concepts[J]. Journal of thermal analysis and calorimetry, 2000, 60(2): 641-658. (  0) 0)
|
| [10] |
STARINK M J. The determination of activation energy from linear heating rate experiments:a comparison of the accuracy of isoconversion methods[J]. Thermochimica acta, 2003, 404(1/2): 163-176. (  0) 0)
|
| [11] |
NIU Shengli, ZHOU Yan, YU Hewei, et al. Investigation on thermal degradation properties of oleic acid and its methyl and ethyl esters through TG-FTIR[J]. Energy conversion and management, 2017, 149: 495-504. (  0) 0)
|
| [12] |
ZHANG Feng, ADACHI D, TAMALAMPUDI S, et al. Real-time monitoring of the transesterification of soybean oil and methanol by Fourier-transform infrared spectroscopy[J]. Energy & fuels, 2013, 27(10): 5957-5961. (  0) 0)
|
| [13] |
张旭明, 张媛媛. 基于TG-FTIR木耳基废弃物热解特性研究[J]. 可再生能源, 2013, 31(9): 74-77. ZHANG Xuming, ZHANG Yuanyuan. Study on pyrolysis of agaric-based waste using TG-FTIR analysis[J]. Renewable energy resources, 2013, 31(9): 74-77. (  0) 0)
|
| [14] |
MA Zhongqing, CHEN Dengyu, GU Jie, et al. Determination of pyrolysis characteristics and kinetics of palm kernel shell using TGA-FTIR and model-free integral methods[J]. Energy conversion and management, 2015, 89: 251-259. (  0) 0)
|
| [15] |
WANG Chang'an, LIU Yinhe, ZHANG Xiaoming, et al. A study on coal properties and combustion characteristics of blended coals in northwestern China[J]. Energy & fuels, 2011, 25(8): 3634-3645. (  0) 0)
|
| [16] |
FLYNN J H, WALL L A. General treatment of the thermogravimetry of polymers[J]. Journal of research of the national bureau of standards-A physics and chemistry, 1966, 70A(6): 487-523. (  0) 0)
|
| [17] |
SBIRRAZZUOLI N, GIRAULT Y, ELÉGANT L. Simulations for evaluation of kinetic methods in differential scanning calorimetry. Part 3-Peak maximum evolution methods and isoconversional methods[J]. Thermochimica acta, 1997, 293(1/2): 25-37. (  0) 0)
|
| [18] |
VYAZOVKIN S. Kinetic concepts of thermally stimulated reactions in solids:a view from a historical perspective[J]. International reviews in physical chemistry, 2000, 19(1): 45-60. (  0) 0)
|
| [19] |
BROWN M E, GALLAGHER P K. Chapter 1-introduction to recent advances, techniques and applications of thermal analysis and calorimetry[J]. Handbook of thermal analysis and calorimetry, 2008, 5: 1-12. (  0) 0)
|
| [20] |
胡荣祖, 高胜利, 赵凤起, 等. 热分析动力学[M]. 2版. 北京: 科学出版社, 2008: 4. HU Rongzu, GAO Shengli, ZHAO Fengqi, et al. Thermal kinetics analysis[M]. 2nd ed. Beijing: Science Press, 2008: 4. (  0) 0)
|
| [21] |
FREUND J E, PERLES B M. Modern elementary statistics: international edition[M]. 2nd ed. 2006: 71-78.
(  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


