2. 中国舰船研究设计中心, 湖北 武汉 430064;
3. 南京理工大学 发射动力学研究所, 江苏 南京 210094
2. China Ship Development and Design Center, Wuhan 430064, China;
3. Institute of Launch Dynamics, Nanjing University of Science and Technology, Nanjing 210094, China
大多数工程机械系统在一定程度上都存在振动问题,它们的结构设计通常需要考虑其振动特性[1]。为了提高水下航行器舵系统的结构性能,更好的计算出舵系统的水弹性,必须准确计算出舵系统的固有频率和振型。在工程问题中,如果不能准确计算结构的振型和频率,很难得到一个具有良好性能的结构系统并且很难进行下一步的振动控制分析[2]。
工程实际中,如水翼艇的水翼,潜艇中的升降舵、艉舵等船舶构件作为复杂的多刚柔体动力学系统,结构参数设计不当时,在流场中高速运动会产生颤振现象导致结构破坏,或发生持续的弱振动现象诱发水噪声,降低水下航行器的隐蔽性[3-5]。而对这些结构系统进行流固耦合仿真的第一步是高效准确的获取结构系统的振动特性。通常力学方法在计算多刚柔耦合体系统振动特性时,需要建立系统总体动力学方程,不仅需要解决涉及的矩阵阶次高计算工作量大的困难,还可能面临计算“病态”问题[6]。寻求水下航行器舵系统等复杂多刚柔耦合体系统动力学快速建模和振动特性快速计算方法,是目前工程上解决大系统的流固耦合问题的迫切需要。芮筱亭等[7-10]建立了多体系统动力学新方法——多体系统传递矩阵法(transfer matrix method for multibody system,MSTMM)。该方法先后实现了线性多体系统的固有振动特性和动力响应及非线性、时变、大运动、受控、一般多体系统动力学研究,无需系统总体动力学方程,程式化程度高、系统矩阵阶次低、可以实现复杂系统的快速建模与快速计算[11-13]。为水下航行器舵系统动力学快速建模和振动特性计算提供了基础。
对于复杂多刚柔体的水下航行器舵系统,部分学者采用有限元法将舵系统的舵叶处理成柔性系统,将舵系统处理为单个柔性舵叶加一根扭簧的简化模型,计算出系统的振动模态,再结合势流理论或CFD理论,计算水翼系统的水弹性问题[14-15]。但很少有人从整个舵系统的角度出发,建立整个舵系统的动力学模型,考虑各部件的结构参数以及连接刚度对系统振动特性的影响。且采用有限元法对简化系统进行建模,依然单元数过多、矩阵阶次高、计算效率低且理论背景复杂、推导过程繁琐。本文基于MSTMM对整个舵系统动力学进行快速建模和仿真并与基于有限元法(finite element method, FEM)的ANSYS仿真软件计算结果进行对比分析。
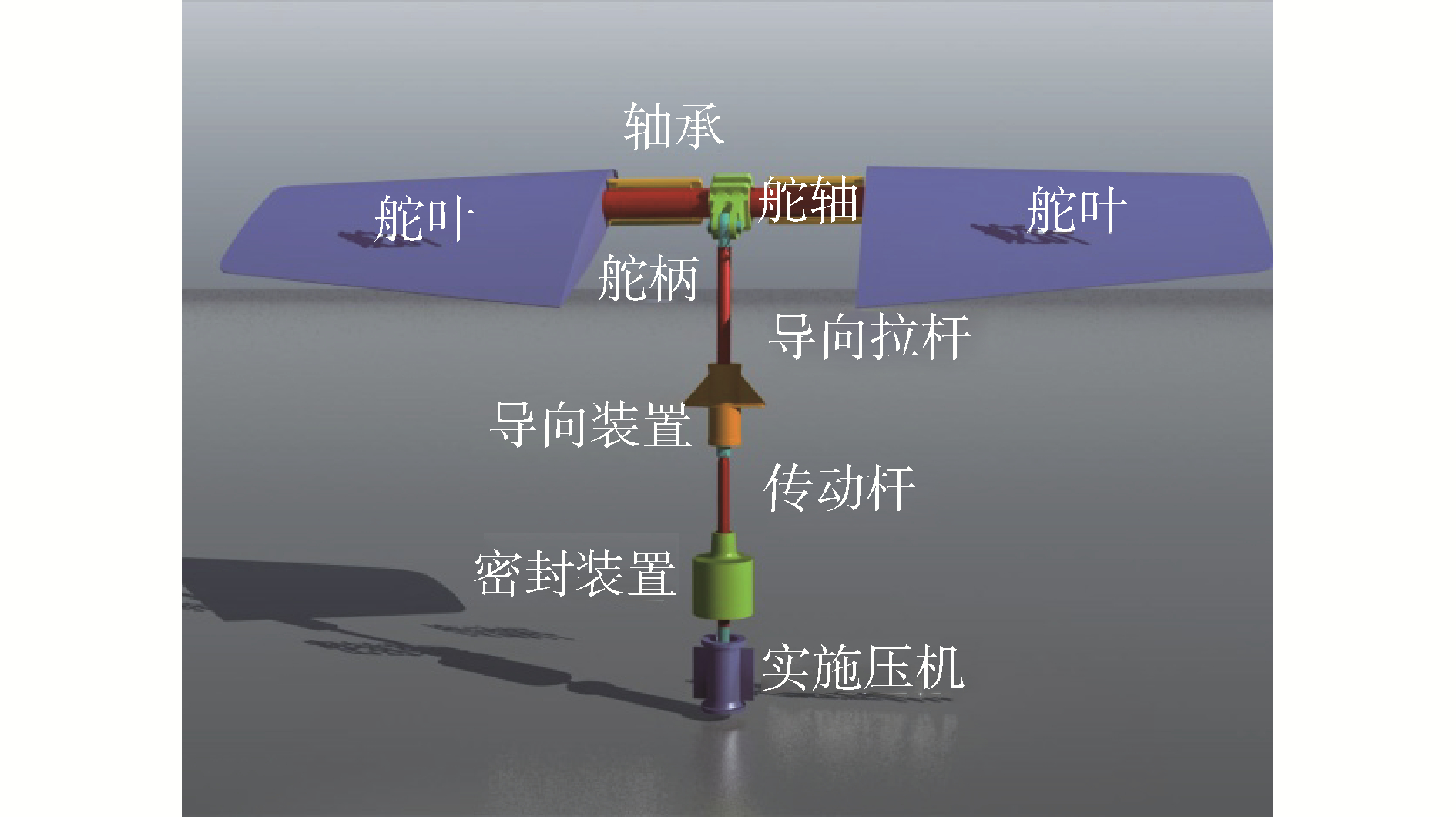
1 水下航行器舵系统动力学建模 1.1 动力学模型水下航行器的舵系统是一个复杂的多刚柔体系统,如图 1所示。舵系统主要由舵叶、舵轴、舵柄、传动杆、拉杆、球铰、柱铰、液压系统组成。该舵系统称为围壳舵,其轴承外表面、导向装置、密封装置、液压缸与该航行器的围壳直接相连,固定在水下航行器上。导向拉杆上下运动带动舵柄转动,舵柄与舵轴固结在一起,因此也带动舵轴转动。传动杆穿过密封装置,只能上下运动。在轴承的两端以及舵叶之间有定位环装置,以确保舵轴没有左右串动。
|
Download:
|
| 图 1 水下航行器舵系统 Fig. 1 The hydroplanes system of an underwater vehicle | |
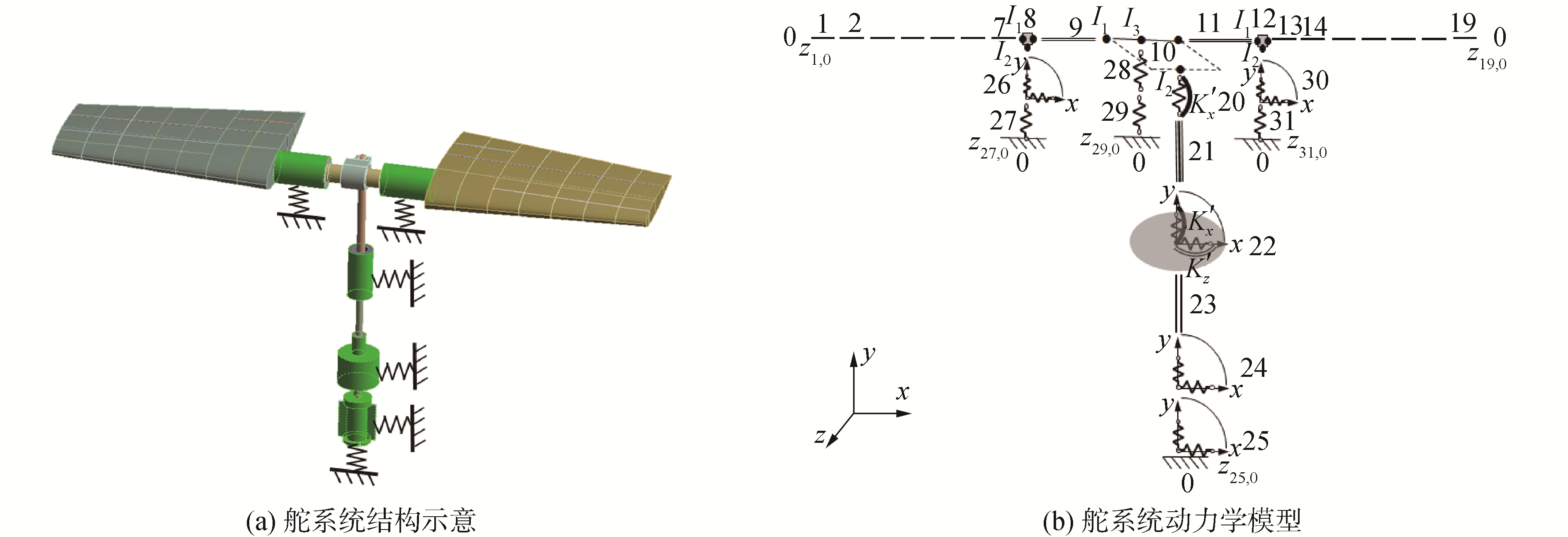
由于水下航行器舵系统的舵叶是位于水下,舵叶表面有细孔,水流可以通过细孔流进流出,假设舵叶内部的水为附加质量,舵叶应变很小,应力应变为线性关系;舵系统的轴承座、导向装置、密封装置、液压缸都是用螺栓连接在水下航行器上。水下航行器质量远远大于舵系统,因此假设水下航行器为固定边界。螺栓连接刚度用弹簧表示,舵系统的结构示意图如图 2(a)所示。考虑舵系统每个部件之间的相互作用,基于MSTMM对整个舵系统进行建模,动力学模型如图 2(b)所示。
|
Download:
|
| 图 2 舵系统结构示意及动力学模型 Fig. 2 The hydroplanes system and its dynamic model | |
在图 2(b)中,舵叶处理为7段考虑轴向振动的、不同结构参数的弯扭耦合梁(元件1~7,13~19);柱铰(元件20)处理为铰元件;球铰以及考虑导向装置与水下航行器的连接刚度,因此在球铰元件(元件22)中添加了x方向的弹簧刚度;舵轴(元件9、11)处理为可以考虑横向、轴向振动以及扭转振动的非耦合梁;轴承与轴承套之间的接触刚度以及定位环与舵叶之间的接触刚度用弹簧铰表示(元件26、28、30);轴承座与水下航行器的连接刚度用弹簧表示(元件27、29、31);拉杆处理为可以考虑x轴方向、轴向振动的非耦合梁(元件21);传动杆在密封装置中只能上下运动,因此处理为杆元件(元件23);舵柄处理为刚体(元件10);液压缸提供的是液压弹簧刚度,同时考虑到密封装置与水下航行器之间的连接刚度,液压缸处理为一个弹簧铰(元件24);液压缸与水下航行器之间的连接刚度处理为一个弹簧铰(元件25);传递方向是从左端点和下端点到右端点,所有元件的状态矢量统一为[X, Y, Θz, Mz, Qx, Qy, Θx, Mx]T。
基于多体系统传递矩阵法[7-8, 16],建立水下航行器舵系统振动特性快速计算方法,以实现对水下航行器舵系统的固有振动特性的准确分析。
1.2 传递方程推导根据多体系统传递矩阵法对系统拓扑结构的定义[7, 16],推导舵系统的传递方程:
| $ \begin{array}{l} {Z_{19,0}} = U_{{\rm{pla}}}^{\rm{R}}{Z_{12,13}} = U_{{\rm{pla}}}^{\rm{R}}\left( {{U_{12,{I_1}}}{Z_{12,11}} + {U_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}}} \right) = \\ U_{{\rm{pla}}}^{\rm{R}}\left( {{U_{12,{I_1}}}{U_{11}}{Z_{10,11}} + {U_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}}} \right) = \\ U_{{\rm{pla}}}^{\rm{R}}\left( {{U_{12,{I_1}}}{U_{11}}\left( {{U_{10,{I_1}}}{Z_{10,9}} + {U_{10,{I_2}}}{Z_{10,20}} + {U_{10,{I_3}}}{Z_{10,28}}} \right) + } \right.\\ \left. {{U_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}}} \right) = \\ U_{{\rm{pla}}}^{\rm{R}}\left( {{U_{12,{I_1}}}{U_{11}}\left( {{U_{10,{I_1}}}{U_9}{Z_{8,9}} + {U_{10,{I_2}}}{U^{col}}{Z_{25,0}} + } \right.} \right.\\ \left. {\left. {{U_{10,{1_3}}}{U_{28}}{U_{29}}{Z_{2,0}}} \right) + {U_{12,{l_2}}}{U_{30}}{U_{31}}{Z_{31,0}}} \right) = \\ U_{{\rm{pla}}}^{\rm{R}}\left( {{U_{12,{I_1}}}{U_{11}}\left( {{U_{10,{I_1}}}{U_9}\left( {{U_{8,{I_1}}}{Z_{8,7}} + {U_{8,{I_2}}}{U_{26}}{U_{27}}{Z_{27,0}}} \right) + } \right.} \right.\\ \left. {\left. {{U_{10,{I_2}}}{U^{{\rm{col}}}}{Z_{25,0}} + {U_{10,{I_3}}}{U_{28}}{U_{29}}{Z_{29,0}}} \right) + {U_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}}} \right) = \\ U_{{\rm{pla}}}^{\rm{R}}\left( {{U_{12,{I_1}}}{U_{11}}\left( {{U_{10,{I_1}}}{U_9}\left( {{U_{8,{I_1}}}U_{{\rm{pla}}}^{\rm{L}}{Z_{1,0}} + {U_{8,{I_2}}}{U_{26}}{U_{27}}{Z_{27,0}}} \right) + } \right.} \right.\\ \left. {{U_{10,{I_2}}}{U^{{\rm{col}}}}{Z_{25,0}} + {U_{10,{I_3}}}{U_{28}}{U_{29}}{Z_{29,0}}} \right) + {U_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}} = \\ U_{{\rm{pla}}}^{\rm{R}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_1}}}{U_9}{U_{8,{I_1}}}U_{{\rm{pla}}}^{\rm{L}}{Z_{1,0}} + \\ U_{{\rm{pla}}}^{\rm{R}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_1}}}{U_9}{U_{8,{I_2}}}{U_{26}}{U_{27}}{Z_{27,0}} + \\ U_{{\rm{pla}}}^{\rm{R}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_3}}}{U_{28}}{U_{29}}{Z_{29,0}} + \\ U_{{\rm{pla}}}^{\rm{R}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_2}}}{U^{{\rm{col}}}}{Z_{25,0}} + U_{{\rm{pla}}}^{\rm{R}}{U_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}} \end{array} $ | (1) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {U_{{\rm{pla}}}^{\rm{R}} = {U_{19}}{U_{18}}{U_{17}}{U_{16}}{U_{15}}{U_{14}}{U_{13}}}\\ {U_{{\rm{pla}}}^{\rm{L}} = {U_7}{U_6}{U_5}{U_4}{U_3}{U_2}{U_1}}\\ {{U^{{\rm{col}}}} = {U_{20}}{U_{21}}{U_{22}}{U_{23}}{U_{24}}{U_{25}}} \end{array}} \right. $ | (2) |
令:
| $ \left\{ {\begin{array}{*{20}{l}} {{T_{1 - 19}} = U_{{\rm{pla}}}^{\rm{R}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_1}}}{U_9}{U_{8,{I_1}}}U_{{\rm{pla}}}^{\rm{L}}}\\ {{T_{27 - 19}} = U_{{\rm{pla}}}^{\rm{R}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_1}}}{U_9}{U_{8,{I_2}}}{U_{26}}{U_{27}}}\\ {{T_{29 - 19}} = U_{{\rm{pla}}}^{\rm{R}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_3}}}{U_{28}}{U_{29}}}\\ {{T_{25 - 19}} = U_{{\rm{pla}}}^{\rm{R}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_2}}}{U^{{\rm{col}}}}}\\ {{T_{31 - 19}} = U_{{\rm{pla}}}^{\rm{R}}{U_{12,{I_2}}}{U_{30}}{U_{31}}} \end{array}} \right. $ | (3) |
因此,式(1)可以写为:
| $ \begin{array}{*{20}{c}} { - {Z_{19,0}} + {T_{1 - 19}}{Z_{1,0}} + {T_{27 - 19}}{Z_{27,0}} + }\\ {{T_{29 - 19}}{Z_{29,0}} + {T_{25 - 19}}{Z_{25,0}} + {T_{31 - 19}}{Z_{31,0}} = 0} \end{array} $ | (4) |
式中Tj-19的下标j-19表示传递方向中从该j稍元件到根元件的传递分支。
| $ \left\{ {\begin{array}{*{20}{l}} {{H_{8,{I_1}}}{Z_{8,7}} = {H_{8,{I_2}}}{U_{26}}{U_{27}}{Z_{27,0}}}\\ {{H_{8,{I_1}}}U_{{\rm{pla}}}^L{Z_{1,0}} = {H_{8,{I_2}}}{U_{26}}{U_{27}}{Z_{27,0}}}\\ {{G_{1 - 8}}{Z_{1,0}} + {G_{27 - 8}}{Z_{27,0}} = 0}\\ {{G_{1 - 8}} = - {H_{8,{I_1}}}U_{{\rm{pla}}}^L}\\ {{G_{27 - 8}} = {H_{8,{I_2}}}{U_{26}}{U_{27}}} \end{array}} \right. $ | (5) |
| $ \left\{ \begin{array}{l} {H_{10,{I_1}}}{Z_{10,9}} = {H_{10,{I_2}}}{Z_{10,20}}\\ {H_{10,{I_1}}}{U_9}{Z_{8,9}} = {H_{10,{I_2}}}{U^{{\rm{col}}}}{Z_{25,0}}\\ {H_{10,{I_1}}}{U_9}\left( {{U_{8,{I_1}}}U_{{\rm{pla}}}^L{Z_{1,0}} + {U_{8,{I_2}}}{U_{26}}{U_{27}}{Z_{27,0}}} \right) = \\ \;\;\;\;\;\;\;{H_{10,{I_2}}}{U^{{\rm{col}}}}{Z_{25,0}}\\ {G_{1 - 10}}{Z_{1,0}} + {G_{27 - 10}}{Z_{27,0}} + {G_{25 - 10}}{Z_{25,0}} = 0\\ {G_{1 - 10}} = - {H_{10,{I_1}}}{U_9}{U_{8,{I_1}}}U_{{\rm{pla}}}^L\\ {G_{27 - 10}} = - {H_{10,{I_1}}}{U_9}{U_{8,{I_2}}}{U_{26}}{U_{27}}\\ {G_{25 - 10}} = {H_{10,{I_2}}}{U^{{\rm{col}}}} \end{array} \right. $ | (6) |
| $ \left\{ {\begin{array}{*{20}{l}} {{H_{10,{{I'}_1}}}{Z_{10,9}} = {H_{10,{I_3}}}{U_{28}}{U_{29}}{Z_{29,0}}}\\ {{H_{10,{{I'}_1}}}{U_9}{Z_{8,9}} = {H_{10,{I_3}}}{U_{28}}{U_{29}}{Z_{29,0}}}\\ {{H_{10,{{I'}_1}}}{U_9}\left( {{U_{8,{I_1}}}U_{{\rm{pla}}}^L{Z_{1,0}} + {U_{8,{I_2}}}{U_{26}}{U_{27}}{Z_{27,0}}} \right) = }\\ {\;\;\;\;\;\;\;{H_{10,{I_3}}}{U_{28}}{U_{29}}{Z_{29,0}}}\\ {G_{1 - 10}^\prime {Z_{1,0}} + G_{27 - 10}^\prime {Z_{27,0}} + G_{29 - 10}^\prime {Z_{29,0}} = 0}\\ {G_{1 - 10}^\prime = - {H_{10,{{I'}_1}}}{U_9}{U_{8,{I_1}}}U_{{\rm{pla}}}^L}\\ {G_{27 - 10}^\prime = - {H_{10,{{I'}_1}}}{U_9}{U_{8,{I_2}}}{U_{26}}{U_{27}}}\\ {G_{29 - 10}^\prime = {H_{10,{I_3}}}{U_{28}}{U_{29}}} \end{array}} \right. $ | (7) |
| $ \left\{ \begin{array}{l} {H_{12,{I_1}}}{Z_{12,11}} = {H_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}}\\ {H_{12,{I_1}}}{U_{12,{I_1}}}{U_{11}}{Z_{10,11}} = {H_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}}\\ {H_{12,{I_1}}}{U_{12,{I_1}}}{U_{11}}\left( {{U_{10,{I_1}}}{Z_{10,9}} + {U_{10,{I_2}}}{Z_{10,20}} + {U_{10,{I_3}}}{U_{28}}{U_{29}}{Z_{29,0}}} \right) = {H_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}}\\ {H_{12,{I_1}}}{U_{12,{I_1}}}{U_{11}}\left( {{U_{10,{I_1}}}{U_9}{Z_{8,9}} + {U_{10,{I_2}}}{U^{{\rm{col}}}}{Z_{25,0}} + {U_{10,{I_3}}}{U_{28}}{U_{29}}{Z_{29,0}}} \right) = {H_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}}\\ - {H_{12,{I_1}}}{U_{12,{I_1}}}{U_{11}}\left( {{U_{10,{I_1}}}{U_9}\left( {{U_{8,{I_1}}}{Z_{8,7}} + {U_{8,{I_2}}}{U_{26}}{U_{27}}{Z_{27,0}}} \right) + {U_{10,{I_2}}}{U^{{\rm{col}}}}{Z_{25,0}} + {U_{10,{I_3}}}{U_{28}}{U_{29}}{Z_{29,0}}} \right) = {H_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}}\\ - {H_{12,{I_1}}}{U_{12,{I_1}}}{U_{11}}\left( {{U_{10,{I_1}}}{U_9}\left( {{U_{8,{I_1}}}U_{{\rm{pla}}}^L{Z_{1,0}} + {U_{8,{I_2}}}{U_{26}}{U_{27}}{Z_{27,0}}} \right) + {U_{10,{I_2}}}{U^{{\rm{col}}}}{Z_{25,0}} + {U_{10,{I_3}}}{U_{28}}{U_{29}}{Z_{29,0}}} \right) = {H_{12,{I_2}}}{U_{30}}{U_{31}}{Z_{31,0}}\\ {G_{1 - 12}}{Z_{1,0}} + {G_{27 - 12}}{Z_{27,0}} + {G_{25 - 12}}{Z_{25,0}} + {G_{29 - 12}}{Z_{29,0}} + {G_{31 - 12}}{Z_{31,0}} = 0\\ {G_{1 - 12}} = - {H_{12,{I_1}}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_1}}}{U_9}{U_{8,{I_1}}}U_{{\rm{pla}}}^L\\ {G_{27 - 12}} = - {H_{12,{I_1}}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_1}}}{U_9}{U_{8,{I_2}}}{U_{26}}{U_{27}}\\ {G_{25 - 12}} = - {H_{12,{I_1}}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_2}}}{U^{{\rm{col}}}}\\ {G_{29 - 12}} = - {H_{12,{I_1}}}{U_{12,{I_1}}}{U_{11}}{U_{10,{I_3}}}{U_{28}}{U_{29}}\\ {G_{31 - 12}} = {H_{12,{I_2}}}{U_{30}}{U_{31}} \end{array} \right. $ | (8) |
式中:Gk-l的下标k-l表示几何方程从该元件k到元件l的传递分支。
1.3 舵系统各部件的传递矩阵常用的梁、杆、刚体、弹簧铰等的传递矩阵可以查阅文献[7]得到。
根据舵叶的变形特性,舵叶一般可以简化为一根弯扭耦合梁。图 2(a)中的舵叶为非等截面水翼,可以将舵叶分成多段等截面不同结构参数分布的弯扭耦合梁。文献[17]已经推导了弯扭耦合梁的传递矩阵,并给出了获取舵叶结构参数的方法及动力学模型中所用的主要参数。从图 1可以看到,由于舵叶是固定在舵轴上,导向拉杆连接的球铰,因此实际模型中,加入了定位环来限制舵轴的左右窜动。在图 2(b)的动力学模型中,将定位环处理为弹簧刚度,因此模型中的舵轴、舵叶、导向拉杆存在x方向的自由度。令文献[17]中的弯扭耦合梁的传递矩阵为DCB=B(1)·B-1(0),那么考虑弯扭耦合梁的轴向振动,得到可以考虑弯曲扭转耦合振动、轴向振动的耦合梁传递矩阵:
| $ {\mathit{\boldsymbol{U}}^{CB}} = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{\beta _r}l} \right)}&0&0&0&{ - \sin \left( {{\beta _r}l} \right)/\left( {{\beta _r}EA} \right)}&0&0&0\\ 0&{D_{11}^{CB}}&{D_{12}^{CB}}&{D_{13}^{CB}}&0&{D_{14}^{CB}}&{D_{15}^{CB}}&{D_{16}^{CB}}\\ 0&{D_{21}^{CB}}&{D_{22}^{CB}}&{D_{23}^{CB}}&0&{D_{24}^{CB}}&{D_{25}^{CB}}&{D_{26}^{CB}}\\ 0&{D_{31}^{CB}}&{D_{32}^{CB}}&{D_{33}^{CB}}&0&{D_{34}^{CB}}&{D_{35}^{CB}}&{D_{36}^{CB}}\\ {{\beta _r}EA\sin \left( {{\beta _r}l} \right)}&0&0&0&{\cos \left( {{\beta _r}l} \right)}&0&0&0\\ 0&{D_{41}^{CB}}&{D_{42}^{CB}}&{D_{43}^{CB}}&0&{D_{44}^{CB}}&{D_{45}^{CB}}&{D_{46}^{CB}}\\ 0&{D_{51}^{CB}}&{D_{52}^{CB}}&{D_{53}^{CB}}&0&{D_{54}^{CB}}&{D_{55}^{CB}}&{D_{56}^{CB}}\\ 0&{D_{61}^{CB}}&{D_{62}^{CB}}&{D_{63}^{CB}}&0&{D_{64}^{CB}}&{D_{65}^{CB}}&{D_{66}^{CB}} \end{array}} \right] $ | (9) |
式中:
刚体的传递矩阵为:
| $ {\mathit{\boldsymbol{U}}_{10,{I_1}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0\\ 0&1&{{b_1}}&0&0&0&{ - {b_3}}&0\\ 0&0&1&0&0&0&0&0\\ 0&{m{\omega ^2}\left( {{b_1} - {c_1}} \right)}&{ - m{\omega ^2}\left( { - {b_2}{c_2} - {b_1}{c_1}} \right) - {\omega ^2}\left( {{J_{zz}} + mc_3^2} \right)}&1&0&{{b_1}}&{ - m{\omega ^2}{b_1}{c_3} + {\omega ^2}{J_{xz}}}&0\\ {m{\omega ^2}}&0&0&0&1&0&0&0\\ 0&{m{\omega ^2}}&{m{\omega ^2}{c_1}}&0&0&1&{ - m{\omega ^2}{c_3}}&0\\ 0&0&0&0&0&0&1&0\\ 0&{m{\omega ^2}\left( { - {b_3} + {c_3}} \right)}&{ - m{\omega ^2}{b_3}{c_1} + {\omega ^2}{J_{xz}}}&0&0&{ - b3}&{ - m{\omega ^2}\left( { - {b_3}{c_3} - {b_2}{c_2}} \right) - {\omega ^2}\left( {{J_{xx}} + mc_1^2} \right)}&1 \end{array}} \right] $ | (10) |
| $ {\mathit{\boldsymbol{U}}_{10,{I_2}}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&1&0&{\left( {{b_1} - {a_1}} \right)}&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&{\left( { - {b_3} + {a_3}} \right)}&0&1 \end{array}} \right] $ | (11) |
| $ {\mathit{\boldsymbol{U}}_{10,{I_3}}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&1&0&{\left( {{b_1} - {d_1}} \right)}&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&{\left( { - {b_3} + {d_3}} \right)}&0&1 \end{array}} \right] $ | (12) |
式中:Jxz、Jxx、Jzz为刚体的质量惯性矩;(c1, c2, c3)为质心位置;(a1, a2, a3)为对应U10, I2的输入点坐标;(d1, d2, d3)为对应U10, I3的输入点坐标;(b1, b2, b3)为输出点处的坐标。以U10, I1对应的输入点位置为原点。
虚拟刚体的传递矩阵为:
| $ {\mathit{\boldsymbol{U}}_{8,{I_1}}} = {\mathit{\boldsymbol{U}}_{12,{I_1}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&1&0&0&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&1&0\\ 0&0&0&0&0&0&0&1 \end{array}} \right] $ | (13) |
| $ {\mathit{\boldsymbol{U}}_{8,{I_2}}} = {\mathit{\boldsymbol{U}}_{12,{I_2}}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&1&0&0&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&1 \end{array}} \right] $ | (14) |
弹簧的传递矩阵为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{U}}_{27}} = {\mathit{\boldsymbol{U}}_{28}} = {\mathit{\boldsymbol{U}}_{29}} = {\mathit{\boldsymbol{U}}_{31}} = }\\ {\left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0\\ 0&1&0&0&0&{ - 1/{K_y}}&0&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&1&0&0&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&1&0\\ 0&0&0&0&0&0&0&1 \end{array}} \right]} \end{array} $ | (15) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{U}}_{25}} = {\mathit{\boldsymbol{U}}_{26}} = {\mathit{\boldsymbol{U}}_{30}} = }\\ {\left[ {\begin{array}{*{20}{c}} 1&0&0&0&{ - 1/{K_x}}&0&0&0\\ 0&1&0&0&0&{ - 1/{K_y}}&0&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&1&0&0&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&1&0\\ 0&0&0&0&0&0&0&1 \end{array}} \right]} \end{array} $ | (16) |
| $ {\mathit{\boldsymbol{U}}_{24}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&{ - 1/{K_x}}&0&0&0\\ 0&1&0&0&0&{ - 1/{K_h}}&0&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&1&0&0&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&1&0\\ 0&0&0&0&0&0&0&1 \end{array}} \right] $ | (17) |
式中:Kx、Ky分别为x和y方向的弹簧刚度;Kh为液压等效弹簧刚度。
柱铰的传递矩阵为:
| $ {\mathit{\boldsymbol{U}}_{20}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0\\ 0&1&0&0&0&{ - 1/{K_y}}&0&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&1&0&0&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&1&{1/{{K'}_x}}\\ 0&0&0&0&0&0&0&1 \end{array}} \right] $ | (18) |
式中K′x为绕x轴的扭转刚度。
球铰的传递矩阵为:
| $ {\mathit{\boldsymbol{U}}_{22}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&{ - 1/{K_x}}&0&0&0\\ 0&1&0&0&0&{ - 1/{K_y}}&0&0\\ 0&0&1&{1/{{K'}_z}}&0&0&0&0\\ 0&0&0&1&0&0&0&0\\ 0&0&0&0&1&0&0&0\\ 0&0&0&0&0&1&0&0\\ 0&0&0&0&0&0&1&{1/{{K'}_x}}\\ 0&0&0&0&0&0&0&1 \end{array}} \right] $ | (19) |
式中K′z为绕z轴的扭转刚度。
弯扭耦合梁的传递矩阵见文献[17],即:
| $ \begin{array}{l} {\mathit{\boldsymbol{U}}_1} = {\mathit{\boldsymbol{U}}_2} = {\mathit{\boldsymbol{U}}_3} = {\mathit{\boldsymbol{U}}_4} = \\ {\mathit{\boldsymbol{U}}_5} = {\mathit{\boldsymbol{U}}_6} = {\mathit{\boldsymbol{U}}_7} = \\ {\mathit{\boldsymbol{U}}_{13}} = {\mathit{\boldsymbol{U}}_{14}} = \\ {\mathit{\boldsymbol{U}}_{15}} = {\mathit{\boldsymbol{U}}_{16}} = {\mathit{\boldsymbol{U}}_{17}} = {\mathit{\boldsymbol{U}}_{18}} = {\mathit{\boldsymbol{U}}_{19}} = {\mathit{\boldsymbol{U}}^{CB}} \end{array} $ | (20) |
多体系统的传递矩阵法[7]的矩阵库中包含具有横向振动、扭转振动的非耦合梁传递矩阵。根据MSTMM矩阵推导方法可以得到非耦合梁模型一的传递矩阵为:
| $ {\mathit{\boldsymbol{U}}^{UB1}} = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{\beta _r}l} \right)}&0&0&0&{ - \sin \left( {{\beta _r}l} \right)/\left( {{\beta _r}EA} \right)}&0&0&0\\ 0&{S(\lambda l)}&{T(\lambda l)/\lambda }&{U(\lambda l)/\left( {EI{\lambda ^2}} \right)}&0&{V(\lambda l)/\left( {EI{\lambda ^3}} \right)}&0&0\\ 0&{\lambda V(\lambda l)}&{S(\lambda l)}&{T(\lambda l)/(EI\lambda )}&0&{U(\lambda l)/\left( {EI{\lambda ^2}} \right)}&0&0\\ 0&{EI{\lambda ^2}U(\lambda l)}&{EI\lambda V(\lambda l)}&{S(\lambda l)}&0&{T(\lambda l)/\lambda }&0&0\\ {\beta EA\sin \left( {{\beta _r}l} \right)}&0&0&0&{\cos \left( {{\beta _r}l} \right)}&0&0&0\\ 0&{EI{\lambda ^3}T(\lambda l)}&{EI{\lambda ^2}U(\lambda l)}&{\lambda V(\lambda l)}&0&{S(\lambda l)}&0&0\\ 0&0&0&0&0&0&{\cos (\gamma l)}&{\sin (\gamma l)}\\ 0&0&0&0&0&0&{ - \gamma Gl\sin \left( {\gamma Ll} \right)}&{\cos (\gamma l)} \end{array}} \right] $ | (21) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {\gamma = \sqrt {\rho {\omega ^2}/G} ,\lambda = \sqrt[4]{{m{\omega ^2}/EI}},S = \frac{{ch + c}}{2},}\\ {T = \frac{{{\rm{sh}} + s}}{2},U = \frac{{{\rm{ch}} - c}}{2},V = \frac{{{\rm{sh}} - s}}{2},}\\ {{\rm{ch}} = \cosh (\lambda l),sh = \sinh (\lambda l),}\\ {c = \cos (\lambda l),s = \sin (\lambda l)} \end{array}} \right. $ | (22) |
l和A分别是梁的长度和截面积。
因此,有:
| $ {\mathit{\boldsymbol{U}}_9} = {\mathit{\boldsymbol{U}}_{11}} = {\mathit{\boldsymbol{U}}^{{\rm{UB1}}}} $ | (23) |
根据MSTMM矩阵库中的轴向振动杆和横向振动梁的传递矩阵形式可以得到考虑轴向和横向振动的平面振动梁的传递矩阵U1为:
| $ {\mathit{\boldsymbol{U}}^{\rm{1}}} = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{\beta _r}l} \right)}&0&0&0&{ - \sin \left( {{\beta _r}l} \right)/\left( {{\beta _r}EA} \right)}&0\\ 0&{S(\lambda l)}&{T(\lambda l)/\lambda }&{U(\lambda l)/\left( {EI{\lambda ^2}} \right)}&0&{V(\lambda l)/\left( {EI{\lambda ^3}} \right)}\\ 0&{\lambda V(\lambda l)}&{S(\lambda l)}&{T(\lambda l)/(EI\lambda )}&0&{U(\lambda l)/\left( {EI{\lambda ^2}} \right)}\\ 0&{EI{\lambda ^2}U(\lambda l)}&{EI\lambda V(\lambda l)}&{S(\lambda l)}&0&{T(\lambda l)/\lambda }\\ {{\beta _r}EA\sin \left( {{\beta _r}l} \right)}&0&0&0&{\cos \left( {{\beta _r}l} \right)}&0\\ 0&{EI{\lambda ^3}T(\lambda l)}&{EI{\lambda ^2}U(\lambda l)}&{\lambda V(\lambda l)}&0&{S(\lambda l)} \end{array}} \right] $ | (24) |
采用方向余弦矩阵将平面振动梁转动90°,转换矩阵R为:
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} 0&{ - 1}&0&0&0&0\\ 1&0&0&0&0&0\\ 0&0&1&0&0&0\\ 0&0&0&1&0&0\\ 0&0&0&0&0&{ - 1}\\ 0&0&0&0&1&0 \end{array}} \right] $ | (25) |
转换后的平面振动梁的传递矩阵U2为:
| $ {\mathit{\boldsymbol{U}}^2} = {\mathit{\boldsymbol{R}}^T}{\mathit{\boldsymbol{U}}^1}\mathit{\boldsymbol{R}} $ | (26) |
根据状态矢量的数量,扩展对应的传递矩阵。因此,非耦合梁模型二传递矩阵UUB2为:
| $ {\mathit{\boldsymbol{U}}^{\mathit{\boldsymbol{UB}}{\rm{2}}}} = \left[ {\begin{array}{*{20}{c}} {U_{11}^2}&{U_{12}^2}&{U_{13}^2}&{U_{14}^2}&{U_{15}^2}&{U_{16}^2}&0&0\\ {U_{21}^2}&{U_{22}^2}&{U_{23}^2}&{U_{24}^2}&{U_{25}^2}&{U_{26}^2}&0&0\\ {U_{31}^2}&{U_{32}^2}&{U_{33}^2}&{U_{34}^2}&{U_{35}^2}&{U_{36}^2}&0&0\\ {U_{41}^2}&{U_{42}^2}&{U_{43}^2}&{U_{44}^2}&{U_{45}^2}&{U_{46}^2}&0&0\\ {U_{51}^2}&{U_{52}^2}&{U_{53}^2}&{U_{54}^2}&{U_{55}^2}&{U_{56}^2}&0&0\\ {U_{61}^2}&{U_{62}^2}&{U_{63}^2}&{U_{64}^2}&{U_{65}^2}&{U_{66}^2}&0&0\\ 0&0&0&0&0&0&1&0\\ 0&0&0&0&0&0&0&1 \end{array}} \right] $ | (27) |
因此,有:
| $ {\mathit{\boldsymbol{U}}_{21}} = {\mathit{\boldsymbol{U}}^{{\rm{UB2}}}} $ | (28) |
杆元件的传递矩阵Urod为:
| $ {\mathit{\boldsymbol{U}}^{{\rm{rod}}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0\\ 0&{\cos \left( {{\beta _r}l} \right)}&0&0&0&{ - \sin \left( {{\beta _r}l} \right)/\left( {{\beta _r}EA} \right)}&0&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&1&0&0&0&0\\ 0&0&0&0&1&0&0&0\\ 0&{{\beta _r}EA\sin \left( {{\beta _r}l} \right)}&0&0&0&{\cos \left( {{\beta _r}l} \right)}&0&0\\ 0&0&0&0&0&0&1&0\\ 0&0&0&0&0&0&0&1 \end{array}} \right] $ | (29) |
因此,
| $ {\mathit{\boldsymbol{U}}_{23}} = {\mathit{\boldsymbol{U}}^{{\rm{rod}}}} $ | (30) |
另外几何矩阵,
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_{8,{I_1}}} = {\mathit{\boldsymbol{H}}_{8,{I_2}}} = {\mathit{\boldsymbol{H}}_{12,{I_1}}} = {\mathit{\boldsymbol{H}}_{12,{I_2}}} = }\\ {\left[ {\begin{array}{*{20}{l}} 1&0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&0&0&0&1&0 \end{array}} \right]} \end{array} $ | (31) |
| $ {\mathit{\boldsymbol{H}}_{10,{I_1}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0\\ 0&1&{{a_1}}&0&0&0&{ - {a_3}}&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&0&0&0&1&0 \end{array}} \right] $ | (32) |
| $ {\mathit{\boldsymbol{H}}_{10,{I_2}}} = {\mathit{\boldsymbol{H}}_{10,{I_3}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&0&0&0&1&0 \end{array}} \right] $ | (33) |
| $ {\mathit{{H}}_{10,{I_1}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0&0&0\\ 0&1&{{d_1}}&0&0&0&{ - {d_3}}&0\\ 0&0&1&0&0&0&0&0\\ 0&0&0&0&0&0&1&0 \end{array}} \right] $ | (34) |
根据式(1)~(5)可以写出舵系统总传递方程:
| $ {\left. {{{\left. {{\mathit{\boldsymbol{U}}_{{\rm{all}}}}} \right|}_{24 \times 48}}{\mathit{\boldsymbol{Z}}_{{\rm{all}}}}} \right|_{48 \times 1}} = 0 $ | (35) |
式中:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{U}}_{{\rm{all}}}} = \left[ {\begin{array}{*{20}{c}} {{{\left. {{\mathit{\boldsymbol{T}}_{1 - 19}}} \right|}_{8 \times 8}}}&{{{\left. {{\mathit{\boldsymbol{T}}_{27 - 19}}} \right|}_{8 \times 8}}}&{{{\left. {{\mathit{\boldsymbol{T}}_{29 - 19}}} \right|}_{8 \times 8}}}&{{{\left. {{\mathit{\boldsymbol{T}}_{25 - 19}}} \right|}_{8 \times 8}}}&{{{\left. {{\mathit{\boldsymbol{T}}_{31 - 19}}} \right|}_{8 \times 8}}}&{ - {{\left. I \right|}_{8 \times 8}}}\\ {{{\left. {{\mathit{\boldsymbol{G}}_{1 - 8}}} \right|}_{4 \times 8}}}&{{{\left. {{\mathit{\boldsymbol{G}}_{27 - 8}}} \right|}_{4 \times 8}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}}\\ {{{\left. {{\mathit{\boldsymbol{G}}_{1 - 10}}} \right|}_{4 \times 8}}}&{{{\left. {{\mathit{\boldsymbol{G}}_{27 - 10}}} \right|}_{4 \times 8}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}}&{{\mathit{\boldsymbol{G}}_{25 - 10}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}}\\ {{{\left. {\mathit{\boldsymbol{G}}_{1 - 10}^\prime } \right|}_{4 \times 8}}}&{{{\left. {\mathit{\boldsymbol{G}}_{27 - 10}^\prime } \right|}_{4 \times 8}}}&{{{\left. {\mathit{\boldsymbol{G}}_{29 - 10}^\prime } \right|}_{4 \times 8}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}}\\ {{{\left. {{\mathit{\boldsymbol{G}}_{1 - 12}}} \right|}_{4 \times 8}}}&{{{\left. {{\mathit{\boldsymbol{G}}_{27 - 12}}} \right|}_{4 \times 8}}}&{{{\left. {{\mathit{\boldsymbol{G}}_{25 - 12}}} \right|}_{4 \times 8}}}&{{{\left. {{\mathit{\boldsymbol{G}}_{29 - 12}}} \right|}_{4 \times 8}}}&{{{\left. {{\mathit{\boldsymbol{G}}_{31 - 12}}} \right|}_{4 \times 8}}}&{{{\left. {\bf{O}} \right|}_{4 \times 8}}} \end{array}} \right]\\ \mathit{\boldsymbol{Z}}_{{\rm{all}}}^{\rm{T}} = {\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{Z}}_{1,0}^{\rm{T}}}&{\mathit{\boldsymbol{Z}}_{27,0}^{\rm{T}}}&{\mathit{\boldsymbol{Z}}_{29,0}^{\rm{T}}}&{\mathit{\boldsymbol{Z}}_{25,0}^{\rm{T}}}&{\mathit{\boldsymbol{Z}}_{31,0}^{\rm{T}}}&{\mathit{\boldsymbol{Z}}_{19,0}^{\rm{T}}} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ | (36) |
边界条件为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{Z}}_{1,0}} = {{\left[ {X,Y,{\mathit{\Theta }_z},0,0,0,{\mathit{\Theta }_x},0} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{Z}}_{27,0}} = {{\left[ {0,0,0,{M_z},{Q_x},{Q_y},{\mathit{\Theta }_x},0} \right]}^{\rm{T}}}}\\ {{Z_{29,0}} = {{\left[ {X,0,{\mathit{\Theta }_z},0,0,{Q_y},{\mathit{\Theta }_x},0} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{Z}}_{25,0}} = {{\left[ {0,0,0,{M_z},{Q_x},{Q_y},0,{M_x}} \right]}^{\rm{T}}}}\\ {{Z_{31,0}} = {{\left[ {0,0,0,{M_z},{Q_x},{Q_y},{\mathit{\Theta }_x},0} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{Z}}_{19,0}} = {{\left[ {X,Y,{\mathit{\Theta }_z},0,0,0,{\mathit{\Theta }_x},0} \right]}^{\rm{T}}}} \end{array}} \right. $ | (37) |
求解式(27)即可求出舵系统固有频率,然后可得到对应于固有频率ωk的系统边界点状态矢量Zall,进而通过元件传递方程得到系统全部联接点的状态矢量,即为系统的振型。
舵系统的弯曲刚度、扭转刚度等参数一般可以由实验获得,本文主要通过前期工作的有限元静力学分析方法获得[17]。由于本文舵系统振动特性计算服务于流固耦合计算,因此只关注前几阶与舵叶振动特性相关的模态,不研究舵系统的较高阶模态。
2 水下航行器舵系统振动特性分析舵系统在水下运作时,舵叶中是充满水的,因此需要计算舵叶中充满水情况下的舵系统振动特性,将舵叶中的水处理为附加质量进行计算。求解特征方程,得到舵叶(舵机液压弹簧刚度Kh=4×108 N/m)内部不含水和充满水2种情况下的舵系统的圆频率值如图 3所示。

|
Download:
|
| 图 3 圆频率计算结果 Fig. 3 Calculation results of circular frequency | |
图 3采用的是文献[13]的搜根方法,图 3(a)的横坐标为圆频率,纵坐标表示Δ值的大小,当Δ值接近于0时即可以求出圆频率。图中显示的竖线即搜根过程,每条竖线下对应的就是该阶模态的圆频率。本文还采用ANSYS软件对该舵系统进行建模,限于篇幅,ANSYS软件的设置细节不在此详述。图 4为采用ANSYS软件计算得到的舵系统前四阶振动模态(舵叶内部充满水情况),单核CPU,采用ANSYS计算一组舵系统振动模态需要38.5 min左右。

|
Download:
|
| 图 4 舵系统模态仿真结果(ANSYS) Fig. 4 Modal simulation results of the hydroplane system(ANSYS) | |
从表 1可以看出,基于MSTMM计算出的频率与ANSYS有限元软件计算结果很接近。可以看出,在考虑舵叶内部充满水的条件下,相较于舵叶内部没有水的情况,舵系统的频率值有所减小。
| 表 1 基于MSTMM和FEM舵系统频率计算结果对比 Table 1 Comparison of MSTMM and FEM for the determination of the natural frequencies of the hydroplanes system |
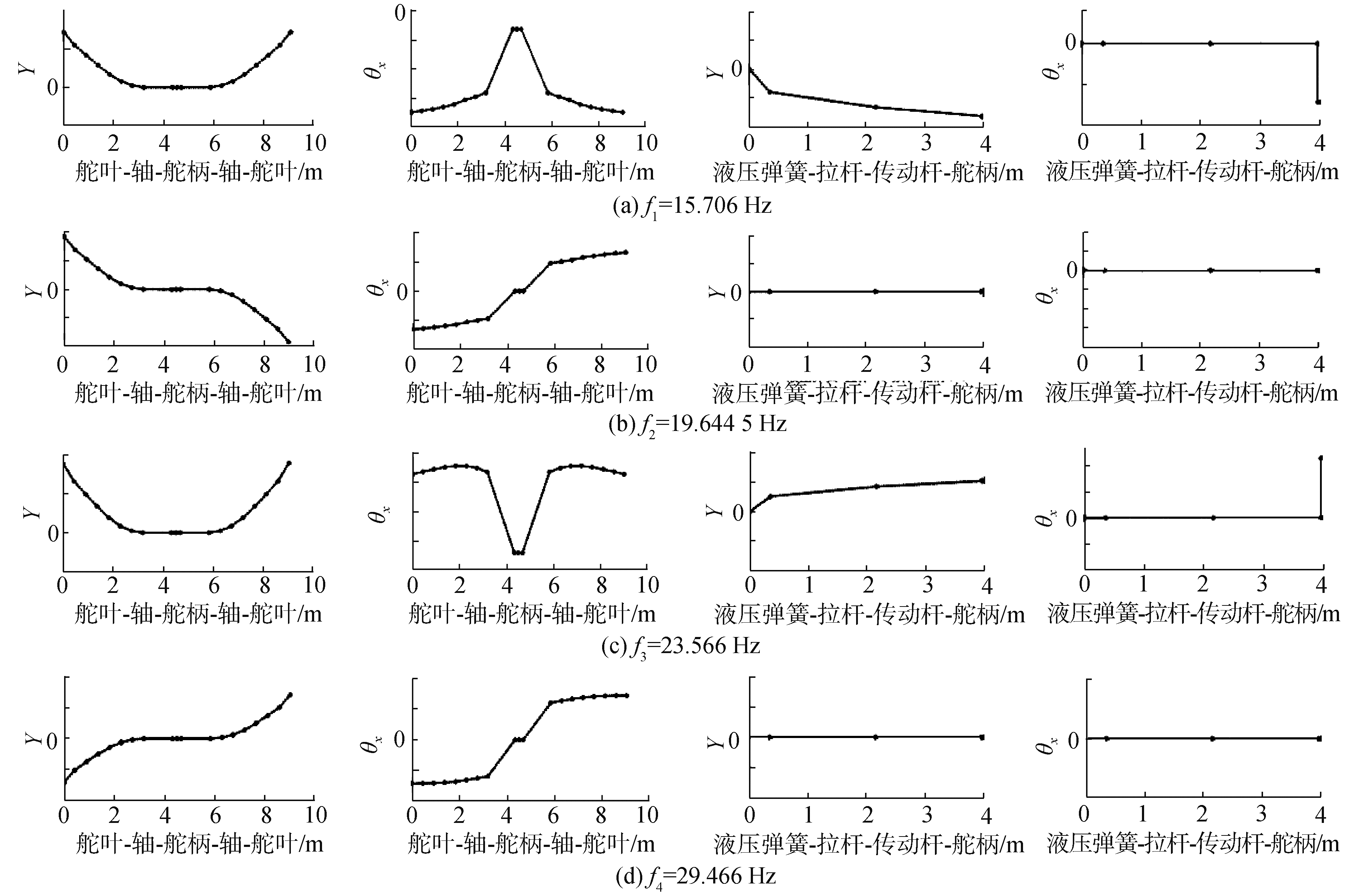
如图 5所示,基于MSTMM的舵系统(内部充满水情况)模态计算结果表明,舵系统前四阶振型在X方向上没有任何振动。基于MSTMM的舵系统(舵叶内部充满水)的Y, Θx方向上的振型如图 6所示。同等计算条件下,计算一组模态,采用MSTMM只需0.25 min左右,相比ANSYS软件大大提高了计算效率。

|
Download:
|
| 图 5 舵系统前四阶X方向振动(MSTMM) Fig. 5 The first fourth x-direction modes of the hydroplane system (MSTMM) | |
|
Download:
|
| 图 6 舵系统前四阶Y, Θx方向振型(MSTMM) Fig. 6 The first fourth Y, Θx-direction modes of the hydroplane system (MSTMM) | |
从图 4~6中可以看出,MSTMM计算结果和ANSYS有限元软件全模型仿真结果十分接近,说明了本文方法的合理性和可行性。舵系统的第1、3阶为对称模态,第2、4阶为反对称模态。从图 6可以看出,第2、4反对称模态中看到,只有舵叶和舵轴这条线有振型,而液压缸到舵柄这条线振型为0,说明第2、4阶模态是舵系统的局部模态。局部模态对系统的整体动力学响应的贡献可以忽略。
基于MSTMM进行舵系统动力学特性计算,可以方便地改变舵系统中的每个部件的参数,并且能快速计算出结果,研究这些参数对舵系统的振动特性的影响。改变液压等效弹簧刚度的大小,分别计算了舵叶内部没有水和充满水2种情况下的舵叶振动频率,计算结果如图 7所示。增加液压弹簧刚度可以增加系统第1、3阶的频率,相当于增加了操纵系统的等效扭转刚度,而增加液压刚度对舵系统的第2、4阶频率没有影响,这是由于第2、4阶模态为局部模态造成的。

|
Download:
|
| 图 7 不同液压刚度情况下的舵系统振动频率 Fig. 7 The hydroplanes system natural frequencies vs. hydraulic stiffness | |
1) 基于MSTMM可以快速建立水下航行器舵系统的动力学模型,且计算效率高。
2) 基于MSTMM可以方便的考虑系统各部件的结构参数和连接刚度对系统振动特性的影响,且可以直观的计算出各振动方向上的振型。
3) 舵系统的1、3阶模态为对称模态,2、4阶模态为反对称模态,且为局部模态。增加液压弹簧刚度可以增加系统第1、3阶的频率,相当于增加了操纵系统的等效扭转刚度,可以抑制舵叶俯仰运动。
| [1] |
THOMSON W T. Theory of vibration with applications[M]. 4th ed. Englewood: Prentice Hall, 1993.
(  0) 0)
|
| [2] |
ABBAS L K, RUI Xiaoting. Free vibration characteristic of multilevel beam based on transfer matrix method of linear multibody systems[J]. Advances in mechanical engineering, 2014, 2014: 792478. (  0) 0)
|
| [3] |
张效慈, 司马灿, 吴有生. 潜艇舵低速颤振现象及其预报[J]. 船舶力学, 2001, 5(1): 70-72. ZHANG Xiaoci, SIMA Can, WU Yousheng. Low-speed flutter phenomenon of submarine rudder and its prediction[J]. Journal of ship mechanics, 2001, 5(1): 70-72. DOI:10.3969/j.issn.1007-7294.2001.01.010 (  0) 0)
|
| [4] |
CHEN Dongyang, ABBAS L K, RUI Xiaoting, et al. Dynamic modeling of sail mounted hydroplanes system-part Ⅱ:hydroelastic behavior and the impact of structural parameters and free-play on flutter[J]. Ocean engineering, 2017, 131: 322-337. DOI:10.1016/j.oceaneng.2017.01.013 (  0) 0)
|
| [5] |
孔建益, 李公法, 侯宇, 等. 潜艇振动噪声的控制研究[J]. 噪声与振动控制, 2006, 26(5): 1-4, 17. KONG Jianyi, LI Gongfa, HOU Yu, et al. Research on vibration and noise controll of submarine[J]. Noise and vibration control, 2006, 26(5): 1-4, 17. DOI:10.3969/j.issn.1006-1355.2006.05.001 (  0) 0)
|
| [6] |
郭勤涛, 张令弥. 结构动力学有限元模型确认方法研究[J]. 应用力学学报, 2005, 22(4): 572-578. GUO Qintao, ZHANG Lingmi. Finite element model validation in structural dynamics[J]. Chinese journal of applied mechanics, 2005, 22(4): 572-578. DOI:10.3969/j.issn.1000-4939.2005.04.015 (  0) 0)
|
| [7] |
芮筱亭. 多体系统传递矩阵法及其应用[M]. 北京: 科学出版社, 2008. RUI Xiaoting. Transfer Matrix method of multibody system and its applications[M]. Beijing: Science Press, 2008. (  0) 0)
|
| [8] |
RUI Xiaoting, WANG Guoping, LU Yuqi, et al. Transfer matrix method for linear multibody system[J]. Multibody system dynamics, 2008, 19(3): 179-207. DOI:10.1007/s11044-007-9092-0 (  0) 0)
|
| [9] |
RUI Xiaoting, HE Bin, LU Yuqi, et al. Discrete time transfer matrix method for multibody system dynamics[J]. Multibody system dynamics, 2005, 14(3-4): 317-344. DOI:10.1007/s11044-005-5006-1 (  0) 0)
|
| [10] |
RONG Bao, RUI Xiaoting, TAO Ling. Discrete time transfer matrix method for launch dynamics modeling and cosimulation of self-propelled artillery system[J]. Journal of applied mechanics, 2013, 80(1): 011008. DOI:10.1115/1.4006869 (  0) 0)
|
| [11] |
ABBAS L K, LI Minjiao, RUI Xiaoting. Transfer matrix method for the determination of the natural vibration characteristics of realistic thrusting launch vehicle-part Ⅰ[J]. Mathematical problems in engineering, 2013, 2013: 764673. (  0) 0)
|
| [12] |
芮筱亭, 陆毓琪, 王国平, 等. 多管火箭发射动力学仿真与试验测试方法[M]. 北京: 国防工业出版社, 2003.
(  0) 0)
|
| [13] |
BESTLE D, ABBAS L, RUI Xiaoting. Recursive eigenvalue search algorithm for transfer matrix method of linear flexible multibody systems[J]. Multibody system dynamics, 2014, 32(4): 429-444. DOI:10.1007/s11044-013-9399-y (  0) 0)
|
| [14] |
ZHANG Lixiang, GUO Yakun, WANG Wenquan. Large eddy simulation of turbulent flow in a true 3D Francis hydro turbine passage with dynamical fluid-structure interaction[J]. International journal for numerical methods in fluids, 2007, 54(5): 517-541. DOI:10.1002/fld.1408 (  0) 0)
|
| [15] |
YOUNG Y L. Fluid-structure interaction analysis of flexible composite marine propellers[J]. Journal of fluids and structures, 2008, 24(6): 799-818. DOI:10.1016/j.jfluidstructs.2007.12.010 (  0) 0)
|
| [16] |
RUI Xiaoting, ZHANG Jianshu, ZHOU Qinbo. Automatic deduction theorem of overall transfer equation of multibody system[J]. Advances in mechanical engineering, 2014, 2014: 378047. (  0) 0)
|
| [17] |
CHEN Dongyang, ABBAS L K, RUI Xiaoting, et al. Dynamic modeling of sail mounted hydroplanes system-Part Ⅰ:Modal characteristics from a transfer matrix method[J]. Ocean engineering, 2017, 130: 629-644. DOI:10.1016/j.oceaneng.2016.12.020 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


