2. 天津水运工程勘察设计院 天津市水运工程测绘技术重点实验室, 天津 300456;
3. 哈尔滨工程大学 水下机器人技术重点实验室, 黑龙江 哈尔滨 150001
2. Tianjin Key Laboratory of Surveying and Mapping for Water Transport Engineering, Tianjin Survey and Design Institute for Water Transport Engineering, Tianjin 300456, China;
3. Science and Technology on Underwater Vehicle Laboratory, Harbin Engineering University, Harbin 150001, China
波浪滑翔器作为新型无人海洋探测平台,从波浪能和太阳能中分别获得前进的动力和电力,克服了大范围、长航时的难题,具有续航能力强、自主控制、绿色环保、价格经济等突出特点[1]。它能长期、自主地执行监测环境、调查水文、预报气象、追踪生物、预警危害、中继通讯等任务。这些特点也使得波浪滑翔器在军事和民用范围内皆具有广泛的应用前景[2]。波浪滑翔器最先由美国的Roger Hine于2005年研制[3]。2年后,他成立了Liquid Robotics公司并进行更加深入的研究[4]。后来,因为其优点多,并且应用需求与发展空间大,波浪滑翔器受到世界众多学者的关注。然而,人们对其的研究主要集中于工程应用,对其动力学模型的理论研究仍然很少。对于任何海洋航行器而言,操纵性能研究是必不可少且极其重要的。建立合适的动力学模型是开展运动机理分析、运动预报、运动控制等研究的基础,而一个优秀的动力学模型往往是简化研究难度的关键。
Kraus等[5]给出了波浪滑翔器沿前进方向和升沉方向的二维模型。齐占峰等[6]利用Kane方程建立了波浪滑翔器在垂直面的多刚体动力学模型。在此基础上,周春琳等[7]将浮体的垂直运动加入到动力学模型中,考虑推力和阻力与波浪运动的耦合。田宝强等[8-9]分别基于牛顿-欧拉方程和拉格朗日方程建立了波浪滑翔器纵剖面动力学模型。上述研究主要考虑波浪滑翔器在竖直平面上的运动,而不能很好地描述波浪滑翔器在水平平面上的运动响应。Smith等[10]对影响波浪滑翔器前进速度的因素的研究。虽然该研究可预测波浪滑翔器的前进速度,但是未考虑波浪滑翔器其他自由度的运动。
现有的海洋机器人动力学模型通常是基于单体的动力学分析建立起来的,而波浪滑翔器是一个多体结构,先前的模型适用性不足,不能清楚地表示波浪滑翔器浮体与滑翔体之间的强耦合关系。D-H方法最早用于描述工业机械臂,能够较好表示多个机械臂之间的关系,且理论发展较成熟,于是Caiti等[11]提出可以借鉴D-H方法用于表示浮体与滑翔体之间的耦合关系。田宝强等[12]在其基础上进一步完善,但是仅仅考虑到二维情况。
本文在国内外波浪滑翔器的动力学模型研究基础上,结合Caiti A的理论基础,利于D-H方法建立三维的波浪滑翔器动力学方程,并进行运动仿真。通过对模型进行动力学仿真,对波浪滑翔器进行动力学分析与操纵性预报。
1 波浪滑翔器 1.1 基本结构波浪滑翔器总体上分为水面浮体、水下滑翔体和系索3大部分,如图 1、2所示。

|
Download:
|
| 图 1 工作中的波浪滑翔器 Fig. 1 Wave glider at work | |

|
Download:
|
| 图 2 波浪滑翔器三维模型 Fig. 2 3-D model of wave glide | |
水面浮体由太阳能电池板、浮体材料包围的密封舱体、控制系统、各类传感器负载以及可充电电池等组成;滑翔体由可转动的翼板、翼板支撑框架及舵机组成;系索主要起到连接浮体和滑翔体作用,并且传递信息。
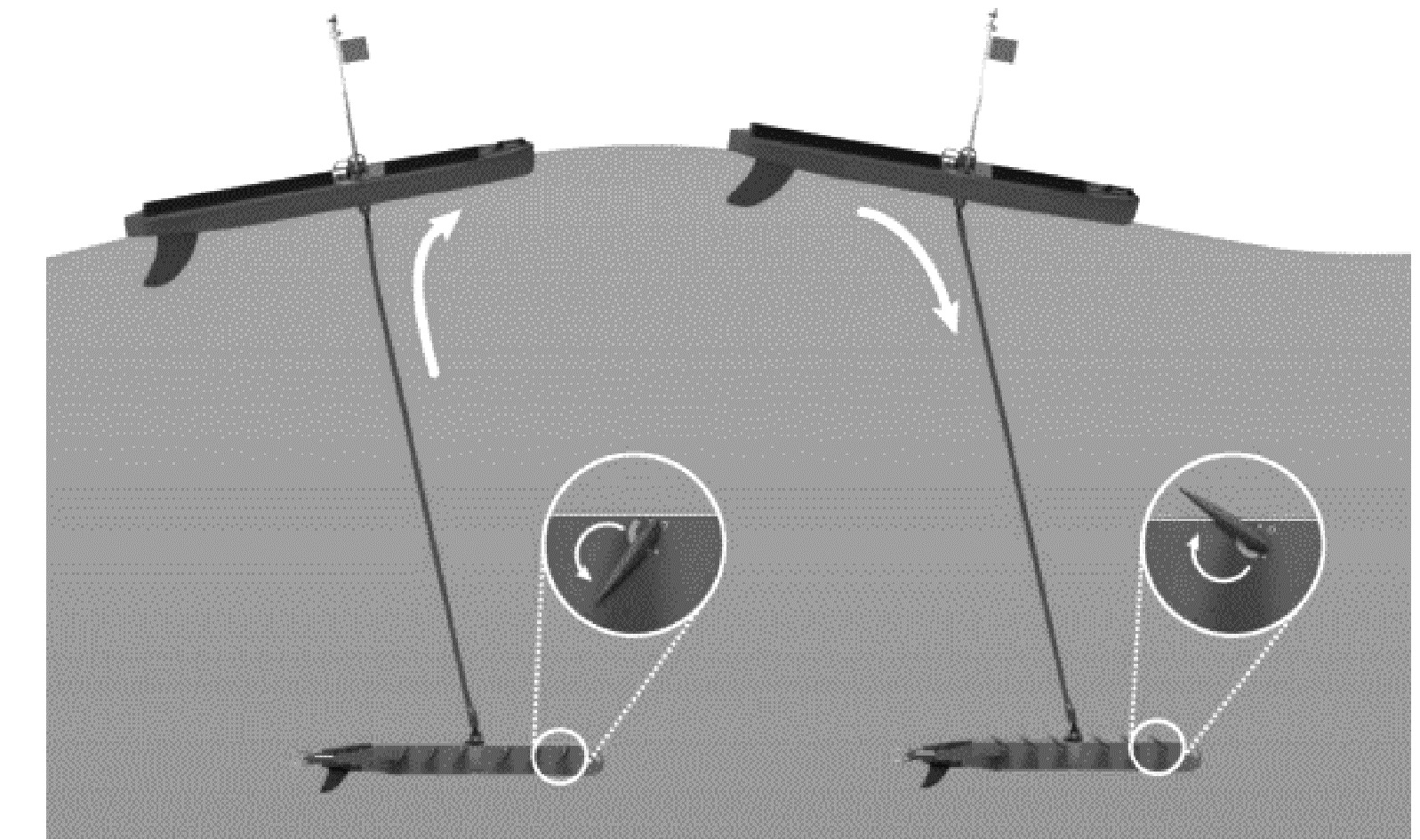
1.2 推进原理如图 3所示,当波浪抬升水面浮体时,在系索的拉力下,水下滑翔体做上升运动。受到水动力的影响,水翼板尾部向下偏转。当攻角在一定范围内时,水翼板产生升力,其分力可分解到水平和垂直2个方向。其中,水平分力推动水下滑翔体向前运动,继而拉动水面浮体,促使其前进。
|
Download:
|
| 图 3 波浪滑翔器上升和下降运动 Fig. 3 Wave glider rises and falls | |
当水面浮体越过波峰时,受到重力的影响,整个系统将向下运动,由于水动力作用,这时水翼板尾部向上翻转。与上升过程一样,由于水动力作用会有升力产生,水平分力方向向前,使整个系统向前运动[13]。
2 动力学模型 2.1 假设为了简化波浪滑翔器动力学模型建模的复杂程度,引用文献[11-12],对波浪滑翔器以及它的环境做出如下假设:
1) 浮体和滑翔体被刚性连接,并且质量恒定不变。
2) 系索应总是处于紧张状态,而且不会在水动力阻力作用下弯曲。
3) 系索节点与浮体重心、滑翔体重心之间的距离忽略不计,因为它们相对于系索的长度都是十分短的。
2.2 D-H方法D-H方法是由Denavit等[14]在1955年最先提出,用4×4齐次变换矩阵来描述机械臂的2个相邻连杆之间的位置和姿态。目前,它已成为一种通用方法,广泛应用于机械臂动力学领域[15]。在每个连杆上固定一个坐标系,来描述其相对位置和姿态关系。所以,每一个连杆可以用ai-1、αi-1、di和θi这4个参数来描述,其中ai-1和αi-1用来描述连杆i-1自身,di和θi用来描述2个相邻连杆之间的相对位置关系。从连杆坐标系i-1变换到坐标系i的坐标转换矩阵可以通过以下步骤获得:绕xi-1轴旋转一个角度αi-1,使得zi轴与zi-1轴互相平行;沿xi-1轴平移一段距离ai-1,使得zi轴与zi-1轴重合;绕zi轴旋转一个角度θi,使得xi-轴与xi-1轴互相平行;沿zi轴平移一段距离di,使得xi-轴与xi-1轴重合。
根据以上步骤,可得知αi-1为两坐标系z轴之间的夹角,ai-1为两坐标系z轴之间的距离,θi为两坐标系x轴之间的夹角,di为两坐标系x轴之间的距离。
所以,从坐标系i变换到坐标系i-1的坐标转换矩阵ii-1T可以表示为:
| $ \begin{array}{l} _i^{i - 1}\mathit{\boldsymbol{T = }}{\rm{Rot}}\left( {x,{\alpha _{i - 1}}} \right){\rm{Trans}}\left( {x,{a_{i - 1}}} \right){\rm{Rot}}\left( {z,{\theta _i}} \right){\rm{Trans}}\left( {z,{d_i}} \right)\\ \left[ {\begin{array}{*{20}{c}} {\cos {\theta _i}}&{ - \sin {\theta _i}}&0&{{\alpha _{i - 1}}}\\ {{\rm{sin}}\theta {\rm{cos}}{\alpha _{i - 1}}}&{\cos {\theta _i}\cos {\alpha _{i - 1}}}&{ - \sin {\alpha _{i - 1}}}&{ - {d_i}\sin {\alpha _{i - 1}}}\\ {\sin {\theta _i}\sin {\alpha _{i - 1}}}&{\cos {\theta _i}\sin {\alpha _{i - 1}}}&{\cos {\alpha _{i - 1}}}&{ - {d_i}\cos {\alpha _{i - 1}}}\\ 0&0&0&1 \end{array}} \right] \end{array} $ |
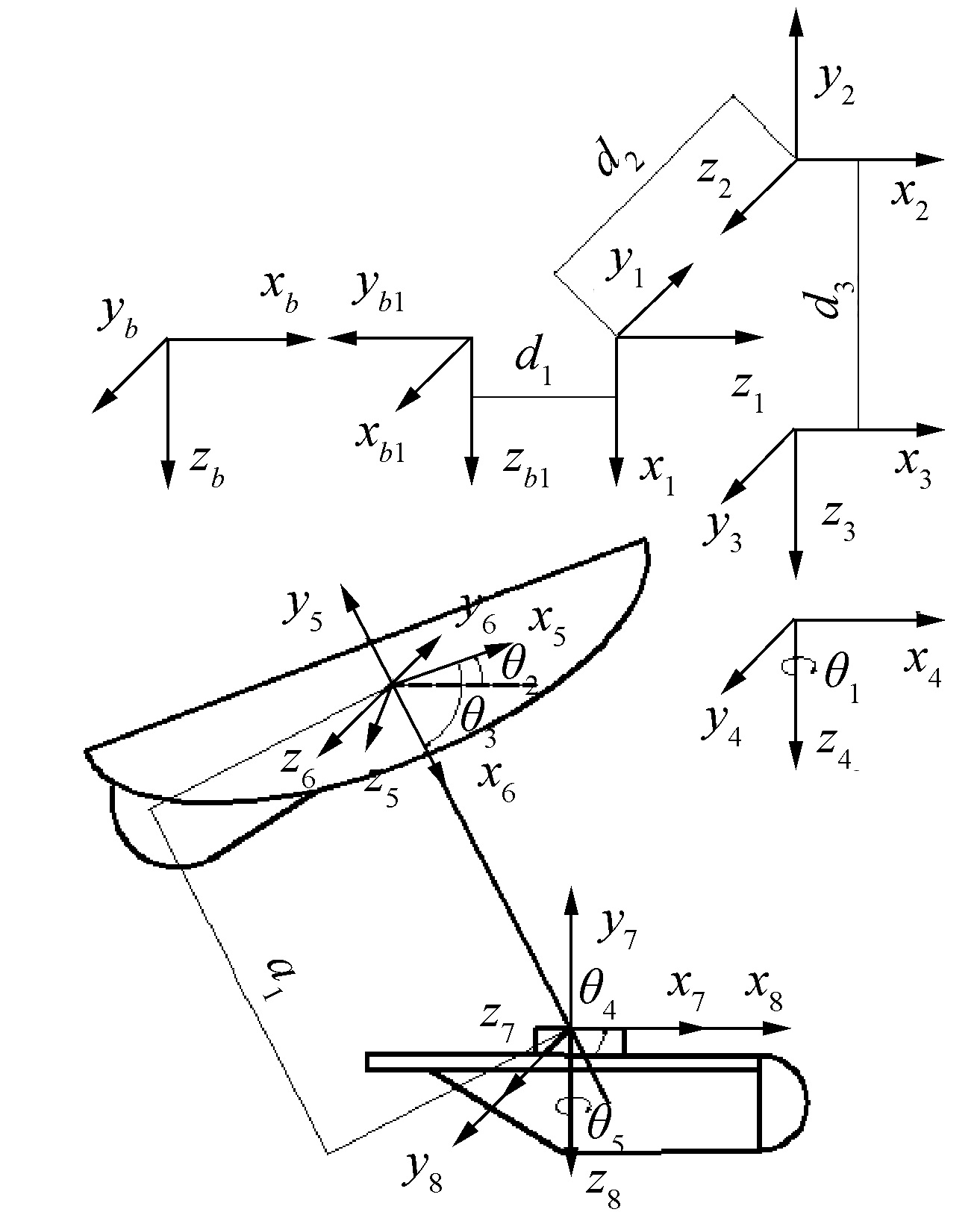
基于D-H方法建立波浪滑翔器的参考坐标系,如图 4所示。为了描述其多体系统,假设基本的参考系xbybzb和水下机器人通常用于导航的坐标系一样是北-东-下(NED)坐标系,而xb1yb1zb1是一个过渡坐标系,实现从xbybzb到x1y1z1的坐标系统转换。
|
Download:
|
| 图 4 波浪滑翔器坐标系系统 Fig. 4 Coordinate systems of wave glider | |
根据D-H方法的定义,波浪滑翔器对应的D-H参数在表 1中总结。
| 表 1 波浪滑翔器D-H参数表 Table 1 Wave glider D-H parameters |
其中d1、d2和d3分别是浮体在x、y、z方向上的位移,θ1是浮体的航向角,θ2为浮体的纵倾角,θ3为浮体船首方向与系索的夹角,θ4为系索与滑翔体船首方向的夹角,θ5为浮体与滑翔体航向角的夹角,a1为系索长度。
所以从滑翔体坐标系8变换到惯性坐标系b的坐标转换矩阵可以由式(1)计算所得:
| $ \begin{array}{*{20}{c}} {_8^b\mathit{\boldsymbol{T = }}_1^b\mathit{\boldsymbol{T}}\left( {{d_1}} \right)_2^1\mathit{\boldsymbol{T}}\left( {{d_2}} \right)_3^2\mathit{\boldsymbol{T}}\left( {{d_3}} \right)_4^3\mathit{\boldsymbol{T}}\left( {{\theta _1}} \right)_5^4\mathit{\boldsymbol{T}}\left( {{\theta _2}} \right)_6^5 \cdot }\\ {\mathit{\boldsymbol{T}}\left( {{\theta _3}} \right)_7^6\mathit{\boldsymbol{T}}\left( {{\theta _4}} \right)_8^7\mathit{\boldsymbol{T}}\left( {{\theta _5}} \right)} \end{array} $ | (1) |
根据刚体动力学,2个相邻的连杆具有关系:
对于旋转关节,有:
| $ \begin{array}{l} ^{i + 1}{\mathit{\boldsymbol{\omega }}_{i + 1}} = _i^{i + 1}{\mathit{\boldsymbol{R}}^i}{\omega _i} + {{\mathit{\boldsymbol{\dot \theta }}}_{i + 1}}^{i + 1}{\mathit{\boldsymbol{z}}_{i + 1}}\\ ^{i + 1}{\mathit{\boldsymbol{v}}_{i + 1}} = _i^{i + 1}\mathit{\boldsymbol{R}}\left( {^i{\mathit{\boldsymbol{v}}_i}{ + ^i}{\mathit{\boldsymbol{\omega }}_i}{{\rm{ \times }}^i}{\mathit{\boldsymbol{p}}_{i + 1}}} \right) \end{array} $ | (2) |
对于移动关节,有:
| $ \begin{array}{*{20}{c}} {^{i + 1}{\mathit{\boldsymbol{\omega }}_{i + 1}} = _i^{i + 1}{\mathit{\boldsymbol{R}}^i}{{\boldsymbol{\omega }} _i}}\\ {^{i + 1}{\mathit{\boldsymbol{v}}_{i + 1}} = _i^{i + 1}\mathit{\boldsymbol{R}}\left( {^i{\mathit{\boldsymbol{v}}_i}{ + ^i}{\mathit{\boldsymbol{\omega }}_i}{{\rm{ \times }}^i}{\mathit{\boldsymbol{p}}_{i + 1}}} \right) + {{\mathit{\boldsymbol{\dot d}}}_{i + 1}}^{i + 1}{\mathit{\boldsymbol{z}}_{i + 1}}} \end{array} $ | (3) |
于是,每个连杆的质心速度可表示为:
| $ \begin{array}{*{20}{c}} {^i{\mathit{\boldsymbol{v}}_{ci}}{ = ^i}{\mathit{\boldsymbol{v}}_i}{ + ^i}{\mathit{\boldsymbol{\omega }}_i}{{\rm{ \times }}^i}{\mathit{\boldsymbol{p}}_{ci}}}\\ {{\mathit{\boldsymbol{v}}_{ci}} = _i^0{\mathit{\boldsymbol{R}}^i}{\mathit{\boldsymbol{\omega }}_i}} \end{array} $ | (4) |
并且,质心速度相对于惯性坐标系可表示为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\omega }}_{ci}} = _i^0{\mathit{\boldsymbol{R}}^i}{\mathit{\boldsymbol{\omega }}_{ci}}}\\ {{\mathit{\boldsymbol{v}}_{ci}} = _i^0{\mathit{\boldsymbol{R}}^i}{\mathit{\boldsymbol{v}}_{ci}}} \end{array} $ | (5) |
式中:ivi和iωi分别是在连杆坐标系i下线速度vi与角速度ωi;i+1zi+1是在坐标系i+1下z轴方向的单位向量;ipi+1是在坐标系i下,坐标系i+1的位置向量。
2.4 动能与势能考虑波浪滑翔器的运动稳定性,水下滑翔体可以通过结构设计和平衡特性来实现平移。可以得到几何关系:
| $ {\theta _2} + {\theta _3} + {\theta _4} = 0 $ | (6) |
即浮体的纵倾角、浮体船首方向与系索的夹角、系索与滑翔体船首方向的夹角,三者之和为0。
为了方便地计算能量,关节变量可以被统一替代:
| $ \mathit{\boldsymbol{q = }}{\left[ {\begin{array}{*{20}{l}} {{d_1}}&{{d_2}}&{{d_3}}&{{\theta _1}}&{{\theta _2}}&{{\theta _4}}&{{\theta _5}} \end{array}} \right]^{\rm{T}}} $ | (7) |
如果在惯性坐标系下,连杆质量为mi,平移速度为vci,质心角速度为ωi,并且相对应质心的惯性张量为Ii。这个连杆的动能可表示为:
| $ {T_w} = \frac{1}{2}{\mathit{\boldsymbol{m}}_i}\mathit{\boldsymbol{v}}_{ci}^{\rm{T}}{\mathit{\boldsymbol{v}}_{ci}} + \frac{1}{2}\mathit{\boldsymbol{\omega }}_i^{\rm{T}}{\mathit{\boldsymbol{I}}_i}{\mathit{\boldsymbol{\omega }}_i} $ | (8) |
波浪滑翔器的动能可表示为:
| $ {T_w} = \sum\limits_{i = 1}^n {{T_i} = \frac{1}{2}{{\mathit{\boldsymbol{\dot q}}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_w}\mathit{\boldsymbol{\dot q}}} $ | (9) |
式中:
考虑到波浪滑翔器在水中航行,这将导致水加速并产生附加质量效应。所以,周围流体的动能为Tf。所以,整体的动能应为波浪滑翔器的动能与周围流体的动能之和:
| $ T = {T_w} + {T_f} = \frac{1}{2}{\mathit{\boldsymbol{\dot q}}^{\rm{T}}}\mathit{\boldsymbol{M\dot q}} $ | (10) |
式中M是广义惯性矩阵,M=Mw+Mf。
如果将惯性坐标系原点的水平设为零势能面,系统的总势能可以写成:
| $ U = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{m}}_i}{\mathit{\boldsymbol{g}}^{{T_0}}}{\mathit{\boldsymbol{p}}_{ci}}} $ | (11) |
由于固定坐标系x1y1z1、x2y2z2、x3y3z3、x4y4z4的连杆1、2、3、4都是虚拟的,因此它们都没有质量,即m1=m2=m3=m4=0。而m5、m6、m7分别等于浮体、系索、滑翔体的质量。
2.5 动力学方程首先定义拉格朗日函数为:
| $ L{\rm{ = }}T - U $ | (12) |
于是,拉格朗日方程可表示为:
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial L}}{{\partial {{\dot q}_i}}}} \right) - \frac{{\partial L}}{{\partial {q_i}}} = {\tau _i} $ | (13) |
所以,在计算和分析的基础上,动力学模型可以以向量形式写成:
| $ \mathit{\boldsymbol{M\ddot q + C}}\left( {\mathit{\boldsymbol{q,\dot q}}} \right)\mathit{\boldsymbol{ + G}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{ = \tau }} $ | (14) |
式中M是广义惯性矩阵。若用mf1、mf2、mf3、If1、If2、If3、If4表示附加惯性质量(转动惯量),则它的每一元素的值为:
| $ {M_{11}} = {m_5} + {m_6} + {m_7} + {m_{f1}} $ |
| $ {M_{22}} = {m_5} + {m_6} + {m_7} + {m_{f2}} $ |
| $ {M_{33}} = {m_5} + {m_6} + {m_7} + {m_{f3}} $ |
| $ {M_{55}} = {I_{5z}} + {I_{f2}},{\mathit{M}_{77}} = {I_{7z}} + {I_{f4}} $ |
| $ \begin{array}{*{20}{c}} {{M_{44}} = \left( {0.25{m_6} + {m_7}} \right){{\left( {{a_1}\cos {\theta _4}} \right)}^2} + {I_{5x}}{{\sin }^2}{\theta _2} + }\\ {{I_{5y}}{{\cos }^2}{\theta _2} + {I_{6x}}{{\sin }^2}{\theta _4} + {I_{6y}}{{\cos }^2}{\theta _4} + }\\ {{I_{7z}} + {I_{f1}}} \end{array} $ |
| $ {M_{66}} = \left( {0.25{m_6} + {m_7}} \right){a_1}^2 + {I_{6z}} + {I_{f3}} $ |
| $ {M_{14}} = {M_{41}} = - \left( {0.5{m_6} + {m_7}} \right){a_1}\sin {\theta _1}\cos {\theta _4} $ |
| $ {M_{16}} = {M_{61}} = - \left( {0.5{m_6} + {m_7}} \right){a_1}\cos {\theta _1}\sin {\theta _4} $ |
| $ {M_{24}} = {M_{42}} = \left( {0.5{m_6} + {m_7}} \right){a_1}\cos {\theta _1}\cos {\theta _4} $ |
| $ {M_{26}} = {M_{62}} = - \left( {0.5{m_6} + {m_7}} \right){a_1}\sin {\theta _1}\sin {\theta _4} $ |
| $ {M_{36}} = {M_{63}} = \left( {0.5{m_6} + {m_7}} \right){a_1}\cos {\theta _4} $ |
| $ {M_{47}} = {M_{74}} = {I_{7z}} $ |
矩阵M的其他元素全部为零。
| $ \begin{array}{*{20}{c}} {{C_1} = - \left( {0.5{m_6} + {m_7}} \right){a_1}\left[ {\cos {\theta _1}\cos {\theta _4}\left( {{{\dot \theta }_1}^2 + {{\dot \theta }_4}^2} \right) - } \right.}\\ {\left. {2{{\dot \theta }_1}{{\dot \theta }_4}\sin {\theta _1}\sin {\theta _4}} \right]} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{C_2} = - \left( {0.5{m_6} + {m_7}} \right){a_1}\left[ {\sin {\theta _1}\cos {\theta _4}\left( {{{\dot \theta }_1}^2 + {{\dot \theta }_4}^2} \right) + } \right.}\\ {\left. {2{{\dot \theta }_1}{{\dot \theta }_4}\cos {\theta _1}\sin {\theta _4}} \right]} \end{array} $ |
| $ {C_3} = - \left( {0.5{m_6} + {m_7}} \right)\left( {{a_1}\sin {\theta _4}} \right){{\dot \theta }_4}^2 $ |
| $ \begin{array}{*{20}{c}} {{C_4} = \left[ {{I_{6x}} - {I_{6y}} - \left( {0.25{m_6} + {m_7}} \right){a_1}^2} \right] \cdot }\\ {\left( {\sin \left( {2{\theta _4}} \right)} \right){{\dot \theta }_1}{{\dot \theta }_4} + \left( {{I_{5x}} - {I_{5y}}} \right)\left( {\sin 2{\theta _2}} \right){{\dot \theta }_1}{{\dot \theta }_2}} \end{array} $ |
| $ {C_5} = - \left( {{I_{5x}} - {I_{5y}}} \right)\left( {\sin {\theta _2}\cos {\theta _2}} \right){{\dot \theta }_1}^2 $ |
| $ \begin{array}{*{20}{c}} {{C_6} = \left[ {{I_{6x}} - {I_{6y}} - \left( {0.25{m_6} + {m_7}} \right){a_1}^2} \right] \cdot }\\ {\left( {\sin {\theta _4}\cos {\theta _4}} \right){{\dot \theta }_1}^2} \end{array} $ |
| $ {{C_7} = 0} $ |
G(q)是重力向量,它的每一元素的值为:
| $ {G_1} = {G_2} = {G_4} = {G_5} = {G_7} = 0 $ |
| $ {G_3} = - \left( {{m_5} + {m_6} + {m_7}} \right)g $ |
| $ {G_6} = - \left( {0.5{m_6} + {m_7}} \right){a_1}g\cos {\theta _4} $ |
根据在虚功原理下的虚位移的广义坐标表达式,可获得广义力τ的表达式,为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\tau }}_1} = \left( {{F_{px}} - {D_g} - {F_{sx}}} \right)\cos \left( {{\theta _1} + {\theta _5}} \right) - }\\ {{F_{sy}}\sin \left( {{\theta _1} + {\theta _5}} \right) - \left( {{D_f} + {D_l}} \right)\cos {\theta _1}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\tau }}_2} = \left( {{F_{px}} - {D_g} - {F_{sx}}} \right)\sin \left( {{\theta _1} + {\theta _5}} \right) + }\\ {{F_{sy}}\cos \left( {{\theta _1} + {\theta _5}} \right) - \left( {{D_f} + {D_l}} \right)\cos \theta } \end{array} $ |
| $ {\mathit{\boldsymbol{\tau }}_3} = {F_{pz}} - {F_w} - {B_f} - {B_l} - {B_g} $ |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\tau }}_4} = \left( {{F_{px}} - {D_g} - {F_{sx}}} \right){a_1}\cos {\theta _4}\sin {\theta _5} + }\\ {{F_{sy}}{a_1}\cos {\theta _4}\cos {\theta _5} + {\tau _s} - {\tau _g} - {\tau _f}} \end{array} $ |
| $ {\mathit{\boldsymbol{\tau }}_5} = {\tau _w} $ |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\tau }}_6} = - \left[ {\left( {{F_{px}} - {D_g} - {F_{sx}}} \right)\cos {\theta _5} - {F_{sy}}\sin {\theta _5} - \frac{1}{2}{D_l}} \right] \cdot }\\ {{a_1}\sin {\theta _4} + \left( {{F_{pz}} - {B_g} - \frac{1}{2}{B_l}} \right){a_1}\cos {\theta _4}} \end{array} $ |
| $ {\mathit{\boldsymbol{\tau }}_7} = {\tau _s} - {\tau _g} $ |
式中:Fpx和Fpz分别是滑翔体水翼产生的合力在水平和垂直2个方向上(滑翔体的随体坐标系)的分力;Df、Dl和Dg分别是浮体、系索和滑翔体的阻力;Bf、Bl和Bg分别是浮体、系索和滑翔体的浮力;Fsx和Fsy分别是滑翔体转舵装置在x轴方向和y轴方向上(滑翔体的随体坐标系)的分力,而τs是转舵装置对滑翔体产生的力矩;Fw和τw分别是波浪对浮体的力和恢复力矩。τg和τf分别是水对浮体和滑翔体的阻力力矩。
3 数值仿真与水池试验 3.1 运动仿真系统搭建将其式(14)中所有加速度项移到方程的左端,所有的非加速度项移到方程的右端,可以得到动力学方程:
| $ \mathit{\boldsymbol{M\ddot q}} = \mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right) - \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{q}} \right) $ | (15) |
若已知波浪滑翔器当前时刻的运动状态参数,就可以得到式(15)等号右边的合值,对常数矩阵M求逆,就可以求解该方程,获得波浪滑翔器的加速度,进而确定波浪滑翔器下一时刻的运动参数,如此往复迭代就可以使得波浪滑翔器在仿真系统中运动起来[16]。
3.2 仿真模型参数本文所采用的模型基本参数主要参考文献[17]。主要参数如表 2。
| 表 2 波浪滑翔器模型基本参数 Table 2 Parameters of wave glider model |
由于系索又细又轻,在计算时可以忽略它的质量和转动惯量。在计算转动惯量时,由于实际质量分布复杂,参考一般船型,可采用经验公式来计算:
| $ \left\{ {\begin{array}{*{20}{l}} {{I_{xx}} \approx m{{\left( {0.33B} \right)}^2}}\\ {{I_{yy}} \approx m{{\left( {0.26{L_{pp}}} \right)}^2}}\\ {{I_{zz}} \approx {I_{yy}}} \end{array}} \right. $ | (16) |
波浪滑翔器整个系统的在各个方向上的附加质量,在x、y和z方向上分别是总质量的0.1、2.1和2.1倍[18-19]。在计算附加惯性矩时,进行如下估算:Jxx≈0.1Ixx,Jyy≈Iyy,Jzz≈Iyy,If1≈I7z,If2≈I5z,If3≈I6z=0,If4≈I7z。仿真计算时,采用文献[17]中计算的不同波幅、不同周期的正弦波浪条件下,水翼产生的驱动力,见表 3。
| 表 3 滑翔体在不同风浪等级下产生的驱动力 Table 3 The driving force of the glider in different wave levels |
而垂直方向上阻力的作用力被认为是相对于波浪力是较小的,在本文中忽略不计。波浪滑翔器航行速度较慢,阻力的主要成分是摩擦阻力。根据弗劳德假设,摩擦阻力等于相同速度、相同长度、相同湿表面积的相当平板摩擦阻力[19]:
| $ {R_f} = \frac{1}{2}\rho {C_f}{U^2}S $ | (17) |
利用表 4中浮体,滑翔体以及系索的阻力系数,可粗略地求得Df、Dg和Dl。
| 表 4 阻力系数和湿表面积估算 Table 4 Resistance coefficient and wet surface area |
本文采用舵的剖面形状为NACA0012型,取弦长0.2 m,展长0.12 m,舵面积0.024 m2,舵轴安装于距离前缘0.3倍的弦长处。转舵装置升力系数CL,阻力系数CD分别表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{C_L} = \frac{L}{{1/2\rho A{V^2}}}}\\ {{C_D} = \frac{D}{{1/2\rho A{V^2}}}} \end{array}} \right. $ | (18) |
为了便于计算,将升力系数CL与舵角δ近似视为正比关系,取舵角δ为30°时的升力系数CL=1.0,将升阻比视为一定值,本文将升阻比取为2,可得:
| $ \left\{ {\begin{array}{*{20}{l}} {{F_{sx}} = 1/2\rho A{C_L}\left( {\dot d_1^2 + \dot d_2^2} \right)}\\ {{F_{sy}} = 1/2\rho A{C_D}\left( {\dot d_1^2 + \dot d_2^2} \right)}\\ {{\tau _s} = 0.6\left( {{F_{sx}}\cos \delta + {F_{sy}}\sin \delta } \right)} \end{array}} \right. $ | (19) |
为验证此动力学模型的正确性和有效性,本文利用哈尔滨工程大学的“海洋漫步者”号波浪滑翔器的水池试验数据进行比对。该波浪滑翔器装备了多种传感器,可以测量浮体和滑翔体的速度,艏向角,首摇角速度等信息。“海洋漫步者”号浮体质量为55 kg,滑翔体质量为40 kg,系索长4 m。
在波高230 mm、波长8 m条件下进行直航试验,仿真试验和水池试验的对比结果如图 5所示。

|
Download:
|
| 图 5 浮体纵向速度对比 Fig. 5 Comparison of longitudinal velocity of the float | |
图 5显示了仿真和水池试验中浮体纵向速度的对比,从图中可以看出水池试验值和仿真计算值有较高的吻合度,误差较小。误差原因可能是水池试验中传感器的采样频率和测量精度有限。
在波高230 mm、波长8 m条件下进行Z形试验,仿真舵角输入和水池舵角相同,结果如图 6所示。

|
Download:
|
| 图 6 仿真与水池试验结果对比 Fig. 6 Comparison of simulation and tank test results | |
从图 6(a)和(b)中可以看出,无论是浮体还是滑翔体,当舵角变化时,在仿真和水池试验中的航向响应的变化趋势是相似的。从图 6(c)和(d)中可以看出,浮体与滑翔体的艏向角的变化趋势在仿真和水池试验中基本一致。仿真是在理想环境下进行的,而水池试验存在机械结构阻力、不规则波载荷、传感器噪声等多种不确定因素,水动力系数和建模假设有限的精度给仿真带来误差,导致仿真结果与水池试验结果存在差异。
根据上述仿真与水池试验的对比,可以判断基于D-H方法的波浪滑翔器动力学模型是具备一定正确性和有效性的,用于仿真分析是可行的。
3.4 数值仿真试验本文数值仿真试验由直航试验、回转试验、Z形试验3个部分组成。
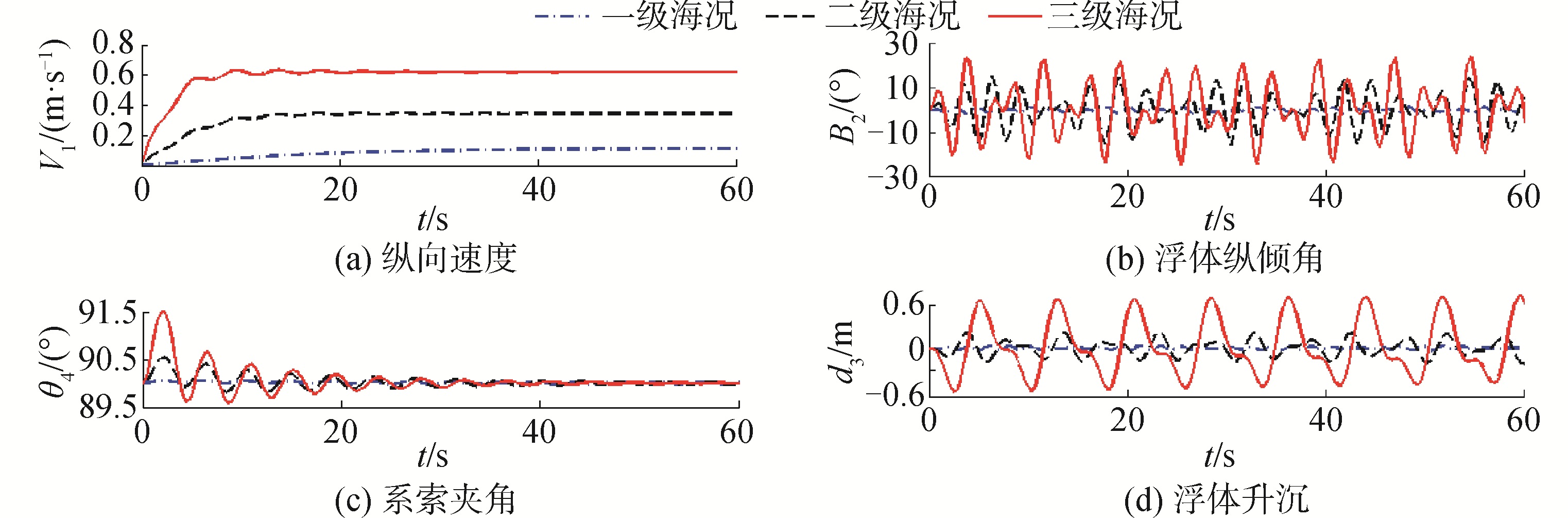
直航试验是分别在1~3级海况下,舵角为0°,波浪滑翔器按纵向直线航行。通过仿真获得波浪滑翔器分别在的纵向速度V1、浮体纵倾角θ2、系索夹角θ4以及浮体升沉d3的曲线如图 7所示。
|
Download:
|
| 图 7 直航试验结果对比 Fig. 7 Comparison of simulation in the tracking of straight line | |
从图 7(a)中可以看出,3种海况下,波浪滑翔器稳定速度分别为0.11、0.35和0.6 m/s。在一定条件下,波浪滑翔器的速度随海况增强而增大。从图 7(b)中可以看出,3种海况下,浮体的纵倾角最大振幅分别为1.5°、15°、20°,浮体的纵倾角最大振幅随海况增强而增大。从图 7(c)中可以看出,系索夹角存在微幅震动,最终基本上在90°附近微幅震动,海况大小对其大小影响不大。从图 7(d)中可以看出,浮体升沉受波浪影响,海况越大波浪振幅和频率越大,浮体升沉的也振幅和频率越大。从整个直航试验可知,可知波浪波幅和频率影响波浪滑翔器对波浪能的利用率,海况越大,波浪能越高,波浪滑翔器航行越快。
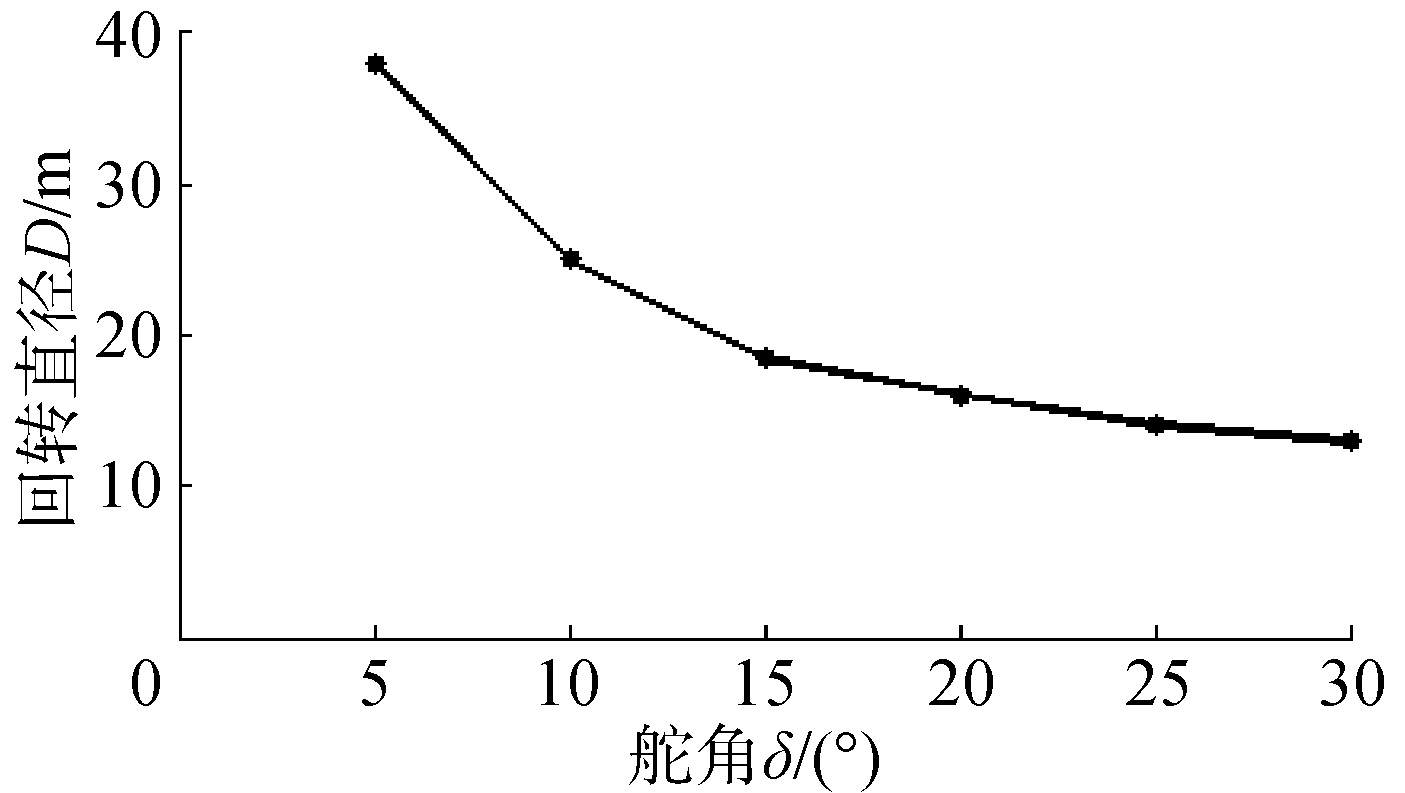
回转试验时,假定在3级海况下,给定垂直舵角,分别为5°、10°、15°、20°、25°、30°。由波浪滑翔器的回转试验仿真曲线可得回转直径,回转直径与舵角的关系如图 8所示。
|
Download:
|
| 图 8 回转直径与舵角的关系曲线 Fig. 8 Relation between turning diameter and rudder angle | |
由图 8可知,在3级海况下,波浪滑翔器的回转直径会随舵角增大而减小,最终收敛约为12 m,即最小回转直径,它大约是浮体长度的4倍。
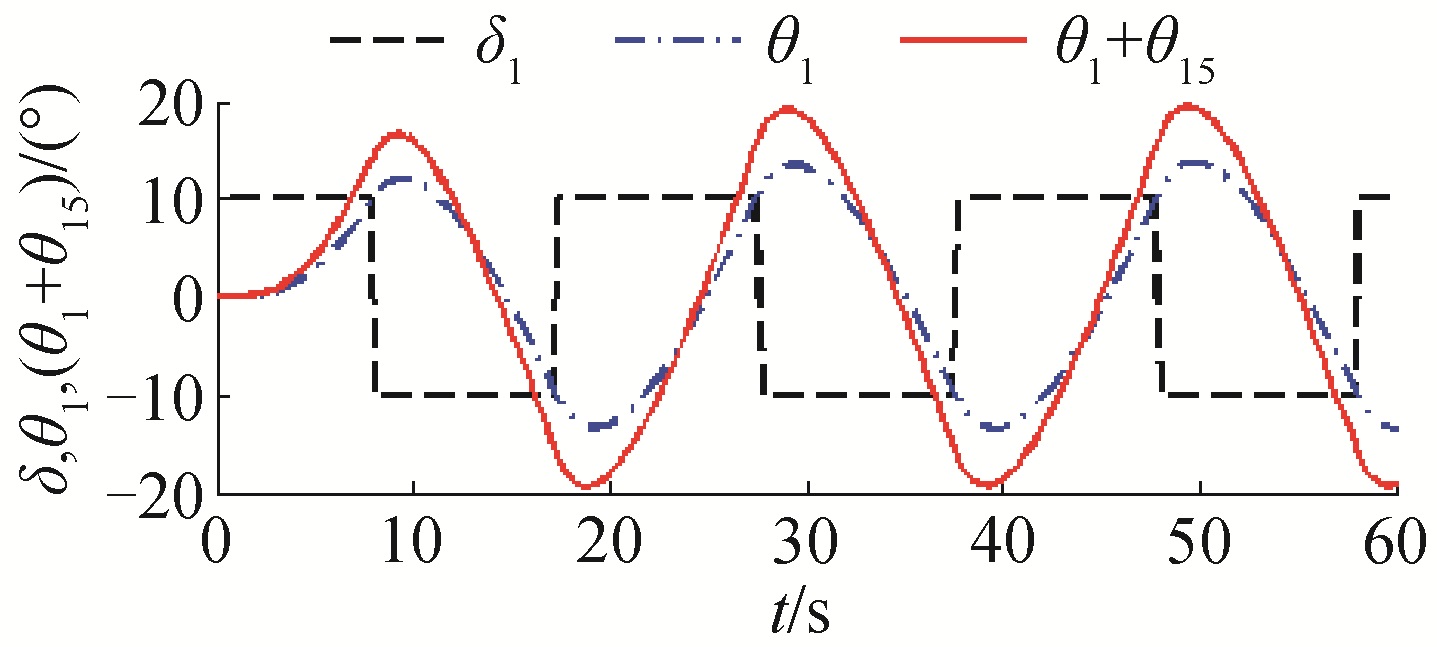
在Z形试验时,同样假定在三级海况下,仿真初始舵角为10°,当浮体艏向角改变到达10°时,舵角阶跃为-10°,当浮体艏向角改变到达-10°时,舵角阶跃为10°,然后按此步骤循环。仿真结果如图 9所示。
|
Download:
|
| 图 9 舵角,浮体与滑翔体艏向角变化曲线 Fig. 9 Relation among δ, θ1, (θ1+θ5) and t | |
从图 9中可以看出,当0 s开始操舵时,波浪滑翔器顺时针运动。在7 s时,舵角从10°阶跃到-10°,波浪滑翔器做逆时针运动。分析可得其初转期为7 s,超约时间为3 s,超越角为3°,周期为20 s。
通过仿真结果之间的对比,可以发现,采用本文方法仿真,可以得到浮体纵向速度v1、浮体横向速度v2、浮体升沉d3、浮体艏向角θ1、浮体纵倾角θ2、滑翔体艏向角(θ1+θ5)、系索与滑翔体夹角θ4等参数。其中,浮体升沉d3和浮体纵倾角θ2是一些传统方法不能计算的。而这2个参数对波浪滑翔器波浪能利用率的计算起着关键作用。因此,本文所建立的波浪滑翔器动力学模型,具有较好的仿真结果。
4 结论1) 该波浪滑翔器动力学模型在利用D-H方法的基础上,更好地表达浮体与滑翔器之间的强耦合关系。
2) 该模型以三维的形式,提供更多运动参数,方便计算波浪滑翔器波浪能利用效率,且部分参数与水池试验结果相吻合。
3) 仿真结果验证了不同海况下的波浪滑翔器运动特性,包括其速度、角速度和系索夹角等,其结果与动力学理论相一致。
然而,水动力计算、模型参数估算、环境影响等问题还需要进一步研究。
| [1] |
廖煜雷, 李晔, 刘涛, 等. 波浪滑翔器技术的回顾与展望[J]. 哈尔滨工程大学学报, 2016, 37(9): 1227-1236. LIAO Yulei, LI Ye, LIU Tao, et al. Unmanned wave glider technology: state of the art and perspective[J]. Journal of Harbin Engineering University, 2016, 37(9): 1227-1236. (  0) 0)
|
| [2] |
徐春莺, 陈家旺, 郑炳焕. 波浪驱动的水面波力滑翔机研究现状及应用[J]. 海洋技术学报, 2014, 33(2): 111-117. XU Chunying, CHEN Jiawang, ZHENG Binghuan. Research status and applications of wave gliders[J]. Journal of ocean technology, 2014, 33(2): 111-117. (  0) 0)
|
| [3] |
MANLEY J E, HINE G. Unmanned Surface Vessels (USVs) as tow platforms: wave glider experience and results[C]//Proceedings of OCEANS 2016 MTS/IEEE Monterey. Monterey, CA, USA, 2016: 1-5.
(  0) 0)
|
| [4] |
HINE R, WILLCOX S, HINE G, et al. The wave glider: a wave-powered autonomous marine vehicle[C]//Proceedings of MTS/IEEE OCEANS 2009. Biloxi, 2009: 1-6.
(  0) 0)
|
| [5] |
KRAUS N, BINGHAM B. Estimation of wave glider dynamics for precise positioning[C]//Proceeding of Oceans 2011 MTS/IEEE KONA. Waikoloa, HI, USA, 2011: 1-9.
(  0) 0)
|
| [6] |
QI Zhanfeng, LIU Wenxia, JIA Lijuan, et al. Dynamic modeling and motion simulation for wave glider[J]. Applied mechanics and materials, 2013, 397-400: 285-290. DOI:10.4028/www.scientific.net/AMM.397-400.285 (  0) 0)
|
| [7] |
ZHOU Chunlin, WANG Boxing, ZHOU Hongxiang, et al. Dynamic modeling of a wave glider[J]. Frontiers of information technology & electronic engineering, 2017, 18(9): 1295-1304. (  0) 0)
|
| [8] |
TIAN Baoqiang, YU Jiancheng, ZHANG Aiqun, et al. Dynamics analysis of wave-driven unmanned surface vehicle in longitudinal profile[C]//Proceeding of OCEANS 2014-TAIPEI. Taipei, China, 2014: 1-6.
(  0) 0)
|
| [9] |
田宝强, 俞建成, 张艾群, 等. 波浪驱动无人水面机器人运动效率分析[J]. 机器人, 2014, 36(1): 43-48, 68. TIAN Baoqiang, YU Jiancheng, ZHANG Aiqun, et al. Analysis on movement efficiency for wave driven unmanned surface vehicle[J]. Robot, 2014, 36(1): 43-48, 68. DOI:10.3969/j.issn.1004-6437.2014.01.010 (  0) 0)
|
| [10] |
SMITH R N, DAS J, HINE G, et al. Predicting wave glider speed from environmental measurements[C]//Proceeding of Oceans 2011 MTS/IEEE KONA. Waikoloa, HI, USA, 2011: 1-8.
(  0) 0)
|
| [11] |
CAITI A, CALABRÒ V, GRAMMATICO S, et al. Lagrangian modeling of the underwater wave glider[C]//Proceeding of OCEANS 2011 IEEE Conference. Santander, 2011: 1-6.
(  0) 0)
|
| [12] |
TIAN Baoqiang, YU Jiancheng, ZHANG Aiqun. Dynamic modeling of wave driven unmanned surface vehicle in longitudinal profile based on D-H approach[J]. Journal of Central South University, 2015, 22(12): 4578-4584. DOI:10.1007/s11771-015-3008-6 (  0) 0)
|
| [13] |
LIU Peng, SU Yumin, LIAO Yulei. Numerical and experimental studies on the propulsion performance of a wave glide propulsor[J]. China ocean engineering, 2016, 30(3): 393-406. DOI:10.1007/s13344-016-0026-6 (  0) 0)
|
| [14] |
DENAVIT J, HARTENBERG R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. ASME journal of applied mechanics, 1955, 22(2): 215-221. (  0) 0)
|
| [15] |
熊有伦, 丁汉, 刘恩沧. 机器人学[M]. 北京: 机械工业出版社, 1993. XIONG Youlun, DING Han, LIU Encang. Robotics[M]. Beijing: China Machine Press, 1993. (  0) 0)
|
| [16] |
苏清磊.大型欠驱动水下机器人操控性能研究[D].哈尔滨: 哈尔滨工程大学, 2014. SU Qinglei. Research on the maneuverability and control performance of large underactuated AUV[D]. Harbin: Harbin Engineering University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D595594 (  0) 0)
|
| [17] |
卢旭.波浪滑翔器总体技术研究[D].哈尔滨: 哈尔滨工程大学, 2015. LU Xu. Research on the general technology of wave glider[D]. Harbin: Harbin Engineering University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10217-1018050784.htm (  0) 0)
|
| [18] |
KOROTKIN A I. Added masses of ship structures[M]. Dordrecht: Springer, 2009.
(  0) 0)
|
| [19] |
张亮, 李云波. 流体力学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2006. ZHANG Liang, LI Yunbo. Hydrodynamics[M]. Harbin: Harbin Engineering University Press, 2006. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


