助推段主要在大气层中,气动力是主要作用力之一。精确地计算火箭受到的气动力,对提高火箭制导精度至关重要。由于气动环境的复杂多变,很难直接建立气动力精确计算模型。目前使用的解决办法是针对特定型号火箭外型,结合空气动力学理论计算和风洞实验校正,给出计算气动力所需的图表、曲线等[1]。工程上,通常提供气动力系数的曲线或插值表,以此来计算火箭飞行过程中的气动力。但是实际飞行过程气动环境复杂,标准气动参数与实际参数存在偏差。这种偏差在制导过程中如果没有处理,一定程度上会影响制导精度,最终增大终端误差。因此,利用辨识算法对气动参数进行实时在线辨识,并将辨识结果用于修正制导指令,对于提高火箭的制导精度有一定研究意义。
摄动制导方法要求在射前计算参考弹道并装载,在飞行过程中将实际弹道参数与参考弹道的偏离量视为小扰动量,再基于摄动理论计算制导指令,使真实弹道始终保持在标准弹道附近[2]。由于运动参数具有可观测性,摄动制导一般选择运动参数扰动(如位置坐标、速度分量、角度值等)作为偏差量来计算制导指令。但是火箭真实飞行过程中的参数偏差量远不止这些运动参数[1]。本文拟将辨识得到的气动系数偏差量视为小扰动量,对传统摄动制导方法进行改进,提高制导精度。
现有的参数估计方法包括递推最小二乘法、递推极大似然法、Wiener滤波和Kalman滤波等,其中Kalman滤波是处理随机估计应用最广泛的方法[3]。为扩展适用范围,Kalman滤波出现了多种改进形式,包括扩展Kalman滤波、无迹Kalman滤波[4-5]、UD分解滤波[6]等。在飞行器气动参数辨识上,文献[7-8]分别应用了具有指数遗忘的最小二乘法和径向基神经网络方法分别对滑翔飞行器和旋翼飞行器进行气动参数辨识,达到较好效果。文献[9-12]研究了扩展Kalman滤波器在飞行器气动参数辨识上的应用,使得扩展Kalman滤波方法得到了广泛应用。本文将基于文献[9]中的基本思想,构建气动参数在线辨识模型,用于修正火箭助推段摄动制导指令,提高末端精度。
1 动力学模型与摄动制导 1.1 火箭助推段动力学模型为了便于后续辨识系统方程的推导,本文拟引入速度坐标系下的动力学方程[13]。由于火箭助推段飞行时间较短,可假设地球为不旋转均质圆球;并假设火箭为对称圆柱体形状,不考虑倾侧角控制。故在速度坐标系下的动力学方程简化为:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot v = \frac{{{P_e}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {\rm{cos}}{\kern 1pt} {\kern 1pt} \beta }}{m} - \frac{{\rho {v^2}{S_m}{C_D}}}{{2m}} - g{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ {\dot h = v{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ {\dot \theta = \frac{{{P_e}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha }}{{mv}} + \frac{{\rho {v^2}{S_m}{C_L}}}{{2mv}} - \frac{{g{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}{v} + \frac{{v{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}{{{R_e} + h}}} \end{array}} \right. $ | (1) |
式中:v表示速度大小;Pe表示轴向推力大小;α为攻角;β为侧滑角;ρ为大气密度;Sm为火箭参考面积;CD、CL为阻力系数和升力系数;θ为速度倾角;Re为地球平均半径;h为飞行高度;m为火箭质量。CD、CL均由标准值与扰动量组成:
| $ \left\{ {\begin{array}{*{20}{l}} {{C_D} = {C_{D0}} + {C_{Dd}}}\\ {{C_L} = {C_{L0}} + {C_{Ld}}} \end{array}} \right. $ | (2) |
式中:CDd、CLd分别为阻力系数和升力系数的扰动量,该扰动量正是本文中要辨识的参量。
1.2 摄动制导模型摄动制导的目的是将火箭的实际飞行轨迹保持在标准弹道附近。在实际飞行过程中,导航系统计算得到火箭实际位置,制导系统将其与存储在箭载计算机中的标准弹道进行对比,经制导方程计算出制导指令。为便于执行机构设计,摄动制导通常分为纵向制导和横向导引,本文仅考虑纵平面内的制导。不考虑姿态变化的动态过程,制导指令俯仰角可简化为[14]:
| $ \varphi (t) = {\varphi _{pr}}(t) + {u_\varphi } $ | (3) |
式中:φpr(t)为t时刻对应的程序俯仰角;uφ为导引控制量,由真实状态和参考状态的偏差计算得到。导引控制量由导引目标量和导引系数组成,即uφ=KδXδXf。本文选择终端速度倾角偏差δθf作为导引目标量。摄动制导通常选择可测量的状态量偏差来计算导引目标量:
| $ \delta {\theta _f} = \frac{{\partial {\theta _f}}}{{\partial v}}\delta v + \frac{{\partial {\theta _f}}}{{\partial \theta }}\delta \theta + \frac{{\partial {\theta _f}}}{{\partial h}}\delta h $ | (4) |
但是根据摄动理论,“扰动”定义为实际弹道飞行条件与标准弹道飞行条件之间的偏差[1]。因此,扰动量除了起始点位置速度外,还包括气温、压强、大气密度等环境参数和质量、秒耗量、气动力系数等弹道参数。本文拟将辨识得到的气动参数偏差作为新的小扰动量。在不考虑气动参数偏差的情况下,终端速度倾角θf是速度大小v、速度倾角θ和高度h的函数,即:
| $ {\theta _f} = {\theta _f}(v,\theta ,h) $ | (5) |
故其摄动方程如式(4)所示。当考虑气动参数扰动时,式(5)可写为:
| $ {\theta _f} = {\theta _f}(v,\theta ,h,{C_D},{C_L}) $ | (6) |
对式(6)求微分:
| $ \delta {\theta _f} = \frac{{\partial {\theta _f}}}{{\partial v}}\delta v + \frac{{\partial {\theta _f}}}{{\partial \theta }}\delta \theta + \frac{{\partial {\theta _f}}}{{\partial h}}\delta h + \frac{{\partial {\theta _f}}}{{\partial {C_D}}}\delta {C_D} + \frac{{\partial {\theta _f}}}{{\partial {C_L}}}\delta {C_L} $ | (7) |
式中:δCD、δCL是气动参数的等时偏差; 在标准模型中,CD是马赫数Ma和高度h的函数,CL是马赫数Ma和攻角α的函数,即:
| $ \left\{ {\begin{array}{*{20}{l}} {{C_D} = {C_D}(Ma,h)}\\ {{C_L} = {C_L}(Ma,\alpha )} \end{array}} \right. $ | (8) |
而Ma=v/a,声速a又是高度的函数。攻角α=φpr-θ,是速度倾角θ的函数。所以在标准情况下,气动参数的等时偏差δCD、δCL可化为:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {\delta {C_D} = \frac{{\partial {C_D}}}{{\partial Ma}}\left( {\frac{{\partial Ma}}{{\partial v}}\delta v + \frac{{\partial Ma}}{{\partial a}}\frac{{\partial a}}{{\partial h}}\delta h} \right) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial {C_D}}}{{\partial h}}\delta h = {A_1}\delta v + {B_1}\delta h} \end{array}\\ \begin{array}{*{20}{l}} {\delta {C_L} = \frac{{\partial {C_L}}}{{\partial Ma}}\left( {\frac{{\partial Ma}}{{\partial v}}\delta v + \frac{{\partial Ma}}{{\partial a}}\frac{{\partial a}}{{\partial h}}\delta h} \right) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial {C_L}}}{{\partial \alpha }}\frac{{\partial \alpha }}{{\partial \theta }}\delta \theta = {A_2}\delta v + {B_2}\delta h + {C_3}\delta \theta } \end{array} \end{array} \right. $ | (9) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{A_1} = \frac{{\partial {C_D}}}{{\partial Ma}}\frac{{\partial Ma}}{{\partial v}}}\\ {{B_1} = \frac{{\partial {C_D}}}{{\partial Ma}}\frac{{\partial Ma}}{{\partial a}}\frac{{\partial a}}{{\partial h}} + \frac{{\partial {C_D}}}{{\partial h}}}\\ {{A_2} = \frac{{\partial {C_L}}}{{\partial Ma}}\frac{{\partial Ma}}{{\partial v}}}\\ {{B_2} = \frac{{\partial {C_L}}}{{\partial Ma}}\frac{{\partial Ma}}{{\partial a}}\frac{{\partial a}}{{\partial h}}}\\ {{C_2} = \frac{{\partial {C_L}}}{{\partial \alpha }}\frac{{\partial \alpha }}{{\partial \theta }}} \end{array}} \right. $ | (10) |
由式(4)可知,标准状况下气动参数的等时偏差可表示为速度大小、高度和速度倾角的等时偏差,将式(9)代入式(4),得到的结果和式(4)等价。但是考虑气动参数扰动时,气动参数等时偏差除了来源于速度大小、高度和速度倾角等时偏差外,还来源于其他未知因素引起的气动参数扰动。结合式(9)可扩展为:
| $ \left\{ {\begin{array}{*{20}{l}} {\delta {C_D} = {A_1}\delta v + {B_1}\delta h + \frac{{\partial {C_D}}}{{\partial {C_{Dd}}}}\delta {C_{Dd}}}\\ {\delta {C_L} = {A_2}\delta v + {B_2}\delta h + {C_3}\delta \theta + \frac{{\partial {C_L}}}{{\partial {C_{Ld}}}}\delta {C_{Ld}}} \end{array}} \right. $ | (11) |
将式(11)代入式(7)中,相同的等时偏差项可以合并,得:
| $ \begin{array}{*{20}{l}} {\delta {\theta _f} = \frac{{\partial {\theta _f}}}{{\partial v}}\delta v + \frac{{\partial {\theta _f}}}{{\partial \theta }}\delta \theta + \frac{{\partial {\theta _f}}}{{\partial h}}\delta h + \frac{{\partial {\theta _f}}}{{\partial {C_{Dd}}}}\delta {C_{Dd}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial {\theta _f}}}{{\partial {C_{Ld}}}}\delta {C_{Ld}}} \end{array} $ | (12) |
而标准弹道的气动参数扰动量均为0,所以式(12)中δCDd=CDd,δCLd=CLd。式化(12)为:
| $ \begin{array}{*{20}{l}} {\delta {\theta _f} = \frac{{\partial {\theta _f}}}{{\partial v}}\delta v + \frac{{\partial {\theta _f}}}{{\partial \theta }}\delta \theta + \frac{{\partial {\theta _f}}}{{\partial h}}\delta h + \frac{{\partial {\theta _f}}}{{\partial {C_{Dd}}}}{C_{Dd}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial {\theta _f}}}{{\partial {C_{Ld}}}}{C_{Ld}}} \end{array} $ | (13) |
式(13)就是考虑气动参数偏差的摄动方程。
2 气动参数在线辨识预测模型 2.1 扩展Kalman滤波辨识模型CDd、CLd为气动参数扰动量,具有一定的随机性,难以用精确模型进行描述。而一阶高斯马尔可夫过程符合大多数物理过程,且数学描述较为简单。因此采用一阶高斯马尔可夫过程对气动参数扰动进行描述[9]:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot C}_{Dd}} = - {\xi _D}{C_{Dd}} + {\omega _{CD}}}\\ {{{\dot C}_{Ld}} = - {\xi _L}{C_{Ld}} + {\omega _{CL}}}\\ {{{\dot \xi }_D} = {\omega _{\xi D}}}\\ {{{\dot \xi }_L} = {\omega _{\xi L}}} \end{array}} \right. $ | (14) |
得到扩展Kalman滤波的系统方程,即:
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{h}}(\mathit{\boldsymbol{X}}) + \mathit{\boldsymbol{V}} $ | (15) |
式中:Y为观测量;V为观测噪声向量。火箭惯性敏感器件可以测量除地球引力外的其余力产生的加速度。因此观测量选择为轴向和法向的视加速度,即Y=[Nx, Ny]T。其中:
| $ \left\{ \begin{array}{l} {N_x} = \frac{{{P_e}}}{m} + \frac{{\rho {v^2}{S_m}}}{{2m}}[({C_{L0}} + {C_{Ld}}){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({C_{D0}} + {C_{Dd}}){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha ] + {\omega _{{N_x}}}\\ {N_y} = \frac{{\rho {v^2}{S_m}}}{{2m}}[({C_{L0}} + {C_{Ld}}){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({C_{D0}} + {C_{Dd}}){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha ] + {\omega _{{N_y}}} \end{array} \right. $ | (16) |
只考虑加速度计的随机漂移,故ωNx、ωNy为高斯白噪声。
扩展Kalman滤波的基本原理如下:
1) 预测方程:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}}_{k + 1}^ - = {\mathit{\boldsymbol{X}}_k} + \int_{{t_k}}^{{t_{\mathit{\boldsymbol{k}} + 1}}} {f(\mathit{\boldsymbol{X}})} }\\ {\mathit{\boldsymbol{P}}_{k + 1}^ - = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k + 1}}{\mathit{\boldsymbol{P}}_k}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^\prime }_{k,k + 1} + {\mathit{\boldsymbol{Q}}_{k + 1}}} \end{array}} \right. $ | (17) |
式中:Qk+1为系统噪声矩阵;Φk, k+1为tk到tk+1时刻的状态转移矩阵,其表达式为:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k,k + 1}} = \mathit{\boldsymbol{I}} + \int_{{t_k}}^{{t_{k + 1}}} {\mathit{\boldsymbol{F}}(\mathit{\boldsymbol{X}})} $ | (18) |
式中:F(X)为状态方程f(X)的雅克比矩阵。
2) 更新方程:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{K}}_{k + 1}} = \mathit{\boldsymbol{P}}_{k + 1}^ - \mathit{\boldsymbol{H}}{\prime _{k + 1}}{{({\mathit{\boldsymbol{H}}_{k + 1}}\mathit{\boldsymbol{P}}_{k + 1}^ - \mathit{\boldsymbol{H}}{\prime _{k + 1}} + {\mathit{\boldsymbol{R}}_{k + 1}})}^{ - 1}}}\\ {{\mathit{\boldsymbol{X}}_{k + 1}} = \mathit{\boldsymbol{X}}_{k + 1}^ - + {\mathit{\boldsymbol{K}}_{k + 1}}({\mathit{\boldsymbol{Y}}_{k + 1}} - \mathit{\boldsymbol{Y}}_{k + 1}^ - )}\\ {{\mathit{\boldsymbol{P}}_{k + 1}} = \mathit{\boldsymbol{P}}_{k + 1}^ - - {\mathit{\boldsymbol{K}}_{k + 1}}{\mathit{\boldsymbol{H}}_{k + 1}}\mathit{\boldsymbol{P}}_{k + 1}^ - } \end{array}} \right. $ | (19) |
式中:Rk+1为观测噪声矩阵;Yk+1为观测量;Yk+1-为根据Xk+1-状态的预测观测量;Hk+1观测方程h(X)的雅克比矩阵。以上就是一个滤波步长的计算流程,其计算结果将作为下一个滤波步长的计算初值。
2.2 限定记忆递推最小二乘法扩展Kalman滤波方法能辨识出当前时刻气动参数扰动量,但是在计算下一时间段内的制导指令时,需要下一时间段内的气动参数扰动量。因此,需要通过已经辨识出来的结果对下一时间段内的气动参数扰动量进行预测。由于气动参数扰动量具有一定的随机性,其与其他状态量的函数关系不明确。因此,建立扰动量的时变多项式模型,再利用参数估计方法对多项式参数进行估计:
| $ \left\{ {\begin{array}{*{20}{l}} {{C_{Dd}} = \sum\limits_{i = 0}^4 {{a_i}} {t^i}}\\ {{C_{Ld}} = \sum\limits_{i = 0}^4 {{b_i}} {t^i}} \end{array}} \right. $ | (20) |
参数估计方法有递推最小二乘法、遗忘因子递推最小二乘法、限定记忆递推最小二乘法等[15]。递推最小二乘法虽然算法简单,但是随着观测数据的增多,会出现“数据饱和”现象,使新数据对估计结果的修正作用减弱。遗忘因子递推最小二乘法通过对旧数据增加“遗忘因子”以减弱数据的作用,而限定记忆递推最小二乘法通过不断地剔除老数据,增加新数据,始终选择固定长度的最新数据(即“数据矩形窗”)进行参数估计。限定记忆递推最小二乘法在一定程度上完全避免了数据饱和现象,更充分地体现了新数据的修正作用。但是为了保证预测结果的合理性,每次预测计算采用的数据量不能过少。本文选择限定记忆递推最小二乘法作为参数估计方法[16]。该方法的计算过程:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {\mathit{\boldsymbol{K}}(k,k + L) = \mathit{\boldsymbol{P}}(k,k + L - 1)\mathit{\boldsymbol{x}}(k + L){{[1 + {\mathit{\boldsymbol{x}}^\prime }(k + L)\mathit{\boldsymbol{P}}(k,k + L - 1)\mathit{\boldsymbol{x}}(k + L)]}^{ - 1}}}\\ {\mathit{\boldsymbol{P}}(k,k + L) = [\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{K}}(k,k + L){\mathit{\boldsymbol{x}}^\prime }(k + L)]\mathit{\boldsymbol{P}}(k,k + L + 1)} \end{array}\\ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat \theta }}(k,k + L) = \mathit{\boldsymbol{\hat \theta }}(k,k + L - 1) + \mathit{\boldsymbol{K}}(k,k + L)[\mathit{\boldsymbol{y}}(k + L) - {\mathit{\boldsymbol{x}}^\prime }(k + L)\mathit{\boldsymbol{\hat \theta }}(k,k + L - 1)}\\ {\mathit{\boldsymbol{K}}(k + 1,k + L) = \mathit{\boldsymbol{P}}(k,k + L)\mathit{\boldsymbol{x}}(k){{[1 - {\mathit{\boldsymbol{x}}^\prime }(k)\mathit{\boldsymbol{P}}(k,k + L)\mathit{\boldsymbol{x}}(k)]}^{ - 1}}} \end{array}\\ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{P}}(k + 1,k + L) = [\mathit{\boldsymbol{I}} + \mathit{\boldsymbol{K}}(k + 1,k + L){\mathit{\boldsymbol{x}}^\prime }(k)]\mathit{\boldsymbol{P}}(k,k + L)}\\ {\mathit{\boldsymbol{\hat \theta }}(k + 1,k + L) = \mathit{\boldsymbol{\hat \theta }}(k,k + L) - \mathit{\boldsymbol{K}}(k + 1,k + L)[\mathit{\boldsymbol{y}}(k) - {x^\prime }(k)\mathit{\boldsymbol{\hat \theta }}(k,k + L)]} \end{array} \end{array} \right. $ | (21) |
式中:L为“数据矩形窗”的长度,
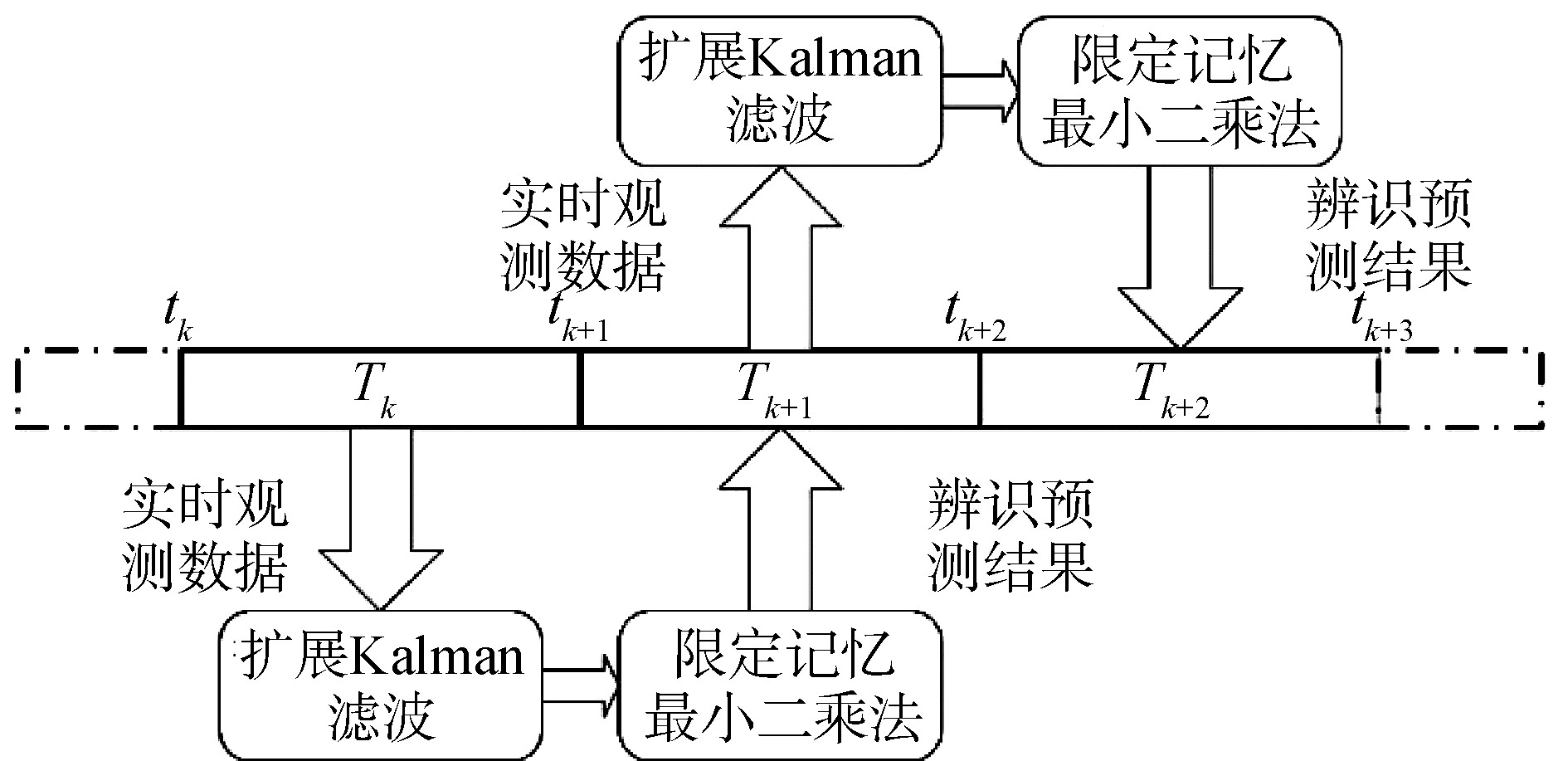
参数在线辨识的关键是实时性,即辨识结果及时应用于下一阶段的制导计算。但在实际飞行过程中,由于存在计算时延,辨识结果不能保持时刻更新。因此,本文考虑采用周期性迭代的方法,来实现在线气动参数实时更新:首先基于实时观测数据,采用扩展Kalman滤波方法对气动参数扰动进行辨识;然后再基于已有的辨识结果,采用限定记忆递推最小二乘法,对下一制导周期的气动参数扰动量进行预测,将预测结果用于下一制导周期的计算。依次循环,便构建了“辨识—预测—计算”迭代更新的在线辨识模型,如图 1所示。
|
Download:
|
| 图 1 气动参数在线辨识在摄动制导中的应用流程 Fig. 1 Flow chart of the aerodynamic parameter online identification in perturbation guidance | |
本文将通过数值仿真对以上方法进行验证。仿真条件如下:对象是某型号的运载火箭,飞行阶段为起飞至一级分离,起飞方式为垂直起飞,状态初值为:[v0, θ0, h0]=[0, π/2, 0],飞行标准程序如图 2所示。

|
Download:
|
| 图 2 数值仿真标准弹道程序俯仰角 Fig. 2 Program pitch angle in numerical simulation | |
为了验证本文设计扩展Kalman滤波的有效性,基于上述对象,设计算例对Kalman滤波器的辨识效果进行验证。
在滤波参数设计中,假设测量噪声仅存在随机漂移,且保持常值:
| $ {\mathit{\boldsymbol{R}}_k} = {\rm{diag}} ({10^{ - 6}},{10^{ - 6}}) $ | (22) |
系统噪声矩阵也保持不变:
| $ {\mathit{\boldsymbol{Q}}_k} = {\rm{diag}} (0,0,0,{10^{ - 4}},{10^{ - 4}},{10^{ - 10}},{10^{ - 10}}) $ | (23) |
系统状态初值:
| $ \begin{array}{l} [{v_0},{\theta _0},{h_0},{C_{Dd0}},{C_{Ld0}},{\xi _{D0}},{\xi _{D0}}] = \\ [0,\pi /2,0,0.001,0.001,0,0] \end{array} $ |
状态误差协方差矩阵的初值为:
| $ {\mathit{\boldsymbol{P}}_0} = {\rm{diag}} (0,0,0,{10^{ - 2}},{10^{ - 2}},{10^{ - 6}},{10^{ - 6}}) $ | (24) |
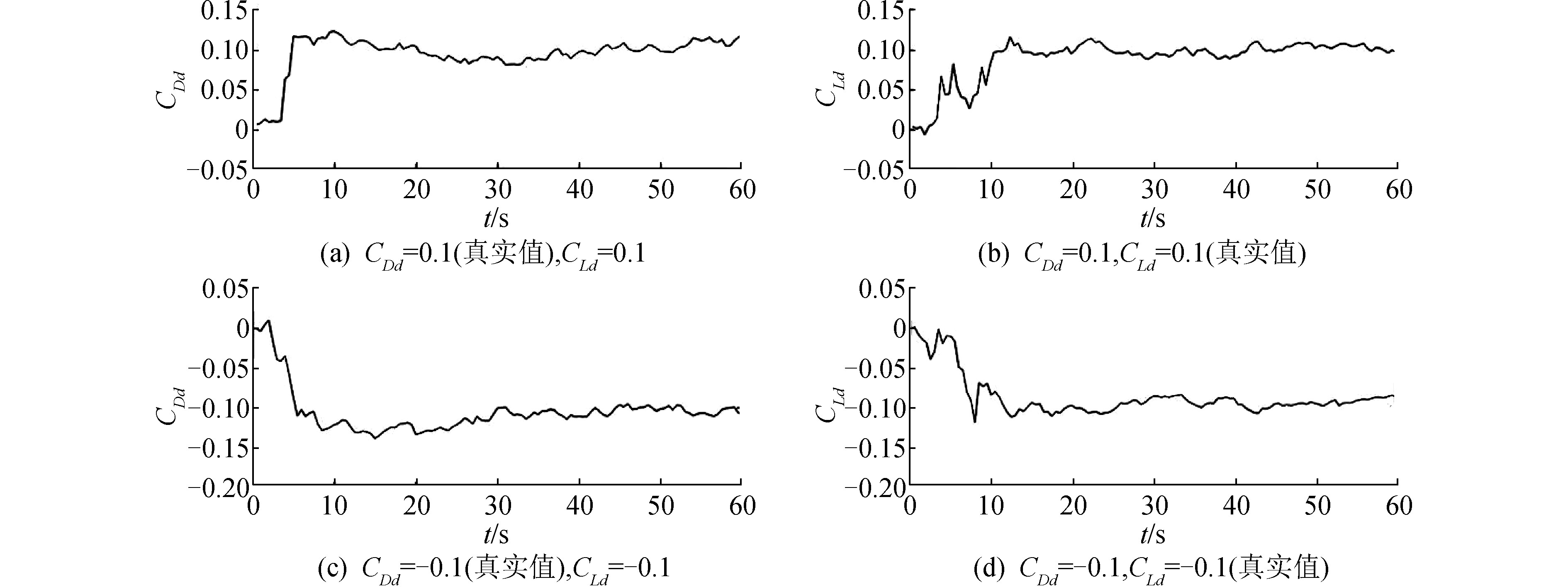
分别设置扰动量真实值为0.1、-0.1,利用本文中的扩展Kalman滤波器进行辨识,辨识结果如图 3所示。从图 3可以发现,滤波器的收敛时间约为10 s,收敛速度较快;辨识误差保持在10%以内,精度较高。
|
Download:
|
| 图 3 扩展Kalman滤波器辨识曲线 Fig. 3 The performance curves of extended Kalman filter | |
为了验证基于气动参数在线辨识的摄动制导方案的有效性,设计仿真对比实验。分别设置多组真实扰动值,计算传统摄动制导方案和基于气动参数在线辨识的摄动制导方案的终端状态偏差。如表 1所示。
| 表 1 气动参数扰动下的终端状态偏差 Table 1 Deviation of terminal state under the aerodynamic parameter disturbance |
对表 1中的结果进行分析,新的摄动制导方案相对于传统摄动制导方案,终端速度倾角偏差和高度偏差有所降低,终端速度偏差改变不大。从能量的角度分析,气动参数扰动量直接影响气动力的大小,进而改变气动力消耗的能量大小。而终端速度直接与终端能量相关,而仅靠制导方法是无法完全弥补能量损耗的,因此新的摄动制导方案对于终端速度偏差没有明显的改善效果。综合以上分析,基于气动参数在线辨识的摄动制导方案相对于传统摄动制导,可以一定程度上减小终端偏差,提高制导精度。
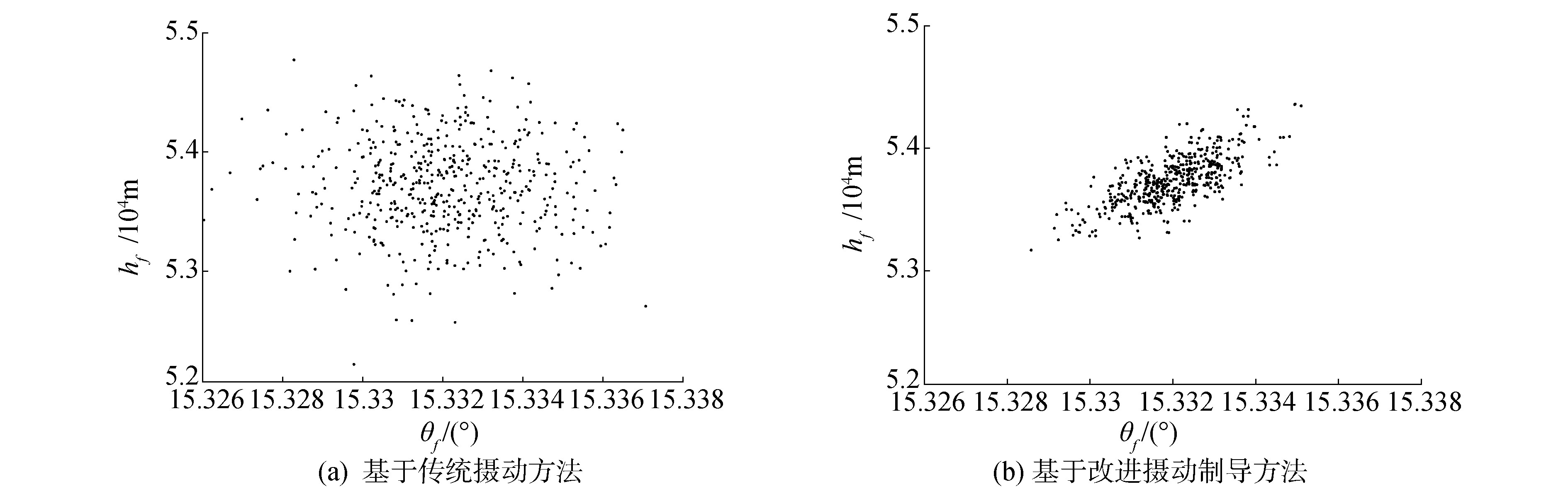
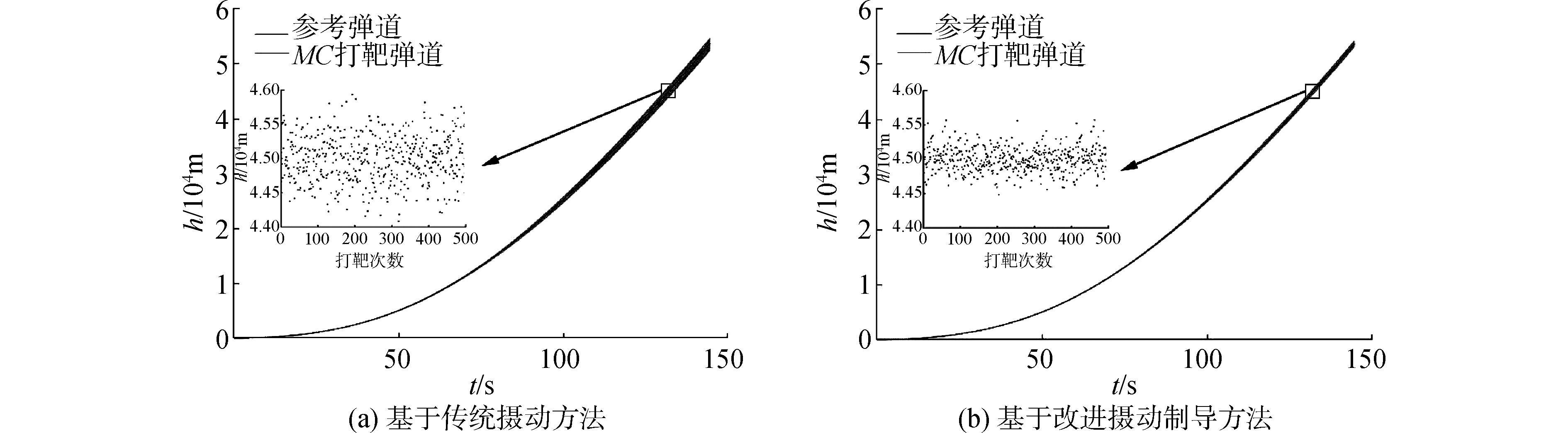
为了进一步验证新的摄动制导方案的可靠性,设计Monte Carlo仿真实验。将气动参数扰动量CDd、CLd设置为随机扰动,均服从零值正态分布,3δ偏差CDd为0.15,CLd为0.015,进行500次Monte Carlo打靶,结果如图 4、5所示。图 4为终端高度-终端速度倾角剖面图,由图可知:基于气动参数在线辨识的摄动制导方法终端高度-速度倾角散布明显小于传统摄动制导:终端高度散布从约2 000 m减小到约1 000 m,终端速度倾角散布从0.016°减小到0.006°。图 5为高度-时间曲线散布对比,由图可知基于气动参数辨识的摄动制导的高度-时间曲线散布明显小于传统摄动制导。综上所述,基于气动参数在线辨识的摄动制导方案不仅能提高终端精度,还能让真实弹道更好地保持在标准弹道附近。
|
Download:
|
| 图 4 Monte Carlo打靶终端状态高度-速度倾角剖面图 Fig. 4 Terminal altitude-velocity profile in Monte Carlo simulation | |
|
Download:
|
| 图 5 Monte Carlo打靶高度-时间曲线 Fig. 5 Altitude-velocity curves in Monte Carlo simulation | |
1) 采用扩展Kalman滤波方法进行气动参数辨识,收敛较快,辨识精度较高;
2) 针对基于气动参数在线辨识的摄动制导方法,设计对比仿真,发现该方法相对于传统摄动制导方法,能有效降低终端状态偏差;并针对随机气动扰动,进行Monte Carlo打靶仿真,发现改进的摄动制导方案能有效地提高弹道收敛性,使弹道更好地保持在标准弹道附近。
| [1] |
陈克俊, 刘鲁华, 孟云鹤. 远程火箭飞行动力学与制导[M]. 北京: 国防工业出版社, 2014: 50. CHEN Kejun, LIU Luhua, MENG Yunhe. Launch vehicle flight dynamics and guidance[M]. Beijing: National Defense Industry Press, 2014: 50. (  0) 0)
|
| [2] |
陈克俊. 载人飞船上升段摄动制导方法探讨[J]. 航天控制, 1992(2): 1-5. CHEN Kejun. An approach to the concept of perturbation guidance of manned spaceraft during ascent phase[J]. Aerospace control, 1992(2): 1-5. (  0) 0)
|
| [3] |
黄小平, 王岩. 卡尔曼滤波原理及应用——MATLAB仿真[M]. 北京: 电子工业出版社, 2015: 2-5. HUANG Xiaoping, WANG Yan. Kalman filter and its application[M]. Beijing: Publishing House of Electronics Industry, 2015: 2-5. (  0) 0)
|
| [4] |
KANDEPU R, FOSS B, IMSLAND L. Applying the unscented Kalman filter for nonlinear state estimation[J]. Journal of process control, 2008, 18(7/8): 753-768. (  0) 0)
|
| [5] |
涂海峰, 贾生伟, 阳丰俊, 等. 基于无迹卡尔曼滤波的巡飞弹气动参数在线辨识方法[J]. 航天控制, 2018, 36(5): 14-18. TU Haifeng, JIA Shengwei, YANG Fengjun, et al. Loitering munition aerodynamic parameter online identification method based on unscented Kalman filter[J]. Aerospace control, 2018, 36(5): 14-18. (  0) 0)
|
| [6] |
冯鹏, 邹世开. 卡尔曼滤波器UD分解滤波算法的改进[J]. 遥测遥控, 2005, 26(1): 10-14. FENG Peng, ZOU Shikai. Improvement of the UD covariance factorization algorithm of Kalman filter[J]. Telemetry & telecontrol, 2005, 26(1): 10-14. (  0) 0)
|
| [7] |
梁子璇, 任章. 基于在线气动参数修正的预测制导方法[J]. 北京航空航天大学学报, 2013, 39(7): 853-857. LIANG Zixuan, REN Zhang. Predictive reentry guidance with aerodynamic parameter online correction[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(7): 853-857. (  0) 0)
|
| [8] |
KUMAR R, GANGULI R, OMKAR S N, et al. Rotorcraft parameter identification from real time flight data[J]. Jounal of aircaft, 2008, 45(1): 333-341. (  0) 0)
|
| [9] |
崔乃刚, 卢宝刚, 傅瑜, 等. 基于卡尔曼滤波的再入飞行器气动参数辨识[J]. 中国惯性技术学报, 2014, 22(6): 755-758. CUI Naigang, LU Baogang, FU Yu, et al. Aerodynamic parameter identification of a reentry vehicle based on Kalman filter method[J]. Journal of Chinese inertial technology, 2014, 22(6): 755-758. (  0) 0)
|
| [10] |
余舜京, 程艳青, 钱炜褀. 跨声速气动参数在线辨识方法研究[J]. 宇航学报, 2011, 32(6): 1211-1216. YU Shunjing, CHENG Yanqing, QIAN Weiqi. Research on transonic aerodynamic parameter online identification[J]. Journal of astronautics, 2011, 32(6): 1211-1216. (  0) 0)
|
| [11] |
GARCIA-VELO J, WALKER B K. Aerodynamic parameter estimation for high-performance aircraft using extended Kalman filtering[J]. Journal of guidance, control, and dynamics, 1997, 20(6): 1257-1260. (  0) 0)
|
| [12] |
CHOWDHARY G, JATEGAONKAR R. Aerodynamic parameter estimation from flight data applying extended and unscented Kalman filter[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Colorado, 2006.
(  0) 0)
|
| [13] |
赵汉元. 飞行器再入动力学和制导[M]. 长沙: 国防科技大学出版社, 1997. ZHAO Hanyuan. Fight vehicle reentry dynamics and guidance[M]. Changsha: National University of Defense Technology Press, 1997. (  0) 0)
|
| [14] |
张迁, 许志, 李新国. 一种多级全固体运载火箭上升段自主制导方法[J]. 宇航学报, 2019, 40(1): 19-28. ZHANG Qian, XU Zhi, LI Xinguo. An autonomous ascent guidance method for multi-stage solid launch vehicles[J]. Journal of astronautics, 2019, 40(1): 19-28. (  0) 0)
|
| [15] |
徐光, 徐楚韶. 参数估计算法的研究[J]. 武汉科技大学学报(自然科学版), 2000, 23(4): 341-343. XU Guang, XU Chushao. Study of the algorithm for parameter estimation[J]. Journal of Wuhan University of Science and Technology (natural science edition), 2000, 23(4): 341-343. (  0) 0)
|
| [16] |
李训艳, 周玉国, 逯倩倩. 限定记忆法辨识带钢热镀锌退火炉模型参数[J]. 计算机时代, 2012(1): 21-23. LI Xunyan, ZHOU Yuguo, LU QianQian. Identification of strip steel galvanized annealing furnace model parameters using fixed memory method[J]. Computer era, 2012(1): 21-23. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


