2. 北京航天计量测试技术研究所, 北京 100076;
3. 中国人民解放军 92578部队, 北京 100161
2. Beijing Aerospace Institute for Metrology and Measurement, Beijing 100076, China;
3. Naval Academy, Beijing 100161, China
层合扇形板结构在航空、航天、机械制造等领域应用广泛。因此开展层合扇形板的振动特性分析研究,获取层合扇形板结构任意边界条件下的典型特征频率,对指导相应结构在工程中的应用具有重要意义。本文基于一阶剪切变形理论建立数学模型,设板厚方向的剪切应变为常数,通过选取适当的剪切修正系数,即可进行中厚板振动特性分析。
当前已有众多研究复合扇形板振动特性的数值方法,如有限元法[1]、微分求积法[2]、改进三角级数法[3]、广义微分求积法[4]、动力松弛法[5],微分求积法[6]等,上述方法虽然可以有效求解复合扇形板振动特性问题,但大多只能应用于刚固、简支、自由等几种特定类型的经典边界,对于各种经典边界、弹性边界及其任意组合的复杂边界下的振动特性研究较少。Li[7]提出改进傅里叶级数法被广泛应用于一般边界条件下的板和壳的振动分析中,本文在该方法的基础上进行了拓展。采用弹簧刚度法模拟一般边界条件,采用基于一阶剪切变形理论的Hamilton方程推导运动方程和边界方程。板结构的位移和旋转分量均展开为三角级数,其由标准三角级数和辅助多项式构成。引入辅助多项式函数以消除传统三角级数的位移及其导数在边界处的不连续性并保证其快速收敛。通过将本方法的计算结果与相关文献进行对比,验证了本方法的准确性和可靠性,并给出了任意边界条件下层合扇形板振动特性的结果。
1 层合扇形板自由振动理论推导 1.1 模型描述层合扇形板由厚度为h、内径为a、外径为b、径向宽度为R、扇形角为φ的多层扇形中厚板层叠而成,其几何尺寸在正交柱坐标系(r, θ, z)中定义,为方便分析还建立了局部坐标系(s, θ, z),其几何模型由图 1(a)给出。本文在各层扇形板边缘处的中性面处施加3组线性弹簧(ku, kv, kw)和2组旋转弹簧(KR, Kθ),并通过改变边界弹簧的刚度值来模拟不同的边界条件[8],见图 1(b)。其中下标deg_0、deg_1、r_0和r_1分别表示边界弹簧在θ=0、θ=φ、s=0和s=R条件下的弹簧刚度。记第k层材料正交各向异性方向与r轴间的夹角为层压角α,见图 1(c)。

|
Download:
|
| 图 1 中厚层合扇形板几何模型示意 Fig. 1 The geometric model of laminated sector plates | |
基于一阶剪切变形理论,层合扇形板的位移函数可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {\bar u(r,\theta ,z,t) = {u_0}(r,\theta ,t) + z{\psi _r}(r,\theta ,t)}\\ {\bar v(r,\theta ,z,t) = {v_0}(r,\theta ,t) + z{\psi _\theta }(r,\theta ,t)}\\ {\bar w(r,\theta ,z,t) = {w_0}(r,\theta ,t)} \end{array}} \right. $ | (1) |
式中:u0、v0和w0分别表示参考平面上相应点在r、θ和z方向的位移;Ψr和Ψθ分别表示绕r和θ方向且垂直于参考面的旋转分量;t表示时间。层合扇形板的应变分量可表示为:
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varepsilon _r} = \varepsilon _r^0 + z{\kappa _r},\;\:{\varepsilon _\theta } = \varepsilon _\theta ^0 + z{\kappa _\theta }}\\ {{\gamma _{r\theta }} = \gamma _{r\theta }^0 + z{\kappa _{r\theta }},\;\:{\gamma _{rz}} = \gamma _{rz}^0,{\gamma _{\theta z}} = \gamma _{\theta z}^0} \end{array} $ | (2) |
式中εr0、εθ0、γrθ0、γrz0和γθz0表示膜应变。
根据胡克定律,层合扇形板的应力-应变关系可表示为:
| $ \left[ {\begin{array}{*{20}{l}} {{\sigma _r}}\\ {{\sigma _\theta }}\\ {{\tau _{r\theta }}}\\ {{\tau _{rz}}}\\ {{\tau _{\theta z}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\bar Q_{11}^k}&{\bar Q_{12}^k}&{\bar Q_{16}^k}&0&0\\ {\bar Q_{12}^k}&{\bar Q_{22}^k}&{\bar Q_{26}^k}&0&0\\ {\bar Q_{16}^k}&{\bar Q_{26}^k}&{\bar Q_{66}^k}&0&0\\ 0&0&0&{\bar Q_{44}^k}&{\bar Q_{45}^k}\\ 0&0&0&{\bar Q_{45}^k}&{\bar Q_{55}^k} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\varepsilon _r}}\\ {{\varepsilon _\theta }}\\ {{\gamma _{r\theta }}}\\ {{\gamma _{rz}}}\\ {{\gamma _{\theta z}}} \end{array}} \right] $ | (3) |
式中:σr、σθ表示r、θ方向上的法向应力;τrθ、τrz和τθz表示柱坐标系中r、θ和z方向上的剪切应力;Qij(i, j=1, 2, 4, 5, 6)表示第k层扇形板的刚度系数。
沿z方向对应力积分,可得力和力矩的积分式:
| $ \begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {{N_r}}\\ {{N_\theta }}\\ {{N_{r\theta }}} \end{array}} \right] = b\int_{ - h/2}^{h/2} {\left[ {\begin{array}{*{20}{c}} {{\sigma _r}}\\ {{\sigma _\theta }}\\ {{\tau _{r\theta }}} \end{array}} \right]} {\rm{d}}z,\left[ {\begin{array}{*{20}{c}} {{M_r}}\\ {{M_\theta }}\\ {{M_{r\theta }}} \end{array}} \right] = b\int_{ - h/2}^{h/2} {\left[ {\begin{array}{*{20}{c}} {{\sigma _r}}\\ {{\sigma _\theta }}\\ {{\tau _{r\theta }}} \end{array}} \right]} z{\rm{d}}z,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{Q_r}}\\ {{Q_\theta }} \end{array}} \right] = \kappa b\int_{ - h/2}^{h/2} {\left[ {\begin{array}{*{20}{c}} {{\tau _{rz}}}\\ {{\tau _{\theta z}}} \end{array}} \right]} {\rm{d}}z} \end{array} $ | (4) |
式中:Nr、Nθ和Nrθ表示各方向的合力;Mr、Mθ和Mrθ表示各方向的合力矩;Qr、Qθ表示各方向的剪切力;κ为剪切校正因子,本文取κ=5/6[9]。
1.3 扇形板中的能量关系层合扇形板内的应变能可定义为:
| $ \begin{array}{l} {U_s} = \frac{1}{2}\int {\int {\int_V ( } } {N_r}\varepsilon _r^0 + {N_\theta }\varepsilon _\theta ^0 + {N_{r\theta }}\gamma _{r\theta }^0 + {M_r}{\kappa _r} + {M_\theta }{\kappa _\theta } + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {M_{r\theta }}{\kappa _{r\theta }} + {Q_r}\gamma _{rz}^0 + {Q_\theta }\gamma _{\theta z}^0)(s + a){\rm{d}}V \end{array} $ | (5) |
将式(2)~(4)代入式(5),可得到用中性面处位移和旋转分量表示的板内应变能。
层合扇形板中的动能可表示为:
| $ T = \frac{{\rho (s + a)}}{2}\int {\int {\int_V {\left[ {{{\left( {\frac{{\partial u}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial w}}{{\partial t}}} \right)}^2}} \right]{\rm{d}}V} } } $ | (6) |
将式(1)中的u、v和w代入式(6), 并对z积分可得层合扇形板内部的动能:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} T = \frac{1}{2}\int_0^R {\int_0^\varphi {\left\{ {{I_0}\left[ {{{\left( {\frac{{\partial {u_0}}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial {v_0}}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial {w_0}}}{{\partial t}}} \right)}^2}} \right] + } \right.} } \\ 2{I_1}\left[ {\left( {\frac{{\partial {u_0}}}{{\partial t}}} \right)\left( {\frac{{\partial {\psi _r}}}{{\partial t}}} \right) + \left( {\frac{{\partial {v_0}}}{{\partial t}}} \right)\left( {\frac{{\partial {\psi _\theta }}}{{\partial t}}} \right)} \right] + {I_2}\left[ {{{\left( {\frac{{\partial {\psi _r}}}{{\partial t}}} \right)}^2} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left. {{{\left( {\frac{{\partial {\psi _\theta }}}{{\partial t}}} \right)}^2}} \right]} \right\}(s + a){\rm{d}}s{\rm{d}}\theta \end{array} $ | (7) |
其中:
| $ \left[ {\begin{array}{*{20}{l}} {{I_0}}&{{I_1}}&{{I_2}} \end{array}} \right] = \int_{ - h/2}^{h/2} \rho \left[ {\begin{array}{*{20}{l}} 1&z&{{z^2}} \end{array}} \right]{\rm{d}}z $ | (8) |
存储在边界弹簧中的应变能可表示为:
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {U_{sp}} = \frac{1}{2}\int_0^\varphi \{ a[k_{r\_0}^uu_0^2 + k_{r\_0}^vv_0^2 + k_{r\_0}^w{w^2} + K_{r\_0}^R\psi _r^2 + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K_{r\_0}^\theta \psi _\theta ^2{]_{s = 0}} + b[k_{r\_1}^uu_0^2 + k_{r\_1}^vv_0^2 + k_{r\_1}^w{w^2} + K_{r\_1}^R\psi _r^2 + } \end{array}\\ K_{r\_1}^\theta \psi _\theta ^2{]_{s = R}}\} {\rm{d}}\theta + \frac{1}{2}\int_0^R \{ [k_{deg \_0}^uu_0^2 + k_{deg\_0}^uv_0^2 + k_{deg \_0}^uw_0^2 + \\ \begin{array}{*{20}{c}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K_{deg \_0}^R\psi _r^2 + K_{deg \_0}^\theta \psi _\theta ^2{]_{\theta = 0}} + [k_{deg \_1}^uu_0^2 + k_{deg \_1}^vv_0^2 + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} k_{deg \_1}^w{w^2} + K_{deg \_1}^R\psi _r^2 + K_{deg \_1}^\theta \psi _\theta ^2{]_{\theta = \varphi }}\} {\rm{d}}s} \end{array} \end{array} $ | (9) |
根据Hamilton原理可得层合扇形板的边界条件和控制方程,其拉格朗日能量泛函L表示为:
| $ {L = T - {U_s} - {U_b} - {U_{bs}} - {U_{sp}}} $ | (10) |
由:
| $ {\delta \int_0^t {(T - {U_s} - {U_{sp}} - {U_{cp}})} {\rm{d}}t = 0} $ | (11) |
可得扇形板的控制方程:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {\frac{{\partial {N_r}}}{{\partial r}} + \frac{{\partial {N_{r\theta }}}}{{r\partial \theta }} - \frac{{{N_\theta }}}{r} = {I_0}{{\left( {\frac{{\partial {u_0}}}{{\partial t}}} \right)}^2} + {I_1}{{\left( {\frac{{\partial {\psi _r}}}{{\partial t}}} \right)}^2}}\\ {\frac{{\partial {N_\theta }}}{{r\partial \theta }} + \frac{{\partial {N_{r\theta }}}}{{\partial r}} + \frac{{{N_{r\theta }}}}{r} = {I_0}{{\left( {\frac{{\partial {v_0}}}{{\partial t}}} \right)}^2} + {I_1}{{\left( {\frac{{\partial {\psi _\theta }}}{{\partial t}}} \right)}^2}} \end{array}\\ \frac{{\partial {Q_r}}}{{\partial r}} + \frac{{\partial {Q_\theta }}}{{r\partial \theta }} = {I_0}{\left( {\frac{{\partial w}}{{\partial t}}} \right)^2}\\ \begin{array}{*{20}{l}} {\frac{{\partial {M_r}}}{{\partial r}} + \frac{{\partial {M_{r\theta }}}}{{r\partial \theta }} - \frac{{{M_\theta }}}{r} - {Q_r} = {I_1}{{\left( {\frac{{\partial {u_0}}}{{\partial t}}} \right)}^2} + {I_2}{{\left( {\frac{{\partial {\psi _r}}}{{\partial t}}} \right)}^2}}\\ {\frac{{\partial {M_\theta }}}{{r\partial \theta }} + \frac{{\partial {M_{r\theta }}}}{{\partial r}} + \frac{{{M_{r\theta }}}}{r} - {Q_\theta } = {I_1}{{\left( {\frac{{\partial {v_0}}}{{\partial t}}} \right)}^2} + {I_2}{{\left( {\frac{{\partial {\psi _\theta }}}{{\partial t}}} \right)}^2}} \end{array} \end{array} \right. $ | (12) |
层合扇形板的边界条件表示为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s = 0:\left\{ {\begin{array}{*{20}{l}} {{N_r} + k_{r\_0}^u{u_0} = 0,\;\:{N_{r\theta }} + k_{r\_0}^v{v_0} = 0}\\ {{M_r} + K_{r\_0}^R{\psi _r} = 0,\;\:{M_{r\theta }} + K_{r\_0}^\theta {\psi _\theta } = 0}\\ {{Q_r} + k_{r\_0}^ww = 0,} \end{array}} \right.\\ \theta = 0:\left\{ {\begin{array}{*{20}{l}} {{N_{r\theta }} + k_{deg\_0}^u{u_0} = 0,\;\:{N_\theta } + k_{deg\_0}^v{v_0} = 0}\\ {{M_{r\theta }} + K_{deg\_0}^R{\psi _r} = 0,\;\:{M_\theta } + K_{deg\_0}^\theta {\psi _\theta } = 0}\\ {{Q_\theta } + k_{deg\_0}^ww = 0} \end{array}} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} s = R:\left\{ {\begin{array}{*{20}{l}} {{N_r} - k_{r\_1}^u{u_0} = 0,}&{{N_{r\theta }} - k_{r\_1}^vv = 0}\\ {{M_r} - K_{r\_1}^R{\psi _r} = 0,}&{{M_{r\theta }} - K_{r\_1}^\theta {\psi _\theta } = 0}\\ {{Q_r} - k_{r\_1}^ww = 0}&{} \end{array}} \right.\\ \theta = \varphi :\left\{ {\begin{array}{*{20}{l}} {{N_{r\theta }} - k_{deg\_1}^u{u_0} = 0,\;\:{N_\theta } - k_{deg\_1}^v{v_0} = 0}\\ {{M_{r\theta }} - K_{deg\_1}^R{\psi _r} = 0,\;\:{M_\theta } - K_{deg\_1}^\theta {\psi _\theta } = 0}\\ {{Q_\theta } - k_{deg\_1}^ww = 0} \end{array}} \right. \end{array} $ | (13) |
本文层合扇形板位移和旋转分量均使用三角级数来表示,但传统三角级数在端点处存在不连续现象,因此引入辅助多项式改善其收敛性,辅助函数的引入使位移容许函数能满足求解域内更高阶导数的存在,从而有效地克服边界上可能存在的不连续问题。
扇形板位移函数的三角级数展开式表示为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {u_0}(s,\theta ,t) = (\sum\limits_{m = 0}^\infty {\sum\limits_{n = 0}^\infty {{A_{mn}}} } {\rm{cos}}({\lambda _{Rm}}s){\rm{cos}}({\lambda _{\varphi n}}\theta ) + \\ \sum\limits_{l = 1}^2 {\zeta _b^l} (\theta )\sum\limits_{m = 0}^\infty {a_m^l} {\rm{cos}}({\lambda _{Rm}}s) + \sum\limits_{l = 1}^2 {\zeta _a^l} (s)\sum\limits_{m = 0}^\infty {b_n^l} {\rm{cos}}({\lambda _{\varphi n}}\theta )){{\rm{e}}^{j\omega t}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {v_0}(s,\theta ,t) = (\sum\limits_{m = 0}^\infty {\sum\limits_{n = 0}^\infty {{B_{mn}}} } {\rm{cos}}({\lambda _{Rm}}s){\rm{cos}}({\lambda _{\varphi n}}\theta ) + \\ \sum\limits_{l = 1}^2 {\zeta _b^l} (\theta )\sum\limits_{m = 0}^\infty {c_m^l} {\rm{cos}}({\lambda _{Rm}}s) + \sum\limits_{l = 1}^2 {\zeta _a^l} (s)\sum\limits_{n = 0}^\infty {d_n^l} {\rm{cos}}({\lambda _{\varphi n}}\theta )){{\rm{e}}^{j\omega t}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} w(s,\theta ,t) = (\sum\limits_{m = 0}^\infty {\sum\limits_{n = 0}^\infty {{C_{mn}}} } {\rm{cos}}({\lambda _{Rm}}s){\rm{cos}}({\lambda _{\varphi n}}\theta ) + \\ \sum\limits_{l = 1}^2 {\zeta _b^l} (\theta )\sum\limits_{m = 0}^\infty {e_m^l} {\rm{cos}}({\lambda _{Rm}}s) + \sum\limits_{l = 1}^2 {\zeta _a^l} (s)\sum\limits_{n = 0}^\infty {f_n^b} {\rm{cos}}({\lambda _{\varphi n}}\theta )){{\rm{e}}^{j\omega t}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _r}(s,\theta ,t) = (\sum\limits_{m = 0}^\infty {\sum\limits_{n = 0}^\infty {{D_{mn}}} } {\rm{cos}}({\lambda _{Rm}}s){\rm{cos}}({\lambda _{\varphi n}}\theta ) + \\ \sum\limits_{l = 1}^2 {\zeta _b^l} (\theta )\sum\limits_{m = 0}^\infty {g_m^l} {\rm{cos}}({\lambda _{Rm}}s) + \sum\limits_{l = 1}^2 {\zeta _a^l} (s)\sum\limits_{n = 0}^\infty {h_n^l} {\rm{cos}}({\lambda _{\varphi n}}\theta )){{\rm{e}}^{j\omega t}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _\theta }(s,\theta ,t) = (\sum\limits_{m = 0} {\sum\limits_{n = 0} {{E_{mn}}} } {\rm{cos}}({\lambda _{Rm}}s){\rm{cos}}({\lambda _{\varphi n}}\theta ) + \\ \sum\limits_{l = 1}^2 {\zeta _b^l} (\theta )\sum\limits_{m = 0}^\infty {k_m^l} {\rm{cos}}({\lambda _{Rm}}s) + \sum\limits_{l = 1}^2 {\zeta _a^l} (s)\sum\limits_{n = 0}^\infty {q_n^l} {\rm{cos}}({\lambda _{\varphi n}}\theta )){{\rm{e}}^{j\omega t}} \end{array} $ | (14) |
式中:λRm=mπ/R、λϕn=nπ/ϕ、Amn、Bmn、Cmn、Dmn和Emn为位移函数二阶三角级数展开的系数。aml、bnl、cml、dnl、eml、fnl、gml、hnl、kml、qnl (l=1, 2)为辅助函数的系数,ζal、ζbl (l=1, 2)表示定义在求解域S=[0, R]×[0, φ]内高阶可导的辅助函数。
从式(14)中可以看出,位移函数分量中最高存在二阶导数,这意味着至少需要允许函数的二阶导数连续才能满足板上任意点的连续性。为此本文选取以下简单的辅助函数,该函数满足求解域内二阶导数连续且三阶导数存在:
| $ \left\{ {\begin{array}{*{20}{l}} {\zeta _a^1(s) = \frac{R}{{2\pi }}{\rm{sin}}\left( {\frac{{\pi s}}{{2R}}} \right) + \frac{R}{{2\pi }}{\rm{sin}}\left( {\frac{{3\pi s}}{{2R}}} \right)}\\ {\zeta _a^2(s) = \frac{{ - R}}{{2\pi }}{\rm{cos}}\left( {\frac{{\pi s}}{{2R}}} \right) + \frac{R}{{2\pi }}{\rm{cos}}\left( {\frac{{3\pi s}}{{2R}}} \right)} \end{array}} \right. $ | (15) |
易证得:
| $ \left\{ {\begin{array}{*{20}{l}} {\zeta _a^1(0) = \zeta _a^1(R) = \zeta _a^{1\prime }(R) = 0,\;\:\zeta _a^{1\prime }(0) = 1}\\ {\zeta _a^2(0) = \zeta _a^2(R) = \zeta _a^{2\prime }(0) = 0,\;\:\zeta _a^{2\prime }(R) = 1} \end{array}} \right. $ | (16) |
同理,ζb1(θ)和ζb2(θ)也满足上述条件,通过对展开项逐项求导可得均匀收敛级数。将式(1)~(4)、(6)~(9)代入式(10),并考虑位移函数构成,根据Rayleigh-Ritz法最终可得如下形式的运动方程:
| $ (\mathit{\boldsymbol{K}} - {\omega ^2}\mathit{\boldsymbol{M}})\mathit{\boldsymbol{E}} = 0 $ | (17) |
式中:K、M和E分别表示扇形板的刚度矩阵、质量矩阵和未知系数矩阵,对上式求解可得到层合扇形板的固有频率,进而可求得相应的振型。
2 数值结果和讨论 2.1 收敛性研究 2.1.1 边界弹簧刚度的影响本文对扇形板的边界使用弹簧来模拟边界约束,设定恰当的弹簧刚度值可模拟扇形板任意的边界条件。通过讨论弹性边界约束参数对层合扇形板无量纲频率参数Ω=ωb2/h(ρm/E2)1/2的影响规律,探讨了不同边界下合适的弹簧刚度取值,进而验证了弹簧刚度法在此类问题应用中的可行性。本算例中模型的几何和材料属性参数为:a/b=0.5,h/b=0.1,E1/E2=15,E2=1×1010 Pa,G12=G13=0.6E2,G23=0.5E2,μ12=0.25,ρ=1 500 kg/m3。为简化分析过程,取弹性约束参数Гu、Гv、Гw、ГR和Гθ表示相应弹簧刚度与抗弯刚度D=E2h3/12(1-μ122)的比值,即Гu=ku/D、Гv=kv/D、Гw=kw/D、ГR=KR/D、Гθ=Kθ/D。此外,定义参数ΔΩ=ΩΓλ-ΩΓλ=10-8,用于表示无量纲频率Ω与参考值的差值,参考值取ΩΓλ=10-8。
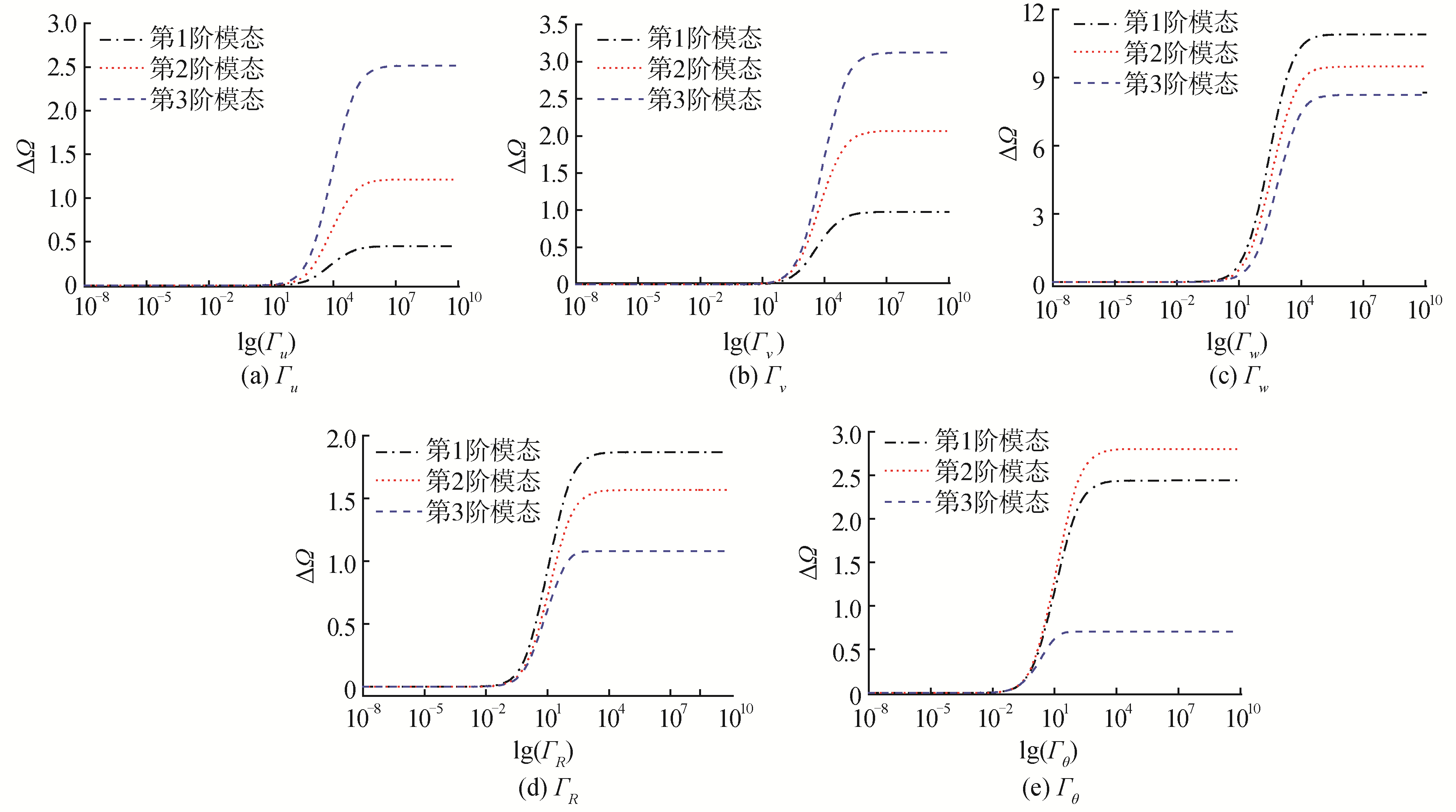
图 2给出了非对称型双层层合扇形板[0°/90°]前三阶频率参数ΔΩ随弹性约束参数Гλ(λ=u, v, w, R, θ)的变化关系。本算例所取边界条件为:s=0、s=R处自由,θ=0处刚固,θ=φ处弹性约束。从图 2可以看出,弹性约束参数Гλ小于10-1时,ΔΩ几乎为零,此时可视自由边界条件;弹性约束参数Гλ在101~106范围内时,ΔΩ与Гλ呈正相关关系,此时可视为弹性边界条件;弹性约束参数Гλ在107以上后ΔΩ基本趋于稳定,此时扇形板的无量纲频率求解已达到收敛,该范围可视为刚固边界条件。
|
Download:
|
| 图 2 双层非对称层合扇形板[0°/90°]的频率参数ΔΩ随弹性约束参数Γλ的变化关系 Fig. 2 The frequency parameters ΔΩ versus the elastic restraint parameters Γλ for laminated sector plate[0°/90°] | |
通过大量分析计算,给出了本算例所给工况下几种经典边界条件对应各弹簧刚度的合理取值(如表 1)。
| 表 1 几种边界条件下各弹簧刚度值的合理取值 Table 1 The suitable values of spring stiffness value under several boundary conditions |
为了检验以上弹簧刚度取值的合理性,将以弹簧模拟不同边界来进行振动特性分析,并与相关文献进行数值对比。为简洁起见,使用字符串来表示边界条件,例如FCSC表示在扇形板s=0、θ=0、s=R和θ=φ处具有F、C、S和C边界条件。除非另有说明,本文层合扇形板无量纲频率参数表示为:Ω=ωb2/h(ρm/E2)1/2,扇形板的材料和几何参数如下:E2=1×1010 Pa,E1/E2=15,G12=G13=0.6E2,G23=0.5E2,μ12=0.25,ρ=1 500 kg/m3。
2.1.2 截断数的影响本节探讨三角级数截断数对层合扇形板无量纲频率收敛性的影响。扇形板的位移函数由三角级数来表示,显然其位移和旋转分量上三角级数的展开阶数M和N对计算收敛性有直接关系,理论上展开阶数越多计算越精确,但相应的计算效率会大幅降低,因此选取合适的展开阶数具有重要的探讨价值。
表 2给出了CCCC边界条件下双层层合扇形板[0°/90°]前六阶固有频率随截断数影响的结果。从表中可以看出本文方法收敛性良好,M=N=8和M=N=16的结果之间的最大差异小于0.077%。因此如不做特殊说明,本文方法在后续计算中三角级数的截断数统一取M=N=12。
| 表 2 CCCC边界下双层[0°/90°]层合扇形板前六阶频率参数收敛性(φ=2π/3, a/b=0.5, h/b=0.2, E1/E2=40) Table 2 Convergence of the first six frequency parameters for a laminated sector plate [0°/90°]with CCCC boundary conditions |
表 3给出了2种方法对不同经典边界条件下多层层合扇形板[0°/90°]5的频率参数计算结果的比较(φ=π/3, a/b=0.1, h/b=0.2, E1/E2=40)。从表 3可知本方法与参考文献相比最大相对误差不超过0.634%,由此可证得本方法的有效性。
| 表 3 不同边界下层合扇形板[0°/90°]5Ω值与文献[10]对比 Table 3 Comparison of the Ω for a laminated sector plate [0°/90°]5 with different boundary conditions |
表 4~6给出了刚固、简支、自由等边界条件下层合扇形板无量纲频率与厚径比、正交各向异性比、层压角等结构参数间的关系。表 4表明无量纲频率随扇形板厚径比的增加而降低(φ=π/2, a/b=0.5, E1/E2=15)。表 5表明频率参数随正交各向异性比的增加而增加(φ=π/2, a/b=0.5, h/b=0.1)。表 6表明扇形板的频率参数随层压角的增大而减小(E1/E2=15, a/b=0.5, h/b=0.1)。图 3给出了CCCC和CFCF边界条件下层合板前三阶阵型图(E1/E2=15, a/b=0.5, h/b=0.1, φ=2π/3)。由图 3可知,同阶阵型下,边界条件的不同会导致其模态特性不尽相同。
| 表 4 不同边界下层合扇形板[0°/90°]2 Ω值与厚径比的关系 Table 4 The Ω for a laminated sector plate[0°/90°]2 with thickness-to-radius ratios in different boundary conditions |
| 表 5 不同边界下层合扇形板[0°/90°]2 Ω值与各向异性比关系 Table 5 The Ω for a laminated sector plate[0°/90°]2 with orthotropy ratios in different boundary conditions |
| 表 6 不同边界下扇形板[0°/90°/90°/0°] Ω值与层压角的关系 Table 6 The Ω for a laminated sector plate[0°/90°/90°/0°] with included angles in different boundary conditions |

|
Download:
|
| 图 3 不同边界下层合扇形板前三阶模态阵型 Fig. 3 The lowest three mode shapes for a laminated sector plate in different boundary conditions | |
层合扇形板在实际工程应用中通常会有更为复杂的一般边界条件约束,表 7和表 8给出了在一般弹性边界约束下层合扇形板的前四阶固有频率。本算例中扇形板的几何尺寸除φ=π外均与图 3相同。从表 7和表 8可以看出,不同的层合方案对层合扇形板的频率也有明显影响。图 4给出了CE3CE3和E3E3E3E3边界条件下层合扇形板[0°/90°/90°/0°]前三阶模态的阵型图,由图 4可知,边界条件的不同使得同阶阵型层合板振动模态呈现明显差异。
| 表 7 不同经典边界和层合方案下层合扇形板的Ω值 Table 7 The Ω for a laminated sector plate with different classical boundary conditions and lamination schemes |
| 表 8 不同弹性边界和层合方案下层合扇形板的Ω值 Table 8 The Ω for a laminated sector plate with different elastic boundary conditions and lamination schemes |

|
Download:
|
| 图 4 2种边界下扇形板[0°/90°/90°/0°]前三阶模态阵型图 Fig. 4 The lowest three mode shapes for a [0°/90°/90°/0°] laminated sector plate with two boundary conditions | |
1) 通过增加辅助函数有效解决了三角级数的连续性问题,计算结果通过与参考文献对比验证了本方法具有较好的准确性。
2) 弹簧刚度法在解决此类问题时可有效应用,使用适当取值的弹簧刚度可较好地模拟各种边界条件约束。
3) 计算结果随三角级数展开阶数的增加快速收敛,通常取较低的阶数就能保证足够的计算精度。
4) 无量纲频率随扇形板厚径比的增大而减小,随正交各向异性比的增大而增大,随层压角的增大而减小。
| [1] |
HOUMAT A. Large amplitude free vibration of shear deformable laminated composite annular sector plates by a sector p-element[J]. International journal of non-linear mechanics, 2008, 43(9): 834-843. DOI:10.1016/j.ijnonlinmec.2008.05.007 (  0) 0)
|
| [2] |
滕兆春, 朱亚文, 蒲育. FGM环扇形板的面内自由振动分析[J]. 计算力学学报, 2018, 35(5): 560-566. TENG Zhaochun, ZHU Yawen, PU Yu. In-plane free vibration analysis of FGM annular sector plates[J]. Chinese journal of computational mechanics, 2018, 35(5): 560-566. (  0) 0)
|
| [3] |
史冬岩, 石先杰, 李文龙. 任意边界条件下环扇形板面内振动特性分析[J]. 振动工程学报, 2014, 27(1): 1-8. SHI Dongyan, SHI Xianjie, LI Wenlong. In-plane vibration analysis of annular sector plates with arbitrary boundary supports[J]. Journal of vibration engineering, 2014, 27(1): 1-8. DOI:10.3969/j.issn.1004-4523.2014.01.001 (  0) 0)
|
| [4] |
ANDAKHSHIDEH A, MALEKI S, AGHDAM M M. Non-linear bending analysis of laminated sector plates using generalized differential quadrature[J]. Composite structures, 2010, 92(9): 2258-2264. DOI:10.1016/j.compstruct.2009.08.007 (  0) 0)
|
| [5] |
GOLMAKANI M E, MEHRABIAN M. Nonlinear bending analysis of ring-stiffened circular and annular general angle-ply laminated plates with various boundary conditions[J]. Mechanics research communications, 2014, 59: 42-50. DOI:10.1016/j.mechrescom.2014.04.007 (  0) 0)
|
| [6] |
MALEKZADEH P. Three-dimensional free vibration analysis of thick laminated annular sector plates using a hybrid method[J]. Composite structures, 2009, 90(4): 428-437. DOI:10.1016/j.compstruct.2009.04.015 (  0) 0)
|
| [7] |
LI W L. Comparison of Fourier sine and cosine series expansions for beams with arbitrary boundary conditions[J]. Journal of sound and vibration, 2002, 255(1): 185-194. (  0) 0)
|
| [8] |
PANG Fuzhen, LI Haichao, WANG Xueren, et al. A semi analytical method for the free vibration of doubly-curved shells of revolution[J]. Computers & mathematics with applications, 2018, 75(9): 3249-3268. (  0) 0)
|
| [9] |
PARK M, CHOI D H. A four-variable first-order shear deformation theory considering the variation of in-plane rotation of functionally graded plates[J]. International journal of steel structures, 2018, 18(4): 1265-1283. (  0) 0)
|
| [10] |
SHARMA A, SHARDA H B, NATH Y. Stability and vibration of thick laminated composite sector plates[J]. Journal of sound and vibration, 2005, 287(1/2): 1-23. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


