2. 北京邮电大学 自动化学院, 北京 100876
2. School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China
软件测试在检验和提升软件设计和实现质量的过程中是非常重要但耗时的环节。在软件开发需要检查版本迭代过程中是否产生了新错误。但是在每次更改后没有必要执行全部测试用例,一方面,多个测试用例可能集中在一段相同的代码上,从而产生冗余和浪费;另一方面,在一个大型项目中执行一次测试套件需要大约1 h[1],频繁的代码更改需要大量时间来进行测试。测试用例集约简旨在保障覆盖率不变的情况下限度地减少执行的测试用例的数量,约简测试用例集,在进行约简时,约简后测试用例集必须要满足跟原始测试用例集具有相同的覆盖率,例如语句覆盖率等[2]。
Harrold等[3]提出测试用例集约简的概念并提出一种启发式方法。在随后的发展中,出现了许多方法,包括贪心算法、启发式算法和整数规划等[4]。Chvatal[5]介绍的种贪心算法是一种经典的用于寻找测试用例集问题的近似最优解的方法。然而,贪心算法并不能尽早处理基本测试用例(唯一可以覆盖其中某测试需求的测试用例),Chen等[6]提出了2种算法来解决这个问题。全君林等[7]提出采用遗传算法,通过遗传算子完成进化过程找到最优或近似最优解。张卫祥等[8]提出了一种改进的基于测试点覆盖和离散粒子群优化算法的方法来提高回归测试效率。但是这类算法会有陷入局部收敛等问题。
本文提出了一种基于萤火虫算法的测试用例集约简算法,利用萤火虫算法发现能够满足测试需求的最简测试用例集,对回归测试进行优化,并通过对实际工程项目进行测试实验,对萤火虫算法的效果、鲁棒性等性能进行检验分析。
1 萤火虫算法及建模本文从覆盖率以及测试开销2个方面进行了综合考虑,利用萤火虫算法空间搜索能力强、收敛快等特点,构建了二值细胞自动机模型,将其应用于测试用例集约简之中,使其可以在快速收敛的情况下,更高效的进行测试用例集约简。
1.1 测试用例集约简测试用例集约简问题输入主要可以概括为:测试用例集T={t1, t2, …, tn},测试需求集R={r1, r2, …, rm},测试关系Z={(t, r)|t∈T,r∈R},其中,如果测试用例t可以检测到测试需求r,则为1,否则为0,测试开销C={c1, c2, …, cm}。
经过约简,得到一个的测试用例集T的子集RS,其中RS的测试用例可以满足所有的测试需求,并且使产生的测试开销尽可能小。
令测试需求集为R={r1, r2, …, rm},测试用例集为T={t1, t2, …, tn},∋t1⊂T,其中:T1满足R,有 ∀Tx⊂T,使得tx的测试开销大于等于T1的测试开销,因此这是一个最小集合覆盖问题,属于典型的NP-Complete问题,所以无法用传统的方法得到最优解。
给出一个测试用例集约简的实例。
如表 1所示,测试用例T内包含5个测试用例{t1, t2, t3, t4, , t5},测试需求集包含6个需求{r1, r2, r3, r4, r5, r6},其中的■代表的是测试关系,每个测试用例分别都对应一个测试开销,实际上这组测试用例是有冗余的,不考虑开销的情况下,只需要{t1, t2}便可以覆盖全部测试点,因此另外3个需要约简的冗余测试用例。
| 表 1 测试用例集实例 Table 1 Test suite example |
将上述问题转化为数学问题:测试用例集和测试需求分别代表矩阵的列和行,测试用例i满足测试需求j的测试关系表示为Sij=1,测试开销表示为一个向量,则可以将表 1转换为:
| $\begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;\begin{array}{*{20}{l}} {} \end{array}\begin{array}{*{20}{l}} {} \end{array}\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {} \end{array}} \end{array}\begin{array}{*{20}{l}} {{r_1}}&{{r_2}}&{{r_3}}&{{r_4}}&{{r_5}}&{{r_6}} \end{array}\;\;\;\;\begin{array}{*{20}{l}} c \end{array}}\\ {F = \begin{array}{*{20}{c}} {{t_1}}\\ {{t_2}}\\ {{t_3}}\\ {\begin{array}{*{20}{l}} {{t_4}}\\ {{t_5}} \end{array}} \end{array}\left[ {\begin{array}{*{20}{c}} 0&1&1&0&1&1\\ 1&0&0&1&0&1\\ 0&0&0&0&1&1\\ 0&1&1&1&0&0\\ 0&0&0&1&0&1 \end{array}} \right]\;\;\;\left[ {\begin{array}{*{20}{l}} {{c_1}}\\ {{c_2}}\\ {{c_3}}\\ {{c_4}}\\ {{c_5}} \end{array}} \right]} \end{array} $ |
即问题可以表示为一个m×n的矩阵,目的是在开销最小的情况下,选择一部分矩阵的行,使其覆盖矩阵所有的列,设向量x表示约简结果,xi=1表示行i被选中,可以覆盖Sij=1各行对应的测试功能点,问题求解目标表示为:
| $ {\rm{min}}f(x) = {\rm{ }}xc $ | (1) |
| $ {\rm{s}}{\rm{.t}}{\rm{.}}\prod\limits_{j = 1}^n {\left( {\sum\limits_{i = 1}^m {\left( {{x_i}{s_{ij}}} \right)} } \right)} > 0 $ | (2) |
式(1)是约简目标,式(2)为约束条件,表示每个测试点都需要被覆盖。
1.2 萤火虫算法描述萤火虫算法(firefly algorithm,FA)是一种基于群体的随机优化算法。文献[9]研究了萤火虫个体间相互吸引与发光亮度之间的关系和萤火虫的移动特性,从而提出了一种新型群智能优化算法,即萤火虫算法。
在萤火虫算法中,空间各点视为萤火虫,发光弱的萤火虫会被发光强的所吸引。根据这一特点,在算法中,将适应度设置为发光强度,适应度越高代表其位置越好,这样适应度低的萤火虫会朝向适应度高的萤火虫移动,从而完成位置的迭代,并找出最优位置,即完成了寻优过程。
萤火虫算法有以下条件:1)所有萤火虫都是同一性别且相互吸引;2)吸引度只与发光强度和距离有关,与发光强度成正比,与距离成反比;3)发光强弱,即适应度,由目标函数决定,在指定区域内与指定函数成比例关系。
算法的数学描述和主要参数如下:1)萤火虫相对荧光亮度:
| $ I{\rm{ }} = {\rm{ }}{I_0}{{\rm{e}}^{ - \gamma {r_{ij}}}} $ | (3) |
式中:I0表示萤火虫的最大亮度,与目标函数有关,位置越优,亮度越大;γ表示光吸收系数,其代表的是荧光会随着距离的增加和传播介质的吸收而逐渐减弱;rij表示的是i和j 2个萤火中之间的欧氏距离。
2) 相互吸引度β:
| $ \beta (r) = {\rm{ }}{\beta _0}{{\rm{e}}^{ - \gamma r_{ij}^2}} $ | (4) |
式中β0为最大吸引度,即距离为0的吸引度。
3) 最优目标迭代:
| $ {x_i}(t{\rm{ }} + 1) = {\rm{ }}{x_i}(t) + {\rm{ }}\beta ({x_j}(t) - {\rm{ }}{x_i}(t)) + {\rm{ }}\alpha \left( {{\rm{rand}} - \frac{1}{2}} \right) $ | (5) |
式中:t表示的是时刻,xi与xj表示萤火虫i、j的空间位置,α为步长因子,rand为随机项,防止产生震荡,为[0, 1]上的均匀分布。
1.3 二元优化问题应用测试用例约简问题属于二元优化问题,因此引入二进制编码,并采用一维二值细胞自动机模型对问题的复杂求解过程进行描述[10],假设问题维度L,则萤火虫细胞列的长度为L,每个细胞的取值Q∈{0, 1},第i只萤火虫的第j维位置表示为xij。采用sign函数对细胞值进行分类,sign函数为:
| $ {s_{ij}} = \frac{1}{{1 + {{\rm{e}}^{ - {x_{ij}}}}}} $ | (6) |
则细胞自动机模型分类的表达示为:
| $ {X_{ij}}(t{\rm{ }} + 1) = \left\{ \begin{array}{l} 0, {\rm{ sign}}({x_{ij}}(t)) < 0.{\rm{ }}5\\ 1, {\rm{ sign}}({x_{ij}}(t)){\rm{ }} \ge {\rm{ }}0.{\rm{ }}5 \end{array} \right. $ | (7) |
式中:t代表的是时刻,萤火虫在0时刻需要遍历一遍分类模型,将位置信息转化为一个0/1序列,从而得到二元离散问题的解。
1.4 基于FA的测试用例集约简本文将FA算法应用于测试用例集约简,算法思想是将萤火虫位置转化为0/1序列,其中0代表舍弃这个测试用例,1代表保留这个测试用例,然后采用传统的贪婪算法得到解。萤火虫算法随机在空间中生成初始点,每个点通过二值细胞自动机模型转化为0或1,并利用萤火虫算法搜索能力强的特点遍历空间,向适应度最好的点收敛,更新位置和适应度,最后得到最好的约简效果。
本文FA的主要步骤为:1)初始化萤火虫算法的基本参数,包括萤火虫数目、位置维度、最大吸引度、步长因子、最大迭代次数;2)随机初始化位置,经过细胞模型分类机,生成细胞阵列,即0/1序列,并根据该序列计算该萤火虫的最大荧光度;3)计算群体中萤火虫之间的相对亮度和吸引度,并进行比较判断移动方向;4)更新萤火虫的位置,对最佳位置萤火虫进行随机移动。5)根据更新后的位置,重新生成细胞阵列,并根据新的0/1序列计算亮度;6)当到达最大搜索次数时,转到下一步;否则进行下一次迭代,迭代次数加1,转到步骤3;7)输出全局极值点,最优萤火虫,以及对应的0/1序列。
1.5 萤火虫算法描述Input: T //测试用例集
Input: C //测试开销
Output: xb //最优解
Begin:
Initialize variables pop, α, β, γ, max GAN
Itialize f=1, firefly population bp
Initialize fireflies′ positions xp
while f < maxGAN:
Find fitness for bp using T and C
Find best solution x′ in xp
if x′>xb:
Update xb
End if
for each i=1,2,…,pop:
for each j=1,2,…,pop:
ifi!=j and fitnessi < =fitnessj:
Update ximove to xj
else if i!= j and fitnessi==fitnessj:
Update xi random
End if
End for
End for
f=f+1
End while
return xb
End
2 实验验证及结果分析本文算法算法是在CPU为i5-4200 2.3 GHz,内存为12G DDR3内存下运行,算法的实现语言为Python 3.6。
2.1 测试数据集本文采用为了研究程序的数据流和控制流的覆盖准则的错误检测能力而提供的标准程序测试套件Siemens Suite[11]。在Siemens程序有7个标准C程序(printtokens、printtokens2、replace、schedule、schedule2、tca、totinfo)和对应的测试用例集合,以及执行这些用例的shell脚本。
2.2 实验探究首先进行测试需求的提取,本文中测试需求的为Siemens Suite中7个程序的分支覆盖,采用gcov[12]进行提取。本文的测试开销用的是每个测试用例执行的时间,总共执行50次后取得平均时间。
每个测试程序分别进行如下操作:在保证覆盖率为100%的情况下,分别在总测试集中随机选择50、200、1 000个测试用例和全集组成新的测试用例集,每组进行随机抽取20次。
本文复原了文献[13]中改进的GRE算法和贪心算法进行对比试验。在实验过程中,分2方面进行比较:1)统计在进行了相同次数的约简实验后,FA、GRE和贪心算法3个算法表现最优的次数,其中20次约简中效果最好的次数,包括约简效果相同实验;2)统计每组实验后约简后的ECRS值。经过实验,得到实验结果,如表 2所示:
| 表 2 实验结果 Table 2 Experimental results |
首先,对测试用例集约简来说,开销的降低是最重要的也是最直接的表现,本文用约简集开销成本(the execution cost of the representative set, ECRS)[14],即RS中的开销总表示约简效果,EECRS表示为:
| $ {E_{{\rm{ECRS}}}} = \sum\limits_{i \in Rs} {{C_{{\rm{cost}}}}(i)} $ | (8) |
式中:Ccost(i)代表第i个测试用例的开销,即ci,EECRS值越小代表约简效果越好。
本文通过与GRE算法和贪心算法进行对比,将3种方法的EECRS值分别进行统计,得到EECRS值分别为78.015、79.846和89.307 ms,萤火虫算法相对GRE算法的EECRS值减少2.3%,相对贪婪算法的EECRS值减少12.6%;从最优次数进行统计,3种算法的最优次数分别为390、293、20次(包括约简效果相同的情况)。从2方面均可以看出萤火虫算法的约简效果是较为可取。
接下来探讨本文测试方法在不同规模测试用例集中表现的差异。通过对7个被测程序的原始测试用例集随机生成不同大小的测试用例集进行约简,实验结果表明:规模为50、100、100和全集的情况下,FA约简得到最优效果的次数占比分别为52.86%、75.00%、65.00%和85.71%,由此可以看出,在较小的测试用例集约简中,萤火虫算法的效果比GRE算法差一些,而随着测试用例集的规模增大,萤火虫算法的效果在3个算法中是最好,具体数据如表 3所示。
| 表 3 不同规模下最优次数 Table 3 The optimal number of times on different scales |
之后讨论本文测试方法在不同工程的测试用例集表现效果。本文一共测试了7个不同的工程,对7个工程的测试结果进行统计,可以得到以下结果,如表 4所示。
| 表 4 不同被测程序下最优次数 Table 4 The optimal number of times under different testing programs |
在7个项目中最优次数占比分别为70%、82.5%、57.5%、76.25%、57.5%、58.75%、85%,均超过了50%,且只有replace和tcas 2个项目的最优次数小于GRE算法。因此总体来说,FA在不同的工程中都有着优异的表现,证明该算法有着良好的鲁棒性。
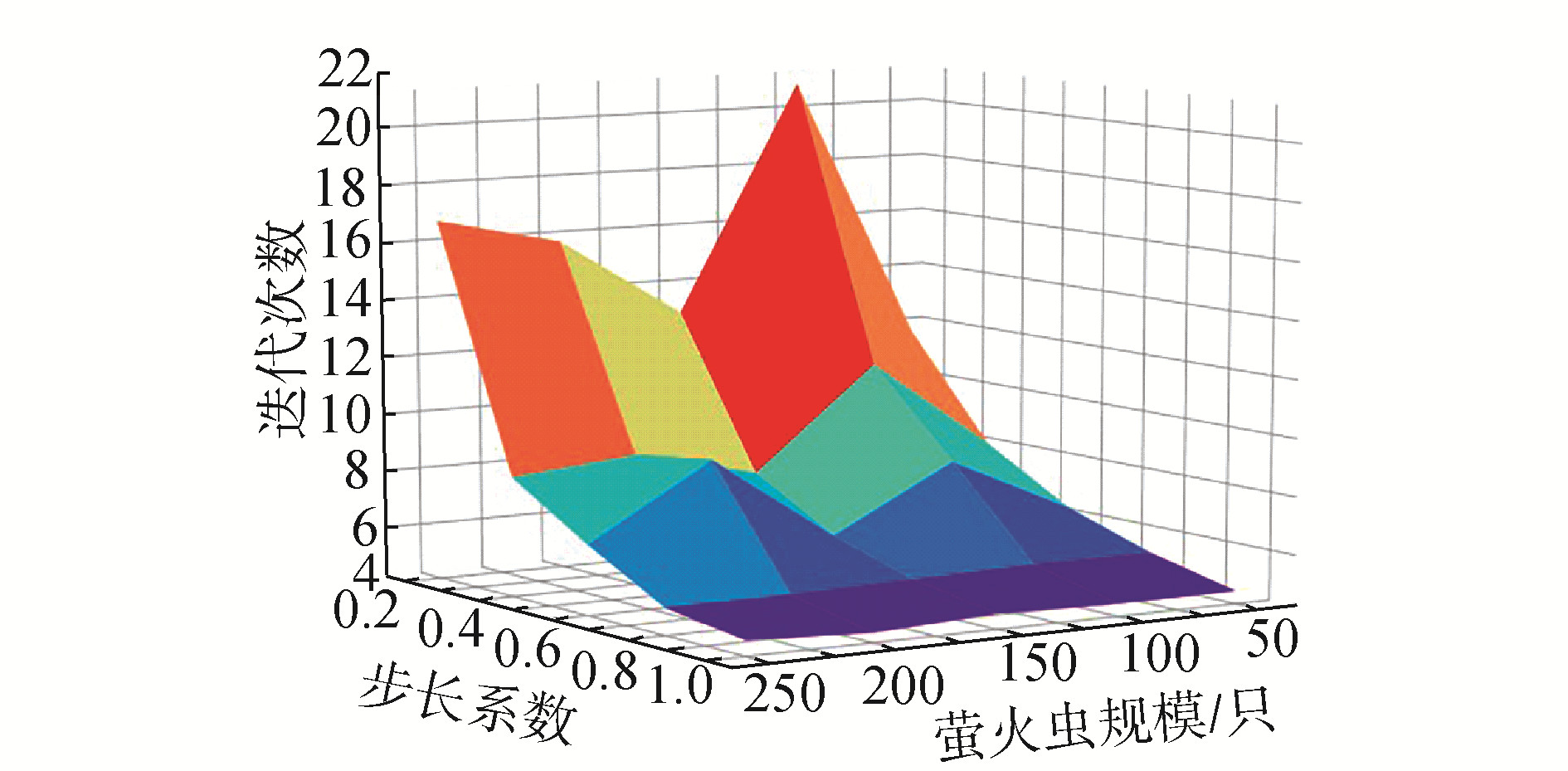
为了验证本文中萤火虫算法在不同参数配置下的求解效率,分别重复实验20次,获得各种配置组合下的平均迭代次数,其主要参数为萤火虫数目和步长系数,其结果如图 1所示。
|
Download:
|
| 图 1 不同参数下迭代次数 Fig. 1 The number of iterations with different parameters | |
从图中可以看出随着步长的减小,迭代次数从总的趋势上来看是上升的,而萤火虫数目则对迭代次数的影响不大,但是随着数目的提升会增强空间搜索的能力。
3 结论1) 本文的萤火虫算法能够在保证对测试需求的覆盖率的情况下,能够高效率、高质量的完成对测试用例集的约简,其效果优于传统的贪婪算法和改进后的GRE算法,同时在对不同规模和不同被测程序的实验中,证明该算法具有良好的鲁棒性。
2) 由于智能算法具有一定的随机性,在对相同实验数据进行约减时,有少量实验可能会陷入局部收敛,无法达到最优值。
后续的研究中,可以对萤火虫算法本身进行更多优化,提升算法的效率及鲁棒性。
| [1] |
GLIGORIC M, ELOUSSI L, MARINOV D. Practical regression test selection with dynamic file dependencies[C]//Proceedings of 2015 International Symposium on Software. Baltimore: ACM, 2015: 211-222.
(  0) 0)
|
| [2] |
HARROLD M J. Reduce, reuse, recycle, recover: techniques for improved regression testing[C]//Proceedings of 2009 IEEE International Conference on Software Maintenance. Edmonton: IEEE, 2009: 5.
(  0) 0)
|
| [3] |
HARROLD M J, GUPTA R SOFFA M L. A methodology for controlling the size of a test suite[J]. ACM transactions on software engineering and methodology, 1993, 2(3): 270-285. DOI:10.1145/152388.152391 (  0) 0)
|
| [4] |
周冲波, 楼俊钢, 程龙. 基于矩阵行列变换的测试用例约简算法[J]. 计算机应用研究, 2013, 30(3): 779-782. ZHOU Chongbo, LOU Jungang, CHENG Long. Test suites reduction based on matrix transformation[J]. Application research of computers, 2013, 30(3): 779-782. DOI:10.3969/j.issn.1001-3695.2013.03.035 (  0) 0)
|
| [5] |
CHVATAL V. A greedy heuristic for the set-covering problem[J]. Mathematics of operations research, 1979, 4(3): 233-235. DOI:10.1287/moor.4.3.233 (  0) 0)
|
| [6] |
CHEN T Y, LAU M F. A new heuristic for test suite reduction[J]. Information and software technology, 1998, 40(5/6): 347-354. (  0) 0)
|
| [7] |
全君林, 陆璐. 基于遗传算法测试用例集极小化研究[J]. 计算机工程与应用, 2009, 45(19): 58-61, 80. QUAN Junlin, LU Lu. Research test case suite minimization based on genetic algorithm[J]. Computer engineering and applications, 2009, 45(19): 58-61, 80. DOI:10.3778/j.issn.1002-8331.2009.19.017 (  0) 0)
|
| [8] |
张卫祥, 齐玉华, 李德治. 基于离散粒子群算法的测试用例优先排序[J]. 计算机应用, 2017, 37(1): 108-113, 169. ZHANG Weixiang, QI Yuhua, LI Dezhi. Test case prioritization based on discrete particle swarm optimization algorithm[J]. Journal of computer applications, 2017, 37(1): 108-113, 169. (  0) 0)
|
| [9] |
YANG Xueshe. Nature-inspired metaheuristic algorithms[M]. Beckington: Luniver Press, 2008.
(  0) 0)
|
| [10] |
程美英, 倪志伟, 朱旭辉. 融合粗糙集和扩散二元萤火虫算法的属性约简方法[J]. 系统工程与电子技术, 2016, 38(10): 2449-2456. CHENG Meiying, NI Zhiwei, ZHU Xuhui. Attribute reduction method combined with spread binary glowworm swarm optimization and rough set[J]. Systems engineering and electronics, 2016, 38(10): 2449-2456. DOI:10.3969/j.issn.1001-506X.2016.10.32 (  0) 0)
|
| [11] |
JEFFREY D, GUPTA N. Improving fault detection capability by selectively retaining test cases during test suite reduction[J]. IEEE transactions on software engineering, 2007, 33(2): 108-123. DOI:10.1109/TSE.2007.18 (  0) 0)
|
| [12] | |
| [13] |
LIN Chuti, TANG Kaiwei, WANG J S, et al. Empirically evaluating greedy-based test suite reduction methods at different levels of test suite complexity[J]. Science of computer programming, 2017, 150: 1-25. DOI:10.1016/j.scico.2017.05.004 (  0) 0)
|
| [14] |
WANG Shuai, ALI S, GOTLIEB A. Cost-effective test suite minimization in product lines using search techniques[J]. Journal of systems and software, 2015, 103: 370-391. DOI:10.1016/j.jss.2014.08.024 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


