2. 天津大学 天津市港口与海洋工程重点实验室, 天津 300072
2. Tianjin Key Laboratory of Port and Ocean Engineering, Tianjin University, Tianjin 300072, China
近年来,化石能源带来的环境问题日趋严重,风能作为可再生清洁能源受到人们的关注。陆上风机技术发展较为成熟,海上风机也因其优势得到迅猛发展,风机逐渐由陆地向海洋发展。出于经济效益考虑,水深超过50 m后宜采用浮式基础,包括半潜型、张力腿型(tension leg platform,TLP)、单柱式(SPAR)等。
针对浮式风机已有大量研究。Koo等[1]针对3种基础型式的风机进行模型试验。Shin等[2]针对OC3-Hywind浮式风机进行了模型试验并分析了风机系统运动特性。Jonkman等[3]开发了气动-水动-伺服-弹性全耦合浮式风机仿真程序,并分析了5 MW风机动力特性,Robertson等[4]运用该仿真程序对几种不同基础型式的浮式风机进行环境载荷分析。Ren等[5]基于计算流体动力学(computational fluid dynamics, CFD)方法计算并分析了风浪联合作用下时域运动响应。Li等[6]考虑下沉运动研究了二阶波浪力和气动载荷对TLP型浮式风机动力响应的影响。
目前大部分研究将浮式风机系统考虑为单刚体。本文将浮式风机系统处理为刚-柔耦合的多体系统,其中基础、轮毂为刚体,塔柱和叶片为柔性体,并考虑了叶片轴向变形对弯曲变形(挥舞和摆振)的影响。采用Jourdain速度变分原理,采用有限单元法离散柔性结构,推导浮式风机刚-柔耦合动力学方程,采用自动变步长的向后差分法求解微分-代数方程组,并依此编制Matlab仿真程序。建立了刚-柔耦合多体系统动力学方程,分析了浮式风力机系统的动力响应。
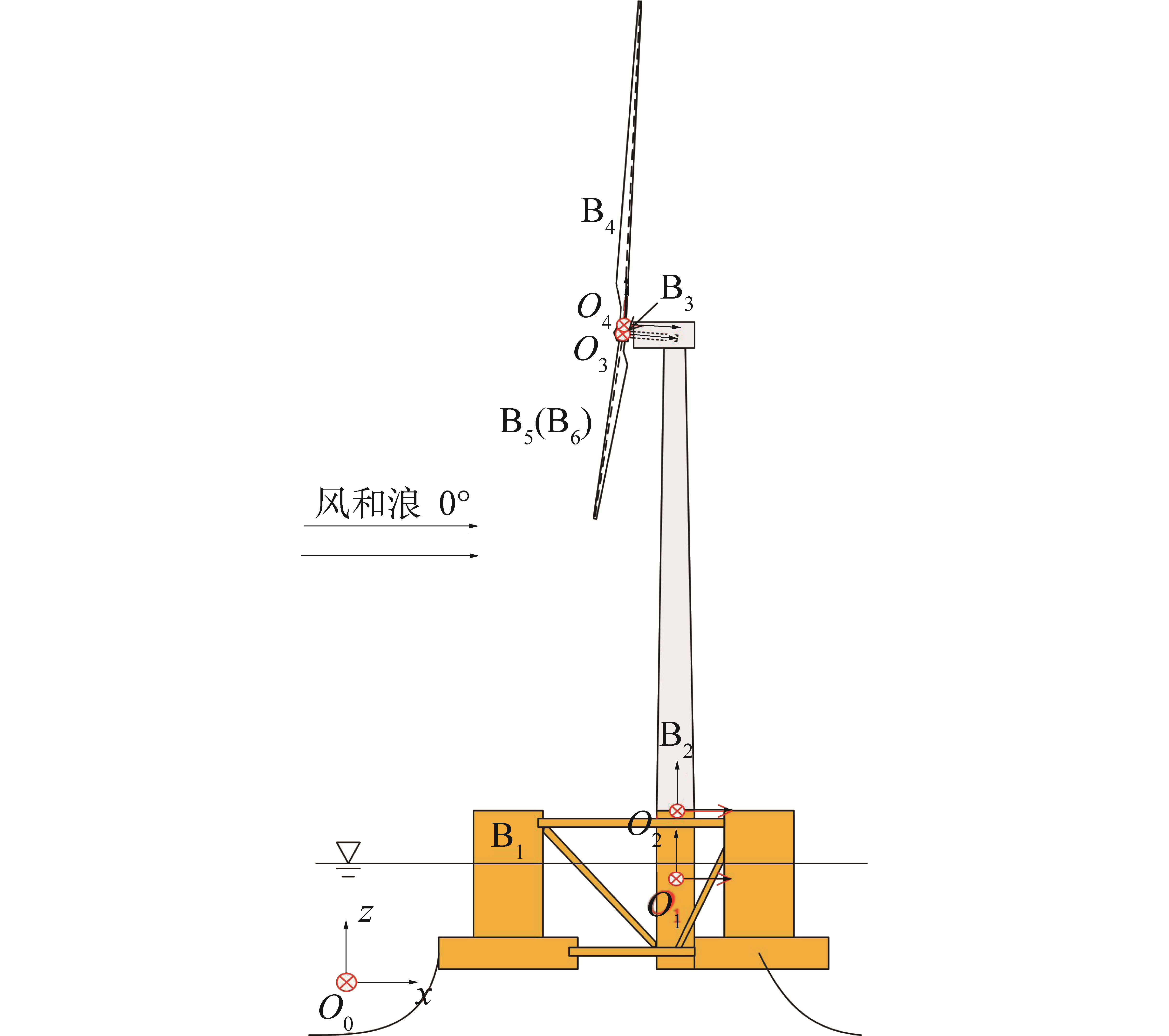
1 浮式风机系统动力学方程 1.1 坐标系的建立为了分析海上浮式风机系统耦合动力响应,本文简化整机系统,将机舱考虑为塔柱末端质量模型,整机系统分为浮式基础刚体(B1)、塔柱柔体(B2)、轮毂刚体(B3)、叶片柔体(B4、B5、B6)。其中刚体部分考虑6个自由度,引入如图 1所示坐标系:1)大地坐标系(O0, e(0)),惯性坐标系;2)浮式基础随体坐标系(O1, e(1)),固结于浮式基础重心;3)塔柱浮动坐标系(O2, e(2)),固结塔柱底端,描述塔柱变形;4)轮毂随体坐标系(O3, e(3)),固结于轮毂中心,随轮毂转动;5)叶片浮动坐标系(O4, e(4))、(O5, e(5))、(O6, e(6)),固结于叶片根部,描述叶片变形。
|
Download:
|
| 图 1 浮式风机示意 Fig. 1 Schematic diagram of floating wind turbine | |
风机系统各体之间的转动位移采用卡尔丹角描述,即绕x轴转动角α、绕y轴转动角β、绕z轴转动角γ,表征转动关系的方向余弦矩阵为[7]:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}\beta {\rm{c}}\gamma }&{ - {\rm{c}}\beta {\rm{s}}\gamma }&{{\rm{s}}\beta }\\ {{\rm{c}}\alpha {\rm{s}}\gamma + {\rm{s}}\alpha {\rm{s}}\beta {\rm{c}}\gamma }&{{\rm{c}}\alpha {\rm{c}}\gamma - {\rm{s}}\alpha {\rm{s}}\beta {\rm{s}}\gamma }&{ - {\rm{s}}\alpha {\rm{c}}\beta }\\ {{\rm{s}}\alpha {\rm{s}}\gamma - {\rm{c}}\alpha {\rm{s}}\beta {\rm{c}}\gamma }&{{\rm{s}}\alpha {\rm{c}}\gamma + {\rm{c}}\alpha {\rm{s}}\beta {\rm{s}}\gamma }&{{\rm{c}}\alpha {\rm{c}}\beta } \end{array}} \right] $ | (1) |
式中:c表示cos;s表示sin。
角速度ω表示在随体坐标下坐标列阵,可用相对惯性基转动角的导数表示,即:
| $ \mathit{\boldsymbol{\omega }} = \mathit{\boldsymbol{D\dot \theta }} $ | (2) |
式中系数矩阵D和广义坐标
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}\beta {\rm{c}}\gamma }&{{\rm{s}}\gamma }&0\\ { - {\rm{c}}\beta {\rm{s}}\gamma }&{{\rm{c}}\gamma }&0\\ {{\rm{s}}\beta }&0&1 \end{array}} \right],\mathit{\boldsymbol{\dot \theta }} = \left[ {\begin{array}{*{20}{c}} {\dot \alpha }\\ {\dot \beta }\\ {\dot \gamma } \end{array}} \right] $ |
角加速度
| $ \mathit{\boldsymbol{\dot \omega }} = \mathit{\boldsymbol{D\ddot \theta }} + \mathit{\boldsymbol{\dot D\dot \theta }} $ | (3) |
式中系数矩阵
| $ \mathit{\boldsymbol{\dot D}} = \left[ {\begin{array}{*{20}{c}} { - \dot \beta {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}\beta {\rm{c}}\gamma - \dot \gamma {\rm{c}}\beta {\rm{s}}\gamma {\kern 1pt} }&{\dot \gamma {\rm{c}}\gamma }&0\\ {\dot \beta {\rm{s}}\beta {\rm{s}}\gamma - \dot \gamma {\rm{c}}\beta {\rm{c}}\gamma }&{ - \dot \gamma {\rm{s}}\gamma }&0\\ {\dot \beta {\rm{c}}\beta }&0&0 \end{array}} \right],\quad \mathit{\boldsymbol{\ddot \theta }} = \left[ {\begin{array}{*{20}{c}} {\ddot \alpha }\\ {\ddot \beta }\\ {\ddot \gamma } \end{array}} \right] $ |
设r0为柔性梁浮动基到惯性基的矢径,ρ为柔性梁上任意点k相对浮动基的矢径,ρ0为未变形时k点关于浮动基的矢径,u为柔性梁关于浮动基的弹性位移,有:
| $ {\mathit{\boldsymbol{r}} = {\mathit{\boldsymbol{r}}_0} + \mathit{\boldsymbol{\rho }}} $ | (4) |
| $ {\mathit{\boldsymbol{\rho }} = {\mathit{\boldsymbol{\rho }}_0} + \mathit{\boldsymbol{u}}} $ | (5) |
因此,柔性梁上k点关于惯性基的速度为:
| $ ^{0}{\mathit{\boldsymbol{\dot{r} }}}{{=}^{0}}{{{\mathit{\boldsymbol{\dot{r} }}}}_{0}}{{+}^{\text{b}}}{\mathit{\boldsymbol{{ }\!\!\omega\!\!\text{ } }}}{{\times }^{\text{b}}}{\mathit{\boldsymbol{{ }\!\!\rho\!\!\text{ } }}}{{+}^{\text{b}}}\overset{° }{{\mathit{\boldsymbol{u }}}}\, $ | (6) |
式中:0()表示惯性基;b()表示浮动基;°表示对浮动基的局部导数。
柔性梁上k点关于惯性基的加速度为:
| $ ^{0}{\mathit{\boldsymbol{\ddot{r} }}}{{=}^{0}}{{{\mathit{\boldsymbol{\ddot{r} }}}}_{0}}{{+}^{\text{b}}}{\mathit{\boldsymbol{\dot{\omega } }}}{{\times }^{\text{b}}}{\mathit{\boldsymbol{\rho }}} {{+}^{\text{b}}}{\mathit{\boldsymbol{u }}}{{+}^{\text{b}}}{\mathit{\boldsymbol{\omega }}}{{\times }^{\text{b}}}{\mathit{\boldsymbol{\omega }}} \times {{{\mathit{\boldsymbol{\rho }}} }^{\text{b}}}+{{2}^{\text{b}}}{\mathit{\boldsymbol{\omega }}} {{\times }^{\text{b}}}\overset{° }{{\mathit{\boldsymbol{u }}}} $ | (7) |
设ui(i=1, 2, 3)为k点的变形位移在浮动基的坐标分量,根据平断面假设ui(i=1, 2, 3)可以用中线上对应点k0的变形位移wi(i=1, 2, 3)表示:
| $ \left\{ {\begin{array}{*{20}{l}} {{u_1} = {w_1} - y\frac{{\partial {w_2}}}{{\partial x}} - z\frac{{\partial {w_3}}}{{\partial x}} + {u_g}}\\ {{u_2} = {w_2}}\\ {{u_3} = {w_3}} \end{array}} \right. $ | (8) |
式中,在小变形假设下,考虑k点的纵向变形位移的二次耦合项[8]:
| $ {u_g} = - \int_0^x {\frac{1}{2}} \left[ {{{\left( {\frac{{{\rm{d}}{w_2}}}{{{\rm{d}}\xi }}} \right)}^2} + {{\left( {\frac{{{\rm{d}}{w_3}}}{{{\rm{d}}\xi }}} \right)}^2}} \right]{\rm{d}}\xi $ |
对于作大范围运动的刚-柔耦合动力学系统,二次耦合项对刚度项的贡献不可不计。就风力机旋转风轮而言,不考虑二次耦合项可能导致数值仿真结果发散。
根据连续介质力学理论,k点处的纵向正应变为:
| $ \varepsilon = \frac{{\partial {w_1}}}{{\partial x}} - y\frac{{{\partial ^2}{w_2}}}{{\partial {x^2}}} - z\frac{{{\partial ^2}{w_3}}}{{\partial {x^2}}} $ | (9) |
不计剪切及扭转效应的柔性梁弹性虚功率为:
| $ \begin{array}{*{20}{l}} {\delta P = \int_0^l {\int_A {\hat \rho } } \delta \dot \varepsilon E\varepsilon {\rm{d}}A{\rm{d}}x = \int_0^l E A\delta \left( {\frac{{\partial {{\dot w}_1}}}{{\partial x}}} \right)\frac{{\partial {w_1}}}{{\partial x}}{\rm{d}}x + }\\ {\int_0^l E {I_{zz}}\delta \left( {\frac{{{\partial ^2}{{\dot w}_2}}}{{\partial {x^2}}}} \right)\frac{{{\partial ^2}{w_2}}}{{\partial {x^2}}}{\rm{d}}x + \int_0^l E {I_{yy}}\delta \left( {\frac{{{\partial ^2}{{\dot w}_3}}}{{\partial {x^2}}}} \right)\frac{{{\partial ^2}{w_3}}}{{\partial {x^2}}}{\rm{d}}x} \end{array} $ | (10) |
目前,变形体的离散技术大致可分为3类:假设模态法、有限元法和部件模态综合法[9]。为了反映旋转叶片的真实振型和频率,本文采用有限元法离散塔柱和叶片。
设单元j长度为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{N}}_{j,1}}(\bar x) = \left[ {\begin{array}{*{20}{l}} {{a_1}}&0&0&0&0&{{a_2}}&0&0&0&0 \end{array}} \right]}&{}\\ {{\mathit{\boldsymbol{N}}_{j,2}}(\bar x) = \left[ {\begin{array}{*{20}{l}} 0&{{b_1}}&{{b_2}}&0&0&0&{{b_3}}&{{b_4}}&0&0 \end{array}} \right]}&{}\\ {{\mathit{\boldsymbol{N}}_{j,3}}(\bar x) = \left[ {\begin{array}{*{20}{l}} 0&0&0&{{b_1}}&{{b_2}}&0&0&0&{{b_3}}&{{b_4}} \end{array}} \right]}&{} \end{array}} \right. $ | (11) |
其中:
| $ {{a_1} = 1 - \hat x,\quad {a_2} = \hat x,\quad {b_1} = 1 - 3{{\hat x}^2} + 2{{\hat x}^3},} $ |
| $ {{b_2} = {l_j}(\hat x - 2{{\hat x}^2} + {{\hat x}^3}),\quad {b_3} = 3{{\hat x}^2} - 2{{\hat x}^3},} $ |
| $ {{b_4} = {l_j}( - {{\hat x}^2} + {{\hat x}^3})} $ |
因此,中线上对应点k0的变形位移wi表示为:
| $ {\mathit{\boldsymbol{w}}_i} = {\mathit{\boldsymbol{N}}_{j,i}}(\bar x){\mathit{\boldsymbol{p}}_j},\quad i = 1,2,3 $ | (12) |
每个单元的节点变形位移列阵pj可通过布尔矩阵Bj及边界条件转化矩阵R从总体变形位移列阵p中“拾取”,即:
| $ {\mathit{\boldsymbol{p}}_i} = {\mathit{\boldsymbol{B}}_j}\mathit{\boldsymbol{Rp}} $ | (13) |
式中:布尔矩阵Bj和边界条件转化矩阵R分别为:
| $ {\mathit{\boldsymbol{B}}_j} = {\left[ {\begin{array}{*{20}{c}} {\bf{0}}&{\bf{0}}& \cdots &{{\mathit{\boldsymbol{I}}_{5 \times 5}}}& \cdots &{\bf{0}}& \cdots &{\bf{0}}\\ {\bf{0}}&{\bf{0}}& \cdots &{\bf{0}}& \cdots &{{\mathit{\boldsymbol{I}}_{5 \times 5}}}& \cdots &{\bf{0}} \end{array}} \right]_{10 \times 5(n + 1)}} $ |
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{l}} {{{\bf{0}}_{5 \times 5n}}}\\ {{\mathit{\boldsymbol{I}}_{5n \times 5n}}} \end{array}} \right] $ |
本文柔性梁均为一端固支的悬臂梁,因此节点1的位移全为0,总体变形位移列阵p表示为:
| $ \begin{array}{l} \mathit{\boldsymbol{p}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{w}}_{12}}}&{{\mathit{\boldsymbol{w}}_{22}}}&{{\mathit{\boldsymbol{\theta }}_{22}}}&{{\mathit{\boldsymbol{w}}_{32}}}&{{\mathit{\boldsymbol{\theta }}_{32}}}& \cdots &{{\mathit{\boldsymbol{w}}_{1n + 1}}}&{{\mathit{\boldsymbol{w}}_{2n + 1}}} \end{array}} \right.\\ {\left. {\begin{array}{*{20}{c}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{\theta }}_{2n + 1}}}&{{\mathit{\boldsymbol{w}}_{3n + 1}}}&{{\mathit{\boldsymbol{\theta }}_{3n + 1}}} \end{array}} \right]^{\rm{T}}} \end{array} $ | (14) |
式中:元素下标第1位表示方向,第2位表示节点数;n为单元数。
将式(11)~(13)代入式(8),并令Ni=Nj, i BjR,则k点相对浮动基的变形位移可表示为
| $ \mathit{\boldsymbol{u}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{N}}_1}\mathit{\boldsymbol{p}} - y\frac{{\partial {\mathit{\boldsymbol{N}}_2}}}{{\partial x}}\mathit{\boldsymbol{p}} - z\frac{{\partial {\mathit{\boldsymbol{N}}_3}}}{{\partial x}}\mathit{\boldsymbol{p}} - \frac{1}{2}{\mathit{\boldsymbol{p}}^{\rm{T}}}\mathit{\boldsymbol{Hp}}}\\ {{\mathit{\boldsymbol{N}}_2}\mathit{\boldsymbol{p}}}\\ {{\mathit{\boldsymbol{N}}_3}\mathit{\boldsymbol{p}}} \end{array}} \right] $ | (15) |
式中耦合形函数为[10]:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}} = {\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{B}}_j^{\rm{T}}\int_0^{\bar x} {\left( {\frac{{\partial \mathit{\boldsymbol{N}}_{j,2}^{\rm{T}}}}{{\partial \bar x}}\frac{{\partial \mathit{\boldsymbol{N}}_{j,2}^{\rm{T}}}}{{\partial \bar x}} + \frac{{\partial \mathit{\boldsymbol{N}}_{j,3}^{\rm{T}}}}{{\partial \bar x}}\frac{{\partial {\mathit{\boldsymbol{N}}_{j,3}}}}{{\partial \bar x}}} \right)} {\rm{d}}\bar x{\mathit{\boldsymbol{B}}_j}\mathit{\boldsymbol{R}} + }\\ {\sum\limits_{i = 1}^{j - 1} {{\mathit{\boldsymbol{R}}^{\rm{T}}}} \mathit{\boldsymbol{B}}_i^{\rm{T}}\int_0^{{l_i}} {\left( {\frac{{\partial \mathit{\boldsymbol{N}}_{j,2}^{\rm{T}}}}{{\partial \bar x}}\frac{{\partial {\mathit{\boldsymbol{N}}_{j,2}}}}{{\partial \bar x}} + \frac{{\partial \mathit{\boldsymbol{N}}_{j,3}^{\rm{T}}}}{{\partial \bar x}}\frac{{\partial {\mathit{\boldsymbol{N}}_{j,3}}}}{{\partial \bar x}}} \right)} {\rm{d}}\bar x{\mathit{\boldsymbol{B}}_j}\mathit{\boldsymbol{R}}} \end{array} $ |
本文通过Jourdain速度变分原理推导空间动力学方程,其形式为:
| $ \int_V \delta \frac{{^0{\rm{d}}{\mathit{\boldsymbol{r}}^{\rm{T}}}}}{{{\rm{d}}t}}\hat \rho \frac{{{{\rm{d}}^2}\mathit{\boldsymbol{r}}}}{{{\rm{d}}{t^2}}}{\rm{d}}V + \delta P - \delta {W_e} = 0 $ | (16) |
式中δWe为外力虚功率。
设广义坐标列阵为:
| $ \mathit{\boldsymbol{q}} = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{r}}_0^{\rm{T}}}&{{\mathit{\boldsymbol{\theta }}^{\rm{T}}}}&{{\mathit{\boldsymbol{p}}^{\rm{T}}}} \end{array}} \right]^{\rm{T}}} $ | (17) |
现代大型风力机都安装伺服控制系统,对于变桨调节的风力机在未达到额定风速之前,以输出功率最大的转速运行,当达到额定风速之后便以额定转速运行。因此需要在轮毂与塔柱之间施加约束条件形如下,其他连接处设为刚性固定:
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_2} = \left[ {\begin{array}{*{20}{c}} {^0{\mathit{\boldsymbol{r}}_{{\rm{0t}}}} + {\mathit{\boldsymbol{A}}_{\rm{t}}}{\mathit{\boldsymbol{\rho }}_{\rm{t}}}{ - ^0}{\mathit{\boldsymbol{r}}_{{\rm{0h}}}}}\\ {{\mathit{\boldsymbol{\theta }}_{\rm{t}}} + {{\left( {\begin{array}{*{20}{c}} {\omega t}&0&0 \end{array}} \right)}^{\rm{T}}} - {\mathit{\boldsymbol{\theta }}_{\rm{h}}}} \end{array}} \right] $ | (18) |
式中:下标t代表塔柱;h代表轮毂;At为塔柱浮动基相对惯性基的余弦矩阵;ρt为考虑塔柱变形的塔柱浮动基到轮毂浮动基的矢径;ω为风轮转速。
因此,约束方程可表示为:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1^{\rm{T}}}&{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_2^{\rm{T}}}&{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_3^{\rm{T}}}&{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_4^{\rm{T}}}&{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_5^{\rm{T}}{]^{\rm{T}}} = 0} \end{array}} \right. $ | (19) |
将式(6)、(7)、(11)、(15)代入动力学方程式(16),对于刚体方程中的变形位移和弹性虚功率为零,并考虑约束方程得到形如下式的第一类拉格朗日方程:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{M\ddot q}} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_q^{\rm{T}}\mathit{\boldsymbol{\lambda }} = \mathit{\boldsymbol{Q}}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_q}\mathit{\boldsymbol{\ddot q}} = - [{{({\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_q}\mathit{\boldsymbol{\dot q}})}_q}\mathit{\boldsymbol{\dot q}} + 2{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{qt}}\mathit{\boldsymbol{\dot q}} + {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{tt}}]} \end{array}} \right. $ | (20) |
式中:()q表示Jacobian矩阵;()t表示对t求偏导数;λ为拉格朗日乘子;M为广义质量阵;Q为广义力阵。式(20)是指标为1的微分-代数方程组,采用传统增广法求解,消去拉格朗日乘子,考虑位置约束和速度约束的违约问题,并采用向后差分法(backward differentiation formulas, BDFs)求解增广后的常微分方程组。本文数值求解为变步长积分,积分精度为10-6。
2 系统载荷计算 2.1 风机叶片非定常气动载荷本文将经典叶素动量理论(blade element momentum, BEM)扩展到局部,计算每个叶素的非定常气动载荷,考虑风剪切、塔影效应、叶尖轮毂损失因子及Glauert修正,在此基础上引入尾流倾斜模型、B-L动态失速模型,经过修正的BEM能计算得到较为准确的气动载荷,满足本文计算要求。
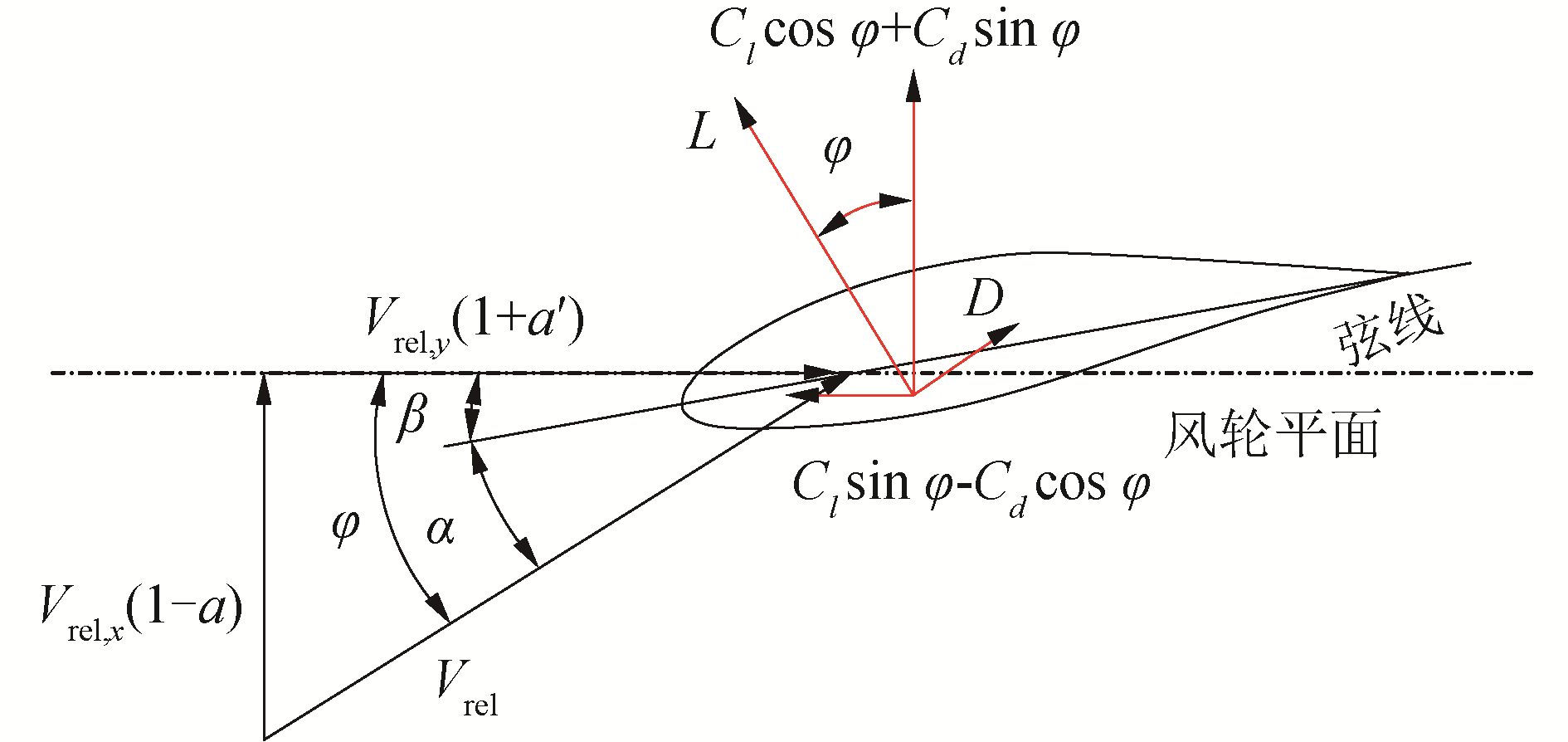
| $ {\rm{tan}}{\kern 1pt} {\kern 1pt} \varphi = \frac{{{V_{{\rm{rel}},x}}(1 - a)}}{{{V_{{\rm{rel}},y}}(1 + {a^\prime })}} $ | (21) |
|
Download:
|
| 图 2 叶素速度及作用力三角关系 Fig. 2 The trigonometric relationship of velocity and force of blade element | |
式中:Vrel, x、Vrel, y分别为来流风速叠加叶片运动速度的轴向和周向速度分量。
针对每个叶素,轴向诱导因子和切向诱导因子可表示为:
| $ {a = {{\left[ {1 + \frac{{8F\pi r{\rm{si}}{{\rm{n}}^2}\varphi }}{{Bc({C_l}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi + {C_d}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi )}}} \right]}^{ - 1}}} $ | (22) |
| $ {{a^\prime } = {{\left[ { - 1 + \frac{{8F\pi r{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{Bc({C_l}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi - {C_d}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi )}}} \right]}^{ - 1}}} $ | (23) |
式中:B为叶片数;Cl、Cd为升阻系数;φ为入流角;F为叶尖/轮毂损失因子:
| $ \begin{array}{*{20}{l}} {F = \frac{4}{{{\pi ^2}}}{\rm{arccos}}\left( {{\rm{exp}}\left( {\frac{B}{2}\frac{{R - r}}{{r{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right)} \right) \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{arccos}}\left( {{\rm{exp}}\left( {\frac{B}{2}\frac{{r - {R_{{\rm{hub}}}}}}{{r{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right)} \right)} \end{array} $ | (24) |
式中:R为风轮半径;Rhub为轮毂半径。
Buhl基于Glauert修正模型,提出当a≥0.4时,推力系数及轴向诱导因子的表达式[12]为:
| $ {C_T} = \frac{8}{9} + \left( {4F - \frac{{40}}{9}} \right)a + \left( {\frac{{50}}{9} - 4F} \right){a^2} $ | (25) |
| $ a = \frac{{18F - 20 - 3\sqrt {{C_T}(50 - 36F) + 12F(3F - 4)} }}{{36F - 50}} $ | (26) |
以上推导过程基于来流风速正对风轮平面,当风轮发生偏航时,尾流将发生倾斜。对于海上浮式风机,当浮式基础发生艏摇,风轮平面发生偏航。因此,必须引入尾流倾斜模型对轴向诱导因子修正。
轴向诱导因子偏航修正可表示为:
| $ {a_{{\rm{skew}}}} = a\left[ {1 + \frac{{15\pi }}{{32}}\frac{r}{R}{\rm{tan}}\frac{\chi }{2}{\rm{cos}}(\theta - {\theta _0})} \right] $ | (27) |
式中:γ为偏航角;θ为风轮方位角;θ0为叶片指向尾流最深处时的方位角。
尾流倾角可用下式近似计算:
| $ \chi = (0.6a + 1)\gamma $ | (28) |
考虑风剪切及塔影效应,计算入流速度。风剪切模型可表示为:
| $ v(z) = {v_{\rm{H}}}{\left( {\frac{z}{H}} \right)^\eta } $ | (29) |
式中:H为轮毂高度;vH为轮毂处风速;η为风切变指数,通常取0.1~0.25。
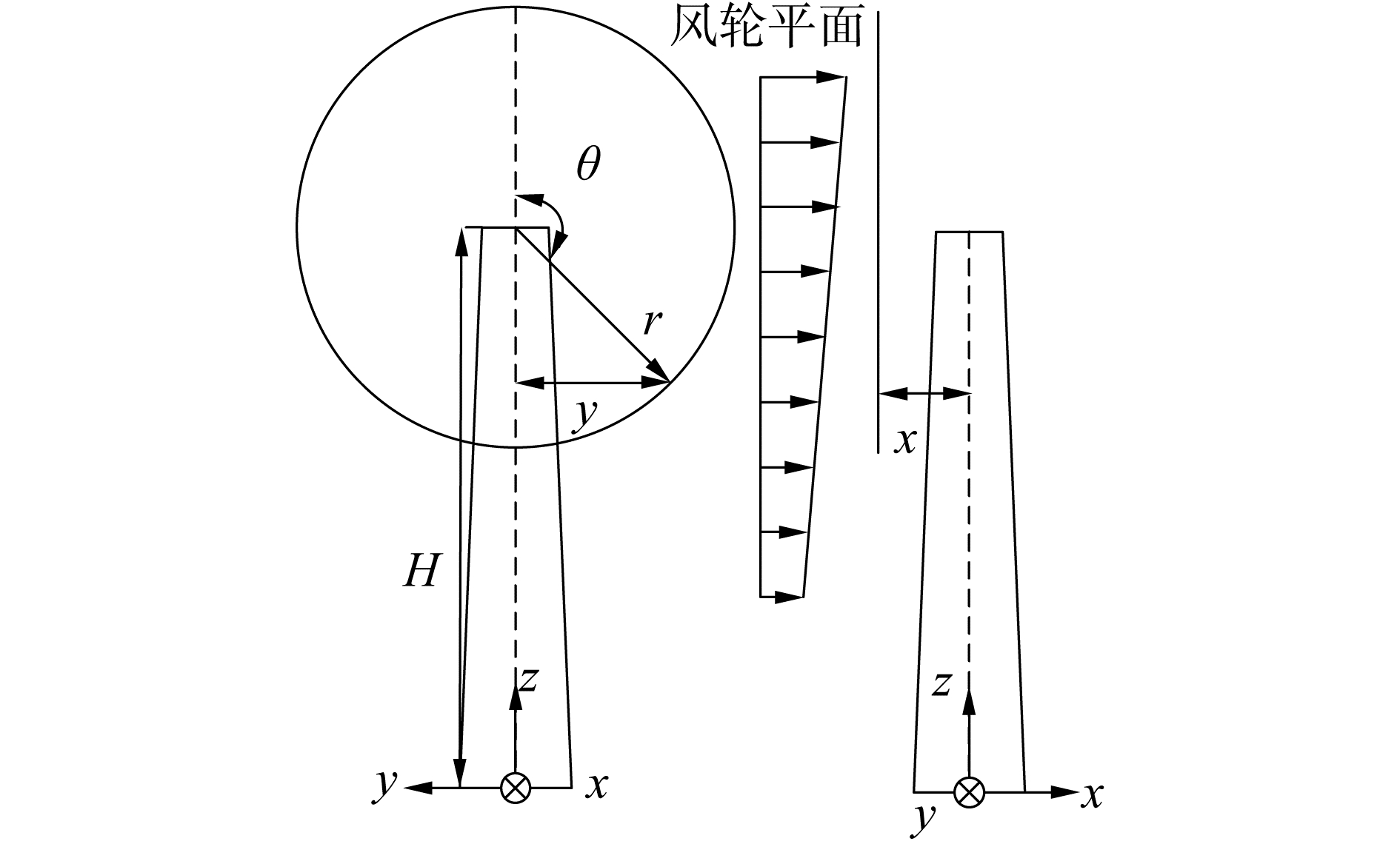
塔柱的存在影响了尾流分布,如图 3所示,对于上风型风力机可采用潜流模型[13]:
| $ A = 1 + {\left( {\frac{{{D_{\rm{T}}}}}{2}} \right)^2}\frac{{{y^2} - {x^2}}}{{{{({y^2} + {x^2})}^2}}} $ | (30) |
|
Download:
|
| 图 3 风剪切和塔影效应示意 Fig. 3 Schematic diagram of wind shear and tower shadow | |
式中:DT为叶素所在高度塔柱直径;x、y为叶素与塔柱中心的距离。式(30)在叶片处于轮毂中心以下,相对塔柱中心±60°区域内成立。当叶片处于轮毂中心之上,相对塔柱中心±60°区域内无塔影效应,其他区域修正为A(0.5-cos θ)+(0.5+cos θ),使得各区域平滑过渡。
因此,考虑风剪切和塔影效应后的来流速度可表示为:
| $ {U_\infty } = Av(z) $ | (31) |
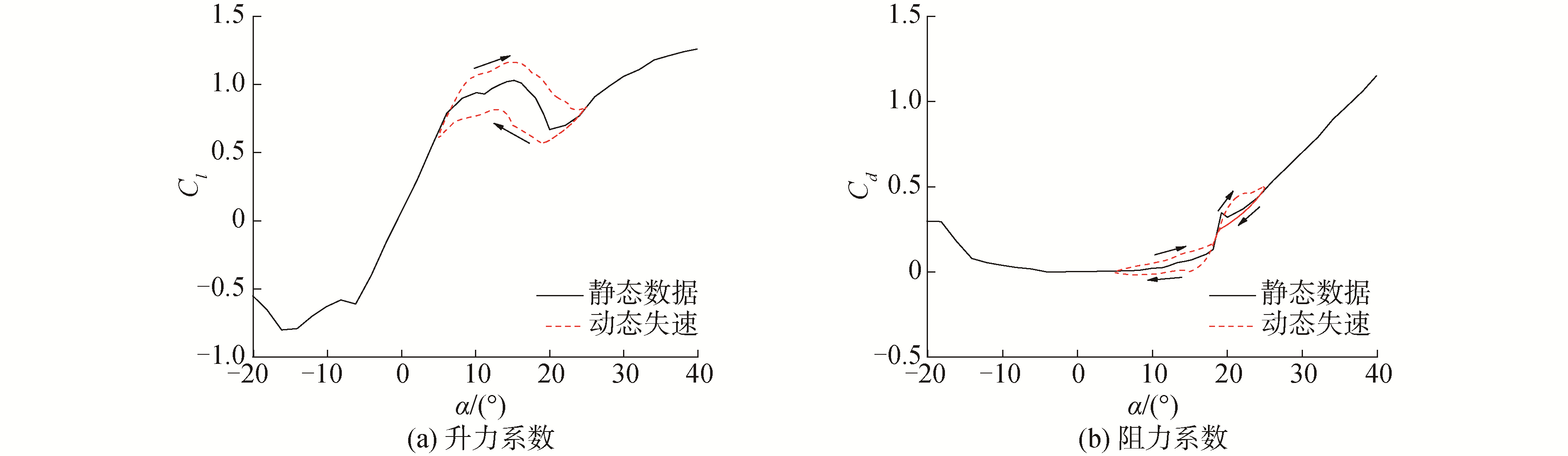
本文使用B-L动态失速模型进行动态失速的模拟,分为非定常附着流、尾缘流动分离及动态失速3个过程[14]。编制Matlab程序,模拟S809翼型动态失速过程,翼型攻角以正弦规律振动α=15+10sin(ωt),衰减频率k=0.051,马赫数M=0.11,并与静态风洞试验数据对比[15], 如图 4所示。
|
Download:
|
| 图 4 动态失速对升阻系数的影响 Fig. 4 The effect of dynamic stall on lift and drag coefficient | |
从图 4可以发现,动态失速体现在升力失速延迟,在失速区动态气动系数与静态数据有明显差异。攻角增加变化时,升力持续增加并且要大于静态升力数据;攻角回程阶段,升力小于静态升力数据,阻力系数也有类似的现象,攻角持续变化气动系数形成迟滞环。气动仿真时,基础的运动以及叶片自身变形使得翼型攻角持续变化,因此有必要考虑动态失速的影响。
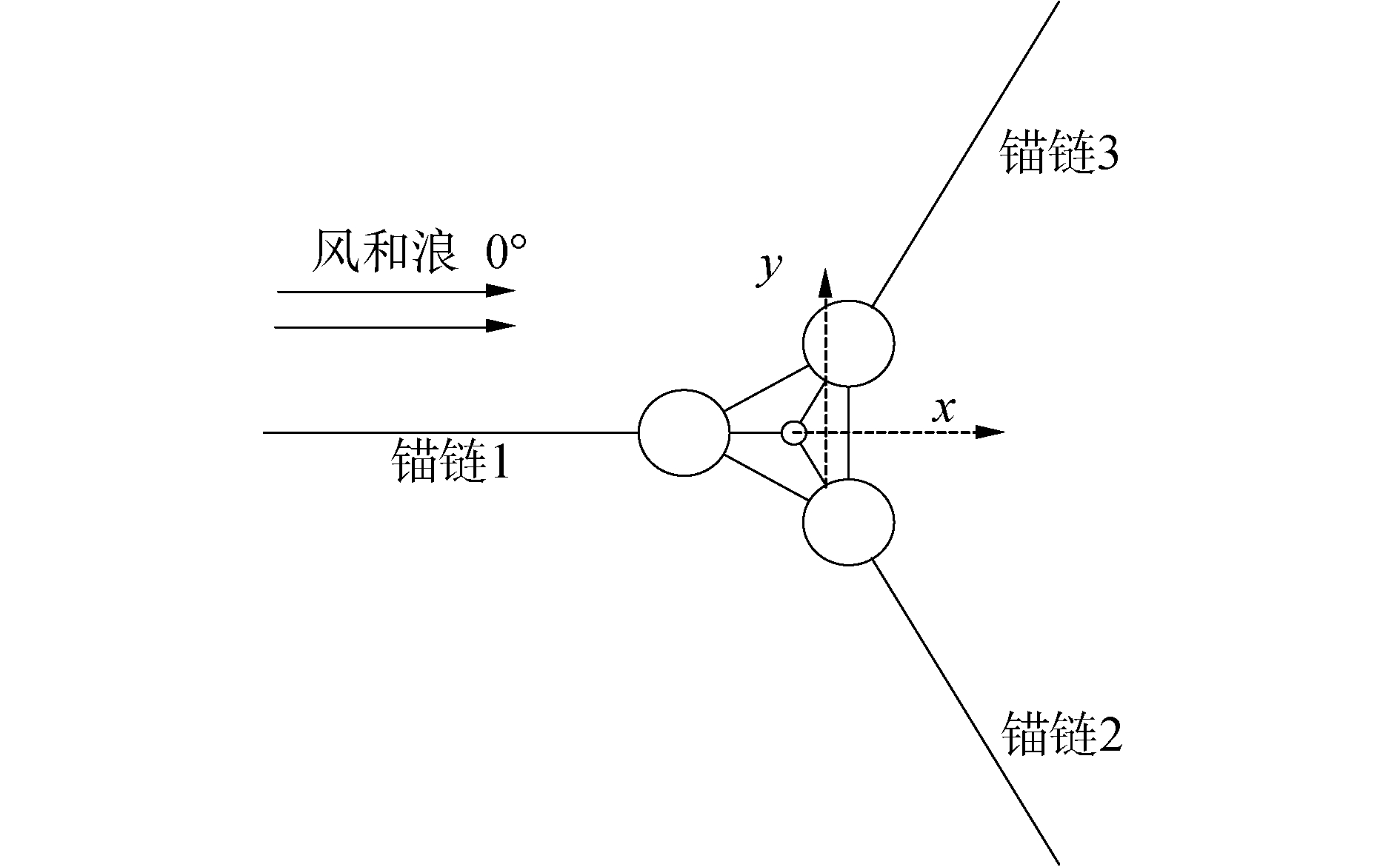
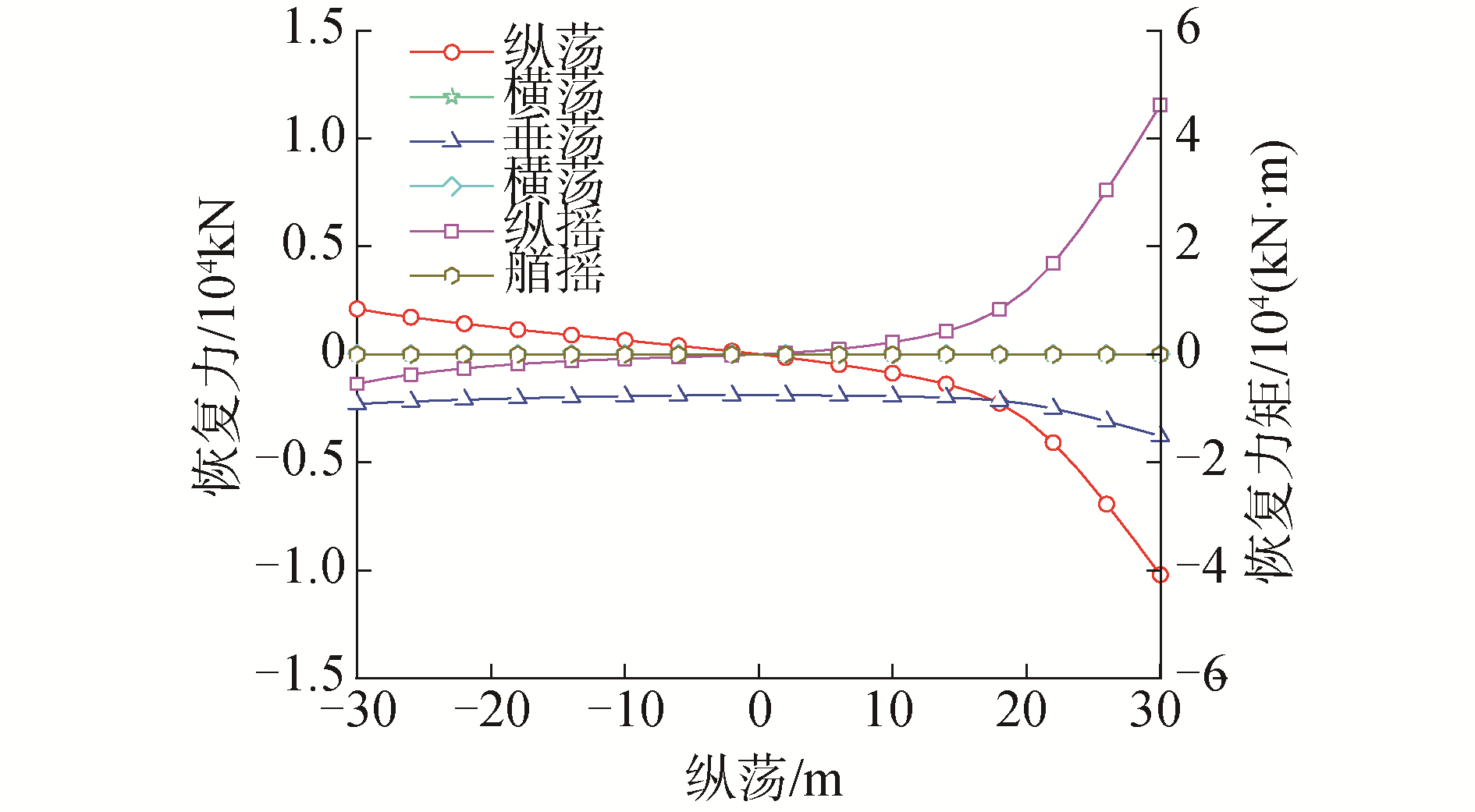
2.2 浮式基础系泊力/矩本文以外载荷的方式考虑系泊系统对浮式风机系统动力学方面的贡献。以浮式风力机OC4-DeepCwind为例,该风机为悬链线式系泊,如图 5。悬链线式系泊根据其形状,忽略水动力的影响,可通过悬链线方程快速估计系泊张力及系泊恢复力(矩)[16]。浮式基础六自由度系泊恢复力(矩)随纵荡位移变化趋势如图 6所示。
|
Download:
|
| 图 5 系泊系统示意 Fig. 5 Schematic diagram of mooring system | |
|
Download:
|
| 图 6 系泊六自由度恢复力和力矩 Fig. 6 Restoring force and moment of mooring system | |
在海洋工程中,小尺度构件用Morison方程计算,大尺度结构物通过三维势流理论计算。本文采用SESAM/Wadam模块进行水动力方面参数的计算,包括一阶波浪力传递函数、附连水质量、势流阻尼、静水恢复刚度。势流理论不计及粘性阻尼,工程中认为粘性阻尼可取临界阻尼β0的5%~8%,即:
| $ {\beta _0} = 2\sqrt {({\mathit{\boldsymbol{M}}_0} + {\mathit{\boldsymbol{M}}_a}) \times {\mathit{\boldsymbol{C}}_i}} $ | (32) |
式中:M0为浮式基础质量;Ma为浮式基础附连水质量;Ci为浮式基础第i自由度的静水恢复刚度。
浮式基础时域控制方程为:
| $ \begin{array}{*{20}{c}} {({\mathit{\boldsymbol{M}}_0} + {\mathit{\boldsymbol{A}}_\infty })\mathit{\boldsymbol{\ddot X}}(t) + \int_0^t h (t - \tau )\mathit{\boldsymbol{\dot X}}(t){\rm{d}}\tau + }\\ {\mathit{\boldsymbol{D\dot X}}(t) + (\mathit{\boldsymbol{K}}_{ij}^{{\rm{ lin }}} + {\mathit{\boldsymbol{C}}_{ij}})\mathit{\boldsymbol{X}}(t) = {\mathit{\boldsymbol{F}}_{\rm{w}}}(t)} \end{array} $ | (33) |
式中:A∞为频率无限大时附连水质量;h(t-τ)为时延函数;D为粘性阻尼系数;Kijlin为线性系泊恢复刚度;Fw(t)为时域波浪载荷。
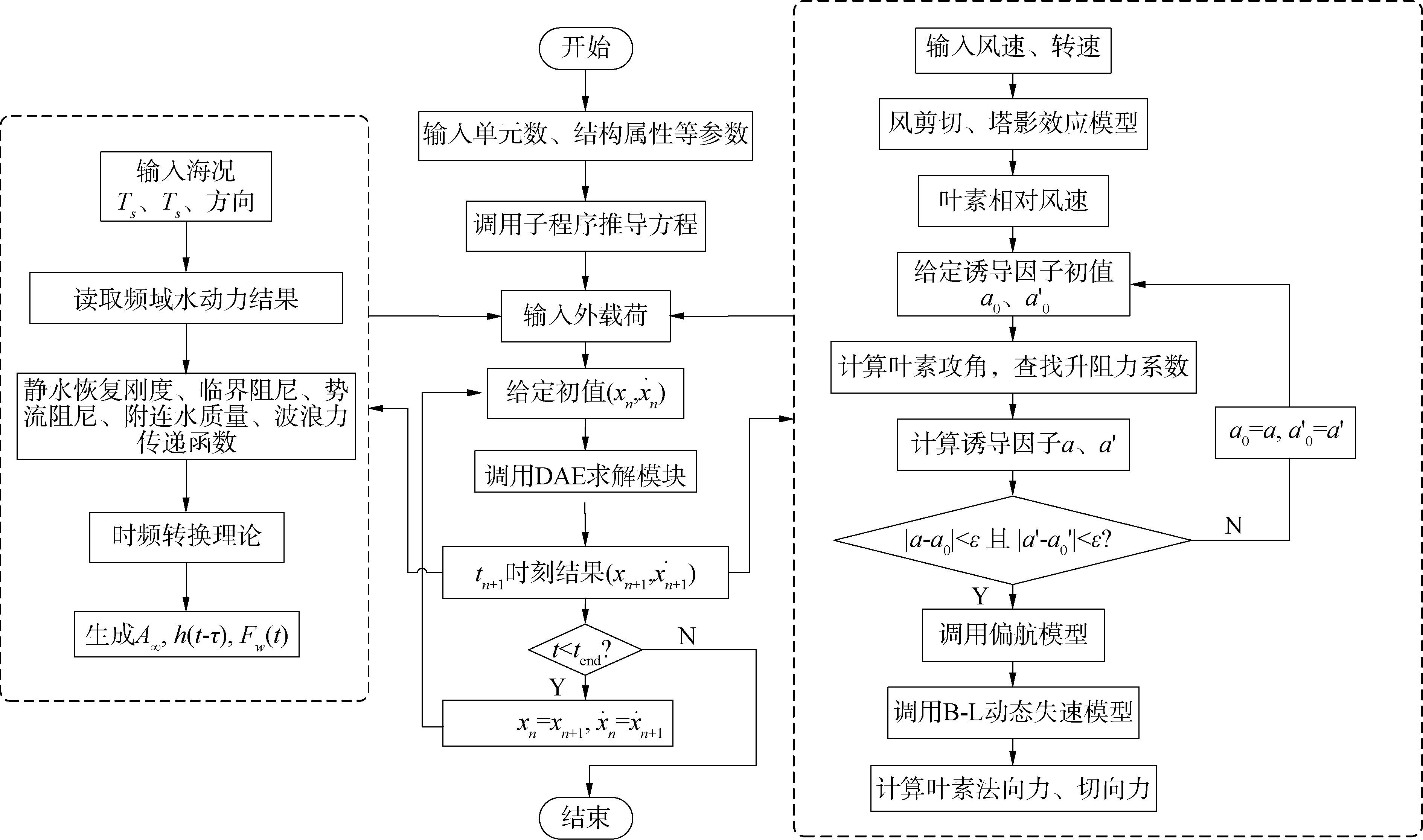
3 半潜式浮式风机算例分析本文以OC4-DeepCwind浮式风机系统为计算模型,相关参数可参考文献[17-18]。综合上述建模过程,可得到如图 7所示程序框图,并编制Matlab仿真程序。
|
Download:
|
| 图 7 仿真程序框图 Fig. 7 Simulation block diagram | |
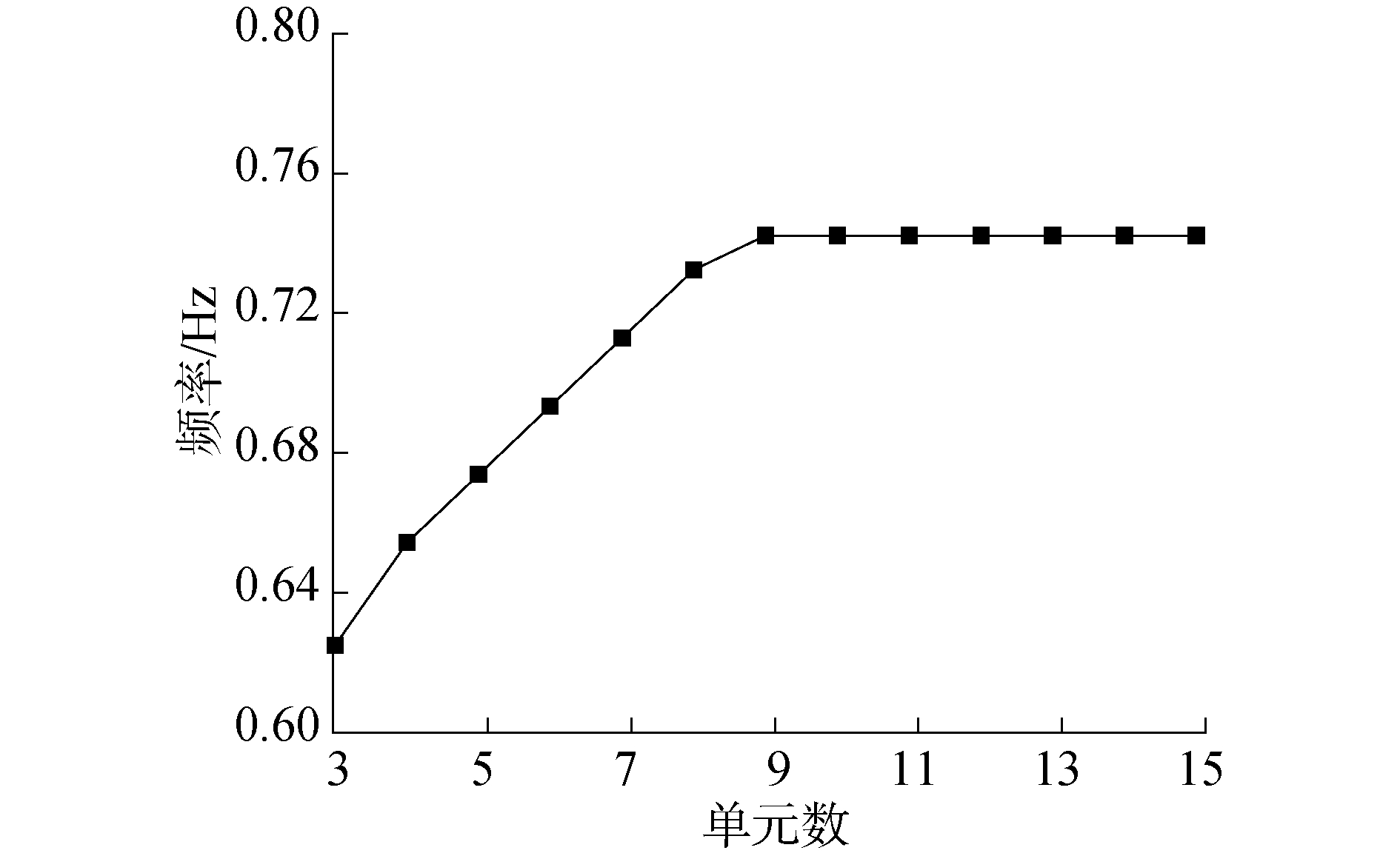
本文采用一次近似耦合模型,考虑二次耦合变形量,体现了叶片离心力和轴向惯性力对挥舞和摆振方向变形的影响,在动力刚度项中产生的附加耦合刚度项。考虑式(16)中δWe=0,且大范围运动已知,则方程退化为非惯性系下自由振动方程。图 8为单根叶片在转速为12.1 r/min时,划分不同单元数目计算一阶挥舞固有频率的结果。
|
Download:
|
| 图 8 验证本文方法单元收敛性 Fig. 8 Verification of the convergence of element | |
图 8结果显示,叶片划分至少9个单元就能得到收敛的计算结果。采用本文程序计算零转速下叶片自由振动,叶片划分10个单元,分析其固有频率,并与FAST和ADAMS计算结果对比[17],如表 1所示,本文程序结果与二者吻合较好。
| 表 1 本文程序结果验证 Table 1 Verification of results by computer program |
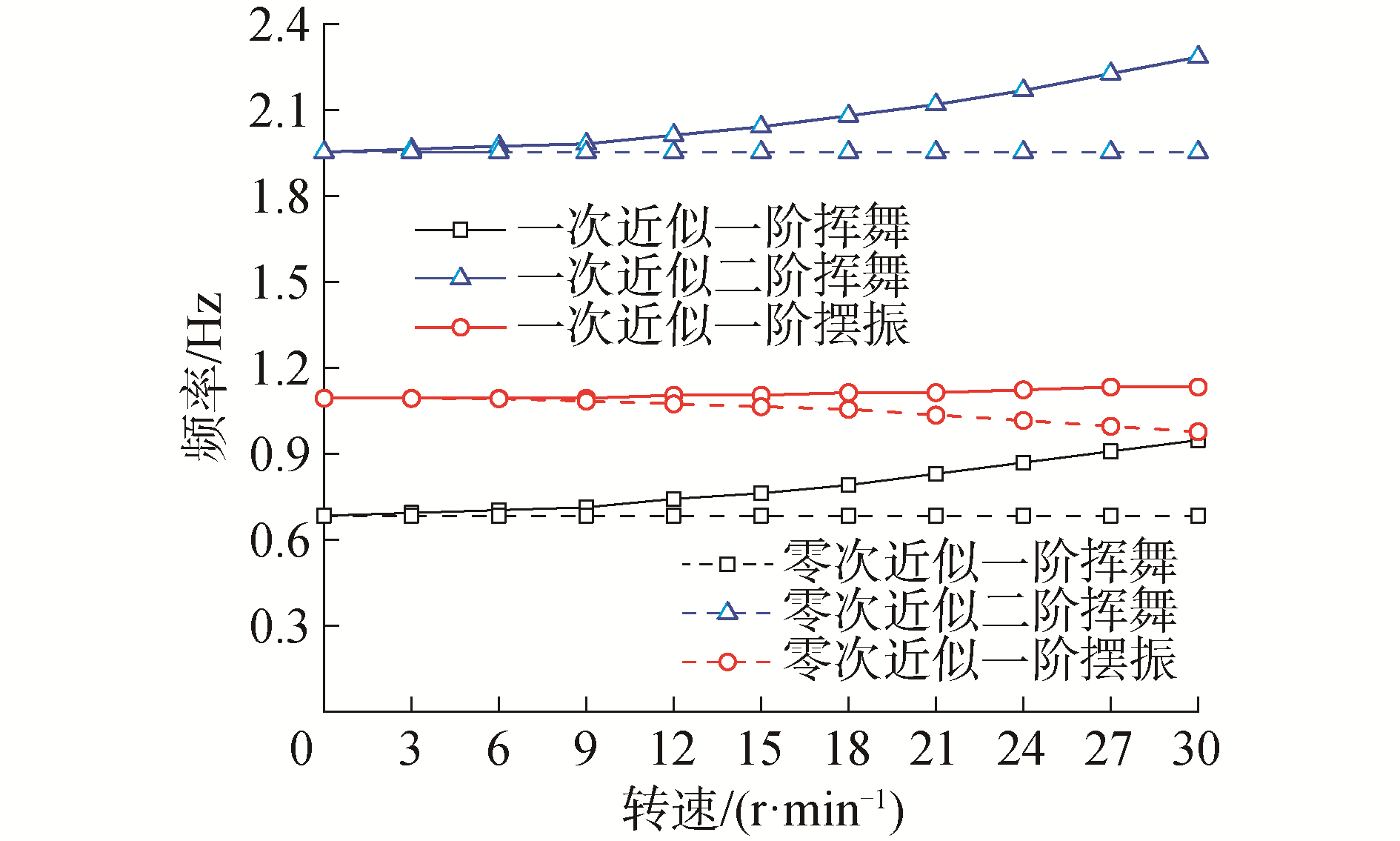
为了揭示叶片大范围运动产生的“动力刚化”现象,将浮式基础固定并且不考虑塔柱柔性变形,采用本文程序给定转速计算叶片自由振动,固有频率随转速变化如图 9所示。
|
Download:
|
| 图 9 叶片固有频率随转速变化关系 Fig. 9 The frequencies of blade vary with rotor speed | |
由图 9可以发现:一次近似耦合模型计算的挥舞和摆振方向固有频率均随着转速的增大而增加,并且转速越高,固有频率增大越快。固有频率的增大,反映出结构刚度的增大。而传统零次近似模型的摆振方向固有频率随转速的增大呈减小的趋势,挥舞方向的刚度不随转速变化。这是因为挥舞方向在旋转平面外,摆振方向在旋转平面内,传统零次近似模型忽略始终为正的附加耦合刚度项。一次近似耦合模型考虑了附加耦合刚度项,保证了旋转叶片各方向的刚度不随转速增大而减小,旋转叶片出现了“动力刚化”现象。
3.2 浮式风机系统动力响应在额定工况下(转速12.1 r/min,风速11.4 m/s),选定海况规则波波高6 m、周期10 s,波浪和风向均为0°,采用本文程序计算浮式风机系统动力响应。
图 10为叶尖挥舞和摆振方向变形,从图中可以看出,一次近似耦合模型的变形量明显小于传统零次近似模型,结果与上述分析的旋转叶片特性相对应,考虑了叶片的“动力刚化”效应。如果采用传统零次近似模型,随着转速不断增大,叶片摆振方向的刚度不断减小,有可能导致叶片变形的仿真失败,与实际情况不符。

|
Download:
|
| 图 10 叶尖变形时域曲线 Fig. 10 Blade tip deformation in time domain | |
|
Download:
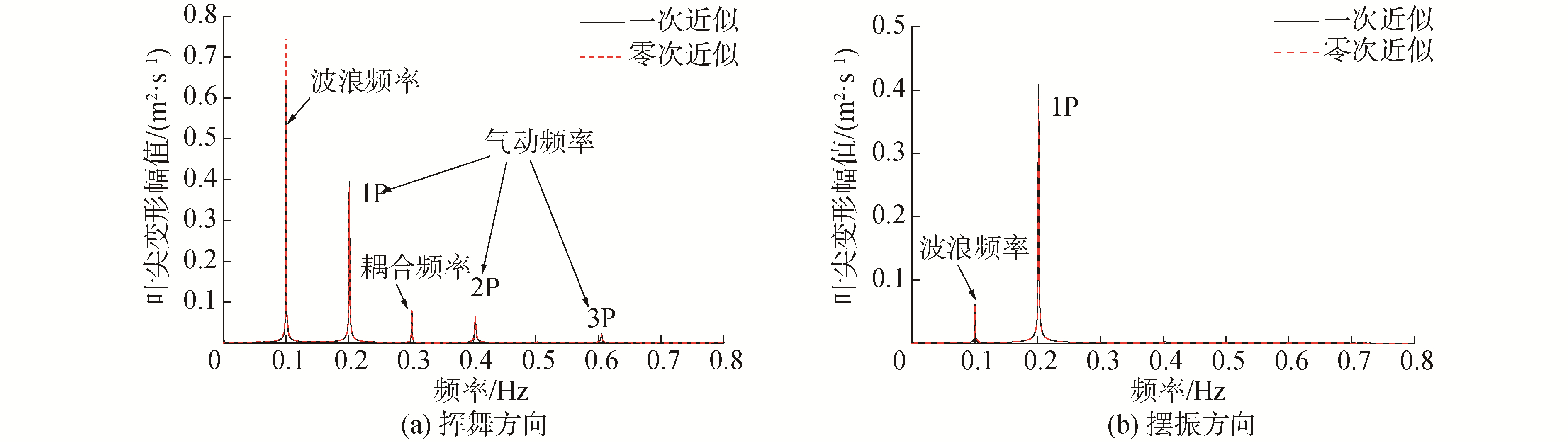
|
| 图 11 叶尖变形频谱分析 Fig. 11 Spectral analysis of blade tip deformation | |
通过频谱分析可以发现,叶片轴向变形二次耦合项只对叶片变形幅值有所影响,并不改变其运动规律。叶片挥舞方向振动频率以波浪和1P(风轮转速)为主,这是由于气动载荷耦合了基础的运动,受波浪影响较大。此外,挥舞变形还存在较为明显的波浪频率与1P的耦合频率、2P以及3P等频率成分。与叶片挥舞方向不同,摆振方向受到的切向气动载荷较小,因此波浪频率响应较小,而摆振方向在风轮旋转过程中受交变重力影响较大,因此摆振方向变形主要以重力引起的1P响应为主导。
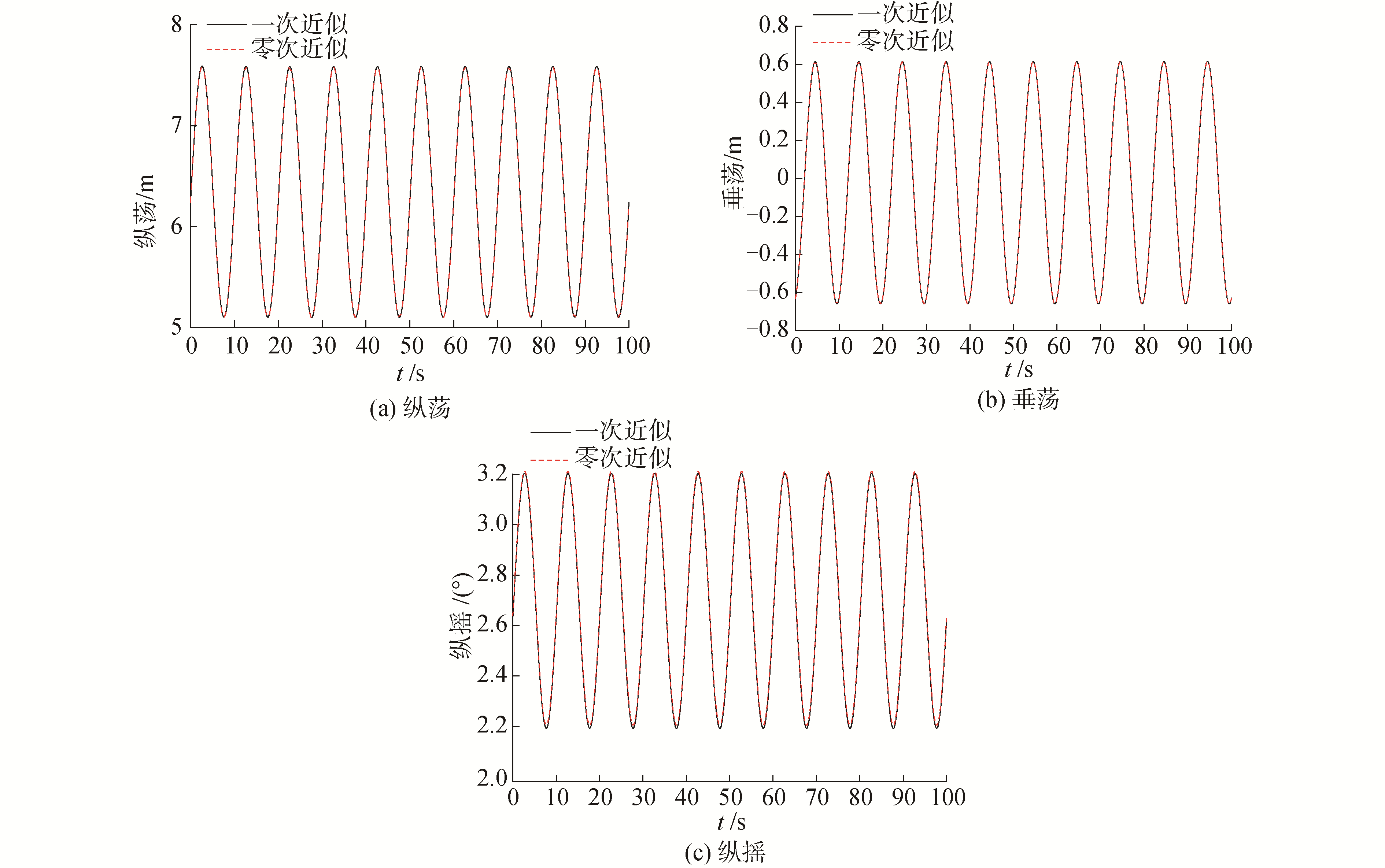
由于篇幅关系,本文只列出风浪作用平面的3个基础自由度响应,即纵荡、垂荡、纵摇。基础纵荡、纵摇和垂荡的运动响应,如图 12所示。
|
Download:
|
| 图 12 浮式基础动力响应 Fig. 12 The dynamic response of floating foundation | |
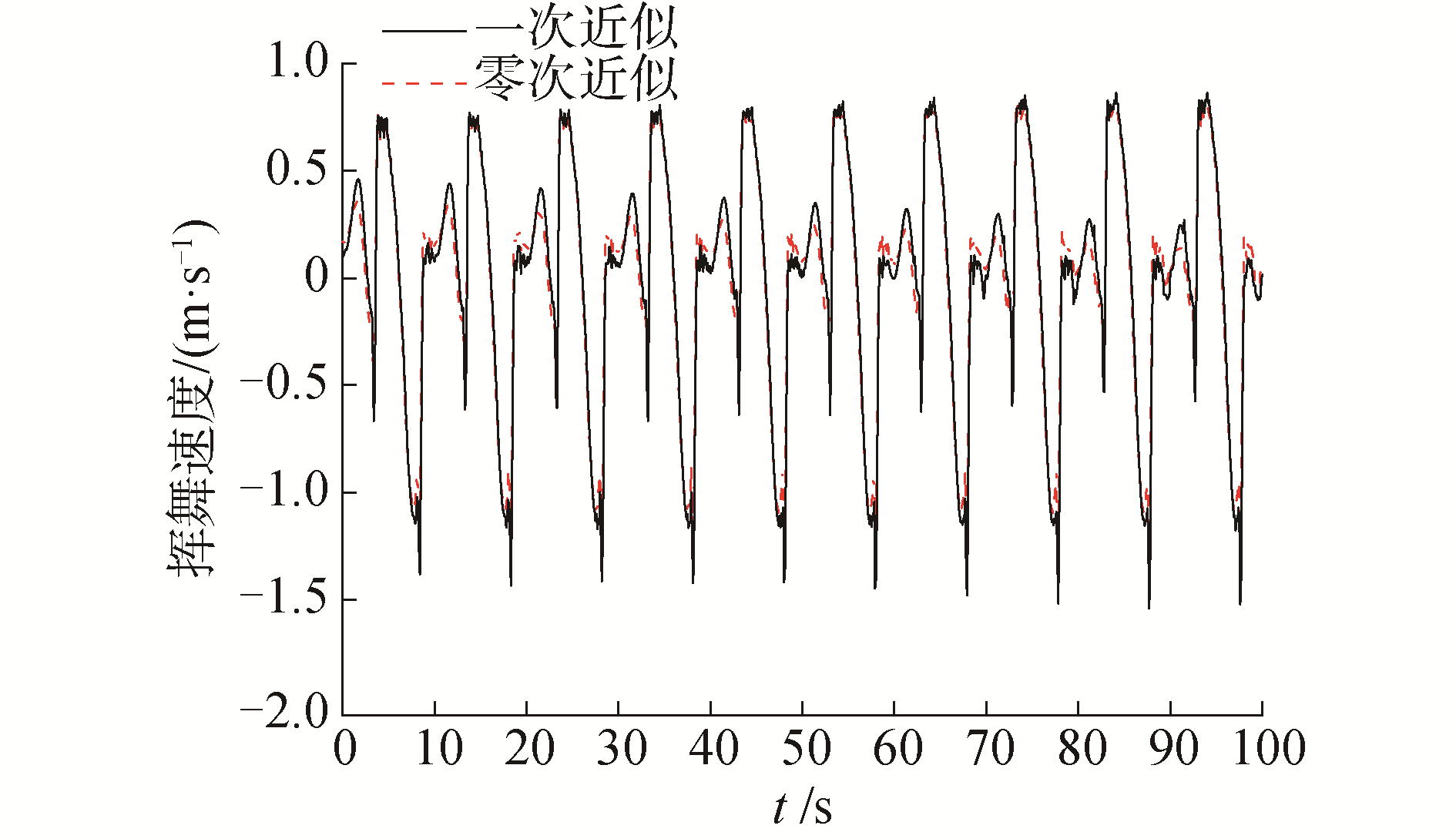
从图 12中可以发现,柔性叶片的2种近似模型对浮式基础的三自由度运动影响不大,这是因为考虑叶片轴向变形二次耦合项对叶片的振动速度影响不大,如图 13所示,因此2种模型计算的气动载荷相差无几。相比较而言,零次近似模型纵摇平衡位置为2.70°,而一次近似模型纵摇的平衡位置为2.71°,一次近似耦合模型的纵摇平衡位置略有增大。
|
Download:
|
| 图 13 叶尖挥舞速度时历曲线 Fig. 13 Blade tip flap velocity in time domain | |
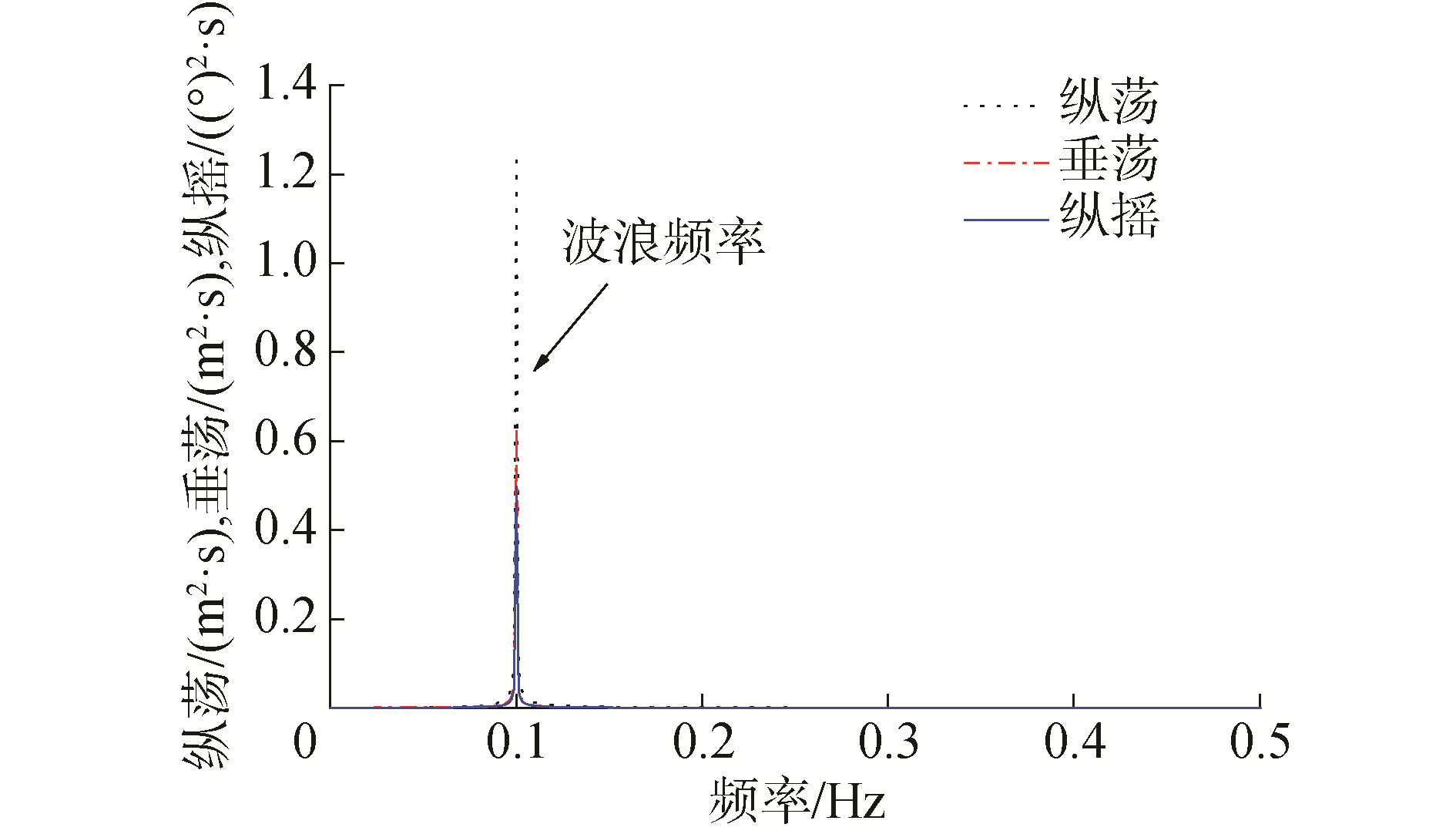
此外,对三自由度作频谱分析,如图 14所示,可以发现,浮式基础运动响应频率基本上以波频为主,气动载荷对基础运动响应频率成分贡献非常小。这是由于水平轴3根叶片在同一旋转平面内,浮式基础所受气动推力相当于叶片沿展向积分求和,叶片之间相位120°,求和之后气动载荷幅值相互抵消大大减小,与波浪载荷波动幅值相比几乎可忽略不计。
|
Download:
|
| 图 14 浮式基础运动响应频谱分析 Fig. 14 Spectral analysis of response of foundation | |
1) 通过计算额定转速下叶片固有频率,验证了本文建模方法的单元收敛性。针对5 MW风机叶片至少划分9个单元可得到收敛的计算结果。仅考虑叶片运动,计算零转速下叶片固有频率,与FAST和ADAMS结果对比吻合较好。
2) 仅考虑叶片运动,计算不同转速下叶片振动,分析其固有频率。传统零次近似模型计算的叶片摆振方向固有频率随转速增大而减小,挥舞方向不发生变化。一次近似耦合模型考虑旋转叶片的“动力刚化”效应,刚度随转速增大而增大,与实际情况相符。
3) 风浪联合作用下,由于一次近似耦合模型考虑了旋转叶片的“动力刚化”效应,叶片振动幅值较小,对叶片振动速度影响较小。叶片挥舞主要以波浪频率和气动1P响应为主,此外还存在二者的耦合频率以及2P、3P响应,摆振方向变形主要受交变重力影响。
4) 在定常风与规则波工况下,气动载荷对基础运动响应频率成分贡献非常小,基础运动响应以波浪频率为主。事实上在某些复杂海况下,气动载荷对基础运动的影响明显增大,因而考虑风机与浮体的耦合效应,对评估风机系统的运动性能至关重要。
| [1] |
KOO B J, GOUPEE A J, LAMBRAKOS K F, et al. Model tests for a floating windturbine on three different floaters[C]//Proceedings of ASME 201231st International Conference on Ocean, Offshore and Arctic Engineering. Rio de Janeiro, Brazil, 2012: 455-465.
(  0) 0)
|
| [2] |
SHIN H. Model test of the OC3-Hywind floating offshore wind turbine[C]//Proceedings of the Twenty-first International Offshore and Polar Engineering Conference. Maui, Hawaii, USA, 2011.
(  0) 0)
|
| [3] |
JONKMAN J M. Dynamics modeling and loads analysis of an offshore floating wind turbine[D]. Boulder: University of Colorado, 2007.
(  0) 0)
|
| [4] |
ROBERTSON A N, JONKMAN J M. Loads analysis of several offshore floating wind turbine concepts[C]//Proceedings of the Twenty-first International Offshore and Polar Engineering Conference. Maui, Hawaii, USA, 2011.
(  0) 0)
|
| [5] |
REN Nianxin, LI Yugang, OU Jinping. Coupled wind-wave time domain analysis of floating offshore wind turbine based on computational fluid dynamics method[J]. Journal of renewable and sustainable energy, 2014, 6(2): 023106. (  0) 0)
|
| [6] |
LI Yan, TANG Yougang, ZHU Qiang, et al. Effects of second-order wave forces and aerodynamic forces on dynamic responses of a TLP-type floating offshore wind turbine considering the set-down motion[J]. Journal of renewable and sustainable energy, 2017, 9(6): 063302. DOI:10.1063/1.5007893 (  0) 0)
|
| [7] |
刘延柱, 潘振宽, 戈新生. 多体系统动力学[M]. 2版. 北京: 高等教育出版社, 2014. LIU Yanzhu, PAN Zhenkuan, GE Xinsheng. Dynamics of multibody systems[M]. 2nd ed. Beijing: Advanced Education Press, 2014. (  0) 0)
|
| [8] |
刘锦阳, 洪嘉振. 刚-柔耦合动力学系统的建模理论研究[J]. 力学学报, 2002, 34(3): 408-415. LIU Jinyang, HONG Jiazhen. Study on dynamic modeling theory of rigid-flexible coupling systems[J]. Acta mechanica sinica, 2002, 34(3): 408-415. DOI:10.3321/j.issn:0459-1879.2002.03.013 (  0) 0)
|
| [9] |
蒋丽忠.柔性多体系统刚-柔耦合动力学建模理论研究[D].上海: 上海交通大学, 1999. JIANG Lizhong. Modeling of rigid-flexible coupling dynamics for flexible multibody systems[D]. Shanghai: Shanghai JiaoTong University, 1999. (  0) 0)
|
| [10] |
刘锦阳.刚-柔耦合动力学系统的建模理论研究[D].上海: 上海交通大学, 2000. LIU Jinyang. Study on dynamic modeling theory of rigid-flexible coupling systems[D]. Shanghai: Shanghai JiaoTong University, 2000. (  0) 0)
|
| [11] |
MORIARTY P J, HANSEN A C. AeroDyn theory manual[R]. Golden, Colorado: National Renewable Energy Laboratory, 2005.
(  0) 0)
|
| [12] |
BUHL JR M L. A new empirical relationship between thrust coefficient and induction factor for the turbulent windmill state[R]. Golden, Colorado: National Renewable Energy Laboratory, 2005.
(  0) 0)
|
| [13] |
BOSSANYI E A. GH bladed theory manual[M]. England: Garrad Hassan and Partners Limited, 2010: 46-47.
(  0) 0)
|
| [14] |
LEISHMAN J G, BEDDOES T S. A semi-empirical model for dynamic stall[J]. Journal of the American helicopter society, 1989, 34(3): 3-17. (  0) 0)
|
| [15] |
RAMSAY R R, HOFFMAN M J, GREGOREK G M. Effects of grit roughness and pitch oscillations on the S801 airfoil[R]. Washington: National Renewable Energy Laboratory, 1996.
(  0) 0)
|
| [16] |
耿宝磊.波浪对深海海洋平台作用的时域模拟[D].大连: 大连理工大学, 2010. GENG Baolei. Time domain simulation of wave action with sea platform in deep water[D]. Dalian: Dalian University of Technology, 2010. (  0) 0)
|
| [17] |
ROBERTSON A, JONKMAN J, MASCIOLA M, et al. Definition of the semisubmersible floating system for phase Ⅱ of OC4[R]. Golden, CO: U.S. Department of Energy, Office of Energy Efficiency & Renewable Energy, 2014.
(  0) 0)
|
| [18] |
JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. Golden, Colorado: National Renewable Energy Laboratory, 2009.
(  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


