2. 中国船舶工业集团有限公司 第七〇八研究所, 上海 200011
2. 708th Research Institute, China State Shipbuilding Corporation Limited, Shanghai 200011, China
无人水面艇(unmanned surface vehicle,USV)是一种自主式海洋运载器。其具有情报收集、环境监测、海上搜救和水文地理勘查等功能,具有十分广泛的应用范围。海洋环境中的风、浪、流等会影响USV的航行性能;而岛屿、礁石和沉船等障碍会影响USV航行的安全性。航迹规划是USV的一个重要研究领域,是保证其安全完成任务的重要条件。根据对外界环境信息的获得途径,USV的航迹规划可以分为基于海洋环境信息的全局航迹规划和基于传感器信息的局部航迹规划[1]。本文研究的是USV全局航迹规划,全局航迹规划是根据已知的航行障碍物建立相应的环境模型,根据任务要求在环境模型中规划出一条连接起始点和目标点的安全航迹。随着全局航迹规划从单目标规划向多目标规划转变,一些智能优化算法被广泛应用[2-10]。
由于USV全局航迹规划涉及到优化算法、控制理论、海洋环境建模以及船舶水动力学等多个领域,使得已有的航迹规划算法很难满足任务要求。目前大多数USV全局航迹规划方法是在全局环境模型中搜索出一条能够避障且航程最短的航迹,少有分析海洋环境对USV全局航迹规划的影响。因此需要从航程最短、能耗最低和安全避障的角度对USV全局航迹问题进行分析,本文提出了一种基于量子蚁群算法(quantum ant colony algorithm, QACA)对USV进行全局航迹规划。量子蚁群算法是将量子计算与蚁群算法(ant colony algorithm, ACA)相结合。采用量子比特对ACA中的信息素编码,得到量子信息素,并根据路径上的量子信息素浓度来选择蚂蚁移动方向。
1 USV及海洋环境建模 1.1 USV的动力学模型文献[11]提出了船舶动力学模型。由于大多数的USV为欠驱动船舶,同时本文主要考虑的是海洋环境对USV航行能耗的影响,因此可以对USV动力学模型进行一定的简化,没有考虑艏摇对航迹规划的影响:
| $ \mathit{\boldsymbol{M\dot \nu }} + \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} + \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} = {\mathit{\boldsymbol{\tau }}_w} + {\mathit{\boldsymbol{\tau }}_{{\text{thr}}}} $ | (1) |
| $ {\mathit{\boldsymbol{\tau }}_w} = {\mathit{\boldsymbol{\tau }}_{{\text{wind}}}} + {\mathit{\boldsymbol{\tau }}_{{\text{wave}}}} + {\mathit{\boldsymbol{\tau }}_{{\text{current}}}} $ | (2) |
式中:M为惯性矩阵;C(ν)为向心力矩阵;D(ν)为阻尼矩阵,D(ν)∈R2×2;τwind、τwave和τcurrent分别表示作用在USV上的风、浪和流等环境干扰力;τthr为推进系统作用在USV上的推力。因此,在式(1)中得到的ν是海洋环境和推进系统共同作用在USV上的速度向量。
1.2 海洋环境建模对USV进行全局航迹规划时,需要分析海洋环境中的风、浪和流对USV的航行性能产生的影响。
1.2.1 风的干扰力模型受到风的干扰力的影响,USV会偏离预定航迹。风的干扰力表现为纵向风压力τwindX和横向风压力τwindY[11]:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\tau }}_{{\rm{wind}}X}} = \frac{1}{2}{\rho _a}{A_f}V_w^2{C_{wx}}\left( {{\alpha _R}} \right)\\ {\mathit{\boldsymbol{\tau }}_{{\rm{wind}}Y}} = \frac{1}{2}{\rho _a}{A_s}V_w^2{C_{wy}}\left( {{\alpha _R}} \right) \end{array} \right. $ | (3) |
式中:ρa为空气密度;Af为船舶水线以上的正投影面积;As为船舶水线以上的侧投影面积;Cwx(αR)和Cwy(αR)分别为纵向和横向的风压力系数;Vw为相对风速。
1.2.2 浪的干扰力模型波浪干扰力作用于船体表现为一阶波浪力和二阶波浪力。二阶漂移力与波高平方成比例,对船舶的航向、航迹有重要的影响。波浪力可以简化为[11]:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\tau }}_{{\rm{wave}}X}} = \frac{1}{2}\rho L\zeta _{\rm{D}}^2{C_{XD}}\left( \lambda \right)\cos \chi \\ {\mathit{\boldsymbol{\tau }}_{{\rm{wave}}Y}} = \frac{1}{2}\rho L\zeta _{\rm{D}}^2{C_{YD}}\left( \lambda \right)\sin \chi \end{array} \right. $ | (4) |
式中:τwaveX为USV受到的纵向波浪干扰力;τwaveY为USV受到的横向波浪干扰力;ρ是海水的密度;ζD为平均波幅;L为船长;χ为海浪遭遇角;CXD(λ)和CYD(λ)为波浪漂移力系数。
1.2.3 流的干扰力模型在海面上航行的船舶会受到流的影响,即改变船舶的位置和姿态,影响船舶的航行效率。在建模过程中,假设流速Vc固定,不随时间和位置的改变而变化:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\tau }}_{{\rm{current}}X}} = \frac{1}{2}\rho {A_{\rm{f}}}V_{\rm{c}}^2{C_X}\left( \beta \right)\\ {\mathit{\boldsymbol{\tau }}_{{\rm{current}}Y}} = \frac{1}{2}\rho {A_{\rm{s}}}V_{\rm{c}}^2{C_Y}\left( \beta \right) \end{array} \right. $ | (5) |
式中:τcurrentX为USV受到的纵向海流干扰力;τcurrentY为USV受到的横向海流干扰力;Af、As为在水面以下船体的正、侧面的投影面积;Vc、β为流相对于船舶的速度和遭遇角;CX(β)和CY(β)分别在纵向和横向的流作用力系数[11]。
1.3 栅格法环境建模栅格法是将环境模型离散为一定数量的栅格,在每个栅格中存储的海浪的波幅、海流的流速、海风的风速及其方向, 以及碍航物位置等信息作为栅格的属性[12]。
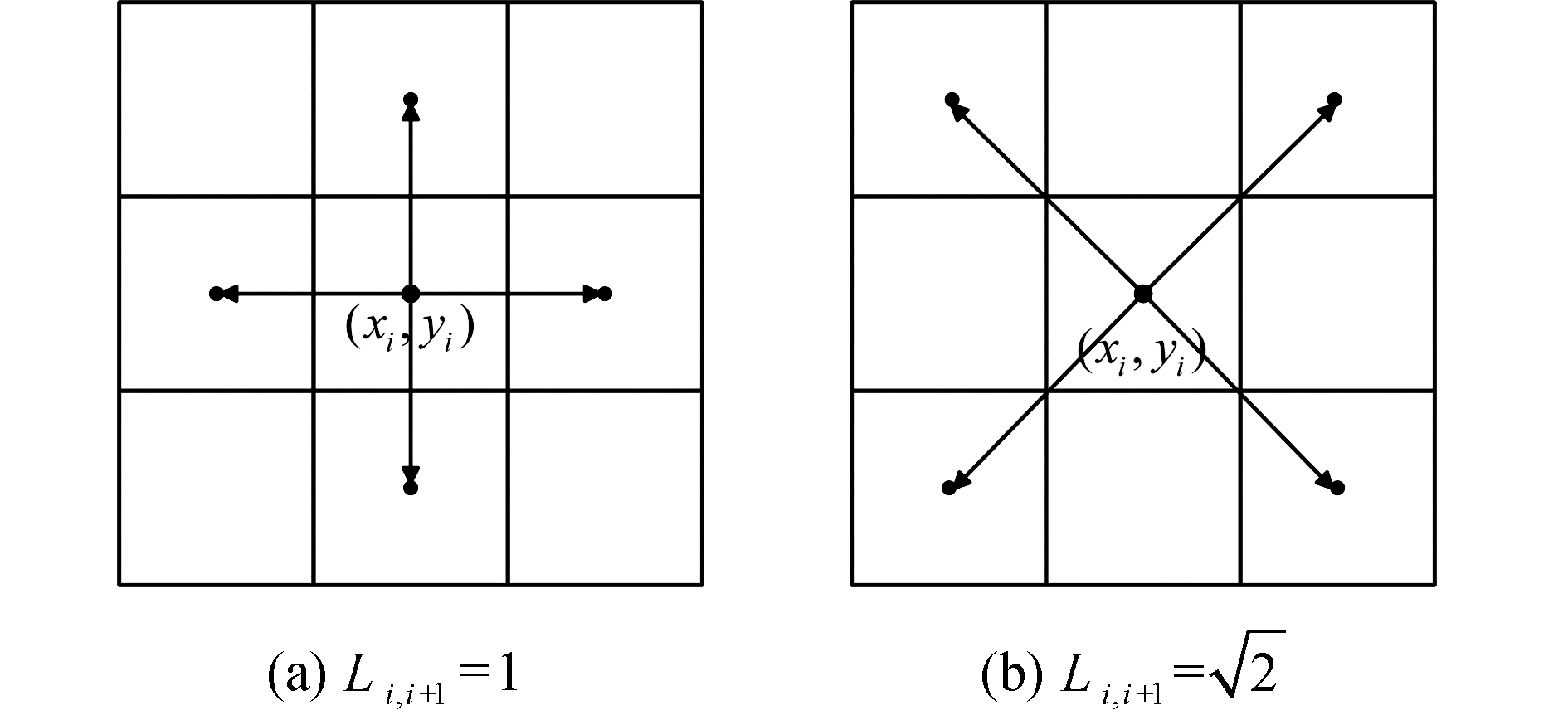
假设USV的当前位置为(xi, yi),而下一时刻USV将要到达的位置为(xi+1, yi+1),则两点间的距离Li, i+1定义为:
| $ {L_{i,i + 1}} = \left\{ \begin{array}{l} \;\;1,\;\;\;\;\;{x_i} = {x_{i + 1}},{y_i} = {y_{i + 1}}\\ \sqrt 2 ,\;\;\;\;其他 \end{array} \right. $ | (6) |
如图 1所示,当Li, i+1=1时,USV将沿着水平或垂直方向前进1个单位距离;而当
|
Download:
|
| 图 1 栅格法的移动规则 Fig. 1 Move rule of grid method | |
航迹规划的综合代价函数是用来评价一条航迹的优劣。首先分析不同的优化目标对航迹产生的影响,这其中包括航迹长度、航行能耗以及航行安全避障,根据任务要求对各个目标函数进行综合加权,形成航迹规划的综合代价函数。
1.4.1 航迹长度USV的航迹总长度为:
| $ L = \sum\limits_{i = 1}^m {{L_{i,i + 1}}} $ | (7) |
式中m为航迹段的数目。
1.4.2 航迹能耗在本文中可以认为USV在航行过程中的能耗全部来源于推进系统。USV在航行过程中的能耗为:
| $ E = \sum\limits_{i = 1}^m {{E_{i,i + 1}}} $ | (8) |
假设USV在节点i和节点i+1间是匀速航行的,这期间的能量消耗Ei, i+1等于推进系统为克服环境干扰阻力对USV所做的功,所以:
| $ E_{i, i+1}=\tau_{w}\left|\boldsymbol{v}_{\mathrm{usv}}\right| t $ | (9) |
| $ t=L_{i, i+1} /|\boldsymbol{v}| $ | (10) |
式中:m为航迹段的数目;νusv为USV推进系统产生的速度;τw为海洋环境干扰力的合力;ν为USV的实际航速,ν可由式(1)得到。
通过式(9)、(10)可以看出,航行能耗的大小与|νusv|成正比,与|ν|成反比。所以,当推进系统产生的推力τthr设定为固定值时,则|νusv|也为固定值,为了获得较低的航行能耗,需要调整USV的航向以充分利用海洋环境力,得到较大的|ν|[13]。
1.4.3 航行安全避障为了确保USV的安全,关键是要实现从起始点航行到目标点的最安全的航迹。则航行安全避障代价函数Psafe为:
| $ {P_{{\rm{safe}}}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{d \ge {d_{{\rm{safe}}}}}\\ {\infty ,}&{d < {d_{{\rm{sfe}}}}} \end{array}} \right. $ | (11) |
式中:d为USV与障碍物中心之间的实际距离;dsafe为USV与障碍物之间的安全距离。
1.4.4 综合代价函数结合以上,建立USV的航迹规划综合代价函数:
| $ \min J=P_{\mathrm{safe}}\left(w_{L} L+w_{E} E\right) $ | (12) |
约束条件为:
| $ \left\{ {\begin{array}{*{20}{l}} {L \le {L_{\max }}}\\ {0 < \left| {{\mathit{\boldsymbol{v}}_i}} \right| \le {\mathit{\boldsymbol{v}}_{\max }}} \end{array}} \right. $ | (13) |
式中:L为航迹长度代价;E为航行能耗代价;wL和wE分别代表相应的代价函数所占的比重,且wL+wE=1;Lmax为USV允许的最大航程;vi为USV在第i段航迹段内的航行速度;vmax为USV允许的最大航行速度。
2 量子蚁群算法 2.1 量子编码与量子旋转门在量子计算中,量子比特是用来描述量子的状态。量子比特有2个可能的状态:|0〉和|1〉,它们分别对应到经典比特的状态0和1。量子比特|φ〉可以表示为|φ〉=α|0〉+β|1〉,其中,α、β分别是量子态|φ〉的概率幅,α、β为复数,且满足|α|2+|β|2=1[14]。量子态|φ〉即为在|0〉和|1〉之间的任意一种不确定的叠加状态[15]。量子态|φ〉有|α|2的概率坍缩到状态|0〉,有|β|2的概率坍缩到状态|1〉。量子态|φ〉也可以使用实数对(cosθ, sinθ)来表示,其中θ为量子态|φ〉的相位[16]。
设个体Xi量子位的个数为n,则Xi可以表示为:
| $ {\mathit{\boldsymbol{X}}_i} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _{i1}}}&{\cos {\theta _{i2}}}& \cdots &{\cos {\theta _{{\rm{in}}}}}\\ {\sin {\theta _{i1}}}&{\sin {\theta _{i2}}}& \cdots &{\sin {\theta _{{\rm{in}}}}} \end{array}} \right] $ | (14) |
式中:Xic=(cosθi1, cosθi2, …, cosθin)和Xis=(sinθi1, sinθi2, …, sinθin)为该量子个体对应的2组解。所以经过量子编码后,每个个体都对应有2组解[17]。这样在个体总数相同的情况下,搜索空间加倍,遍历解空间的能力也得到增强,加快了收敛速度[18]。
量子旋转门是一种酉变换,其公式为:
| $ U\left( \theta \right) = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right] $ | (15) |
式中θ为旋转角度。
量子比特的改变是通过量子旋转门来完成,其更新公式如下:
| $ \left[ {\begin{array}{*{20}{c}} {\cos \varphi _{ij}^{t + 1}}\\ {\sin \varphi _{ij}^{t + 1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \varphi _{ij}^t}\\ {\sin \varphi _{ij}^t} \end{array}} \right] $ | (16) |
式中:[cosφijt, sinφijt]T、[cosφijt+1, sinφijt+1]T分别表示量子旋转门处理前后的量子比特的概率幅[19-20]。
2.2 蚂蚁转移规则与转移概率蚂蚁k由节点i转移到节点j的移动规则为:
| $ \begin{array}{*{20}{c}} {s = }\\ {\left\{ \begin{array}{l} \arg \mathop {\max }\limits_{s \in S} \left\{ {{{\left[ {\tau _{ij}^k\left( t \right)} \right]}^a}{{\left[ {\eta _{ij}^k\left( t \right)} \right]}^b}{{\left[ {{\varepsilon _{ij}}\left( t \right)} \right]}^c}} \right\},\;\;\;\;q \le {q_0}\\ \bar s,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;q > {q_0} \end{array} \right.} \end{array} $ | (17) |
式中:q为在[0, 1]内均匀分布的随机数;q0为某一常数(0≤q0≤1);S为蚂蚁k由节点i出发可能到达的所有节点的集合;
| $ p_{ij}^k\left( t \right) = \frac{{{{\left[ {{\tau _{ij}}\left( t \right)} \right]}^a}{{\left[ {{\eta _{ij}}\left( t \right)} \right]}^b}{{\left[ {{\varepsilon _{ij}}\left( t \right)} \right]}^c}}}{{\sum\limits_{s \in {\rm{allowed}}\left( i \right)} {{{\left[ {{\tau _{ij}}\left( t \right)} \right]}^a}{{\left[ {{\eta _{ij}}\left( t \right)} \right]}^b}{{\left[ {{\varepsilon _{ij}}\left( t \right)} \right]}^c}} }} $ | (18) |
式中:τij(t)为在第t次迭代时节点i到节点j的路径上的信息素浓度;a(a>0)为信息素重要性指数;ηij(t)为在第t次迭代时节点i到节点j的路径上的距离启发信息,其表达式为ηij(t)=1/Lij,Lij为节点i到节点j之间的距离;b(b>0)为距离启发信息重要性指数;εij(t)为在第t次迭代时节点i到节点j的路径上的能耗启发信息,其表达式为εij(t)=1/Eij,Eij为节点i到节点j上USV的能量消耗;c(c>0)为能耗启发信息重要性指数。
2.3 信息素更新规则对每只蚂蚁经过一次一步移动后进行信息素局部更新和对所有蚂蚁完成一次迭代后的得到的最优路径进行全局更新。记蚂蚁当前节点为pi,移动后节点为pj,则信息素局部更新规则为:
| $ \tau \left( {{p_j}} \right) = \left( {1 - {\rho _1}} \right)\tau \left( {{p_i}} \right) + {\rho _1}\Delta {\tau _{ij}} $ | (19) |
式中:τ(pj)为移动后的节点的信息素浓度;τ(pi)为当前节点的信息素浓度;ρ1(0 < ρ1 < 1)为信息素局部更新挥发系数;Δτij为在本次循环中各只蚂蚁在路径(pi→pj)上留存的信息素浓度:
| $ \Delta {\tau _{ij}} = \sum\limits_{k = 1}^n {\Delta \tau _{ij}^k} $ | (20) |
| $ \Delta \tau _{ij}^k = \left\{ \begin{array}{l} Q/{J_k},\;\;\;\;第\;k\;只蚂蚁所走的路径\\ 0,\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (21) |
式中:Q为常数;Jk为蚂蚁k在本次循环中所得的航迹综合代价值。
所有蚂蚁完成一次迭代后,进行信息素全局更新,其规则为:
| $ \tau \left( {{p_j}} \right) = \left\{ {\begin{array}{*{20}{l}} {\left( {1 - {\rho _2}} \right)\tau \left( {{p_j}} \right) + {\rho _2}\Delta {\tau _{{\rm{best}}}},}&{{p_u} = \tilde s}\\ {\left( {1 - {\rho _2}} \right)\tau \left( {{p_j}} \right),}&{{p_u} \ne \tilde s} \end{array}} \right. $ | (22) |
| $ \Delta {\tau _{{\rm{best}}}} = \left\{ \begin{array}{l} Q/{J_e},\;\;\;边\left( {i,j} \right)属于本次循环中的\\ \;\;\;\;\;\;\;\;\;\;\;\;最优路径\\ 0,\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (23) |
式中:ρ2为信息素全局更新挥发系数;Q为常数;Je为本次循环中所得最优路径的航迹综合代价值;
QACA的原理是通过量子比特对ACA中蚂蚁在路径上留下的信息素进行编码,得到量子信息素,并根据路径上的量子信息素浓度来选择蚂蚁的转移方向。并通过量子旋转门改变蚂蚁自身携带的量子比特的相位。算法的具体步骤如下:
1) 初始化量子蚁群。设蚁群中蚂蚁个数为n,则每只蚂蚁会携带2个量子比特,最大迭代次数Nmax,其中t时刻量子蚁群可表示为:A(t)=(τ1t, τ2t, …, τnt),则在第t次迭代中第i(i=1,2,…,n)只蚂蚁个体的量子比特可表示为τijt=[cosφijt, sinφijt]T,通过量子比特来表示各节点上的信息素浓度,即[cosφijt, sinφijt]T表示在第t次迭代时第i只量子蚂蚁在第j个节点上留下的信息素浓度值,φij=2π×Rnd为量子比特的相位;Rnd是(0, 1)之间随机数;
2) 将蚂蚁置于航迹规划空间的起始点上,然后按照蚂蚁的转移规则和转移概率选择节点;
3) 对每只蚂蚁经过一次一步移动后进行信息素局部更新,对所有蚂蚁完成一次迭代后的得到的最优路径进行全局更新;
4) 通过量子旋转门对量子蚁群A(t)的相位进行变换更新;
5) 整个蚁群走过所有的节点,根据蚂蚁对每个节点的选择信息,生成候选解,并计算相应候选解的航迹综合代价值;
6) 若t≥Nmax,则转向步骤7);否则,转向步骤2);
7) 输出得到的最优解的节点及其相应的航迹总代价值,并根据最优解的节点得到最优航迹,算法结束。
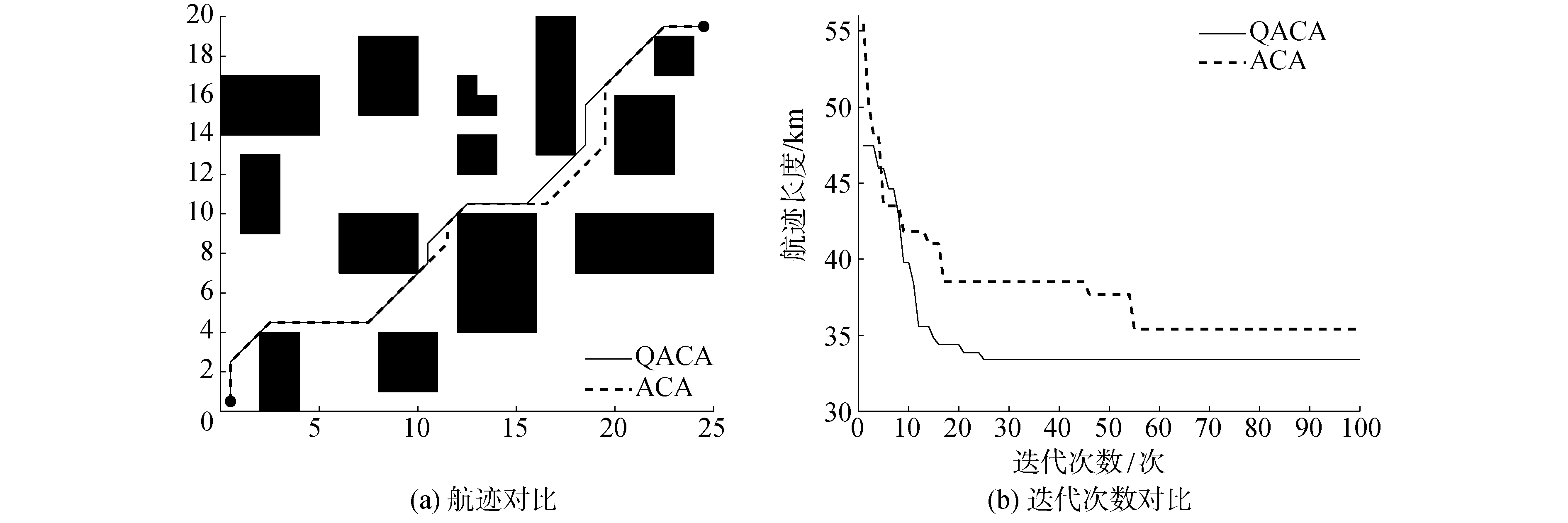
3 航迹规划仿真实验 3.1 QACA和ACA在静态环境中的USV航迹规划在进行基于QACA和ACA的USV航迹规划仿真实验时,设置如下的参数:最大迭代次数Nmax=100,蚁群规模n=100,信息素重要性指数a=2,距离启发信息重要性指数b=2,能耗启发信息重要性指数c=2,信息素挥发指数ρ1=ρ2=0.9;设置实验1中的USV的起始位置为(0.5, 0.5)、目标位置为(24.5, 19.5),实验2中的USV的起始位置为(0.5, 19.5)、目标位置为(24.5, 0.5),单位栅格的长度为1 km。
表 1为实验1、2的QACA和ACA航迹规划仿真结果。通过表 1可以看出,在实验1中QACA的航迹长度比ACA的航迹长度降低了5.65%,QACA收敛到最小值的迭代次数比ACA降低了54.5%。通过表 1可以看出,在实验2中QACA的航迹长度比ACA的航迹长度降低了3.61%,QACA收敛到最小值的迭代次数比ACA降低了44.23%。结果表明:QACA在航迹长度和迭代次数均优于ACA,由于QACA采用了信息素局部和全局2次更新,同时通过量子旋转门对量子蚁群的相位进行更新,这样就能够避免算法陷入局部最优解;因为采用量子比特对信息素进行编码,使得搜索空间加倍,从而具有较快的收敛速度。
| 表 1 实验1、2中QACA和ACA航迹规划仿真数据 Table 1 QACA and ACA path planning simulation data in experiment 1 and 2 |
利用QACA在1.2节所述的海洋环境中对USV进行航迹规划。风速为2 m/s,浪高为2 m,流速为1.5 m/s。|νusv|=5 m/s。USV的起始位置为(0.5, 0.5)、目标位置为(24.5, 19.5)。在实验3中,海风、海浪和海流在北东坐标系下的方向分别设置为30°、60°和45°。在实验4中,海风、海浪和海流在北东坐标系下的方向分别设置为150°、110°和135°。
图 2给出了2种USV的优化航迹。由表 3可以看出,航迹长度因海洋环境的方向而改变,同时相应的航迹能耗也会有所改变。在实验3和实验4中,USV沿着规划出的航迹所消耗的能量比无海洋环境时分别降低了11.25%和1.81%。在图 2(a)可以看出,USV大多数的航行方向与海洋环境方向相近,因此有海洋环境的航迹能耗比无海洋环境时大幅减少。在图 2(b)中,规划出的航迹需要利用海洋环境以节省能耗,因此得到的航迹比无海洋环境的航迹消耗的能量要少。
|
Download:
|
| 图 2 实验3和实验4中有海洋环境与无海洋环境的航迹对比 Fig. 2 Comparison of the path with the marine environment and without the marine environment in experiment 3 and experiment 4 | |
| 表 2 有无海洋环境的航迹数据 Table 2 Path data with and without marine environment |
1) 量子蚁群算法相比较于蚁群算法拥有更快的收敛速度,并且可以有效地避免局部极值;
2) 量子蚁群算法可以在海洋环境中为无人水面艇规划出一条航程最短、航行能耗最低和能够安全避障的全局航迹。
为了更好地解决无人水面艇的航迹规划问题,以及提高量子蚁群算法的优化能力,提出了以下几点展望:
1) 分析航迹规划问题中的各个优化目标之间的相关性,来得到更为合理的航行代价函数;
2) 对量子蚁群算法中涉及到的一些参数进行自适应处理,以实现在算法优化能力的提高;
3) 将量子蚁群算法应用到动态未知环境中的无人水面艇航迹规划。
| [1] |
CHU K, LEE M, SUNWOO M. Local path planning for off-road autonomous driving with avoidance of static obstacles[J]. IEEE transactions on intelligent transportation systems, 2012, 13(4): 1599-1616. DOI:10.1109/TITS.2012.2198214 (  0) 0)
|
| [2] |
NIU Hanlin, LU Yu, SAVVARIS A, et al. An energy-efficient path planning algorithm for unmanned surface vehicles[J]. Ocean engineering, 2018, 161: 308-321. DOI:10.1016/j.oceaneng.2018.01.025 (  0) 0)
|
| [3] |
唐平鹏.复杂海况下水面无人艇分层危险规避方法研究[D].哈尔滨: 哈尔滨工程大学, 2014. TANG Pingpeng. Research on hierarchical obstacle avoidance for unmanned surface vehicle in complicated marine environments[D]. Harbin: Harbin Engineering University, 2014. https://max.book118.com/html/2017/0509/105530768.shtm (  0) 0)
|
| [4] |
KIM H, KIM S H, JEON M, et al. A study on path optimization method of an unmanned surface vehicle under environmental loads using genetic algorithm[J]. Ocean engineering, 2017, 142: 616-624. DOI:10.1016/j.oceaneng.2017.07.040 (  0) 0)
|
| [5] |
MA Yong, HU Mengqi, YAN Xinping. Multi-objective path planning for unmanned surface vehicle with currents effects[J]. ISA transactions, 2018, 75: 137-156. DOI:10.1016/j.isatra.2018.02.003 (  0) 0)
|
| [6] |
WU Peng, XIE Shaorong, LIU Hengli, et al. Autonomous obstacle avoidance of an unmanned surface vehicle based on cooperative manoeuvring[J]. Industrial robot:an international journal, 2017, 44(1): 64-74. DOI:10.1108/IR-04-2016-0127 (  0) 0)
|
| [7] |
AHMED F, DEB K. Multi-objective optimal path planning using elitist non-dominated sorting genetic algorithms[J]. Soft computing, 2013, 17(7): 1283-1299. DOI:10.1007/s00500-012-0964-8 (  0) 0)
|
| [8] |
李明, 李铜桥. 基于非奇异终端滑模的欠驱动UUV航迹跟踪控制[J]. 应用科技, 2018, 45(2): 11-16. LI Ming, LI Tongqiao. Path-following control for an underactuated UUV based on non-singular terminal sliding mode[J]. Applied science and technology, 2018, 45(2): 11-16. (  0) 0)
|
| [9] |
马英凯, 刘志林, 冯江, 等. 基于航向控制的欠驱动船舶曲线航迹控制[J]. 应用科技, 2018, 45(1): 26-32. MA Yingkai, LIU Zhilin, FENG Jiang, et al. Control on the curve track of an underactuated surface vessel based on heading control[J]. Applied science and technology, 2018, 45(1): 26-32. (  0) 0)
|
| [10] |
韩鹏, 刘志林, 周泽才, 等. 基于LOS法的自航模航迹跟踪控制算法实现[J]. 应用科技, 2018, 45(3): 66-70. HAN Peng, LIU Zhilin, ZHOU Zecai, et al. Path tracking control algorithm based on LOS method for surface self-propulsion vessel[J]. Applied science and technology, 2018, 45(3): 66-70. (  0) 0)
|
| [11] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. New York: Wiley, 2011.
(  0) 0)
|
| [12] |
KIM H, KIM D, SHIN J U, et al. Angular rate-constrained path planning algorithm for unmanned surface vehicles[J]. Ocean engineering, 2014, 84: 37-44. DOI:10.1016/j.oceaneng.2014.03.034 (  0) 0)
|
| [13] |
LEE T, KIM H, CHUNG H, et al. Energy efficient path planning for a marine surface vehicle considering heading angle[J]. Ocean engineering, 2015, 107: 118-131. DOI:10.1016/j.oceaneng.2015.07.030 (  0) 0)
|
| [14] |
NARAYANAN A, MOORE M. Quantum-inspired genetic algorithms[C]//Proceedings of IEEE international conference on evolutionary computation. IEEE, 1996: 61-66.
(  0) 0)
|
| [15] |
HAN K H, KIM J H. Quantum-inspired evolutionary algorithm for a class of combinatorial optimization[J]. IEEE transactions on evolutionary computation, 2002, 6(6): 580-593. DOI:10.1109/TEVC.2002.804320 (  0) 0)
|
| [16] |
李士勇, 李盼池. 量子计算与量子优化算法[M]. 哈尔滨: 哈尔滨工业大学出版社, 2009: 108-112. LI Shiyong, LI Panchi. Quantum computation and quantum optimization algorithms[M]. Harbin: Harbin Institute of Technology Press, 2009: 108-112. (  0) 0)
|
| [17] |
李士勇, 柏继云. 连续函数寻优的改进量子扩展蚁群算法[J]. 哈尔滨工程大学学报, 2012, 33(1): 80-84. LI Shiyong, BAI Jiyun. Extended quantum ant colony algorithm for continuous function optimization[J]. Journal of Harbin Engineering University, 2012, 33(1): 80-84. DOI:10.3969/j.issn.1007-7043.201011062 (  0) 0)
|
| [18] |
王芳.基于量子蚁群算法的多无人机协同航迹规划研究[D].哈尔滨: 哈尔滨工业大学, 2015. WANG Fang. Collaborative path planning of UAVs based on quantum ant colony algorithm[D]. Harbin: Harbin Institute of Technology, 2015. (  0) 0)
|
| [19] |
LIU Min, ZHANG Feng, MA Yunlong, et al. Evacuation path optimization based on quantum ant colony algorithm[J]. Advanced engineering informatics, 2016, 30(3): 259-267. DOI:10.1016/j.aei.2016.04.005 (  0) 0)
|
| [20] |
何小锋, 马良. 带时间窗车辆路径问题的量子蚁群算法[J]. 系统工程理论与实践, 2013, 33(5): 1255-1261. HE Xiaofeng, MA Liang. Quantum-inspired ant colony algorithm for vehicle routing problem with time windows[J]. Systems engineering-theory & practice, 2013, 33(5): 1255-1261. DOI:10.3969/j.issn.1000-6788.2013.05.021 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


