2. 深圳航天科技创新研究院, 广东 深圳 518057
2. Shenzhen Academy of Aerospace Technology, Shenzhen 518057, China
目前外骨骼机器人已经基本能够满足人体行走辅助的功能,然而由于外骨骼过高的能耗以及电池容量限制,外骨骼难以长时间工作,因此限制了外骨骼的实际应用。外骨骼的高能耗低续航特点已经成为制约其应用和发展的主要因素之一,因此近些年国内外对外骨骼节能降耗技术的研究格外关注。提高外骨骼续航时间的途径主要有2种:1)提高外骨骼能源的续航能力;2)降低外骨骼驱动关节的能耗。采用第1种途径的代表性研究成果是美国伯克利下肢负重外骨骼(BLEEX)[1-3]和美国洛克希德马丁公司的下肢外骨骼(HULK)[4]。采用新型的能源供给装置能够显著提高外骨骼的续航时间,然而诸如燃料电池等新型能源装置目前尚处于研发阶段,且成本高昂,还无法开展大规模的实际应用,因此在当前新型能源技术尚未成熟的情况下,有必要采用第2种途径来提高外骨骼的续航时间,即通过降低外骨骼驱动关节的能耗来提高续航能力。
目前降低外骨骼驱动关节能耗的主要方法是通过引入被动元件(弹性元件和阻尼元件)实现能量的高效回收和利用,从而降低驱动关节能耗,该方法借鉴了人类行走和奔跑过程中骨骼肌肉的生物力学特性。生物力学研究表明,人体在行走或奔跑过程中主要通过肌肉和韧带来缓冲、存储和释放能量,实现了高效的能量循环利用[5-6]。该方法的代表性研究成果是美国卡内基梅隆大学Collins等[7]学者发表在Nature上的一项研究,该研究提出了一种纯被动式的踝关节助力外骨骼结构,该装置仅由直线弹簧和离合器组成,实现了在没有任何主动驱动元件的情况下,降低了约7%的人体体能消耗。类似的研究还有美国麻省理工学院Walsh等[8]根据人体行走生物力学设计的由弹簧和阻尼构成的外骨骼弹性驱动器;美国特拉华大学SANKAI等[9]的纯被动式康复外骨骼;Spring Walker[10]的被动型外骨骼等。
目前的研究表明采用被动元件降低外骨骼驱动关节能耗以及降低人体行走能耗的可行性和优越性。被动元件的引入使外骨骼具备能量循环利用的能力,从而可以降低驱动关节能耗。为了降低驱动关节能耗,被动元件的参数必须经过合理的匹配,然而目前被动元件参数的匹配主要依赖于工程经验和大量的实验摸索,缺乏系统的理论依据和方法。
1 优化目标与约束条件 1.1 被动元件参数最优匹配优化目标驱动关节的能耗与被动元件的布置方式有关,被动元件的布置方式主要分为串联和并联2类,串联方式的不足是单个元件较小的误差会对整个关节运动产生较大的影响,且元件之间相互耦合导致控制较为复杂,因此本文采用如图 1所示的被动元件的并联方式,各个驱动元件能够相互独立工作,不会对其他元件造成影响,主动驱动力矩、被动弹性力矩和被动阻尼力矩共同作用于人肢体关节,从而对人肢体关节进行助力。

|
Download:
|
| 图 1 外骨骼主-被动元件并联驱动示意 Fig. 1 Exoskeleton active-passive element parallel driver | |
由于被动元件自身并不消耗电能,因此外骨骼驱动关节的能耗来自于主动元件。假设下肢外骨骼一共具有6个驱动关节,分别驱动人双腿的髋关节、膝关节和踝关节,则整个下肢外骨骼系统的能耗为6个驱动关节的功率之和,假设人体行走的步态周期为T,则下肢外骨骼总能耗Pall为:
| $ P_{\mathrm{all}}=\int_{0}^{T} \sum\limits_{i=1}^{6}\left|\tau_{i}(t) \omega_{i}(t)\right| \mathrm{d} t $ | (1) |
式中:τi为各关节电机驱动力矩;ωi为个关节角速度。假设各个关节的被动弹性力矩为Tki,各个关节的被动阻尼力矩为Tci,则外骨骼驱动关节作用于人体关节的合力矩Tai为:
| $ T_{a i}=\tau_{i}+T_{k i}+T_{c i} $ | (2) |
寻求被动元件参数最优匹配的问题本质上是一个优化问题,即在满足各关节合力矩Tai的条件下,寻找主动驱动力矩τi、被动弹性力矩Tki和被动阻尼力矩Tci的最优组合使下肢外骨骼总能耗Pall最小。故该最优问题的目标函数可以表述为:
| $ {\rm{object}}\;\;{\rm{Function}} \to {\mathop{\rm Min}\nolimits} \left( {{P_{{\rm{ all }}}}} \right) $ | (3) |
下面对该优化问题的等式约束条件和不等式约束条件进行分析。
1.2 被动元件参数最优匹配约束条件首先,主动驱动力矩、被动弹性力矩和被动阻尼力矩需要满足等式约束条件(2),即主动驱动力矩、被动弹性力矩和被动阻尼力矩之和需要等于期望的关节合力矩。其次,在一个周期运动过程中,弹性元件的能量变化为零:
| $ P_{k i}=\int_{0}^{T}\left|T_{k i}(t) \omega_{i}(t)\right| \mathrm{d} t=0 $ | (4) |
人体运动实验表明,人肢体关节力矩与肢体角位移成非线性关系[6],故式中被动弹性力矩Tki与关节角度θ成非线性关系,为了方便分析本文将被动弹性力矩Tki泰勒展开,并取前n项近似为:
| $ T_{k i}=\sum\limits_{k=0}^{n} a_{k} \theta_{i}^{k} $ | (5) |
将式(5)代入(4)可得被动弹性力矩的等式约束条件为:
| $ P_{k i}=\int_{0}^{T}\left|\left(\sum\limits_{k=0}^{n} a_{k} \theta_{i}^{k}\right) \cdot \omega_{i}(t)\right| \mathrm{d} t=0 $ | (6) |
被动阻尼力矩的特性为:阻尼力的方向始终与运动方向相反,因此被动阻尼力矩满足的等式约束条件为:
| $ \left\{ \begin{array}{l} T{c_i}\left( t \right) = - {b_i}\left( t \right) \cdot {\mathop{\rm sgn}} \left( {{\omega _i}} \right)\\ {\mathop{\rm sgn}} \left( {{\omega _i}} \right) = \left\{ {\begin{array}{*{20}{c}} {1, }&{{\omega _i} > 0}\\ {0, }&{{\omega _i} = 0}\\ { - 1, }&{{\omega _i} < 0} \end{array}} \right. \end{array} \right. $ | (7) |
除了上述等式约束外,主动驱动力矩、被动弹性力矩和被动阻尼力矩只能在一定范围内变化,故需要满足的不等式约束条件为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _{i\min }} \le {\tau _i} \le {\tau _{i\max }}}\\ {{T_{ki\min }} \le {T_{ki}} \le {T_{ki\max }}}\\ {{T_{ci\min }} \le {T_{ci}} \le {T_{cimax}}} \end{array}} \right. $ | (8) |
为了求解被动元件参数最优匹配的优化问题,需要寻求合适的优化算法。由于被动元件参数最优匹配优化问题未知参数过多且未知量之间仅为弱约束限制,传统优化算法存在计算量巨大、容易陷入局部最优的问题,而诸如遗传算法、蚁群算法、模拟退火算法等现代优化算法,在求解多局部最优问题时容易产生早熟效率低等缺点,为避免上述优化算法的缺点,本文提出一种基于卡尔曼滤波的改进遗传算法,算法流程如图 2所示。

|
Download:
|
| 图 2 改进遗传算法流程 Fig. 2 The flow chart of improved genetic algorithm | |
基本的遗传算法由编码方式、适应度函数、种群初始化、遗传操作(选择、交叉、变异)和终止条件等5个部分组成[11]。为了提高遗传算法的寻优速度和精度,需要减少无效个体的产生数量,使个体尽可能位于可行域内,为此本文提出2个遗传算法的改进措施:1)利用卡尔曼滤波改进初始种群;2)采用自适应交叉算子。
2.1 编码方式由于关节力矩连续变化且要求控制精度高,因此被动元件参数最优匹配的优化问题是一个多变量、连续优化问题。遗传算法常用的二进制编码较长、处理速度较慢且精度较低,因此本文采用实数编码方式,种群中的个体表示为:
| $ \boldsymbol{p}=\left[\begin{array}{lllllllll}{p_{1}} & {\cdots} & {p_{n}} & {p_{n+1}} & {\cdots} & {p_{n+j}} & {\cdots} & {p_{n+m}}\end{array}\right] $ | (9) |
式中p1, p2, …, pn代表被动弹性力矩泰勒展开多项式的前n项系数,本文将被动阻尼力矩分为m等分,其中pn+j为第j个采样点处阻尼力矩。种群个体p需要满足约束条件(2)、(6)、(7)和(8)。
2.2 种群初始化初始种群在满足约束条件的解空间中随机产生。本文利用卡尔曼滤波获得较优的初始种群,具体步骤如下:
1) 将期望关节合力矩存入数据库中;
2) 通过卡尔曼滤波对数据库中的关节合力进行参数辨识,得到被动弹性力矩的泰勒展开多项式系数,即p1,p2,…,pn的值;
3) 将p1p2…pn的值域范围进行二次分配,pimax_new,pimin_new为二次分配时值域的上下限:
| $ \left\{ {\begin{array}{*{20}{c}} {{p_{i\max \_{\rm{new}}}} = {p_i} - {k_0}, }&{1 \le i \le n}\\ {{p_{i\min \_{\rm{new}}}} = {p_i} + {k_0}, }&{1 \le i \le n} \end{array}} \right. $ | (10) |
式中:i为多项式第i项; k0为常数
4) 选择pn+1…pn+j…pn+m的值域范围[0, fjmax],在[0, fjmax]依次对第j项阻尼力矩随机二次分配。
2.3 适应度函数遗传算法的适应度函数用于评价种群子代的优劣,适应度函数值越小说明子代越优秀,因此有更大的概率遗传到下一代。本文采用的适应度函数为:
| $ \begin{array}{*{20}{c}} {{\mathop{\rm eval}\nolimits} (p) = \min \sum\limits_{j = 1}^m {\left( {|\tau (j) - \sum\limits_{i = 1}^n {{p_i}} \theta (j) - } \right.} }\\ {{p_{n + i}}{\mathop{\rm sgn}} (\omega (j)) \cdot \omega (j)| \cdot \Delta t)} \end{array} $ | (11) |
式中:eval(p)是个体p的适应度函数值;τ(j)为关节合力矩的第j个采样点;θ(j)为角位移的第j个采样点;ω(j)为角速度的第j个采样点;Δt为采样时间。
2.4 遗传操作遗传算法是一个反复迭代的过程,个体经过选择、交叉和变异等3个遗传操作后再利用遗传评价函数进行评价,筛选出最优的个体遗传到下一代。
2.4.1 选择选择的目的是保证优秀个体遗传到下一代的概率大于较差的个体,常用的选择方式有:比例选择、排序选择和轮盘赌选择等。本文采用轮盘赌选择方式,个体pi被选择的概率为:
| $ \operatorname{prob}\left(p_{i}\right)=\operatorname{eval}\left(p_{i}\right) / \sum\limits_{j=1}^{n} \operatorname{eval}\left(p_{j}\right) $ | (12) |
式中:prob(pi)为个体pi被选中的概率;
交叉操作将个体两两配对,再将编码中的信息部分交换,从而形成新的个体。交叉操作能使个体不断进化,不同的编码方式所选用的交叉方式也不同,本文采用自适应交叉概率Pc,如式(13)所示,自适应交叉概率随着遗传代数的增加而减小,算法前期交叉概率较大,能够以较高的效率逼近最优解,算法后期交叉概率减小,从而避免较优的个体遭到破坏。
| $ {P_c} = - \left( {{P_{c{\rm{\_start}}}} - {P_{c{\rm{\_end}}}}} \right) \cdot {t^2}/{T^2} + {P_{c{\rm{\_start}}}} $ | (13) |
式中:Pc为每代的交叉概率;Pc_start为初始时刻的交叉概率;Pc_end为结束时刻的交叉概率;T为终止迭代的次数;t为当前的迭代次数。
2.4.3 变异变异操作能使个体编码信息产生突变,能够增加种群的多样性,从而避免陷入局部最优解。本文采用均匀变异法:
| $ \left\{ \begin{array}{l} p_i^{i + 1} = p_i^i + \left( {{p_{i\max }} - p_i^i} \right)c, \;\;\;\;\;w \ge 0.5\\ p_i^{i + 1} = p_i^i - \left( {p_i^i - {p_{i\min }}} \right)c, \;\;\;\;\;w < 0.5 \end{array} \right. $ | (14) |
式中:pii为变异点原编码值;pii+1为变异点新编码值;pimax和pimin为个体i的上下限;c和w为在[0, 1]的随机数。
2.5 终止条件终止条件是遗传算法的收敛条件,当适应度函数已经无法改善或达到最大迭代次数,则遗传算法终止,否则将继续进行遗传算法。
3 膝关节被动元件参数最优匹配本文采用的膝关节助力外骨骼如图 3所示。为了获取人体平地奔跑过程中的膝关节角位移曲线和膝关节力矩曲线,本文首先利用运动捕捉系统和测力台对人体平地奔跑运动进行了数据采集,之后根据实验对象的身高和体重,利用人体五杆动力学模型以及归约化人体动力学参数对平地奔跑过程中的人体矢状面膝关节力矩进行了求解,最后将求解得出的膝关节力矩乘以助力系数(30%)作为外骨骼需要提供的合力矩。

|
Download:
|
| 图 3 直线电机驱动膝关节外骨骼 Fig. 3 Knee exoskeleton driven by linear motor | |
本文采用前面介绍的改进遗传算法寻找膝关节主动驱动力矩、被动弹性力矩和被动阻尼力矩的最优匹配,使膝关节在满足合力矩的情况下能耗最小。本文采用的改进遗传算法的参数设置如表 1所示。
| 表 1 改进遗传算法参数设定值 Table 1 Parameters of improved genetic algorithm |
本文将被动弹性力矩进行泰勒展开并取前n项近似,当多项式项数的增加,达到最优解的遗传代数也相应增加,原因是由于未知数增加从而导致寻优效率下降,然而实验中发现随着多项式项数的增加驱动关节的最优能耗逐渐下降,如表 2所示,当多项式项数n=4时,膝关节的驱动能耗为15.29 J,而实验发现当多项式项数n>4时,驱动关节能耗下降幅度很小,因此多项式项数取4即能获得最优的被动元件参数匹配。
| 表 2 多项式系数与最优能耗 Table 2 Polynomial coefficient and optimal energy consumption |
通过改进遗传算法的求解,能够获得最优驱动关节能耗所对应的最优被动元件参数匹配,即主动驱动力矩、被动弹性力矩和被动阻尼力矩的最优匹配。如图 4所示,改进遗传算法求出的被动弹性力矩、被动阻尼力矩和主动力矩能够较好地重构关节合力矩,并且主动力矩在整个运动周期中相对较小,因此验证了在引入被动元件且被动元件参数最优匹配时,能够在保证关节合力矩的情况下实现驱动力矩最小的目标。为进一步检验本文所提方法对于驱动关节能耗的降低效果,本文计算了在最优被动元件参数匹配下的膝关节驱动能耗。

|
Download:
|
| 图 4 膝关节主-被动力矩重构 Fig. 4 Reconstruction of the active & passive knee torque | |
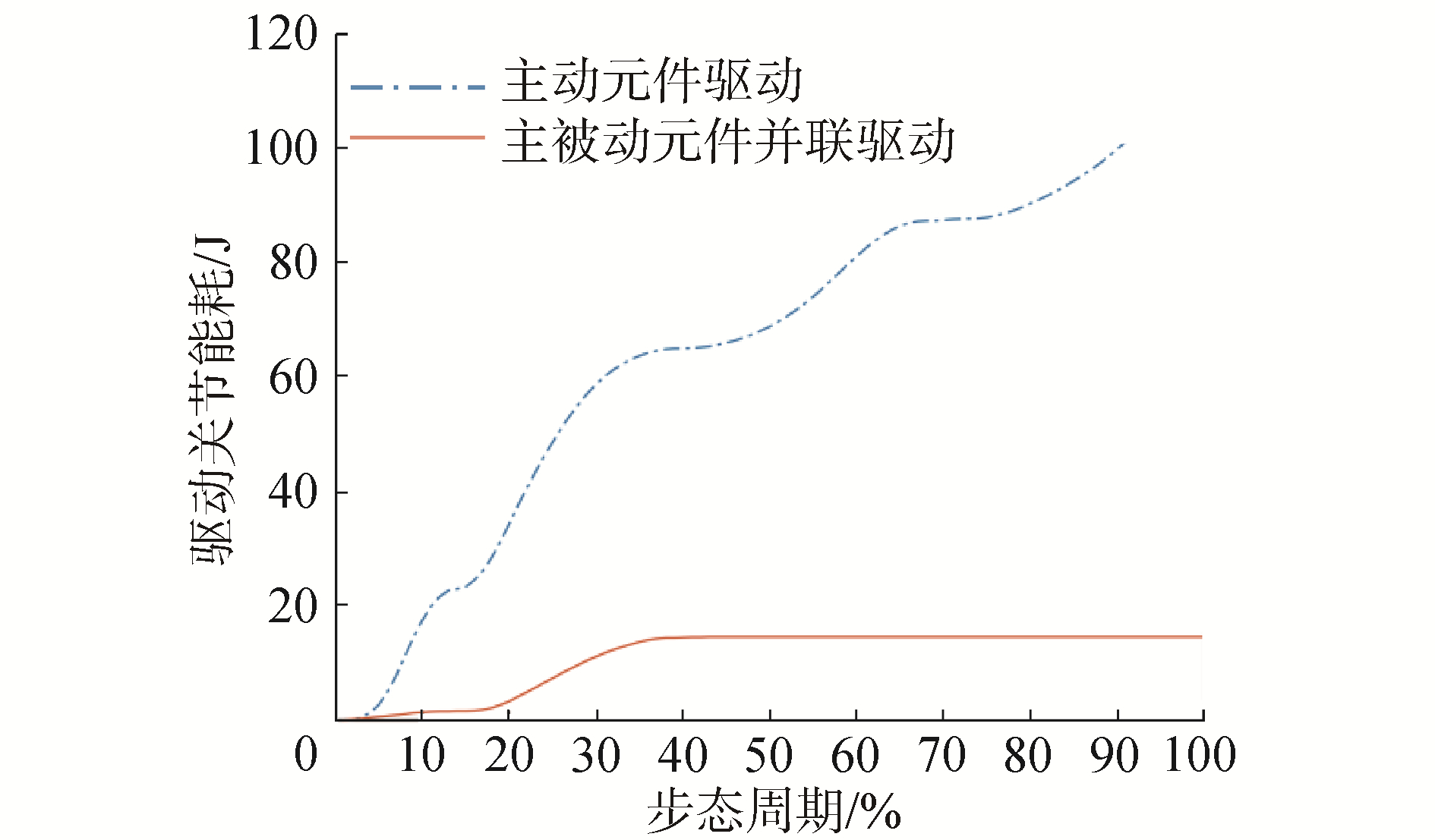
最优被动元件参数匹配下的膝关节驱动能耗如图 5所示,可见在未引入被动元件时驱动关节的能耗明显高于引入被动元件时的能耗,加入被动元件后外骨骼膝关节在一个运动周期内的能耗仅为15.29 J,相比未加入被动元件时的能耗109.32 J,理论上膝关节驱动能耗下降了约86%,说明在最优的被动元件参数匹配时能有效降低驱动关节的能耗。
|
Download:
|
| 图 5 膝关节驱动能耗对比 Fig. 5 Comparison of the energy consumption of knee driver | |
为进一步检验本文提出的被动元件参数最优匹配方法在实际应用中的效果,本文基于如图 6所示的主被动并联驱动单元对顶实验平台验证被动元件参数的最优匹配能否降低驱动能耗。

|
Download:
|
| 图 6 主-被动并联驱动单元对顶实验平台 Fig. 6 Experimental platform of active-passive parallel driver | |
本文设计的主-被动并联驱动单元对顶实验平台主要由2台相同型号的直线电机、弹簧凸轮机构和磁粉制动器组成,其中直线电机2、弹簧凸轮机构和磁粉制动器彼此并联。如图 7所示,直线电机的直线运动由电磁直接驱动,无需借助减速箱,直线电机主要由定子、钕铁硼磁性滑杆、位置温度传感器和驱动器组成,该款直线电机质量3.5 kg,行程1 830 mm,最大输出力572 N,最大输出速度2.9 m/s,定子质量1.93 kg,定子直径48 mm,定子长度289.5 mm,滑杆质量1.46 kg,滑杆直径28 mm,滑杆长度350 mm。

|
Download:
|
| 图 7 直线电机结构 Fig. 7 The structure of linear motor | |
滑杆是一根内部装满汝铁硼磁钢的不锈钢管。定子包括电机线圈、滑杆轴承、位置传感器、温度传感器和电机微处理器。电机停止或运动过程中,内置位置传感器将持续测量和监控电机当前位置,位置偏差将发送给驱动器。直线电机响应速度快,能够精确控制电机的位置、速度和加速度,能够实现高性能的位置伺服和力伺服控制,相比传统电机加减速器的驱动方案,直线电机由于没有减速器且惯量小,因此能够实现响应速度更快且精确更高的力控制,由于外骨骼机器人只有通过精确的力控制才能实现人机之间良好的柔顺交互,因此采用直线电机作为膝关节外骨骼的驱动电机能获得更好的助力效果。
主-被动并联驱动单元对顶实验平台的控制器采用工业PLC(贝加莱,X20CP1586),直线电机的输出轴末端集成了拉压力传感器。弹簧凸轮机构用于产生非线性的被动弹性力矩,弹簧采用刚度为24 N/mm的模具弹簧,磁粉制动器用于模拟非线性的被动阻尼力矩,磁粉制动器最大能够提供6 N/mm制动力矩。被动弹性力矩和被动阻尼力矩通过齿轮齿条机构转化为力矢量,该力矢量与直线电机的输出力矢量平行。
根据前文提出的被动元件参数最优匹配方法,可以指导凸轮的外形设计,使弹簧凸轮机构能够产生最优的被动弹性力矩,同理磁粉制动器产生的阻尼力等于采用前文方法获得的最优被动阻尼力矩。直线电机2用于产生膝关节外骨骼的驱动力,直线电机1用于模拟行走过程中的膝关节位移,需要注意的是由于本文采用如图 3所示的膝关节外骨骼,该外骨骼膝关节利用直线电机驱动,直线电机带动钢丝绳牵拉外骨骼关节,因此外骨骼膝关节的角位移需要映射到直线电机输出轴的直线位移,钢丝绳驱动圆盘的半径e=6.5 cm,膝关节角位移θ和直线电机输出轴位移x的关系为:
| $ x=\theta \cdot e $ | (15) |
如图 6所示,实验对顶平台分为左右2部分,左半部分的直线电机1作位置伺服控制,膝关节运动过程中的角位移映射到直线电机1的直线位移。平台右半部分的直线电机2作力伺服控制,为验证引入被动元件对驱动能耗的影响,本实验分为2组,实验1拆除凸轮弹簧机构和磁粉制动器,此时外骨骼膝关节驱动力完全由直线电机2提供;实验2包含凸轮弹簧机构和磁粉制动器,此时外骨骼膝关节驱动力由直线电机2、凸轮弹簧机构和磁粉制动器共同提供。
2组对照试验的关键是保证试验台右半部分的输出合力和位移与期望值相等,图 8为主-被动并联驱动单元对顶实验平台直线电机输出位移对期望位置的跟踪控制结果,图 9为直线电机输出力对期望力的跟踪控制结果。

|
Download:
|
| 图 8 直线电机位置跟踪控制结果 Fig. 8 The position tracking control property of linear motor | |

|
Download:
|
| 图 9 直线电机力跟踪控制结果 Fig. 9 The force tracking control property of linear motor | |
如图 8所示,直线电机输出位移曲线与期望位置曲线较为接近,绝对误差在3 mm以内,满足目标位置的精度要求。如图 9所示,直线电机输出力与期望力较为接近,输出力绝对误差在8 N以内,电机输出力满足目标输出力的精度要求。通过以上实验数据可知,直线电机位置和力的控制效果好,响应速度快且精度高。
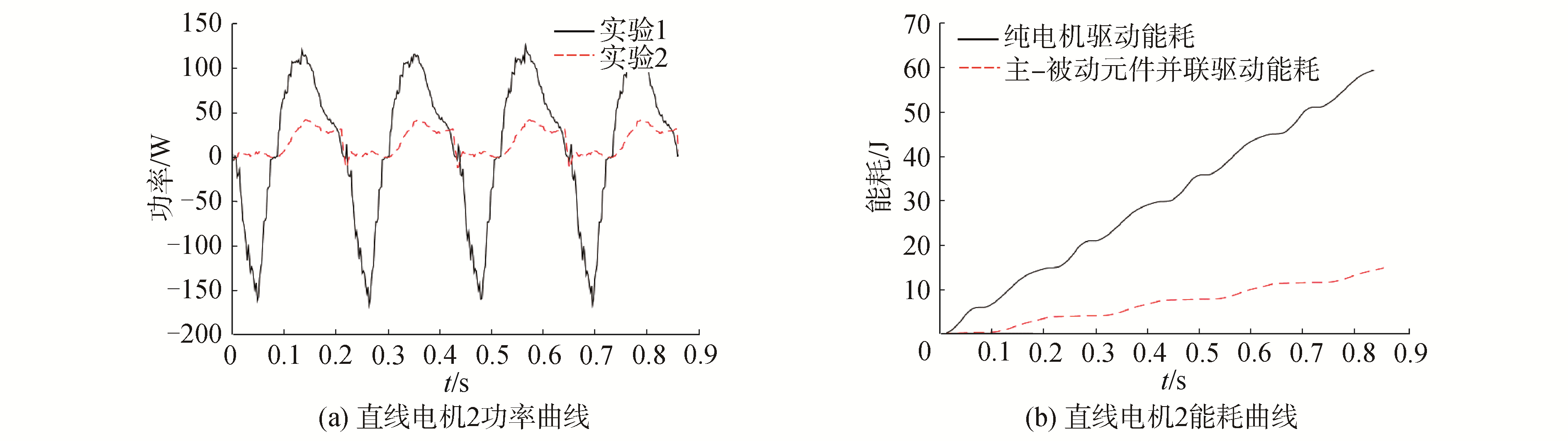
实验1和实验2中直线电机2的功率曲线如图 10(a)所示,可以看到引入被动元件后能够有效降低驱动电机的功率,直线电机2的能耗如图 10(b)所示,同样可以看到引入被动元件后,直线电机2在4个运动周期中消耗的总能量仅为17.61 J,而无被动元件时直线电机2在4个运动周期中消耗的总量为60.38 J,可见引入被动元件后驱动电机的能耗降低了约70.8%,但低于86%的理论能耗下降率。虽然引入被动元件后驱动电机的实际能耗下降率小于理论计算的下降率,但仍然相比于未引入被动元件时的驱动能耗有了较大的降低,从而验证了本文所提的被动元件最优匹配方法的有效性。
|
Download:
|
| 图 10 实验一和实验二驱动电机功率与能耗对比 Fig. 10 Comparison of power and energy consumption of two experiments | |
实际能耗下降率与理论能耗下降率的误差主要由3个方面原因造成。首先,本文仅采用基于卡尔曼滤波的改进遗传算法进行最优参数匹配问题求解,并未与诸如粒子群优化[12]、模拟退火算法[13]、蚁群算法[14]或神经网络算法[15]等其他优化算法进行对比分析,因此本文所提的方法可能仅获得了被动元件参数最优匹配问题的局部最优解,今后的研究中需要进一步尝试采用其他优化算法进行求解,并通过对比分析找到一种最佳的优化方法。其次,本研究中未考虑被动元件存在的摩擦与能量消耗,由于被动元件之间不可避免地存在摩擦损耗,因此即使在最优的被动元件参数匹配下,实际驱动器的能耗下降率仍然低于理论的驱动器能耗下降率。最后,误差原因主要来自于实际被动元件的加工误差和材料性能的误差,由于凸轮轮廓线的计算和加工误差以及弹簧刚度的误差会导致实际被动弹性力矩与理论弹性力矩的误差,并且由于磁粉制动器本身的制造误差以及阻尼力控制的误差,将会造成实际被动阻尼力矩与理论值之间的误差,故被动弹性力矩误差和被动阻力力矩误差共同导致了实际驱动器的能耗与理论能耗之间的误差。
5 结论1) 被动元件参数的最优匹配问题本质上是一个优化问题。优化目标是使驱动关节的能耗最低,约束条件是保证驱动关节的输出合力矩为期望值。被动元件参数最优匹配的目标是在保证驱动关节期望输出合力矩的条件下,通过最优的匹配主动驱动力矩、被动弹性力矩和被动阻尼力矩使驱动关节能耗最低。
2) 基于卡尔曼滤波的改进遗传算法能够求解被动元件参数最优匹配问题。首先利用卡尔曼滤波生成较优的初始种群,使个体尽可能落在可行域内,从而减少无效个体产生的数量;其次利用自适应交叉概率,保证较优的个体能有较大的概率遗传到下一代。
3) 实验表明利用改进遗传算法求出的被动元件最优参数匹配,能够显著降低膝关节外骨骼驱动关节的能耗。
未来的主要研究内容是考虑元件的摩擦损耗并改进优化算法从而提高实际驱动器的节能效果,同时进一步优化被动元件、主动元件以及整个外骨骼驱动关节的结构设计和制造方法,从而获得结构更加紧凑轻便的低能耗外骨骼驱动关节。
| [1] |
KAZEROONI H, RACINE J L, HUANG Lihua, et al. On the control of the berkeley lower extremity exoskeleton (BLEEX)[C]//Proceedings of the 2005 IEEE International Conference on Robotics and Automation. Barcelona, Spain, 2005: 4356-4360.
(  0) 0)
|
| [2] |
STEGER R, KIM S H, KAZEROONI H. Control scheme and networked control architecture for the Berkeley lower extremity exoskeleton (BLEEX)[C]//Proceedings of 2006 IEEE International Conference on Robotics and Automation, 2006. Orlando, FL, USA, 2006: 3469-3476.
(  0) 0)
|
| [3] |
ZOSS A, KAZEROONI H. Architecture and hydraulics of a lower extremity exoskeleton[C]//Proceedings of ASME 2005 International Mechanical Engineering Congress and Exposition. Orlando, Florida, USA, 2005: 1447-1455.
(  0) 0)
|
| [4] |
LOW K H, LIU Xiaopeng, YU Haoyong. Development of NTU wearable exoskeleton system for assistive technologies[C]//Proceedings of IEEE International Conference Mechatronics and Automation. Niagara Falls, Ont., Canada, 2005: 1099-1106.
(  0) 0)
|
| [5] |
HIROSE S, KATO K. Study on quadruped walking robot in Tokyo institute of technology-past, present and future[C]//Proceedings of IEEE International Conference on Robotics and Automation. San Francisco, CA, USA, 2000: 414-419.
(  0) 0)
|
| [6] |
BOBBERT M F, YEADON M R, NIGG B M. Mechanical analysis of the landing phase in heel-toe running[J]. Journal of biomechanics, 1992, 25(3): 223-234. (  0) 0)
|
| [7] |
COLLINS S H, WIGGIN M B, SAWICKI G S. Reducing the energy cost of human walking using an unpowered exoskeleton[J]. Nature, 2015, 522(7555): 212-215. DOI:10.1038/nature14288 (  0) 0)
|
| [8] |
WALSH C J, PASCH K, HERR H. An autonomous, underactuated exoskeleton for load-carrying augmentation[C]//Proceedings of 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing, China, 2007: 1410-1415.
(  0) 0)
|
| [9] |
SANKAI Y. The leading edge of future technology "Cybernics": project HAL-toward robot suits and cyber suits?[C]//Proceedings of the Ninth IEEE International Symposium on Wearable Computers. Osaka, Japan, 2005: xvii.
(  0) 0)
|
| [10] |
Spingwalker[EB/OL]. (2012). http://www.springwalker.com.
(  0) 0)
|
| [11] |
EIBEN A E, SCHUT M C, DE WILDE A R. Boosting genetic algorithms with self-adaptive selection[C]//Proceedings of 2006 IEEE International Conference on Evolutionary Computation. Vancouver, BC, Canada, 2006: 477-482.
(  0) 0)
|
| [12] |
王皓, 高立群, 欧阳海滨. 多种群随机差分粒子群优化算法及其应用[J]. 哈尔滨工程大学学报, 2017, 38(4): 652-660. WANG Hao, GAO Liqun, OUYANG Haibin. Multi-population random differential Particle swarm optimization and its application[J]. Journal of Harbin Engineering University, 2017, 38(4): 652-660. (  0) 0)
|
| [13] |
王国夫, 王鹢, 孙尧, 等. 混合GA与SA求解非线性约束优化[J]. 哈尔滨工程大学学报, 2002, 23(6): 73-76. WANG Guofu, WANG Yi, SUN Yao, et al. Hybrid GA and SA for solving nonlinear constrained optimization problems[J]. Journal of Harbin Engineering University, 2002, 23(6): 73-76. DOI:10.3969/j.issn.1006-7043.2002.06.019 (  0) 0)
|
| [14] |
YANG Yan, KAMEL M S. An aggregated clustering approach using multi-ant colonies algorithms[J]. Pattern recognition, 2006, 39(7): 1278-1289. DOI:10.1016/j.patcog.2006.02.012 (  0) 0)
|
| [15] |
COOK D F, RAGSDALE C T, MAJOR R L. Combining a neural network with a genetic algorithm for process parameter optimization[J]. Engineering applications of artificial intelligence, 2000, 13(4): 391-396. DOI:10.1016/S0952-1976(00)00021-X (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


