2. 哈尔滨工程大学 海洋信息获取与安全工信部重点实验室, 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
近年来,移动水声通信技术在军事和民用方面吸引了大量研究人员的关注。水声信道可利用的有效频带范围极其有限,且典型的水声通信属于宽带或者超宽带信号范畴(即通信带宽与信号载频具有可比性)[1],因此通信平台之间的相对运动引发的多普勒效应不再表现为接收信号的多普勒频移(即窄带多普勒效应),而是导致接收信号的压缩或者扩张效应(即宽带多普勒效应)[2];此外,严重的多途扩展以及复杂的海洋背景噪声干扰均是制约高速移动水声通信发展的关键因素[3-14]。
在20世纪90年代初期,很多水声通信的研究人员均集中在窄带多普勒估计与补偿技术上,典型的接收机方案是联合自适应信道均衡及二阶数字锁相环(DPLL)相位补偿技术,在大量试验验证中均取得了很好的效果[3-4]。为了进一步提升系统性能,一般利用空时处理技术对多路接收信号进行联合处理以便提高接收机输入信噪比及稳健性。Stojanovic等[5]实现了基于单输入多输出(single input multiple output, SIMO)配置条件下的远距离相干水声通信,该接收机由多路分数间隔前馈滤波器、多路数字锁相环及单个反馈滤波器组成,在接收机端采用内嵌二阶PLL的自适应判决反馈均衡器对接收多个通道的数据进行相位补偿及自适应均衡,在最小均方误差(minimum mean square error, MMSE)准则下利用自适应RLS算法对均衡器系数进行有效更新;在准静态条件下给接收机取得了很好的试验数据处理结果。随后,为了降低SIMO接收机的计算复杂度,Stojanovic等[6]提出了一种有效的空时联合处理技术; 基于海试试验数据,对比研究了最优波束形成接收机及有效空时处理接收机的通信性能,证明了这2种接收机是等效的。其采用的有效空时处理技术是利用空间预综合器的预综合矩阵将输入的多路接收信号合并成较少的输出通道以便后续的均衡及相应的解算处理,从而减少了前馈滤波器和相位补偿器的数量,最终降低了接收机的复杂度。在上述基础上,为了进一步降低接收机复杂度并提升系统性能,Stojanovic等[7]提出了基于信道估计的等效判决反馈接收机结构,该接收机由空间预综合器、分数间隔信道估计器、信道因果部分符号间干扰抵消器以及等效分数间隔前馈滤波器组成;试验数据处理结果表明了其提出的接收机的有效性;但Stojanovic仅仅处理了准静态条件的试验数据,而对于宽带信号的多普勒效应而言,该接收机结构并不适用。
针对宽带多普勒的补偿问题,许多学者做了大量的研究[8-15]。Sharif等[8]利用线性插值器对接收到的移动宽带水声通信信号进行多普勒补偿。该接收机联合判决反馈均衡器和线性插值器,通过估计插值因子实现闭环多普勒补偿,成功地处理了平台相对速度为2.6 m/s,加速度为0.9 m/s2的接收信号。此后,Sharif等[9-10]提出了基于接收基阵的宽带信号多普勒补偿接收机。该接收机包含波束形成器、线性插值器和判决反馈均衡器,并利用七元接收基阵在平台相对速度为2.6 m/s,加速度为0.9 m/s2的情况下成功处理通信速率为16 kbit/s的接收信号。至此,该多普勒补偿方式被广泛地应用到水声单载波通信中[11-17]。例如,Goodfellow等[17]将线性插值器和判决反馈均衡器相联系并应用在无线微型无人遥控潜水器中,实现了可靠的高速率非对称全双工通信。Pelekanakis等[15]将线性插值器和空间预综合器运用到多载波系统中,在单输入单输出框架下实现多载波移动通信。
为了消除宽带多普勒效应对移动水声通信性能的影响,提高接收机在时变多途信道条件下的稳健性,本文提出了一种基于自适应宽带多普勒补偿技术的有效空时接收机结构。
1 SIMO水声通信系统模型 1.1 发射系统模型本文主要研究单输入多输出(SIMO)水声通信系统。发送端产生二进制发送信息比特向量,并对其进行相移键控符号映射,而后在映射符号前加入长度为Nt的训练序列,合成长度为Ns的离散发送符号序列x。将离散发送符号序列x通过滚降因子为γ的脉冲成型滤波器g(t)生成基带模拟信号b(t),即:
| $ b\left( t \right) = \sum\limits_{n = 1}^{{N_s}} {{x_n}g\left( {t - nT} \right)} $ | (1) |
式中T为符号间隔。将基带模拟信号b(t)调制到载波频率fc上,并加入一定长度的线性调频信号作为帧同步信号,从而生成通带发射信号。
假设水声信道最大的多途扩展为L个符号间隔,那么在M元接收基阵的第m个基元接收到的经相干解调后的基带信号可被表示为:
| $ \begin{array}{*{20}{c}} {{y_m}\left( t \right) = \sum\limits_{l = 0}^{L - 1} {{\beta _{m,l}}\left( t \right)b\left( {\left( {1 + {\kappa _l}} \right)t - {\tau _l}} \right){{\rm{e}}^{{\rm{j}}2{\rm{ \mathsf{ π} }}{f_c}\left( {{\kappa _l}t - {\tau _l}} \right)}}} + }\\ {{\eta _m}\left( t \right)} \end{array} $ | (2) |
式中:βm, l(t)为第m个基元所对应的随时间变化的第l个多途分量信号的传播损失;κl=vr/c为第l个多途到达信号的多普勒因子;vr为收发平台的相对速度;c为声速;τl为第l途到达信号的相对时延;ηm(t)是与发送信号独立的均值为0、方差为σm, η2的加性高斯白噪声。
1.2 基于自适应锁相环技术的窄带空时接收机该接收机包含空间预综合器,多路锁相环,自适应信道估计,因果部分符号间干扰消除以及分数间隔等效前馈滤波器,其系统结构如图 1所示。系统以T/2符号间隔对M路接收信号进行采样,并输入空间预综合器综合输出J路信号(J < M)。由于受水声信道时变特性的影响,合并输出的J路信号中信道的多途结构和相位偏差不尽相同。为了提高系统的稳健性,接收机采用J个并行的锁相环和自适应信道估计结构对接收数据进行处理。

|
Download:
|
| 图 1 基于自适应锁相环技术的窄带空时接收机结构 Fig. 1 Block diagram of narrowband spatial and temporal receiver based on adaptive PLL | |
信号经过空间预综合器后的第j路输出可表示为:
| $ {r_j}\left( n \right) = \sum\limits_{m = 1}^M {\mathit{\boldsymbol{c}}_{j,m}^ * {\mathit{\boldsymbol{y}}_m}\left( n \right)} = \mathit{\boldsymbol{c}}_j^\dagger \mathit{\boldsymbol{Y}}\left( n \right),j = 1,2, \cdots ,J $ | (3) |
式中:cj为空间预综合器预综合矩阵C的第j列;ym(n)为离散采样信号矩阵Y(n)的第m行;*代表共轭运算;†代表共轭转置运算。
第j路接收信号又可表示为:
| $ {\mathit{\boldsymbol{r}}_j}\left( n \right) = \sum\limits_{i = - {L_c}}^{{L_a}} {{\mathit{\boldsymbol{h}}_j}\left( i \right)d\left( {n - i} \right){{\rm{e}}^{j{\varphi _j}\left( n \right)}} + {\eta _j}\left( n \right)} $ | (4) |
式中:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_j}\left( i \right) = }\\ {{{\left[ {{h_j}\left( {iT + {L_a}T} \right) \cdots {h_j}\left( {iT} \right) \cdots {h_j}\left( {iT - \left( {{L_c} - 1} \right)T} \right)} \right]}^{\rm{T}}}} \end{array} $ | (5) |
表示nT时刻信道的冲击响应hj(0)的第i个移位;Lc和La分别为信道因果部分和非因果部分的长度;φj(n)代表第j个输出通道锁相环跟踪的相位偏差;ηj(n)代表第j个输出通道的加性噪声。所以,第j个输出通道在nT时刻的因果部分符号间干扰为:
| $ \mathit{\boldsymbol{r}}_j^b\left( n \right) = \sum\limits_{i = 1}^{{L_a}} {{\mathit{\boldsymbol{h}}_j}\left( i \right)d\left( {n - i} \right)} $ | (6) |
为了降低其计算量,因果部分符号间干扰的更新可采用移位的方式实现,即:
| $ \mathit{\boldsymbol{r}}_j^b\left( n \right) = \downarrow \mathit{\boldsymbol{r}}_j^b\left( {n - 1} \right) + \mathit{\boldsymbol{\hat h}}\left( 1 \right)\hat d\left( {n - 1} \right) $ | (7) |
式中:↓表示将rjb(n-1)向下移动2位,并将
| $ \mathit{\boldsymbol{r}}_j^f\left( n \right) = {\mathit{\boldsymbol{r}}_j}\left( n \right){{\rm{e}}^{ - {\rm{j}}{\varphi _j}\left( n \right)}} - \mathit{\boldsymbol{r}}_j^b\left( n \right) $ | (8) |
在该情况下,判决反馈均衡器输出的符号估计为:
| $ \tilde d\left( n \right) = \sum\limits_{j = 1}^J {\mathit{\boldsymbol{w}}_j^\dagger \mathit{\boldsymbol{r}}_j^f\left( n \right)} $ | (9) |
式中:wj为第j个输出通道所对应的等效前馈滤波器的权值向量。系统符号判决误差为:
| $ e\left( n \right) = \hat d\left( n \right) - \tilde d\left( n \right) $ | (10) |
式中
为了保证接收算法的整体性能,空间预综合器、多路锁相环和等效前馈滤波器的系数更新均基于最小均方误差(MMSE)原则,而分数间隔信道估计值则是采用随机近似方法。所以,空间预综合器预综合矩阵C的更新为:
| $ \mathit{\boldsymbol{c}}\left( {n + 1} \right) = \mathit{\boldsymbol{c}}\left( n \right) + {A_1}\left\{ {\mathit{\boldsymbol{s}}\left( n \right),e\left( n \right)} \right\} $ | (11) |
| $ \mathit{\boldsymbol{s}}\left( n \right) = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Y}}\left( n \right)\mathit{\boldsymbol{w}}_1^ * {{\rm{e}}^{ - {\rm{j}}{\varphi _1}\left( n \right)}}}\\ \vdots \\ {\mathit{\boldsymbol{Y}}\left( n \right)\mathit{\boldsymbol{w}}_J^ * {{\rm{e}}^{ - {\rm{j}}{\varphi _J}\left( n \right)}}} \end{array}} \right] $ | (12) |
式中c为预综合矩阵C的列向量表示。同理,等效前馈滤波器组的更新为:
| $ \mathit{\boldsymbol{W}}\left( {n + 1} \right) = \mathit{\boldsymbol{W}}\left( n \right) + {A_2}\left( {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{r}}_1^f\left( n \right)}\\ \vdots \\ {\mathit{\boldsymbol{r}}_J^f\left( n \right)} \end{array}} \right],e\left( n \right)} \right) $ | (13) |
式中:W为J个等效前馈滤波器权值向量的列向量表示;A1和A2表示2个自适应更新算法,并且A1和A2可以选取相同算法或者不同算法。本文后续试验数据处理则均采用收敛速度快的自适应RLS算法[18-19]。锁相环采用二阶递归的方式,即:
| $ \theta \left( n \right) = {\mathop{\rm Im}\nolimits} \left\{ {{w^\dagger }\left( n \right)z\left( n \right){{\rm{e}}^{ - j{\varphi _n}}}{{\rm{e}}^ * }\left( n \right)} \right\} $ | (14) |
| $ {\varphi _{n + 1}} = {\varphi _n} + {K_{f1}}\theta \left( n \right) + {K_{f2}}\sum\limits_{i = 0}^n {\theta \left( i \right)} $ | (15) |
式中:Kf1为比例跟踪常量;Kf2为积分跟踪常量。信道估计采用分数阶随机近似的方法,为了保证估计值渐进无偏,引入遗忘因子λ。其递归更新可表示为:
| $ {{\mathit{\boldsymbol{\hat h}}}_j}\left( n \right) = \lambda {{\mathit{\boldsymbol{\hat h}}}_j}\left( {n - 1} \right) + \left( {1 - \lambda } \right){\mathit{\boldsymbol{r}}_{j,\varphi }}\left( n \right){{\hat d}^ * }\left( n \right) $ | (16) |
| $ {\mathit{\boldsymbol{r}}_{j,\varphi }}\left( n \right) = {\mathit{\boldsymbol{r}}_j}\left( n \right){{\rm{e}}^{ - {\rm{j}}{\varphi _j}\left( n \right)}} $ | (17) |
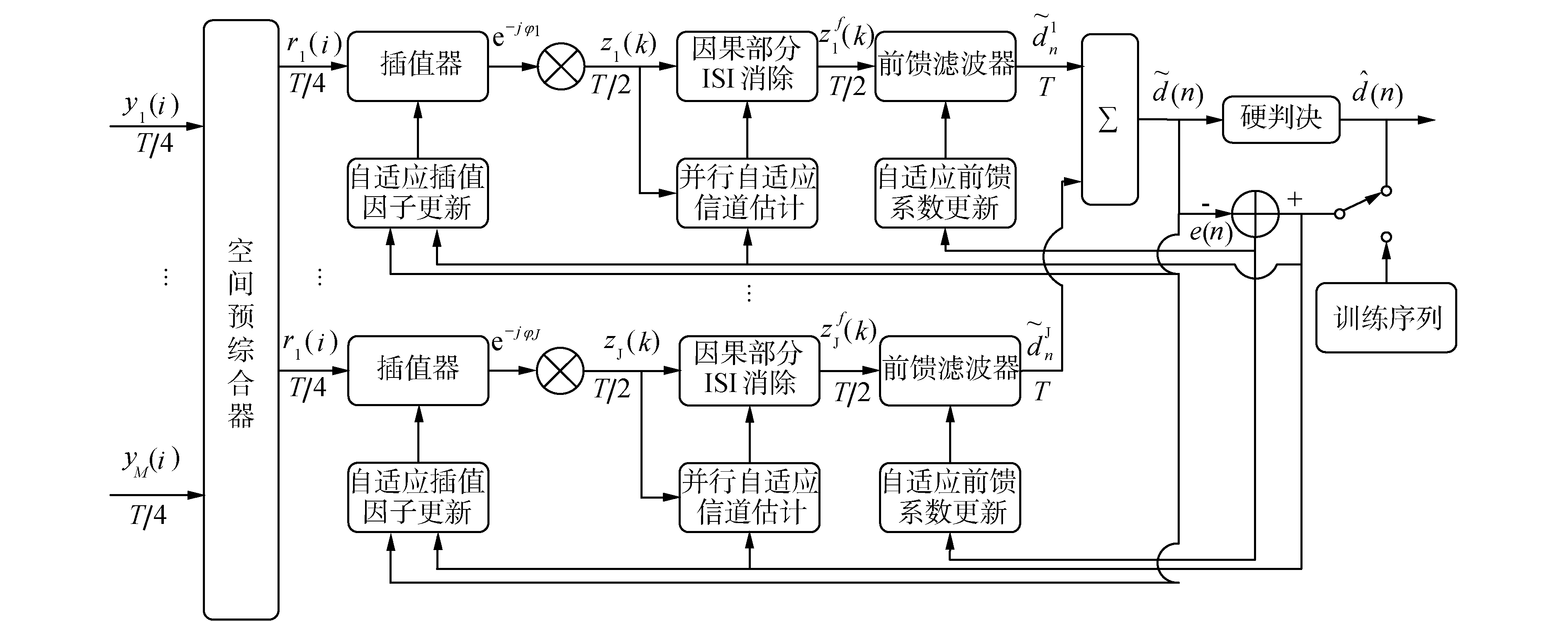
锁相环结构只能跟踪相位的变化,无法解决宽带多普勒效应带来的信号波形的压缩和扩展效应。因此,本文提出一种自适应宽带多普勒补偿方案,能够逐符号地补偿宽带多普勒的影响,其系统框图如图 2所示。
|
Download:
|
| 图 2 基于自适应宽带多普勒补偿技术的有效空时接收机结构 Fig. 2 Block diagram of effective spatial and temporal receiver based on adaptive wideband Doppler compensation technique | |
接收信号以T/4间隔采样后,空间预综合器将M路输入信号综合后输出J路待处理信号。由于水声信道的时变特性,各输出通道信号所包含的多普勒效应和信道的多途结构不尽相同;因此,在接收端配置J个并行插值器和自适应信道估计器。以第j路合并输出信号为例,插值器的更新过程如下:
| $ {\varphi _j}\left( n \right) = {\varphi _j}\left( {n - 1} \right) + 2{\rm{ \mathsf{ π} }}\left( {{I_j}\left( n \right) - 1} \right){f_c}T/2 $ | (18) |
| $ \begin{array}{*{20}{c}} {{z_j}\left( k \right) = \left( {{I_j}\left( n \right){r_j}\left( i \right) + \cdots + } \right.}\\ {\left. {\left( {{I_j}\left( n \right) - 1} \right){r_j}\left( {i + 1} \right)} \right){{\rm{e}}^{ - {\rm{j}}{\varphi _j}\left( n \right)}}} \end{array} $ | (19) |
式中:Ij(n)是第j个插值器的插值因子;φj(n)是第j路输出信号的载波相位偏差估计值,而i和k分别代表以T/4采样间隔和T/2采样间隔的离散样本点;插值器输入信号rj(i)是T/4间隔的空间预综合器输出信号;插值器输出信号zj(k)是对应于T/2间隔的多普勒补偿后的信号。所以,zj(k)也可表示为:
| $ {\mathit{\boldsymbol{z}}_j}\left( n \right) = \sum\limits_{i = - {L_c}}^{{L_a}} {{\mathit{\boldsymbol{h}}_j}\left( i \right)d\left( {n - i} \right){{\rm{e}}^{{\rm{j}}{\varphi _j}\left( n \right)}} + {\eta _j}\left( n \right)} $ | (20) |
由于收发平台具有相对速度,使得信道的多途结构发生变化,且与相对速度呈正相关。为了跟踪信道多途结构的变化,该接收机采用收敛速度较快的RLS算法进行信道估计。因其工作在T/2采样间隔信号上,所以需要2个自适应信道估计器进行并行信道估计,使每个信道估计器的输入信号均为符号间隔采样信号,并将2个信道估计器输出结果进行合并,从而得到T/2间隔信道估计值。其更新过程可被简化为:
| $ {{\mathit{\boldsymbol{\hat h}}}_j}\left( {n + 1} \right) = {{\mathit{\boldsymbol{\hat h}}}_j}\left( n \right) + {\rm{RLS}}\left\{ {{\mathit{\boldsymbol{z}}_j}\left( n \right),\mathit{\boldsymbol{\hat d}}\left( n \right)} \right\} $ | (21) |
根据式(6)、(8)和(9)得到均衡器输出的符号估计值,即:
| $ \mathit{\boldsymbol{z}}_j^b\left( n \right) = \sum\limits_{i = 1}^{{L_a}} {{{\hat h}_j}\left( i \right)\hat d\left( {n - i} \right)} $ | (22) |
| $ \mathit{\boldsymbol{z}}_j^f\left( n \right) = {\mathit{\boldsymbol{z}}_j}\left( n \right) - \mathit{\boldsymbol{z}}_j^b\left( n \right) $ | (23) |
| $ \tilde d\left( n \right) = \sum\limits_{j = 1}^J {\mathit{\boldsymbol{w}}_j^\dagger \mathit{\boldsymbol{z}}_j^f\left( n \right)} $ | (24) |
由于插值器对接收信号重新采样,使得空间预综合器与并行信道估计、因果部分符号间干扰消除器及等效前馈滤波器的输入信号采样率不同。基于MMSE准则更新空间预综合器矩阵时,为了节约计算成本,对输入信号以T/2间隔重新采样,可根据式(11)、(12)进行参数更新。同理,等效前馈滤波器组可根据式(13)进行更新。插值器的更新则是采用最大似然估计,利用相位误差与多普勒成正相关的性质采用跟踪常量更新插值因子,其过程为:
| $ {\theta _{n - 1}} = \arg \left\{ {\tilde d\left( {n - 1} \right){{\hat d}^ * }\left( {n - 1} \right)} \right\} $ | (25) |
| $ I\left( n \right) = I\left( {n - 1} \right) + {K_1}{\theta _{n - 1}} $ | (26) |
式中:θn为nT时刻所对应相位误差;K1为跟踪常量。
2 试验数据处理分析为验证本文提出的基于自适应宽带多普勒补偿技术的有效空时接收机技术的有效性,现对2009年11月6日德克萨斯大学在阿尔湖特拉维斯试验站的试验数据进行分析[20]。试验数据可从文献[21]获得,具体的试验环境和条件可参阅文献[20, 22]。该湖的最大深度约为37 m[23],在发射船上悬挂一个全指向性发射换能器,入水深度为1~8 m;5个接收水听器布放的位置靠近试验站,入水深度为4.6 m。本文处理的数据为发射船高速运动阶段的数据,船速大约1.36 m/s,行驶过程中水深的变化小于5 m。
接收试验信号为QPSK调制,每个数据帧包含4 096个符号,其中前256个符号作为训练序列。发射符号经滚降因子为1的升余弦脉冲成型滤波器生成基带发射信号,而后调制到中心频率为62.5 kHz的载波上;信号带宽为31.25 kHz,符号率为15 625符号/s。
2.1 基于自适应锁相环技术的窄带空时接收机性能分析基于自适应锁相环技术的窄带空时接收机参数设计如下:1)等效前馈滤波器RLS更新算法遗忘因子和简便信道估计更新算法遗忘因子,在训练序列模式下为λ1=0.975,在数据模式下为λ2=0.999;2)空间预综合矩阵RLS更新算法遗忘因子为λ=0.99;3)二阶递归锁相环的跟踪常量为Kf1=2×10-4,积分跟踪常量为Kf2=2×10-5;4)等效前馈滤波器长度和反馈信号长度由信道多途扩展长度决定。其方法为:利用线性调频信号估计输入信道长度及多途结构。线性滤波器长度选取输入信道非因果部分长度的3倍,反馈信号的长度选取大于信道多途扩展长度即可。以第1帧发射信号为例,利用RLS自适应算法在遗忘因子λ=0.975时,估计时变信道结果如图 3所示。

|
Download:
|
| 图 3 时变水声信道 Fig. 3 Time-varying UWA channels | |
从图 3可以看出,水声信道具有明显的时变特性;当收发平台存在相对运动时,信道的多途结构会随着时间发生变化。
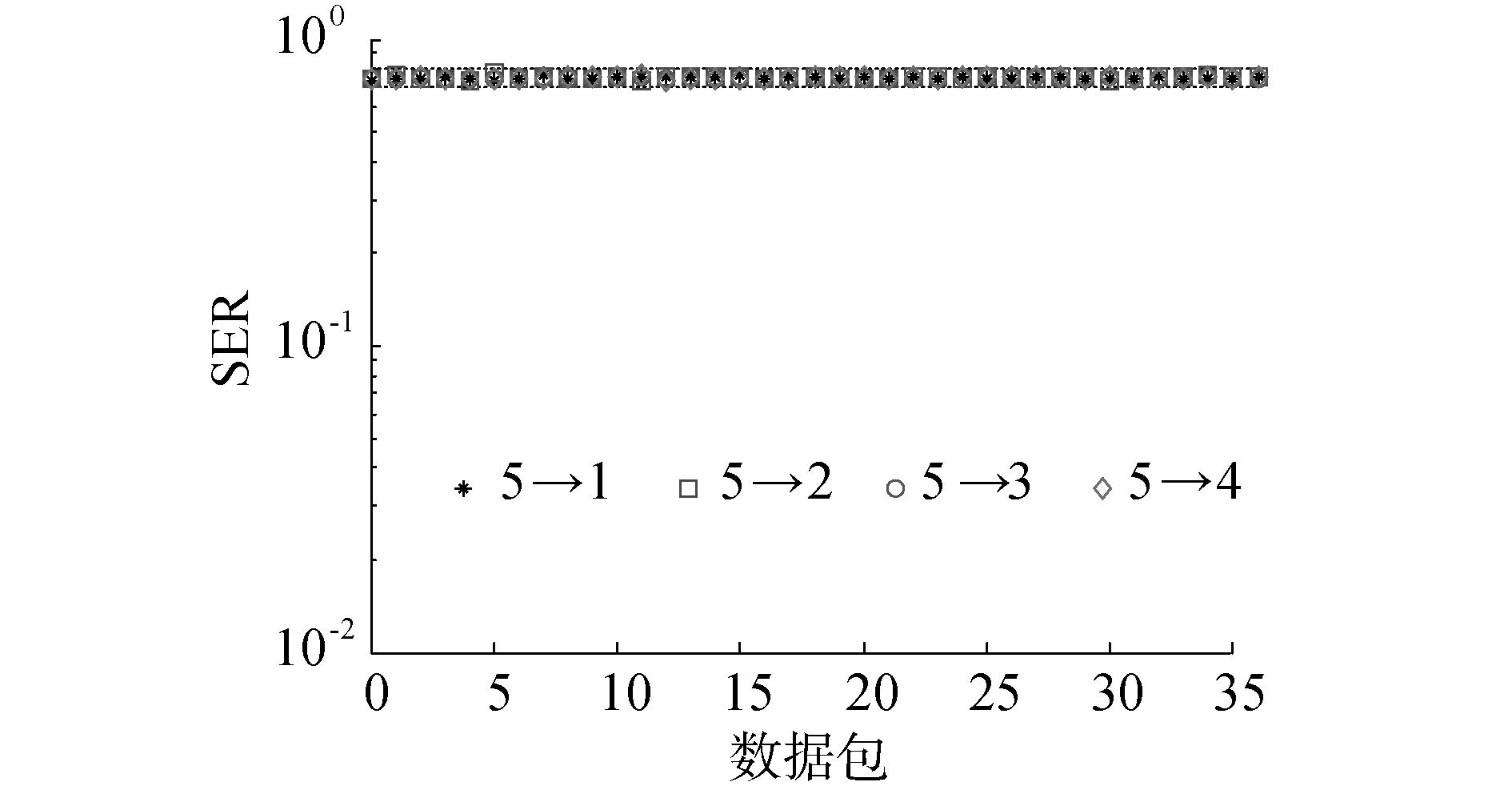
利用基于自适应锁相环技术的窄带空时接收机技术处理上述试验数据。当空间预综合器输入通道数为5时,对应于不同的空间预综合器输出通道数有4种模式,即空间预综合器的5个输入通道可以经过预综合器分别输出1、2、3或4个通道。在这4种模式下,分别处理37帧试验数据,其结果如图 4所示。
|
Download:
|
| 图 4 窄带空时接收机处理结果 Fig. 4 SER for narrowband spatial and temporal receiver | |
从图 4可以看出,在这4种空间预综合模式下接收机误符号率均在0.75左右;说明Stojanovic的接收机结构在接收信号经历宽带多普勒效应条件下完全失效。
2.2 基于自适应宽带多普勒补偿技术的有效空时接收机性能分析利用本文提出的基于自适应宽带多普勒补偿技术的有效空时接收机对该试验数据进行处理。接收机插值器的比例跟踪常量为K1=2×10-3,其余接收机参数均与窄带多普勒假设下的高效多路接收机时一致。
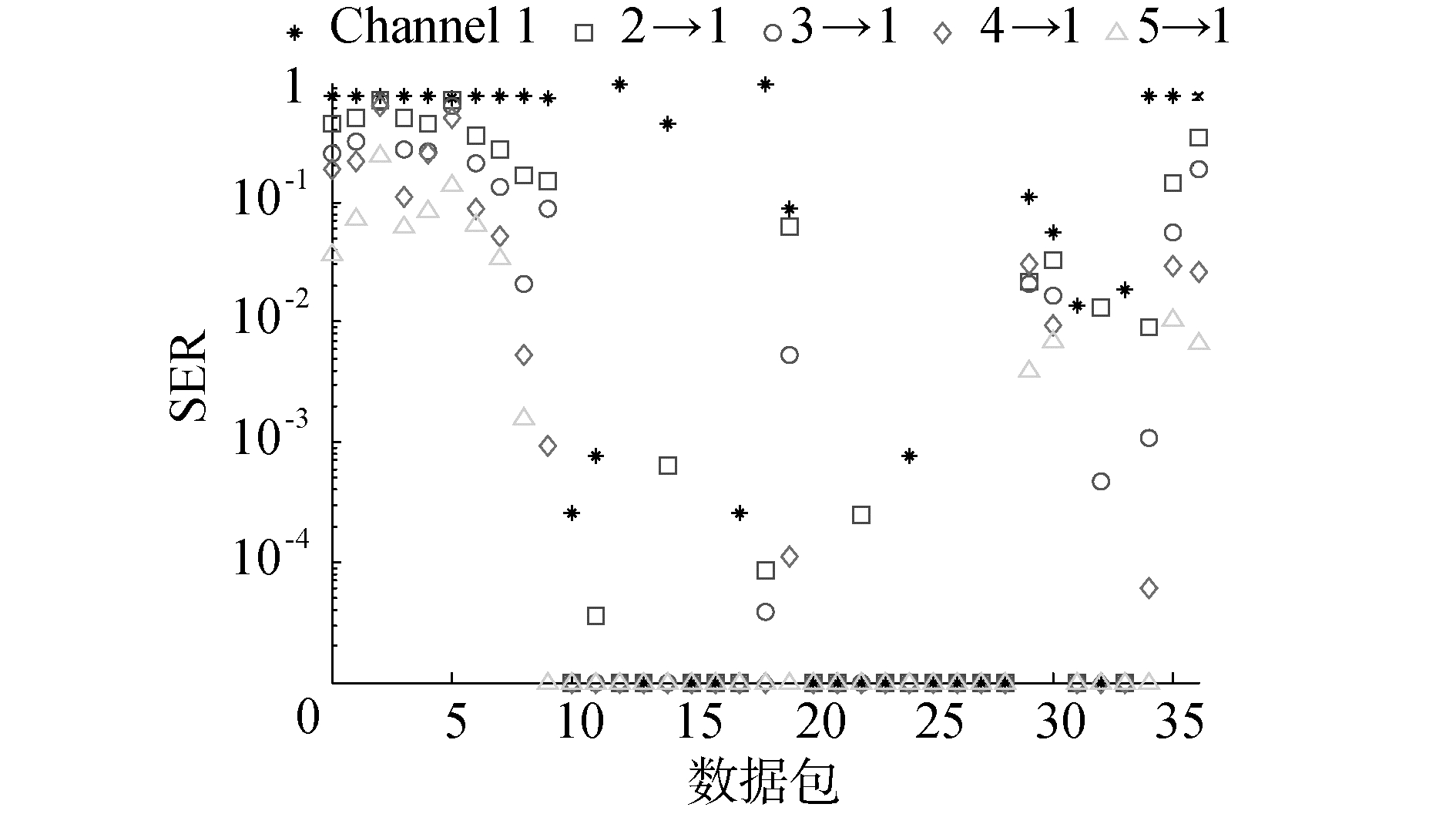
当空间预综合器输出通道数J=1时,在空间预综合器输入通道数M分别为2、3、4和5的条件下,对接收到的37帧信号进行处理;各空间预综合器输入通道的平均误符号率与单路处理结果的对比如图 5所示。
|
Download:
|
| 图 5 预综合后输出通道数为1的处理结果 Fig. 5 SER with one pre-combiner′s output | |
从图 5可以看出,本文提出的接收机处理结果要明显优于单路接收机的处理结果,且随着空间预结合器输入信道数的增多,系统误符号率下降。与图 4中Stojanovic的接收机处理结果相比,本文提出的接收机算法可以有效地处理经历宽带多普勒效应的接收信号。对存在符号判决错误的通道进行最优参数搜索时,其系统误符号率会明显降低[24-25]。
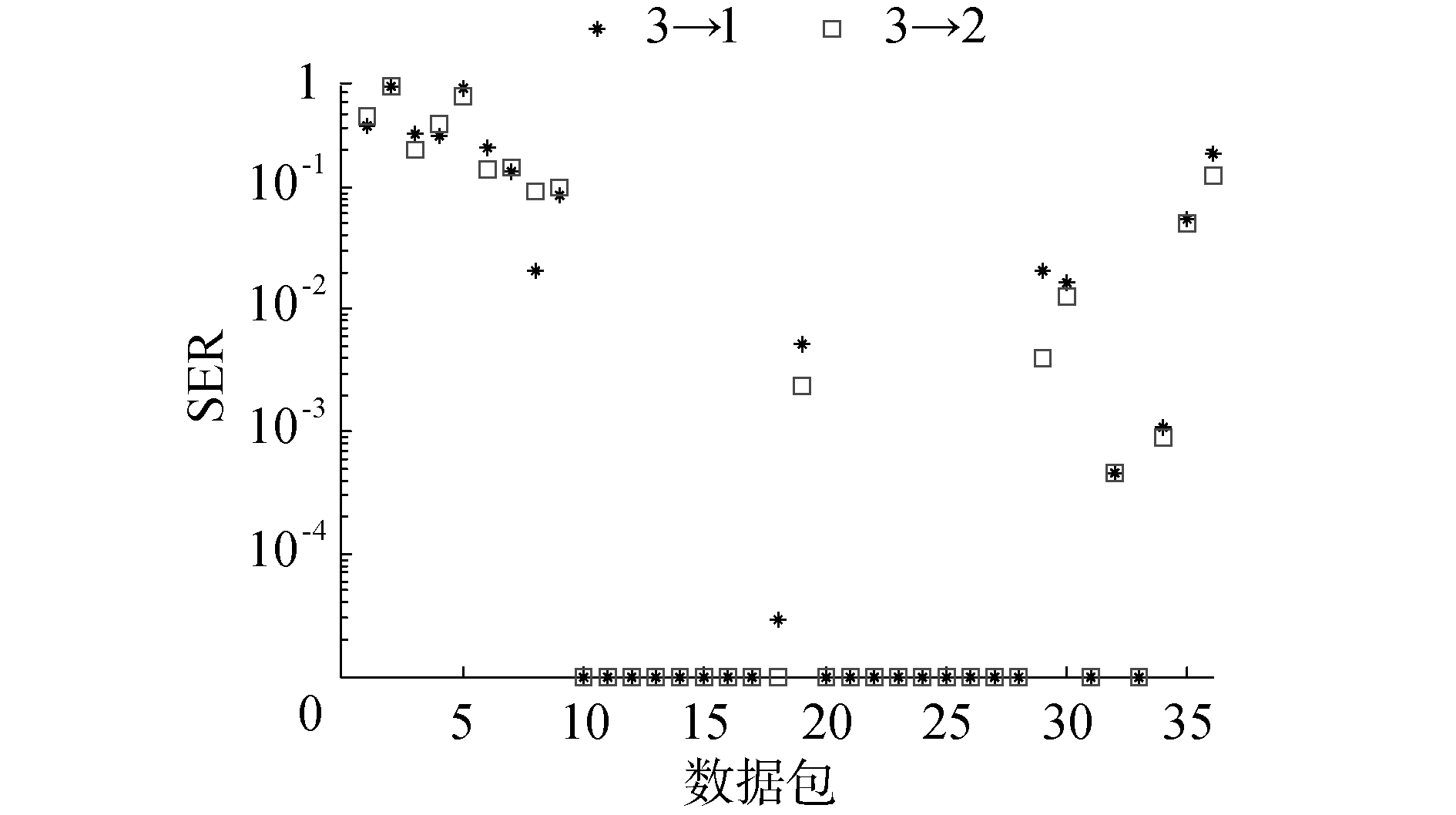
在空间预综合器输入通道数M分别为3、4和5的情况下,针对不同的空间预综合器输出通道进行分析,系统误符号率结果分别如图 6~8所示;均衡器输出信噪比结果如图 9所示,均衡器输出信噪比的计算公式为:
| $ {\rm{SN}}{{\rm{R}}_{{\rm{out}}}} = - 10\lg \left( {\frac{1}{{{N_s}}}\sum\limits_{n = 1}^{{N_s}} {{{\left| {e\left( n \right)} \right|}^2}} } \right) $ | (27) |
|
Download:
|
| 图 6 输入通道数为3时误符号率 Fig. 6 SER for pre-combiner with three input channels | |
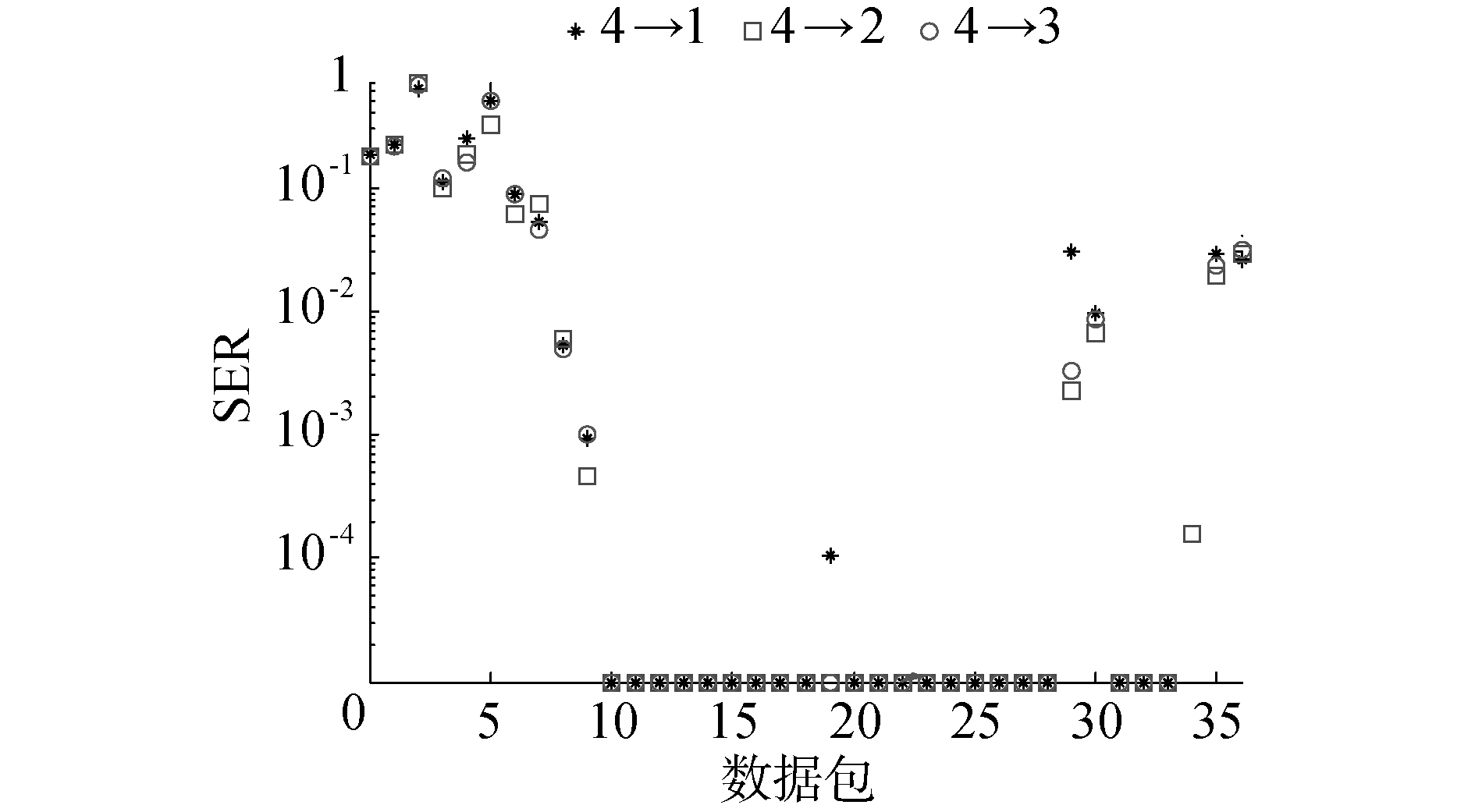
|
Download:
|
| 图 7 输入通道数为4时误符号率 Fig. 7 SER for pre-combiner with four input channels | |

|
Download:
|
| 图 8 输入通道数为5时误符号率 Fig. 8 SER for pre-combiner with five input channels | |

|
Download:
|
| 图 9 3种模式下空间预综合器输入信道数与均衡器输出信噪比 Fig. 9 Number of input channels versus equalizer output SNR versus for the pre-combiner under three modes | |
从图 6可以看出,在空间预综合器输入信道数M为3的条件下,当空间预综合器输出信道J为1时,有19帧数据误符号率为0,有4帧数据误符号率小于1×10-2,当空间预综合器输出信道J为2时,有20帧数据误符号率为0,有5帧数据误符号率小于1×10-2;从图 7中可以看出,在空间预综合器输入信道数J为4的条件下,当空间预综合器输出信道J为1时,有21帧数据误符号率为0,有5帧数据误符号率小于1×10-2,当空间预综合器输出信道为2和3时,有22帧数据误符号率为0,有5帧数据误符号率小于1×10-2;从图 8中可以看出,在空间预综合器输入信道数J为5的条件下,当空间预综合器输出信道为1、2、3和4时,有24帧数据误符号率为0,有5帧数据误符号率小于1×10-2。从图 9中可以看出,在空间预综合器输出通道数J为1时,空间预综合器输入通道数J为5的均衡器输出信噪比比空间预综合器输入通道数J为3的均衡器输出信噪比高1.15 dB;空间预综合器输入通道数J为4的均衡器输出信噪比比空间预综合器输入通道数J为3的均衡器输出信噪比高0.65 dB。在空间预综合器输出通道数J为2时,空间预综合器输入通道数J为5的均衡器输出信噪比比空间预综合器输入通道数为3的均衡器输出信噪比高1.1 dB;空间预综合器输入通道数J为4的均衡器输出信噪比比空间预综合器输入通道数J为3的均衡器输出信噪比高0.5 dB。在空间预综合器输入通道数相同的条件下,输出信噪比随着综合后输出通道数的增多先增大后趋于稳定且不在增加。综上,随着空间预综合器输入通道数的增多,均衡器输出信噪比增大,当空间预综合器的输入通道数相同时,均衡器输出信噪比随着空间预综合器输出通道数的增多而增大至趋于稳定,一般为了兼顾性能以及接收机的复杂度,在本文的条件下选择J为3可以获得很好的性能与复杂度的平衡。
3 结论1) 基于自适应宽带多普勒补偿技术的有效空时接收机技术的输出信噪比在同一空间预综合器输出通道数的条件下,随着空间预综合器输入通道数的增多而变大;在相同空间预综合器输入通道数的条件下,输出信噪比随着综合后输出通道数的增多先增大后趋于稳定。
2) 在系统误符号率方面,基于自适应锁相环技术的窄带空时接收机在处理高速运动平台间的宽带接收信号时,系统误符号率为0.75,系统完全失效;利用本文提出的基于自适应宽带多普勒补偿技术的有效空时接收机技术处理37帧接收数据时,在空间预综合器输入信道数为5的条件下,有24帧数据误符号率为0,有5帧数据误符号率小于1×10-2,表明本文提出的接收机能够满足移动条件下的水声通信的需求。
| [1] |
EGGEN T H, BAGGEROER A B, PREISIG J C. Communication over Doppler spread channels. Part Ⅰ: Channel and receiver presentation[J]. IEEE journal of oceanic engineering, 2001, 25(1): 62-71.
(  0) 0)
|
| [2] |
田坦. 声呐技术[M]. 2版. 哈尔滨: 哈尔滨工程大学出版社, 2010: 23-27.
(  0) 0)
|
| [3] |
JOHNSON M, FREITAG L, STOJANOVIC M. Improved Doppler tracking and correction for underwater acoustic communications[C]//Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing. Munich, Germany, 1997: 575-578.
(  0) 0)
|
| [4] |
STOJANOVIC M, CATIPOVIC J A, PROAKIS J G. Phase-coherent digital communications for underwater acoustic channels[J]. IEEE journal of oceanic engineering, 1994, 19(1): 100-111. DOI:10.1109/48.289455 (  0) 0)
|
| [5] |
STOJANOVIC M, CATIPOVIC J, PROAKIS J G. Adaptive multichannel combining and equalization for underwater acoustic communications[J]. The journal of the acoustical society of America, 1993, 94(3): 1621-1631. DOI:10.1121/1.408135 (  0) 0)
|
| [6] |
STOJANOVIC M, CATIPOVIC J A, PROAKIS J G. Reduced-complexity spatial and temporal processing of underwater acoustic communication signals[J]. The journal of the acoustical society of America, 1995, 98(2): 961-972. DOI:10.1121/1.413521 (  0) 0)
|
| [7] |
STOJANOVIC M. Efficient processing of acoustic signals for high-rate information transmission over sparse underwater channels[J]. Physical communication, 2008, 1(2): 146-161. DOI:10.1016/j.phycom.2008.02.001 (  0) 0)
|
| [8] |
SHARIF B S, NEASHAM J, HINTON O R, et al. A computationally efficient Doppler compensation system for underwater acoustic communications[J]. IEEE journal of oceanic engineering, 2000, 25(1): 52-61. DOI:10.1109/48.820736 (  0) 0)
|
| [9] |
SHARIF B S, NEASHAM J, HINTON O R, et al. Adaptive Doppler compensation for coherent acoustic communication[J]. IEE proceedings-radar, sonar and navigation, 2000, 147(5): 239-246. DOI:10.1049/ip-rsn:20000665 (  0) 0)
|
| [10] |
SHARIF B S, NEASHAM J, HINTON O R, et al. Closed loop Doppler tracking and compensation for non-stationary underwater platforms[C]//Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition. Providence, RI, USA, 2000, 1: 371-375.
(  0) 0)
|
| [11] |
SHAH C P, TSIMENIDIS C C, SHARIF B S, et al. EXIT chart analysis of BICM-ID based receiver for shallow underwater acoustic communications[C]//Proceedings of the 2010 7th International Symposium on Wireless Communication System. York, UK, 2010: 6-10.
(  0) 0)
|
| [12] |
GOODFELLOW G M, NEASHAM J A, TSIMENIDIS C C, et al. High data rate acoustic link for Micro-ROVs, employing BICM-ID[C]//Proceedings of the 2012 Oceans-Yeosu. Yeosu, South Korea, 2012: 1-6.
(  0) 0)
|
| [13] |
SHAH C P, TSIMENIDIS C C, SHARIF B S, et al. Low-complexity iterative receiver structure for time-varying frequency-selective shallow underwater acoustic channels using BICM-ID:design and experimental results[J]. IEEE journal of oceanic engineering, 2011, 36(3): 406-421. DOI:10.1109/JOE.2011.2144670 (  0) 0)
|
| [14] |
PELEKANAKIS K, CHITRE M. Robust equalization of mobile underwater acoustic channels[J]. IEEE journal of oceanic engineering, 2015, 40(4): 775-784. DOI:10.1109/JOE.2015.2469895 (  0) 0)
|
| [15] |
PELEKANAKIS K, CHITRE M. Low-complexity subband equalization of mobile underwater acoustic channels[C]//Proceedings of the Oceans 2015-Genova. Genova, Italy, 2015: 1-8.
(  0) 0)
|
| [16] |
PELEKANAKIS K, CHITRE M. A channel-estimate-based decision feedback equalizer robust under impulsive noise[C]//Proceedings of the 2014 Underwater Communications and Networking. Sestri Levante, Italy, 2014: 1-5.
(  0) 0)
|
| [17] |
GOODFELLOW G M, NEASHAM J A, TSIMENIDIS C C, et al. Investigation of a full duplex acoustic link for a tetherless micro-ROV[C]//Proceedings of OCEANS 2011 IEEE-Spain. Santander, Spain, 2011: 1-7.
(  0) 0)
|
| [18] |
PROAKIS J G. Digital communications[M]. 4th ed. New York: McGraw-Hill, 2000.
(  0) 0)
|
| [19] |
HAYKIN S. Adaptive filter theory[M]. 4th ed. NJ: Prentice-Hall Inc., 2002.
(  0) 0)
|
| [20] |
PERRINE K A, NIEMAN K F, HENDERSON T L, et al. Doppler estimation and correction for shallow underwater acoustic communications[C]//Proceedings of the 2010 Conference Record of the Forty Fourth Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA, 2010: 746-750.
(  0) 0)
|
| [21] |
PERRINE K A, NIEMAN K F, LENT K H, et al. The university of texas at austin applied research laboratories Nov. 2009 five-element acoustic underwater dataset[EB/OL].[2017-02-16]. http://users.ece.utexas.edu/~bevans/projects/underwater/datasets/.
(  0) 0)
|
| [22] |
Lower Colorado River Authority. "Historical Lake Levels: Highland Lakes"[EB/OL]. http://www.lcra.org/water/conditions/historical.html.
(  0) 0)
|
| [23] |
NIEMAN K F, PERRINE K A, LENT K H, et al. Multi-stage and sparse equalizer design for communication systems in reverberant underwater channels[C]//Proceedings of 2010 IEEE Workshop on Signal Processing Systems. San Francisco, CA, USA, 2010: 374-379.
(  0) 0)
|
| [24] |
韩笑, 生雪莉, 殷敬伟, 等. 基于双向判决反馈均衡器的水声通信海试试验研究[J]. 兵工学报, 2016, 37(3): 553-558. HAN Xiao, SHENG Xueli, YIN Jingwei, et al. Experimental demonstration of underwater acoustic communication based on bidirectional decision feedback equalizer[J]. Acta armamentarii, 2016, 37(3): 553-558. DOI:10.3969/j.issn.1000-1093.2016.03.023 (  0) 0)
|
| [25] |
乔钢, 王巍, 刘凇佐, 等. 改进的多输入多输出正交频分复用水声通信判决反馈信道估计算法[J]. 声学学报, 2016, 41(1): 95-104. QIAO Gang, WANG Wei, LIU Songzuo, et al. An improved decision feedback channel estimation algorithm for multiple-output orthogonal frequency division multiplexing underwater acoustic communication[J]. Acta acustica, 2016, 41(1): 95-104. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


