金刚石串珠绳凭借其独特的优点,被应用于各个工程领域之中, 如海底破损油气管道的维修切除[1]。对串珠绳的研制主要考虑串珠绳的切削效率以及串珠绳工作寿命。串珠绳的工作寿命由多个因素制约,存在多种失效形式,导致串珠绳寿命降低[2]。其主要包括串珠绳内部钢丝绳的疲劳失效、断裂失效;橡胶保护套的变形撕裂,串珠绳发生窜珠情况[3];串珠表面金刚石磨粒的腐蚀磨损,脱落失效。对于钢丝绳疲劳寿命以及橡胶保护套的使用寿命经工程实践可以通过控制串珠绳张力大小加以改善,对于串珠表面磨粒的脱离失效,目前认识较为浅薄[4]。Zhou等[5]建立金刚石磨粒二维模型,对单个金刚石磨粒进行应力分析。Amaral等[6]提出三维有限元模型,预测模拟由于烧结过程产生的金刚石磨粒附近金属胎体内的塑性变形以及残余应力。串珠绳表面的金刚石磨粒的过早脱落不仅会加速串珠绳的磨损速度,降低其工作寿命,还会降低绳锯机的切削效率。本文分析串珠绳磨粒脱落机理,探究金刚石磨粒把持力影响因素,为串珠绳的研制提供指导。
1 金刚石磨粒脱落失效分析 1.1 金刚石磨粒脱落机理金属胎体对金刚石磨粒的把持力包括胎体材料对磨粒的机械锁紧、烧结过程中材料热胀冷缩之后产生的挤压应力导致的粘着力以及胎体与磨粒表面通过化学反应产生的表面结合力[7]。磨粒与金属胎体之间的脱落失效主要发生在二者之间结合的界面上。因此金刚石磨粒与金属胎体的结合面强度特性的好坏,代表了金属胎体对磨粒的把持能力强弱。金刚石磨粒从金属胎体表面脱落主要有以下3种可能的失效模式:1)打开模式,由于垂直于界面作用的拉伸应力;2)滑动模式,由于平行于结合界面且垂直于裂纹方向的剪切应力;3)撕裂模式,由于平行于界面并平行于裂纹前部的剪切应力[8]。串珠表面金刚石磨粒与金属胎体结合面的厚度相对于胎体磨粒的尺寸过于微小,几乎可忽略不计,而对磨粒胎体系统来说,结合界面的强度是评价金属胎体对金刚石磨粒把持能力的重要参数。
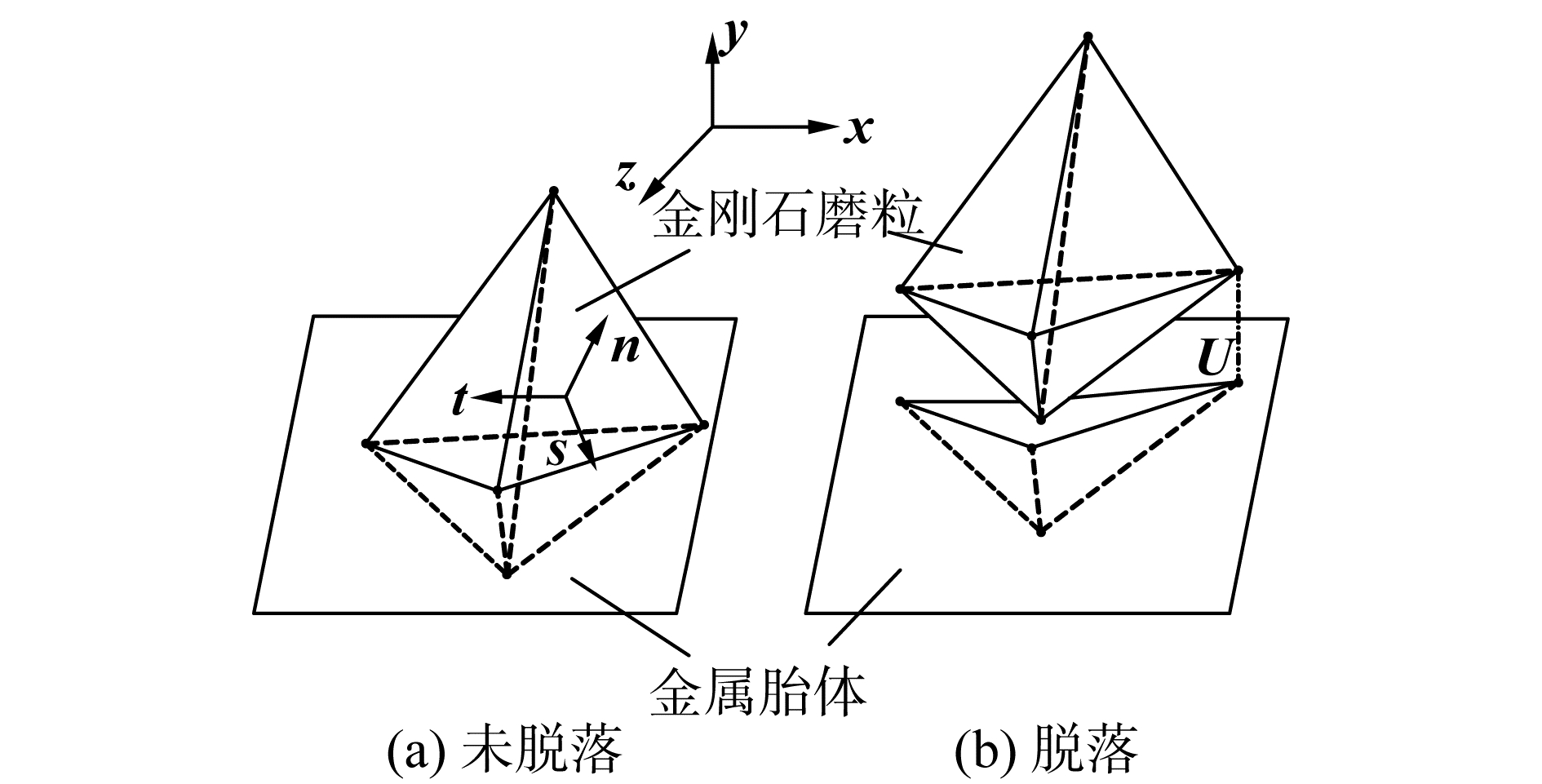
金刚石磨粒从胎体脱落的过程实质上属于界面断裂,是一个复杂的过程。如图 1所示为磨粒脱落示意图。
|
Download:
|
| 图 1 界面断裂磨粒脱落 Fig. 1 Interface fracture particle shedding | |
串珠表面金刚石磨粒与金属胎体结合面的厚度相对于胎体磨粒的尺寸过于微小,几乎可忽略不计,而对磨粒胎体系统来说,结合界面的强度是评价金属胎体对金刚石磨粒把持能力的重要参数。
在磨粒脱落模型的界面中的任何点处的全局坐标中的相对位移矢量U可以表示为:
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\overline x}} }\\ {\mathit{\boldsymbol{\overline y}} }\\ {\mathit{\boldsymbol{\bar z}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}^\mathit{\boldsymbol{ + }}}}\\ {{\mathit{\boldsymbol{y}}^\mathit{\boldsymbol{ + }}}}\\ {{\mathit{\boldsymbol{z}}^\mathit{\boldsymbol{ + }}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}^ - }}\\ {{\mathit{\boldsymbol{y}}^ - }}\\ {{\mathit{\boldsymbol{z}}^ - }} \end{array}} \right] = \sum\limits_{i = 1}^4 {{N_i}} \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}_i^ + }\\ {\mathit{\boldsymbol{y}}_i^ + }\\ {\mathit{\boldsymbol{z}}_i^ + } \end{array}} \right] - \sum\limits_{i = 1}^4 {{N_i}} \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{x}}_i^ - }\\ {\mathit{\boldsymbol{y}}_i^ - }\\ {\mathit{\boldsymbol{z}}_i^ - } \end{array}} \right] $ | (1) |
式中:x+和x-是在全局x方向上结合界面处金刚石磨粒和金属基体的位移分量;xi+和xi-分别为金刚石磨粒单元和金属基体单元第i个节点处的对应位移;Ni为位移的形状函数;全局坐标系中y方向和z方向上的位移分量同理。n,s和t(图 1)表示在局部坐标系中的基准方向量。则局部坐标系中的相对位移δ可以由绝对位移Δ表示:
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{l}} {{\delta _{\rm{n}}}}\\ {{\delta _{\rm{s}}}}\\ {{\delta _{\rm{t}}}} \end{array}} \right] = \mathit{\boldsymbol{Q}}\mathit{\Delta } $ | (2) |
式中:Q为全局坐标系到局部坐标系的变化矩阵。金刚石磨粒从金属胎体脱落的过程可以用双线性弹性-断裂关系来表示。
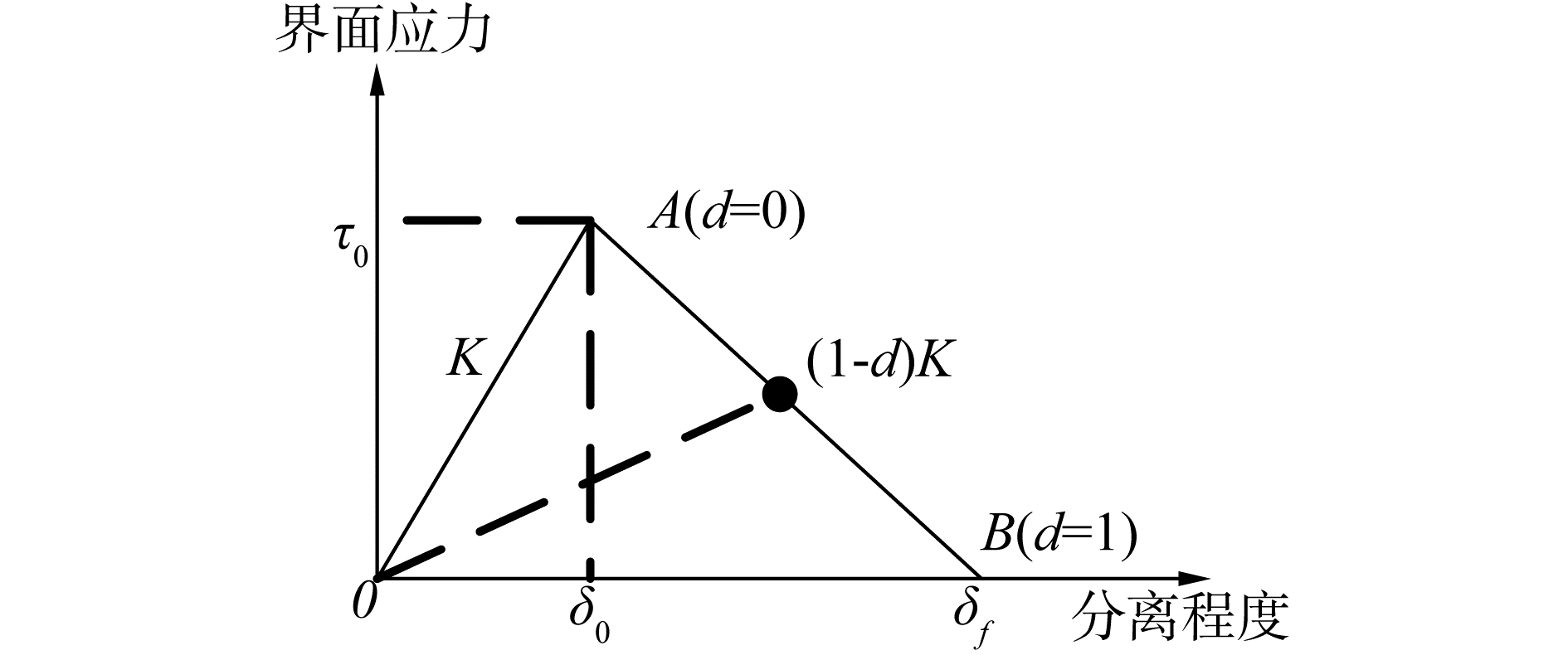
图 2中OA段表示金刚石磨粒金属胎体系统在外界作用下界面发生弹性响应;AB段表示界面的损伤程度;A点表示系统在整个过程中界面产生的极限应力τ0;δ0为界面开始损伤时系统的应变大小;B点表示界面发生完全分离;ΔOAB的面积代表界面的断裂韧性Gc;K表示斜率,结合界面形变处于弹性变形阶段,盈利与分离程度的比值;d表示分离程度。
|
Download:
|
| 图 2 双线性弹性-分离关系 Fig. 2 Relationship of bilinear elasticity-separation | |
实际上,由于串珠绳磨削切割的不同工况,界面断裂的情况更多的是3种模式耦合。在这种情况下,断裂发生的初始应力小于模式Ⅰ中τn,o,模式Ⅱ中τs, 0以及模式Ⅲ中的τt, 0,如图 3所示。

|
Download:
|
| 图 3 混合模式界面破坏模型 Fig. 3 Model of mixed mode interface destruction | |
混合模式下的断裂情况,Cui等[6]提出的二次故障标准适用于此较为合适,当界面发生破坏撕裂,各模式之间的损伤程度总和一定,表现形式为:
| $ {\left( {\frac{{{\tau _{\rm{n}}}}}{{{\tau _{{\rm{n}}, 0}}}}} \right)^2} + {\left( {\frac{{{\tau _{\rm{s}}}}}{{{\tau _{{\rm{s}}, 0}}}}} \right)^2} + {\left( {\frac{{{\tau _{\rm{t}}}}}{{{\tau _{{\rm{t}}, 0}}}}} \right)^2} = 1 $ | (3) |
对于具体到某一颗金刚石磨粒的切削情况,可通过假定金刚石磨粒在各个串珠金属胎体中均匀分布,金刚石磨粒颗粒大小相同计算其平均值。则串珠绳单颗串珠切削时金刚石磨粒的瞬时有效参与数量Ne为[9]:
| $ {N_{\rm{e}}} = {C_{\rm{b}}}{\rm{ \mathsf{ π} }}{d_{\rm{w}}}{L_{\rm{b}}}\eta /2 $ | (4) |
式中:dw为单颗金刚石串珠平均直径;Cb为串珠单位面积上磨粒的数量;Lb为单颗金刚石串珠长度;η为金刚石磨粒接触面有效系数。
2 金刚石磨粒有限元模型 2.1 金刚石磨粒的有限元网络划分及材料属性目前大多数情况下对金刚石磨粒磨损的研究中将其视作为正多边形(2D模型),减轻建模和计算工作量,以Xu[10]提出的二维微机械金刚石磨粒失效模型为代表。
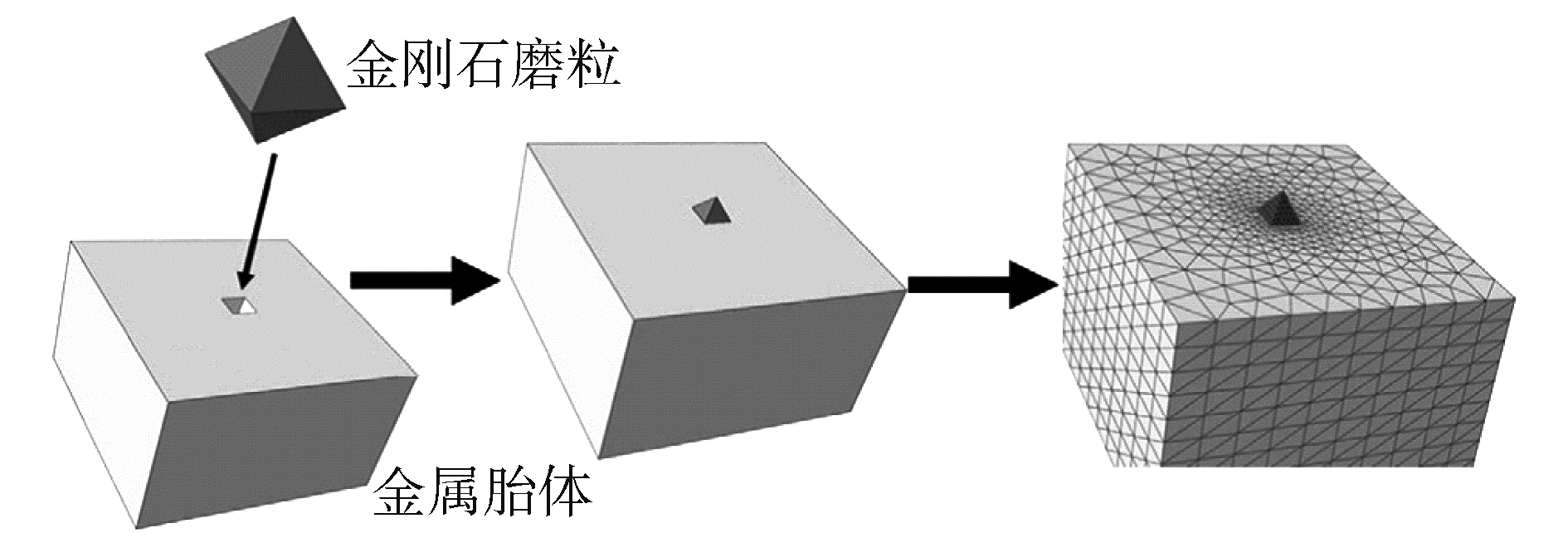
考虑人工制造的金刚石颗粒形状较为规则,为便于建模与研究,假定金刚石磨粒视为8面体结构,边长为0.1 mm,同时选取金属胎体尺寸远大于金刚石磨粒尺寸,保证不影响其应力分布,取胎体边长为2 mm。对系统进行网格划分,取金刚石磨粒网格大小为0.01;金属胎体全局网格大小为0.2;保证分析的准确度,跟金刚石磨粒接触部分进行网格细分为0.01,具体建模如图 4所示。
|
Download:
|
| 图 4 金刚石磨粒有限元模型 Fig. 4 Finite element model of diamond abrasive particle | |
将金刚石磨粒以及金属胎体视为各向同性的弹性体材料,分别为1 100、600 GPa,结合面处因其存在的化学键结合形式,对金刚石磨粒和金属胎体结合的界面另外定义材料参数[11],根据方向不同,强度不同,τn, 0为543 MPa,τs, 0、τt, 0为314 MPa,损伤因子GⅠC为0.14 mJ/mm2,GⅡC、GⅢC为0.33 mJ/mm2。
2.2 磨粒与胎体结合界面强度在金刚石磨粒切削钢材的过程中,磨粒在切向和径向切削力作用下,系统发生弹性变形,同时金刚石磨粒发生轻微的位移响应,随着变形程度加剧,界面处的应力开始线性的增加,当磨粒与金属胎体之间发生断裂之后,应力大小随着位移的增长相应减小。串珠绳切削过程中,忽略串珠绳振动对结果的影响,只考虑由切削应力产生的影响,对其进行仿真分析。图 5为金刚石磨粒受切削力作用时整个系统的应力分布云图。

|
Download:
|
| 图 5 金刚石磨粒应力分布云图 Fig. 5 Stress distribution of diamond abrasive grain | |
在系统刚开始发生断裂时,系统应力主要集中在金刚石磨粒与金属胎体结合界面的接触表面顶点处以及顶点附近,在界面处的应力并不明显。仿真结果与文献[9]提出的二维微机械金刚石磨粒失效模型基本相近,说明结合界面力学性能的不同对于系统的应力分布基本无影响。
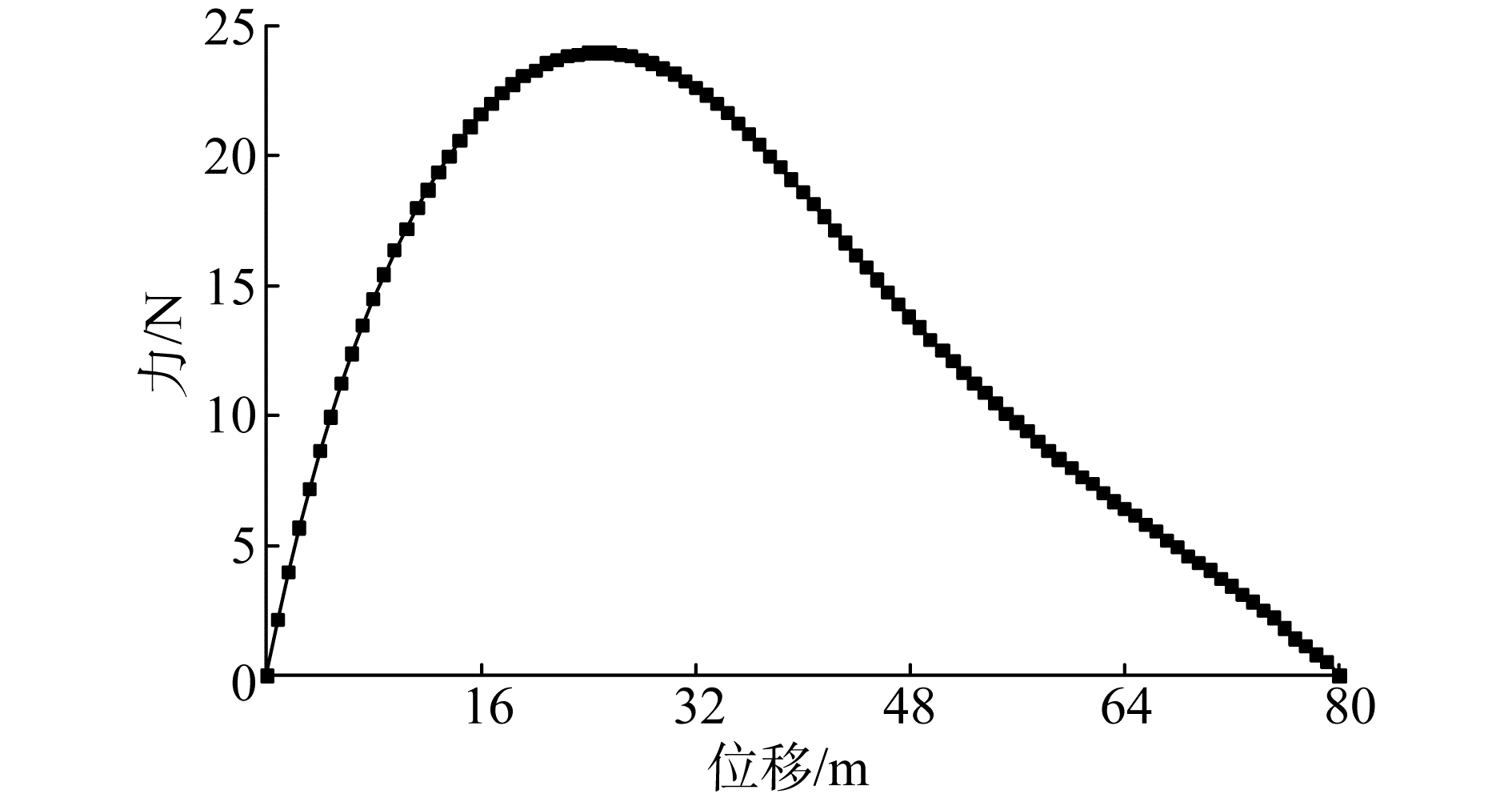
金刚石磨粒表面应力值较高,应力主要集中在各个顶点之处。图 6为位移响应下金刚石磨粒与金属胎体结合表面的最大受力情况。
|
Download:
|
| 图 6 结合面最大受力情况 Fig. 6 The maximum force on the inter face | |
金刚石磨粒在位移载荷的作用下发生偏转,与金属胎体之间在结合界面处发生断裂。在外界载荷的作用下,随着应变的增大,界面接触部分受到的应力逐渐增大,当应变超过一定量时,界面发生断裂,最大应力减小,直至磨粒与金属胎体完全脱离。
3 结合界面强度影响因素分析 3.1 磨粒形状与位姿对界面强度的影响实际切削过程,金刚石磨粒的形状多种多样,位姿也各不相同,不仅仅局限于正八面体[12]。
为得到普遍性规律,对不同形状、不同位姿下的金刚石磨粒界面结合处的应力分布情况进行对比研究,以确定其对界面性能,即把持力强弱的影响。
选取正八面体和正六面体2种形状作为金刚石磨粒模型形状,同时对金刚石磨粒分别施加3个不同方向的水平负载(如图 7),来确定其对界面性能的影响规律。

|
Download:
|
| 图 7 金刚石磨粒本构模型 Fig. 7 Diamond abrasive grain constitutive model | |
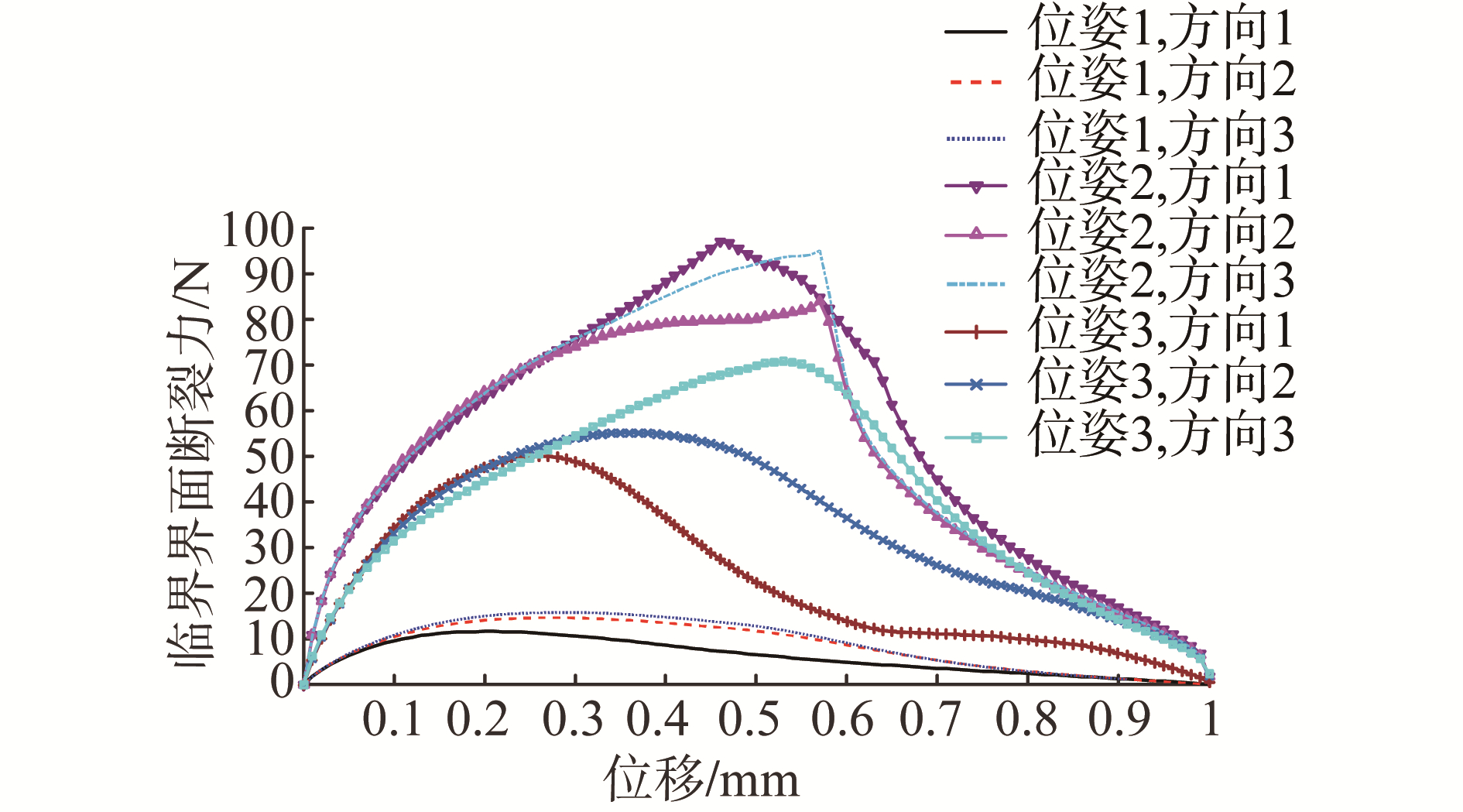
由图 8中数据可知,对于绝大多数情况,负载方向对结合界面的界面性能无显著的影响,对比同种磨粒结构不同位姿下,其临界界面断裂力存在较大的波动。如八面体结构在位姿1下,界面断裂力平均值为23.59 N,在位姿2和位姿3下,其值分别为48.78和44.87 N。在考虑磨粒与金属胎体之间的机械互锁情况下,仍可以说明磨粒的取向对结合界面的强度有较大的影响。
|
Download:
|
| 图 8 不同情况结合界面的临界界面强度 Fig. 8 The critical interface strength of interface in different situations | |
金刚石串珠绳随着切削过程的进行,其上的串珠表面金刚石磨粒的出刃高度也伴随磨损情况的不同有所变化,金属胎体不断地磨损,表层的磨粒不断磨损脱落,同时新的磨粒不断出现。
由于材料性能的差异,两者的磨损速度存在着差别,当胎体磨损速度过快,可能导致磨粒过早的脱落;同时磨粒的磨损速度过快,会导致切削效率的低下。磨粒的出刃高度取决于磨粒的磨损以及金属胎体的磨损,通过研究对比不同磨损情况,量化其对结合界面强度性能的影响情况。
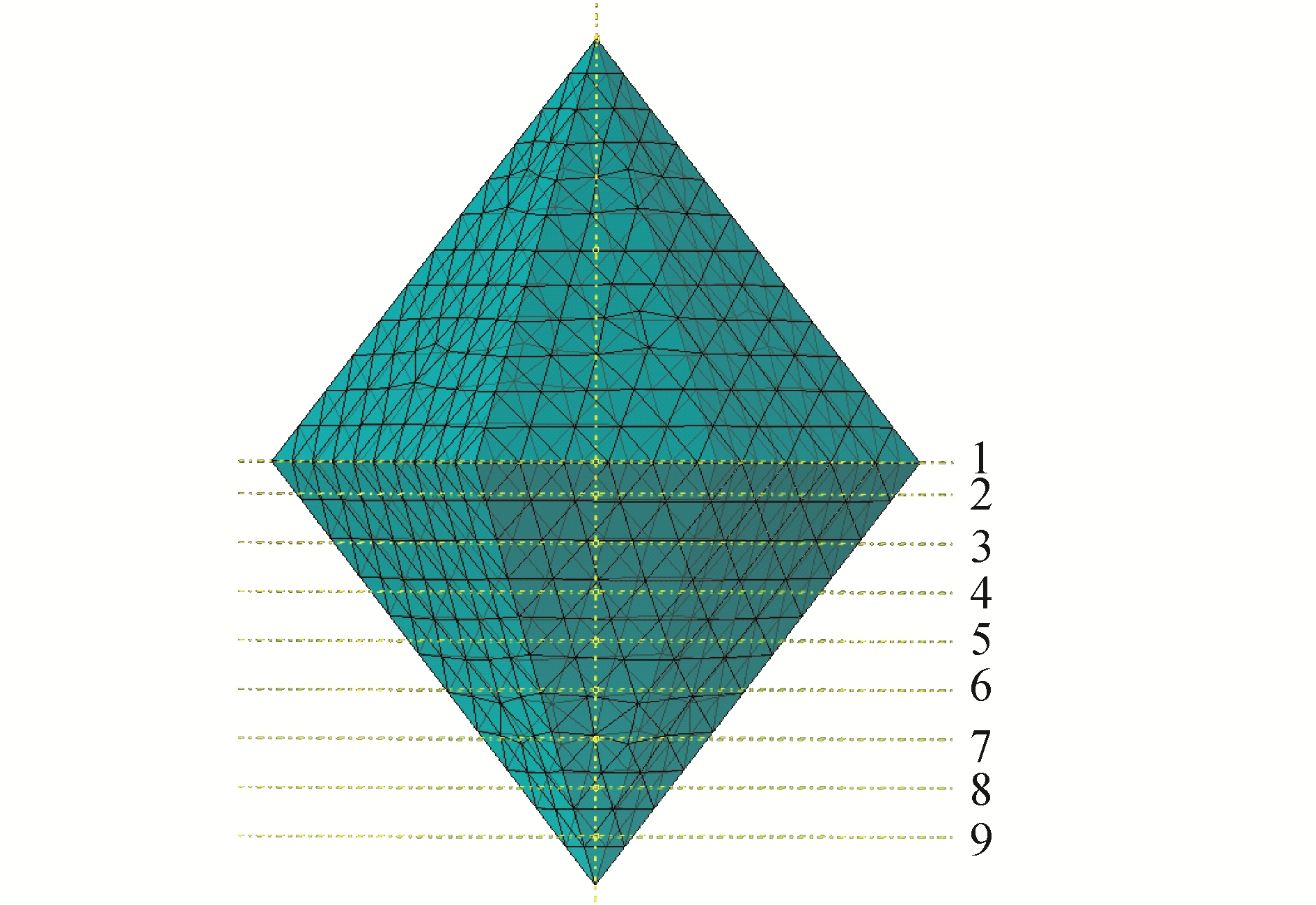
3.2.1 胎体磨损对界面强度的影响考虑不同模型之间存在的差异,以及胎体对磨粒的机械锁紧影响,选择八面体位姿作为研究胎体磨损的参考模型, 如图 9所示。
|
Download:
|
| 图 9 胎体磨损情况分组 Fig. 9 Carcass wear grouped | |
以截面1作为金属胎体磨损对界面强度影响研究的起始截面,保证金刚石磨粒不变化的同时每次分析之后金属胎体高度相应减小0.01 mm,作为新的分析起始截面位置,共计9组数据。
曲线从上到下依次为1~9编号的胎体磨损情况对应的力-位移图,随着位移负载的增大,结合界面处的受力首先大致线性增加到峰值之后再逐渐减小。
图 10可知,随着金属胎体的不断磨损,磨粒的出刃高度增加,结合界面处的临界界面断裂力不断减小,结合界面的强度性能不断下降,磨粒-胎体系统变得更加脆弱,具体数据如表 1所示。

|
Download:
|
| 图 10 不同出刃高度对界面性能的影响 Fig. 10 Effect of different blade height on interface performance | |
| 表 1 胎体磨损情况对应的临界界面断裂力 Table 1 Carcass wear corresponding to the critical interface fracture force |
当金属胎体的磨损速度过快,可能导致磨粒过早的脱落。对于本模型,八面体边长为0.1 mm,通过表中数据可知,当磨粒出刃高度高于0.146 mm时,对应磨损编号为7。此时结合界面的临界断裂力小于2.32 N,结合前文对单颗磨粒受力分析,单颗磨粒平均受切向切削力为0.719 N,考虑瞬时参与切削磨粒数上下波动以及磨粒受冲击载荷的影响,可以推断在这种情况下界面处于断裂边缘,磨粒即将脱落;对于编号8跟9对应的磨损情况,界面临界断裂力分别为1.45和1.11 N,可以视为金刚石磨粒在实际切割过程中已经脱落。
3.2.2 磨粒磨损对界面强度的影响金刚石磨粒出刃高度不仅与胎体磨损情况有关,还与磨粒自身的磨损情况有着直接的关联,本节对磨粒磨损进行详细的仿真分析,同样以八面体作为磨粒结构模型,将磨粒磨损情况划分为6种情况,如图 11所示。通过改变金刚石磨粒的出刃高度代表磨粒的磨损情况。仿真结果如图 12所示,结果显示随着金刚石磨粒出刃高度的减小,界面的强度不断增大。

|
Download:
|
| 图 11 磨粒磨损情况分组 Fig. 11 Abrasive wear grouping | |

|
Download:
|
| 图 12 磨粒磨损对界面强度的影响情况 Fig. 12 Effect of abrasive wear on interface strength | |
综合磨粒磨损与胎体磨损对界面强度影响,将数据进行汇总。结果说明随着磨粒出刃高度的增大,结合界面的强度性能逐渐下降。
3.2.3 磨粒胎体共同磨损对界面强度的影响实际切割过程中,磨粒与胎体的磨损同时进行,为得到更贴合实际的仿真结果,对磨粒与胎体的磨损进行耦合分析,对比相互之间的影响,将磨粒出刃高度分别固定为0.066、0.076和0.086 mm,同时改变磨粒磨损和胎体磨损的情况,研究界面断裂力变化情况,分组如图 13所示。

|
Download:
|
| 图 13 磨粒胎体磨损情况分组 Fig. 13 Abrasive wear of carcass grouping | |
可以预测,当胎体发生磨损,磨粒与胎体之间结合面积减小,结合界面的临界断裂力也将相应减小。
如表 2数据结果显示,当保证出刃高度不发生变化,同时随着磨粒与胎体结合界面深度的减小,临界界面断裂力会相应的减小,仿真结果与预期保持一致。
| 表 2 磨粒胎体磨损耦合分析 Table 2 Carcass wear corresponding to the critical interface fracture force |
对于金刚石串珠而言,金刚石磨粒分布较为密集,需考虑不同磨粒之间存在的相互作用可能对结合界面强度产生影响。目前对于磨粒相互作用的机制研究认识依旧空缺。本节通过改变磨粒间的间隔距离定性分析其对界面强度的影响。
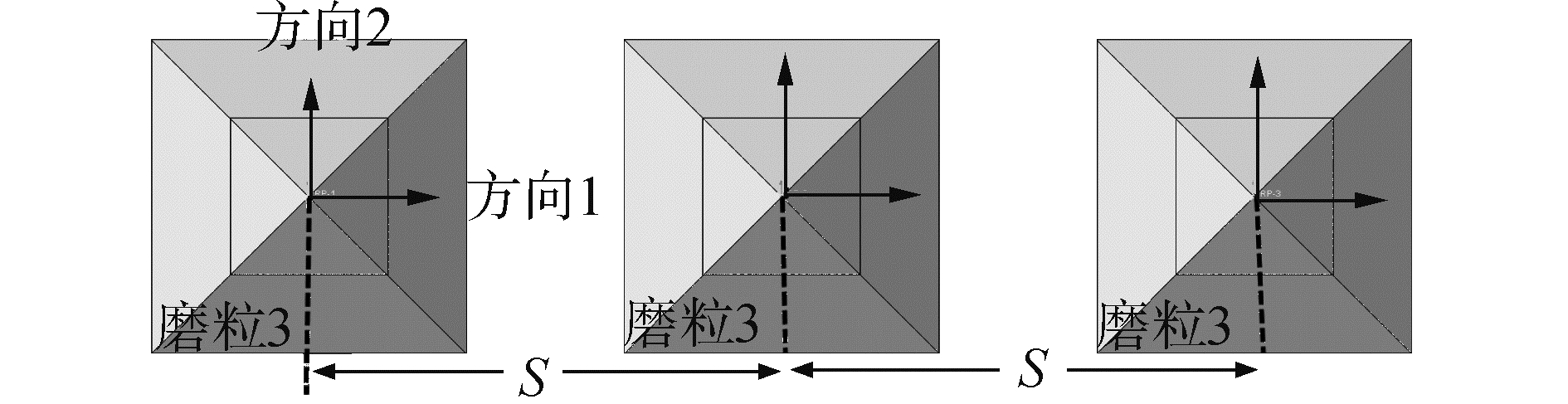
对磨粒间隔距离S划分为0.11、0.12、0.15及0.20 mm这4种情况,对比施加平行于磨粒排列方向和垂直于排列方向载荷情况下结合界面的断裂力变化趋势,如图 14所示。
|
Download:
|
| 图 14 相邻磨粒间相互作用影响 Fig. 14 The interaction between adjacent abrasive particles | |
仿真结果汇总于表 3,由表中数据可以得知,磨粒之间的相互作用会对磨粒与胎体结合界面强度造成一定的影响。
| 表 3 相邻磨粒间相互作用对界面断裂力影响 Table 3 Effect of interaction between adjacent abrasives on interfacial fracture force |
磨粒间相互作用会导致结合界面强度下降,且当磨粒之间间隔距离的增大,其相互影响能力逐渐减小;同时在磨粒排列方向上作用效果更大。可能存在的原因是磨粒胎体系统之间不存在机械包镶力,前面的磨粒在载荷作用下,对胎体有一个挤压变形,对后面的磨粒与胎体之间的结合界面造成一定的影响。
4 结论1) 金刚石串珠表面磨粒的脱落主要由切向切削力导致,与垂直方向受力基本无关。
2) 金刚石磨粒的形状、姿态、磨粒出刃高度对结合界面的强度均有显著的影响,其中磨粒形状、姿态主要影响机械锁紧力的大小,磨粒出刃高度改变结合界面面积大小影响而结合强度。
3) 磨粒间相互作用会导致结合界面强度下降,且当磨粒之间间隔距离增大时,其相互影响能力逐渐减小。
4) 通过对串珠绳串珠表面金刚石磨粒脱落失效机理的研究,为研制高性能的串珠绳打下基础。
| [1] |
刘一波, 徐良. 新兴工业材料加工用金刚石工具[J]. 超硬材料工程, 2016, 28(2): 27-31. LIU Yibo, XU Liang. Diamond tools for processing of the emerging industrial materials[J]. Superhard material engineering, 2016, 28(2): 27-31. DOI:10.3969/j.issn.1673-1433.2016.02.010 (  0) 0)
|
| [2] |
张岚, 孟庆鑫, 王立权, 等. 金刚石串珠失效形式的实验研究[J]. 哈尔滨工程大学学报, 2005, 26(4): 526-530. ZHANG Lan, MENG Qingxin, WANG Liquan, et al. Experiment and study on the failure mode of diamond string bead[J]. Journal of Harbin Engineering University, 2005, 26(4): 526-530. DOI:10.3969/j.issn.1006-7043.2005.04.022 (  0) 0)
|
| [3] |
彭锦雯, 彭啸, 邓卫星. 金刚石串珠绳锯橡胶保护套工作寿命的内因分析[J]. 超硬材料工程, 2016, 28(4): 15-19. PENG Jinwen, PENG Xiao, DENG Weixing. Internal cause analysis of service life of the rubber protective sleeve of diamond beaded wire saw[J]. Superhard material engineering, 2016, 28(4): 15-19. DOI:10.3969/j.issn.1673-1433.2016.04.004 (  0) 0)
|
| [4] |
CHUNG C, TSAY G D, TSAI M H. Distribution of diamond grains in fixed abrasive wire sawing process[J]. The International journal of advanced manufacturing technology, 2014, 73(9/10/11/12): 1485-1494. (  0) 0)
|
| [5] |
ZHOU Y, FUNKENBUSCH P D, QUESNEL D J. Stress distributions at the abrasive-matrix interface during tool wear in bound abrasive grinding-a finite element analysis[J]. Wear, 1997, 209(1/2): 247-254. (  0) 0)
|
| [6] |
LI B, AMARAL P M, REIS L, et al. 3D-modelling of the local plastic deformation and residual stresses of PM diamond-metal matrix composites[J]. Computational materials science, 2010, 47(4): 1023-1030. DOI:10.1016/j.commatsci.2009.12.001 (  0) 0)
|
| [7] |
CUI Weicheng, WISNOM M R. A combined stress-based and fracture-mechanics-based model for predicting delamination in composites[J]. Composites, 1993, 24(6): 467-474. DOI:10.1016/0010-4361(93)90016-2 (  0) 0)
|
| [8] |
DE BORST R, ROTS J G. Occurrence of spurious mechanisms in computations of strain-softening solids[J]. Engineering computations, 1989, 6(4): 272-280. DOI:10.1108/eb023782 (  0) 0)
|
| [9] |
XU J, SHEIKH A H, XU C. Interfacial failure modelling of diamond bits made of particulate composites[J]. Composite structures, 2016, 155: 145-159. DOI:10.1016/j.compstruct.2016.07.075 (  0) 0)
|
| [10] |
XU Jiayi, SHEIKH A H, XU Chaoshui. 3-D Finite element modelling of diamond pull-out failure in impregnated diamond bits[J]. Diamond and related materials, 2017, 71: 1-12. DOI:10.1016/j.diamond.2016.11.006 (  0) 0)
|
| [11] |
ÖZKAN E, SARⅡSIK G, CEYLAN S. Application and productivity analysis of new channel opening method in natural stone quarries with diamond wire cutting machine[J]. Arabian journal of geosciences, 2015, 8(2): 1089-1098. (  0) 0)
|
| [12] |
KIM D, KIM H, LEE S, et al. Characterization of diamond wire-cutting performance for lifetime estimation and process optimization[J]. Journal of mechanical science and technology, 2016, 30(2): 847-852. DOI:10.1007/s12206-016-0139-0 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


