2. 大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024;
3. 大连理工大学 高新船舶与深海开发装备协同创新中心, 辽宁 大连 116024
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China;
3. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration(CISSE), Dalian University of Technology, Dalian 116024, China
船体分段测量数据与其理论模型的有效匹配,是船舶建造精度管理的核心技术[1-3]。匹配技术的本质是绝对定位问题,一般通过算法和统计学规律计算并最小化不同坐标系数据的旋转、平移错位误差。目前,船舶工业主流的分段精度测量设备是全站仪,测量数据常含有粗差,常用的最小二乘匹配结果的鲁棒性易受到粗差影响[4-5]。因此,研究抗粗差的匹配方法对建造精度评定具有重要意义。
近年来对点匹配提已出多种方法[6-8],Besl[9]提出的迭代最近点(iterative closest point,ICP)是应用最广泛的点匹配方法,具有均衡误差特性。常用的抗粗差匹配方法有粗差探测法、随机采样一致性、最小截断二乘法等,粗差探测法是利用统计量方法剔除粗差观测值,但易造成数据剔除的错误判断,应用具有局限性;Fischler等[10]提出的随机采样一致性方法虽可以避免陷入局部最优,但采样次数视具体观测数据而定,没有固定参考值,且门限值难以确定;Doornik[11]采用最小截断二乘法(least trimmed squares,LTS)抗粗差,讨论了样本量与时间关系,当样本量较大时,LTS方法在处理含有粗差的点云数据效率不高。张凯等[12]采用M估计匹配方法,但忽略稳健函数收敛的有效性及稳健函数收敛速度。Guan等[13]建立多目标函数实现权值向量在不同方向上精度要求的误差分配,是另一类不考虑大偏差点的稳健匹配方法。因此研究对含有粗差的点匹配问题,应采用适当的稳健估计建立匹配模型。
为处理粗差所造成的不利影响,本文研究基于退化的M估计抗差方法及稳健函数收敛性问题,算法本质是迭代加权最小二乘(iteratively re-weighted least squares,IRLS)算法,常用于回归模型的鲁棒性分析,文中提出标签法实现点集对应点搜索操作,依据模型当前位姿和M估计准则获取不同精度数据匹配权系数,利用退化-迭代方法削弱粗差对数据匹配精度影响,提高定位解的收敛速率和可靠性,并对抗差函数的收敛性进行分析。
1 数据匹配问题描述及稳健性分析 1.1 数据破匹配问题描述待匹配点与工艺模型匹配定位过程为寻找最优关联矩阵z,设{pi}i=1N为测量数据点集,yi为pi在工艺模型数据集X上的搜索对应点,即yi=ζ(pi, X),ζ为搜索对应点操作。非线性匹配模型可描述为对应点距离的平方和最小:
| $ f(z) = \min \sum\limits_{i = 1}^N {{{\left\| {\mathit{\boldsymbol{R}}{p_i} + \mathit{\boldsymbol{t}} - {y_i}} \right\|}^2}} $ | (1) |
式中:R∈R3×3为旋转矩阵;t∈R3为平移矩阵。关联矩阵为z=[θx θy θz tx ty tz]T,θx、θy、θz分别为绕三坐标轴的旋转角度,tx、ty、tz分别为沿三坐标轴的平移量。
式(1)为常用的最小二乘匹配模型,等价对待每个匹配点对的精度残差Δεi为:
| $ \Delta {\mathit{\boldsymbol{\varepsilon }}_i} = \mathit{\boldsymbol{R}}{p_i} + \mathit{\boldsymbol{t}} - {\mathit{\boldsymbol{y}}_i} = {\left[ {\begin{array}{*{20}{l}} {\Delta {\varepsilon _i}}&{\Delta {\varepsilon _i}}&{\Delta {\varepsilon _i}} \end{array}} \right]^{\rm{T}}} $ | (2) |
本文提出标签法实现yi=ζ(pi, X)操作。对于给定点集{pi}N i=1和{Xi}M i=1,且N≤M, 标签法算法步骤如下:
1) 计算任意点pi到点集{pi}N i=1中所有点距离集{dp, i, h}N h=1,h(h=1, 2, …, N)为{pi}N i=1中点序列;
2) 对距离集{dp, i, h}N h=1进行由小到大排序,距离集更新为{d(p, i, h), j*}N j=1,得到点pi的最近距离序列;
3) 按设定值L∈N+截断pi的最近距离序列,则截断序列集为{d(p, i, h), j*}L j=1,且L≤N;
4) 对应点集{Xi}M i=1按步骤1)、2)操作,更新任意点的最近距离集为{d(X, i, k), j*}M j=1,截断序列集为{d(X, i, k), j*}L j=1;
5) 点pi的{d(p, i, h), j*}L j=1与点Xi的{d(X, i, k), j*}L j=1距离差的平方和(S(p, i, h), 1,S(p, i, h), 2,…,S(p, i, h), M),标记点pi的min(Sp, i, 1,Sp, i, 2,…,Sp, i, M)对应序号;
| $ \left\{ {\begin{array}{*{20}{c}} {\left\{ {{S_{(p,1,h),i}}} \right\}_{i = 1}^M = \sum\limits_{j = 1}^L {{{\left( {d_{(p,1,h),j}^* - d_{(X,i,k),j}^*} \right)}^2}} }\\ \vdots \\ {\left\{ {{S_{(p,N,h),i}}} \right\}_{i = 1}^M = \sum\limits_{j = 1}^L {{{\left( {d_{(p,N,h),j}^* - d_{(X,i,k),j}^*} \right)}^2}} } \end{array}} \right. $ | (3) |
6) 选取适当截断L值,重复步骤3)~5),完成对应点搜索最优操作。
应用式(4)表示对应点匹配率Scon:
| $ {S_{{\rm{con}}}} = \frac{{{\zeta _{{\rm{con}}}}}}{N} $ | (4) |
式中ζcon为应用标签方法的一致对应数。
1.2 稳健性分析直接应用含有粗差的数据进行匹配定位,易导致关联矩阵z偏离真值。如图 1所示,最小二乘回归线受异常点或大偏差点影响偏离理想位姿,稳健估计回归线则能有效抑制粗差对匹配精度的影响,得到较为合理的回归模型。
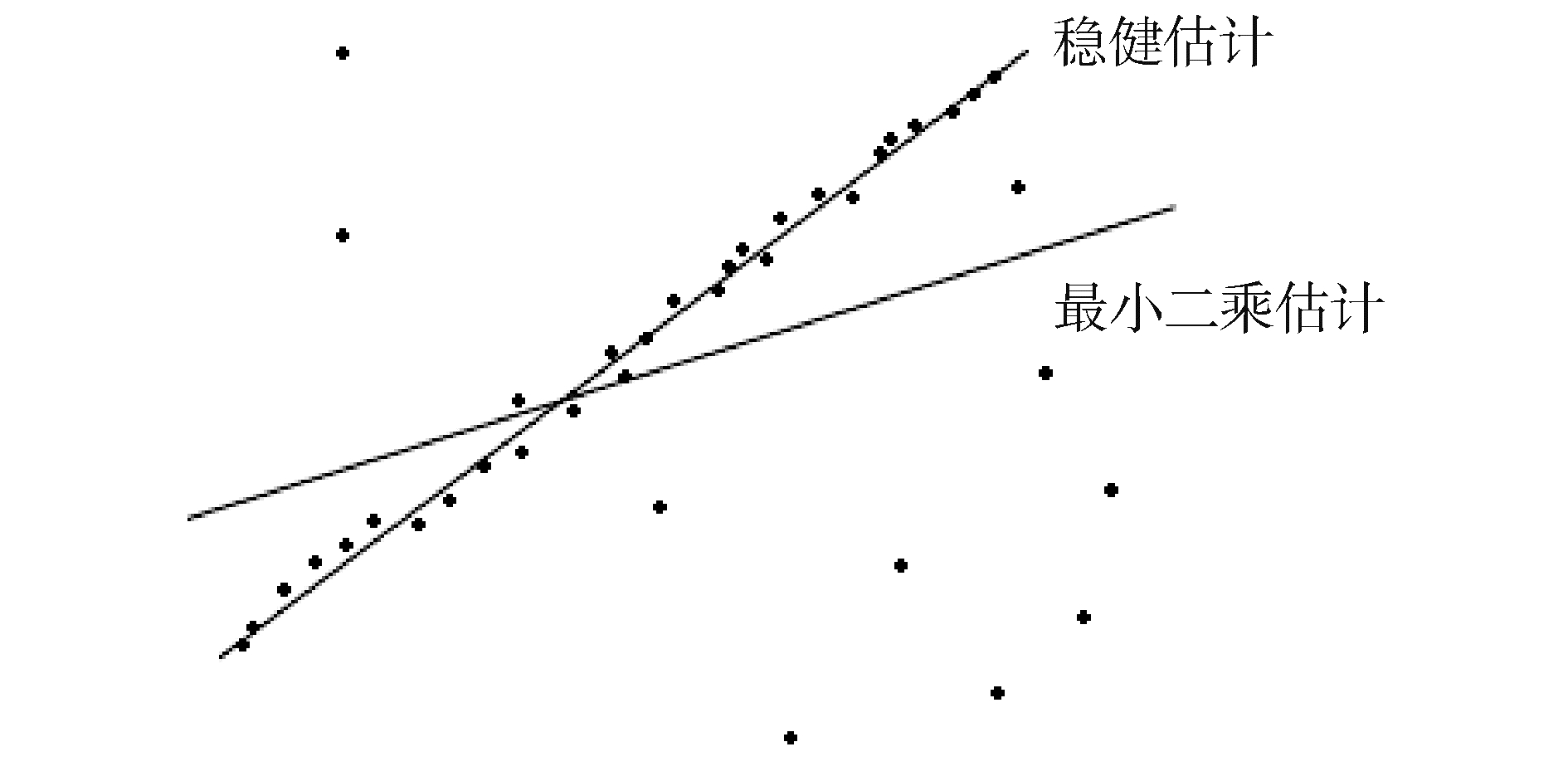
|
Download:
|
| 图 1 线性回归比较 Fig. 1 Comparison of liner regression | |
稳健统计学中认定粗差影响是由于理想正态分布受到了污染,即与总体数据存在显著性差异的数据点,其存在会影响目标函数的解,降低定位解的可靠性[12]。匹配误差的真实分布可用污染分布描述为:
| $ {f_\varepsilon }(\Delta ) = (1 - \alpha )g(\Delta ) + \alpha h(\Delta ) $ | (5) |
式中:α为污染率,即粗差影响概率,满足0≤α < 1;当α=0时,则fε(Δ)=g(Δ),g(Δ)为理想状态下的正态分布,函数估计值等于最小二乘估计值;h(Δ)为任意分布的粗差影响函数,当α→0+时,匹配函数估计越稳健。α的最大值作为衡量目标函数稳健型标准,并把maxα称作为崩溃点值。
M估计算法是通过Δεi的幅值来调整权值ωi,以降低数据粗差权重。如果以最小二乘估计位姿作为初值,则残差maxΔεi的点位置不一定是粗差的位置,计算结果仍不稳健。因此,为了得到稳健的函数估计值,式(1)可用M估计形式表示:
| $ f(z) = \min \sum\limits_{i = 1}^N \rho \left( {\frac{{\left( {d\left( {R{p_i} + t} \right),X} \right)}}{{{\sigma _*}}}} \right) $ | (6) |
式中:ρ(r)为一阶可导偶函数,在区间[0, ∞)内单调递增,满足ψ(r)=ρ′(r)、ρ(0)=0;σ*是Δεi的估计值,
ρ(r)的权函数定义为:
| $ \omega (r) = \left\{ {\begin{array}{*{20}{l}} {\frac{{\psi (r)}}{r},}&{r \ne 0}\\ {\mathop {\lim }\limits_{r \to 0} \frac{{\psi (r)}}{r} = {\psi ^\prime }(0),}&{r \to 0} \end{array}} \right. $ | (7) |
当σ*→0+,对于较大残差值Δεi,函数f(z)收敛速度慢或陷入局部收敛。针对此问题,选用退化方法,即变参数σk替代残差估计值σ*,满足σk-1≥σk≥σ*>0,k表示迭代次数。
为验证退化方法的可靠性,假设σ0>σ1>0,推导可得:
| $ \rho \left( {\frac{r}{{{\sigma _0}}}} \right) \le \rho \left( {\frac{r}{{{\sigma _1}}}} \right) \le \frac{{\sigma _0^2}}{{\sigma _1^2}}\rho \left( {\frac{r}{{{\sigma _0}}}} \right) $ | (8) |
随着k增大,σk逐步退化至σ*,根据式(8)及稳健估计函数性质,函数式(6)满足式(9),使f(z)收敛于全局最小值,提升收敛速度:
| $ \sum\limits_{i = 1}^N \rho \left( {\frac{{{r_i}}}{{{\sigma _k}}}} \right) \le f(z) \le \frac{{\sigma _k^2}}{{\sigma _*^2}}\sum\limits_{i = 1}^N \rho \left( {\frac{{{r_i}}}{{{\sigma _k}}}} \right) $ | (9) |
由式(8)、(9)推导得:
| $ \begin{array}{*{20}{l}} {\frac{{\sigma _k^2}}{{\sigma _*^2}}\sum\limits_{i = 1}^N \rho \left( {\frac{{r_i^k}}{{{\sigma _k}}}} \right) \le \frac{{\sigma _k^2}}{{\sigma _*^2}}\frac{{\sigma _{k - 1}^2}}{{\sigma _k^2}}\sum\limits_{i = 1}^N \rho \left( {\frac{{r_i^k}}{{{\sigma _{k - 1}}}}} \right) = }\\ {\frac{{\sigma _{k - 1}^2}}{{\sigma _*^2}}\sum\limits_{i = 1}^N \rho \left( {\frac{{r_i^k}}{{{\sigma _{k - 1}}}}} \right) \le \frac{{\sigma _{k - 1}^2}}{{\sigma _*^2}}\sum\limits_{i = 1}^N \rho \left( {\frac{{r_i^{k - 1}}}{{{\sigma _{k - 1}}}}} \right)} \end{array} $ | (10) |
因此,在σk退化至σ*时,函数收敛于极小值,即σk→σ*ρ(r/σk)→ρ(r/σ*)。
估计值σk计算式:
| $ {\sigma _k} = \left\{ {\begin{array}{*{20}{l}} {1.90{\rm{Med}}\left( {\left( {d\left( {R{p_i} + t} \right),X} \right)_{i = 1}^N} \right),}&{k = 0}\\ {\xi \left( {{\sigma _{k - 1}} - {\sigma _*}} \right) + {\sigma _*},}&{k > 0} \end{array}} \right. $ | (11) |
式中:Med(·)表示向量元素中值;ξ表示函数的期望退化率,满足0≤ξ < 1;σ*根据数据特征选取。
因此,稳健估计函数f(z)可更新为
| $ \tilde f(z) = \min \sum\limits_{i = 0}^N \rho \left( {\frac{{\left( {d\left( {R{p_i} + t} \right),X} \right)}}{{{\sigma _k}}}} \right) $ | (12) |
统计学理论中用渐进效率来衡量稳健估计的有效性,Δεi为第i个观测值的估计残差,对应的崩溃点值为1/N,渐进效率为1。稳健估计中,为提高数据抗差性,最小二乘估计函数改为增长速度较慢的ρ(r)函数,以牺牲部分渐进效率为代价,提高M估计线性解的稳健性,减少粗差对模型姿态定位精度影响。文献[14, 16]对ρ(r)函数进行了较深入研究,从抑制粗差幅值大小方面考虑,给出常用的3种M估计函数进行分析:Huber估计函数、Cauchy估计函数和Tukey's双边加权函数。
设ρHu(r)、ρCa(r)、ρTu(r)为对应的估计函数,估计函数对应的门限值cHu、cCa、cTu是根据残差性能确定的常数,通常采用渐进方差确定[17-18]:
| $ V(\psi ,F) = \frac{{\int {{\psi ^2}} dF}}{{{{\left( {\int {{\psi ^\prime }} dF} \right)}^2}}} $ | (13) |
假定残差Δεi服从标准正态分布N(0, 1),根据文献[17, 18]得知渐进方差V(ψ, F)→1+,取V(ψ, F)=1.01,计算门限值c为:
| $ \left\{ {\begin{array}{*{20}{l}} {{c_{{\rm{Hu}}}} \approx 2.0138}\\ {{c_{{\rm{Ca}}}} \approx 4.3040}\\ {{c_{{\rm{Tu}}}} \approx 7.0589} \end{array}} \right. $ | (14) |
用M估计函数近似求解旋转矩阵R,无法满足正交性,将导致匹配点集错位。本节研究抗差匹配的线型求解及旋转矩阵的正交近似。
设初始变换参数为R(0)=I、t(0)=0,上标为迭代次数k=0,则0次迭代满足p(0)=R(0)pi+t(0)。假设迭代条件为:
| $ \left\{ {\begin{array}{*{20}{l}} {k = k + 1}\\ {\mathit{\boldsymbol{y}}_i^{(k - 1)} = \zeta \left( {\mathit{\boldsymbol{p}}_i^{(k - 1)},\mathit{\boldsymbol{X}}} \right)}\\ {{\omega _i} = \omega \left( {{{\left\| {\mathit{\boldsymbol{p}}_i^{(k - 1)} - \mathit{\boldsymbol{y}}_i^{(k - 1)}} \right\|}_2}/{\mathit{\boldsymbol{\sigma }}_{k - 1}}} \right)} \end{array}} \right. $ | (15) |
当ωi>0,匹配解算方法公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {\left[ {{\mathit{\boldsymbol{R}}^*},{\mathit{\boldsymbol{t}}^*}} \right] = {\text{argmin}} \sum\limits_{i = 1}^N {{\mathit{\boldsymbol{\omega }}_i}} \left\| {\mathit{\boldsymbol{Rp}}_i^{(k - 1)} + \mathit{\boldsymbol{t}} - \mathit{\boldsymbol{y}}_i^{(k - 1)}} \right\|_2^2}\\ {{\mathit{\boldsymbol{R}}^k} = {\mathit{\boldsymbol{R}}^*}{\mathit{\boldsymbol{R}}^{k - 1}}}\\ {{\mathit{\boldsymbol{t}}^k} = {\mathit{\boldsymbol{R}}^*}{\mathit{\boldsymbol{t}}^{k - 1}} + {\mathit{\boldsymbol{t}}^*}}\\ {\mathit{\boldsymbol{p}}_i^k = {\mathit{\boldsymbol{R}}^*}\mathit{\boldsymbol{p}}_i^{k - 1} + {\mathit{\boldsymbol{t}}^\mathit{\boldsymbol{*}}}} \end{array}} \right. $ | (16) |
为简化迭代指数,每次迭代变换参数(R*, t*)表示为:
| $ \begin{array}{l} \left[ {{\mathit{\boldsymbol{R}}^*},{\mathit{\boldsymbol{t}}^*}} \right] = \mathop {\text{argmin}}\limits_{\mathit{\boldsymbol{R}},\mathit{\boldsymbol{t}}} (\mathit{\boldsymbol{R}},\mathit{\boldsymbol{t}}) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop {\text{argmin}}\limits_{\mathit{\boldsymbol{k}},\mathit{\boldsymbol{t}}} \sum\limits_{i = 1}^N {{\omega _i}} \left\| {\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{p}}_i} + \mathit{\boldsymbol{t}} - {\mathit{\boldsymbol{y}}_i}} \right\|_2^2 \end{array} $ | (17) |
设:
式(17)利用范数定义展开得:
| $ \begin{array}{l} \left[ {{\mathit{\boldsymbol{R}}^*},{\mathit{\boldsymbol{t}}^*}} \right] = \sum\limits_{i = 1}^N {{\omega _i}} \left\| {\mathit{\boldsymbol{p}}_i^{(k - 1)} - {{\mathit{\boldsymbol{\overline p}} }^{(k - 1)}}} \right\|_2^2 + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^N {{\omega _i}} \left\| {\mathit{\boldsymbol{y}}_i^{(k - 1)} - {{\mathit{\boldsymbol{\overline y}} }^{(k - 1)}}} \right\|_2^2 + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\hat \omega \left\| {\mathit{\boldsymbol{R}}\mathit{\boldsymbol{\widehat p}} - \mathit{\boldsymbol{\overline y}} + \mathit{\boldsymbol{t}}} \right\|_2^2 - 2 trace (\mathit{\boldsymbol{RC}}) \end{array} $ | (18) |
式中:
由于
| $ \sum\limits_{i = 1}^N {\left\| {\mathit{\boldsymbol{p}}_i^{(k - 1)} - {{\mathit{\boldsymbol{\overline p}} }^{(k - 1)}}} \right\|_2^2} = \sum\limits_{i = 1}^N {\left\| {{\mathit{\boldsymbol{p}}_i} - \mathit{\boldsymbol{\overline p}} } \right\|_2^2} $ | (19) |
故式(18)中,
若求刚性矩阵变换参数(R*, t*),式(18)等价于:
| $ \left[ {{\mathit{\boldsymbol{R}}^*},{\mathit{\boldsymbol{t}}^*}} \right] = maxtrace (\mathit{\boldsymbol{RC}}) $ | (20) |
对C进行奇异值分解C=UΣV,得到3×3矩阵R*的正交近似解R*=VUT。其中,U和V为3×3正交矩阵,ζ为3×3非负对角矩阵。若反射矩阵det(VUT)=-1, 对应R*=Vdiag(1, 1,-1)UT,平移矩阵
基于对应点搜索方法和M-估计准则,稳健匹配算法过程如下:
1) 借助实测特征数据与工艺模型数据,应用标签法进行对应点搜索操作;
2) 三点位姿粗定位,得到测量数据集的初始位置;
3) 设定参数R(0)=I、t(0)=0,设定最大迭代次数和预设迭代停止条件;
4) 根据偏差函数,建立稳健估计函数式(12);
5) 由式(15)和(16)假设条件,利用R(k)和t(k)更新实测数据点坐标,得到新的匹配位姿,若验证退化-迭代过程满足停止条件,则停止迭代,转下一步;否则令k=k+1,继续匹配;
6) 输出匹配变换参数R、t,计算当前位姿状态时匹配残差。
3 稳健匹配算法收敛性分析为说明稳健匹配的收敛性问题,定义:
| $ \begin{array}{l} \varphi (u) = \phi (v) + {\phi ^\prime }(v)(u - v) = \\ \;\;\;\;\;\;\;\;\;\;\phi (v) + {\phi ^\prime }(v)u - {\phi ^\prime }(v)v \end{array} $ |
假设ρ(s)=ϕ(s2),且s→r,ρ(s)的二阶逼近式为:
| $ \eta (s,r) = \left\{ {\begin{array}{*{20}{l}} {\rho (r) - \frac{{\psi (r)}}{2}r + \frac{{\psi (r)}}{{2r}}{s^2},}&{r \ne 0}\\ {\frac{{{\psi ^\prime }(0)}}{2}{s^2},}&{r = 0} \end{array}} \right. $ | (21) |
式中:s=r时,η(s, r)=ρ(r)、
设si(R, t)=‖Rpi(k-1)+t-yi(k-1)‖2=‖pi(k)-yi(k-1)‖2,ri=si(I, 0)=‖pi(k-1)-yi(k-1)‖2,即当pi(k)=pi(k-1)时,式(21)最小化为:
| $ \begin{array}{*{35}{l}} \begin{matrix} \min \\ R,t \\ \end{matrix}\,\left\{ \sum\limits_{i=1}^{N}{\eta }\left( {{s}_{i}}(R,t),{{r}_{i}} \right) \right\}=\sum\limits_{i=1}^{N}{\left( \rho \left( {{r}_{i}} \right)-\frac{\psi \left( {{r}_{i}} \right)}{2}{{r}_{i}} \right)}+ \\ \frac{1}{2}\sum\limits_{i=1}^{N}{\omega }\left( {{r}_{i}} \right)s_{i}^{2}(R,t)\sum\limits_{i=1}^{N}{\omega }\left( {{r}_{i}} \right)s_{i}^{2}(R,t) \\ \end{array} $ | (22) |
式(22)中,第1行右边第1项独立于参数(R, t),式(22)的2个最小化函数区别仅为系数因子,所以在ω≥0时,有共同解集,则式(22)等同于最小化函数式(17)。
| $ \nabla \tilde f = \sum\limits_{i = 1}^N \psi \left( {{r_i}} \right)\nabla {r_i} = 0 $ | (23) |
式(17)最小化函数h(R, t)表示为h(z)=ωi‖ri‖22关于关联矩阵zj的梯度得:
| $ \nabla h = 2\sum\limits_{i = 1}^N {{\omega _i}} {r_i}\nabla {r_i} = 0 $ | (24) |
根据式(7)知,对于任意ri,式(23)等价于式(24),验证了权函数定义的有效性。
第k次迭代
| $ \sum\limits_{i = 1}^N \eta \left( {s_i^{(k)},r_i^{(k - 1)}} \right) \le \sum\limits_{i = 1}^N \eta \left( {r_i^{(k - 1)},r_i^{(k - 1)}} \right) $ | (25) |
设定
| $ {e_k} \le \sum\limits_{i = 1}^N \eta \left( {s_i^{(k)},r_i^{(k - 1)}} \right) \le {\tilde f_{k - 1}} $ | (26) |
当k+1迭代,由于yik=ζ(pik, X)、rik=‖pik-yik‖2和ωi=ω(rik),计算得
| $ 0 \le {\tilde f_k} \le {e_k} \le {\tilde f_{k - 1}} $ | (27) |
当式(27)成立时,可证明
为验证M估计方法的有效性,采用模拟数据和船体分段实测数据进行试验验证。期望退化率均取ξ=0.9。
4.1 模拟试验采用点云数据进行稳健匹配仿真实验,模型共35 947个点,其中部分点设置扰动误差,并以任意角度旋转、距离平移更新后的数据模型模拟测量数据,污染率为16.54%,设定σ*=a/100,a为粗定位后对应点的距离均值。由于对应点集元素数量相等,应用标签法搜索对应点,设定L=2%×35 947≈719,计算对应点匹配率ζcon=100%。仿真数据实验模型见图 2所示。模型理想位姿、初始位姿、ICP算法和稳健匹配算法的统计结果如表 1所示。

|
Download:
|
| 图 2 数据模拟匹配试验 Fig. 2 Simulated data of registration result | |
| 表 1 匹配误差比较 Table 1 Comparison of registration error |
图 2中黄色三角网格表示测量(模拟)数据,颜色深浅表示误差大小,蓝色三角网格表示理论模型。图 2(a)是测量数据模型与理论模型的理想位姿,图 2(b)是选取未加扰动误差的三点,基于三点法模拟初始位姿,目的是缩小旋转、平移变换错位误差,为后续精匹配提供合理初值。为了分析匹配算法的抗差性,图 2(c)~3(f)是基于初始位姿状态的数据模型进行位姿精确定位,图 2(c)是基于ICP算法的模拟位姿,适用于误差分布均匀的情形,等价对待每个匹配点对,算法不具备抗差性;图 2(d)是采用Huber函数进行目标定位计算共14 328个点,满足|r|≤cHu,由于Huber函数曲线是凸形的,没有完全忽视粗差点对位姿定位影响,但估计函数仍然带有鲁棒性,匹配结果对比于ICP精匹配算法更接近于理想位姿;图 2(e)是采用Cauchy函数实现抗差匹配,计算过程避免了使用分段函数带来的求解困难,估计函数有一定的鲁棒性,对粗差的抑制程度强于Huber函数,弱于Tukey函数;图 2(f)应用Tukey估计函数计算共35 558个点满足|r|≤cTu,算法能有效抑制住初始位姿状态下的低精度数据对位姿定位的影响,匹配结果对比其他匹配算法的模型定位位姿更接近于理想位姿,具有较强的鲁棒性。
表 1中,根据ICP算法的平方根最小特性及c取值大小,各算法对粗差的抑制程度不同,结论为:fTu(z)>fCa(z)>fHu(z)>fICP(z)。
当污染率一定时,应用不同匹配算法,粗差数据对定位结果的影响效果不同,采用ICP精匹配定位精度易受到粗差影响,定位位姿偏离实际位置。在稳健匹配算法中,粗差数据参与匹配过程中被降权,削弱粗差数据对模型位姿定位精度的影响,目标匹配位姿更接近于理想位姿。
4.2 船体分段测量数据的抗差匹配船体分段建造过程中存在装焊误差及累计误差,实体分段特征数字化测量精度受环境、人工操作等影响,与工艺模型存在精度差异,难以完全匹配对齐; 对于含有粗差的测量数据,应用ICP算法会放大粗差对位姿定位准确性的影响。实验采用全站仪采集某船体双层底分段表面特征数据,实测数据整体水平上存在大误差点或离值点,匹配过程中这些粗差点影响分段整体位姿定位,降低定位解的稳健性。
工艺模型采用76个特征点,全站仪采集78个离散点坐标(2点为测量基准点和迁站点),设定σ*=a/100、L=8%·76≈6,对应点匹配率ζcon=100%。图 3表示匹配点对的距离误差,应用ICP算法精确定位时,未考虑粗差对模型位姿定位精度影响,造成匹配位姿偏斜,增加分段修整量。图 3(a)中Huber函数中有0个点满足|r|≤cHu,Huber估计位姿等同于ICP算法定位位姿,导致表 2中ICP算法和Huber函数估计值相同。根据初始位姿对应点距离误差分布,Cauchy函数抗差性较弱,不能有效保证位姿定位精度。图 3(c)中,Tukey估计子有34个点满足|r|≤cHu,距离曲线差异性显著,对比于其他解算方法能降低粗差匹配权重,有效抑制粗差对位姿定位精度影响。

|
Download:
|
| 图 3 匹配误差实验 Fig. 3 Experiment of matching error | |
| 表 2 匹配对比 Table 2 Matching comparison |
模型初始位姿、ICP算法和稳健匹配算法的统计结果如表 2所示。
在同初始位姿基础上,采用稳健匹配方法处理刚性位姿定位问题,降低粗差数据权重,可以减小或避免粗差数据对模型位姿定位精度的影响,提高匹配结果的稳定性。理论上Huber函数、Cauchy函数和Tukey函数稳健匹配方法的均方根误差均比ICP精匹配算法的均方根误差大,是因为ICP算法的目标函数为均方根最小特性,dmin递增和dmax的递减主要是由于cTu>cCa>cHu,对数据粗差的抑制程度不同。在表 2中,由于Huber函数有0个点满足|r|≤cHu,Huber估计函数的匹配目标为均方根最小,等价于ICP算法估计值,即f(z)/N相同。
5 结论1) 残差估计值σk单调递减至σ*,采用理论验证退化方法的可行性,提高迭代算法的收敛速率。
2) 该方法根据渐进方差确定门限值c值,实际应用中可根据数据形式选择合适的影响函数,c值可根据对大误差数据的抑制程度进行设定。
对于采用三维扫描仪获取现场船体分段点云数据,点集数据通常存在扭曲变形、粗差、数据缺失等退化问题,下一步针对点集退化现象进行对应点搜索和精准匹配研究。
| [1] |
管官, 林焰, 申玫, 等. 考虑工程约束的船体分段测量点集匹配方法[J]. 哈尔滨工程大学学报, 2013, 34(5): 541-548. GUAN Guan, LIN Yan, SHEN Mei, et al. Point registration algorithm for hull block measurment with engineering constraints[J]. Journal of Harbin Engineering University, 2013, 34(5): 541-548. (  0) 0)
|
| [2] |
杨贵强.船体分段测量数据配准技术的研究与应用[D].厦门: 集美大学, 2013. YANG Guiqiang.Study and application of measurement data registration technique for hull blocks[D]. Xiamen: JiMei University, 2013. (  0) 0)
|
| [3] |
杨贵强, 刘玉君, 李瑞, 等. 考虑安装工艺的多特征模型匹配定位[J]. 哈尔滨工程大学学报, 2019, 40(8): 1393-1398. YANG Guiqiang, LIU Yujun, LI Rui, et al. Matching localization of multi-feature considering the installation process[J]. Journal of Harbin Engineering University, 2019, 40(8): 1393-1398. (  0) 0)
|
| [4] |
GUO Jianfeng, OU Jikun, WANG Haitao. Robust estimation for correlated observations: two local sensitivity-based downweighting strategies[J]. Journal of geodesy, 2010, 84(4): 243-250. DOI:10.1007/s00190-009-0361-y (  0) 0)
|
| [5] |
方兴, 黄李雄, 曾文宪, 等. 稳健估计的一种改进迭代算法[J]. 测绘学报, 2018, 47(10): 1301-1306. FANG Xing, HUANG Lixiong, ZENG Wenxian, et al. On an improved iterative reweighted least squares algorithm in robust estimation[J]. Actageodaetica et cartographica sinica, 2018, 47(10): 1301-1306. DOI:10.11947/j.AGCS.2018.20170576 (  0) 0)
|
| [6] |
BASTOS L F, TAVARES J M R S. Matching of objects nodal points improvement using optimization[J]. Inverse problems in science and engineering, 2006, 14(5): 529-541. DOI:10.1080/17415970600573767 (  0) 0)
|
| [7] |
MA Jiayi, ZHAO Ji, JIANG Junjun, et al. Non-rigid point set registration with robust transformation estimation under manifold regularization[C]//Proceedings of the 31st AAAI Conference on Artificial Intelligence. Hilton San Francisco Union Square, 2017.
(  0) 0)
|
| [8] |
WANG Gang, ZHOU Qiangqiang, CHEN Yufei. Robust non-rigid point set registration using spatially constrained gaussian fields[J]. IEEE transactions on image processing, 2017, 26(4): 1759-1769. DOI:10.1109/TIP.2017.2658947 (  0) 0)
|
| [9] |
BESL P J, MCKAY N D. A method for registration of 3-D shapes[J]. IEEE transactions on pattern analysis and machine intelligence, 1992, 14(2): 239-256. DOI:10.1109/34.121791 (  0) 0)
|
| [10] |
FISCHLER M A, BOLLES R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. DOI:10.1145/358669.358692 (  0) 0)
|
| [11] |
DOORNIK J A. Robust estimation using least trimmed squares[EB/OL]. (2011-03-14)[2014-08-08].http://econ.au.dk/fileadmin/site_files/filer_oekonomi/subsites/creates/Seminar_Papers/2011/ELTS.pdf.
(  0) 0)
|
| [12] |
张凯, 赵建虎, 张红梅. 一种基于M估计的水下地形抗差匹配算法[J]. 武汉大学学报(信息科学版), 2015, 40(4): 558-562. ZHANG Kai, ZHAO Jianhu, ZHANG Hongmei. Robust underwater terrain matching navigation based on M estimation[J]. Geomatics and Information Science of Wuhan University, 2015, 40(4): 558-562. (  0) 0)
|
| [13] |
GUAN Guan, LIN Yan, SHEN Mei. Measurement points registration for hull blocks based on multi-objective optimization[J]. Journal of information & computational science, 2013, 10(8): 2315-2328. (  0) 0)
|
| [14] |
YANG Y, SONG L, XU T. Robust estimator for correlated observations based on bifactor equivalent weights[J]. Journal of geodesy, 2002, 76(6/7): 353-358. (  0) 0)
|
| [15] |
BERGSTRÖM P, EDLUND O. Robust registration of surfaces using a refined iterative closest point algorithm with a trust region approach[J]. Numerical algorithms, 2017, 74(3): 755-779. DOI:10.1007/s11075-016-0170-3 (  0) 0)
|
| [16] |
KNIGHT N L, WANG Jinling. A comparison of outlier detection procedures and robust estimation methods in GPS positioning[J]. The journal of navigation, 2009, 62(4): 699-709. DOI:10.1017/S0373463309990142 (  0) 0)
|
| [17] |
MARONNA R A, MARTIN R D, YOHAI V J. Robust statistics: theory and methods[M]. New York: John Wiley & Sons, 2006.
(  0) 0)
|
| [18] |
HUBER P J. Robust statistics[M]. New York: Wiley, 1981.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


