世界军事领域正处于深刻变革的时代，一方面高新技术的发展对作战理论、军事装备和作战方法等带来了巨大的影响；另一方面随着计算机技术、网络技术、多媒体技术和建模与仿真技术的发展，实验手段已产生质的飞跃^[1]。在此背景下，军事能力特别是核心作战能力的生成逐步向“理论设计-实验论证-部队演练-实战运用”这一新型发展模式转变，“在实验室中研习战争”成为国防和军队建设转型发展的重要环节^[2]。作战实验指运用科学实验的原理、方法和技术，在可控、可测的虚拟对抗环境中，实证性地研究战争和军队作战行动的特点规律，为军事决策和战争实践提供科学依据^[3]。

目前有关作战实验的研究，主要集中在两方面：一是作战实验支撑技术；二是作战实验优化技术。其中，优化技术研究更多地是建立在解析模型或将仿真系统作为黑箱处理的基础上。文献[4-7]在武器-目标分配的研究中，基于建立的解析模型，分别采用不同的启发式搜索算法进行问题求解。国海峰等^[8]在建立空战过程中无人作战飞机(UCAV)总的态势评价函数基础上，基于统计学原理进行UCAV机动决策优化。陈伟龙等^[9]在建立进攻抢修任务动态调度模型基础上，采用变体遗传算法进行问题求解，以提高决策效率、降低决策风险。阮旻智等^[10]在建立基于任务的携行备件动态配置模型基础上，引入拉格朗日约束因子，构建了多约束条件下的方案优化方法。杨迎辉等^[11]在建立网络化作战信息流转策略的适应性演化模型基础上，采用逐次优化算法搜索最优演化路径。王枭等^[12]将仿真系统作为黑箱，引入Apriori算法提出一种边实验边挖掘的序贯探索方法，以提高战争规律发现效率。文献[13]在研究导弹协同攻击体系目标中，为提高仿真优化效率，将创造性思维引入到问题求解中，基于贝叶斯网络以静态博弈去解析动态博弈过程，虽然考虑了攻防对抗过程，但仍是将仿真系统作为黑箱处理。

全流程攻防对抗是一个动态博弈问题，决策随着态势改变而改变，通常难以建立有效的解析模型表达问题并进行求解。鉴于此，本文提出基于战能控制的作战实验方法，主要研究作战系统的动态能力表达、战能环及战能转化系数，基于分布估计算法的战能转化控制。

1 面向作战实验的动态能力表达 1.1 作战行为

作战行为指代驱动装备系统运转的作战人员行为，包括指挥行为和操纵行为，来源于战术条令，并基于战备远航、训练演习的指挥操纵链路不断丰富和完善。指挥行为主要为作战进程中指挥员口令集，可表示为

$ C = \left\{ {{C_1},{C_2}, \cdots ,{C_{{n_C}}}} \right\} $

(1)

式中n_C表示指挥行为数量。

操纵行为主要为作战进程中，各战位基于指挥员口令、依据操纵规程，对装备系统施加的行为集，可表示为

$ O = \left\{ {{O_1},{O_2}, \cdots ,{O_{{n_O}}}} \right\} $

(2)

式中n_O表示指挥行为数量。

对于每个行为，其带有一套描述各战位人员技能水平的参数，如操纵时间、操纵质量等。

指挥行为与操纵行为之间的关联关系：

${O_i} \triangleleft C = {\mathit{\Omega }_{{O_i} \triangleleft C}} = \left\{ {{C_1}, {C_2}, \cdots , {C_{{n_{{O_i} \triangleleft C}}}}} \right\}$，表示能产生操纵行为O_i的指挥行为集合${\mathit{\Omega }_{{O_i} \triangleleft C}}$。

${C_i} \triangleright O = {\mathit{\Omega }_{{C_i} \triangleright O}} = \left\{ {{O_1}, {O_2}, \cdots , {O_{{n_{{C_i} , O}}}}} \right\}$，表示指挥行为C_i下的操纵行为集合${\mathit{\Omega }_{{C_i} \triangleright O}}$。

1.2 装备系统

装备系统指具有不同作战能力的武器单元或搭载平台，如舰艇平台、声呐系统、雷达系统等^[14]。对于某一作战实体，如坦克、飞机、舰艇，其由装备系统可表示为

$ S = \left\{ {{S_1},{S_2}, \cdots ,{S_{{n_S}}}} \right\} $

(3)

式中n_S表示装备系统数量。

对于作战实体中的每个装备系统，可以采用离散事件系统规范化形式体系进行表示^[15-16]：

$ M = < T,X,S,Y,{\delta _{{\rm{ext}}}},{\delta _{{\rm{int}}}},\lambda ,\tau > $

(4)

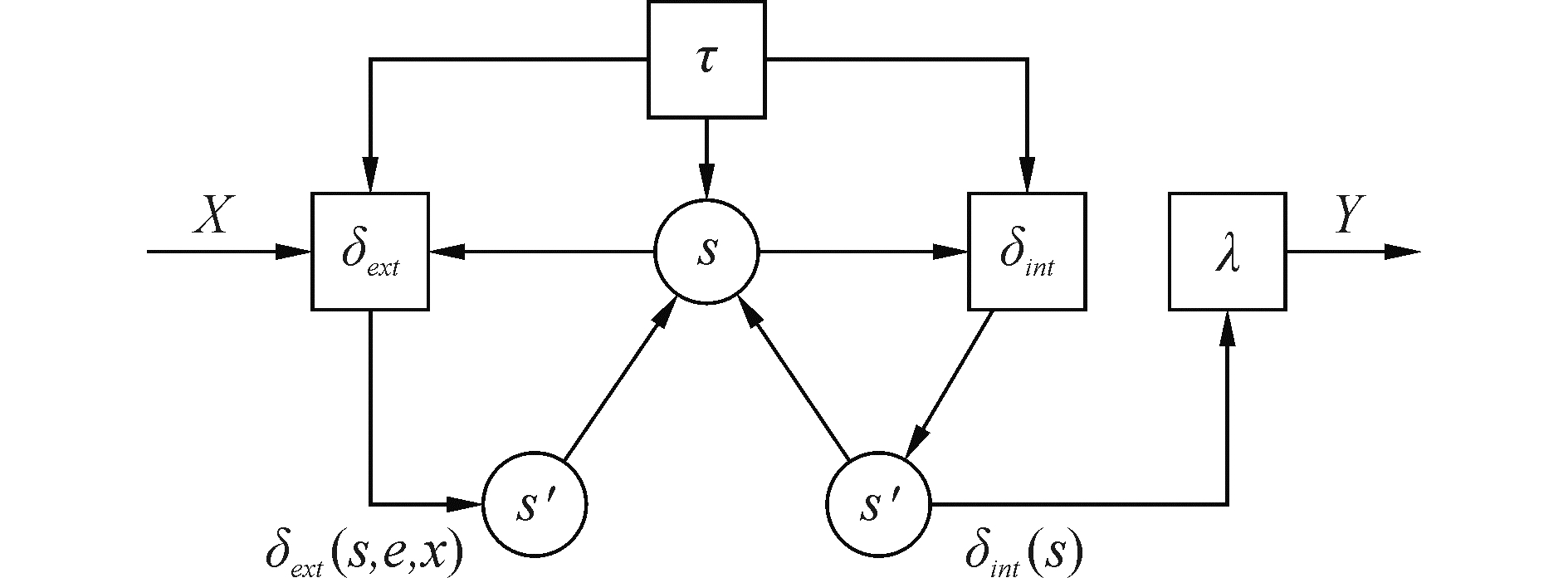
式中：T为时间集合，X为输入集合，S为状态集合，Y为输出集合，δ_ext为外部状态转移函数，δ_int为内部状态转移函数，λ为输出函数，τ为时间推进函数。相互之间的关系如图 1所示。

装备系统的运转是在行为驱动下进行的，操纵行为与装备系统之间的关系为

${S_i} \triangleleft O = {\mathit{\Omega }_{{S_i} \triangleleft O}} = \left\{ {{O_1}, {O_2}, \cdots , {O_{{n_{{S_i} \triangleleft O}}}}} \right\}$，表示能改变装备系统S_i状态的操纵行为集合${\mathit{\Omega }_{{S_i} \triangleleft O}}$；

${O_i} \triangleright S = {\mathit{\Omega }_{{O_i} \triangleright s}} = \left\{ {{S_1}, {S_2}, \cdots , {S_{{n_{{O_i} , S}}}}} \right\}$，表示操纵行为O_i造成状态变化的装备系统集合${\mathit{\Omega }_{{O_i} \triangleright s}}$。

1.3 作战能量

能量是物质运动转换的量度，用来表征物理系统做功的本领。

借鉴物理学中能量定义，将作战能量界定为：作战进程中，作战体系或作战系统所处的一种能力状态，用于表征对敌作战的本领，简称战能。结合作战实体的组分类别及外在表现，对于每一作战实体，其战能可表达为一个七元组^[16]：

$ E = \left( {{E_{Dt}},{E_E},{E_{Df}},{E_A},{E_C},{E_I},{E_G}} \right) $

(5)

式中：E_Dt表示探测战能，E_E表示隐蔽战能，E_Df表示防御战能，E_A表示攻击战能，E_C为指控战能，E_I表示通信战能，E_G表示保障战能。

由能量计算方法可知，每一种能量的表达，最终都落到物理系统的状态，如高速飞行的子弹，其动能为E_k=mv²/2，其中v表达的是子弹的一种运动状态；压缩后的弹簧，其势能为E_p=kx²/2，其中x表达的是弹簧的一种变形状态。鉴于此，基于组分类别和外在表现的可分解性，将各战能分量划分为分量、样式/类别、状态三个层次，其中样式表达作战中更具主观能动性，类别表达作战中主要为客观存在性，作战实验主要是围绕样式展开研究。各战能分量的具体层次性描述为：探测战能、防御战能、隐蔽战能、攻击战能划分为分量、样式、状态，通信战能、指控战能、保障战能划分为分量、类别、状态。

装备系统与作战能量之间的关系为：

${E_i} \triangleleft S = {\mathit{\Omega }_{{E_i} \triangleleft s}} = \left\{ {{S_1}, {S_2}, \cdots , {S_{{n_{{E_i} \triangleleft S}}}}} \right\}$，表示能对作战能量E_i产生影响的装备系统集合${\mathit{\Omega }_{{E_i} \triangleleft s}}$。

${S_i} \triangleright E = {\mathit{\Omega }_{{S_i} \triangleright E}} = \left\{ {{E_1}, {E_2}, \cdots , {E_{{n_{{S_i} \triangleright E}}}}} \right\}$，表示装备系统S_i能够产生影响的作战能量集合${\mathit{\Omega }_{{S_i} \triangleright E}}$。

为统一量纲，所有战能样式采用价值评分进行归一化处理，值越大越优，并通过加权求和形成战能分量。

2 战能环及战能转化系数 2.1 战能环

美国空军上校约翰·博依德(John Boyd)凭借其战斗机飞行员的经验和对能量机动性的研究，于1987年提出了一种作战模型，如图 2所示，它将作战过程简化抽象为由观察(Observe，O)-判断(Orient，O)-决策(Decide，D)-行动(Act，A)4个环节构成的作战回路^[18-19]：

1) 观察，利用各类侦察探测装备对战场环境进行观察和感知，从战场环境中搜集目标的位置、状态、属性等信息；

2) 判断，将观察环节收集到的信息和数据进行处理和融合，并对当前的战场态势进行评估；

3) 决策，依据战场态势制定行动计划和方案；

4) 行动，依据计划方案或上级命令指示实施相应行动。

OODA环具有周期性和嵌套性，周期性意味着一个环结束时，另一个新环的开始，周期性的大小与作战兵力的规模、空间范围、作战样式有关；嵌套性意味着环与环以嵌套的形式关联。目前，OODA被广泛应用于作战问题分析中，它可以很好地表述作战行动的阶段性、递进性，但无法有效诠释作战行动的目的性、并行性。如搜攻任务中，在抵达作战区域时，可为搜索、打击、防御进行提前布势，在搜索阶段同样可为打击、防御进行提前布势等。鉴于此，研究提出战能积蓄-感知-传递-转化的战能环，如图 3所示，其中：

1) 战能积蓄(EA)，在作战进程中，以主行动目标为约束条件，基于作战行为的并行性，开展战能感知、传递和转化的优化布势。

2) 战能感知(EP)，在行为驱动下，充分考虑自身隐蔽情况，基于传感器获取敌方目标信息，主要涉及探测战能、隐蔽战能、保障战能。

3) 战能传递(ED)，在行为驱动下，完成目标分配及方案下发，以实现战能感知到战能转化的变迁，主要涉及指控战能、通信战能、保障战能。

4) 战能转化(ET)，在行为驱动下，基于攻击武器和防御武器，对敌实施攻击或防御，主要涉及攻击战能、防御战能、保障战能。

图 3中的实线表示，完成一次攻防对抗，需要经历战能感知、战能传递、战能转化一个循环；虚线表示，战能感知、战能传递、战能转化与战能积蓄互为输入输出。

2.2 战能转化系数

定义4  作战潜能

面向作战任务，作战体系或作战系统在当前战能下所具备的潜在作战效果，以转化系数进行表征，简称战势。战势不仅与当前战能相关，还受到战能感知、战能传递及作战行动的影响，鉴于此，战势可表示为

$ \eta = \left( {{\eta _1},{\eta _2}, \cdots ,{\eta _{{n_\eta }}}} \right) = f\left( {E,{\rm{EP}},{\rm{ED}},A} \right) $

(6)

式中：E表示当前作战能量；EP表示战能感知，主要由精度进行表征，如位置精度、速度精度；ED表示战能传递，主要由数量进行表征，如单雷攻击、双雷齐射；A表示作战行动，以指挥行为序列进行表征，如鱼雷准备、鱼雷发射。

借鉴频谱分析的部分术语，引入转化效果、转化幅值、转化时间、转化相位、转化密度、转化斜率作为战能转化系数，对战势进行标识。

转化效果η₁：当前作战行动A所能达到的转化效果。通常情况下，转化效果越好的作战方案越优。

转化幅值η₂：最优作战行动A所能达到的转化效果。通常情况下，转化幅值越大，表明通过局部调整可以达到的转化效果越好。

转化时间η₃：当前作战行动A完成战能转化的时间。通常情况下，两个转化效果相同的作战方案，则转化时间越短越好。

转化相位η₄：当前最优作战行动A两者之间距离。两个转化效果相同的作战方案，且转化峰值相同的情况下，则转化相位大的不容易通过局部调整求取最优解。

转化密度η₅：所有作战行动A的转化效果求平均值。两个转化效果相同的作战方案，则转化密度大的越容易通过局部调整求得满意解。

转化斜率η₆：作战行动A所达作战效果的变化趋势。两个转化效果相同的作战方案，则斜率大的越容易通过局部调整获取更好的作战效果。

3 基于分布估计算法的战能转化控制

借鉴棋牌中的动态博弈研究思路^[21-23]，基于战能环及战能转化系数，构建如图 4所示的优化控制框架，总体思路为：将优化算法嵌入到仿真推演中，在作战进程中根据红蓝双方态势，基于战势和战能相结合的评判准则，快速生成满意的行动方案。这样，问题求解是在一种智慧博弈下开展的，相比于传统方法，降低了求解的盲目性。主要由指挥行为编码、行动方案生成^[24]、精英种群选择、概率模型更新、实验数据挖掘组成，其中子图为产生行动方案的展开阐述，战能积蓄贯穿于准备、感知、传递、转化各个阶段。

3.1 指挥行为编码

依据战能感知、传递、转化涉及的系统组件，以及指挥行为与系统组件的关系，对指挥行为进行归类，形成指挥行为集合：

$ \left\{ \begin{array}{l} {\mathit{\Omega }_{{\rm{EP}} \triangleright C}} = \left\{ {{C_1},{C_2}, \cdots {C_{{n_{{\rm{EP}} \triangleright C}}}}} \right\}\\ {\mathit{\Omega }_{{\rm{ED}} \triangleright C}} = \left\{ {{C_1},{C_2}, \cdots {C_{{n_{{\rm{ED}} \triangleright C}}}}} \right\}\\ {\mathit{\Omega }_{{\rm{ET}} \triangleright C}} = \left\{ {{C_1},{C_2}, \cdots {C_{{n_{{\rm{ET}} \triangleright C}}}}} \right\} \end{array} \right. $

(7)

起始阶段，各指挥行为的后续指挥行为等概率存在，即

$ {P_{0,i,j}} = 1/{N_i} $

(8)

式中N_i表示指挥行为C_i后续可能的行为数量。

3.2 行动方案生成

以当前时间节点为起点，建立分别服务于感知、传递、转化的行为流程：

1)在准备阶段，对感知、传递、转化中具有相对独立性的战能分量进行布势，具体步骤为：

步骤1：依次根据转化效果、转化幅值、转化相位、转化斜率、转化密度，基于指挥行为${\mathit{\Omega }_{{\rm{EP}} \triangleright C}}$、${\mathit{\Omega }_{{\rm{ED}} \triangleright C}}$、${\mathit{\Omega }_{{\rm{ET}} \triangleright C}} $并集，确定指挥行为C_i后续指挥行为C_j的概率分布：

$ {\rho _{i,j}} = {\eta _{l,j}}/\sum\limits_{l = 1}^{{N_i}} {{\eta _{l,j}}} $

(9)

式中η_{l, j}中的l表示上述五个值中的一个。

步骤2：如果ρ_{i, j}不同，转步骤3；否则，表明无法获取转化系数，或无法以转化系数进行区别，则设定各战能分量权重相同，以战能聚合函数确定概率分布：

$ \left\{ \begin{array}{l} {\rho _{i,j}} = {e_j}/\sum\limits_{j = 1}^{{N_i}} {{e_j}} \\ {e_{k,j}} = \sum\limits_{k = 1}^7 {{e_{k,j}}} /7 \end{array} \right. $

(10)

式中e_{k, j}表示各战能分量的价值评分。

步骤3：基于ρ_{i, j}、P_{k-1, i, j}，以增量值σ₁构建过渡概率模型，即

$ {P_{k,i,j}}^T = {\sigma _1}{P_{k - 1,i,j}} + \left( {1 - {\sigma _1}} \right){\rho _{i,j}} $

(11)

步骤4：以概率模型P_{k, i, j}^T确定指挥行为C_i的后续指挥行为C_j。

2) 在感知阶段，以感知为主目标，进行指挥行为序列化，具体操作步骤为：

步骤1：如准备阶段的步聚1，不同之处在于基于的指挥行为集合为${\mathit{\Omega }_{{\rm{EP}} \triangleright C}} $。

步骤2：如准备阶段的步骤2，不同之处在于概率分布的计算方式：

$ \left\{ \begin{array}{l} {\rho _{i,j}} = {e_j}/\sum\limits_{j = 1}^{{N_i}} {{e_j}} \\ {e_{k,j}} = \sum\limits_{k = 1}^7 {{\omega _k}{e_{k,j}}} /7 \end{array} \right. $

(12)

式中e_{k, j}表示各战能分量的价值评分。

步骤3：如准备阶段的步骤4。

步骤4：对${\mathit{\Omega }_{{\rm{ED}} \triangleright C}}$、${\mathit{\Omega }_{{\rm{ET}} \triangleright C}}$进行分析，如果存在C_k，其不影响C_j，且效应时间小于C_j，则将其加入到作战流程中。

3) 在传递阶段，以传递为主目标，进行指挥行为序列化，具体操作步骤与2)类似。

4) 在转化阶段，以转化为主目标，进行指挥行为序列化，具体操作步骤与2)类似，不同之处在于其概率分布的确定顺序为转化效果、转化时间、转化幅值、转化相位、转化斜率、转化密度。

3.3 精英种群选择

由于寻优的随机性导致解集在演化过程中具有一定的退化性；为了保证算法能够收敛到全局最优解，将精英策略引入到算法中。对于内外循环，采用同样的种群选择策略，具体方法为：

步骤1：设置一个存储容器C_P，大小为进化种群E_P的规模N_P，用于存储进化过程中产生的精英种群；

步骤2：每次迭代后，从C_P中选择与E_P中不同的个体参与排序，将其中N_P个最优个体作为执行选择操作的基础；

步骤3：每次迭代后，从C_P和E_P中选择N_P个不同的最优个体作为精英种群替换C_P中的精英种群。

3.4 概率模型更新

对于内外循环，采样同样的概率模型更新方法，其中内循环的初始阶段采用外循环的概率模型，且内循环的概率模型更新不影响外循环的概率模型^[25]。对于每个指挥行为，采用增量学习的方式更新概率模型，即：

$ \left\{ \begin{array}{l} {P_{k,i,j}} = {\sigma _2}{P_{k - 1,i,j}} + \left( {1 - {\sigma _2}} \right){{P'}_{k,i,j}}\\ {{P'}_{k,i,j}} = {N_{i,j}}/{N_i} \end{array} \right. $

(13)

式中: k为当前迭代代数，β₂为增量学习系数；N_{i, j}为精英种群中指挥行为C_i后续行为中C_j的数量；N_i为精英种群中指挥行为C_i的数量。

3.5 实验数据挖掘

为有效获取战能转化系数，采用二阶模型进行拟合，即

$ y = {\beta _0} + \sum\limits_{i = 1}^k {{\beta _i}{x_i}} + \sum\limits_{i = 1}^k {{\beta _{i,i}}x_i^2} + \sum\limits_i {\sum\limits_j {{\beta _{i,j}}{x_i}{x_j}} } ,\left( {i \ne j} \right) $

(14)

式中:x=(e, ep, ed, a)，y=(η₁, η₃)。

4 实例分析 4.1 实验设置

红方作战平台A、B受领作战任务，对处于某个作战区域的蓝方作战平台C进行协同搜攻，其中作战平台A为指挥平台，作战平台B为协同平台。进入作战区域前，作战平台A、B需要通过指挥行为达成就位态势；进入作战区域后，作战平台A、B的探测方式为RD₁、RD₂二种，搜索方式为RS₁、RS₂、RS₃三种，机动方式为RM₁、RM₂二种。作战平台C随机地从边界某一点进入作战区域，机动方式BM₁为一种，探测方式为BD₁一种。作战平台C对于探测方式RD₁的隐蔽性要优于作战平台A、B对探测方式BD₁的隐蔽性。

4.2 优化控制 4.2.1 战能设置

基于作战平台A为指挥平台，以作战平台B为协同平台，以加权求和方式确定两者的协同战能：

$ e = {\omega _A}{e_A} + {\omega _B}{e_B} $

(14)

其中，ω_A=0.6、ω_A=0.4。

4.2.2 战势设置

由于作战任务是作战平台A、作战平台B共同完成对作战平台C的搜攻任务，因此转化效果为它们的和：

$ {\eta _1} = {\eta _{1,A}} + {\eta _{1,B}} $

(15)

转化幅值、转化相位、转化斜率、转化密度都建立在此基础上的，由于转化时间独立转化效果，因此作战平台A、B分别保有自己的转化时间。

4.2.3 优化设置

个体产生方式：个体长度为10，时间间隔为5 s，即从当前时刻开始，思考下50 s的作战行动，当未遭遇时，则按照战术条令中的规则开展活动。种群规模为N_P=200；选择概率为P_P=0.3；内部最大迭代次数I_t=100，即战能环的优化控制；外部最大迭代次数O_t=1 000，即仿真实验推演的次数；增量学习系数为σ_i=0.8(i=1, 2)。优化方式分为三种：1)Op₁, 传统的基于分布估计算法的问题求解；2)Op₂, 基于战能环阶段划分的问题求解；3)Op₃, 战能环加转化系数的问题求解。

4.2.4 行为编码

对于作战平台A、B，其作战行动都分别包括：抵达作战区域A₁、侦察战场环境A₂、搜索作战平台CA₃、打击作战平台CA₄、防御作战平台CA₅几大活动。

依据作战平台A主要作战活动，其主要指挥行为集合为

$ C = \left\{ {{C_1},{C_2}, \cdots ,{C_{{n_C}}}} \right\},{n_C} = 17 $

式中：C₁为调整航速、航向、航深的指挥行为，C₁₅为探测方式的指挥行为，C₁₆为搜索方式的指挥行为，C₁₇为机动方式的指挥行为。

指挥行为关系为：

$ \begin{array}{l} {C_1} \to {C_i},{C_i} \to {C_1},{C_3} \to {C_4},{C_4} \to {C_5},\\ {C_5} \to {C_6},{C_6} \to {C_7},{C_8} \to {C_9},{C_9} \to {C_{10}},\\ {C_{10}} \to {C_{11}},{C_6} \to {C_7},{C_3} \triangleright {C_4},{C_4} \triangleright {C_5},\\ {C_5} \triangleright {C_6},{C_5} \triangleright {C_7},{C_8} \triangleright {C_9},{C_9} \triangleright {C_{10}},\\ {C_{10}} \triangleright {C_{11}} \end{array} $

其中，C_i→C_j表示存在序列约束关系，C_i$ \triangleright $C_j表示存在先后约束关系。

4.2.5 实验结果

对每种优化方式开展1 000次重复优化，其中转化效果以对敌毁伤概率进行表征。

1) 转化效果演化进程。

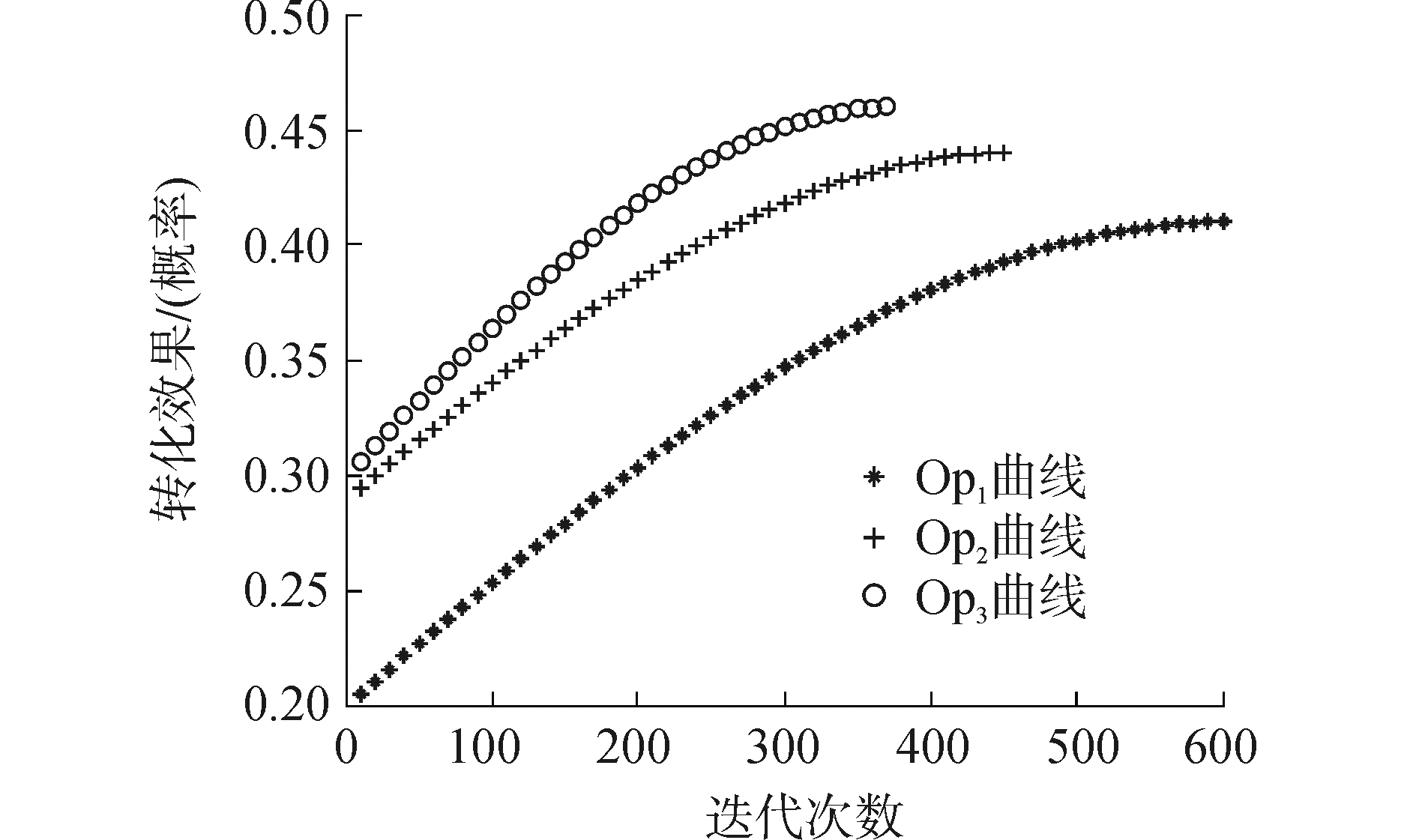
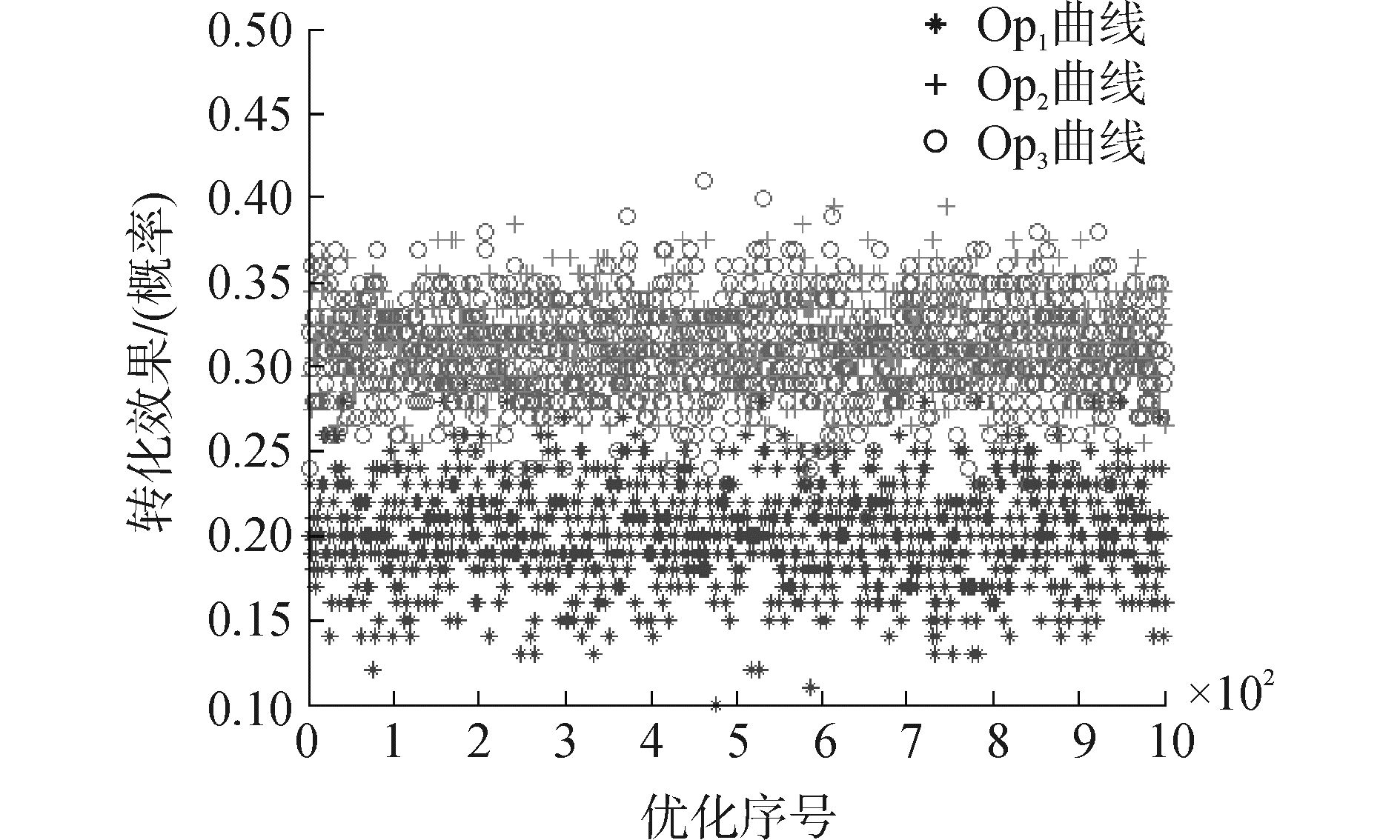
如图 5所示，为某一次三种优化方式转化效果的演化进程；总体上，每次优化过程都服从图 5所示的曲线。第1次迭代结束后，Op₂、Op₃的值要优化于Op₁，这是因为战能环起了作用；Op₂、Op₃的值基本相同，这是因为转化系数还未构建，三者以优化次数作为标识的初始值分布如图 6所示。

2) 优化效果均值方差。

1 000次优化的结果如图 7所示，构建方式为极坐标系：以均值为中心，以距离为极轴，以优化序号标识夹角；统计值如表 1所示。由图及统计值可知，Op₃无论在优化质量还是优化效率方面，都要优于Op₁、Op₂。

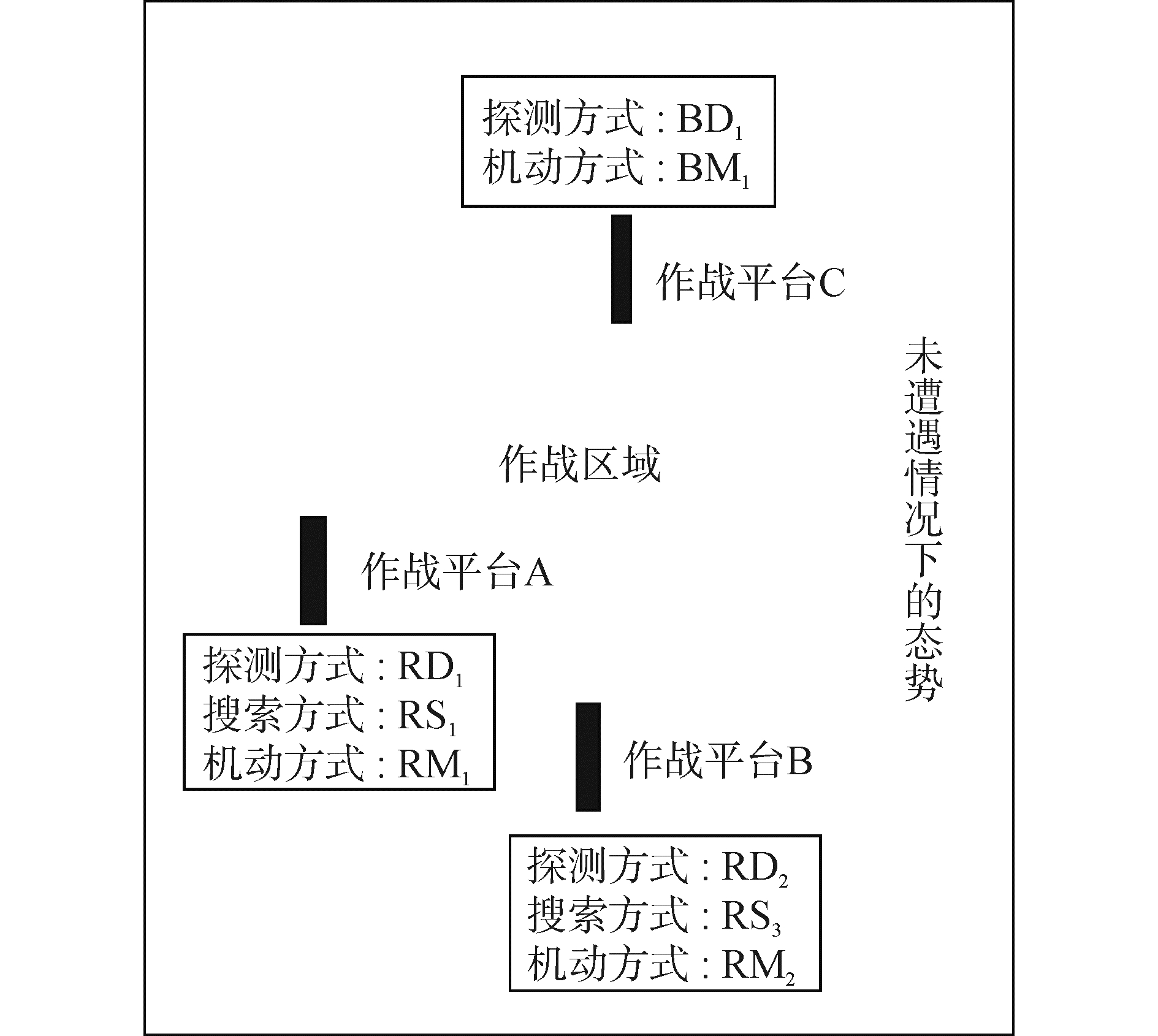
由实验结果可知，战能环及战能转化系数的引入将大大提高方案探索的效率，有利于快速形成战法训法。经实验可得，作战平台A、B采用如图 8所示的就位态势所示进行搜攻任务，作战平台A采用探测方式RD₁、搜索方式RS₁、机动方式RM₁；作战平台B采用探测方式RD₂、搜索方式RS₃、机动方式RM₂。

5 结论

1) 借鉴AlphaGo的思路，将优化算法嵌入到作战进程中，以动态能力作为评价准则，通过红蓝双方智慧博弈来探究作战行为与装备系统的最佳组合；相比于传统方法，能取得更好的优化效率及效果，为研究战争规律提出了一种新的解题思路。

2) 辅助决策存在于部分作战系统中，但通常都属于基于规则库或解析模型的单步决策，即单点最优性；本研究为考虑多时段的博弈决策，具有全局最优性。因此，本研究不仅可以有效服务于战法训法创新；还可为辅助决策系统或智能指控系统的构建提供借鉴，或达到一定成熟度时，作为一型装备装配到作战平台上。

3) 作战大致可分为战略、战役、战术三个层次，本文的立足点为战术博弈，其能力状态的量化分析相对简单；如何量化战役、战略层红蓝双方的动态能力，并据此开展优化分析，以为高层指挥员进行兵力运用提供支持，是下一步研究的方向。