2. 哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
大多数情况下工程只关心广义结构及其邻近介质中的波动,因此需要引入人工边界将感兴趣的有限计算区从无限域中截取出来,并设置人工边界条件模拟外部无限域的能量辐射效应。基于不同的构造思路提出了多种人工边界条件,主要可以分为2类:1)由满足场方程的外行波假定导出,主要有粘性及粘弹性边界[1],Higdon边界及其辅助变量实现[2],透射边界[3]等;2)在人工边界外设置吸收层,如物理阻尼层[4]、Super-grid层[5]、完美匹配层[6]等。另外,近年出现了一种加权混合人工边界[7],其通过在一定层厚范围内对人工边界格式和内域计算格式作线性加权以吸收外行波。
透射边界是廖振鹏等[3]提出的,其基于可描述体波、面波和导波的单向波形式表达式,以离散形式直接模拟外行波穿过边界。透射边界具有高精度、低计算量,且与内域场方程无关,可直接用于各种场方程,并适用于人工边界上的各节点,如角点和分层界面点。这一边界已在地震工程、地球物理、电磁学等数值模拟领域得到应用。然而,在波动数值模拟中透射边界存在数值失稳现象。已有的失稳机理研究结果可归纳为2类:全局反射放大失稳[8]和局域耦合失稳,后者又分为零频飘移失稳[9-10]和高频振荡失稳[11]。局域耦合失稳可通过改变内域离散格式,或人工边界格式,或两者,可消除失稳耦合[12],由此提出了多种有效措施,如采用小量修正透射边界[10]或内域离散格式[13]来消除零频飘移失稳;采用阻尼滤波[14],或调整内域单元长宽比[15],或修改内域有限元刚度[16]来消除高频振荡失稳。
在波动数值模拟中为提高透射边界对大角度入射波的吸收精度,可以通过增大透射边界人工波速来实现,然而此时可能出现反射放大失稳。Liao等[8]基于一维波动集中质量有限元模拟的透射边界反射系数,揭示了透射边界由于人工波速选择不当造成的反射放大失稳现象,其失稳机理是人工边界对波动数值模拟无意义的高频行波的放大效应,以及放大的反射波在有限区域内的反复反射放大,并给出了合理的人工波速选择范围。谢志南等[17]针对一维波动集中质量有限元模拟,理论上论证了当人工波速小于1.5倍的离散空间步距和时间步距的比值时,可避免透射边界反射放大失稳,但指出文中分析不能完全适用于多维情况。另外,上述文献论证反射放大失稳时,均需要将具体的内域离散格式与人工边界格式耦合求解得到反射系数,论证过程复杂,并且如若将内域波动换成另一格式,其结论需重新论证。
对于多维波动,反射放大失稳尚未有过研究,亦未给出合理的人工波速取值范围。但对于多维波动人工边界反射系数已有诸多研究,主要探讨人工边界的吸收精度。反射系数计算方法[18]主要有连续模型解析方法、数值实验方法和离散模型解析方法。第1种方法针对连续模型,然而时域波动数值模拟是在时空离散下进行的,人工边界在离散模型中的表现不同于连续模型。第2种方法基于数值实验结果,然而数值实验结果受诸多因素影响,不能完全反映人工边界反射系数。第3种方法针对离散格式,并采用解析方法,合理地反映了人工边界反射系数,本文采用离散模型解析方法来分析透射边界引发的反射放大失稳。另外,在多维情况下由于透射边界引发更为严重的高频振荡失稳,从而掩盖了反射放大失稳现象。文献[15-16]提出的稳定措施可彻底消除高频振荡失稳,从而为揭示多维波动下的反射放大失稳提供了数值模拟基础。
综上所述,本文针对集中质量有限元模拟的SH波动,基于考虑内域离散的透射边界反射系数,研究透射边界引发的反射放大失稳。
1 反射系数及反射放大失稳各向同性、线弹性SH波动方程:
| $ \rho \frac{\partial^{2} u}{\partial^{2} t}-\nabla \cdot(\mu \nabla u)=f $ | (1) |
式中:u为位移;f为荷载;ρ为密度;μ为弹性模量;∇为哈密顿算子。
由于人工边界附近区域通常采用规则单元,且没有荷载项,因此采用线性集中质量有限元长方形单元及时间中心差分离散上述连续模型可得[19]:
| $ \begin{array}{c} u_{m, n}^{p + 1} = 2u_{m, n}^p - u_{m, n}^{p - 1} + \Delta {\tau ^2}\left[ {\left( {\frac{2}{3} - \frac{1}{{3{\beta ^2}}}} \right)\left( {u_{m - 1, n}^p + u_{m + 1, n}^p} \right) + } \right.\\ \left( { - \frac{1}{3} + \frac{2}{{3{\beta ^2}}}} \right)\left( {u_{m, n - 1}^p + u_{m + 1, n}^p} \right) + \left( {\frac{1}{6} + \frac{1}{{6{\beta ^2}}}} \right)\left( {u_{m + 1, n + 1}^p + } \right.\\ u_{m + 1, n - 1}^p + u_{m - 1, n + 1}^{p + 1} + u_{m - 1, n - 1}^p) - \left( {\frac{4}{3} + \frac{4}{{3{\beta ^2}}}} \right)u_{m, n}^p] \end{array} $ | (2) |
式中:um, np=(mΔx, nΔy, pΔt);Δτ=csΔt/Δx;波速
人工边界采用透射边界[19]:
| $ u_{0}^{p+1}=\sum\limits_{j=1}^{N}(-1)^{j+1} C_{j}^{N} \boldsymbol{u}_{j}^{p+1-j} $ | (3) |
若式(3)中的计算点与内域离散网格节点不重合时,计算点由网格节点空间插值得到。透射边界插值形式:
| $ \left\{\begin{array}{l}{u_{0}^{p+1}=\sum\limits_{j=1}^{N}(-1)^{j+1} C_{j}^{N} \boldsymbol{T}_{j} \boldsymbol{u}_{j}^{p+1-j}} \\ {\boldsymbol{u}_{j}^{p+1-j}=\left[\begin{array}{ccc}{u_{0}^{p+1-j}} & {u_{1}^{p+1-j}} & {\cdots} & {u_{2 j}^{p+1-j}}\end{array}\right]^{\mathrm{T}}} \\ {\boldsymbol{T}_{j}=\left[\begin{array}{lll}{t_{j, 1}} & {t_{j, 2}} & {\cdots} & {t_{j, 2 j+1}}\end{array}\right]}\end{array}\right. $ | (4) |
式中:ujp为沿边界法线距边界jΔx处的网格节点在pΔt时刻的位移,二项式系数CjN=N!/((N-j)!j!)。
| $ t_{j, r}=\sum t_{1, q_{1}} t_{1, q_{2}} \cdots t_{1, q_{j}}, r=1, 2, \cdots, 2 j+1 $ |
式中:记号“∑”表示对所有满足以下条件的项求和:
q1+q2+…+qj=r+j-1, q1, …, qj=1, 2, 3
式中t1, 1=(2-S)(1-S)/2,t1, 2=S(2-S),t1, 3=S(S-1)/2,S=caΔt/Δx,ca为人工波速。
透射边界可以写成算子形式[19]:
| $ \left(1-Z_{t}^{-} A\right)^{N} u_{0}^{p+1}=0 $ | (5) |
其中:A=t1, 1+t1, 2Zx+t1, 3Zx2;Zxujp=uj-1p;Zt±ujp=ujp±1。
由于时域波动数值模拟是在时空离散下进行的,人工边界在离散模型中的表现不同于连续模型。因此,为分析波动模拟中透射边界引发的反射放大失稳,下面给出离散模型中透射边界的反射系数。
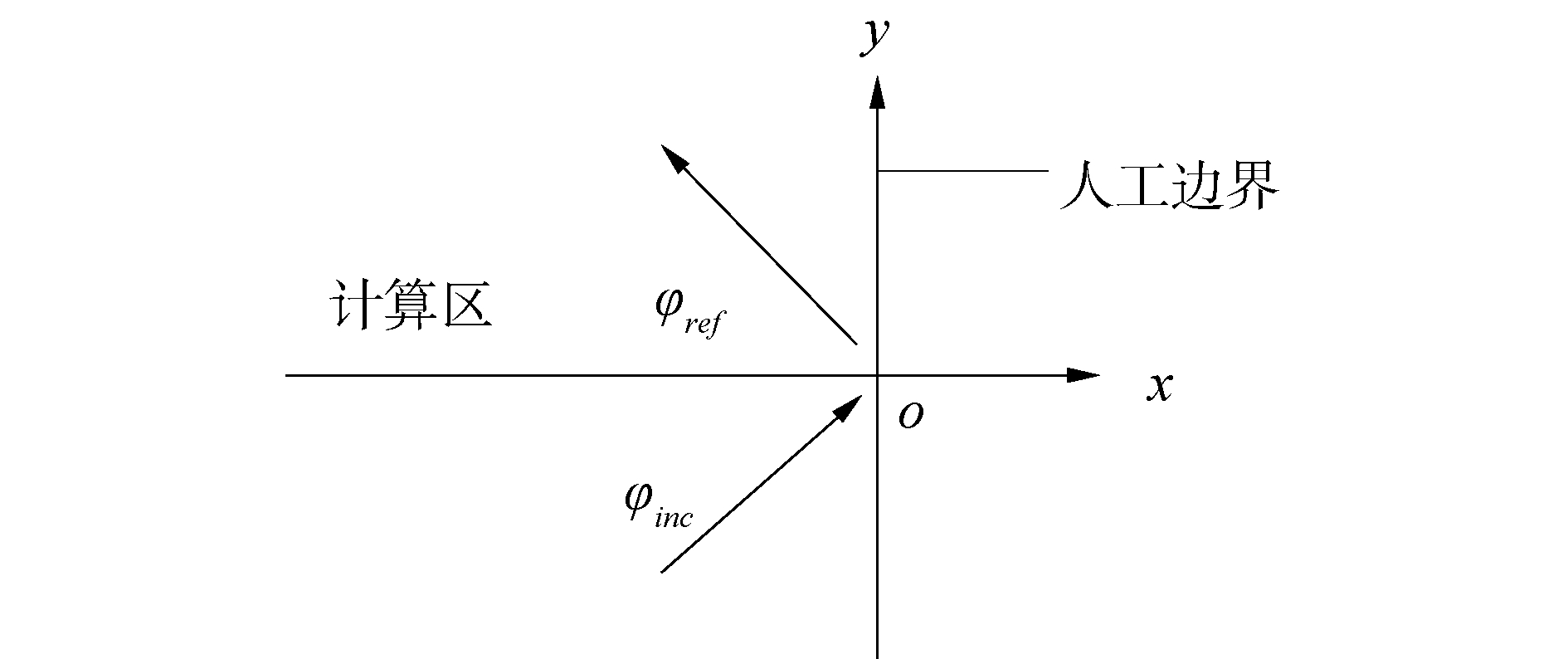
对于右人工边界(如图 1所示),在SH波动情况下,人工边界节点的标量波场可由如下入射波和反射波构成:
|
Download:
|
| 图 1 人工边界示意 Fig. 1 Diagram of artificial boundary | |
| $ \phi=\phi_{\mathrm{inc}}+R \phi_{\mathrm{ref}}=\mathrm{e}^{\mathrm{i} \omega p \Delta t-\mathrm{i} k_{y} n \Delta y}\left(\mathrm{e}^{-\mathrm{i} k_{x} m \Delta x}+R \mathrm{e}^{\mathrm{i} k_{x} m \Delta x}\right) $ | (6) |
式中:R为反射系数;ω为圆频率。沿x和y轴正向的视波数分别为kx=kcos θ,ky=ksin θ,k为波数,θ为平面谐波入射角。由于频散关系的对称性及混淆效应[19],可只考虑第一象限,即ωΔt, kxΔx, kyΔy∈[0, π]。
将式(6)代入式(5),可得反射系数:
| $ R = - {\left( {\frac{{1 - \left( {{t_{1, 1}} + {t_{1, 2}}{{\rm{e}}^{{\rm{i}}{k_x}\Delta x}} + {t_{1, 3}}{{\rm{e}}^{{\rm{i}}2{k_x}\Delta x}}} \right){{\rm{e}}^{ - {\rm{i}}\omega \Delta t}}}}{{1 - \left( {{t_{1, 1}} + {t_{1, 2}}{{\rm{e}}^{ - {\rm{i}}{k_x}\Delta x}} + {t_{1, 3}}{{\rm{e}}^{ - {\rm{i}}2{k_x}\Delta x}}} \right){{\rm{e}}^{ - {\rm{i}}\omega \Delta t}}}}} \right)^N} $ | (7) |
式中ω和kx由内域频散方程确定。
由式(7)可知人工边界作为对外部无限域能量辐射效应的近似模拟,其对波动不仅只在幅值(反射系数的模)上,还会在相位(反射系数的幅角)上产生影响。但对于波动数值模拟,首要考虑的是人工边界反射波的幅值,因此本文所说的反射系数就是指反射系数的模。
将平面谐波
| $ U_{m, n}^{p}=e^{\mathrm{i}\left(\omega p \Delta t-k_{x} m \Delta x-k_{y} n \Delta y\right)} $ | (8) |
代入有限元格式式(2),可得有限元格式的频散方程:
| $ \begin{array}{c} {\sin ^2}\left( {\frac{{\omega \Delta t}}{2}} \right) = \Delta {\tau ^2}\left[ {{{\sin }^2}\left( {\frac{{{k_x}\Delta x}}{2}} \right) + \frac{1}{{{\beta ^2}}}{{\sin }^2}\left( {\frac{{{k_y}\Delta y}}{2} - } \right)} \right.\\ \left. {\frac{2}{3}\left( {1 + \frac{1}{{{\beta ^2}}}} \right){{\sin }^2}\left( {\frac{{{k_x}\Delta x}}{2}} \right){{\sin }^2}\left( {\frac{{{k_y}\Delta y}}{2}} \right)} \right] \end{array} $ | (9) |
利用式(9)计算的反射系数式(7)即为SH波动集中质量有限元模拟中透射边界的反射系数。
当式(7)中的kx和ω由连续模型的频散方程确定,即在连续极限条件下,式(9)取Δt, Δx, Δy→0,由此可得连续模型的频散方程:
| $ \omega^{2}=c_{s}^{2}\left(k_{x}^{2}+k_{y}^{2}\right) $ | (10) |
并取Δτ=S=1,则计算的反射系数即为理想稳态反射系数[19]。
当kyΔy=0,(9)即为SH波动的x方向频散,即为一维波动有限元格式的频散方程:
| $ \sin ^{2}\left(\frac{\omega \Delta t}{2}\right)=\Delta \tau^{2} \sin ^{2}\left(\frac{k_{x} \Delta x}{2}\right) $ | (11) |
利用式(11)计算的反射系数式(7)即为一维波动有限元模拟中透射边界的反射系数[8, 17]。
文献[8, 17]将一维有限元格式和透射边界格式耦合求解得到反射系数,揭示了透射边界引发的反射放大失稳。下面进一步分析SH波动模拟中存在的反射放大失稳,揭示此类失稳与具体的内域离散格式无关,仅是人工波速选择不当造成的,并给出合理的人工波速取值范围,同时分析引起反射放大失稳的波动成分特性。
式(7)中令|R|≤1,可得:
| $ \left|\frac{1-\left(t_{1, 1}+t_{1, 2} \mathrm{e}^{\mathrm{i} k_{x} \Delta x}+t_{1, 3} \mathrm{e}^{\mathrm{i} 2 k_{x} \Delta x}\right) \mathrm{e}^{-\mathrm{i} \omega \Delta t}}{1-\left(t_{1, 1}+t_{1, 2} \mathrm{e}^{-\mathrm{i} k_{x} \Delta x}+t_{1, 3} \mathrm{e}^{-\mathrm{i} 2 k_{x} \Delta x}\right) \mathrm{e}^{-\mathrm{i} \omega \Delta t}}\right| \leqslant 1 $ | (12) |
经化简,可得:
| $ \left|\frac{a+\mathrm{i} b}{a+\mathrm{i} d}\right|=\sqrt{\frac{a^{2}+b^{2}}{a^{2}+d^{2}}} \leqslant 1 $ | (13) |
式中:a=cos(ωΔt)-(t1, 1+t1, 2cos(kxΔx)+t1, 3cos(2kxΔx));b=sin(ωΔt)-(t1, 2sin(kxΔx)+t1, 3sin(2kxΔx));d=sin(ωΔt)+(t1, 2sin(kxΔx)+t1, 3sin(2kxΔx))。
由式(13)易得b2≤d2,因此可得:
| $ \sin (\omega \Delta t)\left(t_{1, 2} \sin \left(k_{x} \Delta x\right)+t_{1, 3} \sin \left(2 k_{x} \Delta x\right)\right) \leqslant 0 $ | (14) |
由于ωΔt、kxΔx∈[0, π],故sin(ωΔt)、sin(kxΔx)≥0,因此有:
| $ t_{1, 2}+2 t_{1, 3} \cos \left(k_{x} \Delta x\right) \leqslant 0 $ | (15) |
即:
| $ S \leqslant \frac{2-\cos \left(k_{x} \Delta x\right)}{1-\cos \left(k_{x} \Delta x\right)} $ | (16) |
由于cos(kxΔx)∈[-1, 1],故
| $ S \leqslant 1.5 $ | (17) |
式(17)是保证透射边界不会发生反射放大失稳的条件。因此,合理的人工波速取值范围为:
| $ c_{a} \leqslant \frac{1.5 \Delta x}{\Delta t}=\frac{1.5 c_{s}}{\Delta \tau} $ | (18) |
本文推导的式(18)与文献[17]针对一维波动的结论一致,但本文上述推导过程(12)~(18)并不涉及具体的内域离散格式,并且由于透射边界格式是一维表达式,在一维、二维和三维中的形式是一致的,因此可以说明本文结论适用于任何一维、二维和三维SH波动,同时与具体的内域离散格式无关,仅是人工波速选择不当造成的。
下面分析引起反射放大失稳的波动成分特性。当S>1.5时,引起反射放大(即|R|>1)的波动成分由式(16)可得:
| $ k_{x} \Delta x>\arccos \left(\frac{S-2}{S-1}\right) $ | (19) |
由式(19)可知,引起失稳的波动对应一波长内包含的单元个数为:
| $ n g=\frac{2 \pi}{k_{x} \Delta x}<2 \pi / \arccos \left(\frac{S-2}{S-1}\right) $ | (20) |
对透射边界式(5)作von-Neumann稳定性分析,可得S≤2。在S∈(1.5, 2]时,可得n最大值为4,即一波长最多包含4个单元,而对波动数值模拟有意义的有效波长内至少应包含6~8个单元[19]。
另外,考虑具体内域离散格式频散,即有限元频散式(9),并取β=1作简化分析,由式(19)可得:
| $ \frac{\omega}{\omega_{u}}>\min \left(\frac{\arcsin \left(\Delta \tau \sqrt{\frac{1}{2 S-2}}\right)}{\arcsin (\Delta \tau)}, \frac{\arcsin \left(\Delta \tau \sqrt{\frac{6 S-7}{6 S-6}}\right)}{\arcsin (\Delta \tau)}\right) $ | (21) |
式中:截止频率ωu=2arcsin(Δτ)/Δt,ωu由式(9)容易得到[19]。由于集中质量有限元的稳定性条件[19]为Δτ≤1,故在Δτ∈(0, 1]及S∈(1.5, 2]情况下,由式(21)可得ω/ωu>1/2,由于对波动数值模拟有意义的频带[19]为ω < (1/4~1/3)ωu,故失稳的频带位于对波动数值模拟无意义的高频带,因此亦可通过高频滤波措施来抑制失稳。
图 2为SH波动二阶透射边界的反射系数,内域采用具体离散格式的频散,即有限元频散式(9)。可以看出,S=1.4时,反射系数均不大于1;而S=1.6时,存在反射系数大于1,并且引起失稳的谐波波数由(19)可得kxΔx∈(arccos(-2/3), π]。

|
Download:
|
| 图 2 不同参数条件下,SH波动集中质量有限元模拟中二阶透射边界的反射系数 Fig. 2 Reflection coefficient of second order transmitting boundary in SH wave simulation with lumped-mass finite element method under different parameter conditions | |
下面采用数值实验验证反射放大失稳现象。集中质量有限元与透射边界结合会导致高频振荡失稳[11],数值实验中更为严重的高频振荡失稳会掩盖反射放大失稳。上文已论证透射边界引发的反射放大失稳与具体的内域离散格式无关,所以采用修正的集中质量有限元[16]来验证反射放大失稳。修正有限元是对传统有限元的单元刚度作了修正,消除了透射边界引发的高频振荡失稳。
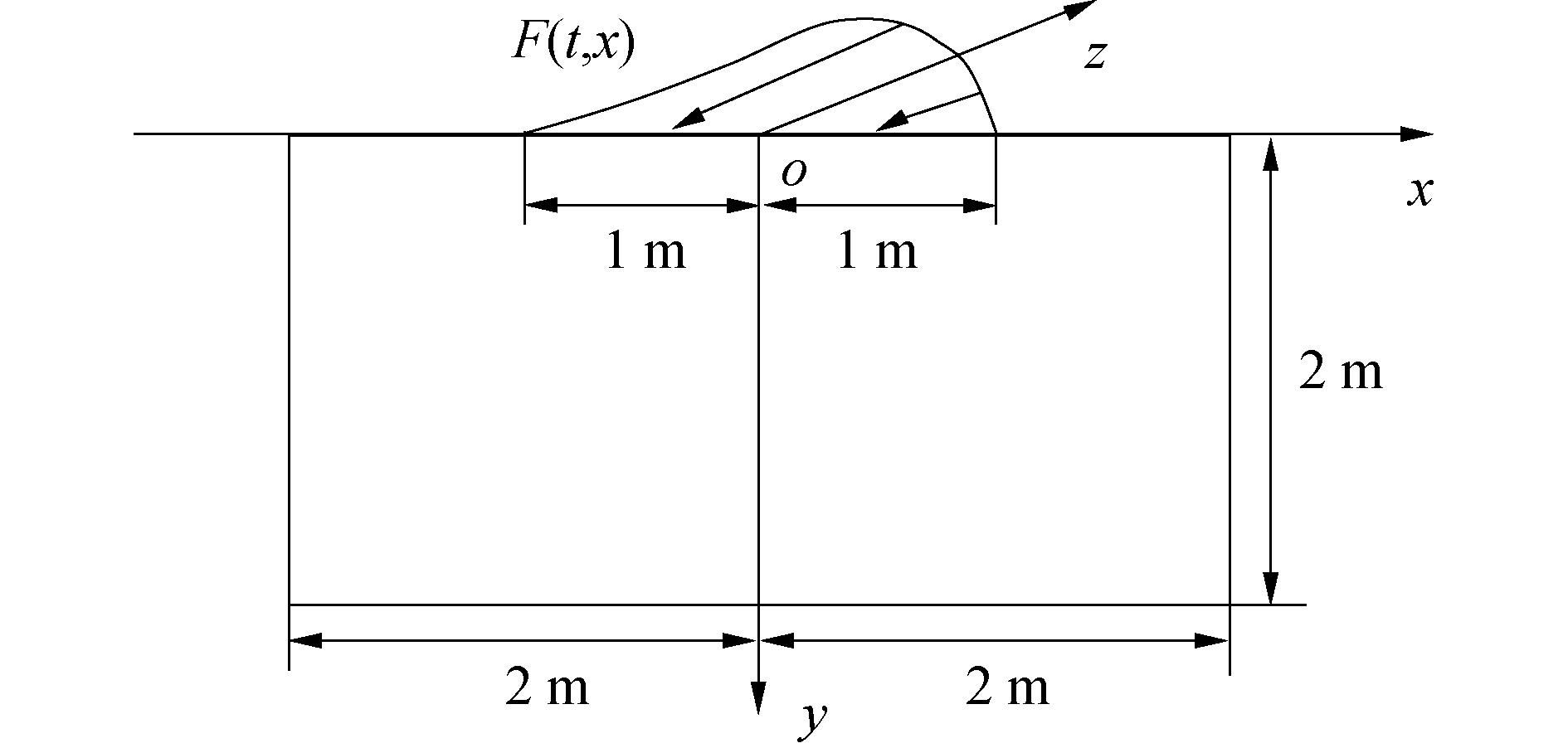
模型的几何关系如图 3所示,剪切波速cs=1 m/s。波源为在自由表面处沿z方向作用的暂态荷载:
|
Download:
|
| 图 3 弹性半空间SH波动模型 Fig. 3 Elastic half-space model of SH wave motion | |
| $ F(t, x)=T(t) D(x) $ | (22) |
其中输入时间函数为三角形脉冲:
| $ T(t)=\left\{\begin{array}{ll}{2 t, } & {0 \leqslant t \leqslant 0.5 ~\mathrm{s}} \\ {2(1-t), } & {0.5 ~\mathrm{s}<t \leqslant 1 ~\mathrm{s}} \\ {0, } & {其他}\end{array}\right. $ | (23) |
荷载空间分布函数D(x)可表示为:
| $ D(x)=\left\{\begin{array}{ll}{1+6\left(x^{3}-x^{2}\right), } & {0 \leqslant x \leqslant 0.5 ~\mathrm{m}} \\ {2(1-x)^{3}, } & {0.5 ~\mathrm{m} \leqslant x \leqslant 1.0 ~\mathrm{m}} \\ {0, } & {x>1.0 ~\mathrm{m}} \\ {S(-x), } & {x<0}\end{array}\right. $ | (24) |
除自由表面外,其余三边均采用透射边界,观测点设置在自由地表(0, 0)处。
图 4为采用传统有限元式(2)和修正有限元[16](数值积分点

|
Download:
|
| 图 4 有限元结合二阶透射边界计算的观测点位移时程 Fig. 4 The Displacement time history of the observation point computed by finite element method with second order transmitting boundary | |
1) SH波动模拟中透射边界引发的反射放大失稳,仅是由透射边界人工波速选择不当所致,与具体的内域离散格式无关;
2) 当人工波速小于1.5倍的离散空间步距和时间步距的比值时,可避免该类失稳。
本文研究结果是针对SH波动的,是对一维研究结果的推广,但对于更为复杂的P-SV波动,透射边界引发的反射放大失稳仍需深入分析。
| [1] |
刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界[J]. 工程力学, 2005, 22(6): 46-51. LIU Jingbo, WANG Zhenyu, DU Xiuli, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems[J]. Engineering mechanics, 2005, 22(6): 46-51. DOI:10.3969/j.issn.1000-4750.2005.06.008 (  0) 0)
|
| [2] |
BAFFET D, BIELAK J, GIVOLI D, et al. Long-time stable high-order absorbing boundary conditions for elastodynamics[J]. Computer methods in applied mechanics and engineering, 2012, 241-244: 20-37. DOI:10.1016/j.cma.2012.05.007 (  0) 0)
|
| [3] |
廖振鹏, 黄孔亮, 杨柏坡, 等. 暂态波透射边界[J]. 中国科学(A辑), 1984(6): 556-564. LIAO Zhenpeng, HUANG Kongliang, YANG Baipo, et al. A Transmitting boundary for transient wave analyses[J]. Scientia sinica (series A), 1984(6): 556-564. (  0) 0)
|
| [4] |
SEMBLAT J F, LENTI L, GANDOMZADEH A. A simple multi-directional absorbing layer method to simulate elastic wave propagation in unbounded domains[J]. International journal for numerical methods in engineering, 2015, 85(12): 1543-1563. (  0) 0)
|
| [5] |
APPELÖ D, COLONIUS T. A high-order super-grid-scale absorbing layer and its application to linear hyperbolic systems[J]. Journal of computational physics, 2009, 228(11): 4200-4217. DOI:10.1016/j.jcp.2009.02.030 (  0) 0)
|
| [6] |
BERENGER J P. Perfectly matched layer (PML) for computational electromagnetics[M]. San Rafael, CA: Morgan & Claypool, 2007: 117.
(  0) 0)
|
| [7] |
LIU Yang, SEN M K. A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation[J]. Geophysics, 2010, 75(2): A1-A6. DOI:10.1190/1.3295447 (  0) 0)
|
| [8] |
LIAO Z P, LIU J B. Numerical instabilities of a local transmitting boundary[J]. Earthquake engineering & structural dynamics, 1992, 21(1): 65-77. (  0) 0)
|
| [9] |
李小军, 廖振鹏. 时域局部透射边界的计算飘移失稳[J]. 力学学报, 1996, 28(5): 627-632. LI Xiaojun, LIAO Zhenpeng. The drift instability of local transmitting boundary in time domain[J]. Acta mechanica sinica, 1996, 28(5): 627-632. DOI:10.3321/j.issn:0459-1879.1996.05.016 (  0) 0)
|
| [10] |
周正华, 廖振鹏. 消除多次透射公式飘移失稳的措施[J]. 力学学报, 2001, 33(4): 550-554. ZHOU Zhenghua, LIAO Zhenpeng. A measure for eliminating drift instability of the multi-transmitting formula[J]. Acta mechanica sinica, 2001, 33(4): 550-554. DOI:10.3321/j.issn:0459-1879.2001.04.015 (  0) 0)
|
| [11] |
景立平, 廖振鹏, 邹经相. 多次透射公式的一种高频失稳机制[J]. 地震工程与工程振动, 2002, 22(1): 7-13. JING Liping, LIAO Zhenpeng, ZOU Jingxiang. A high-frequency instability mechanism in numerical realization of multi-transmitting formula[J]. Earthquake engineering and engineering vibration, 2002, 22(1): 7-13. DOI:10.3969/j.issn.1000-1301.2002.01.002 (  0) 0)
|
| [12] |
廖振鹏, 谢志南. 波动数值模拟的稳定性[J]. 哈尔滨工程大学学报, 2011, 32(9): 1254-1261. LIAO Zhenpeng, XIE Zhinan. Stability of numerical simulation of wave motion[J]. Journal of Harbin Engineering University, 2011, 32(9): 1254-1261. DOI:10.3969/j.issn.1007-7043.2011.09.028 (  0) 0)
|
| [13] |
李小军, 杨宇. 透射边界稳定性控制措施探讨[J]. 岩土工程学报, 2012, 34(4): 641-645. LI Xiaojun, YANG Yu. Measures for stability control of transmitting boundary[J]. Chinese journal of geotechnical engineering, 2012, 34(4): 641-645. (  0) 0)
|
| [14] |
廖振鹏, 周正华, 张艳红. 波动数值模拟中透射边界的稳定实现[J]. 地球物理学报, 2002, 45(4): 553-545. LIAO Zhenpeng, ZHOU Zhenghua, ZHANG Yanhong. Stable implementation of transmitting boundary in numerical simulation of wave motion[J]. Chinese journal of geophysics, 2002, 45(4): 553-545. (  0) 0)
|
| [15] |
谢志南, 廖振鹏. 透射边界高频失稳机理及其消除方法-SH波动[J]. 力学学报, 2012, 44(4): 745-752. XIE Zhinan, LIAO Zhenpeng. Mechanism of high frequency instability caused by transmitting boundary and method of its elimination-SH wave[J]. Chinese journal of theoretical and applied mechanics, 2012, 44(4): 745-752. DOI:10.6052/0459-1879-11-312 (  0) 0)
|
| [16] |
章旭斌, 廖振鹏, 谢志南. 透射边界高频耦合失稳机理及稳定实现——SH波动[J]. 地球物理学报, 2015, 58(10): 3639-3648. ZHANG Xubin, LIAO Zhenpeng, XIE Zhinan. Mechanism of high frequency coupling instability and stable implementation for transmitting boundary——SH wave motion[J]. Chinese journal of geophysics, 2015, 58(10): 3639-3648. DOI:10.6038/cjg20151017 (  0) 0)
|
| [17] |
谢志南, 廖振鹏. 人工边界高频振荡失稳机理的一点注记[J]. 地震学报, 2008, 30(3): 302-306. XIE Zhinan, LIAO Zhenpeng. A note for the mechanism of high-frequency instability induced by absorbing boundary conditions[J]. Acta seismologica sinica, 2008, 30(3): 302-306. DOI:10.3321/j.issn:0253-3782.2008.03.009 (  0) 0)
|
| [18] |
WRENGER J P. Numerical reflection from FDTD-PMLs:a comparison of the split PML with the unsplit and CFS PMLs[J]. IEEE transactions on antennas and propagation, 2002, 50(3): 258-265. DOI:10.1109/8.999615 (  0) 0)
|
| [19] |
廖振鹏. 工程波动理论导论[M]. 2版. 北京: 科学出版社, 2002. LIAO Zhenpeng. Introduction to wave motion theories in engineering[M]. 2nd ed. Beijing: Science Press, 2002. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


