2. 江苏科技大学 船舶与海洋工程学院, 江苏 镇江 212003;
3. 中国舰船科学研究中心 流体力学国家重点实验室, 江苏 无锡 214082
2. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China;
3. State Key Laboratory of Hydrodynamics, China Ship Scientific Research Center, Wuxi 214082, China
海洋能是目前世界上为数不多的可再生能源种类,世界各国对其开发利用给予了足够的重视。潮流能作为海洋能的重要组成部分之一,有能量密度高、可预测性强及相对稳定等优点,据统计全球中可利用开发的潮流能总量达3×1011 kW[1-4]。根据潮流能捕获形式的不同,目前主要有叶轮式和非叶轮式潮流能装置[5],其中叶轮式潮流发电装置是目前较为流行的不能方式,而根据其叶轮旋转方向,可以将潮流能叶轮分为水平式和垂直式叶轮[6-8]。近几十年来,垂直轴潮流能叶轮在“理想潮流环境”中的水动力研究理论及方法已经比较成熟。Coiro[9]针对Koblod垂直轴叶轮,建立了专门的双盘面多流管模型,进而计算了其该水轮机的效率。Camporeale等[10]和张亮等[11]计算了不同型式水轮机的推力、效率等相关性能参数,分别使用流管法和模型实验对其进行了研究,发现利用流管法计算水轮机性能时准确度较高。再此基础上,Li[12]提出了离散涡模型,可以用来计算多个叶轮之间的相互干扰。计算流体力学(computational fluid dynamics, CFD)方法在垂直轴叶轮方面的应用已经取得了很多研究成果。李志川等[13]将CFD方法运用到垂直轴叶轮水动力计算中,并分别讨论了不同偏角形式水轮机,重点研究了叶片数、安装角等对叶轮的水动力性能影响,并通过模型试验证明了CFD方法在垂直轴叶轮研究上的可行性。王凯等[14-15]采用ANSYS软件对两叶片立轴叶轮的艏摇和纵摇运动进行了模拟分析,研究了艏摇和纵摇对浮式立轴水轮机的水动力性能影响。张万超等[16]运用CFD方法,模拟了垂直轴叶轮在均匀流下的受迫摇荡运动,研究了不同摇荡频率下的水动力载荷及相应水动力系数的变化特性。由于旋转机械下的波浪载荷模拟异常困难,波流作用下水轮机水动力的研究非常有限。波流联合作用下的,垂直轴叶轮旋转的同时会伴随波浪摇荡,其运动响应非常复杂,使用常规的CFD方法及软件很难对此问题进行直接模拟。流载荷作用下,叶轮发生旋转运动,而与其固结的浮式载体在波浪作用下会发生摇荡运动。
为了便于研究波浪中垂直轴潮流能叶轮的运动响应及水动力问题,本文将其复杂模型进行简化,假定叶轮在均匀流中作受迫微幅简谐运动,研究不同横摇幅值对浮式立轴潮流能叶轮的水动力影响。
1 计算流体力学数值模拟 1.1 理论基础真实浪流环境下,浮式立轴叶轮的运动如图 1所示,为便于研究,定义密度为ρ的流域中来流速度V的方向为x轴正向。

|
Download:
|
| 图 1 浪流作用下的立轴叶轮模型 Fig. 1 Vertical tidal current turbine under waves and flow | |
针对浮式垂直轴叶轮在浪流作用下的运动工况,为了方便分析,定义无量纲参数为:
叶轮推力系数:
| $ {C_{Fx}} = {F_x}/(0.5\rho {V^2}DH) $ | (1) |
叶轮侧向力系数:
| $ {C_{Fy}} = {F_y}/(0.5\rho {V^2}DH) $ | (2) |
叶轮能量利用率系数:
| $ {C_P} = Q{\omega _0}/(0.5\rho {V^3}DH) $ | (3) |
叶尖速比:
| $ \lambda = R\omega /V $ | (4) |
无因次横摇角速度:
| $ \bar \omega = uL/V = LA\omega {\rm{cos}}\left( {\omega t} \right)/V $ | (5) |
无因次横摇角加速度:
| $ \bar a = \dot uL/V = - A{\omega ^2}{L^2}{\rm{sin}}\left( {\omega t} \right)/{V^2} $ | (6) |
式中:D、R和ω0分别为叶轮直径、半径和旋转角速度;ω、L、u和A分别为横摇频率、臂长、速度与幅值;Z、θ、C和H分别为叶片数量、位置角、弦长、展长;Fx、Fy和Q分别为叶轮受到的推力、侧向力及转矩。
式(1)、(2)中水动力系数可以分为3项:
| $ \left\{ \begin{array}{l} {C_{Fx}} = {C_x} + {n_x}\bar \omega + {m_x}\bar a\\ {C_{Fy}} = {C_y} + {n_y}\bar \omega + {m_y}\bar a \end{array} \right. $ | (7) |
式(7)中nx、ny、mx、my用三角级数形式展开:
| $ \left\{ \begin{array}{l} {n_x} = \frac{{\delta {C_{Fx}}}}{{\delta \bar \omega }} = {\rm{ }}{n_{x, 0}} + \sum\limits_{k = 1}^\infty {{n_{x, k}}} {\rm{sin}}\left( {kz\theta \left( t \right) + {\psi _{\omega x, k}}} \right)\\ {n_y} = \frac{{\delta {C_{Fy}}}}{{\delta \bar \omega }} = {\rm{ }}{n_{y, 0}} + \sum\limits_{k = 1}^\infty {{n_{y, k}}} {\rm{sin}}(kz\theta \left( t \right) + {\psi _{\omega y, k}})\\ {m_x} = \frac{{\delta {C_{Fx}}}}{{\delta \bar a}} = {\rm{ }}{m_{x, 0}} + \sum\limits_{k = 1}^\infty {{m_{x, k}}} {\rm{sin}}(kz\theta \left( t \right) + {\psi _{ax, k}})\\ {m_y} = \frac{{\delta {C_{Fy}}}}{{\delta \bar a}} = {\rm{ }}{m_{y, 0}} + \sum\limits_{k = 1}^\infty {{m_{y, k}}} {\rm{sin}}(kz\theta \left( t \right) + {\psi _{ay, k}}) \end{array} \right. $ | (8) |
最后推力系数可以写成下列级数形式:
| $ \begin{array}{l} {C_{Fx}} = {C_x} + {n_x}\bar \omega + {m_x}\bar a = \\ \;\;\;\;\;\;\;\;{C_{x, 0}} + \sum\limits_{k = 1}^\infty {{C_{x, k}}} {\rm{sin}}(kz\theta \left( t \right) + {\psi _{x, k}}) + \\ \;\;\;\;\;\;\;\;\left\{ {{n_{x, 0}} + \sum\limits_{k = 1}^\infty {[{n_{x, k}}{\rm{sin}}(kz\theta \left( t \right) + {\psi _{\omega x, k}})]} } \right\}\bar \omega + \\ \;\;\;\;\;\;\;\;\left\{ {{m_{x, 0}} + \sum\limits_{k = 1}^\infty {[{m_{x, k}}{\rm{sin}}(kz\theta \left( t \right) + {\psi _{ax, k}})]} } \right\}\bar a \end{array} $ | (9) |
侧向力系数可以写成下列级数形式:
| $ \begin{array}{l} {C_{FY}} = {C_y} + {n_y}\bar \omega + {m_y}\bar a = \\ \;\;\;\;\;\;\;\;\;{C_{y, 0}} + \sum\limits_{k = 1}^\infty {{C_{y, k}}{\rm{sin}}(kz\theta \left( t \right) + {\psi _{y, k}}) + } \\ \;\;\;\;\;\;\;\;\;\left\{ {{n_{y, 0}} + \sum\limits_{k = 1}^\infty {[{n_{y, k}}{\rm{sin}}(kz\theta \left( t \right) + {\psi _{\omega y, k}})]} {\rm{ }}} \right\}\bar \omega + \\ \;\;\;\;\;\;\;\;\;\left\{ {{m_{y, 0}} + \sum\limits_{k = 1}^\infty {[{m_{y, k}}{\rm{sin}}(kz\theta \left( t \right) + {\psi _{ay, k}})]} {\rm{ }}} \right\}\bar a \end{array} $ | (10) |
式(10)和(11)中的CFx和CFy可以通过CFD软件计算得到,再通过最小二乘法拟合得到公式中的各项。
1.2 立轴水轮机模型本文使用翼型为NACA0018的垂直轴三维叶轮模型,叶轮直径D为0.8 m,叶片数Z=2,展长H=0.6 m,弦长C=0.12 m,叶片属于固定偏角形式,安装角为0°。
图 2所示为立轴叶轮横摇运动的计算网格模型。总网格计算域为长35D, 宽和高都为25D的长方形域。叶片周围第1层网格高度为0.000 1,满足第1层网格Y+ < 5(Y+是湍流模型中靠近壁面距离的无量纲量), 旋转域、横摇域和总域之间用滑移网格连接,在计算中网格不存在变形,确保了计算过程中的网格质量,提高了计算精度。3个域之间的相对运动可以模拟立轴叶轮在浪流作用下的横摇运动。

|
Download:
|
| 图 2 三维数值网格 Fig. 2 3D Grid model | |
图 3为立轴叶轮横摇运动计算模型的边界条件设置,设置方法可以参考文献[16]。

|
Download:
|
| 图 3 边界条件 Fig. 3 Boundary conditions | |
图 4为均匀来流下立轴叶轮效率的试验值和CFD计算值得对比图,从图中可以看出实验值和计算值有较高的吻合度,误差较小,在速比2.5时效率达到最大值。通过对比试验和计算工况,计算值和实验值之间的误差可能是由实验中壁面效应和机械摩擦造成的,但是其不影响CFD计算方法在立轴叶轮数值模拟中的准确性。

|
Download:
|
| 图 4 模拟结果与试验结果对比 Fig. 4 Comparsion of experiment and simulation | |
本文研究的立轴叶轮横摇模型主要对比在来流速度1.0 m/s,横摇频率1.2 rad/s, 速比2.5工况下的3个不同横摇幅值(5°、10°和15°)的叶轮推力和侧向力时历曲线的变化规律。
图 5(a)和(c)为立轴浮式叶轮在均匀流无横摇运动下的推力和侧向力的时历曲线,其包络线表现为直线形式。图 5(b)和(d)为浪流作用下的立轴叶轮发生横摇运动时的时历曲线,从图中可以明显看出时历曲线存在周期性波动。特别是侧向力的上下包络线波动更加明显,叶轮的横摇运动方向和叶轮的侧向力方向重合因此侧向力更加明显。

|
Download:
|
| 图 5 横摇和无摇荡状态下对比 Fig. 5 Comparison of turbine under rolling and non-rolling | |
图 6和图 7分别为3个横摇幅值下叶轮推力和侧向力的上下包络线对比图,其中0°代表的是立轴叶轮在均匀来流中无摇荡运动的叶轮推力和侧向力的上下包络线,呈直线形式。3个横摇幅值下的上下包络线呈周期性波动,波动频率和横摇频率一致,这是因为叶轮在浪流联合作用下发生横摇运动,从而引起叶轮推力和侧向力的周期性波动,因此力的波动频率和横摇频率一致。从4幅图中可以看出,推力和侧向力的上下包络线波动幅值都是随着横摇幅值增大而增大。

|
Download:
|
| 图 6 推力系数包络线对比 Fig. 6 Comparison of thrust coefficients′ envelope curves | |

|
Download:
|
| 图 7 侧向力系数包络线对比 Fig. 7 Comparison of lateral force coefficients′ envelope curves | |
为了进一步对比横摇运动下立轴叶轮推力和侧向力的变化规律,分别定义推力和侧向力的平均值和波动幅值:
| $ \left\{ \begin{array}{l} {{\bar C}_{Fx}} = \int_{{t_1}}^{{t_2}} {{C_{Fx}}{\rm{d}}t/({t_2} - {t_1})} \\ {{\bar C}_{Fy}} = \int_{{t_1}}^{{t_2}} {{C_{Fy}}{\rm{d}}t/({t_2} - {t_1})} \\ {{\hat C}_{Fx}} = {C_{Fx{\rm{max}}}} - {C_{Fx{\rm{min}}}}\\ {{\hat C}_{Fy}} = {C_{Fy{\rm{max}}}} - {C_{Fy{\rm{min}}}} \end{array} \right. $ | (11) |
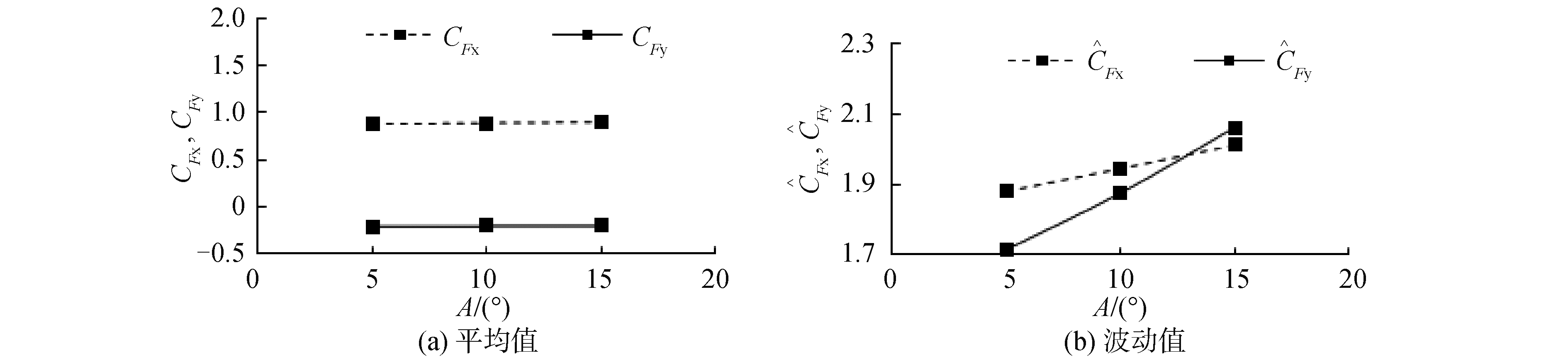
图 8中3个横摇幅值下的推力和侧向力的平均值和波动值对比图。图 8(a)可以看出随着横摇幅值增大,横摇运动下叶轮推力和侧向力平均值基本不变,说明横摇运动对叶轮受力的平均值没有影响。图 8(b)中推力和侧向力的波动幅值随着横摇幅值增大而增大,这是因为叶轮横摇角速度会由于横摇幅值增大而增大,角速度增大从而导致叶轮受力增大。
|
Download:
|
| 图 8 Fig. 8 Force contrast of impeller rolling motion | |
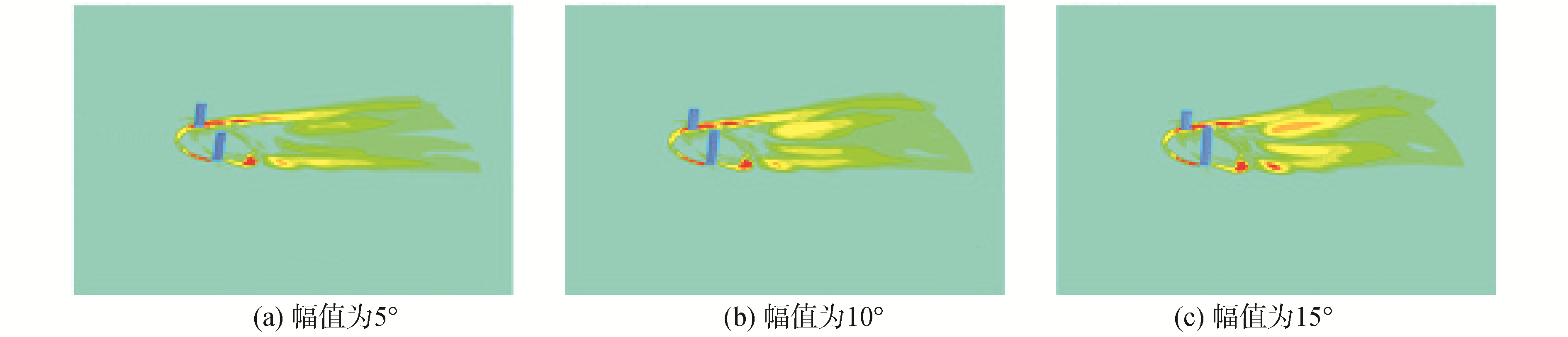
图 9为叶轮横摇运动下3个不同横摇幅值的同一时刻涡量图。随着横摇幅值增大,叶轮尾流中涡量也越大,这是因为横摇幅值增大引起叶轮处合速度增大,从而引起尾涡增大。图 9(c)中叶轮下游尾涡明显多于图 9(a)中的尾涡。
|
Download:
|
| 图 9 浪流作用下水轮机的尾流场涡量对比 Fig. 9 Vortex distributions of turbines under waves and flows | |
在同一水平高度下分别定义横摇运动中叶轮叶片,漏出叶片长度短的为1号叶片,长的为2号叶片。横摇幅值15°的叶轮2号叶片明显高于5°横摇幅值2号叶片高度,这是叶轮横摇幅值不同造成的。随着横摇幅值增加,叶轮下叶片漏出的展长也越大。
图 10对应图 9中的2号叶片表面压力。从图 10中可知,叶片上压力分布形状相似但是压力值不同,随着横摇幅值增大,叶片表面压力逐渐增大。这是因为随着横摇幅值增大,叶轮同一时刻的横摇速度会增大,横摇速度和来流速度叠加导致叶轮盘面的合速度增大,叶轮横摇过程中受到的力也相应增大。

|
Download:
|
| 图 10 横摇运动下叶片压力云图 Fig. 10 Pressure of turbines under waves and flows | |
根据前面CFD计算的横摇幅值为5°、10°和15°工况下的叶轮推力和侧向力时历曲线,利用最小二乘法根据式(10)和式(11)对其进行拟合分析,得到所需的各项系数,并分析其变化规律。表 1为横摇叶轮推力CFx根据式(10)得到的各项系数,表 2为横摇叶轮侧向力CFy根据式(11)得到的各项系数。
| 表 1 不同横摇幅值CFx展开系数表 Table 1 CFx expansion coefficient table under swaying motion |
| 表 2 不同横摇幅值CFy展开系数表 Table 2 CFy expansion coefficient table under swaying motion |
从表 1可知,CFx展开系数中,Cx, 0、Cx, 1和ψx, 1表示均匀水动力项系数,nx, 0、nx, 1和ψωx, 1表示阻尼项系数,mx, 0、mx, 1和ψax, 1表示附加质量项系数。均匀水动力项各系数相差不大,说明不同横摇幅值下叶轮的均匀水动力值相当。ψx, 1、ψωx, 1表明均匀水动力项和阻尼项发生周期性波动。从各项系数来看,随着横摇振幅的增加,阻尼项各项系数绝对值波动幅值不大,总体上微幅增加。附加质量项各系数绝对值在数值上远小于均匀水动力项和阻尼项。因此,横摇运动下叶轮推力的组成成分中均匀水动力和阻尼力占主要作用,附加质量力作用较小。
表 2中横摇侧向力展开各系数中,Cy, 0、Cy, 1和ψy, 1表示侧向力均匀水动力系数,ny, 0、ny, 1和ψωy, 1表示侧向力阻尼力系数,my, 0、my, 1和ψay, 1表示侧向力附加质量力系数。随着横摇幅值增加,均匀水动力各系数变化不大,说明横摇运动下叶轮受力中均匀水动力项不受横摇幅值影响。ψy, 1、ψωy, 1和ψay, 1侧向力中均匀水动力、阻尼力和附加质量力都发生周期性波动,且各项都占据一定比例。
4 结论1) 立轴叶轮在浪流共同作用发生横摇运动时,叶轮的推力和侧向力发生周期性波动,波动频率和横摇频率一致。
2) 横摇运动下叶轮推力和侧向力波动幅值随着横摇幅值增大而增大。
3) 立轴叶轮在浪流作用下的横摇运动的受力平均值不受横摇幅值影响,但受力的波动幅值随横摇幅值增大而增大。
4) 横摇运动下叶轮推力和侧向力系数的各分解项发生周期性波动,推力项中附加质量力所占比例远小于均匀水动力和阻尼力,差一个数量级。侧向力项中3项所占比例在同一数量级。
| [1] |
游亚戈, 李伟, 刘伟民, 等. 海洋能发电技术的发展现状与前景[J]. 电力系统自动化, 2010, 34(14): 1-12. YOU Yage, LI Wei, LIU Weimin, et al. Development status and perspective of marine energy conversion systems[J]. Automation of electric power systems, 2010, 34(14): 1-12. (  0) 0)
|
| [2] |
张理. 我国海洋能开发利用思路的初步探索[J]. 中国造船, 2012, 53(S2): 555-560. ZHANG Li. Preliminary investigation of ocean energy development in China[J]. Shipbuilding of China, 2012, 53(S2): 555-560. (  0) 0)
|
| [3] |
刘富铀, 张俊海, 刘玉新, 等. 海洋能开发对沿海和海岛社会经济的促进作用[J]. 海洋技术, 2009, 28(1): 115-119. LIU Fuyou, ZHANG Junhai, LIU Yuxin, et al. Facilitation of ocean energy development to society and economy of coastal and island area[J]. Ocean technology, 2009, 28(1): 115-119. DOI:10.3969/j.issn.1003-2029.2009.01.028 (  0) 0)
|
| [4] |
张理, 李志川. 潮流能开发现状、发展趋势及面临的力学问题[J]. 力学学报, 2016, 48(5): 1019-1032. ZHANG Li, LI Zhichuan. Development status, trend and the problems of mechanics of tidal current energy[J]. Chinese journal of theoretical and applied mechanics, 2016, 48(5): 1019-1032. (  0) 0)
|
| [5] |
ZHANG Xuewei, ZHANG Liang, WANG Feng, et al. Research on the unsteady hydrodynamic characteristics of vertical axis tidal turbine[J]. China ocean engineering, 2014, 28(1): 95-103. DOI:10.1007/s13344-014-0007-6 (  0) 0)
|
| [6] |
孙科, 梁姝婷, 汤富定, 等. 20kW矩形潮流能发电机组结构设计及优化[J]. 船舶工程, 2014, 36(3): 123-127. SUN Ke, LIANG Shuting, TANG Fuding, et al. Design and optimization of a 20 kW rectangle tidal current turbine[J]. Ship engineering, 2014, 36(3): 123-127. (  0) 0)
|
| [7] |
王凯, 孙科, 张亮. 不同密实度垂直轴潮流能水轮机的相位干扰[J]. 哈尔滨工业大学学报, 2016, 48(8): 179-184. WANG Kai, SUN Ke, ZHANG Liang. Impaction of initial phase angle on performance of the vertical axis tidal turbines with different density[J]. Journal of Harbin Institute of Technology, 2016, 48(8): 179-184. (  0) 0)
|
| [8] |
LI Ye, CALIŞAL S M. Modeling of twin-turbine systems with vertical axis tidal current turbines: part Ⅰ-power output[J]. Ocean engineering, 2010, 37(7): 627-637. DOI:10.1016/j.oceaneng.2010.01.006 (  0) 0)
|
| [9] |
COIRO D P, DE MARCO A, NICOLOSI F, et al. Dynamic behaviour of the patented kobold tidal current turbine: numerical and experimental aspects[J]. Acta polytechnica, 2005, 45(3): 77-84. (  0) 0)
|
| [10] |
CAMPOREALE S M, MAGI V. Streamtube model for analysis of vertical axis variable pitch turbine for marine currents energy conversion[J]. Energy conversion and management, 2000, 41(16): 1811-1827. DOI:10.1016/S0196-8904(99)00183-1 (  0) 0)
|
| [11] |
汪鲁兵, 张亮, 曾念东. 一种竖轴潮流发电水轮机性能优化方法的初步研究[J]. 哈尔滨工程大学学报, 2004, 25(4): 417-422. WANG Lubing, ZHANG Liang, ZENG Niandong. An optimization method for improving hydrodynamic performance of the vertical-axis turbine for tidal streams energy conversion[J]. Journal of Harbin Engineering University, 2004, 25(4): 417-422. DOI:10.3969/j.issn.1006-7043.2004.04.004 (  0) 0)
|
| [12] |
LI Ye. Development of a procedure for predicting power generated from a tidal current turbine farm[D]. Columbia: The University of British Columbia, 2008.
(  0) 0)
|
| [13] |
李志川, 张亮, 孙科, 等. 垂直轴潮流水轮机数值模拟研究[J]. 太阳能学报, 2011, 32(9): 1321-1326. LI Zhichuan, ZHANG Liang, SUN Ke, et al. Numerical simulation of vertical axis tidal turbine[J]. Acta energiae solaris sinica, 2011, 32(9): 1321-1326. (  0) 0)
|
| [14] |
王凯, 孙科, 张亮, 等. 艏摇对立轴潮流能水轮机的水动力性能影响[J]. 上海交通大学学报, 2016, 50(4): 563-568, 574. WANG Kai, SUN Ke, ZHANG Liang, et al. Hydrodynamic performance of vertical axis tidal turbine under yawing motion[J]. Journal of Shanghai Jiao Tong University, 2016, 50(4): 563-568, 574. (  0) 0)
|
| [15] |
王凯, 孙科, 张亮. 不同速比下纵摇运动对立轴叶轮的性能影响[J]. 哈尔滨工业大学学报, 2017, 49(10): 145-152. WANG Kai, SUN Ke, ZHANG Liang. The effect of pitching motion on the hydrodynamic performance of vertical axis turbine under different speed ratios[J]. Journal of Harbin Institute of Technology, 2017, 49(10): 145-152. DOI:10.11918/j.issn.0367-6234.201604107 (  0) 0)
|
| [16] |
张万超, 王凯, 王树齐, 等. 受迫横摇运动浮式立轴叶轮的水动力性能分析[J]. 华中科技大学学报:自然科学学报, 2018, 46(8): 18-23. ZHANG Wanchao, WANG Kai, WANG Shuqi, et al. The hydrodynamic performance analysis of floating vertical-axis tidal turbine considering forced rolling motion[J]. Journal of Huazhong University of Science and Technology (nature science edition), 2018, 46(8): 18-23. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


