2. 天津直升机研发中心, 天津 300270
2. Tianjin Helicopter Research and Development Center, Tianjin 300270, China
金属丝网橡胶是一种新型干摩擦弹性阻尼材料,既有橡胶的弹性阻尼特性,也有金属所具有的所有特性,因而也称金属橡胶材料。这种新型材料自20世纪60年代被各国学者熟知,至今已有50余年,期间对金属橡胶的制备方法、成型工艺、本构模型、各种力学性能等方面的研究一直是国内外热议的学术问题[1-2]。由于其相对于传统橡胶具有更强的承载能力,对环境更强的适应能力,更长的使用寿命,并且特别适用于制备成高低温、大温差、真空及强腐蚀性等特殊工况下的减振及密封构件,金属橡胶被视为在航空航天、船舶、军事武器等领域中替代传统橡胶的重要材料[2]。金属丝网橡胶的减振机理是在受到各种类型的载荷作用时,内部接触的金属丝相对滑移产生干摩擦力,从而消耗能量,起到减振作用。目前,国内对金属橡胶减振器的研究主要集中在本构模型的建立[3-4]、静态力学性能和不同振动激励下的试验测试[5-16],然而在工程实际中,构件的破坏常常是由冲击载荷所引起。冲击是一种普遍的动力学现象,其作用时间短,冲击强度大,应变率大,能够瞬间破坏材料及构件。因此,研究金属丝网橡胶材料的抗冲击性能显得尤为重要,不过目前在此方面研究相对较少,且仍以理论和试验研究为主[16-19],在此前提下,对金属丝网橡胶减振器冲击响应进行有限元仿真研究可以有效地为其他研究提供参考,并突破理论与试验研究的局限性,为工程应用提供更全面的参考。
本文在理论与试验研究的基础上,结合金属丝网橡胶的非线性干摩擦迟滞力学特性,提出一种金属丝网橡胶减振器冲击有限元仿真方法,利用ANSYS LS-DYNA对金属丝网橡胶减振器进行冲击仿真,将仿真结果与试验结果进行对比,验证了冲击仿真方法的可行性,并对仿真误差产生的原因和冲击仿真方法的适用性进行了讨论分析。
1 金属丝网橡胶减振器冲击试验 1.1 试验材料及方法试验采用通孔圆柱型金属丝网橡胶作为减振元件,试件高度20 mm,内径11.6 mm,外径40 mm,金属丝丝径0.2 mm,相对密度ρ为0.16。
| $ \bar \rho = \frac{{{\rho _{{\rm{MR}}}}}}{{{\rho _{\rm{s}}}}} $ | (1) |
式中:ρMR为金属丝网橡胶元件的密度,ρs为金属丝密度。
金属丝网橡胶减振器采取如图 1所示的结构,由底座、支架、紧固螺母、上下端盖、支撑杆和两个金属丝网橡胶试件组成,紧固螺母施加预紧量,使其在振动过程中,通过上下端盖和支撑杆可以将振动过程中产生的上下拉压受力转化成金属丝网橡胶试件所能承受的压力。试验使用的冲击试验装置是江苏东菱振动SY11-600垂直冲击试验机,该试验机由冲击台体、气源系统、测控系统和波形发生器四部分组成,如图 2所示。

|
Download:
|
| 图 1 金属丝网橡胶减振器结构示意图 Fig. 1 Structure schematic diagram of metal-net rubber demper | |

|
Download:
|
| 图 2 冲击测试原理图 Fig. 2 The shock test principle | |
试验时,在测试软件中设置相关试验参数,试验机根据参数将冲击台面上升到设定高度。冲击台释放气压,台面自由下落,与底座上的波形发生器碰撞,产生冲击波形,通过波形发生器和冲击高度调节冲击脉冲持续时间和冲击强度。在冲击台面上和减振器质量块上各放一个加速度传感器,用来测量输入冲击加速度和冲击加速度响应。
对施加了20%预紧量,承载1.3 kg质量块的金属丝网橡胶减振器进行冲击试验,冲击高度h范围控制在150~250 mm。试验图如图 3所示。

|
Download:
|
| 图 3 冲击试验图 Fig. 3 The shock test | |
图 4为冲击试验结果。由图 4可知,在加速度脉冲载荷作用下,金属丝网橡胶减振系统冲击加速度响应为一系列近似正弦脉冲波,且随着时间推移,金属丝网橡胶耗散能量起到减振作用,使波幅值和脉冲波持续时间不断减小[19]。

|
Download:
|
| 图 4 冲击试验结果 Fig. 4 Shock experimental results | |
结合图 4和表 1可知,随着冲击高度的增高,冲击加速度响应峰值变大,冲击加速度响应的衰减速度降低。
| 表 1 冲击试验数据 Tab.1 Shock experimental data |
金属丝网橡胶材料本构关系并无统一模型,相关仿真参数均无法确定,本节仿真采用COMBI165模拟金属丝网橡胶进行计算,输入阻尼系数和力-位移曲线考虑其非线性阻尼特性,解决了材料参数无法确定的问题。
2.1 COMBI165单元COMBI165单元为两节点的一维单元,弹簧和阻尼可以共用相同节点但不能用相同单元,COMBI165单元只用于显式动力分析,支持所有许可的非线性特性,弹簧阻尼单元有两种类型,即平移和旋转。单元的实常数包括:动力放大系数kd、测试速度V0、间隙量CL、失效前的压缩准则CDL、失效后的拉伸极限TDL。实常数并不是必须被定义,如果动力放大系数kd为0,则弹簧的计算被假定为常值,并且被转换成动态值,其关系为
| $ {F_{{\rm{dynamic}}}} = \left( {1 + {k_{\rm{d}}}\frac{V}{{{V_0}}}} \right){F_{{\rm{static}}}} $ | (2) |
式中:Fdynamic是动态弹簧弹力; V是加卸载速度; V0是输入的测试速度; Fstatic是静态弹簧弹力; kd是动力放大系数,设置为0。并且由于减振器中的减振元件金属丝网橡胶在受冲击载荷作用后的变形始终处于弹性范围内,在冲击仿真过程中不需要考虑弹簧单元失效情况,因此,其他单元实常数V0、CL、CDL和TDL均不需要设置参数。
2.2 冲击仿真参数识别采用通用非线性弹簧单元模拟金属丝网橡胶材料的非线性刚度,为减少计算时间,采用两个弹簧单元并联来模拟上下两个金属丝网橡胶减振垫,通用非线性弹簧单元需要输入弹簧的力-位移变形量关系曲线,且曲线必须通过原点,即在弹簧单元位移变形量为0时,弹簧单元弹力也为0,由于金属丝网橡胶减振垫存在预紧压力,若要保证弹簧单元弹力与金属丝网橡胶减振垫的弹性反力相同,必须在极短时间内使弹簧单元弹力迅速升至金属丝网橡胶减振垫的初始预紧压力,会导致弹簧单元弹力和刚度在初始阶段发生阶跃突增,严重影响冲击仿真计算结果的有效性和精度。
为防止弹簧单元力-位移变形量曲线出现阶跃突增阶段,导致刚度急剧增大,本文采取保持刚度相同的办法计算弹簧单元冲击仿真的力-位移变形量关系曲线。
图 1所示的金属丝网橡胶减振器,通过支撑杆和上下挡板的作用,当减振器负载质量部分相对平衡位置向上(下)运动时,上部(下部)的金属丝网橡胶减振垫受压,处于加载状态,下部(上部)的金属丝网橡胶减振垫处于卸载状态,因此,减振器的设计使金属丝网橡胶减振系统始终保持有一个金属丝网橡胶减振垫处于加载状态,另一个金属丝网橡胶减振垫处于卸载状态,采用的两个通用非线性弹簧单元由于对称分布在金属丝网橡胶减振器的上部(或下部),因此,其刚度需要由加载状态金属丝网橡胶减振垫的刚度和卸载状态金属丝网橡胶减振垫的刚度进行叠加得到。
在减振器负载质量部分相对平衡位置上下运动时,设上部金属丝网橡胶减振垫的刚度为k1(s1),下部金属丝网橡胶减振垫的刚度为k2(s2),其中,s1和s2分别为相对应金属丝网橡胶减振垫的位移变形量,则减振系统的总刚度kz为
| $ {k_z} = {k_1}({s_1}) + {k_2}({s_2}) $ | (3) |
根据减振器的结构设计,s1和s2关系为
| $ \frac{{{s_1} + {s_2}}}{2} = 4\;{\rm{mm}} $ | (4) |
单个弹簧单元的非线性刚度为
| $ k = \frac{{{k_z}}}{2} = \frac{{{k_1}({s_1}) + {k_2}({s_2})}}{2} $ | (5) |
由于金属丝网橡胶减振器冲击试验中的预紧量为4 mm(20%),减振系统振动的平衡位置为金属丝网橡胶位移变形量4 mm处。
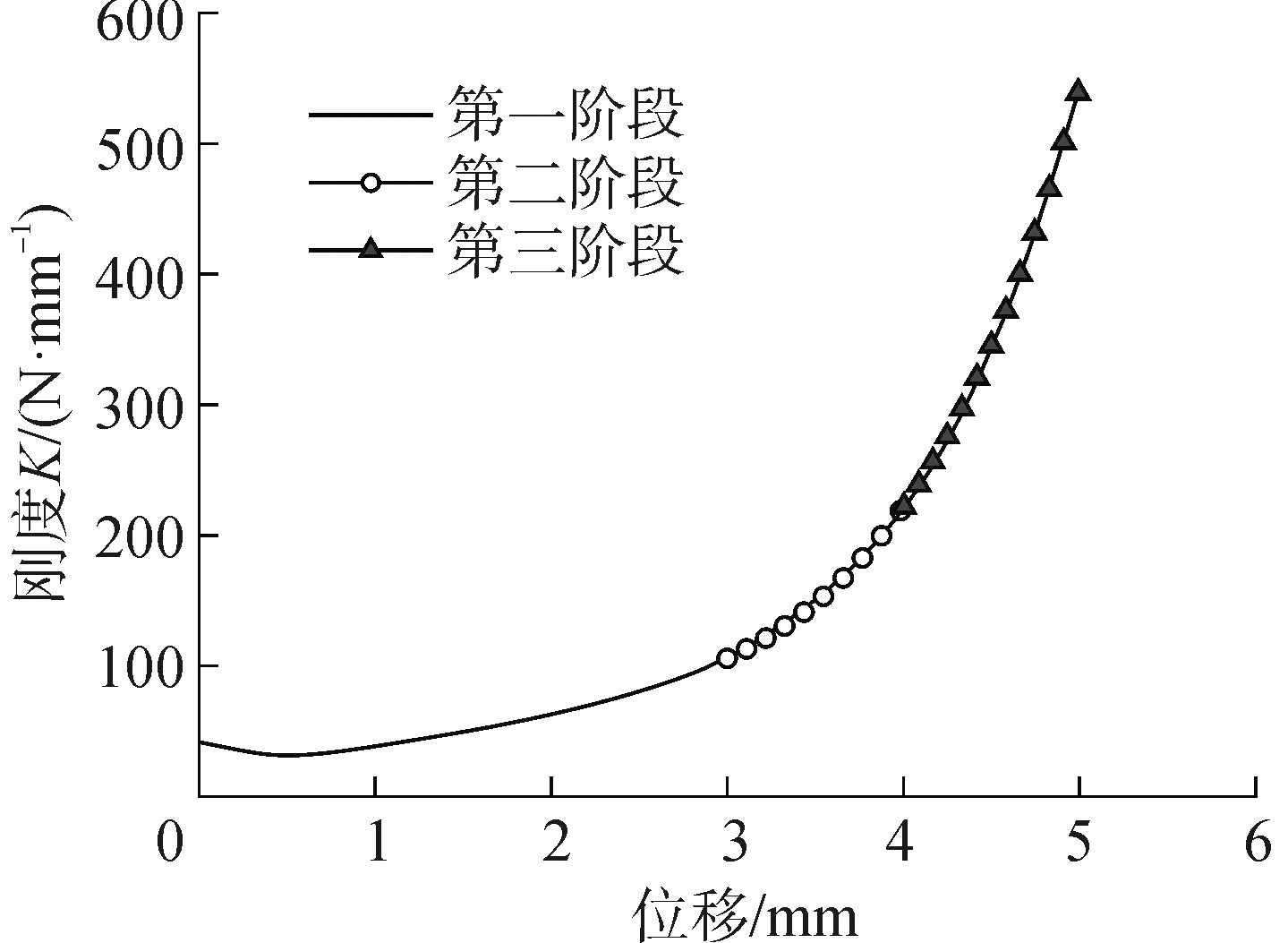
对金属丝网橡胶的非线性刚度进行分段式处理,处理后的分段式非线性刚度如图 5所示,由于金属丝网橡胶减振器冲击试验中所受的冲击载荷相对较小,金属丝网橡胶减振垫的位移变形量小于1 mm,因此,取位移变形3~5 mm阶段非线性刚度进行计算既可以满足要求。
|
Download:
|
| 图 5 非线性刚度分段 Fig. 5 Subsection of nonlinear stiffness | |
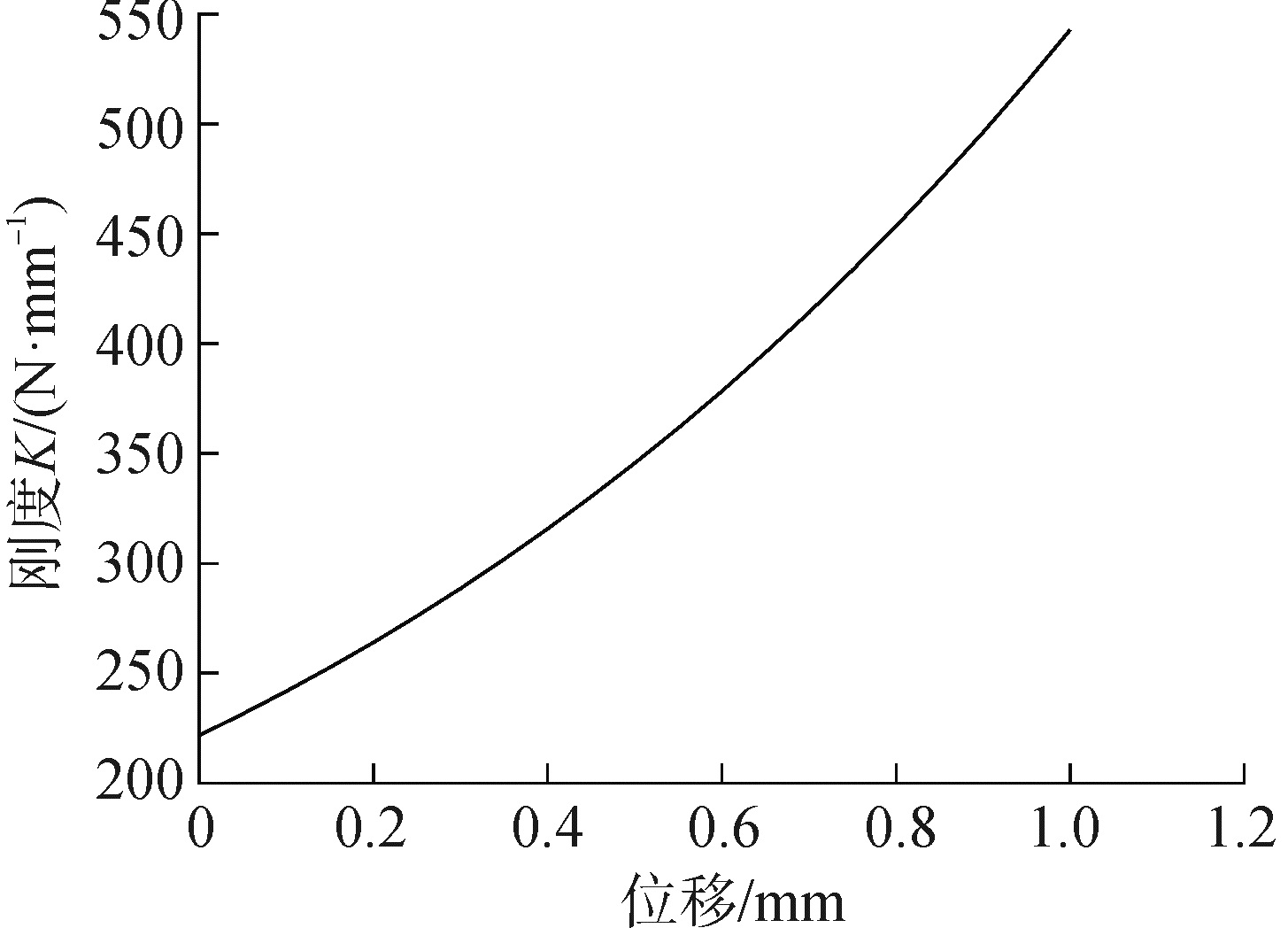
通过式(4)、(5)计算金属丝网橡胶加卸载叠加后的非线性刚度,由于弹簧单元起始位置(减振系统平衡位置)是金属丝网橡胶预紧量4 mm处,因此,将计算所得的非线性叠加刚度曲线初始位置向左平移至X=0处,得到图 6所示的冲击仿真弹簧单元的非线性刚度曲线,并对其积分得到冲击仿真中弹簧单元的力-位移曲线,如图 7所示。
|
Download:
|
| 图 6 弹簧单元的非线性刚度 Fig. 6 Nonlinear stiffness of spring element | |

|
Download:
|
| 图 7 弹簧单元的力-位移曲线 Fig. 7 Force-displacement graph of spring element | |
由于金属丝网橡胶受冲击后的干摩擦缓冲耗能机理过于复杂,无法获得金属丝网橡胶阻尼系数的非线性变化规律,因此,采用近似计算的常阻尼系数作为阻尼单元冲击仿真参数,阻尼系数计算公式为
| $ c = 2\xi \sqrt {m\chi k\left( 0 \right)} $ | (6) |
式中:m为负载质量,k(0)为弹簧单元初始刚度,χ为金属丝网橡胶的显式刚度比例系数,阻尼比ξ可由能量耗散系数近似代替:
| $ \xi \approx \psi = \frac{{\Delta W}}{W} $ | (7) |
式中:负载质量m为1.3 kg时减振系统阻尼系数c为332.15 N·s/m。
2.3 冲击仿真模型及材料参数仿真模型如图 8所示,该模型与真实减振器结构完全一致,代替金属丝网橡胶减振垫的弹簧单元和阻尼单元对称分布在上挡板和底座挡板之间。其中底座部分和上挡板材料为铝合金,质量块、支撑杆和下挡板材料为钢。材料参数如表 2。

|
Download:
|
| 图 8 仿真模型及网格 Fig. 8 Finite element simulation model and mesh | |
| 表 2 材料参数 Tab.2 Material parameters |
由于金属丝网橡胶减振器受冲击载荷后做单轴方向往复振动,对所有节点除Z向运动方向外的其他两个方向施加位移约束,限制减振器X方向和Y方向的运动,使减振器沿Z轴单一方向运动;选取金属丝网橡胶减振器底座部分节点生成组元,并对底座组元施加冲击加速度载荷。
2.5 冲击仿真结果图 9为金属丝网橡胶减振器冲击仿真结果和冲击试验结果对比,从图中可知,利用COMBI165单元模拟金属丝网橡胶减振器冲击试验时,冲击加速度响应曲线衰减趋势与试验相符,能够很好地描述减振器在受到冲击载荷后的加速度响应特征,其结果误差如表 3所示,仿真所得结果冲击加速度响应幅值小于试验结果,首个冲击加速度响应脉冲波持续时间大于试验值;随着冲击激励增大,仿真误差变大,误差不大于23%,这是由于随着冲击载荷增大,减振系统受冲击后的振动幅值增大,弹簧单元的位移变形量增大,仿真刚度与实际刚度误差变大,从而导致仿真计算误差增大。

|
Download:
|
| 图 9 冲击仿真结果和冲击试验结果对比 Fig. 9 Comparison of simulation results and test results | |
| 表 3 冲击仿真结果和冲击实验对比 Tab.3 Comparison of shock simulation results and shock test results |
1) 所提出的仿真方法可以较好的模拟计算金属丝网橡胶减振器在冲击载荷作用下的减振特性。
2) 冲击载荷越大,仿真结果误差越大,不过冲击激励很大时误差并无继续增大的趋势。
3) 仿真误差中峰值误差可控制在25%以内,首次达到峰值时间误差较小,在10%左右。由此可见,所提出的有限元仿真方法可以较好的模拟金属丝网橡胶减振器的冲击力学行为。
| [1] |
董秀萍, 张力. 新型材料金属橡胶建模及应用[M]. 北京: 化学工业出版社, 2010: 1-32. DONG Xiuping, ZHANG Li. New material modeling and application of metal-rubber[M]. Beijing: Chemical Industry Press, 2010: 1-32. (  0) 0)
|
| [2] |
赵程, 贺跃进, 张恒. 金属橡胶的应用研究[J]. 噪声与振动控制, 2006, 26(5): 45-47. ZHAO Cheng, HE Yuejin, ZHANG Heng. Application research of metal-rubber[J]. Noise and vibration control, 2006, 26(5): 45-47. DOI:10.3969/j.issn.1006-1355.2006.05.013 (  0) 0)
|
| [3] |
邹广平, 刘泽, 唱忠良, 等. 金属丝网橡胶的本构关系[J]. 航空动力学报, 2016, 31(10): 2318-2324. ZOU Guangping, LIU Ze, CHANG Zhongliang, et al. Constitutive relation of metal-net rubber[J]. Journal of aerospace power, 2016, 31(10): 2318-2324. (  0) 0)
|
| [4] |
李雨蕾.金属橡胶减振及密封构件的设计与应用[D].哈尔滨: 哈尔滨工程大学, 2013. LI Yulei. Design and application on vibration damping and seal member of metal rubber[D]. Harbin: Harbin Engineering University, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D429283 (  0) 0)
|
| [5] |
王新, 朱梓根. 环形金属橡胶减振器[J]. 航空动力学报, 1997, 12(2): 143-145. WANG Xin, ZHU Zigen. A ring-like metal rubber damper[J]. Journal of aerospace power, 1997, 12(2): 143-145. (  0) 0)
|
| [6] |
ZHANG Dayi, SCARPA F, MA Yanhong, et al. Dynamic mechanical behavior of nickel-based superalloy metal rubber[J]. Materials and design, 2014, 56: 69-77. DOI:10.1016/j.matdes.2013.10.088 (  0) 0)
|
| [7] |
许建东, 郭宝亭, 朱梓根, 等. 金属橡胶材料的振动特性.航空动力学报[J]. 航空动力学报, 2004, 19(5): 619-622. XU Jiandong, GUO Baoting, ZHU Zigen, et al. The vibration performance of metal-rubber material[J]. Journal of aerospace power, 2004, 19(5): 619-622. DOI:10.3969/j.issn.1000-8055.2004.05.008 (  0) 0)
|
| [8] |
JIANG Hongyuan, YAN Hui, AO Hongrui, et al. Calculation of elastic damping characteristics of metal rubber material under variable loads[J]. Chinese journal of mechanical engineering, 2007, 20(6): 33-37. DOI:10.3901/CJME.2007.06.033 (  0) 0)
|
| [9] |
李国富.随机振动下金属橡胶隔振器寿命影响因素分析及实验研究[D].哈尔滨: 哈尔滨工业大学, 2014. LI Guofu. Experimental study and analysis of influencing factors on lifetime of metal rubber isolator under random vibration[D]. Harbin: Harbin Institute of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10213-1014084162.htm (  0) 0)
|
| [10] |
ZHANG B, LANG Z Q, BILLINGS S A, et al. System identification methods for metal rubber devices[J]. Mechanical systems and signal processing, 2013, 39(1/2): 207-226. (  0) 0)
|
| [11] |
闫辉, 姜洪源, 刘文剑, 等. 金属橡胶隔振器随机振动加速度响应分析[J]. 物理学报, 2010, 59(6): 4065-4070. YAN Hui, JIANG Hongyuan, LIU Wenjian, et al. Analysis of acceleration response of metal rubber isolator under random vibration[J]. Acta physica sinica, 2010, 59(6): 4065-4070. (  0) 0)
|
| [12] |
杨春香, 周易, 张虎. 金属橡胶动态隔振性能的实验研究[J]. 航空学报, 2006, 27(3): 536-539. YANG Chunxiang, ZHOU Yi, ZHANG Hu. Research on dynamic performance of metal rubber damper[J]. Acta aeronautica et astronautica sinica, 2006, 27(3): 536-539. DOI:10.3321/j.issn:1000-6893.2006.03.036 (  0) 0)
|
| [13] |
ZHANG Dayi, SCARPA F, MA Yanhong, et al. Compression mechanics of nickel-based superalloy metal rubber[J]. Materials science & engineering:A, 2013, 580: 305-312. (  0) 0)
|
| [14] |
MA Yanhong, ZHANG Qicheng, ZHANG Dayi, et al. The mechanics of shape memory alloy metal rubber[J]. Acta materialia, 2015, 96: 89-100. DOI:10.1016/j.actamat.2015.05.031 (  0) 0)
|
| [15] |
MA Yanhong, LIANG Zhichao, WANG Hong, et al. Theoretical and experimental steady-state rotordynamics of an adaptive air film damper with metal rubber[J]. Journal of sound and vibration, 2013, 332(22): 5710-5726. DOI:10.1016/j.jsv.2013.06.002 (  0) 0)
|
| [16] |
闫辉, 姜洪源, 刘文剑, 等. 金属橡胶冲击隔振系统试验[J]. 航空动力学报, 2009, 24(7): 1518-1522. YAN Hui, JIANG Hongyuan, LIU Wenjian, et al. Experimental research on metal rubber shock isolation system[J]. Journal of aerospace power, 2009, 24(7): 1518-1522. (  0) 0)
|
| [17] |
夏宇宏, 姜洪源, 魏浩东, 等. 金属橡胶隔振器抗冲击性能研究[J]. 振动与冲击, 2009, 28(1): 72-75. XIA Hongyu, JIANG Hongyuan, WEI Haodong, et al. Shock protection characteristics of metal rubber isolators[J]. Journal of vibration and shock, 2009, 28(1): 72-75. DOI:10.3969/j.issn.1000-3835.2009.01.017 (  0) 0)
|
| [18] |
魏浩东.金属橡胶构件抗冲击性能的理论及实验研究[D].哈尔滨: 哈尔滨工业大学, 2007. WEI Haodong. Theoretical and experimental research on metal rubber element anti-shock performance[D]. Harbin: Harbin Institute of Technology, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D447681 (  0) 0)
|
| [19] |
唱忠良, 邹广平, 刘泽, 等. 金属丝网橡胶隔振系统冲击响应[J]. 哈尔滨工程大学学报, 2017, 38(1): 80-85. CHANG Zhongliang, ZOU Guangping, LIU Ze, et al. Shock response of metal-net rubber vibration isolation system[J]. Journal of Harbin Engineering University, 2017, 38(1): 80-85. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


