2. 中国船级社烟台办事处, 山东 烟台 264000
2. China Classification Society, Yantai Office, Yantai 264000, China
随着深水海洋工程的兴起,近些年国内外学者对透水结构在浮式结构物领域中的应用进行了大量研究和探索。岳景云等[1]采用复合边界元素法论证了结构物外壁采用透水结构可大幅降低cosine-type同心圆柱体周围的绕射波动。Koraim等[2]对竖直平行放置的两个透水板在规则波作用下的水动力性能进行了分析,并总结了影响其水动力性能的4个主要因素。Arpita等[3]对规则波与双圆形透水孔板的相互作用进行了水动力分析。利用解析和数值计算的方法,水平放置的双层透水孔板对绕射波动的抑制效果也得到了验证[4, 12~13]。目前,侧立透水孔板对浮式海洋结构物的水动力性能影响机理研究成果相对较少,Il-Hyoung虽然对带有透水侧板的浮式结构物的运动特性进行了分析,但仅限于使用数值模拟方法[5],该问题的理论解析解目前基本处于空白状态。
为了克服以上研究的不足之处,本文以带有侧立透水孔板的浮式结构物为研究对象,基于porous-wavemaker理论[6]和势流理论,构建解析计算模型,对波浪与该浮式结构物的相互作用问题进行了分析,并与现有数值计算以及实验研究成果进行了对比分析[7-9],基于此,得到了透水孔板对浮体波浪散射和所受波浪力的影响机理。
1 构建理论计算模型如图 1所示,一列波高为H,频率为ω,波长为λ的规则波通过一个长度为2a的矩形浮体,浮体浸入水中的高度为s,在浮体下方连接有对称的两块透水孔板,其高度为d-s, 水深为h,以浮体的中心为原点建立笛卡尔坐标系,x轴沿水平方向,z轴沿竖直方向。
|
Download:
|
| 图 1 带侧立透水孔板的浮式结构物 Fig. 1 Schematic of a floating body with vertical porous wall | |
假设流体不可压缩且无粘性,浮体固定不动,流体区域分为三部分(如图 1中的Ⅰ、Ⅱ和Ⅲ),根据势流理论,速度势函数满足拉普拉斯方程:
| $ {\nabla ^2}{\phi _{Dj}} = 0,j = 1,2,3 $ | (1) |
式中:ϕDj表示第j区域的流体势函数,其应该满足的边界条件如下
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}{\phi _{Dj}}}}{{\partial {t^2}}} + g\frac{{\partial {\phi _{Dj}}}}{{\partial {\rm{z}}}} = 0,j = 1,3,\;\;\;z = 0\\ \frac{{\partial {\phi _{Dj}}}}{{\partial {\rm{z}}}} = 0,\;\;\;\;j = 1,2,3,z = - h\\ \frac{{\partial {\phi _{D2}}}}{{\partial {\rm{z}}}} = 0,\;\;\;\;z = - s,\; - a < x < a \end{array} \right. $ | (2) |
流体流经透水孔板的过程中,应该满足的边界条件为
| $ \left\{ \begin{array}{l} \frac{{\partial {\phi _{D1}}}}{{\partial x}} = \frac{{\partial {\phi _{D2}}}}{{\partial x}} = {W_A}\left( {z,t} \right),x = - a, - d < z < - s\\ \frac{{\partial {\phi _{D3}}}}{{\partial x}} = \frac{{\partial {\phi _{D2}}}}{{\partial x}} = {W_B}\left( {z,t} \right),x = a, - d < z < - s \end{array} \right. $ | (3) |
式中:WA(z, t)和WB(z, t)分别表示流体流经透水孔板A和B处时的速度,根据Darcy定理以及线性化的伯努力方程,WA(z, t)和WB(z, t)分别为
| $ {W_A}\left( {z,t} \right) = \frac{{{b_1}}}{\mu }\Delta p = - {G_{01}}\left[ {\frac{{{k_0}}}{\omega }\left( {\frac{{\partial {\phi _{D1}}}}{{\partial t}} - \frac{{\partial {\phi _{D2}}}}{{\partial t}}} \right)} \right] $ |
| $ {W_B}\left( {z,t} \right) = \frac{{{b_2}}}{\mu }\Delta p = - {G_{02}}\left[ {\frac{{{k_0}}}{\omega }\left( {\frac{{\partial {\phi _{D2}}}}{{\partial t}} - \frac{{\partial {\phi _{D3}}}}{{\partial t}}} \right)} \right] $ |
式中:G01和G02是无量纲参数[6],分别表示透水孔板A和B的透水性能,其表达式如下
| $ {G_{01}} = \frac{{\rho \omega {b_1}}}{{\mu {k_0}}},\;\;\;{G_{02}} = \frac{{\rho \omega {b_2}}}{{\mu {k_0}}} $ |
式中:ρ为流体密度;b1和b2具有长度量纲,分别表示透水孔板A和B的材料特性,为常数;μ为流体的动力粘度。矩形浮体下方的速度势函数以及流体流速具有连续性,因此在透水孔板处应满足如下条件
| $ \left\{ \begin{array}{l} \frac{{\partial {\phi _{D1}}}}{{\partial x}} = \frac{{\partial {\phi _{D2}}}}{{\partial x}},\;\;\;\; - h \le z \le - s,x = - a\\ \frac{{\partial {\phi _{D3}}}}{{\partial x}} = \frac{{\partial {\phi _{D2}}}}{{\partial x}},\;\;\;\; - h \le z \le - s,x = a \end{array} \right. $ | (4) |
| $ \left\{ \begin{array}{l} {\phi _{D1}} = {\phi _{D2}},\;\;\;\;x = - a, - h < z < d\\ {\phi _{D3}} = {\phi _{D2}},\;\;\;\;x = a, - h < z < d \end{array} \right. $ | (5) |
在流体区域Ⅰ和Ⅲ中,与浮体表面接触流体的竖直速度为0,即
| $ \frac{{\partial {\phi _{Dj}}}}{{\partial x}} = 0,\;\;\;j = 1,3,\;\;\;\; - s < z < 0 $ | (6) |
该问题的入射波为规则波,其速度势函数为
| $ {\phi _I} = - {\rm{i}}\frac{{gH}}{{2\omega }}{{\rm{e}}^{{\rm{i}}{k_0}\left( {x + a} \right)}}\frac{{\cosh \left[ {{k_0}\left( {z + h} \right)} \right]}}{{\cosh \left( {{k_0}h} \right)}}{{\rm{e}}^{ - {\rm{i}}\omega t}} $ | (7) |
式中:k0为波数,ω和k0满足色散关系式,即
| $ {\omega ^2} = g{k_0}\tanh \left( {{k_0}h} \right) $ |
在无穷远处,速度势函数应满足辐射条件
| $ \mathop {\lim }\limits_{x \to \pm \infty } \left( {\frac{\partial }{{\partial x}} \mp {\rm{i}}{k_0}} \right)\left[ {\begin{array}{*{20}{c}} {{\phi _{D3}}}\\ {{\phi _{D1}} - {\phi _I}} \end{array}} \right] = 0 $ |
矩形浮体在三自由度(纵荡、垂荡以及纵摇)方向上所受到的波浪力为
| $ {F_{ej}} = \int\limits_\mathit{\Gamma } {p{n_j}{\rm{d}}\mathit{\Gamma }} = {\rm{i}}\rho \omega \int\limits_\mathit{\Gamma } {\phi {n_j}{\rm{d}}\mathit{\Gamma }} ,\;\;\;j = 1,2,3 $ | (8) |
式中:nj=(z-ξ)n1-(x-ζ)n2,j=1, 2, 3分别表示纵荡、垂荡以及纵摇三个自由度方向,(ξ, ζ)为浮体纵摇的旋转中心。
2 求解理论模型解析解根据边界条件(2), 采用分离变量法,解流体速度势函数的拉普拉斯方程(1),可以得到流体区域Ⅰ、Ⅱ和Ⅲ内的速度势函数分别为
| $ \begin{array}{l} {\phi _{D1}} = \sum\limits_{m = 0}^\infty {\left[ {{I_m}{{\rm{e}}^{{{\tilde k}_m}\left( {x + a} \right)}} + {R_m}{{\rm{e}}^{ - {{\tilde k}_m}\left( {x + a} \right)}}} \right]} \cdot \\ \;\;\;\;\;\;\;\;\frac{{\cos \left[ {{{\tilde k}_m}\left( {z + h} \right)} \right]}}{{\cos \left( {{{\tilde k}_m}h} \right)}}{{\rm{e}}^{ - {\rm{i}}\omega t}} \end{array} $ | (9) |
| $ \begin{array}{l} {\phi _{D2}} = \left( {{C_0}x + {D_0}} \right){{\rm{e}}^{ - {\rm{i}}\omega t}} + \\ \;\;\;\;\;\;\;\;\sum\limits_{m = 1}^\infty {\left[ {{C_m}\frac{{\cosh \left( {{r_m}x} \right)}}{{\cosh \left( {{r_m}a} \right)}} + {D_m}\frac{{\sinh \left( {{r_m}x} \right)}}{{\sinh \left( {{r_m}a} \right)}}} \right]} \cdot \\ \;\;\;\;\;\;\;\;\cos \left[ {{r_m}\left( {z + h} \right)} \right]{{\rm{e}}^{ - {\rm{i}}\omega t}} \end{array} $ | (10) |
| $ {\phi _{D3}} = \sum\limits_{m = 0}^\infty {\left[ {{T_m}{{\rm{e}}^{{{\tilde k}_m}\left( {x - a} \right)}}} \right]\frac{{\cos \left[ {{{\tilde k}_m}\left( {z + h} \right)} \right]}}{{\cos \left( {{{\tilde k}_m}h} \right)}}{{\rm{e}}^{ - {\rm{i}}\omega t}}} $ | (11) |
式中:Rm、Cm、Dm、Tm(m=0, 1, 2, 3, …)为未知系数,
| $ {{\tilde k}_m} = \left\{ {{\rm{i}}{k_0}, - {k_1}, - {k_2}, - {k_3}, \cdots , - {k_m}, \cdots } \right\} $ |
| $ {r_m} = \frac{{m{\rm{ \mathsf{ π} }}}}{{h - s}} $ |
| $ {I_m} = \left\{ { - {\rm{i}}\frac{{gH}}{{2\omega }},0,0,0, \cdots } \right\} $ |
当x=±a时,联合利用边界条件(4)、(6),结合
| $ \begin{array}{*{20}{c}} {\int_{ - h}^0 {\frac{{\partial {\phi _{D1}}}}{{\partial x}}\cos \left( {{{\tilde k}_n}\left( {z + h} \right)} \right){\rm{d}}z} = \int_{ - h}^{ - s} {\frac{{\partial {\phi _{D2}}}}{{\partial x}}} \cdot }\\ {\cos \left( {{{\tilde k}_n}\left( {z + h} \right)} \right){\rm{d}}z} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {\int_{ - h}^0 {\frac{{\partial {\phi _{D3}}}}{{\partial x}}\cos \left( {{{\tilde k}_n}\left( {z + h} \right)} \right){\rm{d}}z} = \int_{ - h}^{ - s} {\frac{{\partial {\phi _{D2}}}}{{\partial x}}} \cdot }\\ {\cos \left( {{{\tilde k}_n}\left( {z + h} \right)} \right){\rm{d}}z} \end{array} $ | (13) |
同样,在x=±a处,联合利用边界条件(3)、(5)结合cos[rm(z+h)]在流体区域Ⅱ内的积分区间-h<z<-s上的正交特性,可以得到如下方程式(n=0, 1, 2, 3, …):
| $ \begin{array}{*{20}{c}} {\int_{ - h}^{ - d} {{\phi _{D1}}\cos \left( {{r_n}\left( {z + h} \right)} \right){\rm{d}}z} + \int_{ - d}^{ - s} {{{\tilde \phi }_{D1}}\cos \left( {{r_n}\left( {z + h} \right)} \right)} \cdot }\\ {{\rm{d}}z = \int_{ - h}^{ - d} {{\phi _{D2}}\cos \left( {{r_n}\left( {z + h} \right)} \right){\rm{d}}z} ,\;\;\;z = - a} \end{array} $ | (14) |
| $ \begin{array}{*{20}{c}} {\int_{ - h}^{ - d} {{\phi _{D3}}\cos \left( {{r_n}\left( {z + h} \right)} \right){\rm{d}}z} + \int_{ - d}^{ - s} {{{\tilde \phi }_{D3}}\cos \left( {{r_n}\left( {z + h} \right)} \right)} \cdot }\\ {{\rm{d}}z = \int_{ - h}^{ - d} {{\phi _{D2}}\cos \left( {{r_n}\left( {z + h} \right)} \right){\rm{d}}z} ,\;\;\;x = a} \end{array} $ | (15) |
其中
| $ \begin{array}{l} {{\tilde \phi }_{D1}} = \sum\limits_{m = 0}^\infty {\left[ {\left( {{I_m} + {R_m}} \right) - \frac{{{{\tilde k}_m}}}{{{\rm{i}}{G_{01}}{k_0}}}\left( {{I_m} - {R_m}} \right)} \right]} \cdot \\ \;\;\;\;\;\;\;\;\frac{{\cos \left[ {{{\tilde k}_m}\left( {z + h} \right)} \right]}}{{\cos \left( {{{\tilde k}_m}h} \right)}}{{\tilde \phi }_{D3}} = \sum\limits_{D = 0}^\infty {\left( {1 + \frac{{{{\tilde k}_m}}}{{{\rm{i}}{G_{02}}{k_0}}}} \right){T_m}} \cdot \\ \;\;\;\;\;\;\;\;\frac{{\cos \left[ {{{\tilde k}_m}\left( {z + h} \right)} \right]}}{{\cos \left( {{{\tilde k}_m}h} \right)}} \end{array} $ |
将式(9)~(11)分别代入式(12)~(15),用一个趋近于无穷大的实数M替代求和符号中的“∞”,可得到下列线性方程组:
| $ \begin{array}{l} \frac{{{{\tilde k}_n}\left( {{I_n} - {R_n}} \right)}}{{\cos \left( {{{\tilde k}_n}h} \right)}}\left[ {\frac{h}{2} + \frac{{\sin \left( {2{{\tilde k}_n}h} \right)}}{{4{{\tilde k}_n}}}} \right] = \frac{{\sin \left[ {{{\tilde k}_n}\left( {h - s} \right)} \right]}}{{{{\tilde k}_n}}}{C_0} - \\ \sum\limits_{m = 1}^M {\left[ {{C_m}\tanh \left( {{r_m}a} \right) - \frac{{{D_m}}}{{\tanh \left( {{r_m}a} \right)}}} \right]{e_1}} \end{array} $ | (16) |
| $ \begin{array}{l} \frac{{{{\tilde k}_n}{T_n}}}{{\cos \left( {{{\tilde k}_n}h} \right)}}\left[ {\frac{h}{2} + \frac{{\sin \left( {2{{\tilde k}_n}h} \right)}}{{4{{\tilde k}_n}}}} \right] = \frac{{\sin \left[ {{{\tilde k}_n}\left( {h - s} \right)} \right]}}{{{{\tilde k}_n}}}{C_0} - \\ \sum\limits_{m = 1}^M {\left[ {{C_m}\tanh \left( {{r_m}a} \right) + \frac{{{D_m}}}{{\tanh \left( {{r_m}a} \right)}}} \right]{e_1}} \end{array} $ | (17) |
| $ \begin{array}{l} \sum\limits_{m = 0}^M {\left[ {{e_3} + {e_4} + \frac{{{{\tilde k}_m}{e_4}}}{{{\rm{i}}{G_{01}}{k_0}}}} \right]{R_m}} + \sum\limits_{m = 0}^M {\left[ {{e_3} + {e_4} - \frac{{{{\tilde k}_m}{e_4}}}{{{\rm{i}}{G_{01}}{k_0}}}} \right]{I_m}} = \\ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \left( { - a{C_0} + {D_0}} \right)\left( {h - s} \right),\\ 0.5\left( {h - s} \right)\left( {{C_n} - {D_n}} \right), \end{array}&\begin{array}{l} n = 0\\ n \ne 0 \end{array} \end{array}} \right. \end{array} $ | (18) |
| $ \sum\limits_{m = 0}^M {\left( {{e_3} + {e_4} + \frac{{{{\tilde k}_m}{e_4}}}{{{\rm{i}}{G_{02}}{k_0}}}} \right){T_m}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \left( {a{C_0} + {D_0}} \right)\left( {h - s} \right),\\ 0.5\left( {h - s} \right)\left( {{C_n} + {D_n}} \right), \end{array}&\begin{array}{l} n = 0\\ n \ne 0 \end{array} \end{array}} \right. $ | (19) |
该方程组由4(M+1)个线性方程组合而成,其中共含有4(M+1)个未知系数,分别为Cn、Dn、Rn、Tn (n=0, 1, 2, …, M),根据文献[5, 8]分析,以及便于检验计算结果的正确性,取M=40,由此可以对其中的未知系数进行求解。在此基础上可以对一系列的工程问题进行计算,比如浮体系统在纵荡、垂荡以及纵摇三个方向上所受到的水动力以及浮体系统的波浪透射系数Ct(23)和波浪反射系数Cr(20)。
其中,e1、e3、e4的表达式为
| $ \begin{array}{*{20}{c}} {{e_1} = \frac{{{r_m}}}{2}\left\{ {\frac{{\sin \left[ {\left( {{{\tilde k}_n} + {r_m}} \right)\left( {h - s} \right)} \right]}}{{{{\tilde k}_n} + {r_m}}} + } \right.}\\ {\left. {\frac{{\sin \left[ {\left( {{{\tilde k}_n} - {r_m}} \right)\left( {h - s} \right)} \right]}}{{{{\tilde k}_n} - {r_m}}}} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{e_3} = \left\{ {\frac{{\sin \left[ {\left( {{{\tilde k}_m} + {r_n}} \right)\left( {h - d} \right)} \right]}}{{2\cos \left[ {{{\tilde k}_m}h\left( {{{\tilde k}_m} + {r_n}} \right)} \right]}} + } \right.}\\ {\left. {\frac{{\sin \left[ {\left( {{{\tilde k}_m} - {r_n}} \right)\left( {h - d} \right)} \right]}}{{2\cos \left[ {{{\tilde k}_m}h\left( {{{\tilde k}_m} - {r_n}} \right)} \right]}}} \right\}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{e_4} = }\\ {\left\{ {\frac{{\sin \left[ {\left( {{{\tilde k}_m} + {r_n}} \right)\left( {h - s} \right)} \right] - \sin \left[ {\left( {{{\tilde k}_m} + {r_n}} \right)\left( {h - d} \right)} \right]}}{{2\cos \left[ {{{\tilde k}_m}h\left( {{{\tilde k}_m} + {r_n}} \right)} \right]}} + } \right.}\\ {\left. {\frac{{\sin \left[ {\left( {{{\tilde k}_m} - {r_n}} \right)\left( {h - s} \right)} \right] - \sin \left[ {\left( {{{\tilde k}_m} - {r_n}} \right)\left( {h - d} \right)} \right]}}{{2\cos \left[ {{{\tilde k}_m}h\left( {{{\tilde k}_m} - {r_n}} \right)} \right]}}} \right\}} \end{array} $ |
根据式(8),可以得到浮体系统在纵荡、垂荡以及纵摇三个方向上受到的水动力Fe1、Fe2和Fe3分别为
| $ \begin{array}{l} {F_{e1}} = \int_{ - d}^0 { - \rho \frac{{\partial {\phi _{D1}}}}{{\partial t}}\left| {_{x = - a}} \right.{\rm{d}}z} - \int_{ - d}^0 { - \rho \frac{{\partial {\phi _{D3}}}}{{\partial t}}\left| {_{x = a}} \right.{\rm{d}}z} - \\ \;\;\;\;\;\;\;\; \int_{ - d}^{ - s} { - \rho \frac{{\partial {\phi _{D2}}}}{{\partial t}}\left| {_{x = - a}} \right.{\rm{d}}z} + \int_{ - d}^{ - s} { - \rho \frac{{\partial {\phi _{D2}}}}{{\partial t}}\left| {_{x = a}} \right.{\rm{d}}z} = \\ \;\;\;\;\;\;\;\;{\rm{i}}\rho \omega \sum\limits_{m = 0}^M {\frac{{\left( {{I_m} + {R_m} - {T_m}} \right)\left\{ {\sin \left( {{{\tilde k}_m}h} \right) - \sin \left[ {{{\tilde k}_m}\left( {h - d} \right)} \right]} \right\}}}{{{{\tilde k}_m}\cos \left( {{{\tilde k}_m}h} \right)}}} + 2{\rm{i}}\rho \omega a\left( {d - s} \right){C_0} - \\ \;\;\;\;\;\;\;\;{\rm{i}}\rho \omega {\left( {{r_m}} \right)^{ - 1}} \cdot \sum\limits_{m = 1}^M {\left\{ {2{D_m}\sin \left[ {{r_m}\left( {h - d} \right)} \right] - 2{D_m}\sin \left[ {{r_m}\left( {h - s} \right)} \right]} \right\}} \end{array} $ |
| $ \begin{array}{l} {F_{e2}} = \int_{ - a}^a { - \rho \frac{{\partial {\phi _{D2}}}}{{\partial t}}\left| {_{z = - s}} \right.{\rm{d}}x} = 2{\rm{i}}\omega \rho a{D_0} + \\ 2{\rm{i}}\omega \rho \sum\limits_{m = 1}^M {\frac{{{C_m}}}{{{r_m}}}\tanh \left( {{r_m}a} \right)\cos \left[ {{r_m}\left( {h - s} \right)} \right]} \end{array} $ |
| $ \begin{array}{l} {F_{e3}} = \left[ {\int_{ - d}^0 {\left( {{\phi _{D1}}\left| {_{x = - a}} \right. - {\phi _{D3}}\left| {_{x = a}} \right.} \right)\left( {z - \xi } \right){\rm{d}}z} +} \right. \\ \;\;\;\;\;\;\;\; \left. {\int\limits_{ - d}^{ - s} {\left( {{\phi _{D2}}\left| {_{x = - a}} \right. - {\phi _{D2}}\left| {_{x = a}} \right.} \right)\left( {z - \xi } \right){\rm{d}}z} } \right] - \\ \;\;\;\;\;\;\;\;\int_{ - a}^a {\left( {{\phi _{D2}}\left| {_{z = - s}} \right.} \right)x{\rm{d}}x} = {\rm{i}}\rho \omega \sum\limits_{m = 0}^\infty {\left\{ {\left[ {\left( {{I_m} + {R_m} - {T_m}} \right)\frac{{d\sin \left( {{{\tilde k}_m}h - {{\tilde k}_m}d} \right)}}{{{{\tilde k}_m}\cos \left( {{{\tilde k}_m}h} \right)}} - } \right.} \right.} \\ \;\;\;\;\;\;\;\;\left. {\left. {\frac{{\sin \left( {{{\tilde k}_m}h} \right) + \sin \left( {{{\tilde k}_m}h - {{\tilde k}_m}d} \right)}}{{{\xi ^{ - 1}}{{\tilde k}_m}\cos \left( {{{\tilde k}_m}h} \right)}} + \frac{{\cos \left( {{{\tilde k}_m}h} \right) - \cos \left( {{{\tilde k}_m}h - {{\tilde k}_m}d} \right)}}{{{{\tilde k}_m}^2\cos \left( {{{\tilde k}_m}h} \right)}}} \right]} \right\} + \\ \;\;\;\;\;\;\;\;{\rm{i}}\rho \omega \left\{ {a{C_0}\left( {{d^2} - {s^2}} \right) + 2a{C_0}\xi \left( {d - s} \right) - \sum\limits_{m = 1}^M {\frac{{2{D_m}}}{{{r_m}}}} \cdot \left[ {d\sin \left( {{r_m}h - {r_m}d} \right)} \right. } \right.\\ \;\;\;\;\;\;\;\;\left. {\left. { - s\sin \left( {{r_m}h - {r_m}s} \right) + \frac{{\cos \left( {{r_m}h - {r_m}s} \right)}}{{{r_m}}} - \frac{{\cos \left( {{r_m}h - {r_m}d} \right)}}{{{r_m}}}} \right] - \frac{{2{C_0}{a^3}}}{3}} \right\} + \\ \;\;\;\;\;\;\;\;{\rm{i}}\rho \omega \sum\limits_{m = 1}^M {\frac{{2{D_m}\xi }}{{{r_m}}}\left[ {\sin \left( {{r_m}h - {r_m}s} \right) - \sin \left( {{r_m}h - {r_m}d} \right)} \right]} - \\ \;\;\;\;\;\;\;\;{\rm{i}}\rho \omega \left\{ {\sum\limits_{m = 1}^\infty {\left[ {\frac{{2a{D_m}\cos \left( {{r_m}h - {r_m}s} \right)}}{{{r_m}\tanh \left( {{r_m}a} \right)}} - \frac{{2{D_m}\cos \left( {{r_m}h - {r_m}s} \right)}}{{{r_m}^2}}} \right]} } \right\} \end{array} $ |
| $ {C_r} = \left| {\frac{{{R_0}}}{{{I_0}}}} \right|,\;\;\;\;{C_t} = \left| {\frac{{{T_0}}}{{{I_0}}}} \right| $ | (20) |
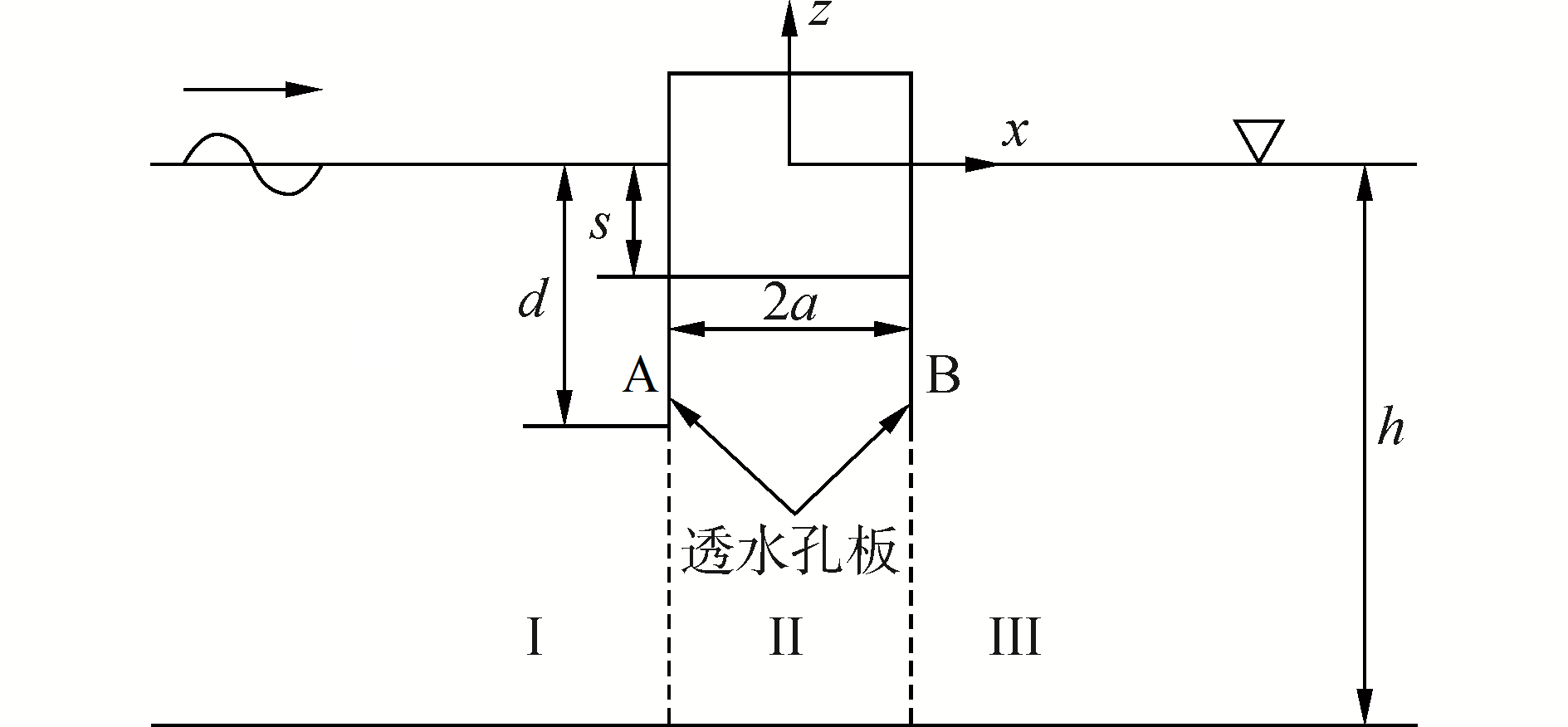
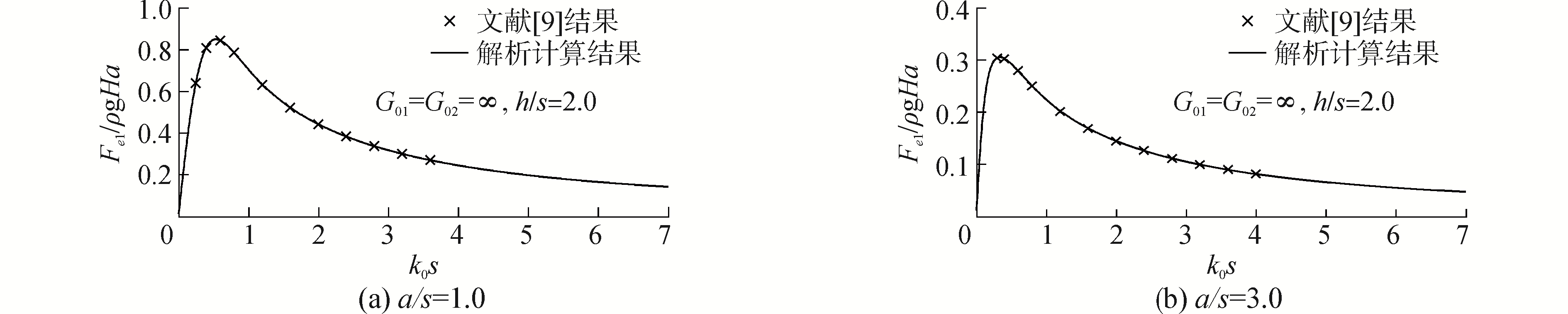
如图 2~7所示分别为浮体在垂荡、纵荡以及纵摇三个方向上所受到的波浪力,当透水系数取无穷大时,即G01=G02=∞,相当于不存在透水孔板的情况,Zheng等[8-9]对该情况下浮体受到的波浪力分别进行了数值计算和解析计算,并分析了入射波长及浮体尺寸对波浪力的影响机理。

|
Download:
|
| 图 2 垂荡力计算结果与文献[9]结果的比较 Fig. 2 Heaving exciting forces comparisons between present solutions and Ref. [9] | |
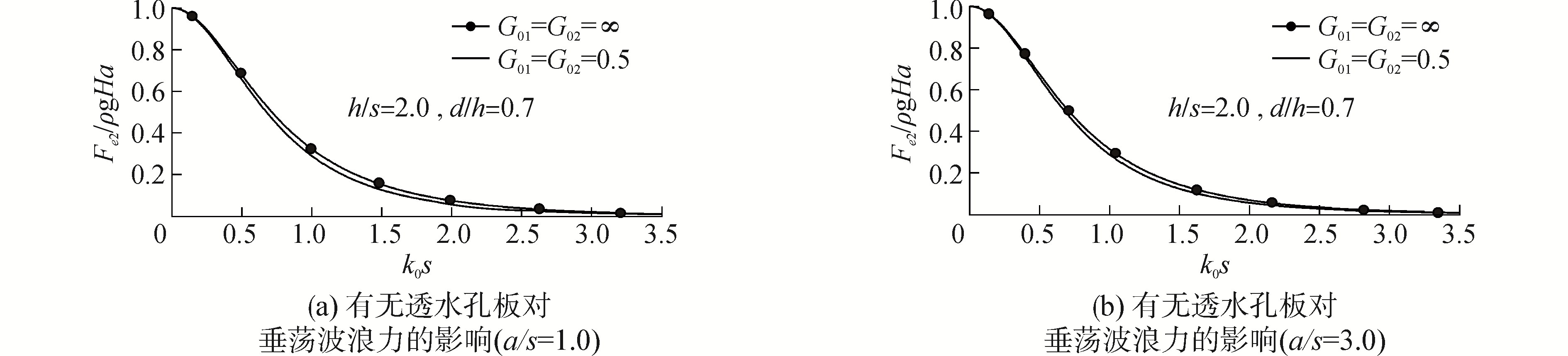
|
Download:
|
| 图 3 垂荡力的计算结果 Fig. 3 Results of heaving exciting forces | |
|
Download:
|
| 图 4 纵荡力计算结果与文献[9]结果的比较 Fig. 4 Surging exciting forces comparisons between present solutions and Ref. [9] | |
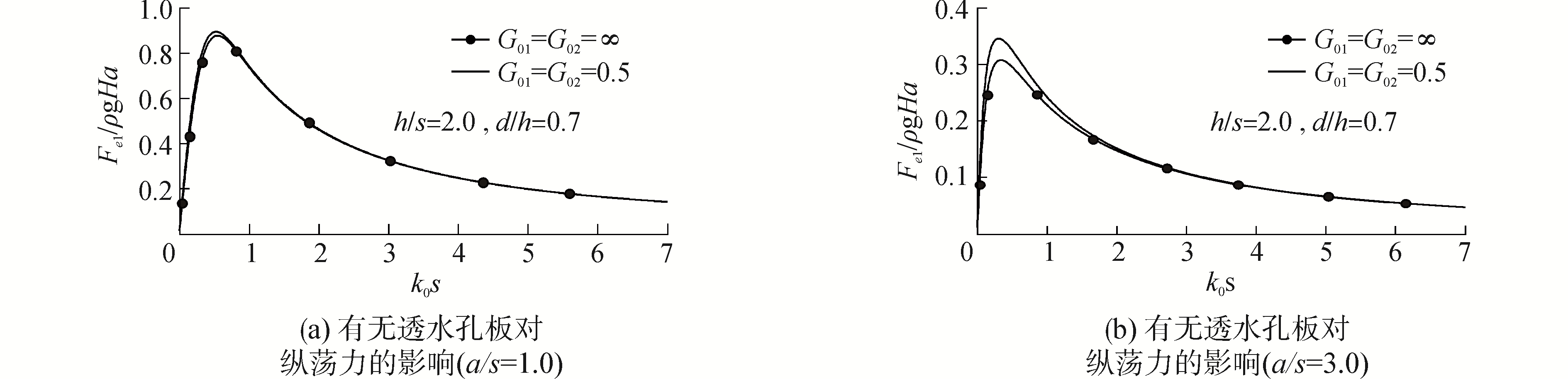
|
Download:
|
| 图 5 纵荡力的计算结果 Fig. 5 Results of surging exciting forces | |

|
Download:
|
| 图 6 纵摇力矩计算结果与文献[9]结果的比较 Fig. 6 Surging exciting forces comparisons between present solutions and Ref. [9] | |
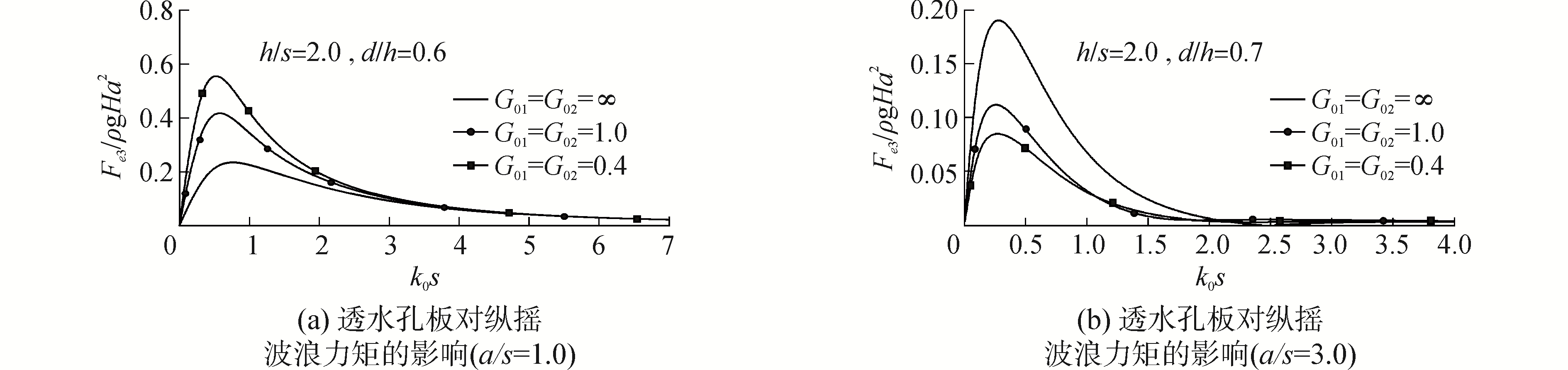
|
Download:
|
| 图 7 纵摇力矩的计算结果 Fig. 7 Results of pitching moments | |
图 2、4、6对比本文的计算结果与Black等[9]的计算结果,本文解析计算结果与Black等的数值计算结果几乎相等,验证了本文提出的理论计算模型的正确性。改变透水孔板A或B的透水系数后发现,随着透水系数的减小,透水孔板的透水能力会相应地降低,其减波、消波能力也被弱化,此时浮体受到波浪的扰动作用得到增强,具体表现为浮体所受到的纵摇力矩和纵荡力呈现上升趋势,尤其是纵摇力矩,上升趋势更为明显。但是此时,由于波浪反射系数增大,透过孔板的入射波较少,浮体受到的垂荡力会有小幅度的降低。
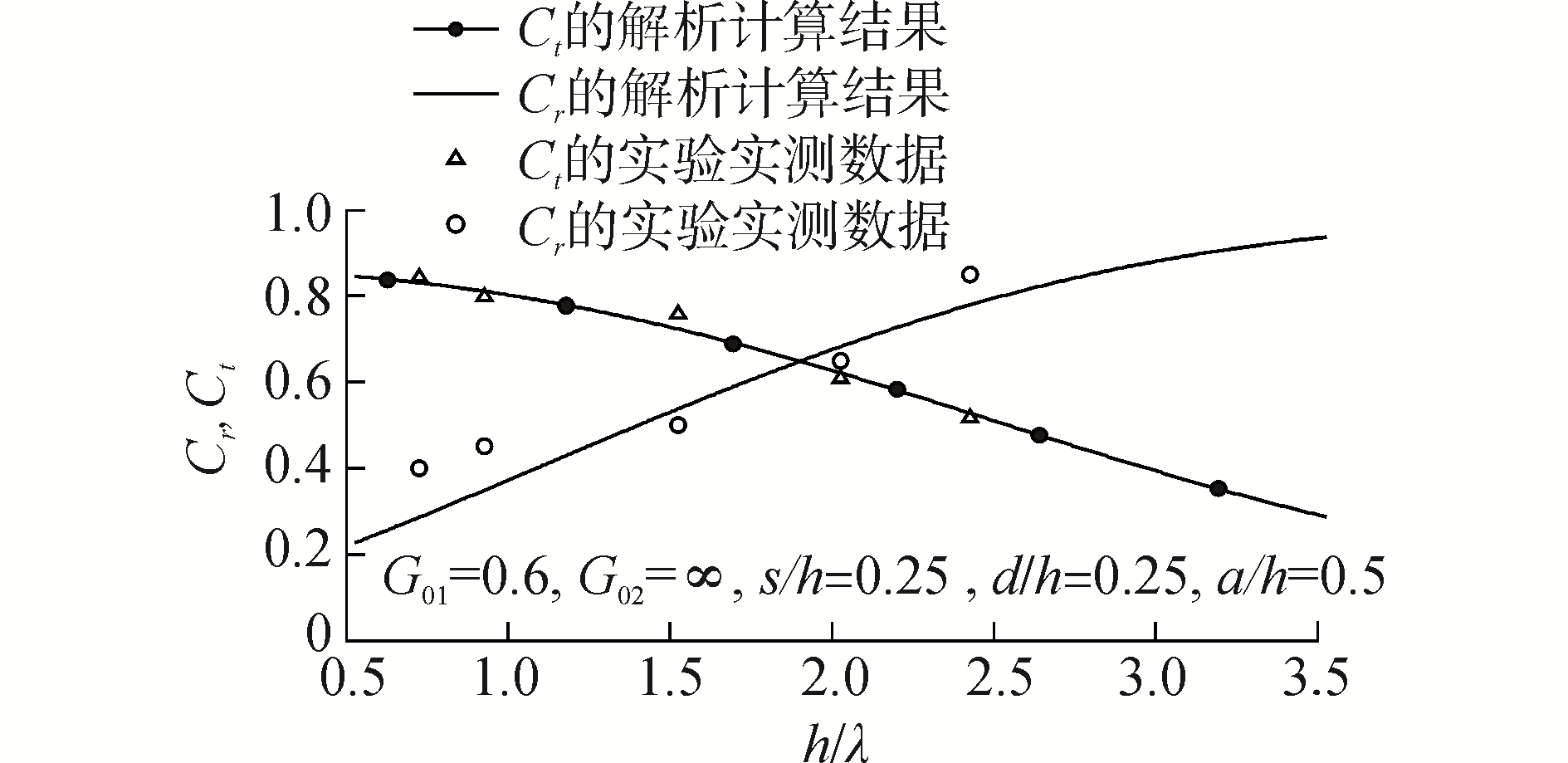
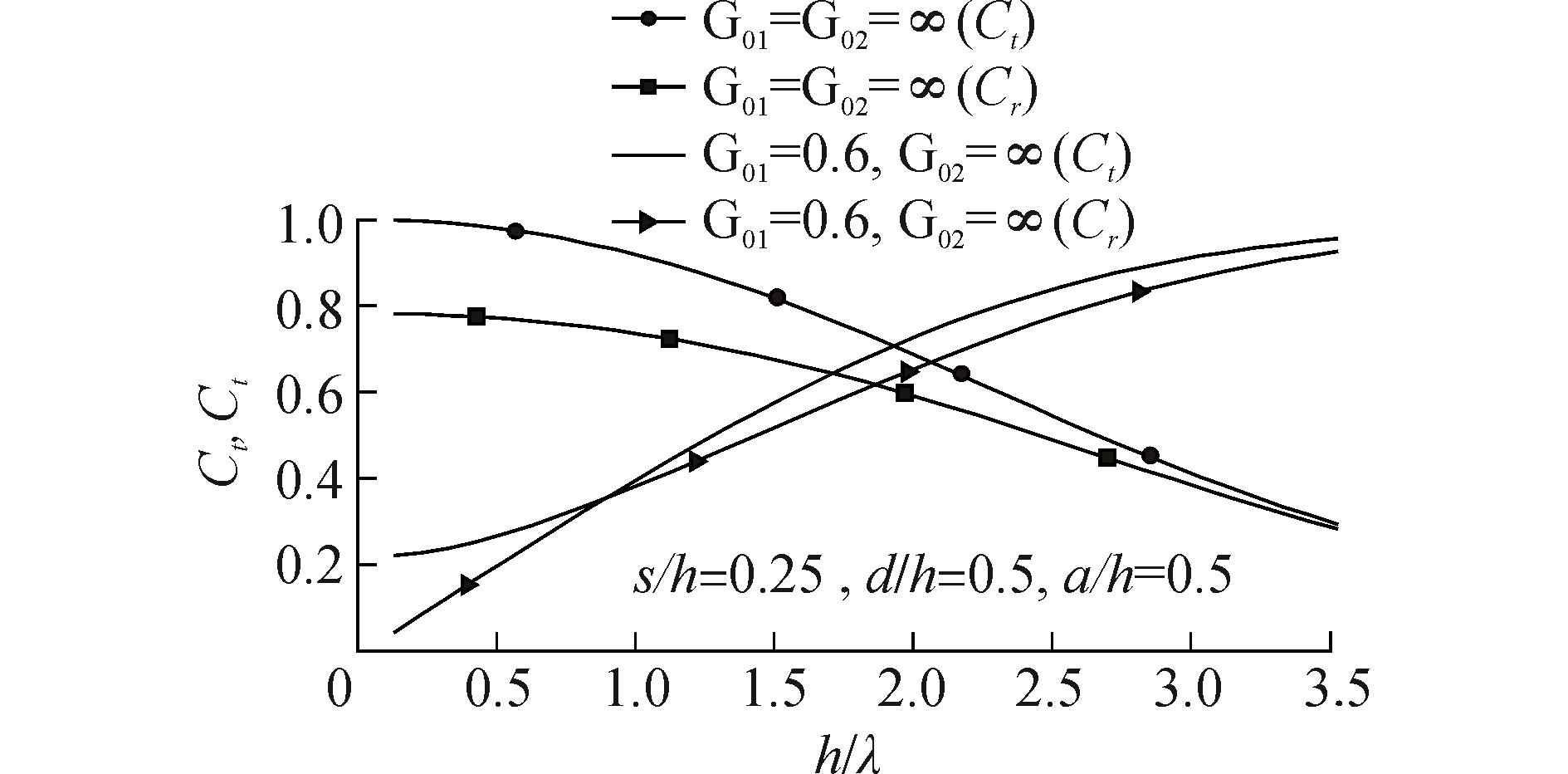
3.2 波浪反射系数和透射系数分析如图 8所示为存在透水孔板的情况下,本文理论计算模型所得的波浪反射系数和透射系数与Koutandos等[7]实测数据的对比分析,从整体上看,透射系数的理论计算结果与实验实测数据基本吻合;对于波浪反射系数,除了个别数据点时,可能存在实验误差之外,理论计算结果与实测数据也基本吻合,从而验证本论文理论计算模型的正确性。图 9所示为透水孔板的透水系数对波浪反射系数和透射系数的影响机理,随着透水系数的降低,透水孔板的透水能力也随之下降,由于入射波为表面重力波,此时大部分波浪无法通过透水孔板,从而使得波浪透射系数随透水系数的降低而呈减小趋势,由于透水孔板对短波的影响不明显[10],所以随着h/λ的增大,减小的趋势越来越弱;而对于波浪反射系数,其数值主要取决于入射波波长及透水孔板的透水系数,对于短波范围而言,波长影响较大,而在长波范围内,透水系数影响较大,转折点处的波长会随实验条件的不同而各异,本实验中转折点处的h/λ=0.56,因此,当h/λ < 0.56时,透水系数越大,波浪反射系数也越大,当h/λ > 0.56时,情况则相反。
|
Download:
|
| 图 8 本文计算的波浪反射系数Cr和透射系数Ct与文献[7]实测数据的对比 Fig. 8 Comparisons between present and measured reflection coefficient (Cr) and transmission coefficient (Ct)[7] | |
|
Download:
|
| 图 9 透水孔板对波浪反射系数和透射系数的影响 Fig. 9 The influences of porous wall to reflection coefficients and transmission coefficients | |
1) 侧立孔板对浮体所受到的垂荡和纵荡波浪力影响作用不明显,尤其是对于小尺度(a/s=1.0)浮体而言,影响作用较小。
2) 对于浮体受到的波浪力矩而言,侧立孔板的影响作用较为明显,入射波长越长、浮体的相对尺寸越大(a/s=3.0),这种影响作用就越为明显。
3) 波浪透射系数随着透水孔板的透水系数的减小而减小,波长越大,这种减小作用就越为明显。波浪反射系数的变化取决于入射波波长和透水孔板的透水系数,短波范围内,入射波波长影响较大;长波范围内,透水系数影响较大。
本文的研究成果为透水孔板在深水浮式结构物领域中的工程应用奠定了一定的理论分析基础,并为下一步开展物理模型试验提供了一定的理论指导。
| [1] |
岳景云, 翁文凯. 透水cosine-type同心圆柱波浪绕射研究[J]. 海洋工程, 2014, 32(6): 1-8. YUE Jingyun, WENG Wenkai. Wave diffraction by a porous cosine-type cylinder with a solid interior cylinder[J]. The ocean engineering, 2014, 32(6): 1-8. DOI:10.3969/j.issn.1005-9865.2014.06.001 (  0) 0)
|
| [2] |
KORAIM A S, HEIKAL E M, RAGEH O S. Hydrodynamic characteristics of double permeable breakwater under regular waves[J]. Marine structures, 2011, 24(4): 503-527. DOI:10.1016/j.marstruc.2011.06.004 (  0) 0)
|
| [3] |
MONDAL A, GAYEN R. Wave interaction with dual circular porous plates[J]. Journal of marine science and application, 2015, 14(4): 366-375. DOI:10.1007/s11804-015-1325-7 (  0) 0)
|
| [4] |
LIU Yong, LI Huajun. Wave scattering by dual submerged horizontal porous plates:further results[J]. Ocean engineering, 2014, 81: 158-163. DOI:10.1016/j.oceaneng.2014.02.004 (  0) 0)
|
| [5] |
CHO I H. Transmission coefficients of a floating rectangular breakwater with porous side plates[J]. International journal of naval architecture and ocean engineering, 2016, 8(1): 53-65. DOI:10.1016/j.ijnaoe.2015.10.002 (  0) 0)
|
| [6] |
CHWANG A T. A porous-wavemaker theory[J]. Journal of fluid mechanics, 1983, 132: 395-406. DOI:10.1017/S0022112083001676 (  0) 0)
|
| [7] |
KOUTANDOS E, PRINOS P, GIRONELLA X. Floating breakwaters under regular and irregular wave forcing:reflection and transmission characteristics[J]. Journal of hydraulic research, 2005, 43(2): 174-188. DOI:10.1080/00221686.2005.9641234 (  0) 0)
|
| [8] |
ZHENG Y H, YOU Y G, SHEN Y M. On the radiation and diffraction of water waves by a rectangular buoy[J]. Ocean engineering, 2004, 31(8/9): 1063-1082. (  0) 0)
|
| [9] |
BLACK J L, MEI C C, BRAY C G. radiation and scattering of water waves by rigid bodies[J]. Journal of fluid mechanics, 1971, 46(1): 151-164. DOI:10.1017/S0022112071000454 (  0) 0)
|
| [10] |
CHO I H, KOH H J, KIM J R, et al. Wave scattering by dual submerged horizontal porous plates[J]. Ocean engineering, 2013, 73: 149-158. DOI:10.1016/j.oceaneng.2013.08.008 (  0) 0)
|
| [11] |
CHU T. Part Ⅰ-Geostatistical interpolation of rain fields using Radar estimates and gauge observations: algorithm design and automation and Part Ⅱ-energy dissipation in fluid flows and wave transformation by porous barriers and submerged cavities[D]. Houston: University of Houston, 2014.
(  0) 0)
|
| [12] |
EVANS D V, PETER M A. Asymptotic reflection of linear water waves by submerged horizontal porous plates[J]. Journal of engineering mathematics, 2011, 69: 135-154. DOI:10.1007/s10665-009-9355-2 (  0) 0)
|
| [13] |
BEHERA H, SAHOO T. Hydroelastifc analysis of gravity wave interaction with submerged horizontal flexible porous plate[J]. Journal of fluids and structures, 2015, 54: 643-660. DOI:10.1016/j.jfluidstructs.2015.01.005 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


