2. 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024
2. State key laboratory coastal and offshore engineering, Dalian University of Technology, Dalian 116024, China
冰载荷是影响极地船舶与海洋结构物安全性与可靠性的主要环境载荷,与冰力学行为密切相关。目前,针对冰受力变形至破坏过程,一些学者综合采用理论推导、数值分析、试验等方法进行了系统的研究。其中,数值分析方法具有简便、可重复性好等特点,可以从不同层面揭示冰破坏机理、冰载荷分布特征和规律,已经成为研究冰力学行为的有效手段。经典数值分析方法在连续性假设下通过偏微分方程进行求解,导致空间导数在裂纹表面和尖端存在奇异性问题,在模拟破坏问题时存在着一定困难[1]。有限元法(FEM)在数值模拟破坏问题时需要预先明确裂纹是否存在以及其尺寸和位置,随着裂纹的扩展需要对网格进行重新划分,计算过程和结果对网格具有强烈依赖性[2]。近年来,随着离散元方法的发展,基于离散元方法的海冰与海洋结构、船体相互作用研究取得了较大的进展,在海冰与船舶结构作用的破坏过程数值模拟方面表现出了一定优势,但由于在离散单元之间采用梁模型,对于连续体阶段的计算往往存在较大误差,在处理本构关系上还需进一步研究和发展[3-4]。
近场动力学[5]是近年来新兴的一种基于非局部理论的无网格方法。该方法基于非局部作用思想,采用积分型控制运动方程,通过非局部力来描述物质点之间的作用力,避免了基于连续性假设求解微分方程的传统方法在处理不连续问题时的奇异性和复杂性,使其在连续介质与非连续介质中同时适用,在处理固体力学中的破坏、断裂等问题时,能够模拟裂纹“自然”发生和扩展过程,在混凝土[6]、复合材料[7]等领域得到了成功的应用。
本文主要目的是探究近场动力学方法在冰材料受力变形至破坏过程数值模拟的可行性。在提出了适用于准静态问题的近场动力学数值计算方法的同时,建立冰的弹脆性近场动力学模型,对冰的三点弯曲试验从变形到破坏全过程进行数值模拟,并与实际试验结果进行对比。
1 近场动力学理论如图 1所示,近场动力学假设占据某一空间域R的物体内任一物质点x,在某一时刻t,与其附近某一范围δ内(称为近场范围)每一个点x′∈R:‖x′-x‖≤δ都存在相互作用力。根据牛顿第二定律,近场动力学基本运动方程为
| $ \begin{array}{l} \rho \mathit{\boldsymbol{\ddot u}}\left( {x, t} \right) = \int_{{H_x}} {\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}}\prime, t} \right)-} \\ \mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}}, t} \right), \mathit{\boldsymbol{x}}\prime-\mathit{\boldsymbol{x}}{\rm{)d}}{V_{x\prime }} + \mathit{\boldsymbol{b}}\left( {\mathit{\boldsymbol{x}}, t} \right) \end{array} $ | (1) |

|
Download:
|
| 图 1 近场范围内物质点的相互作用 Fig. 1 Interaction between material points in horizon | |
式中:ρ为材料密度;u为位移;b代表物质点受到的外载荷密度;Vx′为物质点x′的体积;Hx={x′∈R:‖x′-x‖≤δ }表示物质点x近场范围内其他物质点集合,δ为近场半径;f为本构力函数,表示t时刻物质点x与x′之间的相互作用力,对于各向同性的弹脆性材料[8],其表达式为
| $ \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{\xi }}, \mathit{\boldsymbol{\eta }}} \right) = \frac{{\mathit{\boldsymbol{\xi }} + \mathit{\boldsymbol{\eta }}}}{{\left| {\mathit{\boldsymbol{\xi }} + \mathit{\boldsymbol{\eta }}} \right|}}cs\mu \left( {t, \mathit{\boldsymbol{\xi }}, \mathit{\boldsymbol{\eta }}} \right) $ | (2) |
式中:ξ=x′-x表示两点相对位置;η=u′-u表示两点相对位移;c为连接键弹性系数(microelastic),与材料弹性模量E和泊松比υ有关[9];s为连接键相对伸长率,其表达式为
| $ s = \frac{{\left| {\mathit{\boldsymbol{\xi }} + \mathit{\boldsymbol{\eta }}} \right|-\left| \mathit{\boldsymbol{\xi }} \right|}}{{\left| \mathit{\boldsymbol{\xi }} \right|}} $ | (3) |
材料失效在近场动力学理论中的规定为:当相对伸长率s超过某一临界值s0时,物质点间的连接键将发生不可逆的破坏。连接键的破坏状态用函数μ(t, ξ, η)表示:
| $ \mu \left( {t, \mathit{\boldsymbol{\xi }}, \mathit{\boldsymbol{\eta }}} \right) = \left\{ \begin{array}{l} 1, \;\;\;\;\;s < {s_0}\\ 0, \;\;\;\;\;s \ge {s_0} \end{array} \right. $ | (4) |
根据这一破坏准则,材料在x处的损伤程度可表示为
| $ D\left( {\mathit{\boldsymbol{x}}, t} \right) = 1-\frac{{{\smallint _{{H_x}}}\mu \left( {\mathit{\boldsymbol{x}}, t, \mathit{\boldsymbol{\xi }}, \mathit{\boldsymbol{\eta }}} \right){\rm{d}}{V_\xi }}}{{{\smallint _{{H_x}}}{\rm{d}}{V_\xi }}} $ | (5) |
式中:D表示损伤程度,D=1对应完全破坏状态,D=0对应无损伤状态,0 < D < 1对应不同程度的损伤状态。
2 准静态问题的近场动力学数值计算方法为了数值求解近场动力学运动方程,需要将物体占据的空间域离散成有限数量的物质点,将空间积分方程转化为求解有限和,离散式为
| $ \rho \mathit{\boldsymbol{\ddot u}}_i^n = \sum\limits_p {\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u}}_p^n-\mathit{\boldsymbol{u}}_i^n, {\rm{ }}{\mathit{\boldsymbol{x}}_p}-{\mathit{\boldsymbol{x}}_i}} \right){V_p} + \mathit{\boldsymbol{b}}_i^n} $ | (6) |
式中:n表示计算的第n个时间步;uin=u(xi, tn)表示物质点xi在第n个时间步的位移;Vp为物质点xp的体积,本文中,空间域均匀离散,三维物质点体积为Vp=|Δx|3,二维物质点体积为Vp=|Δx|2k,其中Δx为物质点间距,k为二维物体厚度。方程(6)采用中心差分法进行求解即可得到相应动态问题的解。
近场动力学作为一种动态方法,在计算静态问题时需要通过准静态过程进行近似求解。在准静态问题的求解中,近场动力学一般处理方法是将总时间步数nstep设置成相当大的值,并使载荷在这些时间步内持续缓慢增加,从而消除加速度影响,按照以上动态问题的数值算法求解后即可得到准静态问题的解。由于nstep往往需要取到几万步以上才足以保证计算结果的准确性,因而计算量庞大,对于粒子数量较多的模型将难以施行。为了有效解决这一问题,本文在近场动力学方法中引入动态松弛法求解静态或准静态问题。
动态松弛法是一种以动态方程求解静态问题的方法,利用动态方程的稳态解即静态解原理,通过人为向系统施加阻尼,消耗系统动能迫使系统进入稳定状态,从而求得系统的静态解。由于方法以获得稳定状态为目的,避免了上述动态算法中的缓慢加载过程模拟,往往只需几千步便可求得最终结果,因此相比于动态算法大大提高了计算效率。动态松弛法应用于近场动力学的具体算法如下。
对于方程(6),将求和项记为L,即
| $ \mathit{\boldsymbol{L}}_i^n = \sum\limits_p {\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u}}_p^n-\mathit{\boldsymbol{u}}_i^n, {\rm{ }}{\mathit{\boldsymbol{x}}_p}-{\mathit{\boldsymbol{x}}_i}} \right){V_p}} $ | (7) |
则L=Ku表示内力的体积力密度,其中K表示等效刚度。方程(6)可简写为
| $ \rho \mathit{\boldsymbol{\ddot u}}_i^n = \mathit{\boldsymbol{L}}_i^n + \mathit{\boldsymbol{b}}_i^n $ | (8) |
依照动态松弛法,将人工局部阻尼加入系统,得到近场动力学求解准静态问题的控制方程:
| $ \mathit{\boldsymbol{ \boldsymbol{\varLambda} \ddot u}} + \mathit{\boldsymbol{C\ddot u}} + \mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{b}} $ | (9) |
式中:Λ为对角密度矩阵;C=dΛ为局部阻尼矩阵,d为阻尼系数;b为体积外力密度向量。为了获得方程(9)的稳态解,采用中心差分法求解,递推求解格式为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot u}}}^{1/2}} = \frac{{h{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{-1}}\left( {{\mathit{\boldsymbol{b}}^0}-\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{u}}^0}} \right)}}{2} + \frac{{\left( {2-dh} \right){{\mathit{\boldsymbol{\dot u}}}^0}}}{2}\;\;\;\;\left( {n = 0} \right)\\ {{\mathit{\boldsymbol{\dot u}}}^{n + 1/2}} = \frac{{\left( {2 - dh} \right)}}{{\left( {2 + dh} \right)}}{{\mathit{\boldsymbol{\dot u}}}^{n - 1/2}} + \frac{{2h{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{ - 1}}\left( {{\mathit{\boldsymbol{b}}^n} - \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{u}}^n}} \right)}}{{\left( {2 + dh} \right)}}\;\;\;\;\left( {n \ne 0} \right)\\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{u}}^{n + 1}} = {\mathit{\boldsymbol{u}}^n} + h{{\mathit{\boldsymbol{\dot u}}}^{n + 1/2}} \end{array} $ | (10) |
式中h表示时间步长。计算中每一步需要对稳定状态进行判断以决定是否结束递推计算。本文中,系统稳定状态的判断准则通过系统动能与势能的比值给出:
| $ \varepsilon = \frac{{\frac{1}{2}{{\left( {{{\mathit{\boldsymbol{\dot u}}}^{n-1/2}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{{\mathit{\boldsymbol{\dot u}}}^{n-1/2}}}}{{\frac{1}{2}{{\left( {{\mathit{\boldsymbol{u}}^n}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{L}}^n}}} \le {\varepsilon _{{\rm{tol}}}} $ | (11) |
求解格式(10)中需要确定密度矩阵Λ、阻尼系数d和时间步长h三个参数的取值。根据文献[10],这三个参数不影响稳态解,无须取实际值;因此,选取原则为保证算法以最少时间步数收敛。为了方便计算,时间步长h直接取为1 s。根据圆盘定理,对角虚拟密度矩阵Λ需要满足:
| $ {\lambda _{ii}} \ge \frac{{{h^2}}}{4}\sum\limits_{j = 1}^n {\left| {{K_{ij}}} \right|} $ | (12) |
式中:λii为密度矩阵Λ的对角元素;等效刚度矩阵K由物质点间的相互作用力对相对位移求偏导得到
| $ \sum\limits_{j = 1}^n {\left| {{K_{ij}}} \right|} = \sum\limits_{j = 1} {\left| {\frac{{\partial \mathit{\boldsymbol{f}}\left( {\xi, \eta } \right){V_j}}}{{\partial \eta }}} \right|} $ | (13) |
根据式(12)和(13),密度矩阵最终取为
| $ {\lambda _{ii}} = \frac{{{h^2}}}{4}\frac{1}{{\left| {{\xi _{{\rm{min}}}}} \right|}}c\alpha {V_\delta } $ | (14) |
式中:ξmin为物质点xi的最小键长,即与周围物质点的最小距离;Vδ为物质点近场范围体积; α≥1为安全系数,用以保证密度矩阵满足不等式(12)。
对于阻尼系数的选取,为了加快收敛速度,本文采取自适应阻尼方法,每一个时间步都计算出当前最佳收敛阻尼加入系统。根据文献[11],第n时间步的最佳阻尼为
| $ {d^n} = 2\sqrt {\left( {{{\left( {{\mathit{\boldsymbol{u}}^n}} \right)}^{{\rm{T1}}}}{\mathit{\boldsymbol{K}}^n}{\mathit{\boldsymbol{u}}^n}} \right)/\left( {{{\left( {{\mathit{\boldsymbol{u}}^n}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{u}}^n}} \right)} $ | (15) |
式中:1Kn对角局部刚度矩阵,1Kiin=-(Lin/λii-Ln-1i/λii)/
根据上述推导,编写Fortran程序,将准静态近场动力学算法实现。通过悬臂梁弯曲算例,与理论公式、有限元方法进行比较,验证算法的准确性和计算效率,并对阻尼系数的选取进行了讨论。
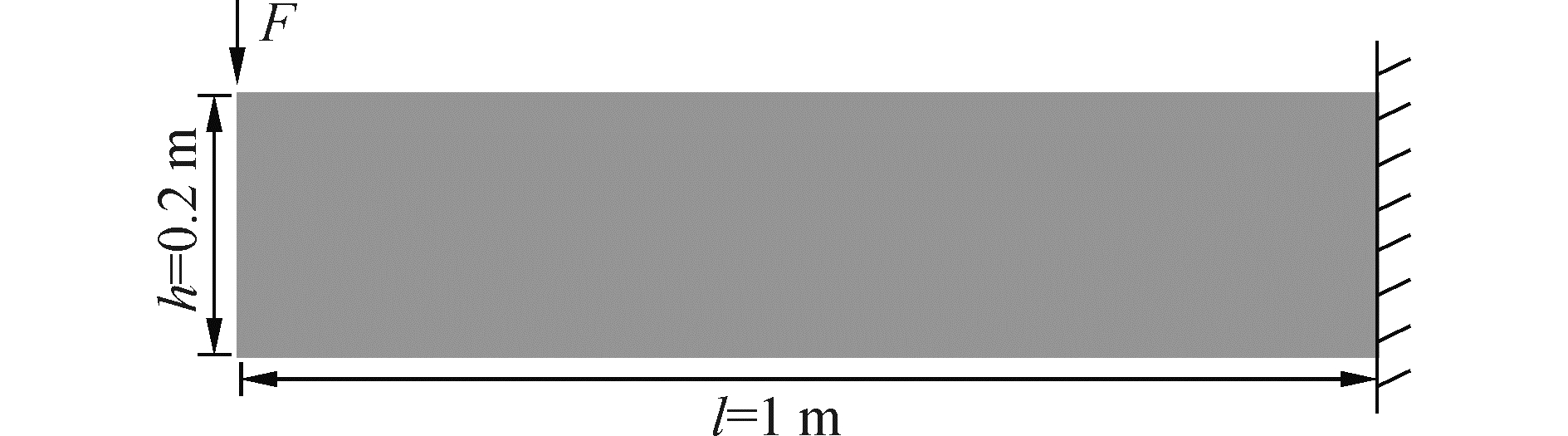
3.1 计算模型悬臂梁长1 m,高0.2 m,自由端受大小为1 000 N、垂直向下的集中力,如图 2所示。材料为均匀、各向同性的弹脆性材料,杨氏模量E=220 GPa,泊松比υ=1/4。
|
Download:
|
| 图 2 受集中力的悬臂梁 Fig. 2 A fixed support beam under concentrated force | |
近场动力学方法模拟中,模型均匀离散成225×45=10 125个物质点,相邻物质点间距为Δx=1/225 m,近场半径取δ=3Δx。悬臂梁右端以三层固定物质点作为虚拟边界层模拟固定位移边界;载荷施加在自由端顶部的物质点上,通过b=F/Vp,将集中力载荷转化为物质点体积力密度。中心差分法时间步长取h=1 s,虚拟密度矩阵和阻尼系数分别按式(14)和(15)计算,安全系数取α=1.2。有限元模拟采用ANSYS软件实现,计算参数、网格间距与近场动力学模型一致。
3.2 计算结果根据理论公式,考虑剪切挠度影响的悬臂梁自由端挠度为
| $ {u_z}\left( L \right) =-F\left( {\frac{{{L^3}}}{{3{\rm{EI}}}} + \frac{L}{{\kappa GA}}} \right) $ | (16) |
式中:G为剪切模量;κ为截面系数,当横截面为矩形时,κ取2/3。
表 1展示了数值模拟和理论公式计算得到的悬臂梁自由端挠度对比。可以看到,近场动力学与理论公式的误差仅为0.40%,计算结果相当接近于理论结果。
| 表 1 悬臂梁自由端挠度对比 Tab.1 Comparison of deflection at the end tip of cantilever beam |
两种数值模拟得到的竖直方向位移云图如图 3所示。可以看到,两种模拟方法的位移分布基本一致,由自由端到固定端,位移从最大位移逐渐减小到0;同一横截面上,两种模拟方法计算得到的位移基本相等。

|
Download:
|
| 图 3 悬臂梁竖直方向位移 Fig. 3 Displacement distribution of cantilever beam | |
为了说明动态松弛法的计算效率,本文同时采用近场动力学动态算法对算例进行模拟求解。按照近场动力学算法稳定性要求,时间步长取5.327×10-7 s,总时间步数nstep分别设置为1万、2万、5万、10万、20万,自由端载荷在这些时间步内均匀增加到1 000 N。
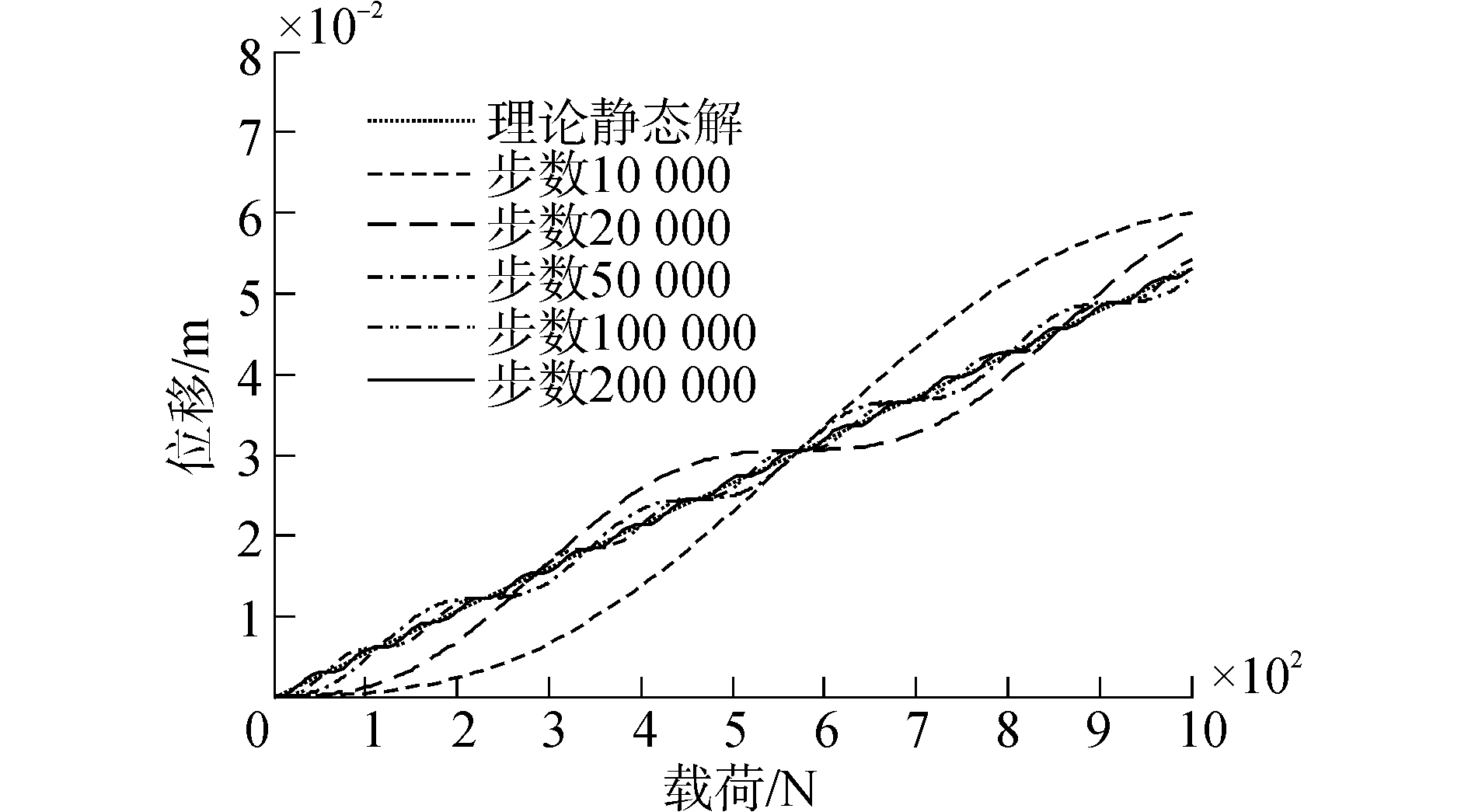
图 4展示了加载过程中载荷与自由端位移的关系曲线,并同理论静态解进行了比较。不难发现,nstep较小时,整个过程的模拟曲线与理论曲线有较大的偏离,此时位移变化率较大,加速度影响难以消除,因此无法准确描述准静态过程和结果;随着nstep的增大,位移变化速率变小,加速度影响逐渐消除,模拟曲线逐渐收敛于理论曲线,当nstep=200 000时,模拟曲线能够很好地逼近理论曲线。表 2展示了载荷施加到1 000 N时数值模拟与理论求解的结果对比,当nstep=10 000时,模拟结果与理论结果之间的误差较大,达到13.21%;随着nstep的增大,误差有减小的趋势,当nstep=200 000时,误差仅为0.14%,结果相当准确。
|
Download:
|
| 图 4 加载过程中载荷与位移的关系 Fig. 4 The force-deflection relationship during loading process | |
| 表 2 载荷1 000 N时模拟结果 Tab.2 Simulation results when loading 1 000 N |
由以上分析不难发现,采用动态算法求解静态或准静态问题时,计算准确度随着nstep的增大而提高;在nstep小于10万步时,无论是过程还是结果,动态方法都无法给出准确的模拟,因此必须使nstep大到一定程度才能够保证模拟结果的准确;相比之下,自适应动态松弛法仅需约12 000个时间步即可计算出准确结果,相比于动态算法大大提高了计算效率。
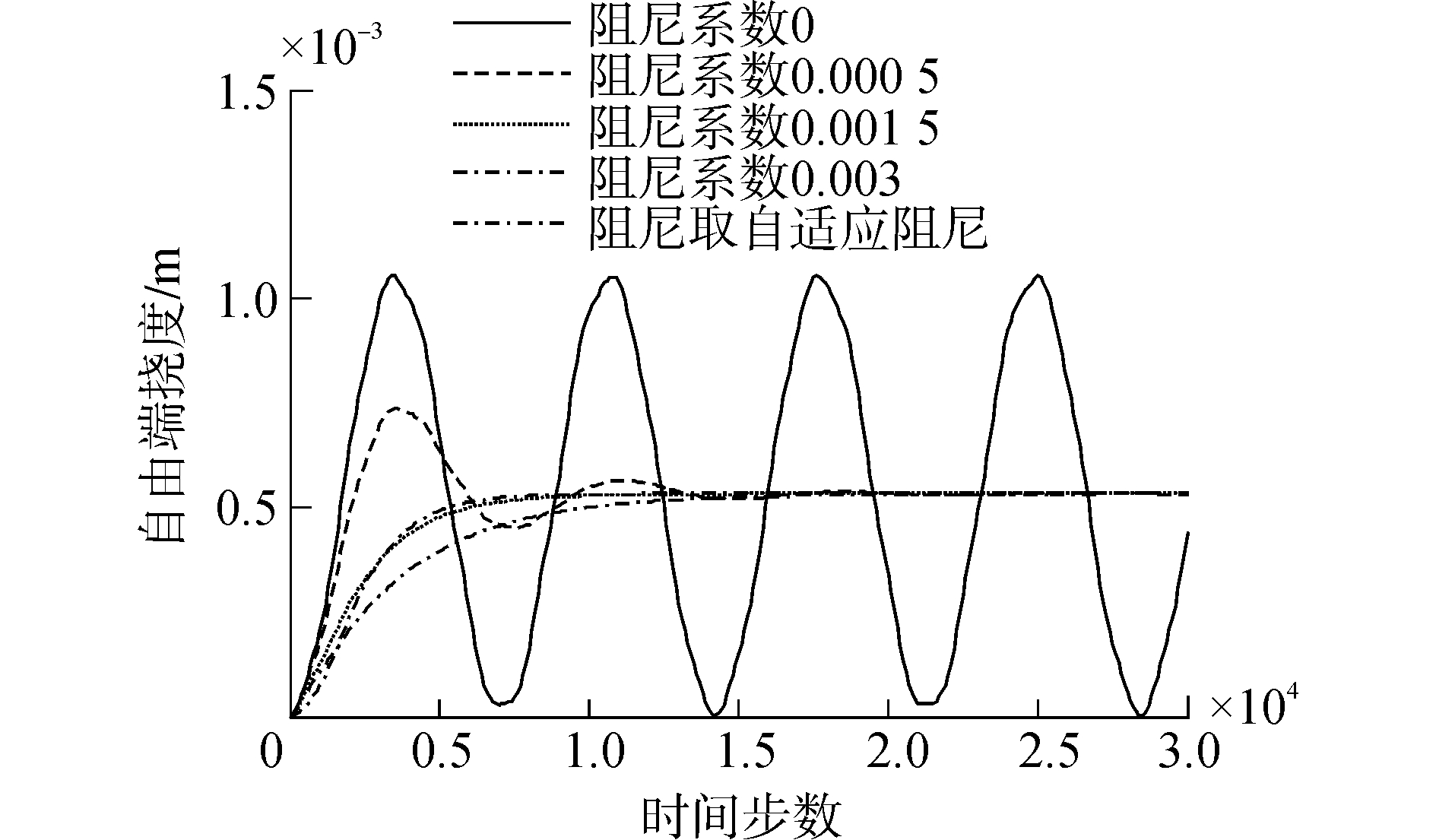
3.4 阻尼系数对收敛性的影响为了考察阻尼系数对准静态算法收敛性的影响,研究自适应阻尼方法与常阻尼方法的差异,采用常数阻尼对悬臂梁进行进一步模拟,常阻尼系数分别取0,0.000 5、0.001 5、0.003。绘制自由端挠度与时间步数的关系曲线如图 5所示。
|
Download:
|
| 图 5 悬臂梁自由端挠度与时间步数的关系 Fig. 5 Relationship between deflection and number of time steps | |
由图 5看到,d=0的无阻尼情况下,悬臂梁保持振动不衰减状态,算法无法收敛;对于d=0.000 5的欠阻尼状态和d=0.003的过阻尼状态,算法最终收敛但收敛速度缓慢;当d=0.001 5时,系统处于临界阻尼状态,收敛速度很快;本文采用的自适应阻尼方法,收敛曲线类似于临界阻尼,收敛速度快于临界阻尼。
4 冰三点弯曲数值模拟 4.1 试验试验使用的冰取自黑龙江省某湖泊,切割成650 mm×70 mm×70 mm的冰试样。试验前,试样放置于冷冻箱内恒温保存24 h以保证试样恒温。
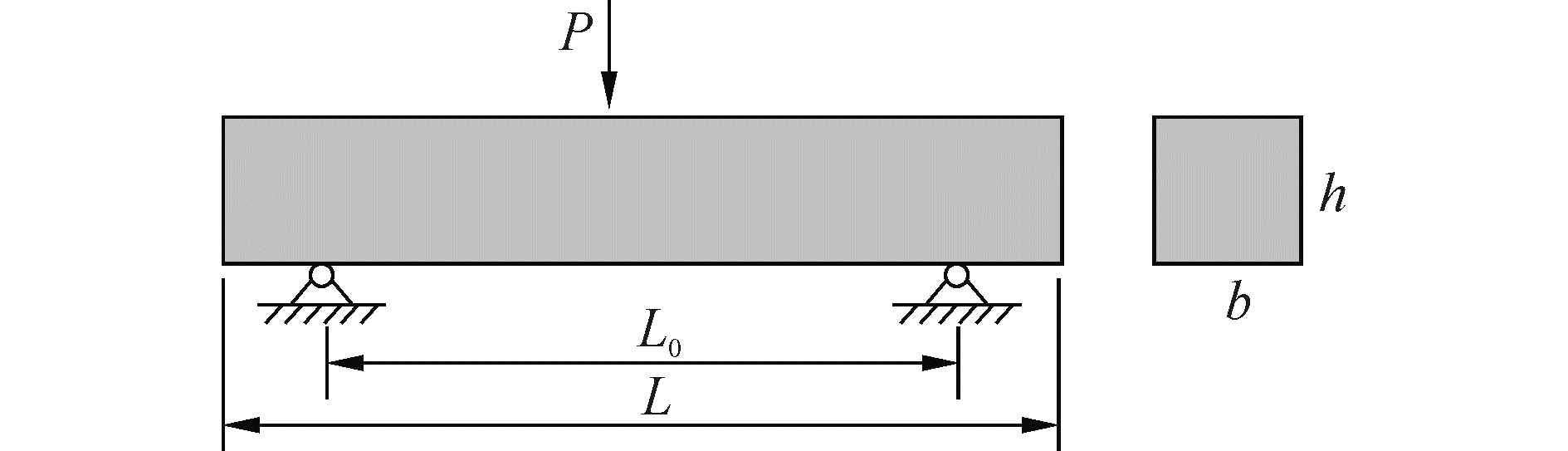
试验原理图如图 6所示,冰试样两端底部自由支持,支座之间距离L0=600 mm,上端中部受竖直载荷P的作用。如图 7所示,试验过程中缓慢增大载荷P,直至冰试样彻底破坏,记录下整个过程中载荷和位移随时间的变化关系。
|
Download:
|
| 图 6 三点弯曲试验原理图 Fig. 6 Schematic diagram of three-point bending test | |

|
Download:
|
| 图 7 三点弯曲试验装置 Fig. 7 Device of three-point bending test | |
本文所取试验组在冰温为10 ℃、应变速率为4.604×10-3的条件下进行试验。冰试样发生破坏时,记录得到:极限载荷为1 127.9 N,极限挠度为0.39 mm,加载历时共1.21 s。试样的杨氏模量的计算公式参考文献[12]:
| $ E = \frac{{P{L^3}}}{{4b{h^3}\delta }} $ | (17) |
式中:P、δ分别为极限载荷和极限挠度;L、b、h为试样的尺寸。计算得到试样杨氏模量为6.83 GPa。
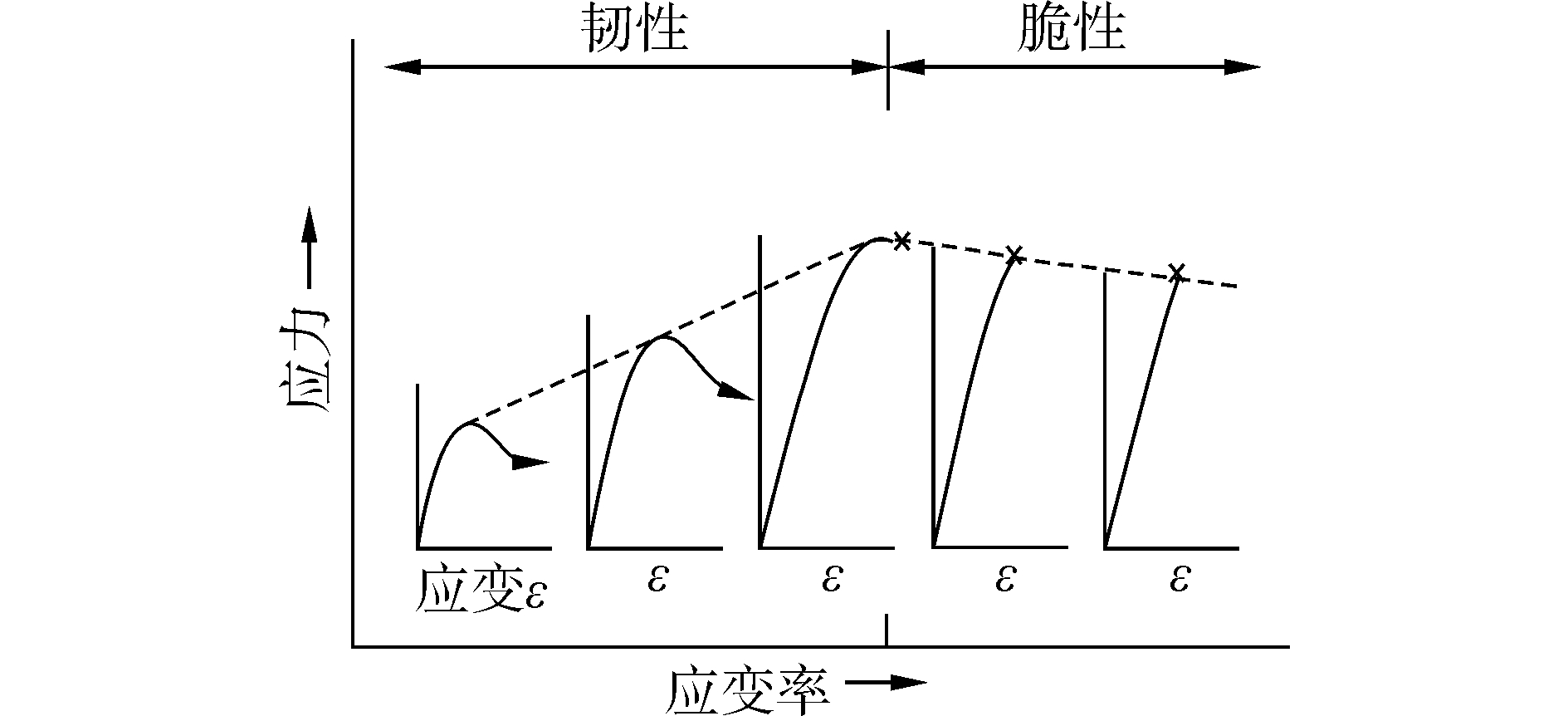
4.2 数值模拟 4.2.1 冰的弹脆性近场动力学模型冰在受力变形至破坏过程中,受加载速率的影响,会出现韧脆转换现象,当加载速度缓慢时,冰表现为韧性材料;高速加载时,冰表现为弹脆性材料[13]。冰力学行为随应变率的变化曲线如图 8所示。从图中可以看出,高应变率下的海冰行为类似于具有脆性破坏的线弹性材料。本文研究的对象是高应变率(应变率大于10-3 s-1)下的淡水冰,可以看作为线弹性材料。
|
Download:
|
| 图 8 冰的性质与应变率的关系 Fig. 8 Relationship between properties of ice and strain rate | |
冰材料近场动力学本构模型如图 9所示,在未破坏的伸长率范围内,物质点间的作用力与相对伸长率成线性关系,而一旦超出范围,连接键立刻发生破坏;考虑到冰的拉压异性,压缩极限伸长率设置为拉伸极限伸长率的4倍[14],即Sc=4St。

|
Download:
|
| 图 9 冰的近场动力学本构模型 Fig. 9 Peridynamic constitutive model of ice | |
数值模拟中,冰试样模型离散为65×7×7=3 185个物质点,相邻物质点间距为Δx=0.01 m,近场半径取δ=3Δx。
实际试验中,冰发生破坏前的加载过程持续1.21 s,按照近场动力学稳定性要求计算得到动态模拟的时间步长为1.65×10-6s,采用动态算法模拟该过程需要约73万个时间步,计算任务十分艰巨,本文采用近场动力学与动态松弛法结合的准静态算法高效解决这一问题。
需要注意的是,对于冰三点弯曲试验的模拟,准静态算法存在两个问题:一是由于算法加入人工阻尼,改变了运动方程,因而无法描述系统实际运动的具体过程;二是由于算法以进入稳定状态为目的,当系统不再进入稳定状态,比如发生破坏时,算法将无法求出正确结果。
针对准静态算法无法描述具体过程的问题,本文采用载荷-位移曲线描述变形过程,为此在运用准静态算法时采用分步加载的方法,通过求取加载过程中特定载荷下的位移得到载荷-位移曲线,从而实现对系统运动过程的描述。
对于准静态算法无法模拟破坏的问题,本文采取的策略是模型未发生破坏的加载过程采用准静态方法模拟,从而提高计算效率;而发生破坏之后采用动态算法进行模拟,从而发挥近场动力学模拟裂纹扩展的独特优势。由于冰模型极限载荷已知,采用准静态算法可以求出极限载荷下冰模型的位移场,在此位移场下微量增加载荷,模型将发生断裂破坏,依此设置极限伸长率s0=3.899×10-4,并采用近场动力学动态数值算法对这一破坏过程进行模拟。
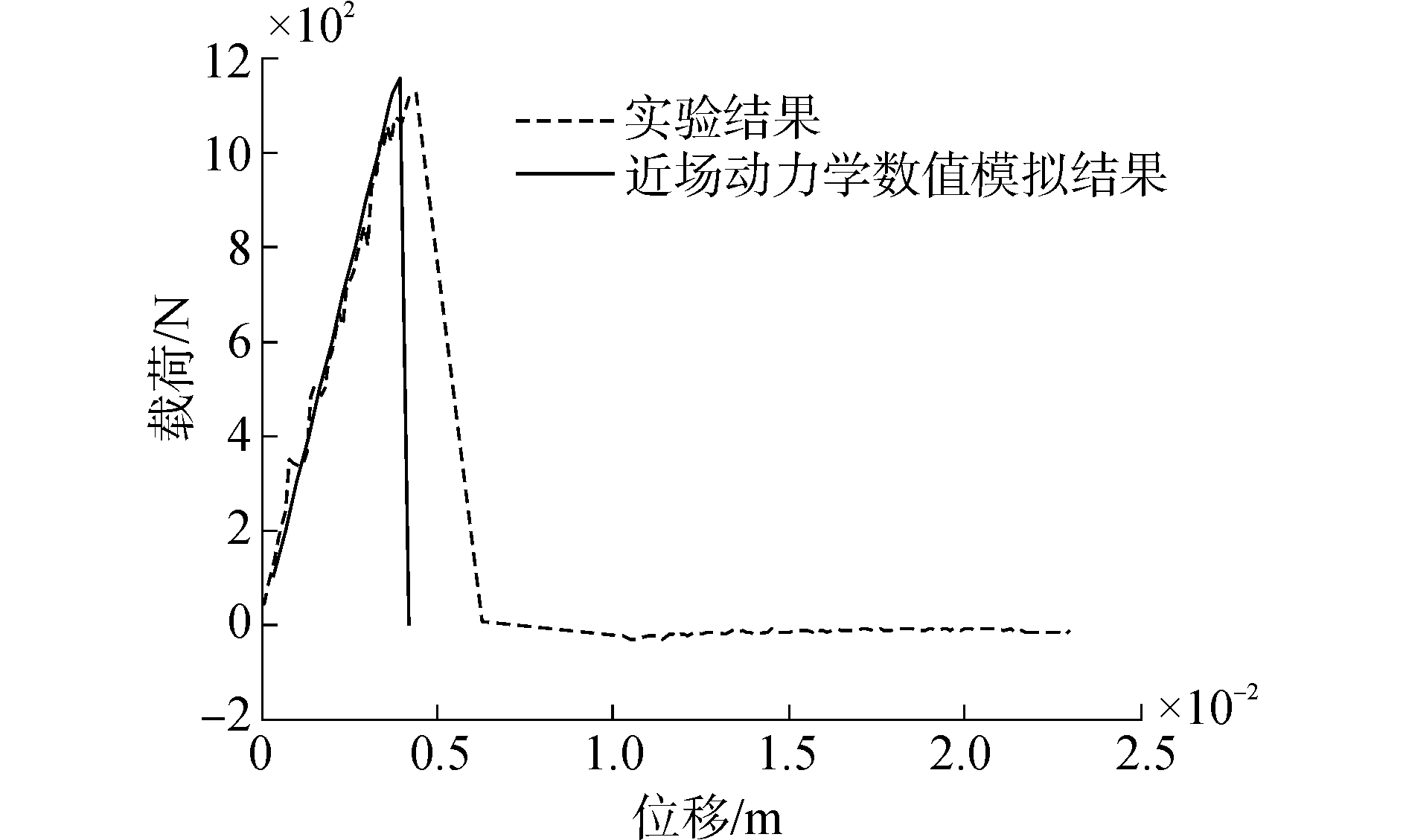
4.2.3 计算结果模拟过程和试验过程的载荷-位移曲线对比如图 10所示。数值模拟采用4.2.1节的弹脆性模型,变形阶段载荷与位移呈线性关系,达到极限载荷后,模型立即发生破坏,表现出脆性,模拟曲线与试验曲线趋势基本一致,变形过程相对误差小于5%。
|
Download:
|
| 图 10 载荷和位移关系 Fig. 10 Relationship between load and displacement | |
图 11展示了动态模拟破坏过程中模型损伤程度云图随时间的变化过程,裂纹从模型中部底端产生,在很短的时间内贯穿模型截面,最终折断模型,裂纹位置与折断结果与试验观察结果一致。

|
Download:
|
| 图 11 裂纹扩展过程 Fig. 11 Crack propagation process | |
模拟结果表明,冰的近场动力学弹脆性模型能够很好地模拟高加载速率下冰的变形与破坏行为,近场动力学在冰力学行为的数值模拟上具有可行性。
5 结论1) 本文将自适应动态松弛法引入近场动力学算法,提出了一种高效率的准静态算法,并通过算例证明了算法的准确性与高效性。
2) 建立的冰材料的近场动力学模型,对冰的三点弯曲变形和裂纹扩展进行了数值模拟研究,结果与试验结果吻合。
3) 近场动力学方法能很好地模拟冰材料变形过程和破坏过程而不需要为破坏产生引进任何外在的破坏准则,是数值研究冰力学行为的有效手段。
今后进一步的研究工作:将进一步考虑冰材料各向异性的影响,另外考虑采用基于GPU并行方式,提高数值计算效率。
| [1] |
SOUIYAH M, MUCHTAR A, ALSHOAIBI A, et al. Finite element analysis of the crack propagation for solid materials[J]. American journal of applied sciences, 2009, 6(7): 1396-1402. DOI:10.3844/ajassp.2009.1396.1402 (  0) 0)
|
| [2] |
WAGNER G J, MOËS N, LIU W K, et al. The extended finite element method for rigid particles in Stokes flow[J]. International journal for numerical methods in engineering, 2001, 51(3): 293-313. DOI:10.1002/nme.169 (  0) 0)
|
| [3] |
狄少丞, 季顺迎. 海冰与自升式海洋平台相互作用GPU离散元模拟[J]. 力学学报, 2014, 46(4): 561-571. DI Shaocheng, JI Shunying. GPU-based discrete element modelling of interaction between sea ice and jack-up platform structure[J]. Chinese journal of theoretical and applied mechanics, 2014, 46(4): 561-571. DOI:10.6052/0459-1879-13-400 (  0) 0)
|
| [4] |
SELVADURAI A P S, SEPEHR K. Two-dimensional discrete element simulations ofice-structure interaction[J]. International journal of solids and structures, 1999, 36(31/32): 4919-4940. (  0) 0)
|
| [5] |
SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the mechanics and physics of solids, 2000, 48(1): 175-209. DOI:10.1016/S0022-5096(99)00029-0 (  0) 0)
|
| [6] |
SILLING S, DEMMIE P, WARREN T L. Peridynamic simulation of high-rate material failure[C]//Proceedings of 2007 ASME Applied Mechanics and Materials Conference. Austin, TX, 2007.
(  0) 0)
|
| [7] |
ASKARI E, XU Jifeng, SILLING S. Peridynamic analysis of damage and failure in composites[C]//Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2006.
(  0) 0)
|
| [8] |
SILLING S A, ASKARI E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computers & structures, 2005, 83(17/18): 1526-1535. (  0) 0)
|
| [9] |
GERSTLE W, SAU N, SILLING S. Peridynamic modeling of plain and reinforced concrete structures[C]//Proceedings of the 18th International Conference on Structural Mechanics in Reactor Technology. Beijing, China, 2005: 54-68.
(  0) 0)
|
| [10] |
OAKLEY D R, KNIGHT N F JR. Adaptive dynamic relaxation algorithm for non-linear hyperelastic structures. I. Formulatio[J]. Computer methods in applied mechanics and engineering, 1995, 126(1/2): 67-89. (  0) 0)
|
| [11] |
BELYTSCHKO T, HUGHES T J R. Computational methods for transient analysis[M]. Amsterdam: North-Holland, 1983: 245-265.
(  0) 0)
|
| [12] |
HAN Hongwei, JIA Qing, HUANG Wenfeng, et al. Flexural strength and effective modulus of large columnar-grained freshwater ice[J]. Journal of cold regions engineering, 2016, 30(2). DOI:10.1061/(ASCE)CR.1943-5495.0000098 (  0) 0)
|
| [13] |
SCHULSON E M. Brittle failure of ice[J]. Engineering fracture mechanics, 2001, 68(17/18): 1839-1887. (  0) 0)
|
| [14] |
KARR D G, DAS S C. Ice strength in brittle and ductile failure modes[J]. Journal of structural engineering, 1983, 109(12). DOI:10.1061/(ASCE)0733-9445(1983)109:12(2802) (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


