日常生活中的很多问题都可以应用约束满足问题[1](constraint satisfaction problem, CSP)来建模表示从而解决,如配置、调度等问题[2];同时学术研究上的很多问题也可以模拟成约束满足问题进行求解,如空间图形表示硬件约束设计和正确性验证研究等,这使得约束满足问题在人工智能领域拥有着十分广泛的应用[3]。CSP的一个解就是给所有的变量在其论域范围内取值,使实例化的变量值组合能满足给定的所有约束[4]。
尽管判断一个CSP是否有解是NP-难问题,但仍有很多对CSP求解的优秀算法[5]。在已有的约束传播技术中,弧相容(AC)出现的最早,也是应用最为广泛的方法[6]。AC3是由Mackworth提出的经典的粗粒度算法,它给出了粗粒度算法的框架[7],即粗粒度算法主要由基本框架和修正检查两部分构成[8]。
本文从框架角度解析了粗粒度弧相容算法的模式, 总结了它们共同的缺陷,即AC3算法、AC2001算法、AC3rm算法的可改进处——那些无效的修正检查[9]。这种冗余的修正检查在弧相容预处理过程中很少出现,而在求解过程中出现较为频繁,为此本文提供一种利用哈希值迅速确定弧是否已经存在于队列中的方法, 避免了这类冗余的弧放回动作, 给出改进后的粗粒度算法的基本框架AC_ArcOnly(AC_AO)可以用于改进目前所有的粗粒度AC算法。最后, 将AC_AO框架应用到AC3、AC2001、AC3rm算法中进行了优化。
1 约束背景知识定义1 约束可满足问题
约束可满足问题(CSP)<X, D, C>包括3部分:变量集X={X1, X2, …, Xn}由n个变量组成;D={D(X1), D(X2), …, D(Xn) }是变量域构成的集合,其中D(Xi)表示变量Xi对应的变量域;C={c1, c2, …, ce}是由e个约束组成的约束集合[10]。
图 1中表示了一个约束满足问题,此CSP有4个变量,X0、X1、X2、X3,变量X0的论域为{0、1、2},变量X1、X2、X3的论域为{0、1}, 3个约束C0、C1、C2表示了变量之间的约束关系,图中的连线表示支持,如X0中的值1与X1中的值0互为支持。图 1(b)表示此CSP问题的解。
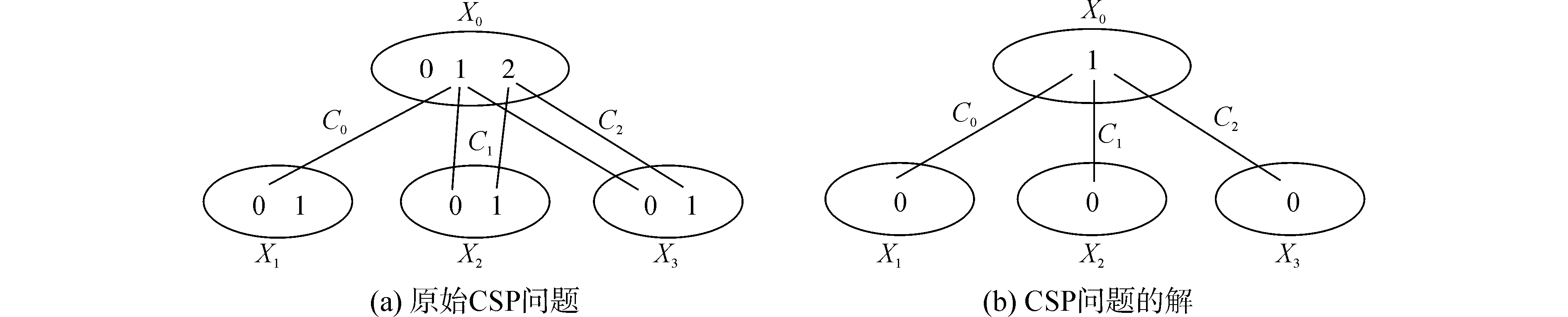
|
Download:
|
| 图 1 CSP问题求解示意图 Fig. 1 CSP problem solving diagram | |
定义2 弧相容(arc consistency, AC)
给定一个二元约束满足问题P, 对于P中的某一条弧(x, Cxy), 如果x值域中的每一个值a都能在y的值域中找到一个值b, 使得(a, b)满足Cxy, 那么称弧(x, Cxy)是弧相容的。一个CSP是弧相容的, 当且仅当它的每一条弧都是弧相容的[11]。
定义3 哈希算法
哈希(Hash)算法, 即散列函数。哈希函数可以将任意长度的输入经过变化以后得到固定长度的输出。
哈希函数是一种单向密码体制, 即它是一个从明文到密文的不可逆的映射, 只有加密过程, 没有解密过程。哈希函数的这种单向特征和输出数据长度固定的特征使得它可以生成消息或者数据。
定理1 已知素数λ, 正整数z(z<λ, z∈N),则针对不同的z有:nλ+z(n, z=0, 1, 2…)所构成的新的数列中的值互不相同。
证明:反证法,若存在n1、n2、z1、z2使得n1λ+z1=n2λ+z2, 则(n1-n2)λ=z2-z1, 因为n1≠n2,所以等式的左边是λ的整数倍,则等式右边一定也是λ的整数倍,而0<z1<λ, 0<z2<λ, -λ<z2-z1<λ, 只能有z2-z1=0,矛盾。假设不成立,原命题成立。
本文用哈希算法生成了弧的唯一的标识,即弧的序列号,既保证了弧序号的唯一性,又能更快地算出弧的序列号,是唯一性保证的基础条件。具体操作是选择一个5位的素数,将此素数与弧中变量x的序列号相乘所得的结果加上约束c的序列号,由于变量的序列号和约束的序列号都是从零开始的流水号,因而,只要约束满足问题约束的条数不超过此素数,就不会有重复的可能,而现实意义下的研究中,一般约束的条数都不过万,因而在实际意义下,此方法产生的哈希值是唯一的。若极特殊问题,约束的条数非常多,则相应扩大素数即可。如假设有2万条约束,那么就选择一个6位的素数,即可保证弧的序列号唯一性。
2 AC框架 2.1 AC算法算法1为粗粒度AC算法的基本框架[12]。其中, Q是待传播队列, 保存所有需要执行修正检查的弧; initialize Q是初始化待传播队列, 如果AC算法用于求解前预处理阶段, 则要将问题中所有的弧加入Q来实现initialize Q。在弧相容检查过程中, 如果有变量的值域改变, 则将从这个变量发出的所有弧加入Q, 对这些弧重新执行修正检查。如果检查过程中发现某一个变量值域为空, 则返回检查失败; 否则, 当Q为空时, 弧相容检查成功。
Algorithm1: AC_frame
begin
initialize Q;
while Q is not empty do
select and remove the arc(xi, c) from Q;
if revise(xi, c) then
if Di= Ø then return fail;
else for each c′ such that xi, xj∈X(c′)
if c′≠c then
Q←Q∪(xj, c′);
return success;
End
本文对经典的弧相容算法AC3算法和当前流行的AC2001算法、AC3rm算法进行前后对比测试,它们都适用于AC框架,不同之处在于它们的修正函数,即算法2 revise3, 算法3 revise2001, 算法4 revise3rm。
图 1(a)中的示例执行的过程是:初始化后,队列Q中弧的条数为6条,是约束个数的2倍。求解过程中,队列Q的长度大于6,则必然有至少一条弧重复存在于队列Q中。算法1执行完第1行后,Q={(x0, c0), (x1, c0), (x0, c1), (x2, c1), (x0, c2), (x3, c2)},执行第2~8行的while循环一次,Q={(x1, c0), (x0, c1), (x2, c1), (x0, c2), (x3, c2),(x0, c0),(x0, c1), (x0, c2)},其中弧(x0, c1), (x0, c2)在队列Q中出现了两次,而出现在后面的两次检查属于检查后的例行检查,毫无意义。因而删掉这种冗余的弧,减少冗余弧的放回,将会减少修正检查,从而提高算法效率。
通过分析,可以得出结论:CSP问题中约束的数目为a,那么初始化后队列Q中的弧的总数为2a条,弧用字母r来表示,则Q={r0, r1, …, r2a-1},r0…r2a-1互不相同,将Q赋予集合的性质,始终保持Q的状态是初始化状态的子集,保持唯一性,避免了检查冗余不必要的弧,就能够缩短求解时间,提高效率。
算法2 revise3是AC3的修正检查过程[13],其中D[x]是x的有限值域,revise3(x, c)是为变量x值域中所有未被删除的值寻找支持,如果产生删值,则返回为真,如果变量的论域被删空,那么弧相容求解失败。
Algorithm2: procedure revise3(x, c)
begin
change←false
for each v belong to D[x], do
if v has no support on c then
remove v from D[i]
change=true;
return change
end
算法3 revise 2001是AC2001的修正检查过程[14],引入了一个last数据结构,记录变量最新的支持,last[c][x][v]表示变量x在约束c和赋值为v的条件下的支持值。检查变量时,优先检查last中的值是否为支持,如果是支持,则不继续检查,如果是不支持,那么从last中的变量中的值开始循环遍历所有值,直到找到支持,并且更新此变量的last数据结构为当前最新支持的值。
Algorithm3: procedure revise2001(x, c)
begin
change←false
for each v belong to D[x], do
if (last[c][x][v]is valid)
continue
if v has no support on c then
remove v from D[i]
change=true
update last[c][x][v]
return change
end
算法4 revise3rm是AC3rm的修正检查过程[15],与revise2001不同的是,在更新last数据结构的时候,不单单更新当前的变量的最新支持值,并且根据约束的双向支持性[16],将变量x的支持值v对应的变量y的支持值b同时进行更新,提高求解效率。
Algorithm4: procedure revise3rm(x, c)
begin
change←false
for each v belong to D[x], do
if (last[c][x][v]is valid)
continue
if v has no support on c then
remove v from D[i]
change=true
update last[c][x][v] and last[c][y][b]
return change
end
从算法中不难看出AC算法执行的主体部分就是在队列Q不为空的前提下,不断从队列Q中取出一条弧,进行一系列的操作,如果被检查的弧减少了,产生的效率提升将是明显的,减少一条弧的检查,意味着减少一次修正检查和修正检查后的一系列判断操作以及放回操作。被检查的弧减少,意味着AC系列算法效率的提高。
2.2 AC_AO算法在AC算法中,队列Q中保存的数据结构是弧arc(x, c),初始化时,将所有弧都放入队列中,弧的总数是约束个数的2倍。改进算法为每条弧分配一个编号,编号的产生是哈希的,此哈希可以保证编号的唯一性。AC算法中,revise函数返回为真时,常常要把一些弧重新放回队列,改进后的算法不再将队列中已经存在的弧放回,只放回那些队列中此时不存在的弧。减少了弧的放回,减少AC算法检查弧的条数,提高了AC算法的执行效率。
3 改进后的AC框架AC_AO算法AC_AO在构造弧的数据结构时,计算完成了弧的序列号,即弧的id。算法AC_AO使用一个队列q单独存储弧的id,这样可以方便检查弧是否在队列中,q与Q的动作是同步的。arc(x, c)_id表示弧(x, c)的id。在弧放回的时候,检查此弧是否在队列q中存在,判断方法是:将自身弧的变量x和变量c的序列号经过哈希计算得到它的弧id,并判断此id是否在队列q中,如果在,那么不放回此弧;若不在队列q中,q中放入此弧的id,Q中放入此弧。
Algorithm5: AC_AO frame
begin
initialize Q
initialize q;
while q is not empty do
select and remove the arc_id from q
select and remove the arc(xi, c) from Q
if Revise(xi, c) then
if Di= Ø then return fail
else for each c′ such that xi, xj∈X(c′)
if c′≠c then
if arc(xj, c′)_id not in q
q←q∪arc(xj, c′)_id
Q←Q∪(xj, c′)
return success
end
定理2 算法5是正确性的。
证明:采用R表示Q中的弧,r表示q中对应的弧的id,a表示约束的个数,执行算法5第1行和第2行。初始化后的结果是Q={R0,R1,…, R2 a-1}, q={r0, r1, …, r2 a-1}, 其中ri是与Rri一一对应的。进入第3行的while循环后,每当从q中取出ri时,随之从Q中取出Ri, 循环中每次执行第4、5行时,Q与q都是一一映射的,当q为空时,Q一定为空。每次执行到第6行,对弧进行修正检查,如果某个变量Xi的值域被删空时,返回弧相容失败,否则,进行第8行的else语句,将与本次检查相关的所有其他约束对应的弧放回到队列中,放回前在算法的第10行判断将要放回的弧id是否在q中,这个判断是哈希判断,O(1)的时间代价,如果在q里,那么不必放回,反之,则将此弧的id放入q中,将弧放入Q中,如算法的第11、12行。整个算法的进行,保证了Q与q的一一映射,保证了算法的正确性。
由此,可得出当一个CSP问题的约束个数为a时,初始化后Q中弧的条数必为2a,如果与之相对应创建一个q,使得元素一一对应,在运行算法的时候,对应的Ri和ri保持同步,那么对Ri存在性的判断可转化为对ri的判断。
AC_AO在AC基础框架上,通过鸽巢原理可知,当队列中弧的数目大于弧的序列号总数,必然产生弧的重复,由不放回队列中已经存在弧的正确性证明可知冗余的弧可以唯一,并且不影响正确求解。由此,保持弧的唯一性,可以减少检查弧的条数,提高算法效率。
4 AC_AO算法与AC系列算法的Benchmark测试用例对比表 1~3中展示了AC系列算法和与之相对应的AC_AO算法在约束传播过程中处理对应问题时检查弧的总条数的对比。
| 表 1 AC3与AC3_AO检查弧总数对比 Tab.1 Comparison of check the total number of arc between AC3 and AC3_AO |
| 表 2 AC3与AC3_AO检查弧总数对比 Tab.2 Comparison of check the total number of arc between AC3 and AC3_AO |
| 表 3 AC3rm与AC3rm_AO检查弧总数对比 Tab.3 Comparison of check the total number of arc between AC3rm and AC3rm_AO |
表 4~6中展示了AC系列算法和与之相对应的AC_AO算法在约束传播过程中,CPU运行时间的对比情况。
| 表 4 AC3与AC3_AO CPU时间对比 Tab.4 Comparison of CPU time between AC3 and AC3_AO |
| 表 5 AC2001与AC2001_AO CPU时间对比 Tab.5 Comparison of CPU time between AC2001 and AC2001_AO |
| 表 6 AC3rm与AC3rm_AO CPU时间对比 Tab.6 Comparison of CPU time between AC3rm and AC3rm_AO |
实验结果表明,改进后的算法中弧检查次数比改进前的算法减少了64%~77%,CPU提速10%~30%优化效果比较明显。
通过实验数据可以看出,由于变量产生删值引起的约束传播,进而导致队列中的弧出现了大量的冗余,经过弧的唯一性处理后,减小了弧的冗余放回,进而减少了修正检查次数,提高了求解的效率。AC3的弧传播次数比AC2001少,而AC2001的弧传播次数比AC3rm少,因而在相同测试用例下,弧的条数是递减的次序,而弧的唯一性的优化着眼于队列中弧的唯一性,队列中弧的条数与放回弧的条数正相关,AC系列算法的不同在于revise函数的不同,因而具有普适性。
实验结果表明,粗粒度弧相容算法,无论是轻量级的算法还是重量级的算法,队列中都存在着大量的冗余弧,保存队列中弧的唯一性,能够大幅度减少冗余弧,弧的修正检查次数减少,提高求解效率。
5 结论1) AC系列算法应用AC_AO框架在复杂度高的约束满足问题上执行效率更高。
2) AC_AO框架在规模大的约束满足问题上执行效率更高。
3) 可以将本文提出的保持弧的唯一性以避免大量的冗余检查的思想应用在其他粗粒度求解约束满足问题的算法系列中,以减少冗余检查,提高效率。
| [1] |
ROSSI F, VAN BEEK P, WALSH T. Handbook of constraint programming[M]. Amsterdam, Netherlands: Elsevier Science, 2006: 26-49.
(  0) 0)
|
| [2] |
ZHOU Jianwei. Improved optimal conditions and iterative parameters for the optimal control problems with an integral constraint in square[J]. Journal of computational and applied mathematics, 2016, 307: 367-373. DOI:10.1016/j.cam.2015.12.014 (  0) 0)
|
| [3] |
HAN Jiangfeng, MIGÍRSKI S. A quasistatic viscoelastic frictional contact problem with multivalued normal compliance, unilateral constraint and material damage[J]. Journal of mathematical analysis and applications, 2016, 443(1): 57-80. DOI:10.1016/j.jmaa.2016.05.012 (  0) 0)
|
| [4] |
MACKWORTH A K. Consistency in networks of relations[J]. Artificial intelligence, 1977, 8(1): 99-118. DOI:10.1016/0004-3702(77)90007-8 (  0) 0)
|
| [5] |
CAI Shaowei, SU Kaile. Local search for Boolean Satisfiability with configuration checking and subscore[J]. Artificial intelligence, 2013, 204: 75-98. DOI:10.1016/j.artint.2013.09.001 (  0) 0)
|
| [6] |
CHOI C W, LEE J H M, STUCKEY P J. Removing propagation redundant constraints in redundant modeling[J]. ACM transactions on computational logic, 2007, 8(4): 23. DOI:10.1145/1276920 (  0) 0)
|
| [7] |
BOUSSEMART F, HEMERY F, LECOUTRE C. Revision ordering heuristics for the Constraint Satisfaction Problem[C]//Proceedings of the 1st International Workshop on Constraint Propagation and Implementation held with CP'04(CPAI'04). Toronto, Canada, 2004: 9-43.
(  0) 0)
|
| [8] |
LEE J H M, ZHU Zichen. Boosting SBDS for partial symmetry breaking in constraint programming[C]//Proceedings of the 28th AAAI Conference on Artificial Intelligence (AAAI 2014). Québec City, Québec, Canada, 2014: 2695-2702. http://dl.acm.org/citation.cfm?id=2892925
(  0) 0)
|
| [9] |
MEHTA D, VAN DONGEN M R C. Reducing checks and revisions in coarse-grained MAC algorithms[C]//Proceedings of the 19th International Joint Conference on Artificial Intelligence. Edinburgh, UK, 2005: 236-241. http://dl.acm.org/citation.cfm?id=1642331
(  0) 0)
|
| [10] |
LEE J H M, LEUNG K L. A stronger consistency for soft global constraints in weighted constraint satisfaction[C]//Proceedings of the 24th AAAI Conference on Artificial Intelligence (AAAI-2010). Atlanta, USA, 2010: 121-127. https://www.researchgate.net/publication/221604924_A_Stronger_Consistency_for_Soft_Global_Constraints_in_Weighted_Constraint_Satisfaction
(  0) 0)
|
| [11] |
LECOUTRE C. Constraint networks:techniques and algorithms[M]. Great Britain, Narendra Jussien, United States: Wiley, 2009: 185-236.
(  0) 0)
|
| [12] |
JAVED K, GOURIVEAU R, ZERHOUNI N, et al. Prognostics of proton exchange membrane fuel cells stack using an ensemble of constraints based connectionist networks[J]. Journal of power sources, 2016, 324: 745-757. DOI:10.1016/j.jpowsour.2016.05.092 (  0) 0)
|
| [13] |
王瑞伟, 李占山, 李宏博. 求解约束可满足问题的eSTR算法优化[J]. 计算机研究与发展, 2016, 53(7): 1586-1595. WANG Ruiwei, LI Zhanshan, LI Hongbo. Optimizing eSTR algorithm for solving constraint satisfaction problems[J]. Journal of computer research and development, 2016, 53(7): 1586-1595. DOI:10.7544/issn1000-1239.2016.20150284 (  0) 0)
|
| [14] |
王涛, 张乾, 李占山, 等. 基于成功回溯的约束推理技术[J]. 吉林大学学报(工学版), 2016, 46(5): 1622-1626. WANG Tao, ZHANG Qian, LI Zhanshan, et al. Reasoning from successful backtracking in constraint programming[J]. Journal of Jilin University (engineering and technology edition), 2016, 46(5): 1622-1626. (  0) 0)
|
| [15] |
李宏博, 梁艳春, 李占山. 概率最大受限路径相容算法[J]. 软件学报, 2015, 26(12): 3140-3150. LI Hongbo, LIANG Yanchun, LI Zhanshan. Probabilistic max restricted path consistency[J]. Journal of software, 2015, 26(12): 3140-3150. (  0) 0)
|
| [16] |
李宏博, 李占山, 王涛. 改进求解约束满足问题粗粒度弧相容算法[J]. 软件学报, 2012, 23(7): 1816-1823. LI Hongbo, LI Zhanshan, WANG Tao. Improving coarse-grained arc consistency algorithms in solving constraint satisfaction problems[J]. Journal of software, 2012, 23(7): 1816-1823. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


