2. 哈尔滨移动公司 无线优化室, 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨 150001
2. Wireless optimization Room, Harbin Mobile Communication Company, Harbin 150001, China;
3. College of Automation, Harbin Engineering University, Harbin 150001, China
风力发电作为应对能源危机与环境问题的重要手段, 目前已成为国内外学者研究的热点[1-4]。大型风电机组可以为国家电网补充电力, 也可以与其他能源技术组成互补发电; 而小型风电机组可以为边远地区提供生产、生活用电, 是孤岛发电、微电网系统、分布式发电等方面的研究热点。而风能的随机性、间歇性和电能质量的苛刻要求使风力发电控制系统面临巨大的挑战。风能转换系统是一个高度非线性、时变的系统, 极不稳定的输入激励, 严重影响系统的稳定性, 在运行范围内对系统的动态性能产生了不可忽视的影响, 常规线性控制方法难以处理风电机组中存在的非线性耦合和不确定因素作用, 因此出现了LQG控制[5]、反馈线性化控制[6]、H∞控制[7]、模糊控制[8]、神经网络控制[9]等一些新的设计思想。虽然这些控制方法在不同程度上提高了风能转换系统的控制特性, 但仍存在控制器阶数较高、计算量大、实现困难等问题。滑模控制是一种鲁棒控制方法, 它非常适用于处理非线性、时变、不确定和扰动等模型失配问题, 由于其具有动态鲁棒性和参数的不确定性, 所以不需要得到系统的精确数据。文献[10]提出了一种基于滑模控制的最大风能追踪方法, 该方法在不依赖风速的情况下, 建立了滑动平面推导出滑模控制率, 实现了最大风能追踪。但此方法所采用的滑模控制存在的抖振会引起机械应力的增加, 限制了其应用。为了解决传统的滑模控制给系统带来的抖振问题, 经常使用积分滑模控制和区间有界的滑模控制技术, 但都是以闭环系统的鲁棒性为代价。
综上所述, 国内外学者对风能转换系统开展了许多关于优化控制方法的研究, 但还少见利用滑模的鲁棒性和预测控制的约束优化相结合的控制方法。针对低功率刚性传动链双馈感应发电机风能转换系统, 本文从改善闭环的动态特性, 降低系统的复杂程度的角度出发, 基于双频环优化控制结构, 运用滑模预测控制实现了在部分负荷状态下的能量转换最大化, 并通过仿真验证了所提方法的稳定性和有效性。
1 WECS的数学模型风能转换系统(wind energy conversion system, WECS)的能量转换链从系统的角度看可以分为四个相互作用的组成部分:空气动力子系统(风力机)、电磁系统的连接单元驱动器(传动系统)、电磁子系统(发电机)和电网, 其结构框图如图 1所示。

|
Download:
|
| 图 1 风能转换系统结构框图 Fig. 1 Structural diagram of WECS systems | |
风速的动态模型是结合具体地点的特殊气象条件建立起来的, 因此风速模型是一个动态随机过程, 由两个部分叠加而成:
| $ v\left( t \right) = {v_s}\left( t \right) + {v_t}\left( t \right) $ | (1) |
式中:vs(t)是长期缓慢变化的低频部分, vt(t)是快速高频变化的湍流部分。
风力机的叶尖速度比是表示叶片速度与风速之比的一个变量, 它由λ来表示:
| $ \lambda = \frac{{R{\mathit{\Omega }_1}}}{v} $ | (2) |
式中:R是叶片长度, Ωl是风轮角速度(低速轴角速度), v是风速。
风力机的捕获功率可以表示为
| $ {P_{{\rm{Wt}}}} = \frac{1}{2}\rho {\rm{ \mathit{ π} }}{R^2}{v^3}{C_{\rm{p}}}\left( \lambda \right) $ | (3) |
式中:ρ为空气密度, Cp(λ)为功率系数。
在WECS中, 发电机与传动机构相连, 因此高速轴的运动方程表达式为
| $ J\frac{{{\rm{d}}{\mathit{\Omega }_{\rm{h}}}}}{{{\rm{d}}t}} = {T_{{\rm{mec}}}} - {T_{\rm{G}}} $ | (4) |
式中:J是高速轴的转动惯量, Ωh是高速轴的旋转角速度, Tmec是机械转矩, TG是电磁转矩。
双馈感应发电机在(d, q)坐标下的电磁转矩方程为
| $ {T_{\rm{G}}} = \frac{3}{2}p{L_{\rm{m}}}\left( {{i_{{\rm{Sq}}}}{i_{{\rm{Rd}}}} - {i_{{\rm{Rq}}}}{i_{{\rm{Sd}}}}} \right) $ | (5) |
式中:p是极对数, Lm是定转子互感, iSd、iSq、iRd、iRq分别是定、转子在(d, q)轴坐标下的电流分量, 则
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{i_{{\rm{Sd}}}}}}{{{\rm{d}}t}} = \frac{{{V_{{\rm{Sd}}}}}}{{{L_{\rm{S}}}}} - \frac{{{R_{\rm{S}}}}}{{{L_{\rm{S}}}}}{i_{{\rm{Sd}}}} - \frac{{{L_{\rm{m}}}}}{{{L_{\rm{S}}}}}\frac{{{\rm{d}}{i_{{\rm{Rd}}}}}}{{{\rm{d}}t}} + {\omega _{\rm{S}}}\left( {{i_{{\rm{Sq}}}} + \frac{{{L_{\rm{m}}}}}{{{L_{\rm{S}}}}}{i_{{\rm{Rq}}}}} \right)\\ \frac{{{\rm{d}}{i_{{\rm{Sq}}}}}}{{{\rm{d}}t}} = \frac{{{V_{{\rm{Sq}}}}}}{{{L_{\rm{S}}}}} - \frac{{{R_{\rm{S}}}}}{{{L_{\rm{S}}}}}{i_{{\rm{Sq}}}} - \frac{{{L_{\rm{m}}}}}{{{L_{\rm{S}}}}}\frac{{{\rm{d}}{i_{{\rm{Rq}}}}}}{{{\rm{d}}t}} - {\omega _{\rm{S}}}\left( {{i_{{\rm{Sd}}}} + \frac{{{L_{\rm{m}}}}}{{{L_{\rm{S}}}}}{i_{{\rm{Rd}}}}} \right)\\ \frac{{{\rm{d}}{i_{{\rm{Rd}}}}}}{{{\rm{d}}t}} = \frac{{{V_{{\rm{Rd}}}}}}{{{L_{\rm{R}}}}} - \frac{{{R_{\rm{R}}}}}{{{L_{\rm{R}}}}}{i_{{\rm{Rd}}}} - \frac{{{L_{\rm{m}}}}}{{{L_{\rm{R}}}}}\frac{{{\rm{d}}{i_{{\rm{Sd}}}}}}{{{\rm{d}}t}} + \left( {{\omega _{\rm{S}}} - \omega } \right)\left( {{i_{{\rm{Rq}}}} + \frac{{{L_{\rm{m}}}}}{{{L_{\rm{R}}}}}{i_{{\rm{Sq}}}}} \right)\\ \frac{{{\rm{d}}{i_{{\rm{Rq}}}}}}{{{\rm{d}}t}} = \frac{{{V_{{\rm{Rq}}}}}}{{{L_{\rm{R}}}}} - \frac{{{R_{\rm{R}}}}}{{{L_{\rm{R}}}}}{i_{{\rm{Rq}}}} - \frac{{{L_{\rm{m}}}}}{{{L_{\rm{R}}}}}\frac{{{\rm{d}}{i_{{\rm{Sq}}}}}}{{{\rm{d}}t}} - \left( {{\omega _{\rm{S}}} - \omega } \right)\left( {{i_{{\rm{Rd}}}} + \frac{{{L_{\rm{m}}}}}{{{L_{\rm{R}}}}}{i_{{\rm{Sd}}}}} \right) \end{array} \right. $ | (6) |
式中:ω是角速度, ω=pΩh, Ωh是发电机的旋转角速度; ωS是定子的场频(rad/s), ωS=dθS/dt; RS、RR分别是定子电阻和转子电阻; LS、LR分别是定子和转子的电感; VSd、VSq、VRd、VRq分别是在(d, q)坐标下的定子和转子电压分量, ΦRd、ΦRq分别是在(d, q)坐标下的转子磁通分量, ΦRd=LRiRd, 令
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}&{{x_2}\left( t \right)}&{{x_3}\left( t \right)}&{{x_4}\left( t \right)} \end{array}} \right]^{\rm{T}}} = \\ \;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {{i_{{\rm{Sd}}}}}&{{i_{{\rm{Sq}}}}}&{{i_{{\rm{Rd}}}}}&{{i_{{\rm{Rq}}}}} \end{array}} \right]^{\rm{T}}}\\ \mathit{\boldsymbol{u}} = {\left[ {\begin{array}{*{20}{c}} {{V_{{\rm{Sd}}}}}&{{V_{{\rm{Sq}}}}}&{{V_{{\rm{Rd}}}}}&{{V_{{\rm{Rq}}}}} \end{array}} \right]^{\rm{T}}} \end{array} \right. $ |
则DFIG状态模型可以表示为一个四阶函数模型:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{h}}}} \right)\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{Bu}}\\ y = {T_{\rm{G}}} = \frac{{3p{L_{\rm{m}}}}}{2}\left( {{x_2}{x_3} - {x_1}{x_4}} \right) \end{array} \right. $ | (7) |
令σ=1-Lm2/(LSLR), 则
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{\rm{h}}}} \right) = \left[ {\begin{array}{*{20}{c}} { - \frac{{{R_{\rm{S}}}}}{{\sigma {L_{\rm{S}}}}}}&{{\omega _{\rm{S}}} + \frac{{p{\mathit{\Omega }_{\rm{h}}}L_{\rm{m}}^2}}{{\sigma {L_{\rm{S}}}{L_{\rm{R}}}}}}&{\frac{{{L_{\rm{m}}}{R_{\rm{R}}}}}{{\sigma {L_{\rm{S}}}{L_{\rm{R}}}}}}&{\frac{{p{\mathit{\Omega }_{\rm{h}}}{L_{\rm{m}}}}}{{\sigma {L_{\rm{S}}}}}}\\ { - \left[ {{\omega _{\rm{S}}} + \frac{{p{\mathit{\Omega }_{\rm{h}}}L_{\rm{m}}^2}}{{\sigma {L_{\rm{S}}}{L_{\rm{R}}}}}} \right]}&{ - \frac{{{R_{\rm{S}}}}}{{\sigma {L_{\rm{S}}}}}}&{ - \frac{{p{\mathit{\Omega }_{\rm{h}}}{L_{\rm{m}}}}}{{\sigma {L_{\rm{S}}}}}}&{\frac{{{L_{\rm{m}}}{R_{\rm{R}}}}}{{\sigma {L_{\rm{S}}}{L_{\rm{R}}}}}}\\ {\frac{{{L_{\rm{m}}}{R_{\rm{R}}}}}{{\sigma {L_{\rm{S}}}{L_{\rm{R}}}}}}&{ - \frac{{p{\mathit{\Omega }_{\rm{h}}}{L_{\rm{m}}}}}{{\sigma {L_{\rm{R}}}}}}&{ - \frac{{{R_{\rm{R}}}}}{{\sigma {L_{\rm{R}}}}}}&{{\omega _{\rm{S}}} - \frac{{p{\mathit{\Omega }_{\rm{h}}}}}{\sigma }}\\ {\frac{{p{\mathit{\Omega }_{\rm{h}}}{L_{\rm{m}}}}}{{\sigma {L_{\rm{R}}}}}}&{\frac{{{R_{\rm{S}}}{L_{\rm{m}}}}}{{\sigma {L_{\rm{S}}}{L_{\rm{R}}}}}}&{\frac{{p{\mathit{\Omega }_{\rm{h}}}}}{\sigma } - {\omega _{\rm{S}}}}&{ - \frac{{{R_{\rm{S}}}}}{{\sigma {L_{\rm{S}}}}}} \end{array}} \right]\\ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{\sigma {L_{\rm{S}}}}}}&0&{ - \frac{{{L_{\rm{m}}}}}{{\sigma {L_{\rm{S}}}{L_{\rm{R}}}}}}&0\\ 0&{\frac{1}{{\sigma {L_{\rm{S}}}}}}&0&{ - \frac{{{L_{\rm{m}}}}}{{\sigma {L_{\rm{S}}}{L_{\rm{R}}}}}}\\ { - \frac{{{L_{\rm{m}}}}}{{\sigma {L_{\rm{S}}}{L_{\rm{R}}}}}}&0&{\frac{1}{{\sigma {L_{\rm{R}}}}}}&0\\ 0&{ - \frac{{{L_{\rm{m}}}}}{{\sigma {L_{\rm{S}}}{L_{\rm{R}}}}}}&0&{\frac{1}{{\sigma {L_{\rm{R}}}}}} \end{array}} \right] \end{array} \right. $ |
WECS有两个时间尺度的动态性能, 分别对应于风速动态模型中的两种频谱变化:风速模型中低频部分的低频动态性能和风速模型湍流部分的高频动态性能。
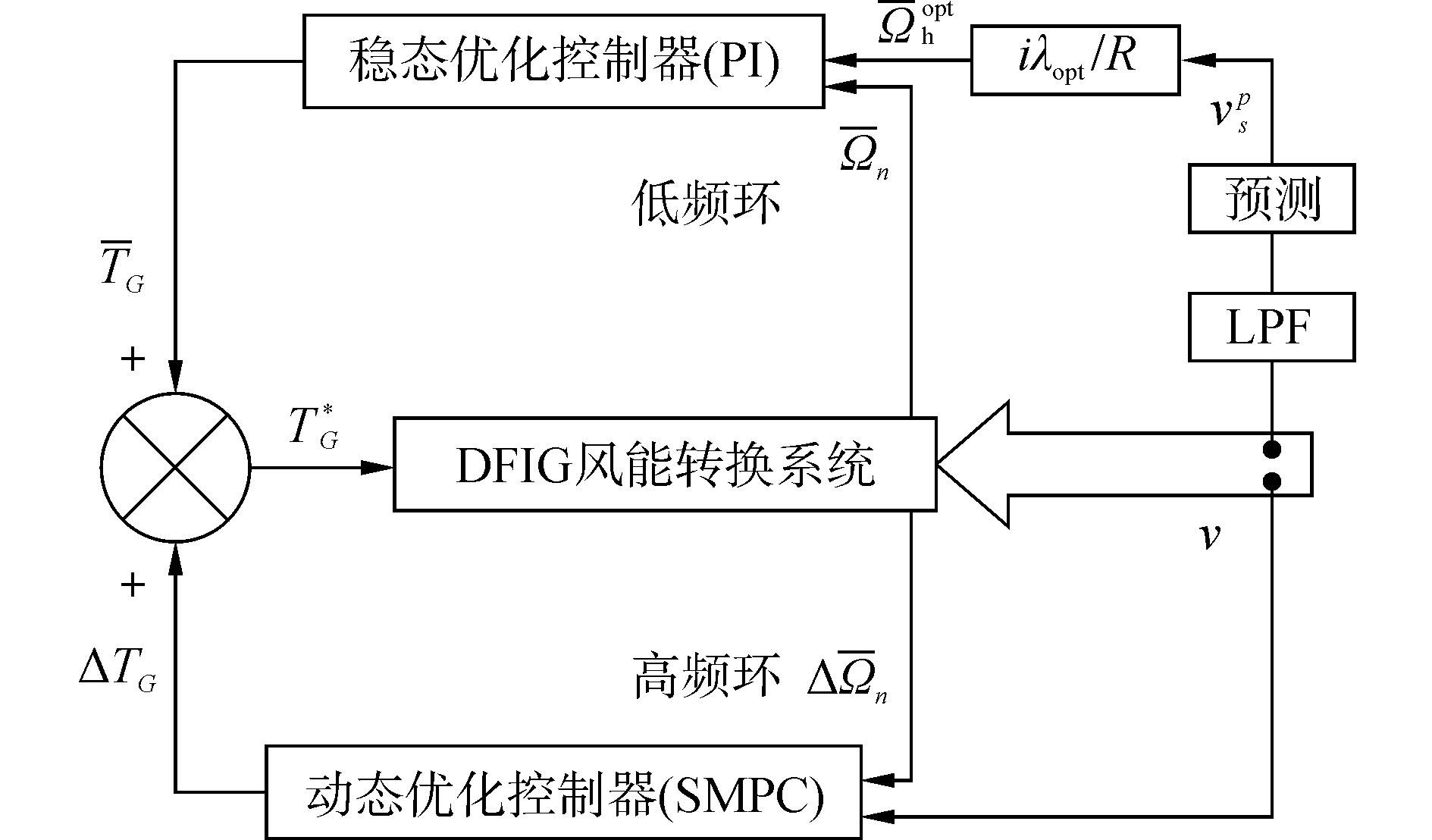
低频部分vs确定风力机特性曲线上的运行点的一般位置, 湍流部分Δv(t)=v-vs=vt通过在这些运行点周围产生高频变化, 从而引起高频动态特性。因此, WECS整体动态特性可以表示为可测量的变量的变化过程。整体动态性能由低频部分引起的低速动态性能和由湍流部分引起的机组动态性能叠加而成, 由此可以设计一个双环控制结构来分别补偿两个动态部分。双环优化控制系统框图如图 2所示。
|
Download:
|
| 图 2 双环优化控制结构框图 Fig. 2 Block diagram of double loop optimal control | |
引入低频环是为了解决WECS能量效率最优化问题, 要求系统运行在变速状态下、工作点运行在最优控制特性(optimal regimes characteristic, ORC)曲线上, 保持最优叶尖速度比λopt, 稳态优化控制器的参考值是依据风速低频分量vs计算得到, 则
| $ \mathit{\bar \Omega }_{\rm{h}}^{{\rm{opt}}} = {v_s}i{\lambda _{{\rm{opt}}}}/R $ | (8) |
为了避免由于时间延迟而产生相应的稳定性问题, 本文采用先低通滤波(LPF)然后再基于ARMA模型预测得到风速的低频分量vs。
令vsf为LPF的输出, vsp是通过滤波和预测得到的vs的估计值, 利用ARMA模型的递归思想, 可以由vsf对第k个vsp值进行预测:
| $ v_{{s_k}}^p = \sum\limits_{i = 1}^n {{a_i}v_{{s_{k - i}}}^f} + \sum\limits_{j = 1}^m {{b_j}\left( {v_{{s_{k - j}}}^p - v_{{s_{k - j}}}^f} \right)} $ | (9) |
高频环的优化标准:设定高频环的控制目标为降低风速的高频分量对λ(t)准确跟踪λopt的影响, 最大化功率系数, 提高系统的鲁棒稳定性。
考虑到低频环能够实现维持工作点运行在ORC上, 所以振荡动态性能的参数就是时不变的, 因此预测控制问题所对应的被控对象可以看成是时不变系统。在高频模型中, 以归一化变化量为状态变量, 得到线性时不变状态方程。
状态变量为x(t)=[ΔΩl(t) ΔTwt(t)]T, 系统输入为u(t)=ΔTG(t), 系统输出为z(t)=Δλ(t), 则系统的状态方程为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}}\left( \mathit{\boldsymbol{t}} \right) = \mathit{\boldsymbol{A}}x\left( t \right) + \mathit{\boldsymbol{B}}u\left( t \right) + \mathit{\boldsymbol{L}}e\left( t \right)\\ z = \mathit{\boldsymbol{C}}x\left( t \right) \end{array} \right. $ | (10) |
式中:
本文应用预测控制的思想建立一种滑模变结构控制策略。假定预测模型为线性定常离散时间的状态空间模型其形式为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + \mathit{\boldsymbol{Bu}}\left( k \right)\\ \mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{Cx}}\left( k \right) \end{array} \right. $ | (11) |
选择线性滑模函数为[11]
| $ s\left( k \right) = Cx\left( k \right) $ | (12) |
以式(11)作为预测模型, 设预测时域为N, 对未来k+p(p=1, 2…, N-1)时刻的滑模函数预测值为
| $ {s_y}\left( {k + p} \right) = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^p}\mathit{\boldsymbol{x}}\left( k \right) + \sum\limits_{i = 1}^p {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{i - 1}}\mathit{\boldsymbol{Bu}}\left( {k + p - i} \right)} $ | (13) |
考虑到系统中存在的不确定因素, 利用当前实测滑模函数值s(k)与预测值sy(k)之差对未来时刻的预测值进行反馈校正:
| $ \begin{array}{*{20}{c}} {{{\hat s}_y}\left( {k + p} \right) = {s_y}\left( {k + p} \right) + {h_p}\left[ {s\left( k \right) - {s_y}\left( k \right)} \right] = }\\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^p}\mathit{\boldsymbol{x}}\left( k \right) + \sum\limits_{i = 1}^p {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{i - 1}}\mathit{\boldsymbol{Bu}}\left( {k + p - i} \right)} + }\\ {{h_p}\left[ {s\left( k \right) - {s_y}\left( k \right)} \right]} \end{array} $ | (14) |
其中
| $ {s_y}\left( k \right) = \mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^p}\mathit{\boldsymbol{x}}\left( {k - p} \right) + \sum\limits_{i = 1}^p {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{i - 1}}\mathit{\boldsymbol{Bu}}\left( {k - i} \right)} $ |
利用预测控制的思想设计控制规则, 目标函数的表达式为
| $ \begin{array}{*{20}{c}} {{J_p} = \sum\limits_{i = 1}^N {{q_i}{{\left[ {{{\hat s}_y}\left( {k + i} \right) - {s_r}\left( {k + i} \right)} \right]}^2}} + }\\ {\sum\limits_{j = 1}^M {{r_j}{{\left[ {u\left( {k + j - 1} \right)} \right]}^2}} } \end{array} $ | (15) |
式中:sr(k+i)为滑模参考轨迹, N、M分别为预测时域和控制时域, qi、rj为加权系数。
滑模参考轨迹选取目前常用的指数趋近率作为滑模参考轨迹:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {{s_r}\left( {k + p} \right) = \left( {1 - qT} \right){s_r}\left( {k + p - 1} \right) - }\\ {\varepsilon T{\mathop{\rm sgn}} \left( {{s_r}\left( {k + p} \right)} \right)} \end{array}\\ {s_r}\left( k \right) = s\left( k \right) \end{array} \right. $ | (16) |
式中:ε>0, q>0, 1-qT>0, T为采样周期。
由式(15)目标函数可以写成
| $ \begin{array}{*{20}{c}} {{J_p} = {{\left[ {{{\mathit{\boldsymbol{\hat S}}}_y}\left( {k + 1} \right) - {\mathit{\boldsymbol{S}}_r}\left( {k + 1} \right)} \right]}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left[ {{{\mathit{\boldsymbol{\hat S}}}_y}\left( {k + 1} \right) - } \right.}\\ {\left. {{\mathit{\boldsymbol{S}}_r}\left( {k + 1} \right)} \right] + {\mathit{\boldsymbol{U}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{RU}}\left( k \right) = \left[ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}x\left( k \right) + \mathit{\boldsymbol{GU}}\left( k \right) + } \right.}\\ {{{\left. {\mathit{\boldsymbol{HE}}\left( k \right) - {\mathit{\boldsymbol{S}}_r}\left( {k + 1} \right)} \right]}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left[ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}x\left( k \right) + \mathit{\boldsymbol{GU}}\left( k \right) + } \right.}\\ {\left. {\mathit{\boldsymbol{HE}}\left( k \right) - {\mathit{\boldsymbol{S}}_r}\left( {k + 1} \right)} \right] + {\mathit{\boldsymbol{U}}^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{RU}}\left( k \right)} \end{array} $ | (17) |
其中
| $ {{\mathit{\boldsymbol{\hat S}}}_r}\left( {k + 1} \right) = {\left[ {{{\hat s}_y}\left( {k + 1} \right),{{\hat s}_y}\left( {k + 2} \right), \cdots ,{{\hat s}_y}\left( {k + N} \right)} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{S}}_r}\left( {k + 1} \right) = {\left[ {{s_r}\left( {k + 1} \right),{s_r}\left( {k + 2} \right), \cdots ,{s_r}\left( {k + N} \right)} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{U}}\left( k \right) = {\left[ {u\left( k \right),u\left( {k + 1} \right), \cdots ,u\left( {k + M - 1} \right)} \right]^{\rm{T}}}, $ |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{E}}\left( k \right) = \left[ {s\left( k \right) - {s_y}\left( {k\left| {k - 1} \right.} \right),s\left( k \right) - {s_y}\left( {k\left| {k - 2} \right.} \right),} \right.}\\ {{{\left. { \cdots ,s\left( k \right) - {s_y}\left( {k\left| {k - N} \right.} \right)} \right]}^{\rm{T}}},} \end{array} $ |
| $ \mathit{\boldsymbol{Q}} = {\rm{diag}}\left( {{q_1},{q_2}, \cdots ,{q_N}} \right), $ |
| $ \mathit{\boldsymbol{R}} = {\rm{diag}}\left( {{r_1},{r_2}, \cdots ,{r_M}} \right), $ |
| $ \mathit{\boldsymbol{H}} = {\rm{diag}}\left( {{h_1},{h_2}, \cdots ,{h_N}} \right), $ |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{CA}}}\\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^2}}\\ \mathit{\boldsymbol{M}}\\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^N}} \end{array}} \right];\mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{CB}}}&\mathit{\boldsymbol{0}}&\mathit{\boldsymbol{L}}&\mathit{\boldsymbol{0}}\\ {\mathit{\boldsymbol{CAB}}}&{\mathit{\boldsymbol{CB}}}&\mathit{\boldsymbol{L}}&\mathit{\boldsymbol{0}}\\ \mathit{\boldsymbol{M}}&\mathit{\boldsymbol{M}}&\mathit{\boldsymbol{M}}&\mathit{\boldsymbol{M}}\\ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{N - 1}}\mathit{\boldsymbol{B}}}&{\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{N - 2}}\mathit{\boldsymbol{B}}}&\mathit{\boldsymbol{L}}&{\mathit{\boldsymbol{CB}}} \end{array}} \right] $ |
令∂Jp/∂U(k)=0, 可得:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}\left( k \right) = {{\left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{QG}} + \mathit{\boldsymbol{R}}} \right)}^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left[ {{\mathit{\boldsymbol{S}}_r}\left( {k + 1} \right) - } \right.}\\ {\left. {\mathit{\boldsymbol{ \boldsymbol{\varPhi} x}}\left( k \right) - \mathit{\boldsymbol{HE}}\left( k \right)} \right]} \end{array} $ | (18) |
无约束和有约束条件下得到的均是一个控制量序列U, 但实际只取第一个控制量作用于系统:
| $ \begin{array}{*{20}{c}} {u\left( k \right) = \left[ {1,0, \cdots ,0} \right]{{\left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{QG}} + \mathit{\boldsymbol{R}}} \right)}^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left[ {{\mathit{\boldsymbol{S}}_r}\left( {k + } \right.} \right.}\\ {\left. {\left. 1 \right) - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}x\left( k \right) - \mathit{\boldsymbol{HE}}\left( k \right)} \right]} \end{array} $ | (19) |
通过上述分析和设计, 基于双频环的风能转换系统的滑模预测控制的设计过程如下:
1) 由风速计测量出风速v的大小, 由编码器测量得到高速轴的转速Ωh;
2) 通过对风速v进行预测得到低频风速v;
3) 求得风速湍流分量Δv=v-v和其标准化值Δv=Δv/v;
4) 对信号Ωh进行低通滤波得到高速轴转速的低频分量Ωh;
5) 求得高速轴转速的高频分量的标准化值ΔΩh=(Ωh-Ωh)/Ωh;
6) v和Ωh作为低频环的输入信号, 控制输入的稳态分量TG是稳态优化的输出;
7)Δv和ΔΩh作为高频环的输入, 高频环的设计基于上述滑模预测控制算法, 可以得到控制输入的动态分量ΔTG;
8) 总控制输入TG*通过稳态分量和动态分量相加得到:TG*=TG+ΔTG。
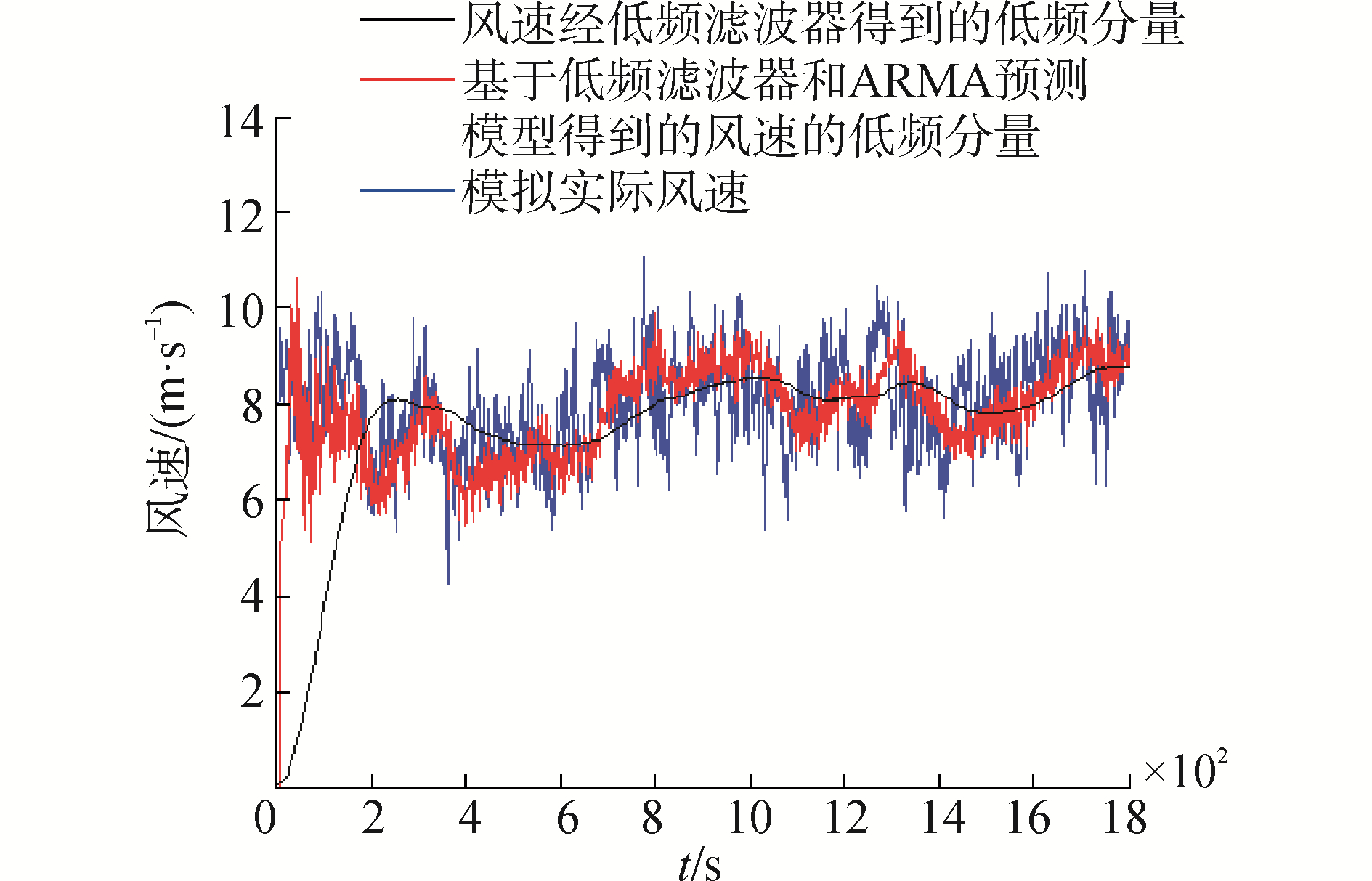
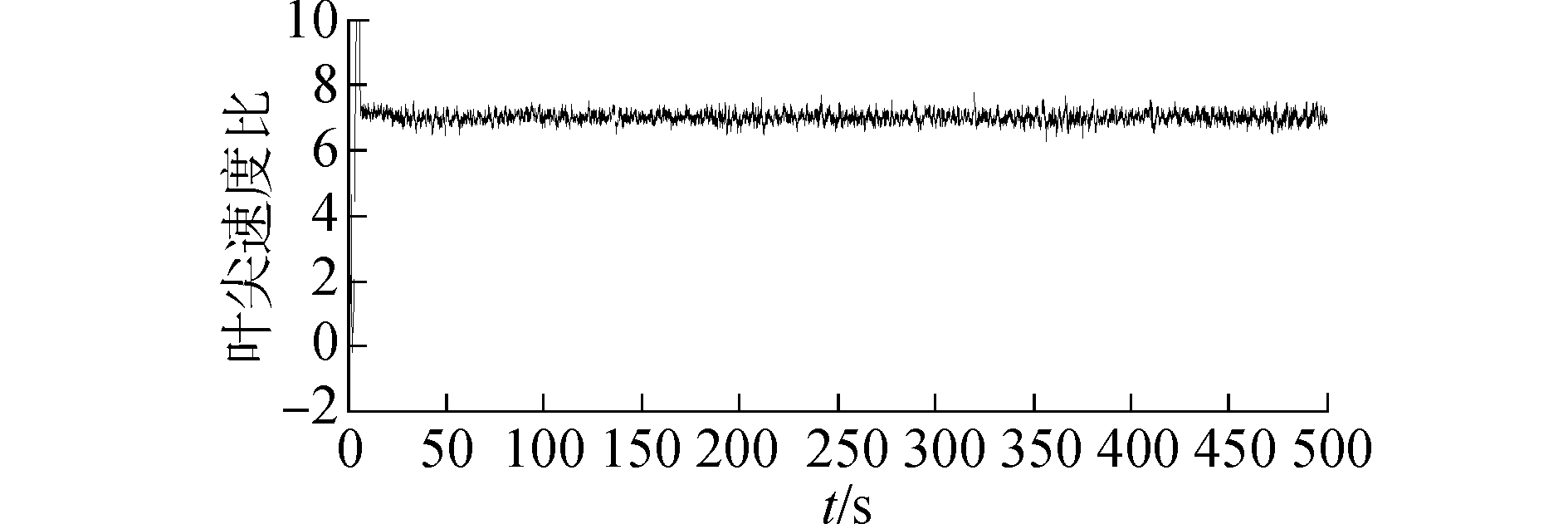
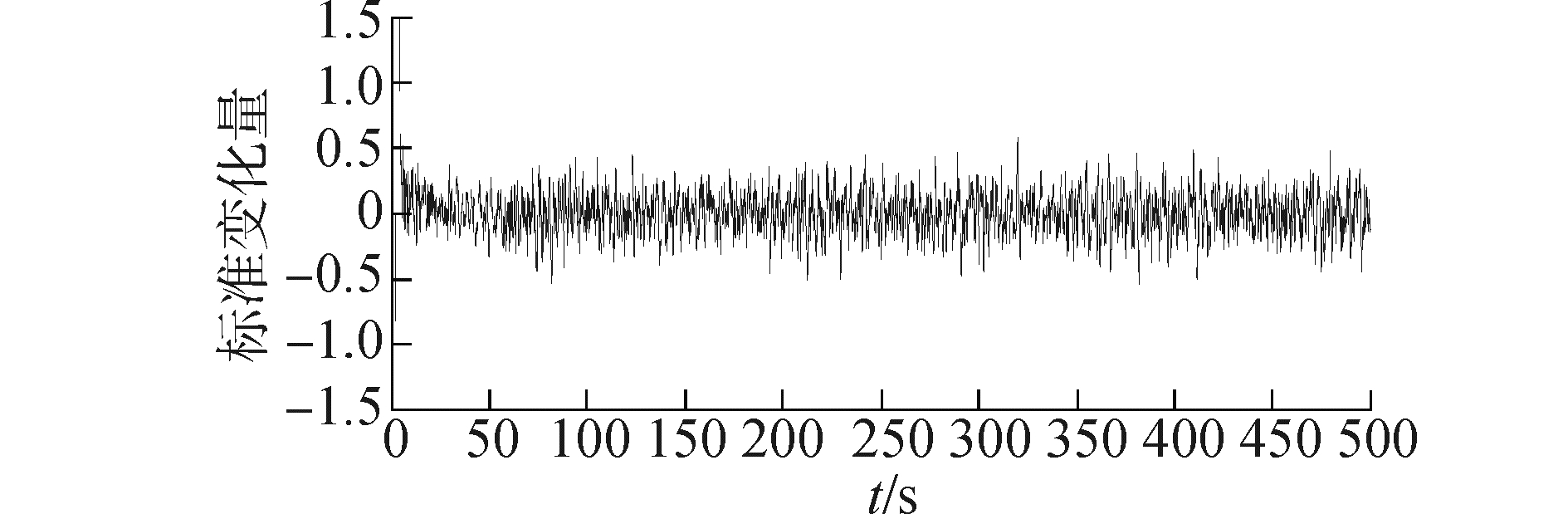
3 仿真结果为验证所提出控制方法在系统中的有效性, 利用MATLAB/Simulink仿真软件在6 kW的DFIG刚性传动链的风能转换系统中对本文提出的控制方法进行验证。选取文献[12]中的系统参数如表 1所示。模拟的平均风速为7.5 m/s, 滤波器阶数m=4, 回归矢量次数n=5, 预测时域N=5, qi=2, ri=0.1, hi=1。图 3给出了风速预测与采用简单的低通滤波器的对比效果图, 从仿真结果可以看出采用预测方法处理可以更准确的估计出风速的低频分量, 预测值更接近实际的低频风速; 图 4显示了叶尖速度的稳态值维持在其最优值λopt=7附近; 图 5和图 6分别给出了表征能量效率的叶尖速度标准化变化量和与机械负荷强度相关的电磁转矩标准化变化量的变化过程, 从仿真结果可以看出基于滑模预测控制方法的双频环优化控制可以确保较低的转矩偏差, 叶尖速度振动幅值不超过5%。将本文提出的控制策略与文献[13]对比研究, 基于相同仿真条件图 7得到了功率系数的变化过程, 体现了空气动力效率的变化; 图 8给出了跟踪ORC的闭环系统性能, 显示了工作点与最优运行点之间的接近程度。对比研究表明在高频环采用滑模预测控制比滑模控制获得较高的效率, 能够实现高的风能捕获。
| 表 1 DFIG低功率刚性传动链WECS的基本参数 Tab.1 Basic parameters of the low-fiequency rigid transmission chain WECS of DFIG |
|
Download:
|
| 图 3 风速预测和低频滤波效果对比 Fig. 3 Comparison of wind speed prediction and low frequency filtering effect | |
|
Download:
|
| 图 4 风力机的叶尖速度比 Fig. 4 Tip speed ratio of wind turbine | |

|
Download:
|
| 图 5 叶尖速度比的标准变化 Fig. 5 The normalized change of tip speed ratia | |
|
Download:
|
| 图 6 电磁转矩的标准变化 Fig. 6 The normalized change of electromagnetic torque | |

|
Download:
|
| 图 7 功率系数的变化过程 Fig. 7 The change process of power coefficient | |

|
Download:
|
| 图 8 工作点与ORC的相对关系 Fig. 8 The relative relationship between the operating point and the ORC | |
1) 本文通过分析低功率刚性传动链双馈感应发电机的风能转换系统的特点, 建立了WECS的数学模型, 基于WECS的两个时间尺度的动态性能, 利用双频环优化控制结构解决了系统效率的最大化与控制输入投入的最小化的平衡问题。
2) 利用ARMA模型对低通滤波器分离出的风速进行预测, 实现了vs(t)的准确估计, 该方法能够减少低频分量的延迟。
3) 为弥补双频环控制结构对参数、模型不确定的敏感性, 提出高频环滑模预测控制方法。该方法充分利用滑模的鲁棒性和预测控制的滚动优化与反馈校正思想, 有效的避免了滑模控制高频切换带来的抖振现象, 在部分负荷状态下减小了控制输入量的变化, 降低了机械疲劳, 提高了能源利用效率。
| [1] |
BAÑOS R, MANZANO-AGUGLIARO F, MONTOYA F G, et al. Optimization methods applied to renewable and sustainable energy:a review[J]. Renewable and sustainable energy reviews, 2011, 15(4): 1753-1766. DOI:10.1016/j.rser.2010.12.008 (  0) 0)
|
| [2] |
侯喆瑞, 张鑫, 张嵩. 风力发电的发展现状与关键技术研究综述[J]. 智能电网, 2014, 2(2): 22-27. HOU Zherui, ZHANG Xin, ZHANG Song. Review on development status and key technologies of wind power[J]. Smart grid, 2014, 2(2): 22-27. (  0) 0)
|
| [3] |
YANG Yun, MOK K T, TAN S C, et al. Nonlinear dynamic power tracking of low-power wind energy conversion system[J]. IEEE transactions on power electronics, 2015, 30(9): 5223-5236. DOI:10.1109/TPEL.2014.2363561 (  0) 0)
|
| [4] |
ELNAGGAR M, FATTAH H A A, ELSHAFEI A L. Maximum power tracking in WECS (Wind energy conversion systems) via numerical and stochastic approaches[J]. Energy, 2014, 74: 651-661. DOI:10.1016/j.energy.2014.07.031 (  0) 0)
|
| [5] |
ROCHA R. A sensorless control for a variable speed wind turbine operating at partial load[J]. Renewable energy, 2011, 36(1): 132-141. DOI:10.1016/j.renene.2010.06.008 (  0) 0)
|
| [6] |
BALOCH M H, WANG Jie, KALOI G S. Stability and nonlinear controller analysis of wind energy conversion system with random wind speed[J]. International journal of electrical power & energy systems, 2016, 79: 75-83. (  0) 0)
|
| [7] |
HOWLADER A M, URASAKI N, YONA A, et al. Design and implement a digital H∞ robust controller for a MW-class PMSG-based grid-interactive wind energy conversion system[J]. Energies, 2013, 6(4): 2084-2109. DOI:10.3390/en6042084 (  0) 0)
|
| [8] |
LIU P, YANG W T, YANG Changen, et al. Sensorless wind energy conversion system maximum power point tracking using Takagi-Sugeno fuzzy cerebellar model articulation control[J]. Applied soft computing, 2015, 29: 450-460. DOI:10.1016/j.asoc.2015.01.019 (  0) 0)
|
| [9] |
WEI Chun, ZHANG Zhe, QIAO Wei, et al. An adaptive network-based reinforcement learning method for MPPT control of PMSG wind energy conversion systems[J]. IEEE transactions on power electronics, 2016, 31(11): 7837-7848. DOI:10.1109/TPEL.2016.2514370 (  0) 0)
|
| [10] |
张凤, 阎秀恪, 兰宏光, 等. 基于滑模控制的风机最大风能追踪[J]. 沈阳工业大学学报, 2014, 36(6): 625-630. ZHANG Feng, YAN Xiuke, LAN Hongguang, et al. Maximum power point tracking of wind turbine based on sliding mode control[J]. Journal of Shenyang University of Technology, 2014, 36(6): 625-630. DOI:10.7688/j.issn.1000-1646.2014.06.05 (  0) 0)
|
| [11] |
宋立忠, 陈少昌, 姚琼荟. 滑模预测离散变结构控制[J]. 控制理论与应用, 2004, 21(5): 826-829. SONG Lizhong, CHEN Shaochang, YAO Qionghui. Discrete variable structure control algorithm based on sliding mode prediction[J]. Control theory & applications, 2004, 21(5): 826-829. (  0) 0)
|
| [12] |
MUNTEANU I, BRATCU A I, CUTULULIS N A, et al. Optimal control of wind energy systems:towards a global approach[M]. London: Springer, 2008: 1-254.
(  0) 0)
|
| [13] |
孟涛, 纪志成. 风能转换系统双频环滑模控制[J]. 电机与控制学报, 2009, 13(S1): 152-156. MENG Tao, JI Zhicheng. Two-frequency-loop control for wind energy conversion system based on sliding-mode contro[J]. Electric machines and control, 2009, 13(S1): 152-156. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


