2. 武汉船舶通信研究所, 湖北 武汉 430079
2. Wuhan Maritime Communication Research Institute, Wuhan 430079, China
在经典的压缩感知(compressed sensing,CS)理论中[1], 未知的稀疏信号由单一的观测向量恢复, 被称为单测量向量(single measurement vector,SMV)模型。然而在诸多场合,多测量向量(multiple measurement vector,MMV)模型有着更为广泛的应用,如脑磁图数据处理、合成孔径雷达成像、稀疏宽带信号MWC采样等[2]问题,均需要完成对稀疏目标信号多次或并行压缩采样的数据进行整体重构。
MMV模型的稀疏重构(sparse reconstruction,SR)算法主要分为两类:一类是分解MMV问题为多个独立的SMV问题[3];另一类算法则建立了MMV联合稀疏模型,将SMV模型的SR算法推广到MMV模型中应用。Eldar Y C等证明了相对于SMV模型算法,MMV模型可以显著提高未知稀疏信号的成功重构的概率[4-6]。常规的MMV模型算法,如凸优化算法MMV-proc[7]、M-FOCUSS[8]、贪婪算法MMV-OMP[9]、MSBL[10]等,在收敛速度和重构精度上都有较好的性能,但都假设原稀疏信号不同量测列的稀疏度和支撑集相同。针对在信号模型不满足严格的联合稀疏约束条件下常规算法性能显著下降的问题,文献[11]提出了一种多量测向量快速重构算法(MMVFR),该算法利用最速下降法在统一框架下重构信号支撑集,能够适用于任意稀疏结构的MMV模型的求解,但MMVFR算法的稀疏优化目标函数没有考虑噪声的影响,尤其当噪声为方差很大的非高斯冲击噪声时,重构性能将急剧下降。文献[12]提出了一种基于SMV模型的Lorentzian-ISL0重构算法,提高了在冲击噪声背景下的压缩感知雷达参数估计精度。
针对常规MMV模型算法对联合稀疏结构的限制和MMVFR算法噪声鲁棒性不足的问题,本文提出了一种冲击噪声下任意稀疏结构的MMV模型稀疏重构算法(MMVLL2-ISL0)。该算法首先构建了矩阵平滑l0范数优化目标函数,利用Lorentzian范数拟合噪声的误差项;然后利用固定步长共轭梯度法进行优化求解。
1 任意稀疏结构的MMV信号模型SMV是CS框架下常用信号模型,即已知测量矩阵Φ∈RM×N(M≪N)以及未知信号x在该矩阵下的线性测量值y∈RM,即
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} x}} $ | (1) |
测量值y是信号x从N维空间到M维空间的线性投影,包含了重构原始信号x所需要的全部信息。
然而在许多实际应用中常涉及多个测量向量,每个测量向量均与一个未知信号向量相对应,并且各个未知向量均是具有公共支撑集的稀疏信号。针对这种联合稀疏结构信号模型的重构问题称之为多测量向量问题,其模型可表示如下
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} X}} $ | (2) |
式中:X=[x(1), x(2), …, x(L)], x(l)∈RN×1由L个稀疏的列向量组成,且假设这些向量具有K个公共非零行,即联合K稀疏;Y=[y(1), y(2), …, y(L)], y(l)∈RM×1为采样值矩阵;L为测量向量的总列数。MMV重构问题本质上是通过求解具有稀疏约束的优化问题来获得最稀疏解:
| $ \arg \min \sum\limits_{l = 1}^L {{{\left\| {{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|}_{{l_0}}}} ,{\rm{st}}.\;{\mathit{\boldsymbol{y}}^{\left( l \right)}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{\left( l \right)}},l = 1,2, \cdots ,L $ | (3) |
式中:x(l)表示矩阵X的第l个列向量;y(l)表示矩阵Y的第l个列向量。MMV模型的求解实际上可以视为求解一系列的具有稀疏约束的SMV问题,属于典型组合优化问题,并且由于MMV问题中增加了测量向量数量和未知向量间的联合稀疏结构,相比SMV问题,可以改进重构性能。
通常,由于信号的稀疏结构具有时变性和特殊的信号结构,传统MMV模型的联合稀疏性假设不能准确描述此类信号的稀疏特性。本文假设MMV模型具有任意稀疏结构(MMV of arbitrary sparse structure, ASS-MMV),即矩阵X的不同列向量的稀疏度和支撑集均不要求相同,更符合实际应用。图 1给出了传统MMV模型和任意稀疏结构的MMV模型示意图。

|
图 1 MMV模型示意图 Fig.1 Schematic of MMV model |
式(2)为压缩感知无噪声MMV模型,而在实际应用中,由于存在不可忽略的测量噪声或者模型噪声,测量值矩阵受到噪声和干扰影响。因此存在噪声的MMV模型可表示为
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} X}} + \mathit{\boldsymbol{W}} $ | (4) |
式中:W=[w(1), w(2), …, w(L)], w(l)∈RM×1,W为加性噪声。在压缩感知框架下,噪声W主要分为两类:高斯白噪声和冲击噪声。对于噪声模型下MMV求解问题可以将式(3)修正为如下形式:
| $ \arg \min \sum\limits_{l = 1}^L {{{\left\| {{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|}_{{l_0}}}} + \lambda {\rm{loss}}\left( {{\mathit{\boldsymbol{y}}^{\left( l \right)}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right) $ | (5) |
式中:loss(y(l)-Φx(l))为误差项,λ≥0为正则化参数,控制着允许误差和稀疏性之间的平衡。当W为高斯噪声时,可以采用l2范数来拟合误差项,此时式(5)有如下表示
| $ \arg \min \sum\limits_{l = 1}^L {{{\left\| {{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|}_{{l_0}}}} + \lambda \left\| {{\mathit{\boldsymbol{y}}^{\left( l \right)}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|_2^2 $ | (6) |
由文献[13]可知,压缩感知最优重构下的信号的最小均方误差与噪声的方差成正比,当W为脉冲噪声时,其特点是方差很大,误差项中会出现较大幅值元素,存在离散的异值点,l2范数将会线性放大残差的影响。
Carrillo等在文献[14]中指出:利用Lorentzian范数来拟合误差项时,由于导函数的有界软回降特性,对误差项中幅值较大的元素惩罚较重,其作用与l1范数相同;对误差项中幅值较小的元素惩罚较轻,其作用与l2范数相同,能够鲁棒性地削弱异值点对重构结果的影响。Lorentzian范数的定义如下
| $ {\left\| \mathit{\boldsymbol{u}} \right\|_{L{L_{2,\gamma }}}} = \sum\limits_{m = 1}^M {\log \left( {1 + {\gamma ^{ - 2}}\mathit{\boldsymbol{u}}_m^2} \right)} ,\gamma > 0 $ | (7) |
式中:u∈RM×1为列向量,‖·‖LL2, γ表示向量u的Lorentzian范数;γ为Lorentzian范数的尺度参数,并决定了LL2范数对误差项异常值的鲁棒性。定理1给出了l2范数和LL2范数之间的关系。
定理1 对于任意u∈RM和γ>0,下面不等式都成立:
| $ {\gamma ^2}{\left\| \mathit{\boldsymbol{u}} \right\|_{L{L_{2,\gamma }}}} \le \left\| \mathit{\boldsymbol{u}} \right\|_2^2 \le {\gamma ^2}M\left( {{{\rm{e}}^{{{\left\| \mathit{\boldsymbol{u}} \right\|}_{L{L_{2,\gamma }}}}}} - 1} \right) $ | (8) |
证明:由于对数函数有性质log(1+x)≤x, x≥0,设xm=um2/γ2,则
| $ \begin{array}{*{20}{c}} {{\gamma ^2}{{\left\| \mathit{\boldsymbol{u}} \right\|}_{L{L_{2,\gamma }}}} = {\gamma ^2}\sum\limits_{m = 1}^M {\log \left( {1 + {x_m}} \right)} \le }\\ {\sum\limits_{m = 1}^M {{\gamma ^2}{x_m} = \left\| \mathit{\boldsymbol{u}} \right\|_2^2} } \end{array} $ | (9) |
式(8)的第一个不等式成立。
根据Lorentzian范数的定义有:
| $ \begin{array}{*{20}{c}} {{{\left\| \mathit{\boldsymbol{u}} \right\|}_{L{L_{2,\gamma }}}} = \sum\limits_{m = 1}^M {\log \left( {1 + {x_m}} \right)} \ge }\\ {\mathop {\max }\limits_m \log \left( {1 + {x_m}} \right) = \log \left( {1 + \frac{{\left\| \mathit{\boldsymbol{u}} \right\|_\infty ^2}}{{{\gamma ^2}}}} \right)} \end{array} $ | (10) |
式(10)整理可得‖u‖∞≤γ(e‖u‖LL2, γ-1)1/2,又由于‖u‖22≤M‖u‖∞2,式(6)的第二个不等式成立。得证。
另外,Lorentzian范数为连续可导函数,在求解式(6)问题时,可以利用最优化算法迭代求解。本文利用Lorentzian范数替换式(6)中l2范数来拟合误差项,冲击噪声下MMV模型求解问题可表示成如下混合L0-LL2范数优化模型:
| $ \arg \min \sum\limits_{l = 1}^L {{{\left\| {{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|}_{{l_0}}}} + \lambda {\left\| {{\mathit{\boldsymbol{y}}^{\left( l \right)}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|_{L{L_{2,\gamma }}}} $ | (11) |
式中:‖y(l)-Φx(l)‖LL2, γ表示测量值矩阵第l列重构误差项的Lorentzian范数,可表示为
| $ \begin{array}{*{20}{c}} {{{\left\| {{\mathit{\boldsymbol{y}}^{\left( l \right)}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|}_{L{L_{2,\gamma }}}} = }\\ {\sum\limits_{m = 1}^M {\log \left( {1 + {\gamma ^{ - 2}}{{\left( {\mathit{\boldsymbol{Y}}\left[ {m,l} \right] - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left[ {m,:} \right]\mathit{\boldsymbol{X}}\left[ {:,l} \right]} \right)}^2}} \right)} } \end{array} $ | (12) |
压缩感知MMV模型信号重构可以归纳为目标函数L(X)最优化问题:
| $ L\left( \mathit{\boldsymbol{X}} \right) = \sum\limits_{l = 1}^L {{{\left\| {{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|}_{{l_0}}}} + \lambda {\left\| {{\mathit{\boldsymbol{y}}^{\left( l \right)}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|_{L{L_{2,\gamma }}}} $ | (13) |
式(13)中l0范数属于伪范数,具有高度不连续性,导致无法用解析方法求解,属于NP-Hard问题。SL0算法是通过一类光滑的高斯函数逼近零范数,把零范数问题转化为求函数极值,从而用解析方法直接求解l0范数最小问题,不仅提高了重构概率,与凸优化算法(l1范数代替l0范数)相比,大大缩短了运算时间。基于平滑l0范数和Lorentzian范数的最优化目标函数为
| $ L\left( \mathit{\boldsymbol{X}} \right) = \sum\limits_{l = 1}^L {{F_\sigma }\left( {{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right) + \lambda {{\left\| {{\mathit{\boldsymbol{y}}^{\left( l \right)}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|}_{L{L_{2,\gamma }}}}} $ | (14) |
式中
| $ {f_\sigma }\left( \mathit{\boldsymbol{s}} \right) = \exp \left( { - {\mathit{\boldsymbol{s}}^2}/2{\sigma ^2}} \right) $ | (15) |
式中:σ为常数,衡量逼近矢量s的l0范数的精确度和平滑度之间的关系。根据高斯函数的性质可得
ASS-MMV模型快速重构算法利用SL0算法在每个σ值处只需收敛到最优值附近的特点,设定初始的稀疏向量最小二乘解为X0=ΦH(ΦΦH)-1Y,选取参数σ的递减区间[σmax, σmin],为了保证重构中每一列所对应的目标函数都可以在初次迭代时落入最优值区间,避免陷入局部最优解,令σmax=4max[max(x0(l))]足够大,此时对任意元素xi值函数fσ(xi)>0.96≈1。该算法在统一的参数设置下,采用数值优化算法并行地对多向量进行整体重构。
3.2 固定步长共轭梯度法求解式(14)最优解通常采用迭代方法:
| $ {\mathit{\boldsymbol{x}}_{k + 1}} = {\mathit{\boldsymbol{x}}_k} + {a_k}{\mathit{\boldsymbol{d}}_k} $ | (16) |
式中:xk为第k次迭代点,dk为第k次搜索方向,ak为第k次迭代步长,不同的ak和dk构造方法决定了算法复杂度和精确度。本文采用一种基于固定步长公式的共轭梯度算法,搜索方向dk的定义为
| $ {\mathit{\boldsymbol{d}}_k} = \left\{ \begin{array}{l} - {\mathit{\boldsymbol{g}}_k},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 1\\ - {\mathit{\boldsymbol{g}}_k} + {\beta _k}{\mathit{\boldsymbol{d}}_{k - 1}},\;\;\;\;k \ge 2 \end{array} \right. $ | (17) |
式中:-gk为负梯度方向,k为当前迭代步数,参数βk表达式为
| $ \beta _k^{FR} = \frac{{{{\left\| {{\mathit{\boldsymbol{g}}_k}} \right\|}^2}}}{{{{\left\| {{\mathit{\boldsymbol{g}}_{k - 1}}} \right\|}^2}}} $ | (18) |
为了保证ASS-MMV模型快速重构算法迭代过程能在统一的参数设置下进行,避免对每一列向量独立进行步长因子ak的线搜索,式(19)给出了一个无需矩阵运算的固定步长更新公式:
| $ {a_k} = - \mu \frac{{\mathit{\boldsymbol{g}}_k^{\rm{T}}{\mathit{\boldsymbol{d}}_k}}}{{{{\mathit{\boldsymbol{\tilde y}}}^{\rm{T}}}{\mathit{\boldsymbol{d}}_k}/\delta }} $ | (19) |
式中:0<μ<λ2/L2,L为Lipschitz常数,δ为一个保证xk+δdk在讨论区间内的足够小的正数,
式(17)和式(19)中只需计算函数值和梯度值,不存在二阶导数计算和矩阵操作,可以显著减小ASS-MMV模型重构过程的计算量和存储量。目标函数L(X)的梯度为
| $ \begin{array}{*{20}{c}} {\nabla L\left( \mathit{\boldsymbol{X}} \right) = \sum\limits_{l = 1}^L {\frac{\partial }{{\partial {\mathit{\boldsymbol{x}}^{\left( l \right)}}}}{F_\sigma }\left( {{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right)} + }\\ {\lambda \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}^{\left( l \right)}}}}{{\left\| {{\mathit{\boldsymbol{y}}^{\left( l \right)}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|}_{L{L_{2,\gamma }}}}} \end{array} $ | (20) |
式(20)中等号右边第一项为
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial {\mathit{\boldsymbol{x}}^{\left( l \right)}}}}{F_\sigma }\left( {{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right) = {{\left[ {\frac{{\partial {f_\sigma }\left( {\mathit{\boldsymbol{x}}_1^{\left( l \right)}} \right)}}{{\partial \mathit{\boldsymbol{x}}_1^{\left( l \right)}}}, \cdots ,\frac{{\partial {f_\sigma }\left( {\mathit{\boldsymbol{x}}_N^{\left( l \right)}} \right)}}{{\partial \mathit{\boldsymbol{x}}_N^{\left( l \right)}}}} \right]}^{\rm{T}}} = }\\ {{{\left[ {\frac{{\mathit{\boldsymbol{x}}_1^{\left( l \right)}}}{{{\sigma ^2}}}{f_\sigma }\left( {\mathit{\boldsymbol{x}}_1^{\left( l \right)}} \right), \cdots ,\frac{{\mathit{\boldsymbol{x}}_N^{\left( l \right)}}}{{{\sigma ^2}}}{f_\sigma }\left( {\mathit{\boldsymbol{x}}_N^{\left( l \right)}} \right)} \right]}^{\rm{T}}} = P\frac{{{\mathit{\boldsymbol{x}}^{\left( l \right)}}}}{{{\sigma ^2}}}} \end{array} $ | (21) |
式中:P=diag{fσ(x(l))}∈RN×N,为对角矩阵。式(20)中等号右边第二项为
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial {\mathit{\boldsymbol{x}}^{\left( l \right)}}}}{{\left\| {{\mathit{\boldsymbol{y}}^{\left( l \right)}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{\left( l \right)}}} \right\|}_{L{L_{2,\gamma }}}} = }\\ {\sum\limits_{m = 1}^M {\frac{{{\gamma ^2}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left[ {m,:} \right]X\left[ {:,l} \right] - Y\left[ {m,l} \right]} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left[ {m,:} \right]}}{{{\gamma ^2} + {{\left( {\mathit{\boldsymbol{Y}}\left[ {m,l} \right] - \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left[ {m,:} \right]\mathit{\boldsymbol{X}}\left[ {:,l} \right]} \right)}^2}}}} = }\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{H}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{\left( l \right)}} - {\mathit{\boldsymbol{y}}^{\left( l \right)}}} \right)} \end{array} $ | (22) |
式中:Q=diag{γ2/[γ2+(y(l)-Φx(l))2]}∈RM×M为对角矩阵。经过上述分析,MMVLL2-ISL0算法的具体步骤如下:
输入:采样矩阵Φ,测量值矩阵Y;
初始化:
1) 取σ=σi,判断σ>σmin是否成立,若成立,重构结束,否则继续执行循环迭代;
2) 令内循环次数k=1,利用稀疏信号估计值
3) 计算固定步长共轭梯度法的搜索方向dk和迭代步长ak;
4) 更新第k+1次估计值
5) 判断k<K,则返回步骤2,否则返回步骤1;
输出:恢复稀疏信号
下面通过运算量分析比较算法的重构速度,以一次加法或乘法为运算量单位。分别与SMV-SL0算法、Lorentzian-ISL0算法、OMPMMV算法和MMVFR算法进行比较。
若使用SMV-SL0算法逐列求解MMV模型问题,则计算出运行一次SL0算法运算量之后,总的运算量为其L倍,约为
| $ O\left( {MNLK + L\left( {{M^3} + 2{M^2}N + 4MN} \right)} \right) $ |
Lorentzian-ISL0算法同样需要逐列求解MMV模型问题,总的运算量约为
| $ O\left( {MNLK + L\left( {{M^3} + 2{M^2}N + 4MN + M} \right)} \right) $ |
OMPMMV算法求解MMV模型,其运算量主要集中在求逆运算,运算量约为
| $ O\left( {{M^2}NK + {M^3} + 2MNL} \right) $ |
MMVFR算法运算量包括两部分:支撑集初始重构和贝叶斯组检验。支撑集初始重构部分经过K次迭代后的运算量约为O(MNLK+M3),忽略影响较小的步骤,总的运算量约为
| $ O\left( {MNLK + {M^3} + 4MN + 2{M^2}NL} \right) $ |
MMVLL2-ISL0算法运算量主要集中在步骤3和步骤4中的搜索方向、迭代步长、可行域投影及初始的求伪逆运算,迭代K次后总的运算量约为
| $ O\left( {MNLK + {M^3} + 2MNL + 2{M^2}NL} \right) $ |
当迭代次数一样时,5种算法运算量关系为
| $ \begin{array}{*{20}{c}} {{C_{{\rm{OMPMMV}}}} < {C_{{\rm{MMVFR}}}} < {C_{{\rm{MMVLL2 - ISL0}}}} < }\\ {{C_{{\rm{SMV - SL0}}}} < {C_{{\rm{Lorentzian - ISL0}}}}} \end{array} $ |
由于MMVLL2-ISL0算法采用了固定步长的共轭梯度法,可以提高收敛速率,迭代次数的降低减少了算法的运算量,仿真实验将进一步分析。
4 实验仿真与分析本节将采用Matlab仿真试验平台,对本文提出算法的性能进行验证分析。在仿真中,采用对称参数α=0的对称α稳定分布(symmetric alpha stable,SαS)对冲击噪声进行建模,由于α稳定分布没有封闭的PDF表达式,用其特征函数定义来表示:
| $ \varphi \left( t \right) = \exp \left\{ {j\mu t - \gamma {{\left| t \right|}^\alpha }} \right\} $ |
式中:α(0<α≤2)为特征指数,决定了α稳定分布的拖尾厚度,α越小对应的尖峰噪声越严重,PDF的拖尾越厚重,非高斯程度也越强;γ(γ≥0)为分散系数,类似于高斯分布的方差,决定了稳定分布变量偏离其均值的程度;μ(-∞<μ<∞)对应于分布的位置参数。特别地,当α=2时α稳定分布对应于高斯分布。同时,由于α稳定分布(α<2)只存在分数低阶矩,没有有限的二阶矩,其方差也不存在,因此采用以下的广义信噪比:
| $ {\rm{SNR}} = 10\lg \left( {{{\left\| \mathit{\boldsymbol{x}} \right\|}^2}/N\gamma } \right) $ |
实验1 不同信号稀疏结构下各算法重构性能对比。任意稀疏结构的MMV模型的信号维度为N=256,列数为[3, 6, …, 36],稀疏度为[1, 16]任意值,且每列的稀疏位置任意,压缩比ρ=M/N=0.5,感知矩阵为高斯矩阵。图 2为特征指数α=2,信噪比15 dB时,各算法重构误差随信号向量数变化的曲线,其中蒙特卡洛仿真次数为500。相对重构误差定义为
| $ {\rm{error}} = \frac{1}{{{N_{mc}}}}\sum\limits_{n = 1}^{{N_{mc}}} {{{\left\| {{{\hat X}_n} - X} \right\|}_F}} /{\left\| X \right\|_F} $ |
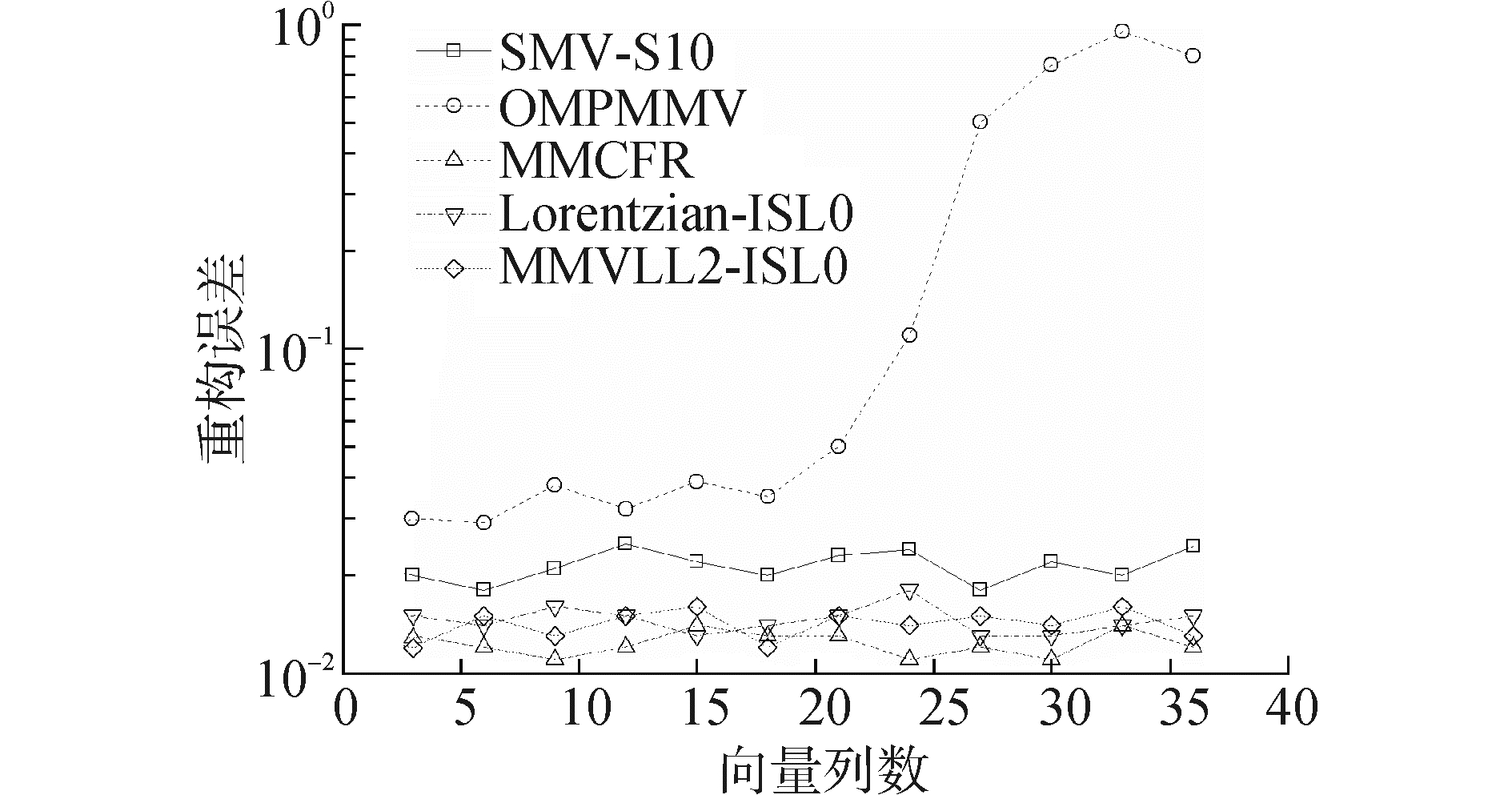
|
图 2 不同算法重构误差对比 Fig.2 Comparison of recovery error for different algorithms |
式中:Nmc为蒙特卡洛仿真次数,
从图 3可以看出,不同算法运行时间均随着信号列数的增加而增加。由于SMV-SL0算法和Lorentzian-ISL0算法分解MMV问题为多个独立的SMV问题,算法运行时间较长,且随信号列数的增加而显著增加。由于修正牛顿算法收敛速度优于最速下降法,在向量列数大于15时SMV-SL0算法运行时间超过Lorentzian-ISL0算法;而MMVFR和MMVLL2-ISL0算法采用矩阵形式的处理方法在统一参数框架下并行重构,不需要每列逐一重构,算法耗时较少。MMVLL2-ISL0算法每次迭代运算量略大于MMVFR算法,前者由于采用了固定步长的共轭梯度算法,提高了收敛速率,减少了运行耗时。从图 1、2中可以看出,本文算法在重构精度和运算速度上具有较好的性能。

|
图 3 不同算法重构速度对比 Fig.3 Comparison of recovery speed for different algorithms |
实验2 不同冲击噪声背景下各算法重构性能对比。任意稀疏结构的MMV模型的信号列数为16,其他参数与实验1相同。图 4描绘的是两种特征指数的冲击噪声条件下,不同算法重构误差随信噪比的变化,其中蒙特卡洛仿真次数为500。
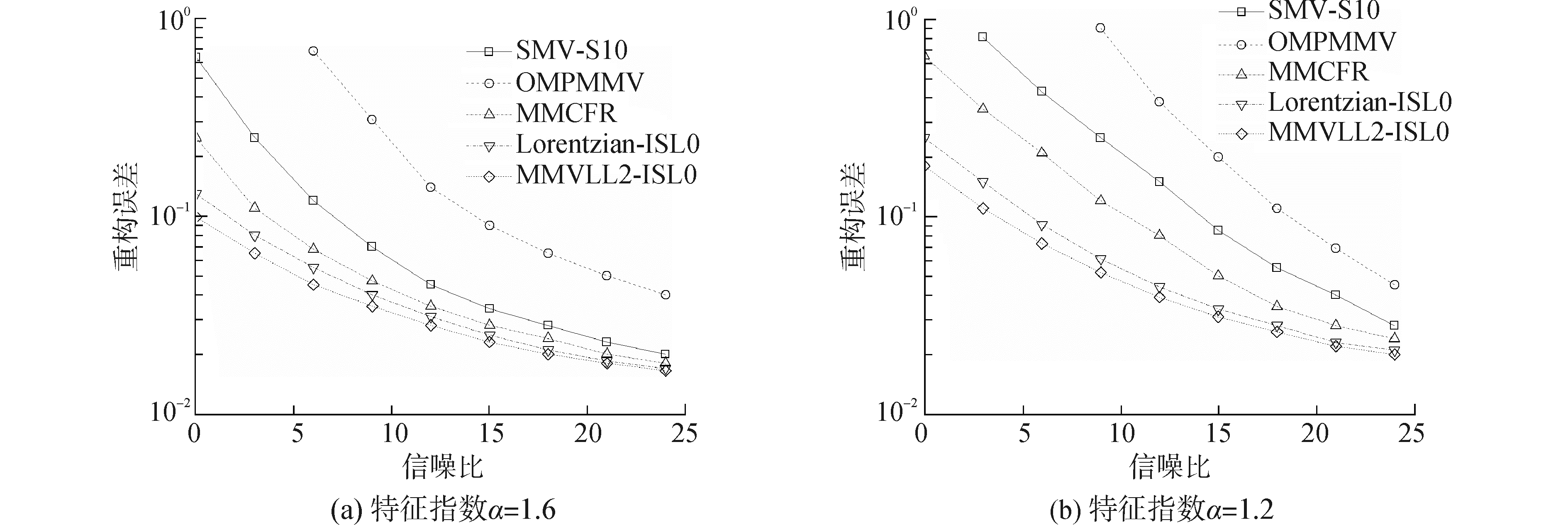
|
图 4 不同算法重构误差随信噪比的变化曲线 Fig.4 The variation curves of reconstruction error for different algorithms with SNR |
图 4(a)冲击噪声特征指数为α=1.6,可以看出,各算法的重构误差均随着信噪比的提高而呈现递减趋势。MMVLL2-ISL0和Lorentzian-ISL0算法采用Lorentzian范数作为约束条件,其软回降特性可以鲁棒性地去除观测向量中的异值元素对于重构结果的影响,重构性能最优。图 4(b)冲击噪声特征指数为α=1.2,可以看出随着噪声非高斯强度增大,各算法的重构性能均有不同程度的下降,但受冲击噪声影响的程度不同。本文所提算法性能波动较小,且冲击噪声越强,优势越明显。在高信噪比时,MMVFR、MMVLL2-ISL0、Lorentzian-ISL0算法重构误差接近。仿真验证了本文算法的有效性和实时性。
5 结论1) 基于Lorentzian范数约束的矩阵平滑零范数最小化构造了稀疏优化目标函数,建立了冲击噪声背景下任意稀疏结构的多量测向量重构模型。
2) 推导了具有固定步长的共轭梯度算法,实现了ASS-MMV模型的快速重构。
3) 与已有算法相比,本文算法降低了对信号模型联合稀疏度的要求,实现了任意稀疏结构的MMV问题的高效重构;由于采用Lorentzian范数拟合误差项,其软回降特性有效降低了冲击噪声对重构性能的影响。
正则化参数控制着允许误差和稀疏性之间的平衡,下一步有必要研究不同冲击噪声分布下正则化参数的估计问题。
| [1] |
DONOHO D L. Compressed sensing[J]. IEEE transactions on information theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 (  0) 0)
|
| [2] |
金坚, 谷源涛, 梅顺良. 压缩采样技术及其应用[J]. 电子与信息学报, 2010, 32(2): 470-475. JIN Jian, GU Yuantao, MEI Shunliang. An introduction to compressed sampling and its applications[J]. Journal of electronics & information technology, 2010, 32(2): 470-475. (  0) 0)
|
| [3] |
ELDAR Y C, MISHALI M. Robust recovery of signals from a structured union of subspaces[J]. IEEE transactions on information theory, 2009, 55(11): 5302-5316. DOI:10.1109/TIT.2009.2030471 (  0) 0)
|
| [4] |
FANG Hao, VOROBYOV S A, JIANG Hai, et al. Permutation meets parallel compressed sensing:how to relax restricted isometry property for 2D sparse signals[J]. IEEE transactions on signal process, 2014, 62(7): 196-210. (  0) 0)
|
| [5] |
ELDAR Y C, RAUHUT H. Average case analysis of multi-channel sparse recovery using convex relaxation[J]. IEEE transactions on information theory, 2010, 56(1): 505-519. DOI:10.1109/TIT.2009.2034789 (  0) 0)
|
| [6] |
TANG G, NEHORAI A. Performance analysis for sparse support recovery[J]. IEEE transactions on information theory, 2010, 56(3): 1383-1399. DOI:10.1109/TIT.2009.2039039 (  0) 0)
|
| [7] |
SUN L, LIU J, CHEN J, et al. Efficient recovery of jointly sparse vectors[C]//Advances in Neural Information Processing Systems. Vancouver, British Columbia, Canada, 2009:1812-1820. http://dl.acm.org/citation.cfm?id=2984093.2984296
(  0) 0)
|
| [8] |
韩学兵, 张颢. 模型噪声中的稀疏恢复算法研究[J]. 电子与信息学报, 2012, 34(8): 1813-1818. HAN Xuebing, ZHANG Hao. Research of sparse recovery algorithm based on model noise[J]. Journal of electronics & information technology, 2012, 34(8): 1813-1818. (  0) 0)
|
| [9] |
PENG Xiyuan, ZHANG Miao, ZHANG Jingchao, et al. An alternative recovery algorithm based on SL0 for multiband signals[C]//Instrumentation and Measurement Technology Conference (I2MTC), 2013 IEEE International. IEEE, 2013:114-117. http://ieeexplore.ieee.org/document/6555392/
(  0) 0)
|
| [10] |
WIPF D P, RAO B D. An empirical bayesian strategy for solving the simultaneous sparse approximation problem[J]. IEEE transactions on signal processing, 2007, 55(7): 3704-3716. DOI:10.1109/TSP.2007.894265 (  0) 0)
|
| [11] |
李少东, 陈文峰, 杨军, 等. 任意稀疏结构的多量测向量快速稀疏重构算法研究[J]. 电子学报, 2015, 43(4): 708-715. LI Shaodong, CHEN Wenfeng, YANG Jun, et al. Study on the fast sparse recovery algorithm via multiple measurement vectors of arbitrary sparse structure[J]. ACTA electronica sinica, 2015, 43(4): 708-715. (  0) 0)
|
| [12] |
代林, 崔琛, 余剑, 等. 冲击噪声下基于Lorentzian范数的CSR参数估计[J]. 华中科技大学学报:自然科学版, 2015(7): 66-71. DAI Lin, CUI Chen, YU Jian, et al. Parameter estimation for CSR under inpulsive noise based on Lorentzian norm[J]. Journal of Huazhong University of Science and Technology:natural science edition, 2015(7): 66-71. (  0) 0)
|
| [13] |
CANDES E, TAO T. The Dantzig selector:statistical estimation when is much larger than n[J]. Annals of statistics, 2007, 35: 2313-2351. DOI:10.1214/009053606000001523 (  0) 0)
|
| [14] |
CARRILLO R E, BARNER K E, AYSAL T C. Robust sampling and reconstruction methods for sparse signals in the presence of impulsive noise[J]. IEEE transactions on selected topics in signal processing, 2010, 4(2): 392-408. DOI:10.1109/JSTSP.2009.2039177 (  0) 0)
|
| [15] |
HUANG Jinhong, ZHOU Genjiao. A conjugate gradient method without line search and the convergence analysis[C]//2013 Fourth International Conference on Emerging Intelligent Data and Web Technologies. Xi'an, China, 2013:734-736. http://doi.ieeecomputersociety.org/10.1109/EIDWT.2013.133
(  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


