2. 三峡大学 土木与建筑学院, 湖北 宜昌 443002;
3. 华南理工大学 土木与交通学院, 广东 广州 510640
2. College of Civil Engineering and Architecture, China Three Gorges University, Yichang 443002, China;
3. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China
由于大跨度人行桥是轻柔、低阻尼结构,在行人荷载作用下易发生振动。国内外人致振动灾害现象时有发生,2010年,四川省洪雅县的一座钢索桥在游客行走下激发桥梁大幅振动,最终导致桥梁垮塌,事故造成28人死亡[1];2000年,伦敦千禧桥由于行人的荷载引起大幅振动而导致桥梁关闭[1],因此,人致振动灾害问题引起了国内外学者的广泛关注。目前计算人致结构振动的方法,多数采用有限元方法和数值分析方法进行人致振动响应分析。F.P. Figueiredo等[2]分析了现有的行人确定型荷载模型,运用ANSYS有限元软件分析某简支梁桥的模态,并采用不同荷载模型施加到有限元模型上,分析了其动力响应。采用有限元方法和数值方法进行计算时,每次计算都需要进行一次瞬态响应分析,工作量巨大,效率低。解析解是一种精确解的计算方法,目前在人致桥梁振动研究中采用解析解的方法较少,温青等[3]基于稳态简谐激励,通过数值仿真分析和现场试验研究了某人行桥的模态参数。ORESTE S. BURSI等[5]基于行人多点输入激励,研究了某斜拉桥的动力响应的概率分布。LUCA BRUNO等[5]基于多尺度模型,分析了人行桥随机荷载作用下动力响应。潘宁等[6]假定人群行走工况下楼板上各点的功率谱密度函数相同,研究了人群荷载作用下楼板的动力响应。C.C. Caprani[7-8]提出基于精细积分计算人行桥的振动响应的方法,结合模态精细积分法和闭式解,计算了恒定荷载、线性变换荷载、正弦荷载作用下人行桥的动力响应。Giuseppe Piccardo等[9]以单人等效荷载研究了行人与人行桥共振的动力放大系数。宋志刚[10]基于社会力模型,考虑行人与人行桥相互作用,将行人作用力分解为固有侧向力和附加侧向力,研究了行人作用下柔性人行桥侧向振动放大系数。徐若天[11]通过试验测得行人的步行荷载曲线,提出了单人荷载作用下,大跨度楼盖的加速度反应谱曲线,对影响反应谱曲线的参数进行了分析,并运用反应谱曲线计算了某楼盖在单人荷载作用下的加速度。陈隽[12]以加速度反应谱曲线为基础,研究了单人双脚不离地上下往复运动作用下楼盖的最大动力响应。但是目前行人引起人行桥振动的解析计算中,求解过程复杂,不便于计算和应用。设计计算中需要能够高效准确的计算行人作用下人行桥振动响应的方法。
针对以上问题,基于解析解理论,首先将行人荷载考虑为确定性模型,推导了单个过桥时振动响应的解析表达式,引入假设将解析表达式进行简化,从而得到人致简支梁桥简单实用的计算方法,以期方便地计算人行桥结构的动力响应。在动力响应简化表达式的基础上给出了人致桥梁振动频率响应函数。最后,结合某人行桥结构,运用简化公式及前人的研究成果分别进行时程分析,并运用频率响应函数计算动力响应最大值与前人的研究成果进行对比。
1 单人行走作用下结构响应及简化计算 1.1 人行荷载单个行人行走时的荷载模型,其表达式为
| $ {F_p}\left( t \right) = G + \sum\limits_{k = 1}^n {G{\alpha _k}\sin \left( {2{\rm{ \mathsf{ π} }}k{f_p}t - {\phi _k}} \right)} $ | (1) |
式中:Fp(t)为单个行人的荷载,G为人的体重,k为谐波阶数,αk为行人k阶动载系数,fp为行人行走的频率,ϕk为k阶谐波的相位,t为时间。由于竖向取前三阶已满足精度要求[13]。前三阶动载系数α1、α2、α3取值见文献[13]。
1.2 单人行走作用下结构响应解析解假设简支梁单位长度的质量为m,阻尼为c,抗弯刚度为EI。行人荷载作用下的简支梁动力学模型如图 1所示。

|
Download:
|
| 图 1 单人作用下简支梁动力学模型 Fig. 1 The dynamic model of a simple supported beam under single pedestrian action | |
令
| $ \begin{array}{*{20}{c}} {{{\ddot q}_n}\left( t \right) + 2{\zeta _n}{\omega _n}{{\dot q}_n}\left( t \right) + \omega _n^2{q_n}\left( t \right) = \frac{{2G}}{{mL}}\sin \frac{{n{\rm{ \mathsf{ π} }}vt}}{L} + }\\ {\sum\limits_{k = 1}^3 {\frac{{G{\alpha _k}}}{{mL}}\left[ {\cos \left( {{\omega _{kn1}}t} \right) - \cos \left( {{\omega _{kn2}}t} \right)} \right]} } \end{array} $ | (2) |
式中:
| $ {\omega _p} = 2{\rm{ \mathsf{ π} }}{f_p},{\omega _{0n}} = \frac{n}{p}{\omega _p}, $ |
| $ {\omega _{kn1}} = {\omega _p}\left( {k - \frac{n}{p}} \right),\;\;\;\;{\omega _{kn2}} = {\omega _p}\left( {k + \frac{n}{p}} \right) $ |
式中:
| $ \begin{array}{*{20}{c}} {{q_n}\left( t \right) = \frac{{2G}}{{mL\omega _n^2}}\left[ {{A_{0n}}\sin \left( {{\omega _{0n}}t + {\varphi _{0n}}} \right) + } \right.}\\ {\left. {{s_{0n}}{A_{B0n}}{{\rm{e}}^{ - {\zeta _n}{\omega _n}t}}\sin \left( {{\omega _{Bn}}t + {\varphi _{B0n}}} \right)} \right] + \sum\limits_{k = 1}^3 {\frac{{{\alpha _k}G}}{{mL\omega _n^2}}} \cdot }\\ {\left[ {{A_{kn1}}\sin \left( {{\omega _{kn2}}t + {\omega _{kn2}}} \right) + {A_{kn2}}\sin \left( {{\omega _{kn2}}t + } \right.} \right.}\\ {\left. {\left. {{\varphi _{kn2}}} \right) + {s_{kn}}{A_{Bkn}}{{\rm{e}}^{ - {\zeta _n}{\omega _n}t}}\sin \left( {{\omega _{Bn}}t + {\varphi _{Bkn}}} \right)} \right]} \end{array} $ |
式中:
| $ {A_{0n}} = \frac{{\omega _n^2}}{{\sqrt {{{\left( {\omega _n^2 - \omega _{0n}^2} \right)}^2} + {{\left( {2{\zeta _n}{\omega _n}{\omega _{0n}}} \right)}^2}} }}, $ |
| $ \tan {\varphi _{0n}} = \frac{{ - 2{\zeta _n}{\omega _n}{\omega _{0n}}}}{{\omega _n^2 - \omega _{0n}^2}},\;\;\;\;{\varphi _{B0n}} = 0 $ |
| $ {A_{B0n}} = \sqrt {C_{0n}^2} ,\;\;\;\;{s_{0n}} = - {\mathop{\rm sgn}} \left( {{C_{0n}}} \right), $ |
| $ {C_{0n}} = \frac{{{\zeta _n}}}{{\omega _n^2\sqrt {1 - \zeta _n^2} }}\left( {\omega _n^2 + \omega _{0n}^2} \right)A_{0n}^2 $ |
| $ {A_{kn1}} = \frac{{\omega _n^2}}{{\sqrt {{{\left( {\omega _n^2 - \omega _{kn1}^2} \right)}^2} + {{\left( {2{\zeta _n}{\omega _n}{\omega _{kn1}}} \right)}^2}} }}, $ |
| $ {A_{kn2}} = \frac{{ - \omega _n^2}}{{\sqrt {{{\left( {\omega _n^2 - \omega _{kn2}^2} \right)}^2} + {{\left( {2{\zeta _n}{\omega _n}{\omega _{kn2}}} \right)}^2}} }} $ |
| $ \tan {\varphi _{kn1}} = \frac{{\omega _n^2 - \omega _{kn1}^2}}{{2{\zeta _n}{\omega _n}{\omega _{kn1}}}},\;\;\tan {\varphi _{kn2}} = \frac{{\omega _n^2 - \omega _{kn}^2}}{{2{\zeta _n}{\omega _n}{\omega _{kn2}}}}, $ |
| $ {A_{Bkn}} = \sqrt {C_{kn}^2 + D_{kn}^2} ,\tan {\varphi _{Bkn}} = \frac{{{D_{kn}}}}{{{C_{kn}}}},{s_{kn}} = - {\mathop{\rm sgn}} \left( {{C_{kn}}} \right), $ |
| $ {C_{kn}} = \frac{{{\zeta _n}}}{{\omega _n^2\sqrt {1 - \zeta _n^2} }}\left[ {\left( {\omega _n^2 + \omega _{kn1}^2} \right)A_{kn1}^2 - \left( {\omega _n^2 + \omega _{kn2}^2} \right)A_{kn2}^2} \right] $ |
| $ {D_{kn}} = \frac{1}{{\omega _n^2}}\left[ {\left( {\omega _n^2 - \omega _{kn1}^2} \right)A_{kn1}^2 - \left( {\omega _n^2 - \omega _{kn2}^2} \right)A_{kn2}^2} \right] $ |
由于人行桥的阻尼比ζn
| $ \begin{array}{*{20}{c}} {\ddot q\left( t \right) = - \frac{{2G}}{{mL\omega _n^2}}\left[ {{A_{0n}}\omega _{0n}^2\sin \left( {{\omega _{0n}}t + {\varphi _{0n}}} \right) + } \right.}\\ {\left. {{s_{0n}}{A_{B0n}}{{\rm{e}}^{ - {\zeta _n}{\omega _n}t}}\omega _{Bn}^2\sin \left( {{\omega _{Bn}}t + {\varphi _{B0n}}} \right)} \right] - }\\ {\sum\limits_{k = 1}^3 {\frac{{{\alpha _k}G}}{{mL\omega _n^2}}\left[ {{A_{kn1}}\omega _{kn1}^2\sin \left( {{\omega _{kn1}}t + {\varphi _{kn1}}} \right) + } \right.} }\\ {{A_{kn2}}\omega _{kn2}^2\sin \left( {{\omega _{kn2}}t + {\varphi _{kn2}}} \right) + }\\ {\left. {{s_{kn1}}{A_{Bkn}}{{\rm{e}}^{ - {\zeta _n}{\omega _n}t}}\omega _{Bn}^2\sin \left( {{\omega _{Bn}}t + {\varphi _{Bkn}}} \right)} \right]} \end{array} $ | (3) |
当行人与人行桥共振时,人致桥梁振动的响应最大,因此取n=1,则单个行人的荷载可以等效为
| $ {F_p}\left( {x,t} \right) = {F_0}\sin \left( {2{\rm{ \mathsf{ π} }}{f_1}t} \right)\delta \left( {x - ct} \right) $ | (4) |
式中:x描述一维结构的横轴;δ为Dirac函数;F0=αG,是力的幅值;α为动载系数。因此,共振时的动力学方程为
| $ \begin{array}{*{20}{c}} {{{\ddot q}_n}\left( t \right) + 2{\zeta _n}{\omega _n}{{\dot q}_n}\left( t \right) + \omega _n^2{q_n}\left( t \right) = }\\ {\frac{{{F_0}}}{{mL}}\left[ {\cos \left( {{\omega _{7n}}t} \right) - \cos \left( {{\omega _{8n}}t} \right)} \right]} \end{array} $ | (5) |
当人致桥梁产生共振时,ωp=ωn。
| $ {\omega _{7n}} = {\omega _n}\left( {1 - \frac{n}{p}} \right) = {\omega _n}\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right) $ |
| $ {\omega _{8n}} = {\omega _n}\left( {1 + \frac{n}{p}} \right) = {\omega _n}\left( {1 + \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right) $ |
方程(5)的解为
| $ \begin{array}{*{20}{c}} {{q_n}\left( t \right) = \frac{{{F_0}}}{{mL\omega _n^2}}\left[ {{A_{7n}}\sin \left( {{\omega _{7n}}t + {\varphi _{7n}}} \right) + } \right.}\\ {\left. {{A_{8n}}\sin \left( {{\omega _{8n}}t + {\varphi _{8n}}} \right) + {s_n}{A_{Bn}}{{\rm{e}}^{ - {\zeta _n}{\omega _n}t}}\sin \left( {{\omega _{Dn}}t + {\varphi _{Dn}}} \right)} \right]} \end{array} $ |
式中:
| $ {A_{7n}} = \frac{{\omega _n^2}}{{\sqrt {{{\left( {\omega _n^2 - \omega _{7n}^2} \right)}^2} + {{\left( {2{\zeta _n}{\omega _n}{\omega _{7n}}} \right)}^2}} }}, $ |
| $ {A_{8n}} = \frac{{ - \omega _n^2}}{{\sqrt {{{\left( {\omega _n^2 - \omega _{8n}^2} \right)}^2} + {{\left( {2{\zeta _n}{\omega _n}{\omega _{8n}}} \right)}^2}} }} $ |
| $ \tan {\varphi _{7n}} = \frac{{\omega _n^2 - \omega _{7n}^2}}{{2{\zeta _n}{\omega _n}{\omega _{7n}}}},\tan {\varphi _{8n}} = \frac{{\omega _n^2 - \omega _{8n}^2}}{{2{\zeta _n}{\omega _n}{\omega _{8n}}}}, $ |
| $ {A_{B7n}} = \sqrt {C_n^2 + D_n^2} ,\tan {\varphi _{B7n}} = \frac{{{D_n}}}{{{C_n}}} $ |
| $ {s_n} = - {\mathop{\rm sgn}} \left( {{C_{7n}}} \right),{\omega _{Dn}} = {\omega _n}\sqrt {1 - {\zeta _n}} , $ |
| $ {C_{7n}} = \frac{{{\zeta _n}}}{{\omega _n^2\sqrt {1 - \zeta _n^2} }}\left[ {\left( {\omega _n^2 + \omega _{7n}^2} \right)A_{7n}^2 - \left( {\omega _n^2 + \omega _{8n}^2} \right)A_{8n}^2} \right] $ |
| $ {D_{7n}} = \frac{1}{{\omega _n^2}}\left[ {\left( {\omega _n^2 - \omega _{7n}^2} \right)A_{7n}^2 - \left( {\omega _n^2 - \omega _{8n}^2} \right)A_{8n}^2} \right] $ |
定义与人行桥结构的阻尼、振型阶数、跨径及行人步长有关系统参数为
由于人行桥的阻尼比一般为:0.2%≤ζn≤3.0%,因此n/p=ζn/εn→0上面的式子可以简化为
| $ {A_{7n}} \cong \frac{{{\varepsilon _n}}}{{2{\zeta _n}}}\frac{1}{{\sqrt {1 + \varepsilon _n^2} }} = - {A_{8n}}, $ |
| $ \tan {\varphi _{7n}} = \frac{n}{{p{\zeta _n}}} = \frac{1}{{{\varepsilon _n}}} \cong - \tan {\varphi _{8n}}, $ |
| $ {C_{7n}} = - \frac{{{\varepsilon _n}}}{{1 + \varepsilon _n^2}},{D_{7n}} = - \frac{{{\varepsilon _n}}}{{{\zeta _n}\left( {1 + \varepsilon _n^2} \right)}} $ |
| $ {A_{B7n}} \cong \frac{{{\varepsilon _n}}}{{{\zeta _n}\left( {1 + \varepsilon _n^2} \right)}},\tan {\varphi _{B7n}} \cong \frac{1}{{{\zeta _n}}} \to \infty , $ |
| $ {\varphi _{B7n}} \to \frac{{\rm{ \mathsf{ π} }}}{2},s = - 1,{\omega _{Dn}} = {\omega _n}\sqrt {1 - \zeta _n^2} \cong {\omega _n} $ |
加速度响应可以简化为
| $ \begin{array}{*{20}{c}} {\ddot q\left( t \right) \cong - \frac{{{\alpha _1}G}}{{mL}}\left\{ {\frac{{{\varepsilon _n}}}{{{\zeta _n}}}\frac{1}{{1 + \varepsilon _n^2}}\left[ {\sqrt {1 + \varepsilon _n^2} \sin \left( {\frac{{{\zeta _n}}}{{{\varepsilon _n}}}{\omega _n}t - } \right.} \right.} \right.}\\ {\left. {\left. {\left. {\arctan \frac{1}{{{\varepsilon _n}}}} \right) + {{\rm{e}}^{ - {\zeta _n}{\omega _n}t}}} \right]\cos \left( {{\omega _n}t} \right)} \right\} = - \omega _n^2H\left( t \right)\cos \left( {{\omega _n}t} \right)} \end{array} $ | (6) |
由式(6)可得:
| $ \begin{array}{*{20}{c}} {H\left( t \right) = \frac{{{\alpha _1}G}}{{\omega _n^2mL}}\left\{ {\frac{{{\varepsilon _n}}}{{{\zeta _n}}}\frac{1}{{1 + \varepsilon _n^2}}\left[ {\sqrt {1 + \varepsilon _n^2} \sin \left( {\frac{{{\zeta _n}}}{{{\varepsilon _n}}}{\omega _n}t - } \right.} \right.} \right.}\\ {\left. {\left. {\left. {\arctan \frac{1}{{{\varepsilon _n}}}} \right) + {{\rm{e}}^{ - {\zeta _n}{\omega _n}t}}} \right]} \right\}} \end{array} $ |
H(t)的最大值为人行桥动力响应包络曲线,对H(t)求导, 令
| $ \cos \left( {\frac{{{\zeta _n}}}{{{\varepsilon _n}}}{\omega _n}t - \arctan \frac{1}{{{\varepsilon _n}}}} \right) = \frac{{{\varepsilon _n}}}{{\sqrt {1 + \varepsilon _n^2} }}{{\rm{e}}^{ - {\zeta _n}{\omega _n}t}} $ | (7) |
由于求方程(7)的精确解较为困难,故求其近似解,假设:
| $ a\left( t \right) = \cos \left( {\frac{{{\zeta _n}}}{{{\varepsilon _n}}}{\omega _n}t - \arctan \frac{1}{{{\varepsilon _n}}}} \right) $ |
| $ b\left( t \right) = \frac{{{\varepsilon _n}}}{{\sqrt {1 + \varepsilon _n^2} }}{{\rm{e}}^{ - {\zeta _n}{\omega _n}t}} $ |
函数a(t)、b(t)在a(t)=0、b(t)=0处,两条切线的交点即为方程的解,交点为
| $ t' = \frac{{{\varepsilon _n}}}{{{\zeta _n}{\omega _n}}}\left[ {\frac{{\rm{ \mathsf{ π} }}}{2} + \arctan \frac{1}{{{\varepsilon _n}}} - \frac{{{\varepsilon _n}}}{{{{\rm{e}}^{{\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{2} + \arctan \frac{1}{{{\varepsilon _n}}}} \right)}}\sqrt {1 + \varepsilon _n^2} }}} \right] $ |
因此,在t′时刻单人行走时引起人行桥的振动响应最大,加速度包络线为
| $ \begin{array}{*{20}{c}} {\ddot q\left( t \right) = \frac{{{\alpha _1}G}}{{mL}} \cdot \frac{{{\varepsilon _n}}}{{{\zeta _n}}} \cdot \frac{1}{{1 + \varepsilon _n^2}}\left[ {\sqrt {1 + \varepsilon _n^2} \cdot } \right.}\\ {\cos \frac{{{\varepsilon _n}}}{{{{\rm{e}}^{{\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{2} + \arctan \frac{1}{{{\varepsilon _n}}}} \right)}}\sqrt {1 + \varepsilon _n^2} }} + }\\ {\left. {{{\rm{e}}^{ - {\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{2} + \arctan \frac{1}{{{\varepsilon _n}}} - \frac{{{\varepsilon _n}}}{{{{\rm{e}}^{{\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{2} + \arctan \frac{1}{{{\varepsilon _n}}}} \right)}}\sqrt {1 + \varepsilon _n^2} }}} \right)}}} \right]} \end{array} $ | (8) |
由式(8),定义μ为瞬态共振响应函数, 令
| $ \begin{array}{*{20}{c}} {\mu \left( {{\varepsilon _n}} \right) = \frac{{{\varepsilon _n}}}{{{\zeta _n}}}\frac{1}{{1 + \varepsilon _n^2}}\left[ {\sqrt {1 + \varepsilon _n^2} \cdot } \right.}\\ {\cos \frac{{{\varepsilon _n}}}{{{{\rm{e}}^{{\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{2} + \arctan \frac{1}{{{\varepsilon _n}}}} \right)}}\sqrt {1 + \varepsilon _n^2} }} + }\\ {\left. {{{\rm{e}}^{ - {\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{2} + \arctan \frac{1}{{{\varepsilon _n}}} - \frac{{{\varepsilon _n}}}{{{{\rm{e}}^{{\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{2} + \arctan \frac{1}{{{\varepsilon _n}}}} \right)}}\sqrt {1 + \varepsilon _n^2} }}} \right)}}} \right]} \end{array} $ | (9) |
根据式(9)绘出人致桥梁振动共振响应包络图如图 2,由图可知:随着人行桥结构的阻尼比ζn增加,共振响应包络值μ迅速减小,当阻尼比大于0.01后,共振响应包络值变化不明显;随着系统参数εn增加,共振响应包络值迅速增大,当系统参数大于1.5后,共振响应包络值变化不大。

|
Download:
|
| 图 2 人致桥梁振动共振响应包络图 Fig. 2 Envelope diagram of the resonance response of the bridge vibration induced by human | |
当行人行走频率与桥梁的固有频率相差较远时,行人激励频率与桥梁的n阶振动频率的比值定义为
| $ {\gamma _n} = \frac{\omega }{{{\omega _n}}} $ | (10) |
因此,式(9)、(10)可以用γn来表示为
| $ {A_{in1}} = \frac{1}{{\sqrt {{{\left[ {1 - \gamma _n^2\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)} \right]}^2} + {{\left[ {2{\zeta _n}{\gamma _n}\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)} \right]}^2}} }}, $ |
| $ {A_{in2}} = \frac{{ - 1}}{{\sqrt {{{\left[ {1 - \gamma _n^2\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)} \right]}^2} + {{\left[ {2{\zeta _n}{\gamma _n}\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)} \right]}^2}} }} $ |
| $ \tan {\varphi _{in1}} = \frac{{1 - \gamma _n^2{{\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)}^2}}}{{2{\zeta _n}{\gamma _n}\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)}}, $ |
| $ \tan {\varphi _{in2}} = \frac{{1 - \gamma _n^2{{\left( {1 + \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)}^2}}}{{2{\zeta _n}{\gamma _n}\left( {1 + \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)}}, $ |
| $ {A_{Bin}} = \sqrt {C_{in}^2 + D_{in}^2} $ |
| $ \begin{array}{*{20}{c}} {{C_{in}} = \frac{{{\zeta _n}}}{{\sqrt {1 - \zeta _n^2} }}\left[ {1 + \gamma _n^2{{\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)}^2}} \right]A_{in}^2 - }\\ {\left. {\left( {1 + \gamma _n^2{{\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)}^2}} \right)A_{in}^2} \right]}\\ {{D_{in}} = \left[ {1 - \gamma _n^2{{\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)}^2}} \right]A_{in}^2 - }\\ {\left. {\left( {1 + \gamma _n^2{{\left( {1 - \frac{{{\zeta _n}}}{{{\varepsilon _n}}}} \right)}^2}} \right)A_{in}^2} \right],i = 1,2,3} \end{array} $ | (11) |
由于0.2%≤ζn≤3.0%,所以
| $ {A_{1n}} = \frac{1}{{\left| {1 - \gamma _n^2} \right|}} \cong - {A_{2n}},{\varphi _{0n}} \to 0, $ |
| $ {C_{1n}} = - \frac{{4\gamma _n^2}}{{{{\left( {1 - \gamma _n^2} \right)}^2}}}\frac{{\zeta _n^2}}{{{\varepsilon _n}}} $ |
| $ {D_{1n}} \cong - \frac{{4\gamma _n^2}}{{\left( {1 - \gamma _n^2} \right)^2}}\frac{{{\zeta _n}}}{{{\varepsilon _n}}},{A_{B1n}} = \frac{{4\gamma _n^2}}{{{{\left( {1 - \gamma _n^2} \right)}^2}}}\frac{{{\zeta _n}}}{{{\varepsilon _n}}}, $ |
| $ {\varphi _{B0n}} = \frac{{\rm{ \mathsf{ π} }}}{2} $ |
同理可得:
| $ {A_{0n}} \cong 1,{\varphi _{0n}} \to 0,{C_{0n}} = \frac{{{\zeta _n}\left( {\varepsilon _n^2 + \gamma _n^2\zeta _n^2} \right)}}{{\varepsilon _n^2}}, $ |
| $ {D_{0n}} \cong \frac{{\left( {\varepsilon _n^2 - \gamma _n^2\zeta _n^2} \right)}}{{\varepsilon _n^2}},{A_{B3n}} = \frac{{\left( {\varepsilon _n^2 - \gamma _n^2\zeta _n^2} \right)}}{{\varepsilon _n^2}}, $ |
| $ {\varphi _{B0n}} = \frac{{\rm{ \mathsf{ π} }}}{2} $ |
| $ {A_{3n}} = \frac{1}{{\left| {1 - \gamma _n^2} \right|}} \cong - {A_{4n}},{\varphi _{3n}} = {\varphi _{4n}} \to \frac{{\rm{ \mathsf{ π} }}}{2}, $ |
| $ {C_{3n}} = - \frac{{4\gamma _n^2}}{{{{\left( {1 - \gamma _n^2} \right)}^2}}}\frac{{\zeta _n^2}}{{{\varepsilon _n}}},{\varphi _{B0n}} = \frac{{\rm{ \mathsf{ π} }}}{2}, $ |
| $ {D_{3n}} \cong - \frac{{4\gamma _n^2}}{{{{\left( {1 - \gamma _n^2} \right)}^2}}}\frac{{{\zeta _n}}}{{{\varepsilon _n}}},{A_{B3n}} = \frac{{4\gamma _n^2}}{{{{\left( {1 - \gamma _n^2} \right)}^2}}}\frac{{{\zeta _n}}}{{{\varepsilon _n}}} $ |
| $ {A_{5n}} = \frac{1}{{\left| {1 - \gamma _n^2} \right|}} \cong - {A_{6n}},{\varphi _{5n}} = {\varphi _{6n}} \to \frac{{\rm{ \mathsf{ π} }}}{2}, $ |
| $ {C_{5n}} = - \frac{{4\gamma _n^2}}{{{{\left( {1 - \gamma _n^2} \right)}^2}}}\frac{{\zeta _n^2}}{{{\varepsilon _n}}},{\varphi _{B0n}} = \frac{{\rm{ \mathsf{ π} }}}{2}, $ |
| $ {D_{5n}} \cong - \frac{{4\gamma _n^2}}{{{{\left( {1 - \gamma _n^2} \right)}^2}}}\frac{{{\zeta _n}}}{{{\varepsilon _n}}},{A_{B5n}} = \frac{{4\gamma _n^2}}{{{{\left( {1 - \gamma _n^2} \right)}^2}}}\frac{{{\zeta _n}}}{{{\varepsilon _n}}} $ |
因此,加速度可以简化为
| $ \begin{array}{*{20}{c}} {{{\ddot q}_n}\left( t \right) = - \frac{{2G\gamma _n^2}}{{mL}}\left[ {\sin \left( {{\gamma _n}{\omega _n}\frac{{{\zeta _n}}}{{{\varepsilon _n}}}t} \right) - } \right.}\\ {\left. {\frac{{{\zeta _n}}}{{{\varepsilon _n}}} \cdot \frac{2}{{1 - \gamma _n^2}}{{\rm{e}}^{ - {\zeta _n}{\omega _n}t}}\cos \left( {{\omega _{Bn}}t} \right)} \right] - }\\ {\sum\limits_{k = 1}^3 {\frac{{{\alpha _k}G}}{{mL}} \cdot \frac{{2\gamma _n^2}}{{\left| {1 - \gamma _n^2} \right|}}} \left[ {\sin \left( {{\gamma _n}{\omega _n}t} \right)\sin \left( {{\gamma _n}{\omega _n}\frac{{{\zeta _n}}}{{{\varepsilon _n}}}t} \right) - } \right.}\\ {\left. {\frac{{{\zeta _n}}}{{{\varepsilon _n}}} \cdot \frac{2}{{1 - \gamma _n^2}}{{\rm{e}}^{ - {\zeta _n}{\omega _n}t}}\cos \left( {{\omega _{Bn}}t} \right)} \right]} \end{array} $ | (12) |
对式(12)近似处理,得到其包络线为
| $ \begin{array}{*{20}{c}} {V\left( t \right) = {{\ddot q}_n}\left( t \right) = \left( { - \frac{{2G\gamma _n^2}}{{mL}} - \frac{{{\alpha _1}G}}{{mL}} \cdot \frac{{2\gamma _n^2}}{{\left| {1 - \gamma _n^2} \right|}} - } \right.}\\ {\left. {\frac{{{\alpha _2}G}}{{mL}} \cdot \frac{{2\gamma _n^2}}{{\left| {1 - \gamma _n^2} \right|}} - \frac{{{\alpha _3}G}}{{mL}} \cdot \frac{{2\gamma _n^2}}{{\left| {1 - \gamma _n^2} \right|}}} \right)}\\ {\left[ {\sin \left( {{\gamma _n}{\omega _n}\frac{{{\zeta _n}}}{{{\varepsilon _n}}}t} \right) - \frac{{{\zeta _n}}}{{{\varepsilon _n}}} \cdot \frac{2}{{\left| {1 - \gamma _n^2} \right|}}{{\rm{e}}^{ - {\zeta _n}{\omega _n}t}}} \right]} \end{array} $ | (13) |
对V(t)求导,并令
| $ {t^{2'}} = \frac{{{\varepsilon _n}}}{{{\omega _n}}}\left( {\frac{{\rm{ \mathsf{ π} }}}{{2{\zeta _n}{\gamma _n}}} - \frac{2}{{\gamma _n^2\left| {1 - \gamma _n^2} \right|}} \cdot {e^{ - \frac{{{\varepsilon _n}{\rm{ \mathsf{ π} }}}}{{2{\gamma _n}}}}}} \right) $ |
所以加速度的瞬态响应函数分别为
| $ \begin{array}{*{20}{c}} {\frac{{ - mL}}{{\left( {G\left| {1 - \gamma _n^2} \right| + {\alpha _1}G + {\alpha _2}G + {\alpha _3}G} \right)}}V\left( {{t^{2'}}} \right) = }\\ {\frac{{2\gamma _n^2}}{{\left| {1 - \gamma _n^2} \right|}} \cdot \left[ {\sin \left( {\frac{{2{\zeta _n}{\gamma _n}}}{{\left| {1 - \gamma _n^2} \right|}} \cdot {{\rm{e}}^{ - \frac{{{\varepsilon _n}{\rm{ \mathsf{ π} }}}}{{2{\gamma _n}}}}}} \right) + } \right.}\\ {\left. {\frac{{{\zeta _n}}}{{{\varepsilon _n}}} \cdot \frac{{2{\gamma _n}{\zeta _n}}}{{\left| {1 - \gamma _n^2} \right|}} \cdot {{\rm{e}}^{ - {\zeta _n}{\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{{2{\zeta _n}{\gamma _n}}} - \frac{2}{{\left| {1 - \gamma _n^2} \right|}} \cdot {{\rm{e}}^{ - \frac{{{\varepsilon _n}{\rm{ \mathsf{ π} }}}}{{2{\gamma _n}}}}}} \right)}}} \right]} \end{array} $ | (14) |
式(14)是频率参数γn,结构阻尼比ζn,系统响应平稳性参数εn的函数,称为人致桥梁振动频响函数,也称为放大系数。取二者中的较小值,得出结构的加速度瞬态频率响应函数分别为
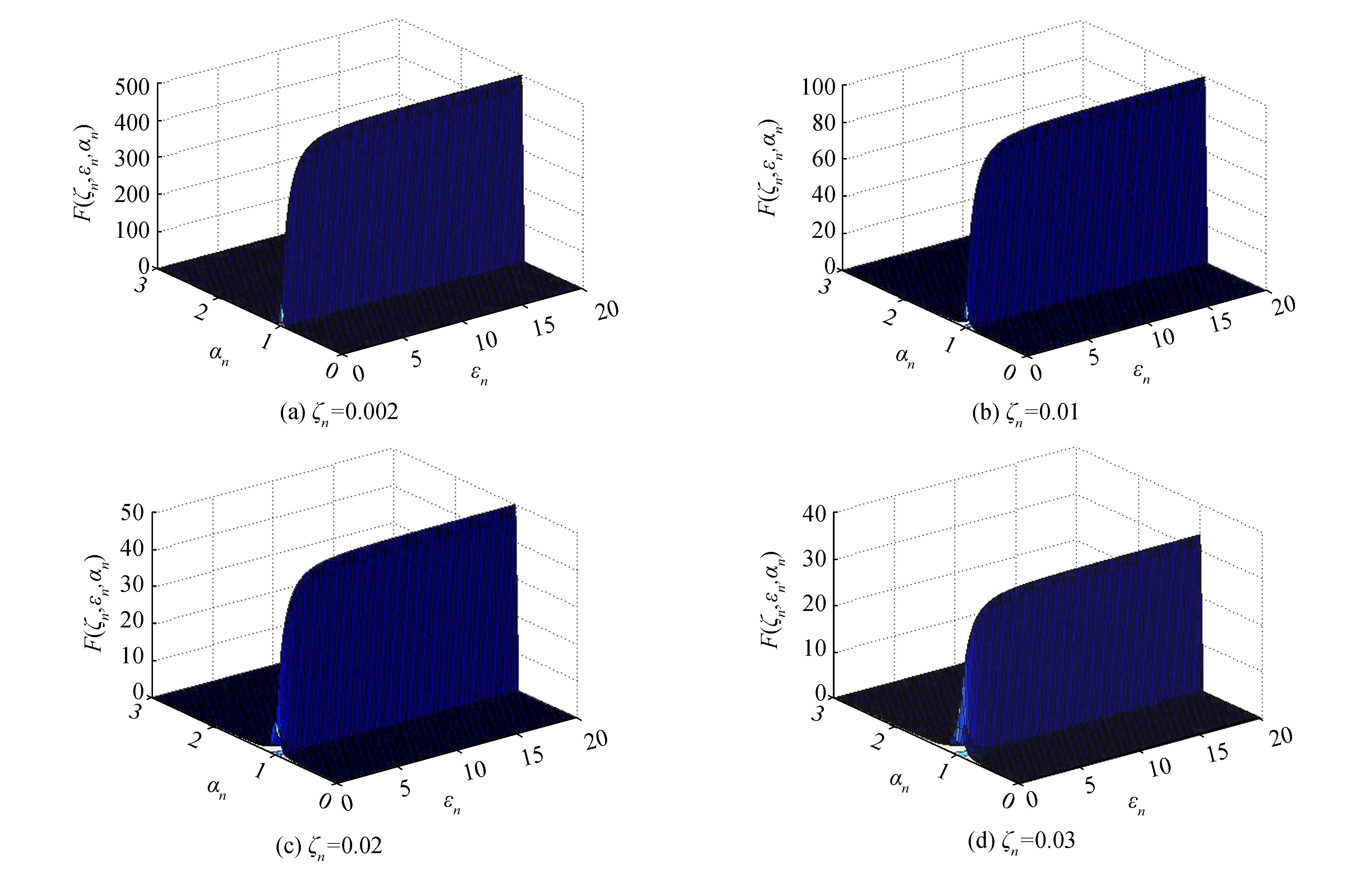
| $ \begin{array}{*{20}{c}} {{F_{\ddot q}}\left( {{\zeta _n},{\varepsilon _n},{\gamma _n}} \right) = }\\ {\min \left\{ {\frac{{2\gamma _n^2}}{{\left| {1 - \gamma _n^2} \right|}} \left[ {\cos \left( {\frac{{2{\zeta _n}}}{{{\gamma _n}\left| {1 - \gamma _n^2} \right|}} \cdot {{\rm{e}}^{ - \frac{{{\varepsilon _n}{\rm{ \mathsf{ π} }}}}{{2{\gamma _n}}}}}} \right)} \right.} \right. - }\\ {\left. {\frac{{{\zeta _n}}}{{{\varepsilon _n}}} \cdot \frac{2}{{\left| {1 - \gamma _n^2} \right|}} \cdot {{\rm{e}}^{ - {\zeta _n}{\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{{2{\zeta _n}{\gamma _n}}} - \frac{2}{{\gamma _n^2\left| {1 - \gamma _n^2} \right|}} \cdot {e^{ - \frac{{{\varepsilon _n}{\rm{ \mathsf{ π} }}}}{{2{\gamma _n}}}}}} \right)}}} \right];}\\ {\frac{{{\zeta _n}}}{{{\varepsilon _n}}} \cdot \frac{1}{{1 + \varepsilon _n^2}}\left[ {\sqrt {1 + \varepsilon _n^2} \cos \frac{{{\varepsilon _n}}}{{{{\rm{e}}^{{\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{2}+\arctan \frac{1}{{{\varepsilon _n}}}} \right)}}\sqrt {1 + \varepsilon _n^2} }} + } \right.}\\ {\left. {\left. {{{\rm{e}}^{ - {\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{2}+\arctan \frac{1}{{{\varepsilon _n}}} - \frac{{{\varepsilon _n}}}{{{{\rm{e}}^{{\varepsilon _n}\left( {\frac{{\rm{ \mathsf{ π} }}}{2}+\arctan \frac{1}{{{\varepsilon _n}}}} \right)}}\sqrt {1 + \varepsilon _n^2} }}} \right)}}} \right]} \right\}} \end{array} $ | (15) |
根据式(15)绘制了不同阻尼比情况下加速度瞬态频率响应函数如图 3,由图 3可知:随着阻尼比的增大,加速度瞬态频率响应值逐渐减小。在激励频率靠近桥梁固有频率的区域时,系统参数εn对加速度瞬态频率响应值的影响远大于激励频率远离桥梁固有频率区域;在激励频率越靠近桥梁的固有频率时,当εn较小时,加速度瞬态频率响应值随着εn的增大而迅速增大,随后影响逐渐减弱。
|
Download:
|
| 图 3 人行桥瞬态加速度频率响应函数图 Fig. 3 The frequency response function of the transient acceleration of pedestrian bridge | |
某人行桥跨径L=36 m,桥面宽B=3 m,人群行走的有效宽度为2.5 m,单位长度质量为1 500 kg/m,抗弯刚度为3.444×109N·m2,阻尼比为0.005。其前三阶频率分别为1.836 Hz、7.337 Hz、16.481 Hz。行人在该桥上行走可激起前两阶频率共振,对应的行走速度分别为:1.304 m/s,5.209 m/s,时间步长取为0.01 s。分析其一阶频率响应是共振、非共振的加速度时程。
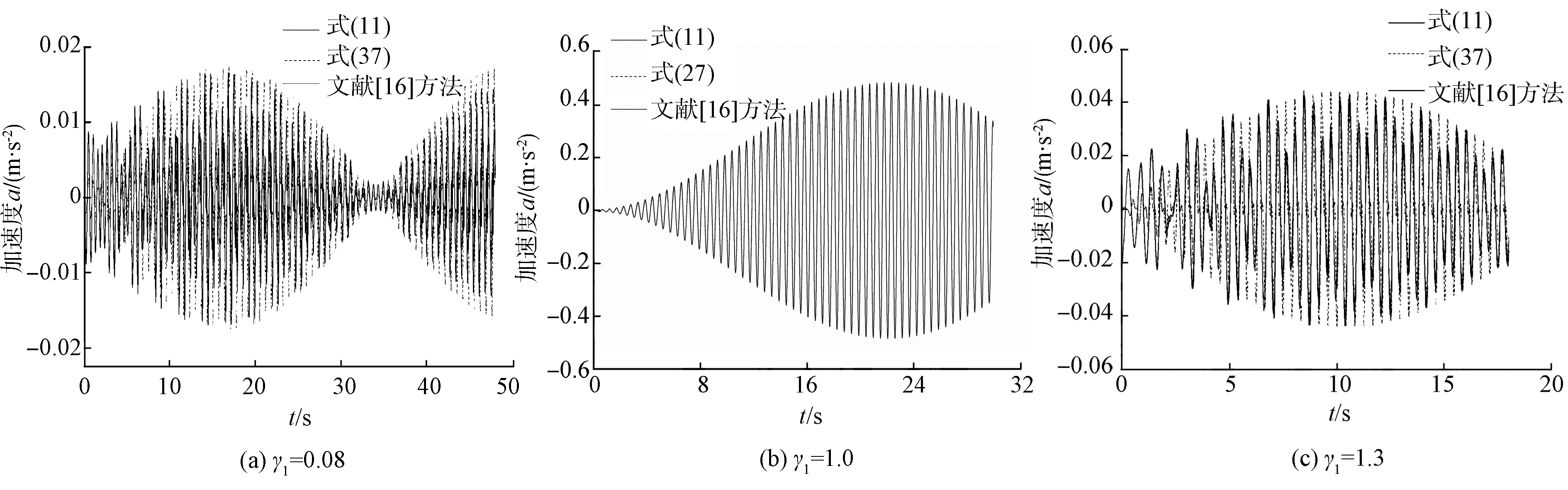
图 4给出了3种频率比时加速度时程响应对比,从图 4可知:在图 4(a)、(c)中文献[13]的时程值比文中方法索计算的结果偏小,这是由于文献[13]中只考虑行人自重和一阶谐波荷载。式(8)、(13)的计算结果与式(11)、文献[13]中的方法进行对比,时程曲线相吻合,且简化后的最大响应值基本上能够包络简化前的值。说明文中的方法是合理正确的,用简化公式进行计算在保证精度的前提下,计算效率更高。
|
Download:
|
| 图 4 各种频率比情况两种加速度时程响应对比 Fig. 4 Comparison of two kinds of acceleration time history response of different frequency ratio | |
分别利用瞬态加速度频率响应函数式(15)和时程法求得人致桥梁振动的最大加速度响应对比如表 1。从表 1可知:利用瞬态加速度频率响应函数计算的结构最大加速度响应与时程分析得到的最大加速度相近,误差较小,共振时,误差最小。且与现有规范的计算方法、研究成果的结果相接近,说明文中提出的解析解方法、及其简化计算方法是可靠的。BS5400方法计算得到的结果偏小,由于BS5400方法没有考虑行人荷载中的高阶谐波分量的影响,所以计算得到的结果偏小;而EC5-2方法计算得到的结果与文中的计算很接近,说明文中的方法是合理正确的。
| 表 1 单人行走作用下人行桥竖向加速度对比表(εn=0.5,ζn=0.005) Tab.1 A walking pedestrian bridge under effect of vertical acceleration comparison table |
1) 随着阻尼比的增大,加速度瞬态频率响应值逐渐减小;激励频率不同,系统参数εn对频率响应值得影响不同;当激励频率远离桥梁的固有频率时,激励频率对其影响较小。
2) 通过与前人的研究结果进行比较,证明本文的方法具有较高的精度,同时可以避免进行时程和基于动力可靠度分析时的复杂计算, 提高了人致桥梁振动的计算效率,进一步研究可开展人群荷载激励下的简化计算研究。
| [1] |
秦敬伟. 基于双足步行模型的人体-结构相互作用[D]. 北京: 北京交通大学, 2013, 1-5 QIN Jingwei. Human-structure interaction based on the bipedal walking model[D]. Beijing: Beijing Jiaotong University, 2013, 1-5. http://cdmd.cnki.com.cn/Article/CDMD-10004-1014178364.htm (  0) 0)
|
| [2] |
FIGUEIREDO F P, DA SILVA J G S, DE LIMA L R O, et al. A parametric study of composite footbridges under pedestrian walking loads[J]. Engineering structures, 2008, 30(3): 605-615. DOI:10.1016/j.engstruct.2007.04.021 (  0) 0)
|
| [3] |
温青, 华旭刚, 陈政清, 等. 基于稳态简谐激励的人行桥模态参数识别[J]. 中国公路学报, 2017, 30(2): 98-106. WEN Qing, HUA Xugang, CHEN Zhengqing, et al. Modal parameters identification of footbridges based on steady-state sinusoidal excitations[J]. China journal of highway and transport, 2017, 30(2): 98-106. (  0) 0)
|
| [4] |
BURSI O S, CAZZADOR E, USSIA A. Probabilistic analysis of a twin deck curved cable-stayed footbridge subjected to multiple inputs and corrosion[J]. Engineering structures, 2015, 105: 87-98. DOI:10.1016/j.engstruct.2015.09.034 (  0) 0)
|
| [5] |
BRUNO L, CORBETTA A. Uncertainties in crowd dynamic loading of footbridges:A novel multi-scale model of pedestrian traffic[J]. Engineering structures, 2017, 147: 545-566. DOI:10.1016/j.engstruct.2017.05.066 (  0) 0)
|
| [6] |
潘宁, 杜文博, 倪志伟, 等. 计算人群行走楼板响应的随机振动方法[J]. 建筑科学, 2016, 32(5): 36-43. PAN Ning, DU Wenbo, NI Zhiwei, et al. Random vibration method for calculating floor vibration response under crowd walking[J]. Building science, 2016, 32(5): 36-43. (  0) 0)
|
| [7] |
CAPRANI C C, KEOGH J, ARCHBOLD P, et al. Enhance-ment factors for the vertical response of footbridges subjected to stochastic crowd loading[J]. Computers & structures, 2012, 102-103: 87-96. (  0) 0)
|
| [8] |
CAPRANI C C. A modal precise integration method for the calculation of footbridge vibration response[J]. Computers & structures, 2013, 128: 116-127. (  0) 0)
|
| [9] |
PICCARDO G, TUBINO F. Simplified procedures for vibration serviceability analysis of footbridges subjected to realistic walking loads[J]. Computers & structures, 2009, 87(13/14): 809-903. (  0) 0)
|
| [10] |
宋志刚, 张尧. 人-桥侧向动力相互作用下侧振动的动力放大系数分析[J]. 振动与冲击, 2015, 34(1): 19-23. SONG Zhigang, ZHANG Yao. Analysis of the dynamic amplification factor of lateral structural vibration induced by crowd-bridge interaction[J]. Journal of vibration and shock, 2015, 34(1): 19-23. (  0) 0)
|
| [11] |
徐若天, 陈隽, 叶艇, 等. 大跨度楼盖步行荷载作用的加速度反应谱研究[J]. 建筑结构学报, 2015, 36(4): 133-140. XU Ruotian, CHEN Jun, YE Ting, et al. Acceleration response spectrum for predicting floor vibration due to occupant walking[J]. Journal of building structures, 2015, 36(4): 133-140. (  0) 0)
|
| [12] |
陈隽, 王磊, 楼佳悦, 等. 单人Bounce荷载下楼盖结构加速度反应谱设计[J]. 振动与冲击, 2015, 34(5): 14-19, 38. CHEN Jun, WANG Lei, LOU Jiayue, et al. Acceleration response spectrum for predicting floor vibration due to single human bounce load[J]. Journal of vibration and shock, 2015, 34(5): 14-19, 38. (  0) 0)
|
| [13] |
陈璞. 人行桥振动舒适度的设计与评价理论研究[D]哈尔滨: 哈尔滨工业大学, 2008: 21-32. CHEN Pu. Theoretical study on vibration Serviceability design and evaluation of footbridge[D]. Harbin: Harbin Institute of Technology, 2008: 21-32 http://cdmd.cnki.com.cn/Article/CDMD-10213-2009290957.htm (  0) 0)
|
| [14] |
BRITISH STANDARDS INSTITUTION BS5400. Steel, concrete and composite bridges[S]. London: British Standards Institution, 1978.
(  0) 0)
|
| [15] |
Human induced vibrations of steel structure. EN 03-08, Design of Footbridge[S]. England, Backgrarnd Document, 2008.
(  0) 0)
|
| [16] |
European Union ENV 1995-2: 1997 EUROCODE 5: Design of Timber Structures-Part 2: Bridges[S]. Brussels, Belgium, European Committee for Standardization, 1997.
(  0) 0)
|
| [17] |
ALLEN D E, MURRAY T M. Design criterion for vibrations due to walking[J]. Engineering journal, 1993, 30(4): 117-129. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


