2. 环境保护部核与辐射安全中心, 北京 100088;
3. 中国核动力研究设计院 第一研究所, 四川 成都 610041
2. Nuclear and Radiation Safety Center, Ministry of Environmental Protection, Beijing 100088, China;
3. The First Sub-institute, Nuclear Power Institute of China, Chengdu 610041, China
随着我国“海洋强国”战略的提出,海洋开发对能源的需求日益迫切。浮动核电站作为一种安全、经济的核电新形式,能够有效地解决海上能源短缺的问题,开展相关的研发工作势在必行。利用系统分析程序评估海洋条件对反应堆安全的影响并制定相应的设计规范是我国浮动核电站研发和安审工作中亟待解决的问题。目前主流的反应堆系统分析程序如RELAP5、TRACE、RETRAN等均是基于陆基核电厂开发而来[1],无法针对浮动核电站开展系统安全分析,因此有必要开发适用于海洋条件的反应堆热工水力系统分析程序。
目前海洋条件下反应堆系统分析程序的开发主要可分为两类,即小型自编程序的开发和商用程序改进。由于小型自编程序[2-5]往往模型算法简单且适用对象单一,难以满足浮动核电站的研发和安审工作的需要。对于商用程序的改进,日本Ishida等[6]和韩国Jae-Hak Kim等[7]分别基于RETRAN程序开发了海洋条件瞬态分析程序RETRAN-02/GRAV和RETRAN-03/INT,并采用实验验证了程序计算的准确性;我国鄢炳火等针对RELAP5程序进行了海洋条件的二次开发,但所开发程序针对摇摆运动,没有研究复杂海洋条件对反应堆安全的影响[8]。谭长禄等基于RELAP5开发了海洋条件系统分析程序RELAP5/MC,但程序未开展实验验证,对复合海洋条件下反应堆系统安全分析的适用性不明[9-10]。
针对当前相关研究的不足,本文建立了描述复合海洋条件下惯性加速度的数学模型,通过在RELAP5中添加海洋条件计算模块,开发了适用于复杂海洋条件下反应堆热工水力分析的系统分析程序。采用实验验证和程序间对比验证的方法,对程序在运动条件下的计算准确性进行验证。
1 海洋条件惯性加速度模型建立海洋条件是指核动力船舶受海面风浪、船体机动等影响而产生的不同运动形式。通常采用倾斜、起伏、摇摆这三种基本运动形式来进行海洋条件的建模分析。为方便描述海洋条件下的流体运动,引入两个右手坐标系:固定于地球的世界坐标系O0X0Y0Z0和固定于运动控制体上的局部坐标系O1X1Y1Z1。
由于海洋条件下的局部坐标系O1X1Y1Z1是一种非惯性系,牛顿运动定律不成立,需要建立非惯性系下的动量守恒方程。式(1) 为非惯性系下积分形式的动量守恒方程表达式[11]:
| $\begin{align} & \iiint\limits_{{{\tau }'}}{\frac{{D}'{v}'}{Dt}}\rho \rm{d}{\tau }'=\iiint\limits_{{{\tau }'}}{\left[ \mathit{\boldsymbol{f}}-{{\mathit{\boldsymbol{a}}}_{0}}-\mathit{\boldsymbol{ }}\!\!\omega\!\!\rm{ }\times \left( \mathit{\boldsymbol{ }}\!\!\omega\!\!\rm{ }\times \mathit{\boldsymbol{{r}'}} \right)-\mathit{\boldsymbol{ }}\!\!\beta\!\!\rm{ }\times \mathit{\boldsymbol{{r}'}}- \right.} \\ & \quad \quad \quad \quad \quad \quad \left. 2\mathit{\boldsymbol{ }}\!\!\omega\!\!\rm{ }\times \mathit{\boldsymbol{{v}'}} \right]\rho \rm{d}{\tau }'+\iint\limits_{{{A}'}}{{{\mathit{\boldsymbol{p}}}_{n}}}\rm{d}{A}' \\ \end{align}$ | (1) |
同惯性系下的动量守恒方程相比,式(1) 增加了中括号中的后四项,分别为平移加速度、向心加速度、切向加速度和科氏加速度。因此,为应用海洋条件下流体的动量守恒方程,需要对船体运动所引入的附加惯性加速度进行数学建模。
1.1 倾斜运动倾斜运动会引起反应堆几何姿态的改变,这不仅会造成容器中水位的变化,还会引起反应堆冷热源间有效高度差的改变,进而影响自然循环的热驱动力。因此,倾斜运动数学描述的重点为倾斜后系统水力学控制体竖直提升高度的计算。
空间位置坐标为(x0, y0, z0)的控制体倾斜后的新坐标(x1, y1, z1)可以用三维旋转矩阵表示:
| $\begin{array}{l} \left[ {\begin{array}{*{20}{l}} {{x_1}}\\ {{y_1}}\\ {{z_1}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\cos r} & { - \sin r} & 0\\ {\sin r} & {\cos r} & 0\\ {\;0} & {\;0} & 1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\cos \beta } & 0 & {\sin \beta }\\ {\;0} & 1 & {\;0}\\ { - \sin \beta } & 0 & {\cos \beta } \end{array}} \right].\\ \quad \quad \quad \left[ {\begin{array}{*{20}{l}} 1 & {\;0} & {\;0}\\ 0 & {\cos \alpha } & { - \sin \alpha }\\ 0 & {\sin \alpha } & {\cos \alpha } \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{x_0}}\\ {{y_0}}\\ {{z_0}} \end{array}} \right] \end{array}$ | (2) |
式中:α、β、γ分别为控制体绕世界坐标系X0、Y0、Z0轴倾斜的角度。计算得到的控制体新坐标中的z1即为倾斜后控制体在世界坐标系Z0轴方向上的竖直提升高度hz。
1.2 起伏运动起伏是指船舶周期性的上下平动,它不会改变系统的几何姿态。通常情况下,起伏运动可被简化描述为一种简谐变化规律。在世界坐标系中,起伏条件下流体的惯性加速度aheaving可以表示为
| ${\mathit{\boldsymbol{a}}_{{\rm{heaving}}}} = - \mathit{\boldsymbol{a}}\left( t \right) = \frac{{4{{\rm{ \mathsf{ π} }}^2}{x_m}}}{{{T^2}}}\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}t}}{T}} \right)\mathit{\boldsymbol{k}}$ | (3) |
式中:xm为起伏位移的最大值,T为起伏周期,k为世界坐标系中Z0轴正向的单位向量。
起伏运动的本质为一种竖直方向上的变加速直线运动,对于一般形式的直线加速运动也可以采用同样的方式表示:
| ${\mathit{\boldsymbol{a}}_{{\rm{line}}}} = - {a_x}\left( t \right)\mathit{\boldsymbol{i}} - {a_y}\left( t \right)\mathit{\boldsymbol{j}} - {a_z}\left( t \right)\mathit{\boldsymbol{k}}$ | (4) |
式中:ax、ay、az分别为船体沿世界坐标系X0、Y0、Z0轴方向的直线加速度。
1.3 摇摆运动摇摆是指船舶绕某一轴线进行的往复运动,它不仅会引起系统几何姿态的变化,还会引入附加的切向加速度和向心加速度。在核动力船舶实际运行时,其摇摆运动可能发生在任意方向上,为模拟船舶受海洋条件影响的实际运动情况,需建立绕任意轴摇摆的惯性加速度模型。
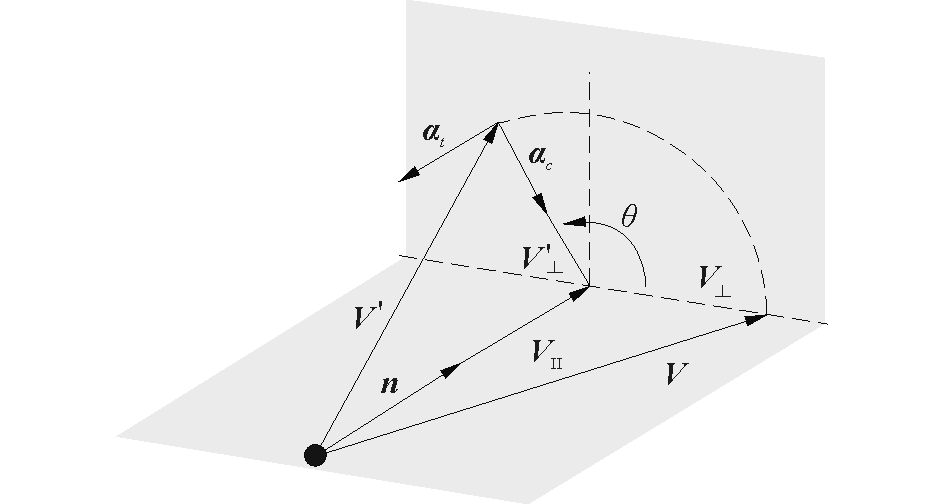
如图 1所示,在向量V=(x0, y0, z0)绕任意单位向量n=(nx, ny, nz)旋转θ角度过程中,任意时刻新向量V′的空间坐标(xt, yt, zt)可以由式(5) 计算的得到[12]:
| $\left[ {\begin{array}{*{20}{l}} {{x_t}}\\ {{y_t}}\\ {{z_t}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{l}} {n_x^2\left( {1 - \cos {\theta _t}} \right) + \cos {\theta _t}} & {{n_x}{n_y}\left( {1 - \cos {\theta _t}} \right) - {n_z}\sin {\theta _t}} & {{n_x}{n_z}\left( {1 - \cos {\theta _t}} \right) - {n_z}\sin {\theta _t}}\\ {{n_x}{n_y}\left( {1 - \cos {\theta _t}} \right) - {n_z}\sin {\theta _t}} & {n_y^2\left( {1 - \cos {\theta _t}} \right) + \cos {\theta _t}} & {{n_y}{n_z}\left( {1 - \cos {\theta _t}} \right) - {n_x}\sin {\theta _t}}\\ {{n_x}{n_z}\left( {1 - \cos {\theta _t}} \right) - {n_y}\sin {\theta _t}} & {{n_y}{n_z}\left( {1 - \cos {\theta _t}} \right) - {n_x}\sin {\theta _t}} & {n_z^2\left( {1 - \cos {\theta _t}} \right) + \cos {\theta _t}} \end{array}} \right]\\\left[ {\begin{array}{*{20}{l}} {{x_0}}\\ {{y_0}}\\ {{z_0}} \end{array}} \right]$ | (5) |
|
图 1 向量旋转示意图 Fig.1 Diagram of vector rotation |
将向量V=(x0, y0, z0)分解成与单位向量n平行的向量Vll=(V·n)n和垂直的向量V⊥=V-Vll,则向量V距旋转中心的距离R=V⊥。
同理,旋转后的向量V′=(xt, yt, zt)也可以分解成平行于n的Vll和垂直于n的V′⊥,则该时刻与V′⊥同向的单位向量nc可以计算得到;又因为切向加速度垂直于向量n和向量nc,则与切向加速度同向的单位向量nt可以表示为
| ${\mathit{\boldsymbol{n}}_t} = {\mathit{\boldsymbol{n}}_c} \times \mathit{\boldsymbol{n}}$ | (6) |
向心加速度矢量ac和切向加速度矢量at可以表示为
| $\begin{array}{l} {\mathit{\boldsymbol{a}}_c} = - {w^2}R{\mathit{\boldsymbol{n}}_c} = \left( {{a_{cx}},{a_{cy}},{a_{cz}}} \right)\\ {\mathit{\boldsymbol{a}}_c} = \beta R{\mathit{\boldsymbol{n}}_t} = \left( {{a_{tx}},{a_{ty}},{a_{tz}}} \right) \end{array}$ | (7) |
所以绕任意轴摇摆控制体的惯性加速度就可以表示为
| ${\mathit{\boldsymbol{a}}_{{\rm{rolling}}}} = - \left( {{a_{tx}} + {a_{cz}}} \right)\mathit{\boldsymbol{i}} - \left( {{a_{ty}} + {a_{cy}}} \right)\mathit{\boldsymbol{j}} - \left( {{a_{tz}} + {a_{cz}}} \right)\mathit{\boldsymbol{k}}$ | (8) |
基于以上典型运动形式的海洋条件描述,可以组合得到多运动形式耦合的复合海洋条件惯性加速度模型:
| ${\mathit{\boldsymbol{a}}_{{\rm{couple}}}} = {\mathit{\boldsymbol{a}}_{{\rm{line}}}} + {\mathit{\boldsymbol{a}}_{{\rm{heaving}}}} + {\mathit{\boldsymbol{a}}_{{\rm{rolling}}}}$ | (9) |
复合海洋条件所引起的系统控制体空间位置的改变,仍可采用式(5) 计算得到。
2 海洋条件反应堆系统分析程序开发RELAP5程序是美国Idaho国家实验室开发的一款用于轻水堆设计安全评审的最佳估算瞬态分析程序,采用两流体、非均匀、非平衡的两相流模型,能够模拟包括破口事故、全场断电等几乎所有的核电厂运行瞬态及安全事故,在世界范围内得到了广泛的认可和应用[13]。本文基于建立的海洋条件惯性加速度模型,通过修改RELAP5程序的动量方程并添加海洋条件计算模块,实现对RELAP5程序的二次开发。
RELAP5中采用的扩展形式的气相和液相动量方
程[13]分别为
| $\begin{array}{l} {\alpha _g}{\rho _g}A\frac{{\partial v_g^2}}{{\partial t}} + \frac{1}{2}{\alpha _g}{\rho _g}A\frac{{\partial v_g^2}}{{\partial x}} = - {\alpha _g}A\frac{{\partial P}}{{\partial x}} + {\alpha _g}{\rho _g}{B_x}A - \\ \quad \quad \quad \left( {{\alpha _g}{\rho _g}A} \right){\rm{FWG}} \cdot {v_g} + {\mathit{\Gamma }_g}A\left( {{v_{gI}} - {v_g}} \right) - \\ \quad \quad \quad \quad \quad \quad \left( {{\alpha _g}{\rho _g}A} \right){\rm{FIG}}\left( {{v_g} - {v_f}} \right) - \\ \quad \quad C{\alpha _g}{\alpha _f}{\rho _m}A\left[ {\frac{{\partial \left( {{v_g} - {v_f}} \right)}}{{\partial t}} + {v_f}\frac{{\partial {v_g}}}{{\partial x}} - {v_g}\frac{{\partial {v_f}}}{{\partial x}}} \right]\\ {\alpha _f}{\rho _f}A\frac{{\partial v_f^2}}{{\partial t}} + \frac{1}{2}{\alpha _f}{\rho _f}A\frac{{\partial v_f^2}}{{\partial x}} = - {\alpha _f}A\frac{{\partial P}}{{\partial x}} + {\alpha _f}{\rho _f}{B_x}A - \\ \quad \quad \quad \left( {{\alpha _f}{\rho _f}A} \right){\rm{FWF}}{v_f} + {\mathit{\Gamma }_g}A\left( {{v_{fI}} - {v_f}} \right) - \\ \quad \quad \quad \quad \quad \left( {{\alpha _f}{\rho _f}A} \right){\rm{FIF}}\left( {{v_f} - {v_g}} \right) - \\ C{\alpha _g}{\alpha _f}{\rho _m}A\left[ {\frac{{\partial \left( {{v_f} - {v_g}} \right)}}{{\partial t}} + {v_g}\frac{{\partial {v_f}}}{{\partial x}} - {v_f}\frac{{\partial {v_g}}}{{\partial x}}} \right] \end{array}$ | (11) |
式中:等式右边各项依次为:压力梯度项、体积力项、壁面摩擦项、界面质量传输导致的动量传递项、界面摩擦阻力项、虚拟质量力项。
在RELAP5中,重力等体积力是通过Bx引入动量方程的。考虑到海洋条件带来的附加惯性力与重力具有相似的性质[6, 9],可以将附加惯性力沿世界坐标系分解后,参照与重力相同的处理方式引入RELAP5的动量方程,则处理后的等效加速度a可以表示为
| $\mathit{\boldsymbol{a}}{\rm{ = }} - {a_x}\mathit{\boldsymbol{i}} - {a_y}\mathit{\boldsymbol{j}} + \left( {{g_0} - {a_z}} \right)\mathit{\boldsymbol{k}}$ | (12) |
式中:g0为重力加速度,ax、ay、az分别为海洋条件附加惯性加速度在世界坐标系X0、Y0、Z0轴正向上的分量。
图 2为修改后的RELAP5瞬态计算流程示意图。海洋条件参数及相关数据的输入在时间控制模块之后执行,海洋条件附加惯性力的引入及其相关计算在RELAP5瞬态计算中的水力学计算模块中执行。

|
图 2 修改后REALP5瞬态计算流程图 Fig.2 Flow chart of modified RELAP5 transient calculation |
由于目前针对海洋条件下流体的流动传热、阻力特性、CHF等的研究还处于机理性研究阶段,相关的理论模型尚不完善。因此本研究未进行海洋条件下本构关系式的修改,依然采用RELAP5原有的本构关系式。
3 程序验证本文采用哈尔滨工程大学开展的摇摆条件下单相强迫循环实验[14]对引入海洋条件的RELAP5程序在运动条件下强迫循环工况计算的准确性进行验证;同时利用同类型程序RETRAN-02/GRAV[6]和RELAP5/MC[9],通过建立相似的自然循环回路模型,对比各程序的计算结果来验证本文程序在运动条件下自然循环工况计算的准确性。
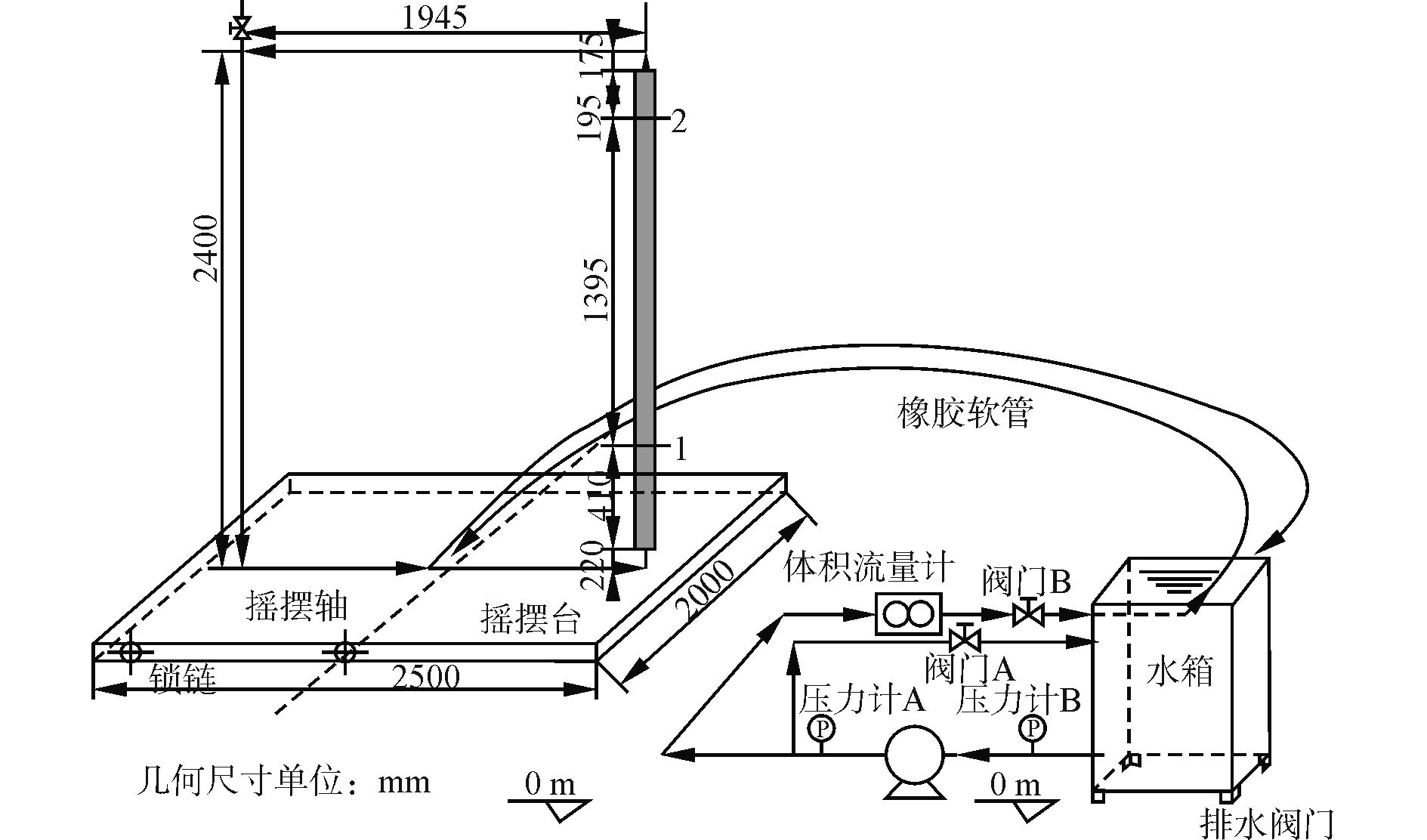
3.1 摇摆条件下单相强迫循环实验验证该实验主要研究了摇摆运动下竖直窄矩形通道内单相水低速流动时流量的波动特征。图 3为实验回路的系统布置简图。主实验回路被固定在摇摆实验台上,通过橡胶软管与主实验回路相连的水箱、离心水泵等设备不参与摇摆运动,具体实验过程及系统相关参数详见文献[14]。图 4为该实验回路的RELAP5节点划分示意图。控制体尺寸按实验装置实际尺寸进行设置,系统运行状态为常温常压,Y轴为摇摆轴。为尽可能模拟实验真实情况,水泵被布置在摇摆上,并通过合理设置稳压器的空间坐标来消除摇摆的影响。
|
图 3 单相强迫循环实验回路示意图 Fig.3 Schematic diagram of single-phase forced circulation experiment |

|
图 4 单相强迫循环实验回路RELAP5节点图 Fig.4 RELAP5 nodalization for single-phase forced circulation loop |
计算过程中,通过调节RELAP5程序中的阀门开度及各部件的阻力参数,使系统流量和压降等参数的计算值与静态实验值相匹配。设置与实验工况相同的摇摆运动参数(周期、振幅)进行计算,并将计算结果与实验结果进行对比分析。本文选用表 1所示三种不同的实验工况进行分析验证。
| 表 1 各实验工况摇摆运动参数及静态流量汇总 Tab.1 Main parameters of rolling motion and static flow rate for different experiment conditions |
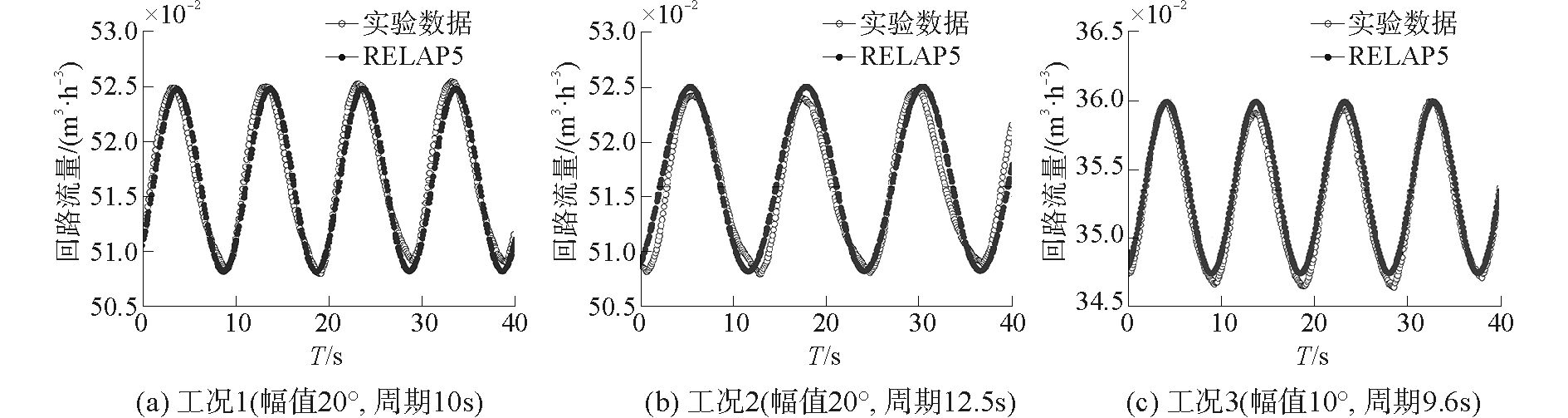
图 5为三组实验工况的RELAP5计算结果与实验数据对比。计算得到的回路流量波动趋势与实验数据符合较好,流量波动周期及相位与实际情况基本相同,但在流量波动极值处存在偏差。综合考虑RELAP5对实验台架进行简化建模过程中引入的误差,可以认为本程序对于摇摆条件下强迫循环工况计算的适用性较好。
|
图 5 计算结果与实验数据对比 Fig.5 Comparisons of calculation results and experimental data |
本节采用日本Ishida等开发的RETRAN-02/GRAV[6]与国内谭长禄等开发的RELAP5/MC程序[9-10]进行对比验证。受公开文献中相关计算模型参数完整性的限制,只能通过对比相似系统的热工水力参数受海洋条件影响的变化趋势来验证本文程序。综合考虑文献[6, 10]中所采用的自然循环回路形式,建立如图 6所示的并联双回路单相自然循环计算模型,具体参数详见表 2。

|
图 6 并联双回路自然循环系统RELAP5节点图 Fig.6 RELAP5 nodalization for parallel two loops natural circulation system |
| 表 2 计算模型主要参数汇总 Tab.2 Main parameters of calcution model |
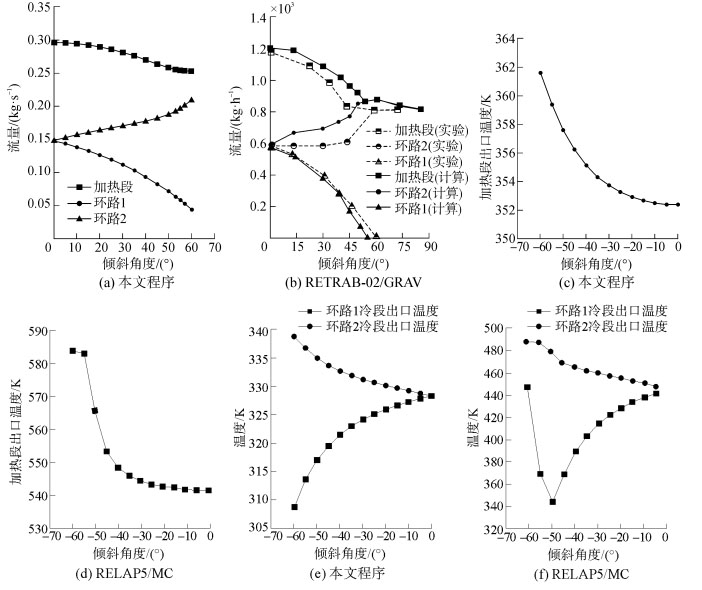
图 7为RETRAN-02/GRAV、RELAP5/MC与本文程序对不同横斜角度(绕Y轴)下并联双回路自然循环系统的计算结果对比,其中图 7(b)中的实心点代表程序计算结果,空心点为Iyori等实验结果[15]。可以看出,三种程序得到的系统流量和温度随横摇角度变化趋势基本相同:随着倾斜角度的增加,支路的自然循环流量随着其相对位置的上升或下降而增加或减小,流经加热器的总流量逐渐减少。这主要是由倾斜造成的回路冷热源高度差的改变而引起的自然循环热驱动压头的变化所导致的。由于加热功率恒定,各回路的出口温度与其流量的变化保持对应关系。需要说明的是,对比图 7(e)与图 7(f),当倾斜角度大于-50°时,RELAP5/MC计算得到的环路1冷段出口温度出现了跃升。这主要是因为文献[9]中采用的自然循环回路尺寸及系统参数与本文模型并不完全相同,当倾斜角度接近-60°时,文献[9]中相对位置下降的环路1出现了零流量,导致系统换热能力下降而造成温度上升。
|
图 7 横斜条件下并联双回路自然循环系统计算结果对比 Fig.7 Comparisons of calculation results for parallel two loops natural circulation system under heeling condition |
考虑到各程序采用的计算回路尺寸等参数不同所造成的偏差,可以认为本文程序对倾斜条件下自然循环工况计算具有较好的适用性。
3.2.2 起伏条件图 8为本文程序计算得到的双回路自然循环系统在起伏条件下的系统流量波动情况。可以看出,在竖直方向变加速度的影响下,自然循环流量围绕其静态值呈正/余弦规律波动。同竖直方向的加速度变化相比,流量的波动存在约1.7 s的延迟,这主要是由于流道阻力造成的。同两个支路相比,加热段的流量波动幅度更大。相同的变化趋势在Ishida等的计算中也被得到[6]。

|
图 8 起伏海洋条件下系统流量随时间变化曲线(幅值0.6 g,周期9 s) Fig.8 Results of nature circulation flow rate under heaving condition(amplitude 0.6 g, period 9 s) |
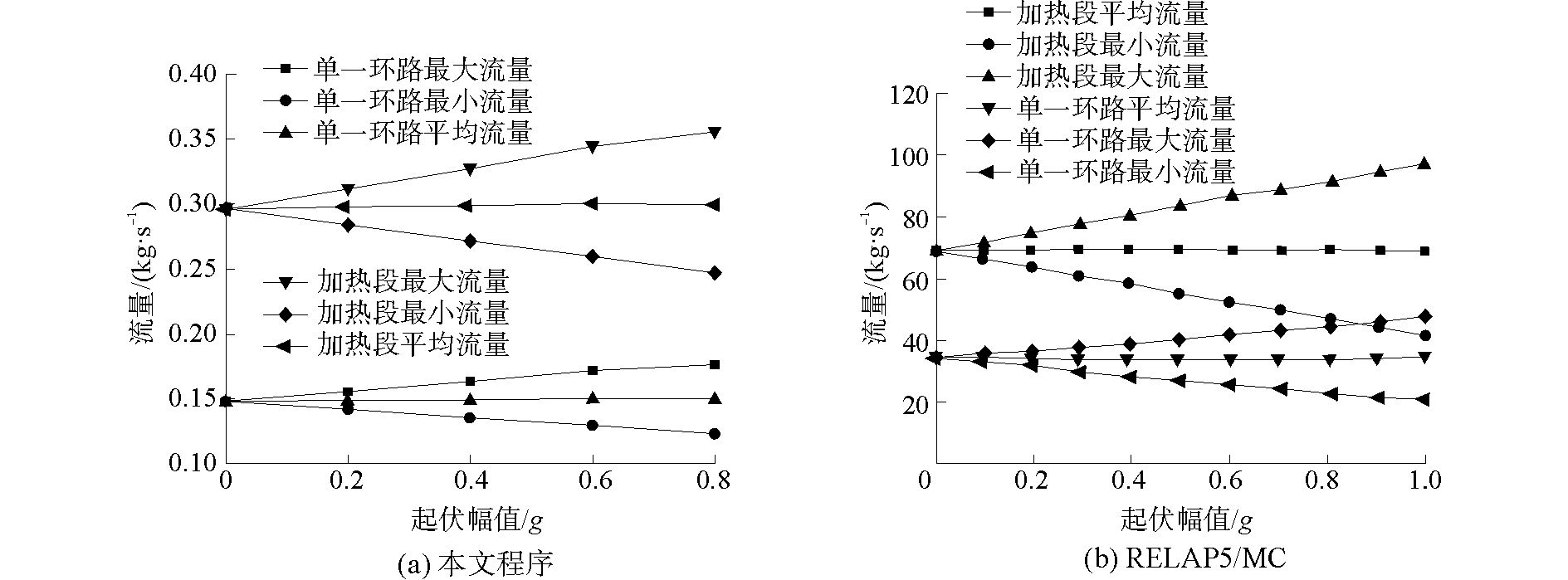
起伏运动参数的变化会对自然循环系统的热工水力特性产生影响。图 9(a)和图 9(b)分别为本文程序和RELAP5/MC计算得到的起伏幅值对自然循环流量的影响情况。两种程序得到的影响规律基本相同:随着起伏运动幅值的增加,自然循环系统各回路的流量波动幅度逐步变大。
|
图 9 系统流量受起伏幅值变化影响曲线对 Fig.9 Effects of heaving amplitudes on system flow rate calculated by two codes |
图 10和图 11分别为本文程序和RELAP5/MC计算得到的横摇条件下(绕Y轴)双回路自然循环系统的流量波动情况。两种程序得到的流量变化趋势基本相同,即摇摆条件下加热段的流量几何保持恒定,两个并联环路的流量波动相位相反,且冷热段流量的变化相对于摇摆角度存在延迟。

|
图 10 横摇条件下运动参数和系统流量变化曲线(幅值10°,周期10 s) Fig.10 Curves of motion parameters and system flow rate under rolling condition (amplitude 10°, period 10 s) |

|
图 11 横摇条件下系统流量变化曲线-RELAP5/MC[9](幅值45°,周期10 s) Fig.11 System flow rate curves under rolling condition-RELAP5/MC[9] (amplitude 45°, period 10 s) |
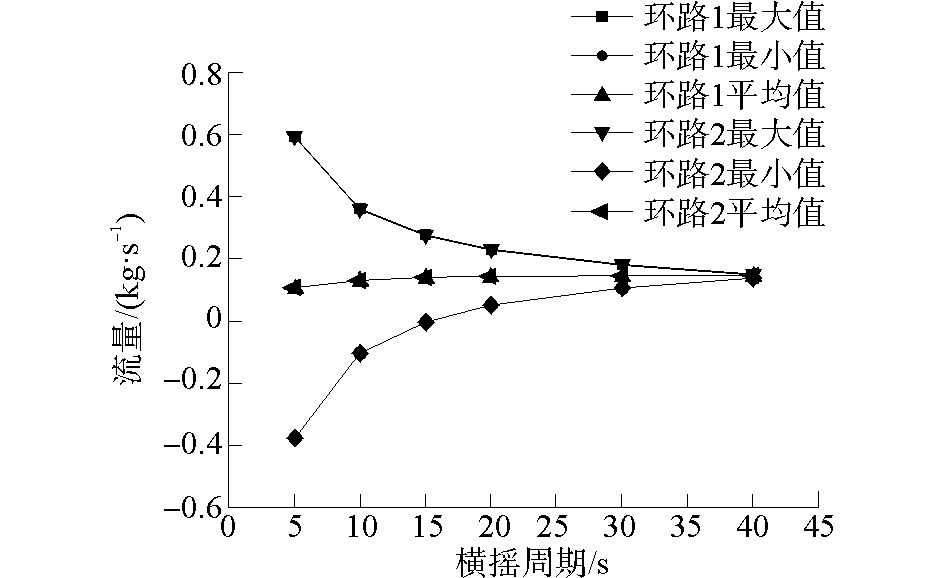
摇摆运动参数的变化会对自然循环系统的热工水力特性产生影响。图 12和图 13分别为本文程序计算得到的横摇周期和幅值对双回路自然循环系统流量波动的影响情况。
|
图 12 系统流量随横摇周期的变化曲线(固定摇摆幅值20°) Fig.12 Effects of rolling period on system flow rate (conatant rollling amplitude 20°) |

|
图 13 系统流量随横摇幅值的变化曲线(固定摇摆周期20 s) Fig.13 Effects of rolling amplitude on system flow rate (conatant rollling period 20 s) |
从图中可以看出,支路流量的波动幅度随周期的增加而减小,并在周期约为40 s时振荡幅度达到最小值。随着摇摆幅值的增加,支路流量的平均值减小,但流量波动幅度增大。相似的变化趋势在谭长禄等的计算[10]中也被得到。通过程序间对比验证的方式,对本程序在运动条件下自然循环工况计算的适用性进行了评价。结果表明,相同工况下程序间计算结果的变化趋势符合良好,证实了本文海洋条件模型建立和程序修改的正确性。
4 结论1) 本文通过建立不同运动条件下流体的惯性加速度模型,基于RELAP5程序开发得到适用于复杂海洋条件的反应堆热工水力系统分析程序。
2) 本文程序计算结果与摇摆运动下竖直通道内单相水低速流动实验结果比较吻合,不同运动条件下程序的结果趋势与RETRAN-02/GRAV和RELAP5/MC程序符合较好。
未来在海洋条件本构关系式模型修改和实验验证方面还需开展进一步的工作。经过后续不断改进验证,该程序可成为我国浮动核电站设计研发及安全评审的有力工具。
| [1] |
靖剑平, 张春明, 陈妍, 等. 浅谈核电领域中的热工水力分析程序[J]. 核安全, 2012, 3: 70-74. JING Jianping, ZHANG Chunming, CHEN Yan, et al. Discussion on the thermal-hydraulic analysis codes in the field of nuclear power[J]. Nuclear safety, 2012, 3: 70-74. DOI:10.3969/j.issn.1672-5360.2012.03.016 (  0) 0)
|
| [2] |
庞凤阁, 高璞珍, 王兆祥, 等. 海洋条件对自然循环影响的理论研究[J]. 核动力工程, 1995, 16(4): 330-335. PANG Fengge, GAO Puzhen, WANG Zhaoxiang, et al. Theoretical research for effect of ocean conditions on natural circulation[J]. Nuclear power engineering, 1995, 16(4): 330-335. (  0) 0)
|
| [3] |
张金玲. 压水堆核动力装置稳态及瞬态热工安全分析程序的研制和应用[D]. 西安: 西安交通大学, 1995. ZHANG Jinling. The development and applications of the steady andtransient-state thermal-safety analysis code for PWR nuclear power equipment[D]. Xi'an:Xi'an Jiaotong University, 1995. http://d.wanfangdata.com.cn/Thesis/Y204509 (  0) 0)
|
| [4] |
谭思超, 高璞珍, 苏光辉. 摇摆运动条件下自然循环流动的实验和理论研究[J]. 哈尔滨工程大学学报, 2007, 28(11): 1213-1217. TAN Sichao, GAO Puzhen, SU Guanghui. Experimental and theoretical study on natural circulation flow under rolling motion condition[J]. Journal of Harbin Engineeirng University, 2007, 28(11): 1213-1217. DOI:10.3969/j.issn.1006-7043.2007.11.005 (  0) 0)
|
| [5] |
姜胜耀, 杨星团, 宫厚军, 等. 起伏因素影响自然循环流动的机理分析[J]. 原子能科学技术, 2009, 43(1): 92-96. JIANG Shengyao, YANG Xingtuan, GONG Houjun, et al. Mechanism of natural circulation taking account into heaving movement[J]. Atomic energy science and technology, 2009, 43(1): 92-96. (  0) 0)
|
| [6] |
ISHIDA T. Development of analysis code for thermal hydro-dynamics of marine reactor under multi-dimensional ship motions, retran-02/grav[R]. Tokyo:Japan Atomic Energy Research Inst., 1992.
( 0) 0)
|
| [7] |
KIM J H, KIM T W, LEE S M, et al. Study on the natural circulation characteristics of the integral type reactor for vertical and inclined conditions[J]. Nuclear engineering & design, 2001, 207(1): 21-31. ( 0) 0)
|
| [8] |
鄢炳火, 于雷. 摇摆条件下热工水力程序的研制与验证[J]. 原子能科学技术, 2012, 46(1): 15-19. YAN Binghuo, YU Lei. Development and validation of thermal hydraulic code in rolling motion[J]. Atomic energy science and technology, 2012, 46(1): 15-19. (  0) 0)
|
| [9] |
谭长禄, 张虹, 赵华. 基于RELAP5的海洋条件下反应堆热工水力系统分析程序开发[J]. 核动力工程, 2009, 30(6): 53-56. TAN Changlu, ZHANG Hong, ZHAO Hua. Development ofocean-condition code based on RELAP5[J]. Nuclear power engineering, 2009, 30(6): 53-56. (  0) 0)
|
| [10] |
谭长禄. 基于RELAP5的海洋条件程序研究[D]. 成都: 中国核动力研究设计院, 2008. TAN Changlu. Development ofocean-condition code based on RELAP5[D]. Chengdu:Nuclear Power Institute of China, 2008. http://www.cnki.com.cn/Article/CJFDTOTAL-HDLG200906012.htm (  0) 0)
|
| [11] |
高璞珍, 庞凤阁, 王兆祥. 核动力装置一回路冷却剂受海洋条件影响的数学模型[J]. 哈尔滨工程大学学报, 1997, 18(1): 24-27. GAO Puzhen, PANG Fengge, WANG Zhaoxiang. Mathematical model of primary coolant in nuclear power plant influenced by ocean conditions[J]. Journal of Harbin Engineeirng University, 1997, 18(1): 24-27. (  0) 0)
|
| [12] |
DUNN F, PARBERRY I. 3D math printer for graphics and game development[M]. Beijing: Tsinghua University Press, 2005: 93-94.
( 0) 0)
|
| [13] |
CARLSON K, RIEMKE R, ROUHANI S, et al. RELAP5/MOD3 Code Manual Volume I:Code Structure, System Models and Solution Methods[R]. Washington DC:US NRC NUREG/CR-5535, 1990.
( 0) 0)
|
| [14] |
王占伟. 摇摆运动下冷却剂低流速流动、传热特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. WANG Zhanwei.The flow and heat transfer characteristics of low flow rate flow under rolling motion conditions[D]. Harbin:Harbin Engineering University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014132992.htm (  0) 0)
|
| [15] |
MURATA H, IYORI I, KOBAYASHI M. Natural circulation characteristics of a marine reactor in rolling motion[J]. Nuclear engineering & design, 1990, 118(2): 141-154. ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


