声子晶体是类比于光子晶体概念提出来的,通常来说,将介电常数不同的材料按照周期排列光子晶体,将弹性模量常数不同的材料按照周期排列形成声子晶体。当弹性波在声子晶体结构中传播时会存在在某些频率范围内响应较微小,甚至为零的情况,这种范围称为振动带隙。声子晶体这一振动带隙特性有着极为强大的理论研究价值,并且在工程应用方面有着及其广阔的应用价值。目前声子晶体的应用方面仍然处于研发阶段,其在机械加工过程中的减振降噪以及精密仪器的无振工作环境等方面有着较为广泛的应用前景[1]。
一维声子晶体结构较为简单,并且在实际应用之中较为贴合,有着较为广阔的应用空间与潜在价值。虽然较二维、三维声子晶体的研究较少,但是在减振降噪等方面较易得到工程应用[2]。目前,对于弹性波在一维声子晶体中的传输特性研究,主要的数值研究方法包含:传递矩阵法、集中质量法以及平面波展开法等。传递矩阵法计算一维声子晶体结构对于弹性波的传输特性计算较为简单,计算量较小,但是对于二维以及三维声子晶体的计算工作量较大,计算过程较为复杂[3];集中质量法是将连续介质的质量集中在有限的节点或者横切面上,将连续的系统进行离散化处理,将整体结构转化为有限自由度的系统进行计算;平面波展开法计算相对简单,但是该方法的收敛速度较慢,其计算精度强烈依赖于平面波的波数[4]。通常随着波数增加,计算结果的精度逐渐增大,但是收敛的速度逐渐变慢。
目前一维声子晶体结构对于弹性波的传输特性研究主要集中于一维等截面声子晶体结构以及一维阶梯变截面声子晶体结构,但是对于一维均匀变截面声子晶体结构的研究较少。本文利用回传射线矩阵法(method of reverberation-ray matrix, MRRM)对一维均匀变截面声子晶体结构对于轴向波的传输特性进行研究。
本文基于Euler-Bernoulli梁理论,通过推导横向波与轴向波的控制微分方程,利用回传射矩阵法建立了一维均匀变截面声子晶体分析模型。研究弹性纵波在一维均匀变截面声子晶体中的传输特性,并且对组成形式、材料参数、物理参数等的影响程度以及影响规律进行比较研究。通过比较分析振动范围内带隙的起始频率、截止频率、带隙宽度以及带隙范围内的最大衰减程度的变化规律来得到各个参数对一维均匀变截面声子晶体对弹性波的传输特性的影响。
1 模型建立与描述通常定义理想的声子晶体结构是由无限大的平板在某一方向上进行周期性排列,其余方向上为无限大。然而在实际工程应用中并不存在这样的模型,对于有限尺寸的声子晶体模型,其在工程应用上具有较实际的工程应用价值。通常将这种模型称为声子晶体结构,将经典的声子晶体定义为典型声子晶体结构[5]。
本文建立一维均匀变截面声子晶体结构的求解模型如图 1所示,通过将两种材料单元在单一方向上进行周期排列,进而得出相应的一维声子晶体结构,每个单元的截面特性都随长度方向发生均匀变化且截面单元为圆台体。

|
图 1 声子晶体结构 Fig.1 Structure of phononic crystals |
材料A和材料B构成的均匀变截面结构几何参数定义为材料A结构的长度为l1,材料B的结构长度为l2。对于每一个均匀变截面单元而言,其左端端面半径,即小端面半径r1=a,右端端面半径,即大端面半径r2=b,如图 1(b)所示。其余组成参数设置为定义晶格常数N=l1+l2,组分比u=l1/(l1+l2),截面积比s=(r2/r1)2。
2 回传射线矩阵法回传射线矩阵法的基本思想是基于单元划分思想,将每一个均匀变截面结构划分为若干单元,在每个单元内建立相应的对偶坐标系[6]。将单元的控制微分方程进行傅里叶变换,进而将时域内的偏微分方程转化为频域范围内的常微分方程,并且将波动解写成简谐波的形式;根据简谐波在各自坐标系中的传播方向,将简谐波分为入射波和出射波;根据单元划分以及节点定义的情况,将单元的相位关系矩阵以及节点的散射关系矩阵通过引入转换关系矩阵得出总体结构的回传射线矩阵,求解相应的入射波波幅向量以及出射波波幅向量,代入相应的公式,求解出相应的物理量,通过数据处理,得出对应的频率响应函数曲线。
2.1 结构定义以及单元划分基于回传射线矩阵法的单元思想,对总体结构进行结构定义与单元划分。假设一维均匀变截面声子晶体结构具有K个均匀变截面结构,并且沿x轴方向上进行周期排列,即将每一个均匀变截面材料视为一个结构,对各个单元结构进行定义,如图 2所示。
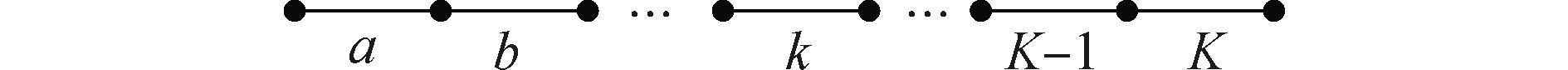
|
图 2 结构定义 Fig.2 The definition of structure |
将每一均匀变截面结构划分为若干等截面单元周期排列的单元结构,在各个单元范围内进行对偶坐标系的建立及数值计算处理,具体离散化处理如图 3所示。

|
图 3 单一结构离散示意图 Fig.3 The discrete schematic of single structure |
对于均匀变截面结构的具体划分,其离散方法的定义如图 4所示,a和b为变截面单元左右两端的半径,rj和rj+1是分割单元左右两端的半径,rj, o是离散单元半径,αj是与划分长度dj有关的位置系数,从质心位置O到左右两端端面的长度分别为αjdj和(1-αj)dj,l为均匀变截面结构的长度,则图中离散单元左右端面的半径可以定义为

|
图 4 单个结构离散化示意图 Fig.4 The discrete schematic of single structure |
| $ \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {r_j} = a + \frac{{b - a}}{l}\sum\limits_{j = 1}^{j - 1} {{d_j}} ,\\ {r_1} = {r_a}, \end{array}&\begin{array}{l} 0 < \sum\limits_{j = 1}^j {{d_f}} < l\\ {r_{j + 1}} = {r_b} \end{array} \end{array}} \right. $ | (1) |
对于每一个离散单元,单元的质心O处于中心位置,通过数学理论知识,根据圆台的体积以及相关的几何知识,则质心处的半径rj, o以及比例系数αj的表达式为
| $ {r_{j,o}} = {\left( {\frac{{r_j^3 + r_{j + 1}^3}}{2}} \right)^{1/3}},{\alpha _j} = \frac{{{r_{j,o}} - {r_j}}}{{{r_{j + 1}} - {r_j}}} $ | (2) |
对于等截面情况,式(2) 可以表达为:rj, o=rj, αj=0.5。
经过上述描述,将每一个均匀变截面结构离散化为多个等截面圆柱单元的连接。通过将单个均匀变截面单元的离散化处理,进而将整个一维均匀变截面声子晶体结构进行离散化处理,为了后续的理论研究打下基础。
经过上述均匀变截面单元的离散化处理,将各个离散单元结构进行节点定义以及单元划分,如图 5所示,通常应用字母对各个节点进行定义并划分n个单元。

|
图 5 节点定义与单元划分 Fig.5 The definition of node and division unit cell |
基于回传射线矩阵法的思想,通过建立对应的对偶坐标系,在各个单元内进行回传射线矩阵的建立以及各物理量的求解[7]。
2.2.1 广义力与广义位移向量根据单元的控制微分方程,基于Euler-Bernoulli梁理论,结合傅里叶变换,建立相应的理论分析模型[8]。如图建立笛卡尔坐标系,在相应的单元范围内依据单元平衡方程得出轴向运动微分方程,并且求出对应的齐次解。
根据图 6中单元轴向力的平衡条件,N(x, t)、E(x)、A(x)、ρ(x)、u(x, t)分布定义为相应截面轴向力、弹性模量、横截面面积、密度和轴向位移。图 6中,N和u分别代表轴向力和轴向位移的简写形式。

|
图 6 单元受力示意图 Fig.6 The force diagrams of unit |
根据单元的轴向力平衡条件以及轴向位移协调条件,可以得出相应的平衡方程,具体方程如下
| $ \left\{ \begin{array}{l} \frac{{\partial N\left( {x,t} \right)}}{{\partial x}} = \rho \left( x \right)A\left( x \right)\frac{{{\partial ^2}u\left( {x,t} \right)}}{{\partial {t^2}}}\\ N\left( {x,t} \right) = E\left( x \right)A\left( x \right)\frac{{\partial u\left( {x,t} \right)}}{{\partial x}} \end{array} \right. $ | (3) |
将上述方程进行傅里叶变换,同时可以得出相应的位移齐次解,轴向力齐次解,具体表述如下
| $ \left\{ \begin{array}{l} u\left( {x,\omega } \right) = {\mathit{\boldsymbol{a}}_1}\left( \omega \right){{\rm{e}}^{{\rm{i}}{k_1}x}} + {\mathit{\boldsymbol{d}}_1}\left( \omega \right){{\rm{e}}^{ - {\rm{i}}{k_1}x}}\\ N\left( {x,\omega } \right) = {\xi _1}{\mathit{\boldsymbol{a}}_1}\left( \omega \right){{\rm{e}}^{{\rm{i}}{k_1}x}} + {\xi _1}{\mathit{\boldsymbol{d}}_1}\left( \omega \right){{\rm{e}}^{ - {\rm{i}}{k_1}x}} \end{array} \right. $ | (4) |
式中:
根据单元的剪切力平衡以及弯矩平衡关系式可以相应的得到单元的弯曲运动微分方程,进而求得对应的弯曲运动齐次解的表达式,其中v(x, ω)表示为频域范围内纵向位移表达式。具体形式如下
| $ \begin{array}{l} v\left( {x,\omega } \right) = {\mathit{\boldsymbol{a}}_2}\left( \omega \right){{\rm{e}}^{{\rm{i}}{k_2}x}} + {\mathit{\boldsymbol{d}}_2}\left( \omega \right){{\rm{e}}^{ - {\rm{i}}{k_2}x}} + {\mathit{\boldsymbol{a}}_3}\left( \omega \right){{\rm{e}}^{{\rm{i}}{k_3}x}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{d}}_3}\left( \omega \right){{\rm{e}}^{ - {\rm{i}}{k_3}x}} \end{array} $ | (5) |
根据相应的物理量之间的关系表达式,可以求出其余物理量的简谐波形式。定义E(x)为材料的弹性模量,G(x)为材料的弹性模量,ρ(x)为材料的密度,A(x)为材料的横截面面积,I(x)为材料的横截面二次矩,Q(x, ω)为梁的剪力,M(x, ω)为梁的弯矩, φ(x, ω)为梁的转角位移。具体如下
| $ \left\{ \begin{array}{l} M\left( {x,\omega } \right) = - EI\left[ {k_2^2\left( {{\mathit{\boldsymbol{a}}_2}\left( \omega \right){{\rm{e}}^{{\rm{i}}{k_2}x}} + {\mathit{\boldsymbol{d}}_2}\left( \omega \right){{\rm{e}}^{ - {\rm{i}}{k_2}x}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {k_3^2\left( {{\mathit{\boldsymbol{a}}_3}\left( \omega \right){{\rm{e}}^{{\rm{i}}{k_3}x}} + {\mathit{\boldsymbol{d}}_3}\left( \omega \right){{\rm{e}}^{ - {\rm{i}}{k_3}x}}} \right)} \right]\\ Q\left( {x,\omega } \right) = {\rm{i}}EI\left[ {k_2^2\left( {{\mathit{\boldsymbol{a}}_2}\left( \omega \right){{\rm{e}}^{{\rm{i}}{k_2}x}} + {\mathit{\boldsymbol{d}}_2}\left( \omega \right){{\rm{e}}^{ - {\rm{i}}{k_2}x}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {k_3^2\left( {{\mathit{\boldsymbol{a}}_3}\left( \omega \right){{\rm{e}}^{{\rm{i}}{k_3}x}} + {\mathit{\boldsymbol{d}}_3}\left( \omega \right){{\rm{e}}^{ - {\rm{i}}{k_3}x}}} \right)} \right]\\ \varphi \left( {x,\omega } \right) = {\rm{i}}\left[ {{k_2}\left( {{\mathit{\boldsymbol{a}}_2}\left( \omega \right){{\rm{e}}^{{\rm{i}}{k_2}x}} + {\mathit{\boldsymbol{d}}_2}\left( \omega \right){{\rm{e}}^{ - {\rm{i}}{k_2}x}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{k_3}\left( {{\mathit{\boldsymbol{a}}_3}\left( \omega \right){{\rm{e}}^{{\rm{i}}{k_3}x}} + {\mathit{\boldsymbol{d}}_3}\left( \omega \right){{\rm{e}}^{ - {\rm{i}}{k_3}x}}} \right)} \right] \end{array} \right. $ | (6) |
其中:波数k2, k3的表达式分别为
| $ {k_2} = \sqrt[4]{{\frac{{\rho A}}{{EI}}}}\sqrt \omega ,\;\;\;\;\;{k_3} = {\rm{i}}\sqrt[4]{{\frac{{\rho A}}{{EI}}}}\sqrt \omega $ |
根据轴向位移u(x, ω),剪切位移v(x, ω)以及转角位移φ(x, ω),定义为广义位移向量F=[u v φ]T;相应地,将轴向力N(x, ω),剪切力Q(x, ω)以及弯矩M(x, ω)定义为广义力向量V=[N Q M]T。
2.2.2 相位关系在每个单元内,根据单元内的对偶变换关系,得出单元内的相位关系[9]:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{a}}^{ij}}\left( \omega \right) = {\mathit{\boldsymbol{P}}^{ij}}\left( {{l^{ij}},\omega } \right){\mathit{\boldsymbol{d}}^{ji}}\left( \omega \right)\\ {\mathit{\boldsymbol{a}}^{ji}}\left( \omega \right) = {\mathit{\boldsymbol{P}}^{ij}}\left( {{l^{ij}},\omega } \right){\mathit{\boldsymbol{d}}^{ij}}\left( \omega \right) \end{array} \right. $ | (7) |
式中aij为单元ij内的入射波向量,dij为相应的出射波向量。
根据单元内的相位关系,可以得出单元内的相位关系矩阵:
| $ {\mathit{\boldsymbol{a}}^{ij}} = {\mathit{\boldsymbol{P}}^{ij}}\overline {{\mathit{\boldsymbol{d}}^{ij}}} $ | (8) |
式中,aij和
根据单一结构范围内的节点定义顺序,将单元相位关系矩阵组装成为单一结构相位关系矩阵:
| $ {\mathit{\boldsymbol{P}}^k} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}^{12}}}&{}&{}&{}&{}\\ {}& \ddots &{}&{}&{}\\ {}&{}&{{\mathit{\boldsymbol{P}}^{ij}}}&{}&{}\\ {}&{}&{}& \ddots &{}\\ {}&{}&{}&{}&{{\mathit{\boldsymbol{P}}^{\left( {n - 1} \right)n}}} \end{array}} \right]_{6n \times 6n}} $ |
根据单一结构范围内的相位关系矩阵,得出对应结构范围内的相位关系式:
| $ {\mathit{\boldsymbol{a}}^k} = {\mathit{\boldsymbol{P}}^k}\overline {{\mathit{\boldsymbol{d}}^k}} ,\;\;\;\;k = 1,2, \cdots ,K $ | (9) |
式中:ak和
根据单一结构在总体范围之中的节点定义与单元划分,可以得出总体范围内的相位关系矩阵:
| $ \mathit{\boldsymbol{P}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}^a}}&{}&{}&{}&{}\\ {}& \ddots &{}&{}&{}\\ {}&{}&{{\mathit{\boldsymbol{P}}^k}}&{}&{}\\ {}&{}&{}& \ddots &{}\\ {}&{}&{}&{}&{{\mathit{\boldsymbol{P}}^K}} \end{array}} \right]_{6nK \times 6nK}} $ |
同理可以得出总体结构范围内的相位关系式:
| $ \mathit{\boldsymbol{a}} = \mathit{\boldsymbol{P\bar d}} $ | (10) |
式中a和d为整体范围内的入射波向量和出射波向量。
2.2.3 散射关系在各个单元的节点处,利用单元对偶坐标与整体坐标之间的转换关系,结合外力源向量,根据广义力平衡关系以及广义位移协调关系,可以得出节点处的散射关系表达式:
| $ {\mathit{\boldsymbol{d}}^i} = {\mathit{\boldsymbol{S}}^i}{\mathit{\boldsymbol{a}}^i} + {\mathit{\boldsymbol{s}}^i},\;\;\;i = 1,2, \cdots ,n $ | (11) |
式中:Si为单元范围内节点的散射关系矩阵,si为与外载荷有关的向量。
根据单一结构内的节点定义,可以得出单一结构内的散射关系矩阵:
| $ \mathit{\boldsymbol{S}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}^0}}&{}&{}&{}&{}\\ {}& \ddots &{}&{}&{}\\ {}&{}&{{\mathit{\boldsymbol{S}}^i}}&{}&{}\\ {}&{}&{}& \ddots &{}\\ {}&{}&{}&{}&{{\mathit{\boldsymbol{S}}^n}} \end{array}} \right]_{6n \times 6n}} $ |
根据单一结构内的相位关系矩阵,可以得出单一结构内的散射关系式:
| $ {\mathit{\boldsymbol{d}}^k} = {\mathit{\boldsymbol{S}}^k}{\mathit{\boldsymbol{a}}^k} + {\mathit{\boldsymbol{s}}^k},k = 1,2, \cdots ,K $ | (12) |
式中:Sk为单一结构范围内节点的散射关系矩阵,sk为与外载荷有关的向量。根据总体范围内结构定义与节点划分,结合各单一结构之间的节点散射关系矩阵、边界条件进而得出整体结构范围的散射关系矩阵:
| $ \mathit{\boldsymbol{S}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}^a}}&{}&{}&{}&{}\\ {}& \ddots &{}&{}&{}\\ {}&{}&{{\mathit{\boldsymbol{S}}^k}}&{}&{}\\ {}&{}&{}& \ddots &{}\\ {}&{}&{}&{}&{{\mathit{\boldsymbol{S}}^K}} \end{array}} \right]_{6nK \times 6nK}} $ |
同理求出总体结构范围的散射关系表达式:
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Sa}} + \mathit{\boldsymbol{s}} $ | (13) |
式中:S为整体结构范围内节点的散射关系矩阵,s为与外载荷有关的向量。
2.2.4 总体关系矩阵的组装为进一步对总体关系矩阵进行组装,需要引入转换关系矩阵对相位关系矩阵进行转换。由上文可知,出射向量d和d二者均含有相同的组成元素,只是排列顺序不一致。引入转换矩阵U,转换矩阵的特点为其每一行每一列有且只有一个元素为1,其余为零,并且其转换矩阵的逆矩阵为其自身[10]。可以将总体结构的相位关系矩阵写为a=PUd。将总体相位关系式与总体散射关系表达式,消除入射波向量a,可以得出d=(I-R)-1s,其中定义R=SPU为回传射线矩阵。
2.2.5 振动特性与频响曲线根据结构受到的周期载荷,将输入激励产生的动态响应写成稳态响应模式,以轴向输入位移为例,定义输入位移uo(t)=uo(ω)eiωt。同理将各个单元ij内的广义力向量Fij以及广义位移向量Vij的稳态响应形式可以表示为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{F}}^{ij}}\left( {{x^{ij}},t} \right) = {\mathit{\boldsymbol{F}}^{ij}}\left( {{x^{ij}},{\omega ^{ij}}} \right){{\rm{e}}^{{\rm{i}}\omega t}}\\ {\mathit{\boldsymbol{V}}^{ij}}\left( {{x^{ij}},t} \right) = {\mathit{\boldsymbol{V}}^{ij}}\left( {{x^{ij}},{\omega ^{ij}}} \right){{\rm{e}}^{{\rm{i}}\omega t}} \end{array} \right. $ | (14) |
将相应的激励频率代入到对应的广义力向量以及广义位移向量的表达式之中,结合简谐波的表达形式,可以得出在任意频率下,任意位置、时间处的输出响应值,具体形式写为
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}}\left( {x,t} \right) = \left[ {{\mathit{\boldsymbol{A}}_{FO}}\left( {x,\omega } \right)} \right]\mathit{\boldsymbol{PU + }}\left. {{\mathit{\boldsymbol{D}}_{FO}}\left( {x,\omega } \right)} \right] \cdot }\\ {{{\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{R}}\left( \omega \right)} \right)}^{ - 1}}\mathit{\boldsymbol{s}}\left( \omega \right){{\rm{e}}^{{\rm{i}}\omega t}}} \end{array}\\ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{V}}\left( {x,t} \right) = \left[ {{\mathit{\boldsymbol{A}}_{VO}}\left( {x,\omega } \right)} \right]\mathit{\boldsymbol{PU + }}\left. {{\mathit{\boldsymbol{D}}_{VO}}\left( {x,\omega } \right)} \right] \cdot }\\ {{{\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{R}}\left( \omega \right)} \right)}^{ - 1}}\mathit{\boldsymbol{s}}\left( \omega \right){{\rm{e}}^{{\rm{i}}\omega t}}} \end{array} \end{array} \right. $ | (15) |
式中:F(x, t)和V(x, t)分别表示整体广义力向量和广义位移向量,s(ω)为外载荷向量。相应地,可以得出AFO和DFO表示整体广义位移的传播矩阵;AVO和DVO表示整体广义力的传播矩阵。
以广义位移向量为例,根据输入激扰表达式,即式(14),得出输入激扰振幅值,即∣Fo(x, t)∣。同理,根据式(15) 可以得出相应的振动频率响应幅值,即∣F(x, t)∣。由激励输入端输入相应的激扰,得出响应拾取端的振动频率响应幅值曲线,将结果进行处理,得出相应的频率响应函数H,分析其传输特性。具体公式如下
| $ H = 20 \times \lg \left( {\frac{{\left| {F\left( {x,t} \right)} \right|}}{{\left| {{F_o}\left( {x,t} \right)} \right|}}} \right) $ | (16) |
本节对三周期一维均匀变截面声子晶体对于轴向波的传输特性行计算,并且对一维均匀变截面声子晶体模型对于轴向波的传输特性进行有限元仿真分析。
一维均匀变截面声子晶体模型,对于铝其材料参数为:铝:密度ρA=2 799 kg/m3,弹性模量常数EA=7.21×1010 Pa,泊松比νA=0.33。有机玻璃:密度ρB=1 442 kg/m3,弹性模量EB=0.32×1010 Pa,泊松比νB=0.36。
对于一维均匀变截面声子晶体结构,其物理参数为:材料A的长度l1=50 mm,材料B的长度l2=50 mm,晶格常数N=l1+l2=100 mm;组分比u=l1/(l1+l2)=0.5;均匀变截面结构的左端面端面半径r1=0.5 mm,右端面端面半径r2=2 mm,则定义截面积比s=(r2/r1)2=16。
为减小一维均匀变截面声子晶体结构模型与理想声子晶体结构模型之间的差距,本节采用自由边界条件进行计算[2],如图 7所示。取一维均匀变截面声子晶体模型的左端面为激励输入端,输入振幅为1 mm的轴向位移激扰,取右端面为激励拾取端,得出输出响应值。

|
图 7 有限元分析示意图 Fig.7 The diagram of FEM |
本节采用有限元分析法中使用较为广泛的仿真模拟软件Ansys Workbench,采用谐响应分析模块进行计算,具体加载方式如图 7所示,激励幅值为1 mm; 采用自由网格划分法,具体算法采用Full算法。
图 8给出了分别利用有限元分析法与回传射线矩阵法得到的频率响应函数曲线。从图 8中可以看出,两者之间的计算结果吻合较好,因此可以证明基于回传射线矩阵法所建立的一维均匀变截面声子晶体分析模型的正确性。此外还可以看出,在0~17 kHz的频率范围内,一维均匀变截面声子晶体对于轴向波的传输特性曲线存在一个较为明显的带隙,并且在振动带隙的范围内存在着较大的衰减程度。

|
图 8 数值计算与有限元仿真 Fig.8 The comparison of numerical and FEM |
在验证本文所建立的一维均匀变截面声子晶体分析模型的正确性的基础上,本小节还将进一步研究一维声子晶体的组成形式,各物理参数、组成参数对一维均匀变截面声子晶体对于轴向波传输特性的影响。
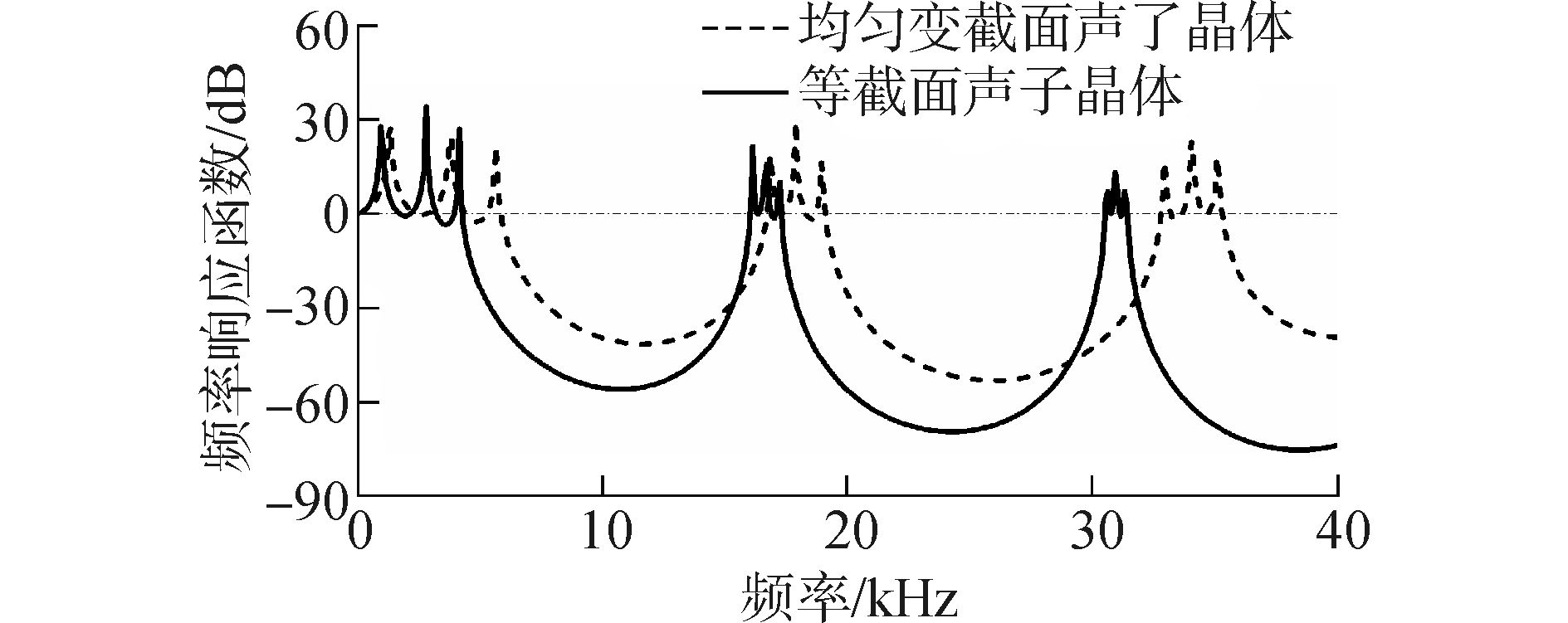
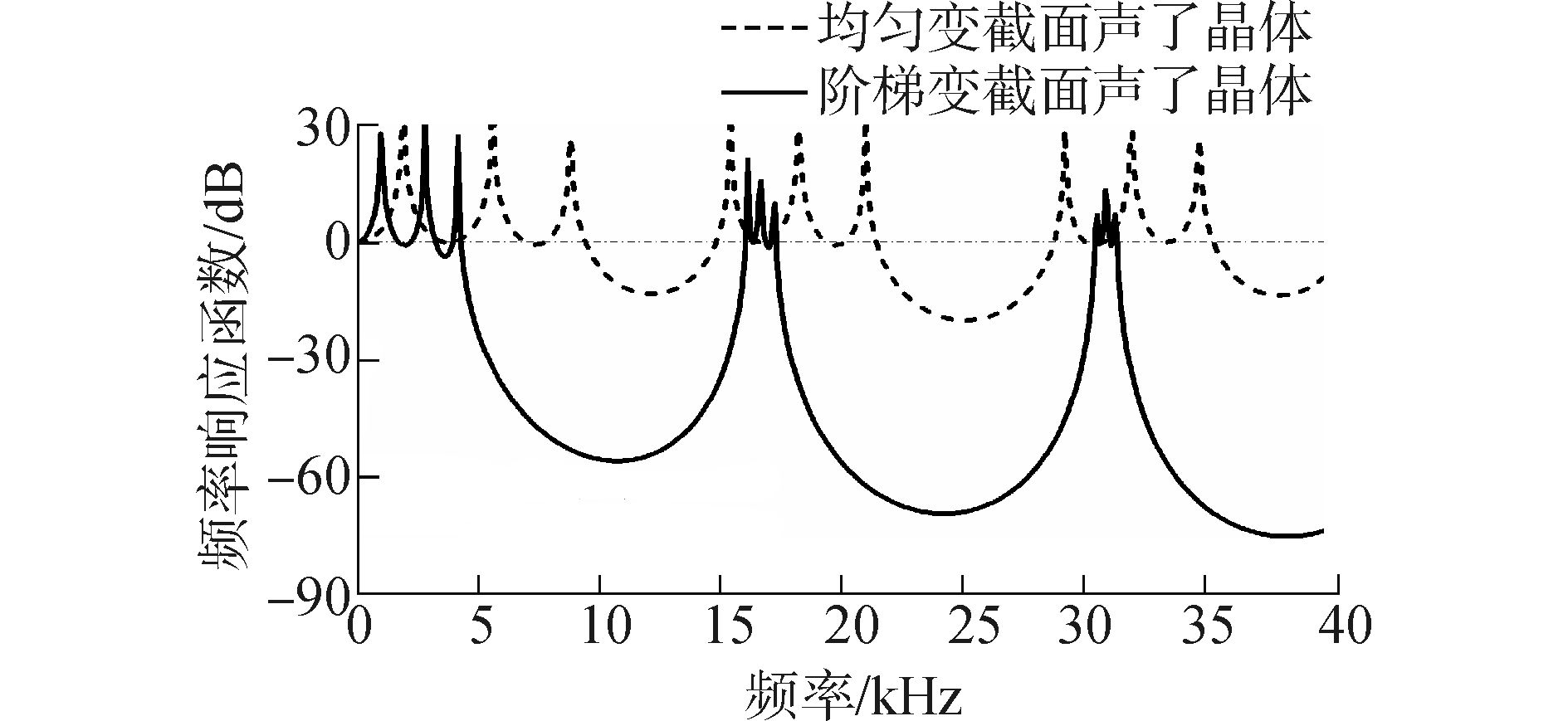
3.2.1 声子晶体组成形式的影响为比较分析一维均匀变截面声子晶体结构、一维等截面声子晶体结构和一维阶梯变截面声子晶体结构之间的区别。在此,将一维均匀变截面声子晶体分别与等截面、阶梯变截面声子晶体结构的频率响应函数曲线记性比较分析,得出相应结论。图 9和图 10分别给出了一维均匀变截面声子晶体与一维等截面声子晶体结构和一维阶梯变截面声子晶体结构之间对于轴向波传输特性的对比曲线图。一维等截面声子晶体结构的横截面为r=0.5 mm,一维阶梯变截面声子晶体结构的小截面段半径为r1=0.5 mm,大截面段半径为r2=2 mm。此外,对于其他参数,两种声子晶体结构保持一致。
|
图 9 均匀变截面与等截面声子晶体对应的频响曲线 Fig.9 The frequency response curve to the constant section and variable section phononic crystals |
|
图 10 均匀变截面与阶梯变截面声子晶体对应的频响曲线 Fig.10 The frequency response curve to the variable section and ladder section phononic crystals |
从图 9中可以看出,在0~40 kHz的频率范围内,一维均匀变截面变截面声子晶体在相应的振动带隙范围内存在着较大的衰减程度,对输入的衰减作用存在着较大的影响。并且可以看出,就第一振动带隙而言,一维均匀变截面声子晶体的振动带隙较大,具有较为广阔的衰减范围。
从图 10中可以看出,在0~40 kHz的频率范围内,一维均匀变截面声子晶体结构对于轴向波的传递作用具有较大的衰减带隙,同时经过比较可以看出,在相应的振动带隙范围之内,均匀变截面声子晶体对应的频率响应函数曲线具有较大的衰减程度,能够起到较为良好的减振衰减作用。
3.2.2 晶格常数N的影响为了比较研究晶格常数N对一维均匀变截面声子晶体结构对于轴向波传递的影响,将不同晶格常数对应的频率响应函数曲线进行绘制。保持组分比不变,通过改变晶格常数的值,得出不同晶格常数对应的频率响应函数曲线。由图 11中可以看出,在0~40 kHz的频率范围内,各个晶格常数对应的曲线具有两个较为明显的振动带隙,因第一带隙较为明显,并且具有较为良好的变化规律以及变化趋势。因此,选取第一带隙为研究对象,比较研究晶格常数对一维均匀变截面声子晶体结构振动特性的影响。
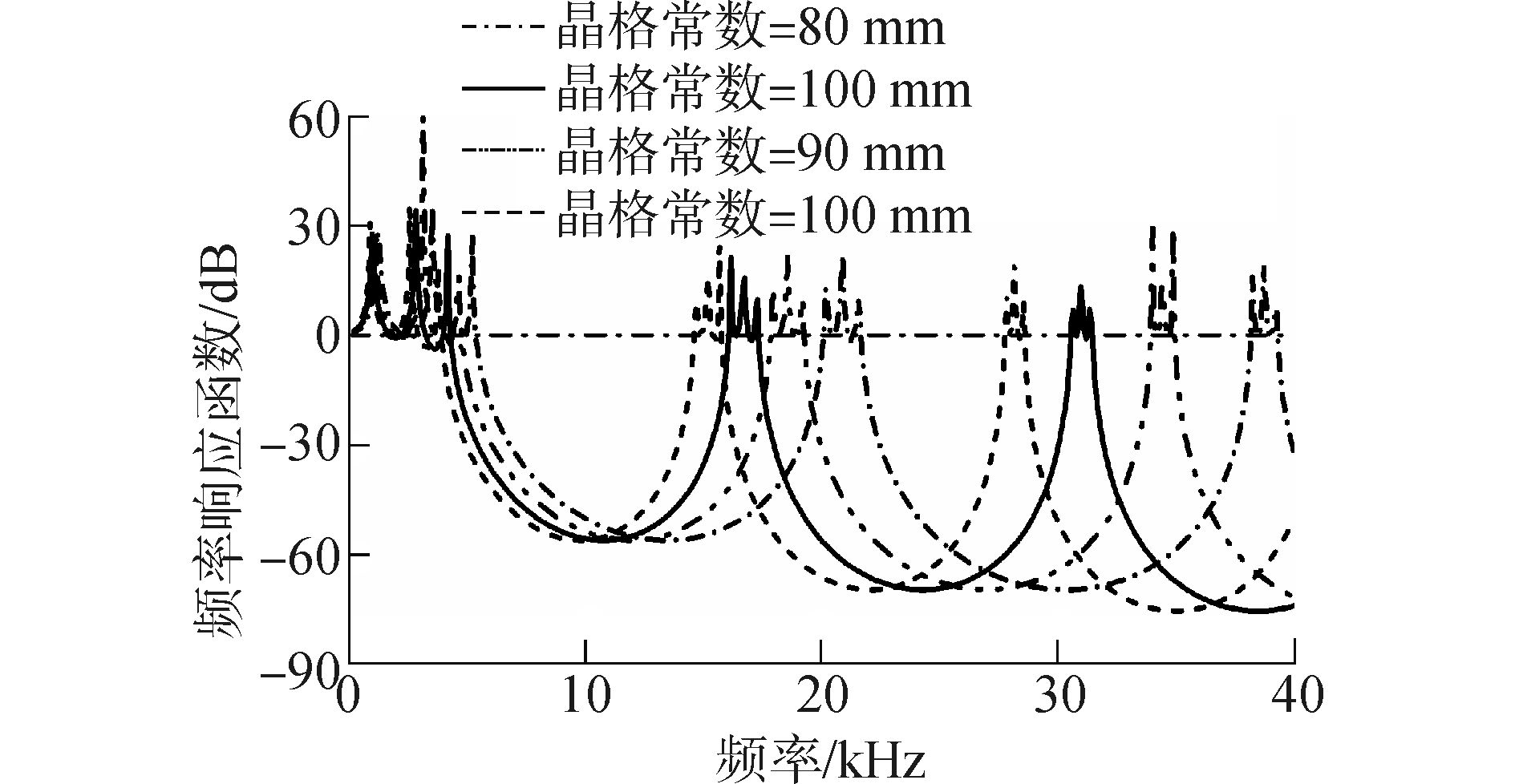
|
图 11 不晶格常数对应的频率响应曲线 Fig.11 The frequency curve of different lattice constants |
图 12为晶格常数对带隙的起始频率、截止频率、带隙宽度的影响规律。从图中可以看出,随着晶格常数的增加,第一振动带隙的起始频率以及截止频率均存在着递减的变化趋势,并且可以明显看出,截止频率的递减程度较起始频率的递减程度较为明显;对于带隙的宽度而言,随着晶格常数的增大,第一振动带隙范围内的带隙宽度逐渐减小;对于第一振动带隙范围内的最大衰减程度而言,随着晶格常数的增大,带隙范围内的最大衰减程度基本保持不变,维持在稳定的变化范围之内。

|
图 12 晶格常数对第一振动带隙的影响 Fig.12 The effect of the lattice constants to the first band gap |
为了比较分析研究组分比u对一维均匀变截面声子晶体结构振动特性的影响,保持晶格常数N的不变,通过改变组分比u的值,得出相应的频率响应函数曲线,通过比较带隙范围内的起始频率,截止频率,带隙宽度以及带隙范围内的最大衰减程度的影响,总结其变化规律。
图 13为各个组分比对应的频率响应函数曲线。不难发现,在0~40 kHz的频率范围内,各个组分比对应的频率响应函数曲线均存在着两个较大的振动带隙,因第一带隙较为明显,并且具有较为良好的变化规律,因此以第一带隙为研究对象,比较分析组分比对一维均匀变截面声子晶体振动特性的影响。图 14为组分比对带隙的起始频率,截止频率,带隙宽度的影响规律。可以看出,随着组分比的增大,带隙的起始频率基本保持不变,维持在稳定的频率范围之内;对于带隙的截止频率而言,可以看出,随着组分比的增加,带隙的截止频率逐渐降低;对于带隙宽度,随着组分比的增大,带隙宽度存在着减小的趋势;对于带隙范围内的最大衰减程度而言,随着组分比的增大,带隙范围内的最大衰减程度逐渐递减,并且存在着较大的递减趋势。

|
图 13 不同组分比对应的频率响应函数曲线 Fig.13 The frequency curve of different filling fraction |

|
图 14 组分比对第一振动带隙的影响 Fig.14 The effect of the filling fraction to the first band gap |
为了比较分析研究截面积比对一维均匀变截面声子晶体结构振动特性的影响,通过改变截面积比的值,得出相对应的频率响应函数曲线,总结其变化规律,得出相应的结论。
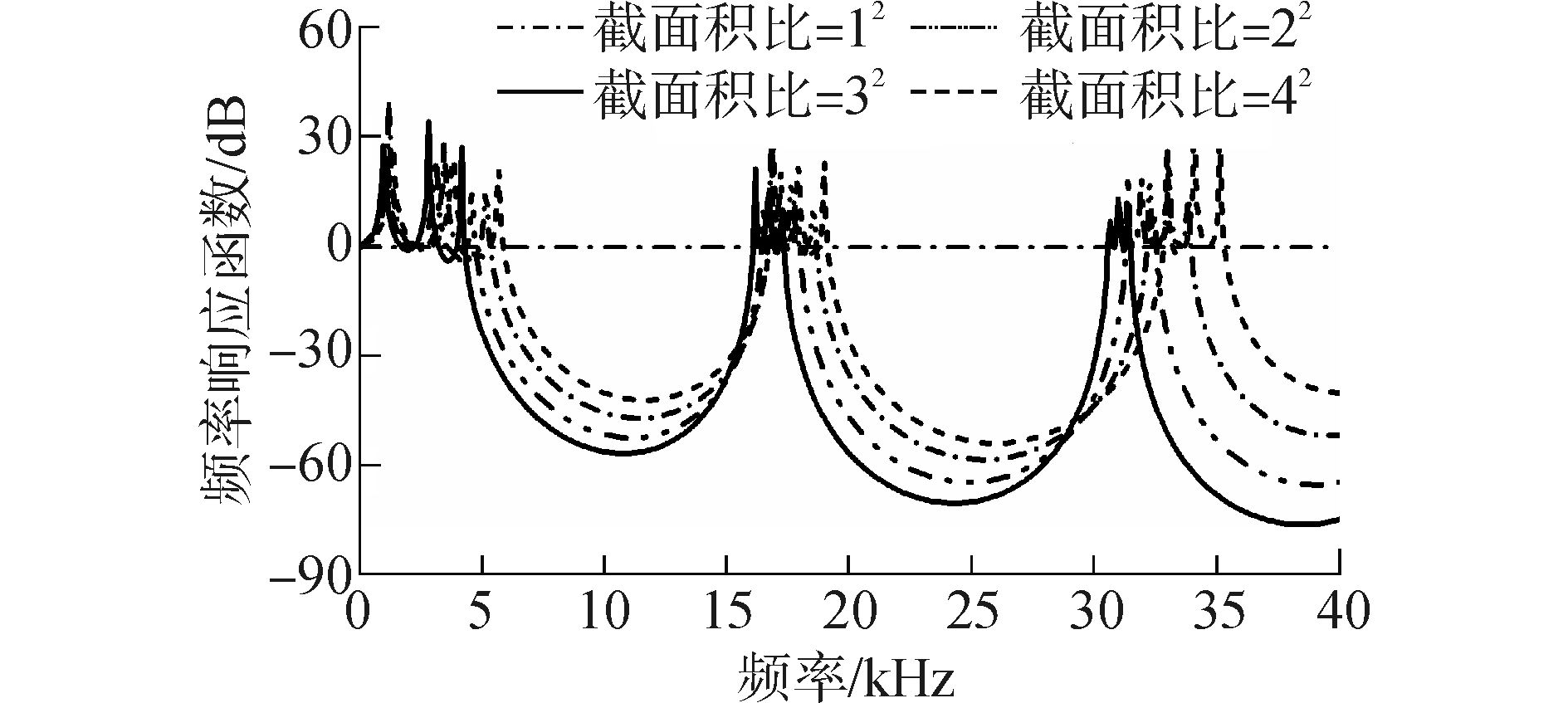
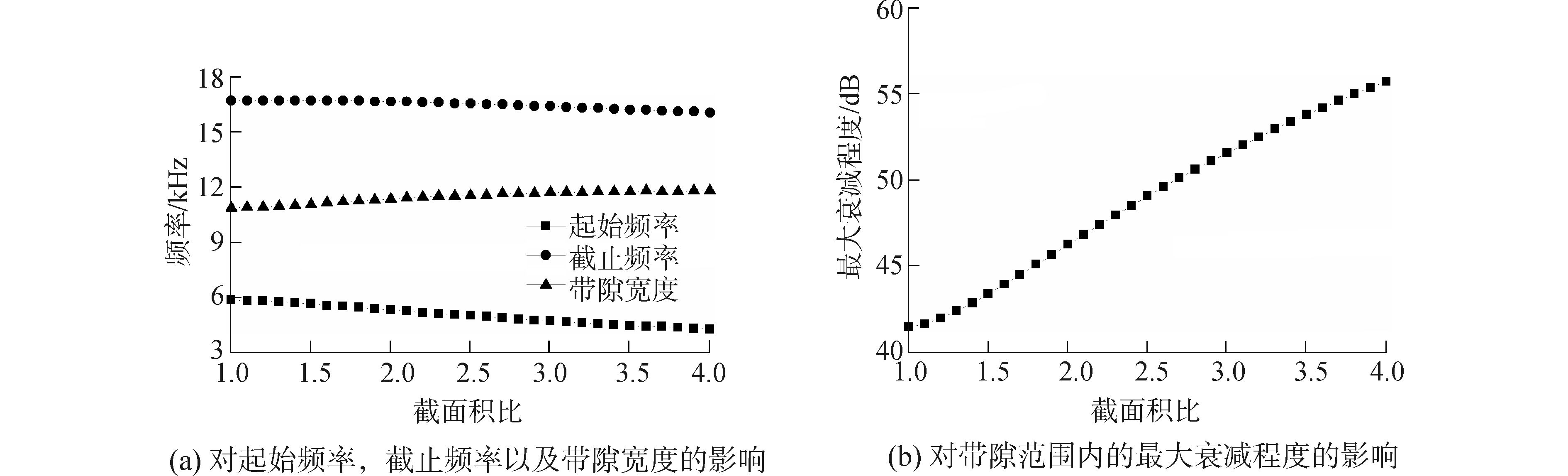
图 15为各个截面积比对应的频率响应函数曲线。在相应的频率范围之中,各个截面积比对应的频率相应函数曲线均存在两个较为明显的振动带隙,因第一带隙观察较为方便,并且具有较为明显的变化规律。因此以第一带隙为研究对象,比较分析研究截面积比对一维均匀变截面声子晶体振动特性的影响。图 16为截面积比对带隙的起始频率,截止频率,带隙宽度的影响规律。随着截面积比的增大,带隙的起始频率逐渐减小,存在着递减的趋势; 对于带隙的截止频率而言,可以看出,基本保持不变,维持在稳定的频率范围之内;对于带隙宽度而言,随着截面积比的增大,带隙宽度逐渐增大;对于带隙范围内的最大衰减程度而言,随着组分比的增大,带隙范围内的最大衰减程度逐渐增大。
|
图 15 不同截面积比对应的频率相应函数曲线 Fig.15 The frequency curve of different sectional area ratio |
|
图 16 截面积比对第一振动带隙的影响 Fig.16 The effect of the sectional area ratio to the first band gap |
本文基于欧拉-伯努利梁理论,结合回传射线矩阵法对一维均匀变截面声子晶体结构对于轴向波的振动特性进行研究,并讨论分析各个参数对其的影响程度和变化规律。
1) 基于有限元法,对一维变截面声子晶体结构对于轴向波的频率响应函数曲线进行计算并与回传射线矩阵法进行对比,证明本算法计算的正确性,为后续研究奠定基础。
2) 基于不同的结构形式,分别对一维等截面及一维阶梯变截面声子晶体结构对轴向波的传输特性曲线进行计算,并与一维均匀变截面声子晶体结构进行对比。可以看出,一维均匀变截面声子晶体结构的传输特性曲线具有较为宽大的减振带隙并且在带隙范围内存在着较大的衰减程度,起到较为良好的减振作用。
3) 基于影响参数的不同,讨论分析了各物理参数及结构参数对一维变截面声子晶体结构对于轴向波的传输特性的影响,分析相应的变化规律,为后续的研究提供相应的理论基础。
| [1] |
CICEK A, SALMAN A, KAYA O A, et al. Phononic crystal surface mode coupling and its use in acoustic Doppler velocimetry[J]. Ultrasonics, 2016, 65: 78-86. DOI:10.1016/j.ultras.2015.10.017 ( 0) 0)
|
| [2] |
LUCKLUM R, LI J, ZUBTSOV M. 1D and 2D phononic crystal sensors[J]. Procedia engineering, 2010(5): 436-439. ( 0) 0)
|
| [3] |
温激鸿, 韩小云, 王刚, 等. 声子晶体研究概述[J]. 功能材料, 2003(04): 364-367. WEN Jihong, HAN Xiaoyun, WANG Gang, et al. Review of phononic crystals[J]. Journal of functional materials, 2003(04): 364-367. DOI:10.3321/j.issn:1001-9731.2003.04.004 (  0) 0)
|
| [4] |
郁殿龙, 刘耀宗, 邱静, 等. 一维声子晶体振动特性与仿真[J]. 振动与冲击, 2005(02): 92-94. YU Dianlong, LIU Yaozong, QIU Jing, et al. Vibration property and simulation of one dimension phononic crystals[J]. Journal of vibration and shock, 2005(2): 92-94. (  0) 0)
|
| [5] |
GUO Y, CHEN W, ZHANG Y. Guided wave propagation in multilayered piezoelectric structures[J]. Science in China series G:physics, mechanics and astronomy, 2009, 52(7): 1094-1104. DOI:10.1007/s11433-009-0130-1 ( 0) 0)
|
| [6] |
郭永强. 回传射线矩阵法的理论及其应用[D]. 杭州: 浙江大学, 2008: 32-34. GUO Yongqiang, The method of reverberation-ray matrixand Its Applications[D]. Hangzhou:Zhejiang University, 2008:32-34. http://cdmd.cnki.com.cn/Article/CDMD-10335-2008071079.htm (  0) 0)
|
| [7] |
MIAO F, SUN G, ZHU P. Developed reverberation-ray matrix analysis on transient responses of laminated composite frame based on the first-order shear deformation theory[J]. Composite structures, 2016, 143: 255-271. DOI:10.1016/j.compstruct.2016.02.030 ( 0) 0)
|
| [8] |
ZHOU Y Y, CHEN W Q, LV C F, et al. Reverberation-ray matrix analysis of free vibration of piezoelectric laminates[J]. Journal of sound and vibration, 2009, 326(3): 821-836. ( 0) 0)
|
| [9] |
PAO Y H, CH EN. Elastodynamic theory of framed structures and reverberation-ray matrix analysis[J]. Acta Mechanica, 2009, 204(1-2): 61-79. DOI:10.1007/s00707-008-0012-z ( 0) 0)
|
| [10] |
ZHU J, CHEN W, YE G. Reverberation-ray matrix analysis for wave propagation in multiferroic plates with imperfect interfacial bonding[J]. Ultrasonics, 2011, 52(1): 125-132. ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


