2. 武汉理工大学 交通学院, 湖北 武汉 430063
2. School of Transportation, Wuhan University of Technology, Wuhan 430063, China
含能物质爆炸时其能量释放迅速,产生的高温高压爆轰产物急剧膨胀,爆轰产物和空气交界面产生极强冲击波。在开敞空间中,冲击波随传播距离快速衰减。而当爆炸发生在约束空间时,由于冲击波传播过程中受到约束空间壁面限制,将产生多次反射和汇聚,以及持续时间较长的准静态压力,对结构和人员产生更加严重的毁伤效应。近年来,国内外学者在爆炸冲击波的传播特性和计算方法方面做了大量的研究工作。Edri等开展了长方形TNT药柱在约束空间内的爆炸实验[1],并分析了炸药形状、起爆位置[2]对爆炸冲击波的影响规律。Feldgun等采用Autodyn程序,研究了约束空间长方体TNT药柱爆炸载荷特性,并将数值计算得到的冲击波时历曲线与实验结果进行了对比,发现数值模拟结果小于试验测量,误差是由网格尺寸及爆炸产物的后燃烧效应等因素造成的[3-4]。Benselama等采用二阶精度有限差分格式对球形TNT装药在开敞空间爆炸过程进行了数值模拟,研究表明,对于瞬时爆轰产物采用理想气体状态方程或JWL状态方程对计算结果影响不大[5]。
爆炸产生的冲击波包含激波强间断、接触间断和光滑流场结构,对爆炸冲击波流场的精确模拟需要有效且高精度的激波捕捉格式。自从Harten提出总变差递减(total variation diminishing,TVD)格式后[6],相关的高分辨率、高精度激波捕捉格式(如ENO和WENO等)得到了重视和快速发展。TVD格式是单调的,总变差不增,在间断附近能够抑制过大的非物理振荡、保持比较好的锐利形态[7-8]。然而TVD格式的精度较低并且不是全场一致的,在光滑区域最多可达二阶精度,在极值点附近只有一阶精度。Harten等提出了ENO格式,该格式采用自适应模板技术,在所有可能的插值模板中通过对节点模板自适应的单调选择和扩展来选取相对最光滑的模板进行高阶多项式插值[9]。有效避免了插值模板中出现的间断问题,从而可以无振荡的处理间断解,达到高分辨率的目的,其计算精度可以通过格式设计达到7阶。Liu等提出了WENO(weighted essentially non-oscillation scheme)格式[10],SHU等发展了该格式[11-14]。WENO在格式的有效性、通量的光滑性和收敛解的稳定性方面均优于ENO格式。在国内,张涵信构造了无参数、无振荡的NND格式[15],该格式也是属于TVD格式的一种,该格式计算精度为2阶,计算量小且编程简单,在高超声速空气动力学相关问题研究中得到了广泛应用。
本文首先提出了现有的五阶WENO格式的修改格式,利用加权函数将数值耗散局限在间断区域附近,而对于光滑流场区域则利用无耗散通量部分进行计算。采用经典算例验证了改进格式的计算精度。基于FORTRAN平台和改进的五阶WENO有限差分格式,开发了约束空间内爆炸冲击波高精度三维数值计算程序,通过与实验结果的对比分析验证了本文提出的数值计算程序的可靠性和准确性,在此基础上通过程序计算并分析炸药位置、泄爆孔位置以及泄爆孔大小等参数对约束空间爆炸载荷特性影响规律。
1 控制方程及维数分裂 1.1 欧拉方程本文对于TNT装药爆轰过程采用瞬时爆轰假定。装药瞬时爆轰后描述流场的控制方程采用三维无粘可压缩欧拉方程[16]:
| $ {\mathit{\boldsymbol{U}}_t} + {\mathit{\boldsymbol{E}}_x} + {\mathit{\boldsymbol{F}}_y} + {\mathit{\boldsymbol{G}}_z} = 0 $ | (1) |
其中,
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{U = }}\left[ \begin{array}{l} \rho \\ \rho u\\ \rho v\\ \rho w\\ E \end{array} \right],\;\;\;\mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {\rho u}\\ {\rho {u^2} + p}\\ {\rho uv}\\ {\rho uw}\\ {u\left( {E + p} \right)} \end{array}} \right],}\\ {\mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\rho v}\\ {\rho vu}\\ {\rho {v^2} + p}\\ {\rho vw}\\ {v\left( {E + p} \right)} \end{array}} \right],\;\;\;\;\mathit{\boldsymbol{G = }}\left[ {\begin{array}{*{20}{c}} {\rho w}\\ {\rho wu}\\ {\rho wv}\\ {\rho {w^2} + p}\\ {w\left( {E + p} \right)} \end{array}} \right]} \end{array} $ | (2) |
| $ E = \rho e + \frac{1}{2}\rho {u^2} + \frac{1}{2}\rho {v^2} + \frac{1}{2}\rho {w^2} $ | (3) |
| $ p = \left( {\gamma - 1} \right)\rho e $ | (4) |
式中:ρ是密度,u、v、w是x、y、z方向上的速度分量,p为流体压力,E是单位体积流体的总能量,e是比内能。
1.2 Strang维数分裂对于多维欧拉方程的计算,一般采用维数分裂的方法进行处理。利用Strang维数分裂法,将欧拉方程分解为x、y、z 3个方向求解:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{E}}\left( \mathit{\boldsymbol{U}} \right)}}{{\partial \mathit{\boldsymbol{U}}}}\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial x}} = 0 $ | (5) |
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{U}} \right)}}{{\partial \mathit{\boldsymbol{U}}}}\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial y}} = 0 $ | (6) |
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{G}}\left( \mathit{\boldsymbol{U}} \right)}}{{\partial \mathit{\boldsymbol{U}}}}\frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial z}} = 0 $ | (7) |
欧拉方程属于双曲型偏微分方程,需要根据其特性来选择合适的数值计算方法进行求解。本文的程序中采用改进的五阶WENO有限差分格式进行欧拉方程的数值离散和求解。
2.1 特征矩阵对x、y、z 3个方向对流项通量所对应的Jacobia矩阵进行特征矩阵求解[16]的过程是将对流项通量首先映射到特征空间进行特征分裂,然后再将特征分裂后的对流项数值通量映射回原物理空间,最终实现对流项通量在物理空间的分裂。
Jacobia矩阵∂E(U)/∂U的左特征矩阵L为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_1} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}\left( {{b_2} + \frac{u}{c}} \right)}&{ - \frac{1}{2}\left( {{b_1}u + \frac{1}{c}} \right)} \end{array}} \right.}\\ {\left. {\begin{array}{*{20}{c}} { - \frac{1}{2}{b_1}v}&{ - \frac{1}{2}{b_1}w}&{\frac{1}{2}{b_1}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_2} = \left[ {\begin{array}{*{20}{c}} {1 - {b_2}}&{{b_1}u}&{{b_1}v}&{{b_1}w}&{ - {b_1}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_3} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}\left( {{b_2} - \frac{u}{c}} \right)}&{ - \frac{1}{2}\left( {{b_1}u - \frac{1}{c}} \right)} \end{array}} \right.}\\ {\left. {\begin{array}{*{20}{c}} { - \frac{1}{2}{b_1}v}&{ - \frac{1}{2}{b_1}w}&{\frac{1}{2}{b_1}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_4} = \left[ {\begin{array}{*{20}{c}} { - w}&0&0&1&0 \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_5} = \left[ {\begin{array}{*{20}{c}} { - v}&0&1&0&0 \end{array}} \right]} \end{array} $ | (8) |
Jacobia矩阵∂E(U)/∂U的右特征矩阵R为,
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_1} = \left[ {\begin{array}{*{20}{c}} 1\\ {u - c}\\ v\\ w\\ {H - uc} \end{array}} \right],\;\;\;\;\;{\mathit{\boldsymbol{R}}_2} = \left[ {\begin{array}{*{20}{c}} 1\\ u\\ v\\ w\\ {\frac{{{u^2} + {v^2} + {w^2}}}{2}} \end{array}} \right],}\\ {{\mathit{\boldsymbol{R}}_3} = \left[ {\begin{array}{*{20}{c}} 1\\ {u + c}\\ v\\ w\\ {H + uc} \end{array}} \right],\;\;\;\;\;\;\;{\mathit{\boldsymbol{R}}_4} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 1\\ w \end{array}} \right],\;\;\;\;\;\;\;{\mathit{\boldsymbol{R}}_5} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1\\ 0\\ v \end{array}} \right]} \end{array} $ | (9) |
Jacobia矩阵∂F(U)/∂U的左特征矩阵L为,
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_1} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}\left( {{b_2} + \frac{v}{c}} \right)}&{ - \frac{1}{2}{b_1}u} \end{array}} \right.}\\ {\left. {\begin{array}{*{20}{c}} { - \frac{1}{2}\left( {{b_1}v + \frac{1}{c}} \right)}&{ - \frac{1}{2}{b_1}w}&{\frac{1}{2}{b_1}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_2} = \left[ {\begin{array}{*{20}{c}} {1 - {b_2}}&{{b_1}u}&{{b_1}v}&{{b_1}w}&{ - {b_1}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_3} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}\left( {{b_2} - \frac{v}{c}} \right)}&{ - \frac{1}{2}{b_1}u} \end{array}} \right.}\\ {\left. {\begin{array}{*{20}{c}} { - \frac{1}{2}\left( {{b_1}v - \frac{1}{c}} \right)}&{ - \frac{1}{2}{b_1}w}&{\frac{1}{2}{b_1}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_4} = \left[ {\begin{array}{*{20}{c}} { - w}&0&0&1&0 \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_5} = \left[ {\begin{array}{*{20}{c}} { - u}&1&0&0&0 \end{array}} \right]} \end{array} $ | (10) |
Jacobia矩阵∂F(U)/∂U的右特征矩阵R为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_1} = \left[ {\begin{array}{*{20}{c}} 1\\ u\\ {v - c}\\ w\\ {H - vc} \end{array}} \right],\;\;\;\;\;{\mathit{\boldsymbol{R}}_2} = \left[ {\begin{array}{*{20}{c}} 1\\ u\\ v\\ w\\ {\frac{{{u^2} + {v^2} + {w^2}}}{2}} \end{array}} \right],}\\ {{\mathit{\boldsymbol{R}}_3} = \left[ {\begin{array}{*{20}{c}} 1\\ u\\ {v + c}\\ w\\ {H + vc} \end{array}} \right],\;\;\;\;\;\;\;{\mathit{\boldsymbol{R}}_4} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 1\\ w \end{array}} \right],\;\;\;\;\;\;\;{\mathit{\boldsymbol{R}}_5} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1\\ 0\\ u \end{array}} \right]} \end{array} $ | (11) |
Jacobia矩阵∂G(U)/∂U的左特征矩阵L为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_1} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}\left( {{b_2} + \frac{w}{c}} \right)}&{ - \frac{1}{2}{b_1}u} \end{array}} \right.}\\ {\left. {\begin{array}{*{20}{c}} { - \frac{1}{2}{b_1}v}&{ - \frac{1}{2}\left( {{b_1}w + \frac{1}{c}} \right)}&{\frac{1}{2}{b_1}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_2} = \left[ {\begin{array}{*{20}{c}} {1 - {b_2}}&{{b_1}u}&{{b_1}v}&{{b_1}w}&{ - {b_1}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_3}\left[ {\begin{array}{*{20}{c}} {\frac{1}{2}\left( {{b_2} - \frac{w}{c}} \right)}&{ - \frac{1}{2}{b_1}u}&{ - \frac{1}{2}{b_1}v} \end{array}} \right.}\\ {\left. {\begin{array}{*{20}{c}} { - \frac{1}{2}\left( {{b_1}w - \frac{1}{c}} \right)}&{\frac{1}{2}{b_1}} \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_4} = \left[ {\begin{array}{*{20}{c}} { - v}&0&1&0&0 \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_5} = \left[ {\begin{array}{*{20}{c}} { - u}&1&0&0&0 \end{array}} \right]} \end{array} $ | (12) |
Jacobia矩阵∂G(U)/∂U的右特征矩阵R为
| $ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_1} = \left[ {\begin{array}{*{20}{c}} 1\\ u\\ v\\ {w - c}\\ {H - wc} \end{array}} \right],}&{{\mathit{\boldsymbol{R}}_2} = \left[ {\begin{array}{*{20}{c}} 1\\ u\\ v\\ w\\ {\frac{{{u^2} + {v^2} + {w^2}}}{2}} \end{array}} \right],} \end{array}}\\ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_3} = \left[ {\begin{array}{*{20}{c}} 1\\ u\\ v\\ {w + c}\\ {H + wc} \end{array}} \right],}&{{\mathit{\boldsymbol{R}}_4} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 1\\ v \end{array}} \right],}&{{\mathit{\boldsymbol{R}}_5} = \left[ {\begin{array}{*{20}{c}} 0\\ 1\\ 0\\ 0\\ u \end{array}} \right]} \end{array}} \end{array} $ | (13) |
式中:
WENO格式的基本思想是通过线性组合低阶通量来得到高阶通量,其数值离散和推导过程如下[14, 17],对于五阶WENO格式单元面xi+1/2处的数值通量fi+1/2的3种重构方式分别为
| $ f_{i + 1/2}^0 = \frac{1}{3}{f_i} + \frac{5}{6}{f_{i + 1}} - \frac{1}{6}{f_{i + 2}} $ | (14) |
| $ f_{i + 1/2}^1 = - \frac{1}{6}{f_{i - 1}} + \frac{5}{6}{f_i} + \frac{1}{3}{f_{i + 1}} $ | (15) |
| $ f_{i + 1/2}^2 = \frac{1}{3}{f_{i - 2}} - \frac{7}{6}{f_{i - 1}} + \frac{{11}}{6}{f_i} $ | (16) |
式中:fk(k=i-2, i-1, i, i+1, i+2) 分别表示点xk处的数值通量。fi+1/2k(k=0, 1, 2) 表示3个子模板{xi, xi+1, xi+2}, {xi-1, xi, xi+1}, {xi-2, xi-1, xi}上三阶精度的数值通量。
五阶WENO格式利用上述的3种模板的凸组合计算数值通量fi+1/2,即
| $ {f_{i + 1/2}} = {\omega _0}f_{i + 1/2}^0 + {\omega _1}f_{i + 1/2}^1 + {\omega _2}f_{i + 1/2}^2 $ | (17) |
ωk(k=0, 1, 2) 表示WENO格式的非线性权重。
对于光滑情形,将
| $ \begin{array}{l} {f_{i + 1/2}} = \frac{1}{{12}}\left( { - {f_{i - 1}} + 7{f_i} + 7{f_{i + 1}} - {f_{i + 2}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{6}\left( {{\omega _0} - \frac{1}{2}} \right)\left( {{D_1} - 2{D_2} + {D_3}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{1}{3}{\omega _2}\left( {{D_0} - 2{D_1} + {D_2}} \right) \end{array} $ | (18) |
式中:
| $ \left\{ \begin{array}{l} {D_0} = {f_{i - 2}} - {f_{i - 1}},{D_1} = {f_{i - 1}} - {f_i}\\ {D_2} = {f_i} - {f_{i + 1}},{D_3} = {f_{i + 1}} - {f_{i + 2}} \end{array} \right. $ | (19) |
式(18) 中的ωk根据下式求得
| $ \left\{ \begin{array}{l} {\omega _k} = \frac{{{\alpha _k}}}{{\sum\limits_{s = 0}^2 {{\alpha _s}} }},{\alpha _k} = \frac{{{d_k}}}{{\left( {\varepsilon + {\beta _k}} \right)}},k = 0,1,2\\ {d_0} = \frac{3}{{10}},{d_1} = \frac{6}{{10}},{d_2} = \frac{1}{{10}} \end{array} \right. $ | (20) |
式中:dk(k=0, 1, 2) 表示WENO格式的线性权重。ε为避免分母为零的小数,取为ε=10-6。
其中,3个子模板光滑因子βk(k=0, 1, 2) 的表达式如下
| $ \left\{ \begin{array}{l} {\beta _0} = {D_2}\left( {10{D_2} - 11{D_3}} \right) + 4D_3^2\\ {\beta _1} = {D_1}\left( {4{D_1} - 5{D_2}} \right) + 4D_2^2\\ {\beta _2} = {D_0}\left( {4{D_0} - 11{D_1}} \right) + 10D_1^2 \end{array} \right. $ | (21) |
为了提高爆炸冲击波计算精度,本文参考文献[18]的思想提出改进的五阶WENO格式。将五阶WENO格式数值通量分解为无耗散部分和耗散部分,并利用加权函数将数值耗散局限在间断区域附近,从而更好地捕捉间断;而对于光滑流场区域则利用无耗散通量部分进行计算,提高流场的计算分辨率。下面给出改进的五阶WENO格式具体推导过程。
将式(18) 中的数值通量分解为四阶中心差分无耗散通量和数值耗散通量,两部分通量分别为
| $ f_{i + 1/2{\rm{\_non}}\_{\rm{diss}}}^{{\rm{WENO}}5} = \frac{1}{{12}}\left( { - {f_{i - 1}} + 7{f_i} + 7{f_{i + 1}} - {f_{i + 2}}} \right) $ | (22) |
| $ \begin{array}{l} f_{i + 1/2\_{\rm{diss}}}^{{\rm{WENO}}5} = \frac{1}{6}\left( {{\omega _0} - \frac{1}{2}} \right)\left( {{D_1} - 2{D_2} + {D_3}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{3}{\omega _2}\left( {{D_0} - 2{D_1} + {D_2}} \right) \end{array} $ | (23) |
改进格式最终可以写成
| $ f_{i + 1/2}^{{\rm{HYBRID}}} = f_{i + 1/2{\rm{\_non}}\_{\rm{diss}}}^{{\rm{WENO}}5} + \left( {1 - {\sigma _{i + 1/2}}} \right)f_{i + 1/2\_{\rm{diss}}}^{{\rm{WENO}}5} $ | (24) |
式(24) 中σi+1/2为加权函数,其表达式为
| $ {\sigma _{i + 1/2}} = {\left( {\frac{1}{{1 + {{\left( {\frac{{\tau + \varepsilon }}{{\beta _{j + 1/2}^{{\rm{hybrid}}}}}} \right)}^m}}}} \right)^p} $ | (25) |
| $ \tau = \max \left[ {{\rm{abs}}\left( {{\beta _0} - {\beta _1}} \right),{\rm{abs}}\left( {{\beta _1} - {\beta _2}} \right),{\rm{abs}}\left( {{\beta _2} - {\beta _0}} \right)} \right] $ | (26) |
| $ \beta _{j + 1/2}^{{\rm{hybrid}}} = \min \left( {{\beta _0},{\beta _1},{\beta _2}} \right) $ | (27) |
式(25) 中ε=1.0×10-6,m、p均为大于1的整数,通过多次数值试验确定本文中m、p参数分别为m=2, p=2。
2.3 时间项数值离散时间项采用三阶TVD-RK法求解,格式如下
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{U}}^{\left( 1 \right)}} = {\mathit{\boldsymbol{U}}^{\rm{n}}} + \Delta t\mathit{\boldsymbol{L}}\left( {{\mathit{\boldsymbol{U}}^{\rm{n}}}} \right)\\ {\mathit{\boldsymbol{U}}^{\left( 2 \right)}} = \frac{3}{4}{\mathit{\boldsymbol{U}}^{\rm{n}}} + \frac{1}{4}{\mathit{\boldsymbol{U}}^{\left( 1 \right)}} + \frac{1}{4}\Delta t\mathit{\boldsymbol{L}}\left( {{\mathit{\boldsymbol{U}}^{\left( 1 \right)}}} \right)\\ {\mathit{\boldsymbol{U}}^{n + 1}} = \frac{1}{3}{\mathit{\boldsymbol{U}}^{\rm{n}}} + \frac{1}{3}{\mathit{\boldsymbol{U}}^{\left( 2 \right)}} + \frac{2}{3}\Delta t\mathit{\boldsymbol{L}}\left( {{\mathit{\boldsymbol{U}}^{\left( 2 \right)}}} \right) \end{array} \right. $ | (28) |
式中:U表示守恒通量,Un表示n时刻的守恒通量,U(1), U(2)表示中间变量,Un+1表示n+1时刻的守恒通量,Δt表示时间步长,L(·)表示运算算子。
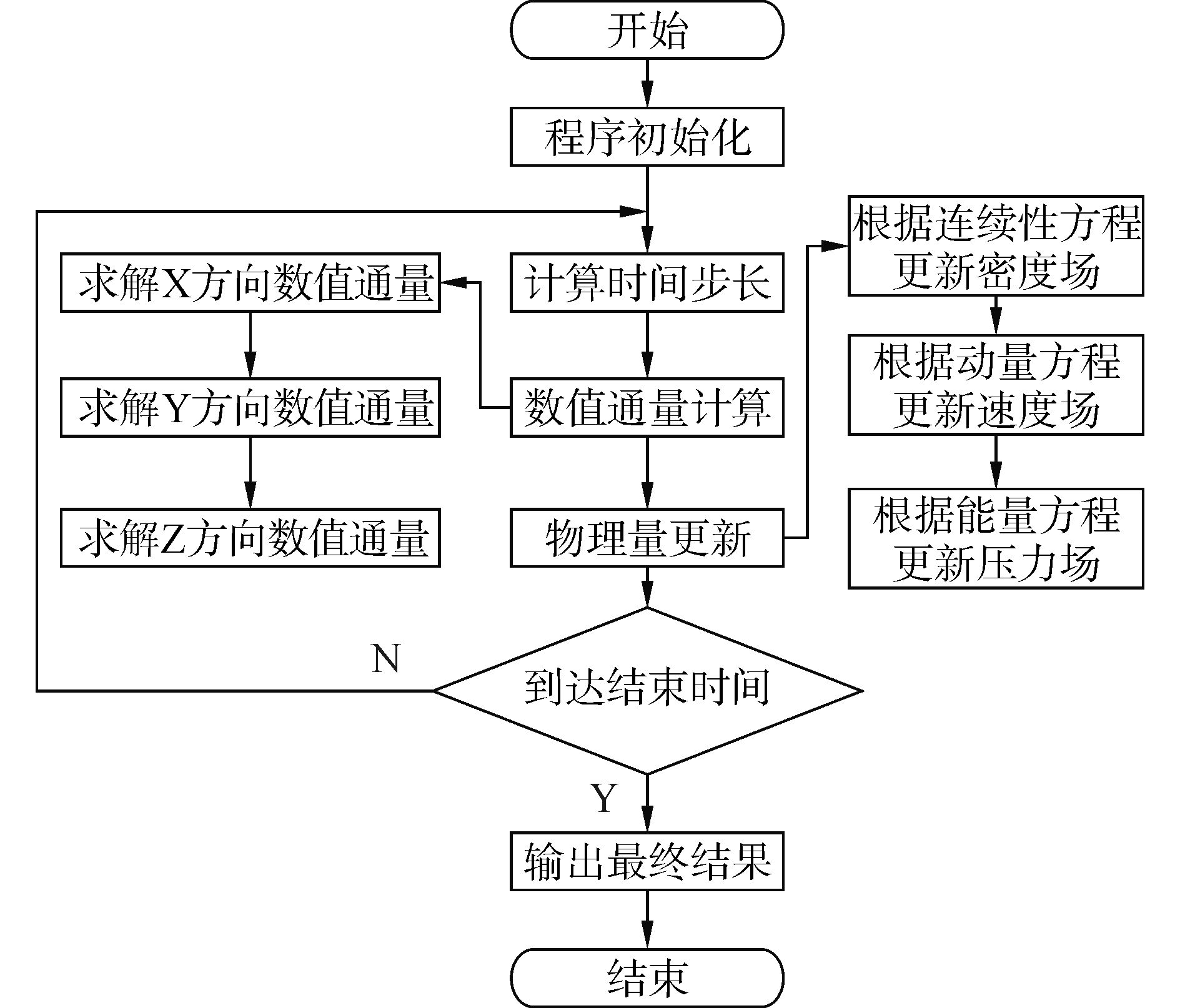
2.4 数值计算方法的程序实现本文所开发的约束空间内爆炸冲击波高精度三维数值计算程序,基于FORTRAN平台,采用主程序和子程序相结合方式进行上述数值计算方法的实现,程序实现流程如图 1所示。1) 根据具体的物理条件,确定计算域的尺度、网格大小、计算结束时间等参数,对程序进行初始化。2) 根据数值计算的稳定性条件确定时间步长。3) 通过主程序调用子程序的方式实现x、y、z 3个方向数值通量的计算。4) 根据计算得到的总通量,由连续性方程更新密度场,由动量方程更新速度场,由能量方程更新压力场、温度场等标量场。5) 判断计算时间是否达到结束时间,若达到,则直接输出最终计算结果;否则,返回到2) 进行程序的循环。
|
图 1 程序实现流程 Fig.1 Program implementation process |
本文采用经典的激波与熵波的相互作用案例来验证改进WENO格式的计算精度,该问题主要描述冲击波与局部密度扰动区的相互作用过程[12]。计算初始条件为
| $ \left( {\rho \;u\;p} \right) = \left\{ {\begin{array}{*{20}{c}} {\left( {\begin{array}{*{20}{c}} {3.857\;143}&{2.629\;369}&{10.333\;33} \end{array}} \right),}\\ { - 5 \le x < - 4}\\ {\left( {1 + 0.2\sin 5x\;0\;1} \right),\;\;\;\; - 4 \le x \le 5} \end{array}} \right. $ | (29) |
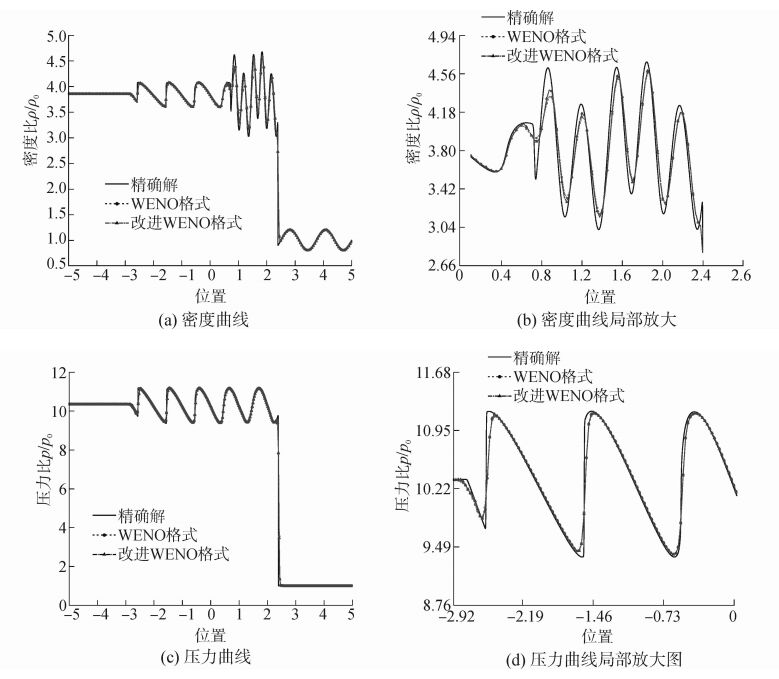
两端边界条件设置为流出边界,网格数为400,计算结束的无量纲时间为1.8(参照文献[12]处理方法),计算对比结果如图 2所示。图 2(a)、(c)分别给出WENO格式、改进的WENO格式数值计算结果与精确解的对比图,为了比较两种格式的差异性,将密度和压力曲线进行局部放大,见图 2(b)、(d)。
|
图 2 两种数值格式计算密度和压力曲线对比图 Fig.2 Comparisons of density and pressure curve between two different numerical schemes |
通过对比发现,本文改进的WENO格式对激波间断具有较好的捕捉能力,在间断附近其耗散比WENO格式小,捕捉到的间断更陡峭,见图 2(d)。对于光滑流场结构,本文改进的WENO格式给出更高精度的结果,见图 2(b)。从计算结果的对比来看,本文采用的加权函数可以有效地检测到间断,在远离间断区域减小数值耗散,在间断局部区域施加足够耗散以捕捉间断。
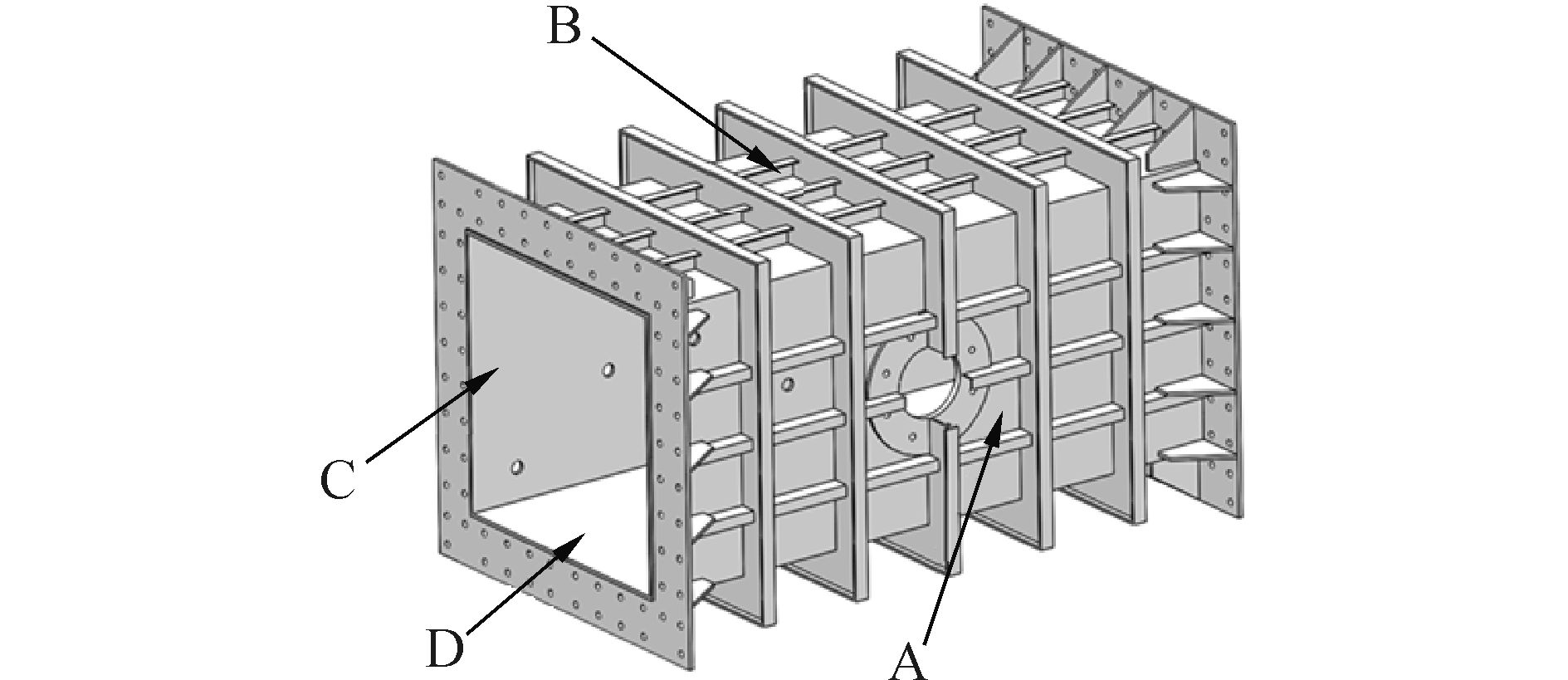
4 数值计算程序的实验验证 4.1 实验装置为了验证本文数值程序对于三维约束空间TNT爆炸冲击波演化过程模拟计算的可靠性和准确性,作者团队开展了相关的实验研究。实验装置是内部尺寸为1 800 mm×800 mm×800 mm的长方体结构,如图 3所示。箱体壁面A上开有可以调节孔径大小的泄爆孔,如图 4所示。箱体壁面A上安装2个压力传感器,分别编号为NO.1和NO.2;壁面B上安装1个压力传感器,编号为NO.3;壁面C上安装2个压力传感器,编号分别为NO.4和NO.5,各压力传感器具体布置位置如图 5所示。

|
图 3 爆炸箱体 Fig.3 Blast chamber |
|
图 4 爆炸箱体壁面编号 Fig.4 Wall numbers of the blast chamber |

|
图 5 压力传感器测点布置位置示意图 Fig.5 Sketch of arrangement of pressure transducers |
实验中采用55 g和110 g 2种柱形TNT,具体的尺寸和参数见表 1,实验工况列于表 2。
| 表 1 柱形TNT尺寸和参数 Tab.1 Size and parameters of the cylindrical TNT |
| 表 2 实验爆炸工况 Tab.2 Cases of the experiment |
炸药的爆炸场包含向内部传播的稀疏波以及向外部空气域传播的冲击波等复杂波系结构。由于本文实验采用的TNT药柱尺寸较小,假定柱形TNT装药瞬时爆轰,并根据能量等效的原则,采用理想气体状态方程计算瞬时爆轰后高温高压气体产物的压力,具体的参数见表 3。通过初步计算发现,由于TNT药柱尺寸较小,所能填充的网格数较少,会给计算过程造成一定的误差。本文对于装药采用特殊的处理方法,根据质量和能量守恒,将柱形TNT装药瞬时爆轰后高温高压气体产物尺寸扩大2倍后的参数作为程序的初始条件,见表 4。
| 表 3 空气和爆轰气体产物的参数 Tab.3 Parameters of the air and detonation gas |
| 表 4 尺寸扩大后TNT爆轰产物参数 Tab.4 Parameters of the expanded TNT explosives |
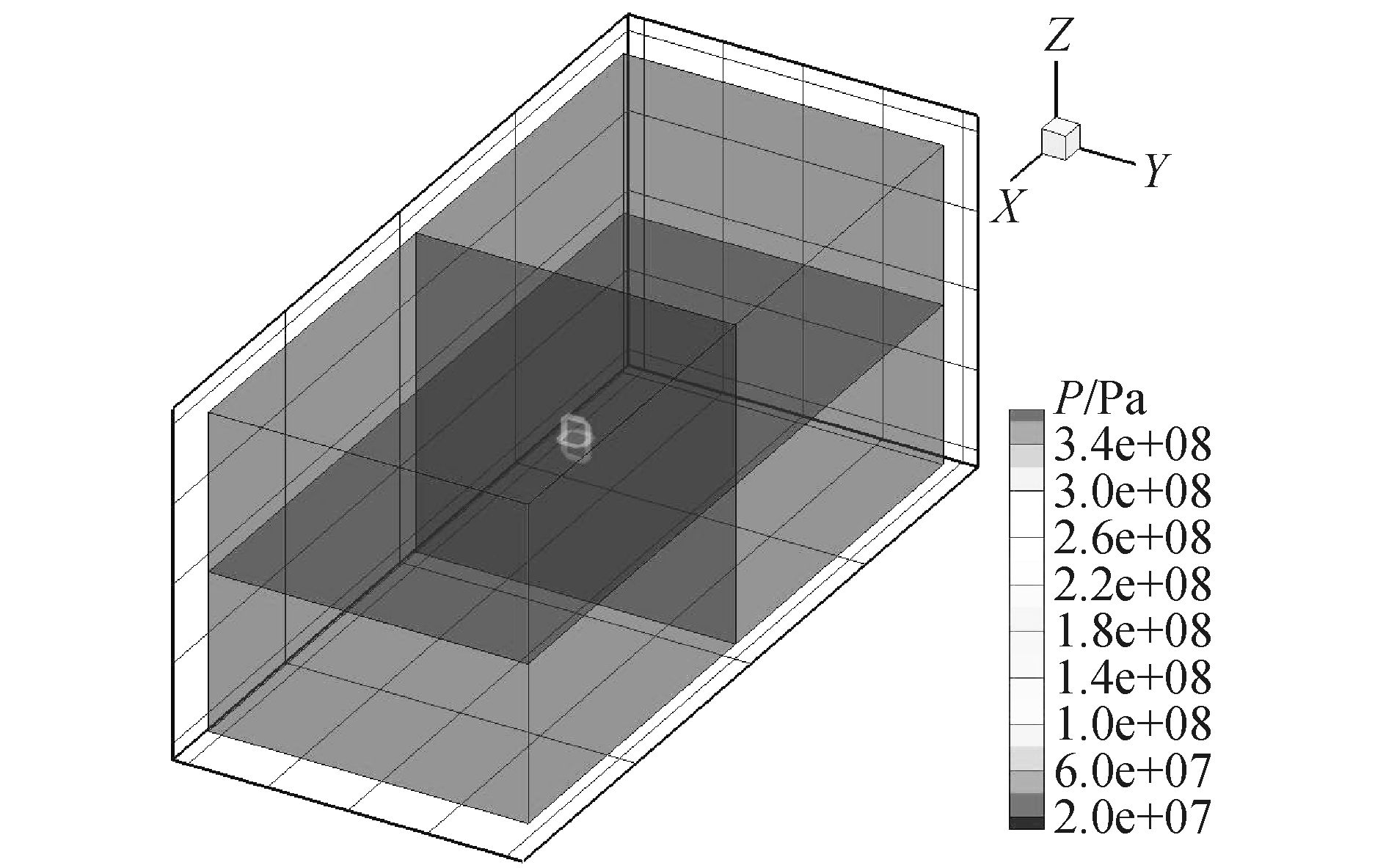
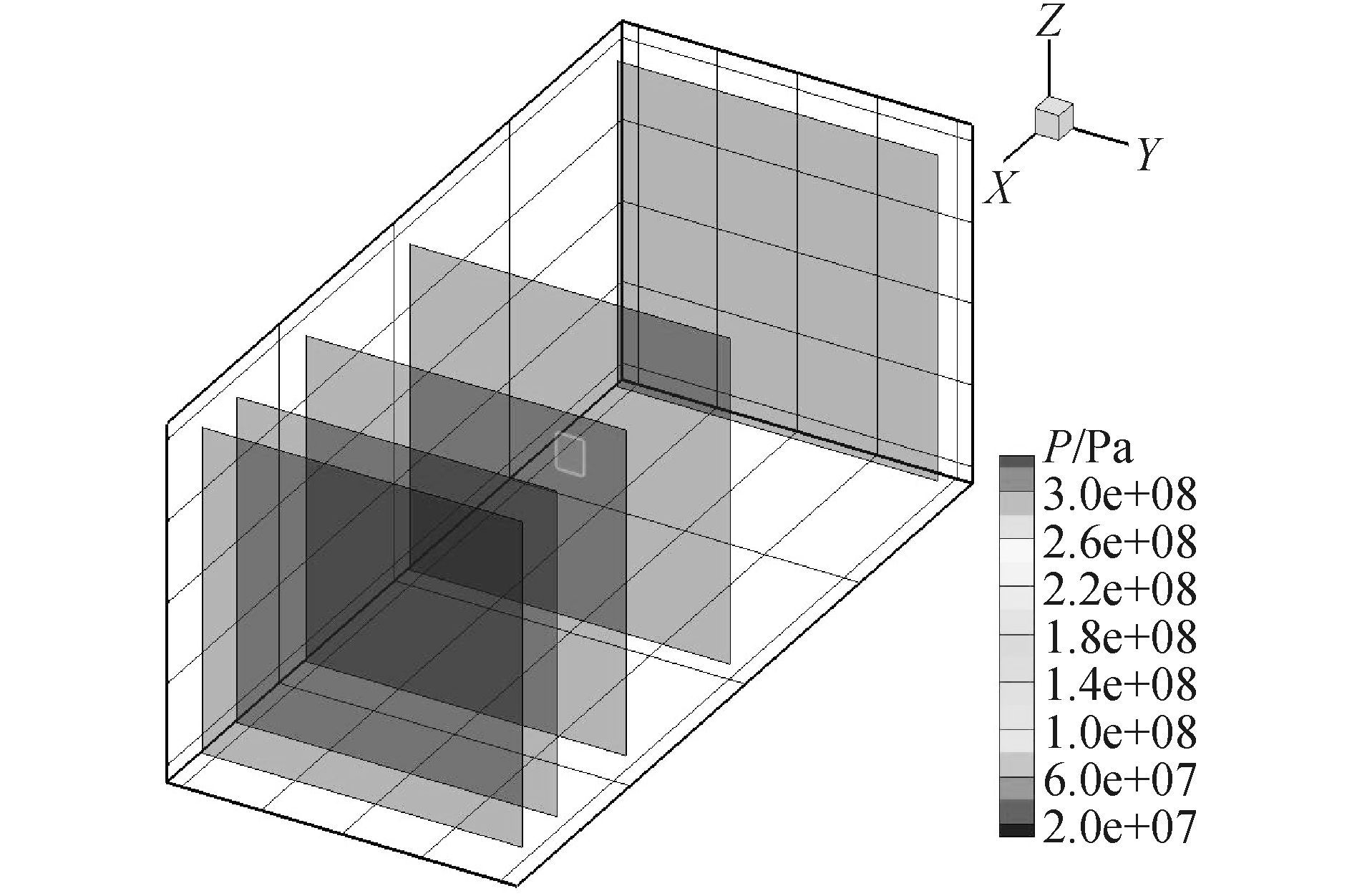
三维程序中计算初始状态见图 6,中间柱形区域表示TNT瞬时爆轰产物,周围区域为箱体内部的空气,其尺寸为箱体内部尺寸,由于壁面结构刚度很大,在计算中处理为刚性反射壁面,箱体开孔处设置为流出边界。基于计算时间和计算精度的考虑,本文程序中网格数设置为180×80×80。为了显示压力场随时间变化的整个过程,计算过程中设定了5个切面(见图 7),分别位于x1=0 mm,x2=900 mm,x3=1 350 mm,x4=1 650 mm和x5=1 800 mm处。切面x1和x5分别位于爆炸箱体长度方向的2个端面处;切面x2位于箱体中间;切面x3位于壁面压力测点NO.1、NO.3和NO.4的位置处;切面x4位于壁面压力测点NO.2和NO.5的位置处。
|
图 6 爆炸箱体及初始条件 Fig.6 The blast chamber and initial condition |
|
图 7 爆炸箱体切面位置 Fig.7 Initial slices of the blast chamber |
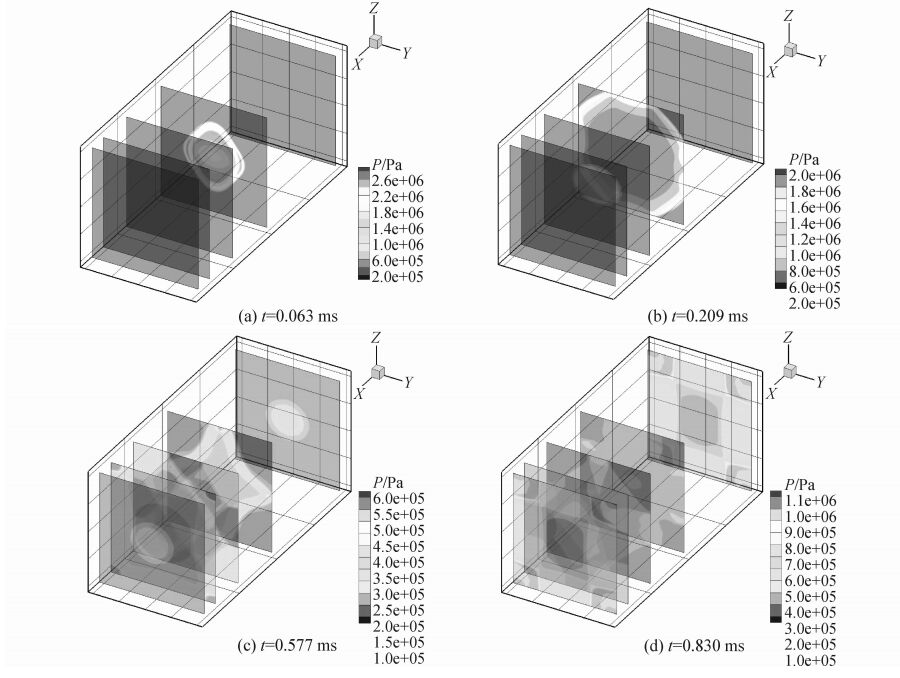
为了显示整个爆炸过程爆炸箱体内部爆炸波的传播过程,选取4个典型时刻显示其压力分布。从图 8(a)可以看出,爆炸波到达壁面之前,装药爆轰产物处于三维柱对称自由膨胀过程,从图中可以看出,柱形装药高压区由初始柱形逐渐演变成椭圆形,且椭圆长轴分布在径向。径向冲击波强度要大于轴向冲击波强度,传播过程区别于典型的球形装药一维球对称膨胀。从图 8(b)可以看出,冲击波初次达到箱体宽度和高度方向的壁面,并发生规则反射,同时高压气体从泄爆孔处泄出。随着计算时间的推进,爆炸波到达爆炸箱体长度方向的壁面并发生规则反射,如图 8(c)所示。随着不同壁面的反射冲击波的汇聚叠加和多次反射,约束空间内部的流场趋于复杂,如图 8(d)所示。
|
图 8 爆炸箱体压力场分布 Fig.8 Pressure field of the whole blast chamber |
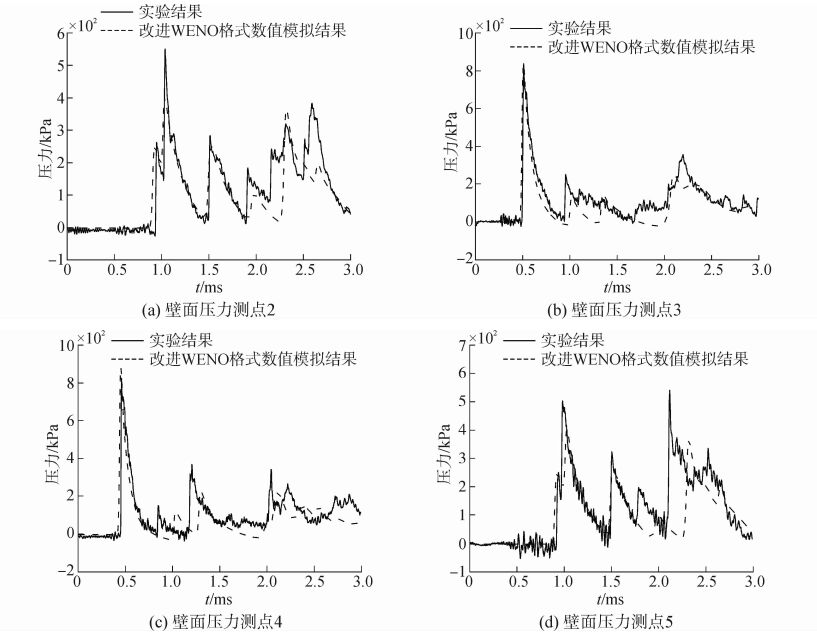
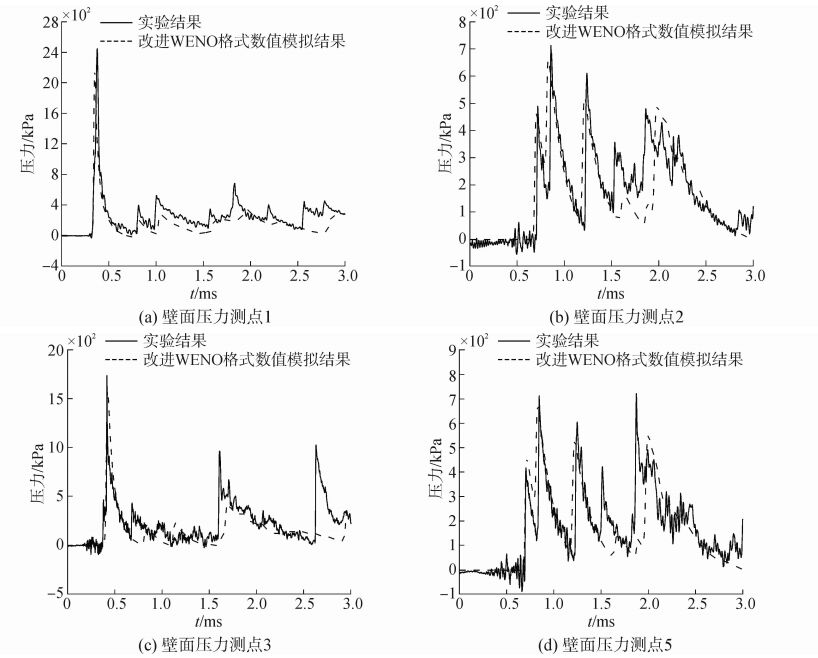
由于在实验过程中工况1的测点NO.1没有采集到有效的数据,因此主要对比测点NO.2,NO.3,NO.4和NO.5的压力时间历程,具体的对比结果见图 9。对于工况2,实验中测点NO.4没有采集到有效的数据,因此对于爆炸工况2,主要对比测点NO.1,NO.2,NO.3和NO.5的压力时间历程,具体的对比结果见图 10。
|
图 9 工况1实验和数值模拟压力测点对比 Fig.9 Comparisons of experimental and numerical simulation of overpressure time histories in CASE 1 |
|
图 10 工况2实验和数值模拟压力测点对比 Fig.10 Comparisons of experimental and numerical simulation of overpressure time histories in CASE 2 |
从试验数据可以看出,当爆炸发生在约束空间时,冲击波的压力演化过程较开敞环境的情况更加复杂,其包括初始冲击波和约束壁面的反射冲击波,且来自不同壁面的反射冲击波在靠近爆炸箱体两端的压力测点处产生明显的叠加效应,如图 9(a)、(d)和图 10(b)、(d)所示,使得反射冲击波叠加后的压力值峰值显著高于初始冲击波的压力峰值。而靠近爆炸箱体中部的测点则包含持续时间相对较长的冲击波衰减过程,如图 9(b)、(c)和图 10(a)、(c)所示。此外,从测点的冲击波压力时程曲线来看,图 9中NO.3和NO.4测点存在相似性,而图 9中NO.1和NO.3测点存在较大的差异,即虽然测点NO.1,NO.3和NO.4测点与装药的几何距离相差不大,而在工况1和工况2中其压力时程差异较大。分析原因发现,工况1中柱形装药的高度与直径比为1.06,近似相等,装药轴向和径向产生的冲击波强度基本相同;而工况2中柱形装药的高度与直径比为1.35,装药用于产生径向冲击波的能量明显高于装药用于产生轴向冲击波的能量,从而造成工况2中测点NO.1和NO.3的差异。由于NO.1位于装药径向方向,NO.3位于装药轴向方向,因此,测点NO.1的压力明显大于测点NO.3的压力。
采用本文程序计算得到2个工况各测点压力时程如图 9和图 10中的虚线所示,从对比情况来看,程序数值计算的结果较好的反应出冲击波在约束空间内的反射和叠加效应,与试验得到的规律较一致。对于不同的药量,计算得到的初始冲击波反射压力与试验数据吻合较好;也准确地反应出了壁面反射冲击波的叠加效应,如图 9(a)、(d)和图 10(b)、(d)所示。对于靠近爆炸点位置,数值计算得到的冲击波时历曲线也捕捉到了初始反射冲击波和壁面反射冲击波,且初始反射冲击波的峰值压力与实验值吻合较好,但壁面反射冲击波的压力值和到达时间存在一些差异,程序计算得到的值相对较小,达到时间也略有滞后,如图 9(b)、(c)和图 10(a)、(c)所示。其主要原因是本文程序中较理想的处理了炸药的爆轰,即采用瞬时爆轰的假定,而实际的炸药爆轰过程复杂且影响因素较多,将对后续的冲击波强度产生不确定性影响;此外,在程序中引入数值粘性处理冲击波强间断面的方法和采用了理想气体状态方程也是造成差异的原因。
5 约束空间爆炸载荷的影响因素分析本节主要通过验证的程序对约束空间爆炸载荷影响因素进行分析。在数值计算中,箱体体积及形状保持不变,柱形药量取为768 g,其具体尺寸为:半径50 mm,高度60 mm,密度为1 630 kg/m3。经多次数值试验,网格数确定为90×40×40。
5.1 炸药与泄爆孔相对位置对爆炸载荷的影响主要分两种相对位置工况进行研究:1) 泄爆孔位置不变,改变炸药的位置;2) 炸药位置不变,改变泄爆孔的位置。泄爆孔的半径取为160 mm。
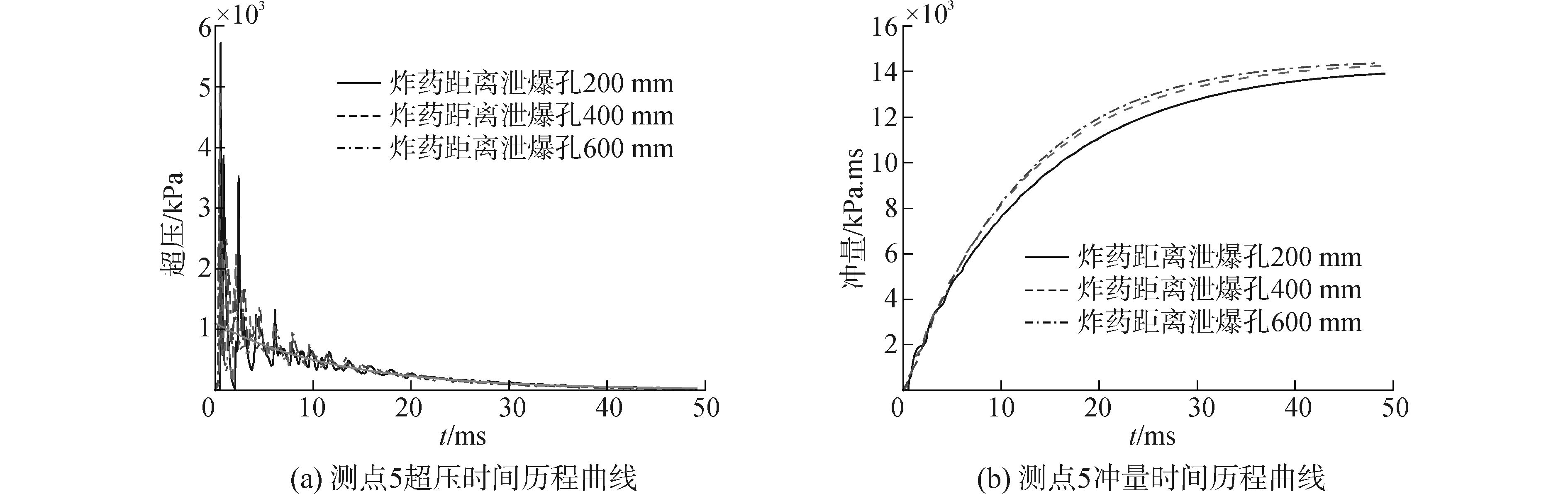
工况1:泄爆孔位置设置在箱体壁面A的中间。炸药的位置设置在垂直于泄爆孔平面并通过孔心的轴线上,采用3种不同的炸药位置,分别为:距离泄爆孔200、400、600 mm。具体的计算结果见图 11。
|
图 11 不同炸药位置测点5载荷时间历程曲线 Fig.11 Pressure and impulse of gauging point 5 for different explosive positions |
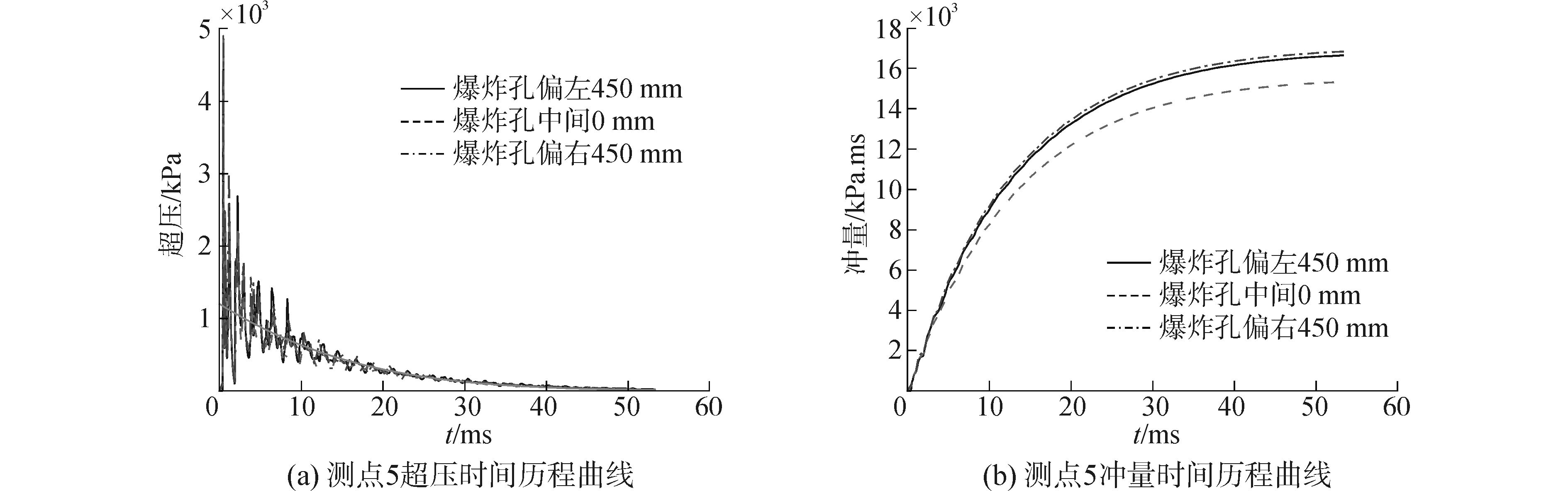
工况2:炸药的位置设置在爆炸箱体中间,泄爆孔设置在爆炸箱体壁面A的长度方向上,且泄爆孔的中心点均位于爆炸箱体壁面A的半高线上。共设定3种不同的泄爆孔位置,分别为:爆炸箱体半长度平面偏左450 mm、中间0 mm、偏右450 mm。具体的计算结果见图 12。
|
图 12 不同泄爆孔位置测点5载荷历程曲线 Fig.12 Pressure and impulse of gauging point 5 for different venting hole positions |
根据图 11(a)、12(a)可知,炸药与泄爆孔的相对位置显著影响爆炸箱体壁面测点的前期爆炸波峰值,而对爆炸载荷的整体超压时间历程影响较小,准静态泄压曲线(见图 11(a)、12(a)中的无波动缓降曲线)基本重合。根据图 11(b)、12(b)可知,炸药与泄爆孔的距离影响冲击波冲量的时间历程,减小炸药与泄爆孔的距离能降低爆炸箱体内部冲量,这主要是由于当炸药离泄爆孔越近,在整个爆炸过程中,从泄爆孔处泄出的能量越多。
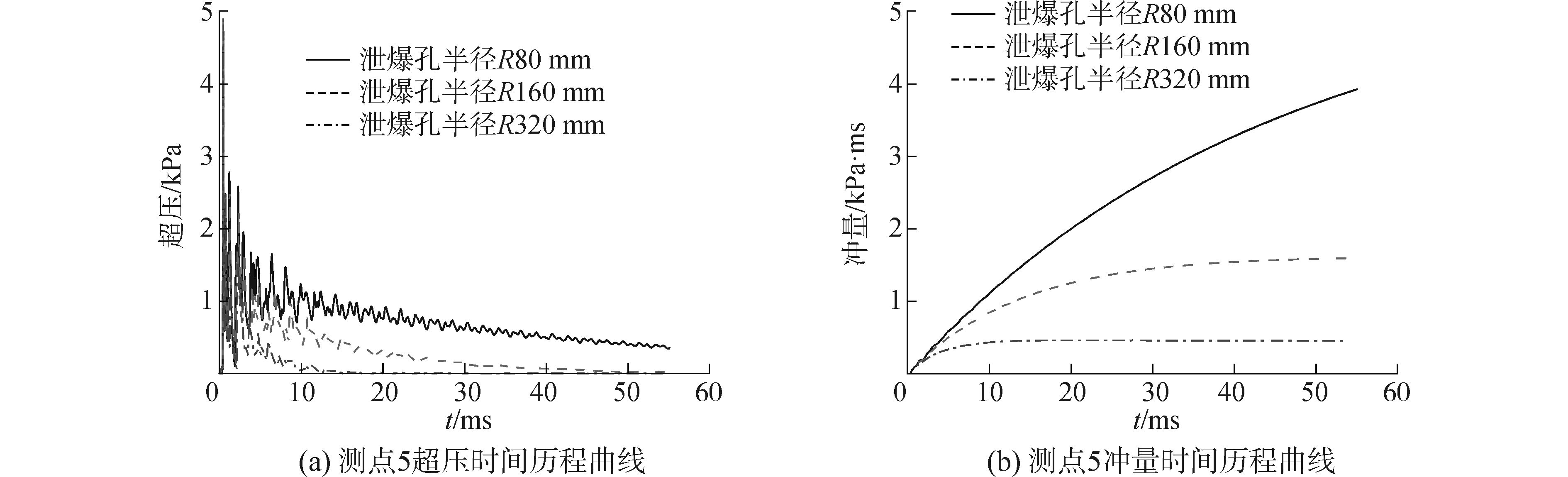
5.2 泄爆孔大小对爆炸载荷的影响炸药的位置设置在爆炸箱体中间,泄爆孔位置设置在爆炸箱体壁面A的中间。共设定3种不同的泄爆孔半径,分别为:R80、R160、R320 mm。
根据图 13(a)可知,泄爆孔的大小对爆炸箱体壁面测点的超压时间历程影响较大,泄爆孔半径越大,超压衰减越快。根据图 13(b)可知,泄爆孔的大小显著影响冲击波冲量的时间历程,增大泄爆孔半径能显著降低爆炸箱体内部冲量。
|
图 13 不同泄爆孔大小测点5载荷历程曲线 Fig.13 Pressure and impulse of gauging point 5 for different size of venting holes |
爆炸发生在约束空间时,爆炸冲击波将在约束壁面间多次反射,并产生叠加增强效应,对其复杂演化传播规律的准确描述是内爆炸冲击波载荷评估的前提。
1) 本文采用改进的五阶WENO有限差分格式编写了三维约束空间高精度爆炸冲击波数值计算程序,较好地捕捉到炸药爆炸场中稀疏波、冲击波和接触间断等复杂波系结构,同时开展了约束空间柱形TNT爆炸场试验验证程序计算的可靠性和正确性。
2) 基于验证的程序初步研究了炸药位置、泄爆孔位置以及泄爆孔大小对约束空间爆炸载荷特性的影响规律。
3) 本文开发的三维约束空间高精度爆炸冲击波数值程序可以较好地计算包含高压比、高密度比的TNT强爆炸冲击波载荷,为结构抗爆设计提供可靠的载荷输入。
| [1] |
EDRI I, SAVIR Z, FELDGUN V R, et al. On blast pressure analysis due to a partially confined explosion:Ⅰ. experimental studies[J]. International journal of protective structures, 2011, 25(3): 1-20. ( 0) 0)
|
| [2] |
WU C, LUKASZEWICZ M, SCHEBELLA K, et al. Experimental and numerical investigation of confined explosion in a blast chamber[J]. Journal of loss prevention in the process industries, 2013, 26(4): 737-750. DOI:10.1016/j.jlp.2013.02.001 ( 0) 0)
|
| [3] |
FELDGUN V R, KARINSKI Y S, YANKELEVSKY D Z. Some characteristics of an interior explosion within a room without venting[J]. Structural engineering & mechanics, 2011, 38(5): 633-649. ( 0) 0)
|
| [4] |
FELDGUN V R, KARINSKI Y S, EDRI I, et al. On blast pressure analysis due to a partially confined explosion:Ⅱ. numerical studies[J]. International journal of protective structures, 2012, 3(1): 61-80. DOI:10.1260/2041-4196.3.1.61 ( 0) 0)
|
| [5] |
BENSELAMA A M, WILLIAM-LOUIS J P, MONNOYER F. A 1D-3D mixed method for the numerical simulation of blast waves in confined geometries[J]. Journal of computational physics, 2009, 228(18): 6796-6810. DOI:10.1016/j.jcp.2009.06.010 ( 0) 0)
|
| [6] |
HARTEN A. High resolution schemes for hyperbolic conservation laws, J. computer physics[J]. Journal of computational physics, 1983, 135(3): 357-393. ( 0) 0)
|
| [7] |
COLELLA P, WOODWARD P R. The piecewise parabolic method (PPM) for gas-dynamical simulations[J]. Journal of computational physics, 1984, 54(1): 174-201. DOI:10.1016/0021-9991(84)90143-8 ( 0) 0)
|
| [8] |
SWEBY P K. High resolution schemes using flux limiters for hyperbolic conservation laws[J]. Siam journal on numerical analysis, 1984, 21(5): 995-1011. DOI:10.1137/0721062 ( 0) 0)
|
| [9] |
HARTEN A, ENGQUIST B, OSHER S, et al. Uniformly high order accurate essentially non-oscillatory schemes, Ⅲ[J]. Journal of computational physics, 1987, 71(2): 231-303. DOI:10.1016/0021-9991(87)90031-3 ( 0) 0)
|
| [10] |
LIU X D, OSHER S, CHAN T. Weighted essentially non-oscillatory schemes[J]. Journal of computational physics, 1994, 115(1): 200-212. DOI:10.1006/jcph.1994.1187 ( 0) 0)
|
| [11] |
SHU C W, OSHER S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J]. Journal of computational physics, 1988, 77(2): 439-471. DOI:10.1016/0021-9991(88)90177-5 ( 0) 0)
|
| [12] |
JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of computational physics, 1996, 126(1): 202-202. DOI:10.1006/jcph.1996.0130 ( 0) 0)
|
| [13] |
SHU C W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws[M]. Berlin Heidelberg: Springer, 1998: 325-432.
( 0) 0)
|
| [14] |
SHU C W. High order weighted essentially nonoscillatory schemes for convection dominated problems[J]. Siam review, 2009, 51(1): 82-126. DOI:10.1137/070679065 ( 0) 0)
|
| [15] |
ZHANG H, ZHUANG F. NND schemes and their applications to numerical simulation of two-and three-dimensional flows[J]. Advances in applied mechanics, 1991, 210(2): 193-256. ( 0) 0)
|
| [16] |
曹乐. 利用level set方法捕捉气、水界面的三维数值研究[D]. 合肥: 中国科学技术大学, 2009. CAO Le. Three-dimensional computations on capturing of gas-water interface by level set method[D]. Hefei:University of Science and Technology of China, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10358-2010019317.htm (  0) 0)
|
| [17] |
谢昌坦. 气-水可压缩流物质界面的R-M不稳定性研究[D]. 哈尔滨: 哈尔滨工程大学, 2011. XIE Changtan. The study on R-M instability of the material interface in gas-water compressible flow[D]. Harbin:Harbin Engineering University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10217-1012264213.htm (  0) 0)
|
| [18] |
KIM D, KWON J H. A high-order accurate hybrid scheme using a central flux scheme and a WENO scheme for compressible flowfield analysis[J]. Journal of computational physics, 2005, 210(2): 554-583. DOI:10.1016/j.jcp.2005.04.023 ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


