2. College of Ocean Science and Engineering, Shanghai Maritime University, Shanghai 201306, China
海流经过立管时,在立管下游产生尾流和漩涡,周期发放的漩涡对立管产生垂直于流向的涡激升力,引起立管的涡激振动,涡激振动是立管发生破坏的关键因素之一[1]。由于海流速度沿水深变化的非均匀性及流固耦合的复杂性,涡激振动的准确预报是一个巨大的难题[2]。
目前,研究涡激振动的方法主要有两种,即模型试验法和数值模拟法[3]。数值模拟法主要有3类方法:1) 基于切片理论的CFD方法,这类模型大多将二维Navier-Stokes方程的求解与梁模型结合在一起,通过求解方程得到作用在圆柱上的力,然后将力反馈到圆柱上求得结构的动力响应。2) 基于圆柱受迫振动实验数据的经验模型,常用的有DNV模型、LIC模型、MARINTE模型等。这些模型的基本假定是涡激振动发生在一个或有限个离散频率上,基于这些经验模型进行涡激振动预报的软件有SHEAR7、VIVA、VIVANA等。3) 介于上述两者之间的尾流振子模型,也称半经验模型。通过相互独立的方式分别建立圆柱振子运动方程和流体振子运动方程,然后利用它们共同预报流体-弹性系统的动力响应[4-6]。
立管下端一般通过万向节与海底井口相连,上端通过升沉补偿装置 (又称张紧器) 与平台相连。张紧器给立管提供较大的顶张力,支持立管的重量,使立管保持张紧垂直状态,避免立管长度过大致使底部发生屈曲。对于浅海立管 (水深一般小于300 m),由于其刚度较大,自重对立管轴向张力分布影响不大,多忽略自重影响做恒张力处理[7];浅海海流流速沿水深变化不如深海明显,柱体受波流联合作用明显,一般涡激振动分析时可作均匀流处理[8];此外浅海立管固有频率主要受自身刚度控制,涡激振动“锁频”现象明显,最大响应多出现在立管中上部[9]。
对于深海立管,长径比迅速增大,立管固有频率主要受张力控制,而且深海海底流速低,涡泄频率与立管低阶固有频率接近,此外立管自重大、柔度高、顶部张力集中等因素也增加了立管涡激振动问题的复杂性。因此对深海立管的涡激振动现象亟需更深入的研究。
为预报深海立管涡激振动并揭示其动力特性,本文考虑立管自重影响及线性剪切流,建立立管涡激振动方程,基于Van der Pol尾流振子模型,采用有限差分法计算立管的振动响应,并通过与模型试验对比验证该数值模型的可靠性,最后研究流速及顶张力对立管涡激振动的影响。
1 立管涡激振动分析模型针对长细比很大的深海立管,考虑立管自重引起的轴向变张力和剪切流引起的涡激升力,简化后的立管模型示意如图 1所示。

|
| 图1 立管模型示意图 Figure 1 Simply supported riser |
基于欧拉梁的弯曲振动理论,建立深海立管涡激振动方程:
| $ \begin{array}{*{20}{c}} {EI\frac{{{\partial ^4}x\left( {z,t} \right)}}{{\partial {z^4}}} - \frac{\partial }{{\partial z}}\left[ {\left( {{T_z}wz} \right) \cdot \frac{{\partial x\left( {z,t} \right)}}{{\partial z}}} \right] + }\\ {\bar m\frac{{{\partial ^2}x\left( {z,t} \right)}}{{\partial {t^2}}} = {f_x}\left( {z,t} \right)} \end{array} $ | (1) |
式中:x(z, t) 为立管水平位移;EI是弯曲刚度;m是立管单位长度等效质量 (包括附连水质量和内流质量);w为立管单位长度湿重;Tt=ftopwL为张紧器提供的顶张力,L为立管长度,ftop为顶张力系数,一般为1.1~1.6。
fx(z, t) 是单位长度外激励,由漩涡泄放产生的涡激升力fL(z, t) 和立管振动产生的流体阻尼力ft(z, t) 组成:
| $ {f_y}\left( {z,t} \right) = {f_L}\left( {z,t} \right) - {f_t}\left( {z,t} \right) $ | (2) |
式中:
立管两端边界条件视为铰接:
| $ w\left( {z,t} \right) = 0,\frac{{{\partial ^2}w\left( {z,t} \right)}}{{\partial {z^2}}} = 0\left( {z = 0,z = L} \right) $ | (3) |
考虑立管与流体之间的流-固耦合影响,基于Van der Pol方程描述漩涡的尾流特性[10]:
| $ \ddot q + \varepsilon {\Omega _f}\left( {{q^2} - 1} \right)\dot q + \Omega _f^2q = F $ | (4) |
式中:ε=0.3。变量m可以表示成局部脉动的升力系数CL与固定圆柱升力系数CL0之比,q=2CL/CL0,CL0=0.3。Ωf是漩涡脱落的圆频率,满足Strouhal关系,Ωf=2πStU/D,St=0.2。F是结构对流场的反作用力,与结构的加速度成正比,
联立方程 (1)、(4),深海立管涡激振动预报模型为
| $ \left\{ \begin{array}{l} EI\frac{{{\partial ^4}x\left( {z,t} \right)}}{{\partial {z^4}}} - \frac{\partial }{{\partial z}}\left[ {\left( {{T_z}wz} \right) \cdot \frac{{\partial x\left( {z,t} \right)}}{{\partial z}}} \right] + \bar m\frac{{{\partial ^2}x\left( {z,t} \right)}}{{\partial {t^2}}} = \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{4}{\rho _w}D{C_{L0}}\eta {U^2} - \frac{1}{2}{\rho _w}D{C_D}\left| {\dot x} \right.\left| {\dot x} \right.\\ \ddot \eta + \varepsilon {\Omega _f}\left( {{\eta ^2} - 1} \right)\dot \eta + \Omega _f^2\eta = \frac{A}{D}\ddot x \end{array} \right. $ | (5) |
由式 (5) 可知,深海立管涡激振动预报模型体现了流固耦合的特性,拖曳力阻尼是非线性的,所以模态叠加法不再适用,本文应用有限差分法对方程 (5) 在时间和空间上离散,以求解立管的振动响应。
应用中心差分格式,将立管长度平均分为N份,得到N个计算单元和N+1个节点,单元长度为ΔN=L/N,立管顶端的节点编号为0,第二个为1,依次分布直到N。根据边界条件 (3),顶端节点0和底端节点N的运动形式是已知的,于是得到关于时间t的2(N-1) 个二阶常微分方程组,应用四阶Runge-Kutta法数值求解[3]。
3 涡激振动试验为验证深海立管涡激振动数值计算的可靠性,在天津大学水利工程仿真与安全国家重点实验室船舶拖曳水池中 (137 m×7 m×3 m) 进行了深海立管涡激振动试验。
受水池深度限制,立管试验模型横向布置,由拖车匀速带动模拟均匀流。采用应变片监测立管应力变化。试验装置设备主要包括立管模型 (Teflon管)、万向节、钢丝绳、弹簧、滑轮、测速仪和张力计等。试验测量设备包括电阻应变片、电阻应变仪、信号采集仪和振动信号采集分析软件等。立管实体及模型参数如表 1所示。
| 名称 | 立管实体 (钢管) | 试验模型 (Teflon管) |
| 立管长度/m | 1 500 | 5 |
| 立管外径/m | 0.304 8 | 0.016 |
| 立管壁厚/m | 0.013 6 | 0.001 |
| 弹性模量/Pa | 2×1011 | 7.38×108 |
| 材料密度/(kg·m-3) | 7 850 | 2 178 |
| 海水密度/(kg·m-3) | 1 025 | 1 000 |
| 内流密度/(kg·m-3) | 800 | 1 000 |
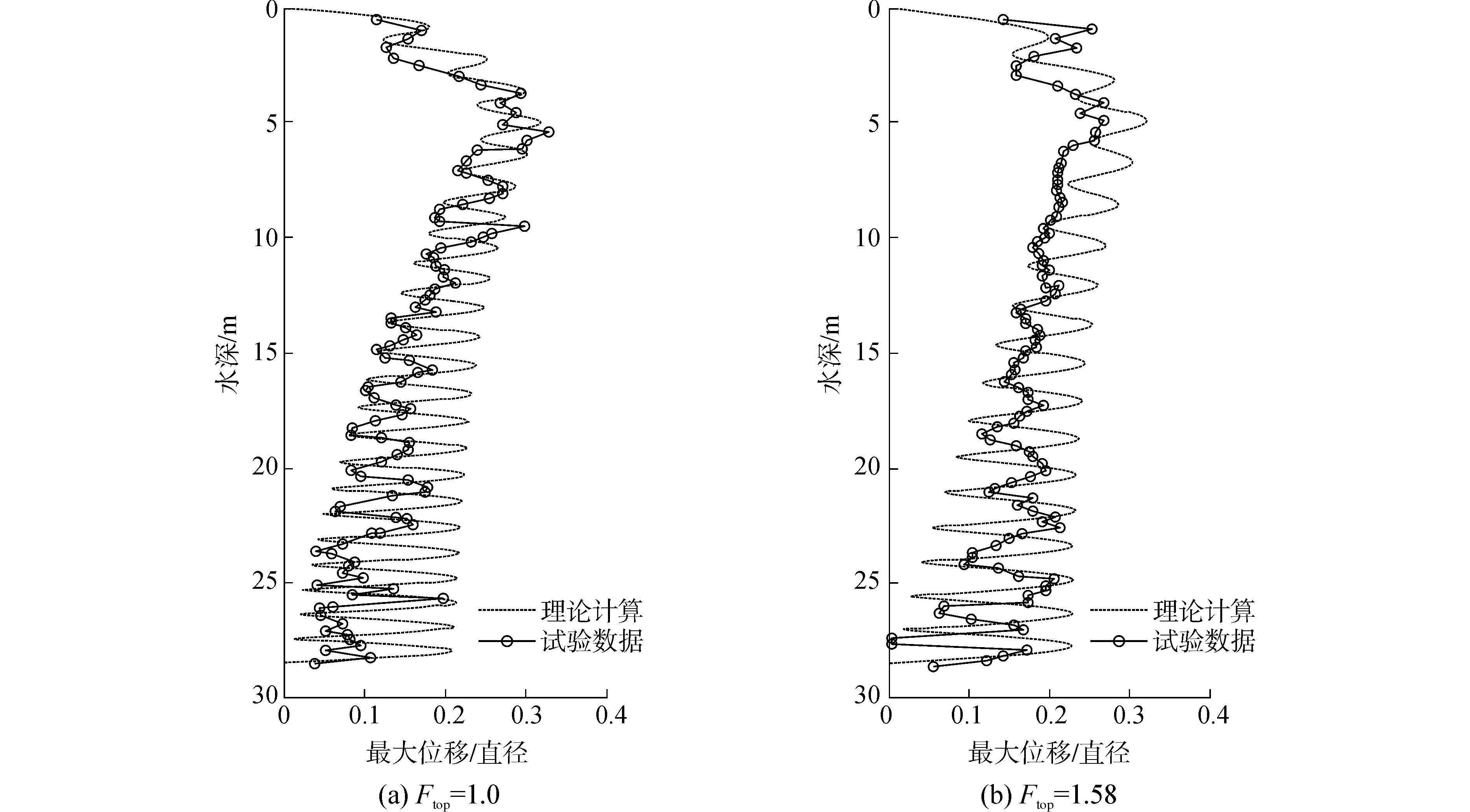
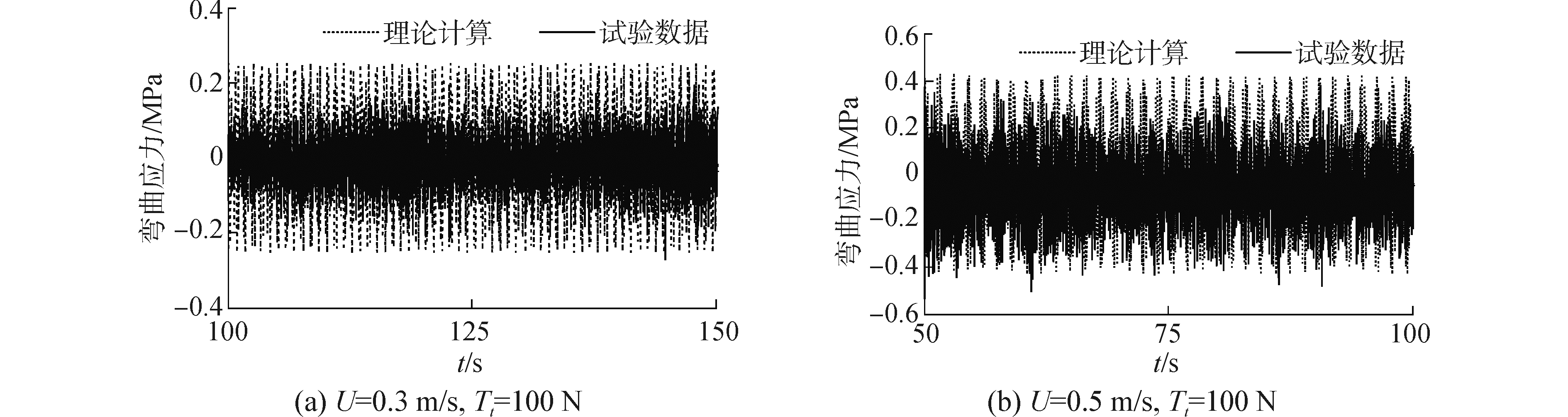
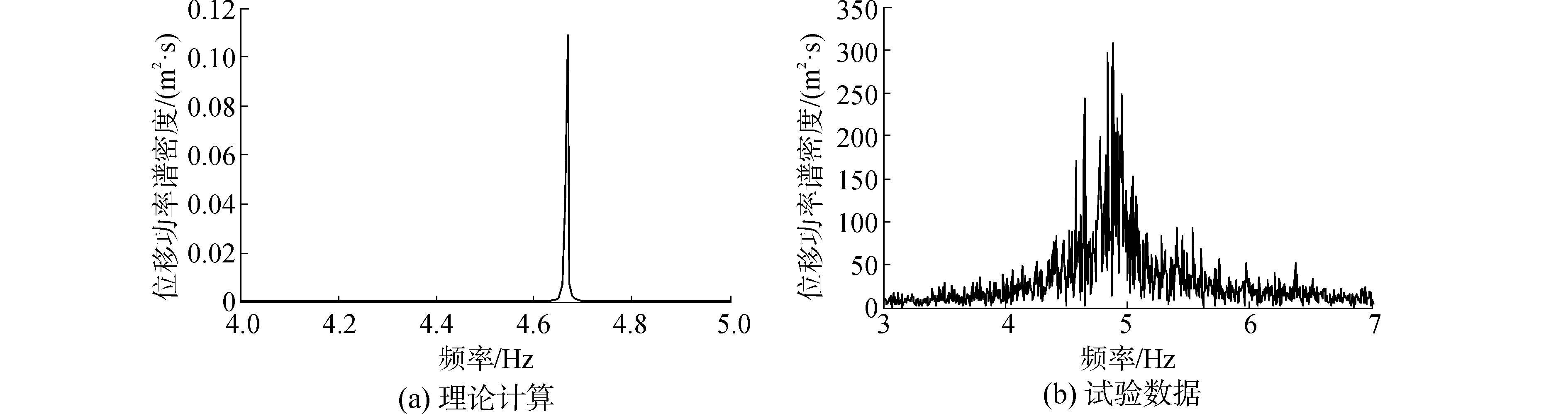
理论计算得到振动应力、振动频率和振动位移与试验中测量的数据对比如图 2~4所示。
|
| 图2 中点应力时程曲线 Figure 2 Bending stress time-history of riser at midpoint |
|
| 图3 振动频谱分析 (U=0.5 m/s, Tt=100 N) Figure 3 Frequency spectrum of riser (U=0.5 m/s, Tt=100 N) |
经过大量的试验对比验证,说明本文采用的涡激振动预报模型是合理的,Matlab编程计算的结果是可靠的。
5 影响因素分析 5.1 流速对立管涡激振动的影响不考虑波浪的影响,海面流速一般为0.1~1 m/s [12]。当顶张力系数ftop=1.3时,计算不同流速下立管的振动响应,根据立管每一点的位移时程曲线和弯曲应力时程曲线,得到立管振动的最大位移和最大弯曲应力,图 5、6是选取高、中、低三种流速:0.2、0.5和0.8 m/s计算得到的最大位移和最大弯曲应力对比图。

|
| 图5 立管涡激振动位移最大值 Figure 5 The maximum displacement of riser in VIV |

|
| 图6 立管涡激振动弯曲应力最大值 Figure 6 The maximum bending stress of riser in VIV |
由图 5看出,流速越大,立管涡激振动激发模态越高,但最大振动位移略有减小,说明立管涡激振动位移主要受低阶模态控制;低流速时振动位移最大值在立管底部,高流速时振动位移最大值在立管中上部。
由图 6看出,流速越大,立管涡激振动弯曲应力越大,说明立管涡激振动弯曲应力主要受高阶模态控制;不管何种流速,弯曲应力最大值始终在立管底部。
不同流速下立管振动最大位移、最大弯曲应力及振动主频率的统计如表 2所示。可以看出:
| 流速/ (m·s-1) |
最大位 移/m |
水深 /m |
最大弯曲 应力/MPa |
水深 /m |
主频率/ (rad·s-1) |
| 0.1 | 0.243 8 | 1 246 | 0.29 | 1 268 | 0.256 4 |
| 0.2 | 0.234 6 | 1 384 | 1.52 | 1 398 | 0.644 0 |
| 0.3 | 0.216 3 | 1 432 | 3.55 | 1 435 | 1.043 3 |
| 0.4 | 0.213 1 | 1 442 | 5.91 | 1 455 | 1.196 6 |
| 0.5 | 0.192 5 | 652 | 8.42 | 1 463 | 1.944 2 |
| 0.6 | 0.185 3 | 648 | 10.89 | 1 468 | 2.423 7 |
| 0.7 | 0.182 2 | 612 | 14.09 | 1 472 | 2.853 2 |
| 0.8 | 0.175 7 | 589 | 15.8 | 1 475 | 3.159 8 |
| 0.9 | 0.151 7 | 580 | 17.97 | 1 478 | 3.620 1 |
| 1.0 | 0.151 1 | 525 | 20.29 | 1 481 | 4.080 1 |
1) 振动位移:流速越大,最大位移越小,最大值出现的位置越靠近立管上部。原因分析:小流速产生的涡激升力小,主要激起低阶模态,低阶模态产生的位移较大,特别是立管底部由于内部张力较小,因此有较大的位移;大流速激起高阶模态,高阶模态产生的位移较小,立管中上部由于涡激升力大,导致有较大的振动位移。
2) 振动弯曲应力:流速越大,激发模态越高,弯曲应力越大,最大弯曲应力均集中在立管底部。原因分析:弯曲应力大小由振动位移的二次导数决定,振动位移二次导数随模态及水深的变化趋势同立管模态曲率随模态和水深的变化趋势是一致的,即深海立管涡激振动位移的二次导数最大幅值在立管底部,在振动位移相差不大的情况下,位移二次导数的最大幅值随模态阶次升高而增大[3]。
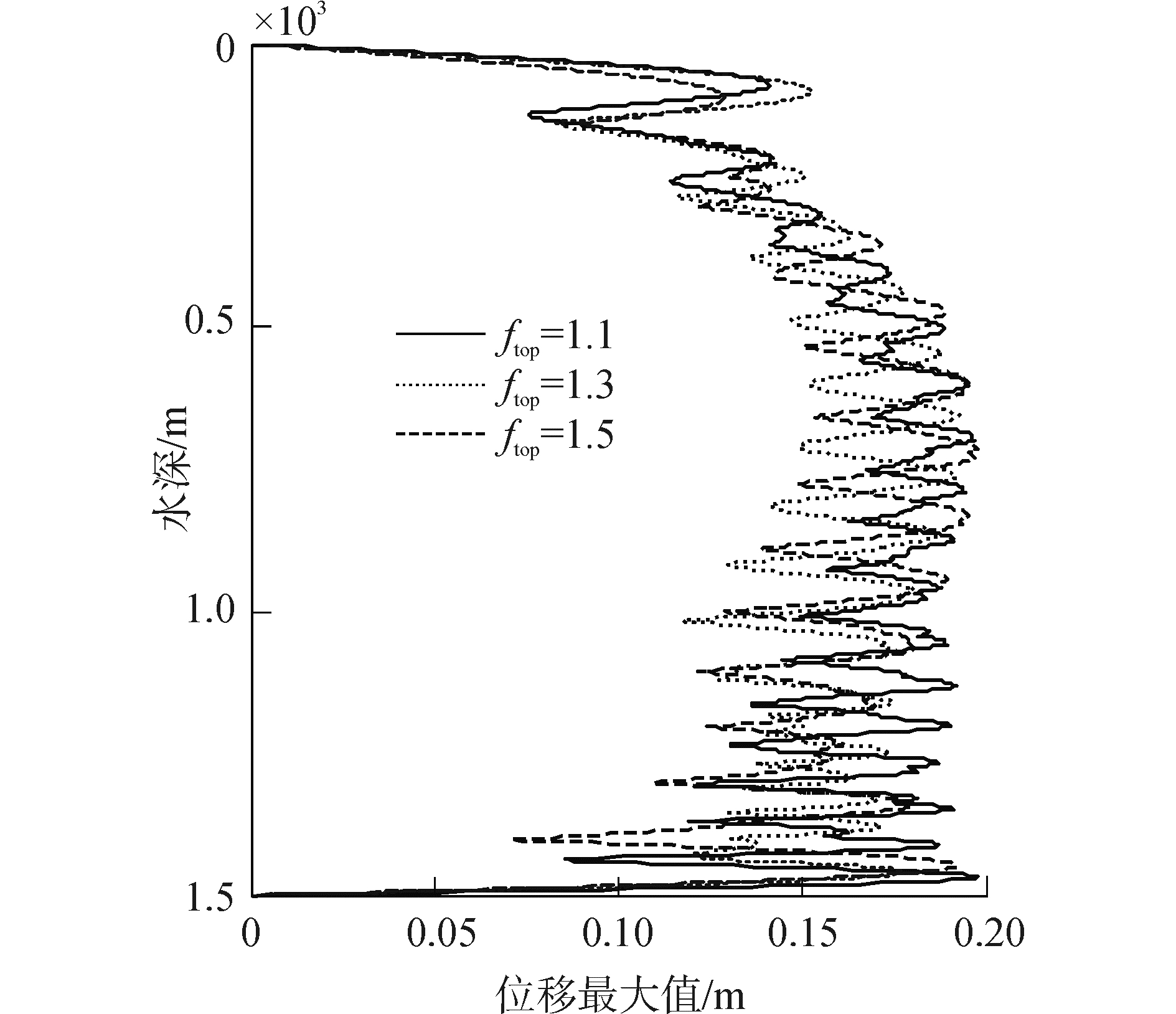
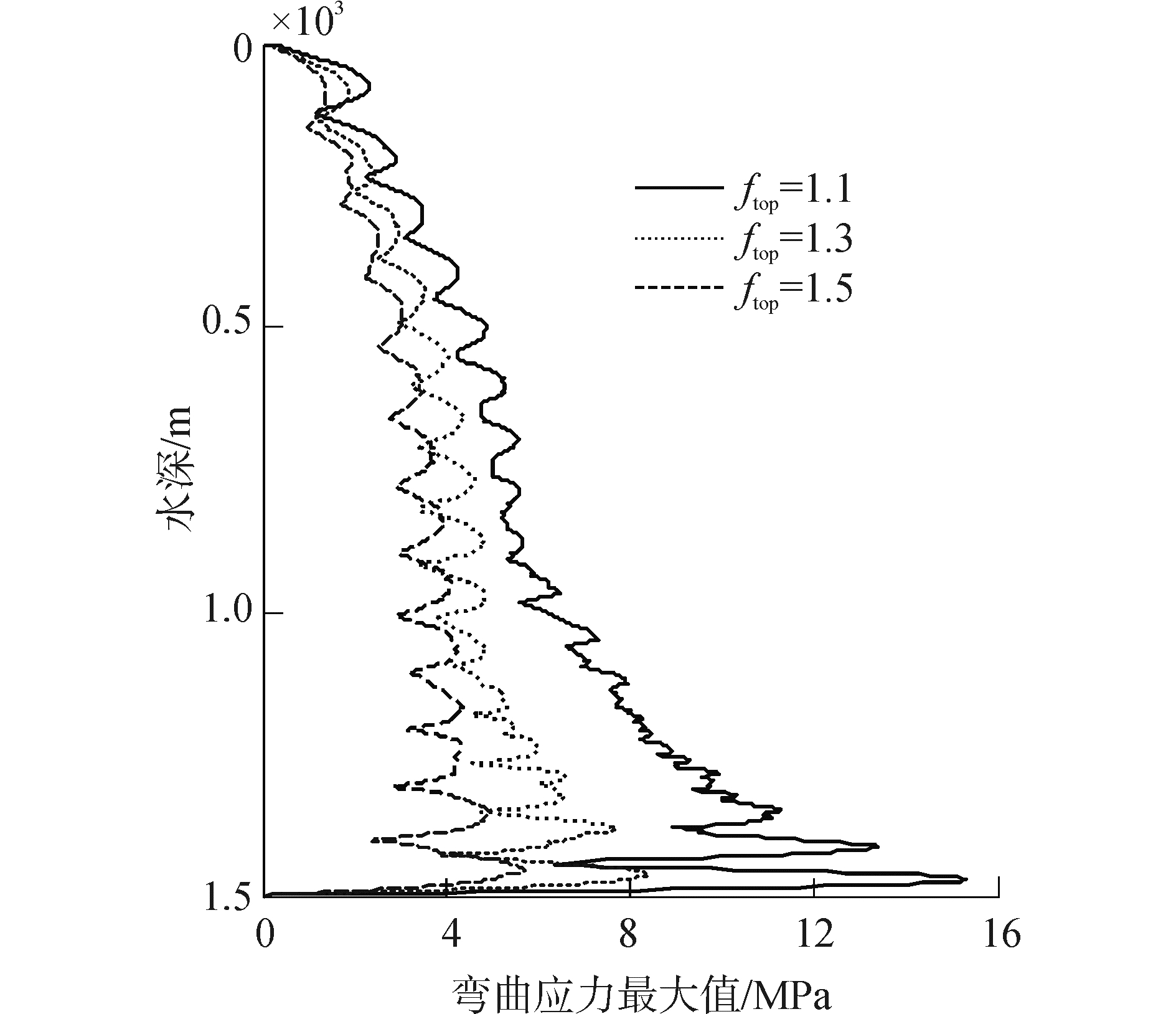
5.2 顶张力对立管涡激振动的影响当U0=0.5 m/s时,计算顶张力系数ftop分别为1.1、1.3和1.5时立管振动的最大位移和最大弯曲应力,如图 7、8所示。
|
| 图7 立管涡激振动位移最大值 Figure 7 The maximum displacement of riser in VIV |
|
| 图8 立管涡激振动弯曲应力最大值 Figure 8 The maximum bending stress of riser in VIV |
可以看出,顶张力增大,立管振动位移略有增大,但立管弯曲应力明显减小。这是因为顶张力系数增大,则立管内部张力增大,相当于增大了立管的弯曲刚度,立管模态固有频率升高,在同等流速下由于涡激频率不变,导致立管激起模态降低,从而使立管振动位移增大,弯曲应力减小。这是深海立管所特有的性质,与普通梁或浅海立管横向振动随轴向力变化的规律是不一致的。
立管振动响应频谱分析如图 9所示。由图 9可以发现,改变顶张力系数,立管涡激振动主频率变化不大。说明立管振动主频率主要受涡激升力频率的控制,也就是受流速的控制。

|
| 图9 立管涡激振动响应频谱对比图 Figure 9 Frequency spectrum of riser in VIV |
1) 流速越大,涡泄频率越高,立管涡激振动激发模态越高,立管振动主频率越大,振动应力也越大;
2) 顶张力增大,立管固有频率升高,在同等流速下虽然立管振动响应主频率变化不大,但导致立管激起振动的模态降低,从而使立管振动应力减小。
| [1] | XUE Hongxiang, WANG Kunpeng, TANG Wenyong. A practical approach to predicting cross-flow and in-line VIV response for deepwater risers[J]. Applied ocean research, 2015, 52: 92–101. DOI:10.1016/j.apor.2015.05.005 |
| [2] | SRINIL N. Analysis and prediction of vortex-induced vibrations of variable-tension vertical risers in linearly sheared currents[J]. Applied ocean research, 2011, 33(1): 41–53. DOI:10.1016/j.apor.2010.11.004 |
| [3] |
张杰. 深海立管参激-涡激联合振动与疲劳特性研究[D]. 天津: 天津大学, 2014.
ZHANG Jie. Vortex-induced vibration and fatigue analysis of deepwater risers considering parametric excitations[D]. Tianjin:Tianjin University, 2014. |
| [4] |
魏东泽, 白兴兰, 顾恩凯. 考虑流固耦合的立管涡激振动研究[J].
中国造船, 2014, 55(3): 108–116.
WEI Dongze, BAI Xinglan, GU Enkai. Study on vortex-induced vibration of riser considering fluid-structure interaction[J]. Shipbuilding of China, 2014, 55(3): 108–116. |
| [5] |
唐世振. 考虑顺流向振动的深水顶张力立管涡激振动分析[D]. 青岛: 中国海洋大学, 2010.
TANG Shizhen. Study of the vortex induced vibration for the deepwater top tensioned risers considering the in-line vibration[D]. Qingdao:Ocean University of China, 2010. |
| [6] | YAMAMOTO C T, MENEGHINI J R, SALTARA F, et al. Numerical simulations of vortex-induced vibration on flexible cylinders[J]. Journal of fluids and structures, 2004, 19(4): 467–489. DOI:10.1016/j.jfluidstructs.2004.01.004 |
| [7] |
张杰, 唐友刚. 深海立管固有振动特性的进一步分析[J].
船舶力学, 2014, 18(1/2): 165–171.
ZHANG Jie, TANG Yougang. Further analysis on natural vibration of deep-water risers[J]. Journal of ship mechanics, 2014, 18(1/2): 165–171. |
| [8] |
董艳秋. 波、流联合作用下海洋平台张力腿的涡激非线性振动[J].
海洋学报, 1994, 16(3): 121–129.
DONG Yanqiu. Nonlinear vibration analysis of tension leg under combined wave-current[J]. Acta oceanologica sinica, 1994, 16(3): 121–129. |
| [9] |
郭海燕, 傅强, 娄敏. 海洋输液立管涡激振动响应及其疲劳寿命研究[J].
工程力学, 2005, 22(4): 220–224.
GUO Haiyan, FU Qiang, LOU Min. Vortex-induced vibrations and fatigue life of marine risers conveying flowing fluid[J]. Engineering mechanics, 2005, 22(4): 220–224. |
| [10] | FACCHINETTI M L, DE LANGRE E, BIOLLEY F. Coupling of structure and wake oscillators in vortex-induced vibrations[J]. Journal of fluids and structures, 2004, 19(2): 123–140. DOI:10.1016/j.jfluidstructs.2003.12.004 |
| [11] | FUJIWARA T, UTO S, KANADA S. An experimental study of the effects that change the vibration mode of riser VIV[C]//ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering. Rotterdam, The Netherlands:ASME, 2011:487-492. |
| [12] | GAO Yun, ZONG Zhi, SUN Lei. Numerical prediction of fatigue damage in steel catenary riser due to vortex-induced vibration[J]. Journal of hydrodynamics, ser. B, 2011, 23(2): 154–163. DOI:10.1016/S1001-6058(10)60099-6 |