图像复原问题一直是图像处理领域中的研究热点之一,对其的研究不仅具有重要的理论指导意义,在实际应用中也有着十分迫切的需求。作为经典的图像反问题模型,图像复原广泛的应用于光学成像、医疗成像、遥感、空间探索等多个应用领域[1-2]。模糊图像复原是图像复原问题的一个重要分支,它的目的是解决如何从模糊退化图像中获得清晰的原始图像。本文主要围绕线性且空间不变模糊核下的图像盲复原问题进行深入研究。
盲复原的目的是利用观测退化图像来同时估计模糊算子和理想原始图像。文献[3]指出,由于退化模型的欠定性,从贝叶斯分析的角度出发,复原图像的求解可以转化为一个具有约束项的正则化问题。因此,复原质量的高低也就取决于这一问题中正则先验形式的选取。李一兵等联合拉东变换及傅里叶变换估计点扩展函数的先验信息,再通过对模糊类别分类,解决水下图像的盲复原问题[4]。J.Ya等将贝叶斯分析与变分法相结合,成功的应用于运动模糊图像的复原,但这种基于最大后验的思想容易产生数据的过拟合[5]。Y.Q Dong等根据图像的局部特性,提出了一种多尺度的变参数全变差(total variation)方法,以牺牲计算复杂度为代价使复原图像的质量得到改善[6]。J. Li等引入非局部模型,提出一种基于多维非局部的全变差模型,解决遥感图像的复原问题[7]。为了解决更大规模图像复原问题,H. Chang等提出了基于域分解的非局部全变差方法,将复原过程在多个子域并行处理,并利用Bregman迭代算法对各子域模型进行求解[8]。上述的这些方法在图像复原中尽管取得了一定的效果,但其基本思想仍是在空域讨论图像的先验特性,使得正则化先验项的构造受到了限制。
近年来,稀疏表示作为一种新兴的图像表示模型,得到了学者们的广泛关注并成功地应用于图像复原领域。J.F Cai等研究发现在框架表示方法下,模糊核与图像都呈现较好的稀疏性,并以次作为先验提出了基于稀疏近似的模糊图像盲复原[9]。H.C Zhang等提出基于稀疏的图像盲复原方法,讨论在自适应学习字典下的稀疏图像复原以及模糊矩阵估计方法[10]。D. Krishnan等提出一种基于l1/l2范数的图像先验模型和稀疏模糊核约束的算法,实现图像快速复原[11]。文献[12]利用自然图像的在梯度域的稀疏性构造先验约束,并在贝叶斯后验理论的启发下建立多幅观测图像的联合概率密度函数,用于具有多帧源图像的盲复原问题。W.S Dong等基于聚类的思想,认为图像的稀疏编码应接近其所在类的聚类中心,提出了中心化编码的图像复原方法[13]。但在该方法中,模糊核的估计是独立完成的部分,未将其加入复原框架。M. Hanif等从非负矩阵分解的角度出发,提出基于非负稀疏模型的盲复原方法[14]。但在这一方法中需要花费额外的计算量来估计图像的基矩阵。此外,该模型中仅以l2范数约束模糊核的平滑性,难以获得较好的估计性能。文献[15]同时探究了图像的非局部稀疏和全变差约束,建立联合统计复原模型,取得了较好的效果。在此基础上,为了充分利用图像的自相似性,将全变差与稀疏相结合,L. Jun等又提出一种基于组稀疏的全变差图像复原方法[16]。唐述等运用图像的局部结构提取策略,分别对退化核及图像实施多正则约束,进而消除模糊[17]。
上述基于稀疏模型的图像复原方法,主要讨论在正交变换(如小波变换、傅里叶变换)或是冗余字典表示下的模糊复原,这些表示方法称为图像的合成表示模型。文献[18]指出,相比上述的合成表示模型,采用冗余表示的紧框架分析模型能够进一步降低目标函数的函数值,以取得更高的复原精度。但对于这一模型,需要针对性的设计有效的重构算法用于模型的求解。与此同时,受到上述部分方法的启发,采用将模糊核约束与复原优化目标放入同一优化框架的思想,使二者在迭代中相互促进,进一步提高复原质量。基于上面的想法,本文将讨论具有冗余表示能力的紧框架分析模型下的模糊图像盲复原方法并建立相应的迭代复原框架。针对模糊核估计问题,同时进行核稀疏约束及核一阶微分平滑约束,共同发挥两种约束的优势,提高核估计精度。此外,针对紧框架分析模型下的复原求解,设计了一种基于Moreau envelope函数的数值算法,有效的解决分析模型中存在的不可微性和不可分离性,获得优化目标的近似解。
1 基于紧框架的盲复原模型框架是由Duffin和Schaeffer于1952年在非调和傅里叶分析中引入的,框架与基底都是用于表示某一空间中的元素的一组向量集合,所不同的是框架并不要求表示向量间的线性无关性[19]。
定义1 设{φj}j∈J是RN中的一组元素序列,若存在正数A,B(0<A, B<+∞),使得对于∀f∈RN,都有
| $A{\left\| \mathit{\boldsymbol{f}} \right\|^2} \le \sum\limits_{j \in J} {{{\left| {\left\langle {f,{\varphi _j}} \right\rangle } \right|}^2}} \le B{\left\| \mathit{\boldsymbol{f}} \right\|^2}$ | (1) |
式中:{φj}j∈J为空间中的一个框架,A,B为框架的界。
在上述定义中,若A=B则称框架{φj}j∈J为空间中的紧框架。一般称{φj}j∈J为该框架的合成表示模型,即
| $\mathit{\boldsymbol{f = }}\left[ {\begin{array}{*{20}{c}} {{\varphi _1}}&{{\varphi _2}}& \cdots \end{array}} \right]\alpha $ | (2) |
式中:α为空间元素f在框架{φj}j∈J下的合成系数。同时,该框架还有一对应的分析表示模型Ψ,且满足Ψ=[φ1 φ2 …]H。
1.2 盲复原模型的建立针对稀疏l1范数的图像复原,令Φ=[φ1 φ2 …],在上述框架含义的引导下,可以采用如下的两种基本形式:
合成模型:
| $\mathop {\min }\limits_\alpha \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{h}} \otimes \mathit{\boldsymbol{ \boldsymbol{\varPhi} \alpha }}} \right\|_2^2 + \lambda {{\left\| {\bf{ \pmb{\mathsf{ α}} }} \right\|}_1}} \right\}$ | (3) |
分析模型:
| $\mathop {\min }\limits_x \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{h}} \otimes \mathit{\boldsymbol{x}}} \right\|_2^2 + \lambda {{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} x}}} \right\|}_1}} \right\}$ | (4) |
从两种模型的表达式可以看出,相对于分析模型,式(3) 的估计过程是以图像在合成算子Φ中的表示系数α为变量而进行的。当采用规范正交框架时,分析模型与合成模型是等价的。在一般情况下,规范正交框架不如冗余框架更能有效的表示图像丰富的几何结构。文献[20-21]指出,在采用冗余框架的条件下,分析模型比合成模型具有更好的收敛性能和更高的重构精度。对于模糊核,若将其看作一幅图像,其反应的是成像设备的运动轨迹。一般情况下,这样的轨迹呈现较细且平滑连续的特性。从图像处理的角度出发,轨迹的细特性映射为图像的稀疏性,即仅有少量像素有较大值而其他像素值接近于0。根据这一思想,文献[10]中利用梯度图像,通过约束核稀疏性的对其进行估计,但该方法并未体现对于平滑连续的约束。鉴于上述观点的分析,在核稀疏的基础上,进一步利用核的一阶梯度同时约束其平滑特性。综上,针对盲复原问题,本文建立如下的综合迭代优化模型:
| ${x^J} = \arg \mathop {\min }\limits_x \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{h}}^J} \otimes \mathit{\boldsymbol{x}}} \right\| + \mu {{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} x}}} \right\|}_1}} \right\}$ | (5) |
| $\begin{array}{l} {h^{J + 1}} = \mathop {\arg \min }\limits_h \left\{ {\frac{1}{2}\left\| {\nabla \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{h}} \otimes \nabla {\mathit{\boldsymbol{x}}^J}} \right\| + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\gamma {{\left\| \mathit{\boldsymbol{h}} \right\|}_1} + \eta \left\| {\nabla \mathit{\boldsymbol{h}}} \right\|_2^2} \right\}\\ \;\;\;\;\;\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;{\mathit{\boldsymbol{h}}_i} \ge 0,\;\;\;\;\sum\limits_i {{\mathit{\boldsymbol{h}}_i} = 1} \end{array}$ | (6) |
式中:∇表示梯度运算,‖·‖1和‖·‖2分别表示L1、L2范数,μ、η、γ为相应的正则化参数。
在上述优化模型中,式(6) 在基于梯度图像的前提下同时约束了核的稀疏性及其一阶微分的平滑特性,获得更准确估计核。而对于式(5) 的优化问题,研究表明:一方面可以灵活的适用于多种表示基函数;另一方面,在基于紧框架的重构问题中, 相比合成模型,分析模型能获得几何意义下的收敛解和更低的优化目标函数值[22]。同时,结合式(6) 中的模糊核估计表达式,使得式(5) 中的优化变为一个非盲的复原过程。此外,在迭代过程中,式(5)、(6) 中的优化结果又可相互促进,进一步提高复原质量。但值得注意的是,传统的用于合成模型的快速数值算法不能直接应用于式(5) 中的分析模型的求解,本文将在下面一节详细讨论数值算法的设计。
2 复原模型的数值算法 2.1 关于xJ的优化子问题对于式(7) 中基于分析模型的复原优化函数,一个重要的挑战就是如何设计有效的数值算法对其进行求解。内点法是解决此类问题的有效方法之一,但随着信号维度的增长,其收敛的速度会迅速的下降,不适于解决像图像复原这样的大规模问题。对于合成模型,已有很多现成有效的数值求解算法,如基于代理函数思想的迭代收缩阈值算法(iterative shrinkage thresolding alogrithm, ISTA)和快速迭代收缩阈值算法(fast iterative shrinkage thresholding alogrithm, FISTA)等,这些算法在收敛速度和收敛精度方面达到了较好的平衡,适合于大规模问题[23]。但在式(7) 的分析优化模型中,‖Ψx‖1是一具有不可微性和不可分离性的凸函数,这使得ISTA和FISTA方法不能直接应用于式(7) 中的复原模型。在此分析基础之上,本文提出一种基于Moreau envelope函数的交替迭代数值算法,利用Moreau envelope函数对不可微项的近似平滑作用,使模型得以有效的求解。
Moreau envelope函数可以作为优化函数中不可微项的一种平滑近似,进而得到问题的近似解[24]。为了方便后续的说明,这里引入近似算子符号。对于凸函数g(x),称如下的表达式为g(x)的近似算子:
| ${\rm{pro}}{{\rm{x}}_{\lambda g}}\left( \mathit{\boldsymbol{x}} \right) = \mathop {\arg \min }\limits_u \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{u}}} \right\|_2^2 + \lambda g\left( \mathit{\boldsymbol{u}} \right)} \right\}$ | (7) |
设函数:
| ${g_\mu }\left( \mathit{\boldsymbol{x}} \right) = \mathop {\min }\limits_u \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{u}}} \right\|_2^2 + \mu g\left( \mathit{\boldsymbol{u}} \right)} \right\}$ | (8) |
则gμ(x)称为函数g(x)的Moreau envelope函数,且gμ(x)具有以下性质:
1)
2) gμ(x)是一个连续可微函数,且它的梯度∇gμ(x)的Lipschitz指数为1/μ。
由上述两条性质可以得出,gμ(x)的梯度为
| $\nabla {g_\mu }\left( \mathit{\boldsymbol{x}} \right) = \frac{1}{\mu }\left( {x - {\rm{pro}}{{\rm{x}}_{\mu g}}\left( \mathit{\boldsymbol{x}} \right)} \right)$ | (9) |
鉴于上面的分析,由于式(7) 中的第二项是具有不可微和不可分离性质的凸函数,使得FISTA方法不能直接应用于模型的求解。因此可以利用Moreau envelope函数的连续可微性质作为该凸函数的一种近似平滑替代,使梯度计算成为可能,并结合式(9) 中的近似算子消除不可分离性对模型求解的影响。令g(Ψx)=‖Ψx‖1,将式(7) 改写为如下平滑近似形式:
| ${x^{J + 1}} = \mathop {\arg \min }\limits_x \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{y}} - {\mathit{\boldsymbol{h}}^{J + 1}} \otimes \mathit{\boldsymbol{x}}} \right\|_2^2 + {g_\mu }\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} x}}} \right)} \right\}$ | (10) |
令
| $\nabla f\left( \mathit{\boldsymbol{x}} \right) = {\left( {{\mathit{\boldsymbol{h}}^{J + 1}}} \right)^{\rm{H}}} \otimes \left( {{\mathit{\boldsymbol{h}}^{J + 1}} \otimes \mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)$ | (11) |
设
| ${\mathit{\boldsymbol{x}}^{J + 1}} = \arg \min \left\{ {H\left( \mathit{\boldsymbol{x}} \right) \equiv f\left( \mathit{\boldsymbol{x}} \right) + {g_\mu }\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} x}}} \right)} \right\}$ | (12) |
由于式(12) 中的两个函数f(x)和gμ(Ψx)均为可微函数并联合式(9)、(11), 给出下面的双迭代变量的更新策略,∇f(pk+1)、∇gμ(xk)分别为
| $\nabla f\left( {{\mathit{\boldsymbol{p}}^{k + 1}}} \right) = {\left( {{\mathit{\boldsymbol{h}}^{J + 1}}} \right)^{\rm{H}}} \otimes \left( {{\mathit{\boldsymbol{h}}^{J + 1}} \otimes {\mathit{\boldsymbol{p}}^{k + 1}} - \mathit{\boldsymbol{y}}} \right)$ | (13) |
| $\nabla {g_\mu }\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}^k}} \right) = \frac{1}{\mu }{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{\rm{H}}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}^k} - {\rm{pro}}{{\rm{x}}_{\mu g}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}^k}} \right)} \right)$ | (14) |
式中,
| $\begin{array}{l} {\rm{pro}}{{\rm{x}}_{\mu g}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}^k}} \right) = {S_\mu }\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}^k}} \right) = \\ \max \left( {\left| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}^k}} \right| - \mu ,0} \right){\mathop{\rm sgn}} \left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}^k}} \right) \end{array}$ | (15) |
则式(16) 可改写为
| $\nabla {g_\mu }\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}^k}} \right) = \frac{1}{\mu }{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}^{\rm{H}}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}^k} - {S_\mu }\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}{\mathit{\boldsymbol{x}}^k}} \right)} \right)$ | (16) |
从上面的推导过程可以看出,利用近似算子proxμg(Ψxk)可以有效的消除式(7) 中第二项不可分离性的影响,使模型得以求解。借鉴FISTA中的分析方法,令
| ${\mathit{\boldsymbol{x}}^{k + 1}} = \arg \min \left( {\mathit{\boldsymbol{x}}:H\left( {\mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{q}}^k}} \right),H\left( {\mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{x}}^k}} \right)} \right)$ | (17) |
式中:LH表示函数H(x)的Lipschitz指数,式(19) 表示xk+1取qk或xk中令H(x)较小的那一个。这里,迭代参量pk+1的更新表达式为
| ${t_{k + 1}} = \frac{{1 + \sqrt {1 + 4t_k^2} }}{2}$ | (18) |
| ${\mathit{\boldsymbol{p}}^{k + 1}} = {\mathit{\boldsymbol{x}}^k} + \frac{{{t_k}}}{{{t_{k + 1}}}}\left( {{\mathit{\boldsymbol{q}}^k} - {\mathit{\boldsymbol{x}}^k}} \right) + \frac{{{t_k} - 1}}{{{t_{k + 1}}}}\left( {{\mathit{\boldsymbol{x}}^k} - {\mathit{\boldsymbol{x}}^{k - 1}}} \right)$ | (19) |
此外,文献[24]还指出,当μ较大时能够给gμ(x)的求解带来一个较好的初值。而同时,随着μ的减小,又能够使得优化函数的精度和收敛速度获得一定的提升。因此本文中将采用递减式的μ取值,加快算法的收敛速度并提高收敛精度。
2.2 模糊核估计算法为了对式(8) 进行求解,这里给出一种基于交替迭代的核估计算法。引入辅助变量l,将式(8) 改写为如下的形式:
| $\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat h = }}\mathop {\arg \min }\limits_h \left\{ {\frac{1}{2}\left\| {\nabla \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{h}} \otimes \nabla {\mathit{\boldsymbol{x}}^J}} \right\|_2^2 + } \right.}\\ {\left. {\gamma {{\left\| \mathit{\boldsymbol{l}} \right\|}_1} + \eta \left\| {\nabla \mathit{\boldsymbol{h}}} \right\|_2^2} \right\}}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\mathit{\boldsymbol{l = h}},{\mathit{\boldsymbol{h}}_i} \ge 0,\sum\limits_i {{\mathit{\boldsymbol{h}}_i} = 1} } \end{array}$ | (20) |
利用交替优化技术[25],式(22) 可以拆分为下面的两个优化子问题:
| $\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}^{k + 1}} = \arg \min \left\{ {\frac{1}{2}\left\| {\nabla \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{h}} \otimes \nabla {x^J}} \right\|_2^2 + } \right.}\\ {\left. {\eta \left\| {\nabla \mathit{\boldsymbol{h}}} \right\|_2^2 + \frac{\rho }{2}\left\| {{\mathit{\boldsymbol{l}}^k} - \mathit{\boldsymbol{h + }}{\mathit{\boldsymbol{a}}^k}} \right\|_2^2} \right\}} \end{array}$ | (21) |
| ${\mathit{\boldsymbol{l}}^{k + 1}} = \mathop {\arg \min }\limits_l \left\{ {\eta {{\left\| \mathit{\boldsymbol{l}} \right\|}_1} + \frac{\rho }{2}\left\| {\mathit{\boldsymbol{l}} - {\mathit{\boldsymbol{h}}^{k + 1}}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{a}}^k}} \right\|_2^2} \right\}$ | (22) |
| ${\mathit{\boldsymbol{a}}^{k + 1}} = {\mathit{\boldsymbol{a}}^k} + \left( {{\mathit{\boldsymbol{l}}^{k + 1}} - {\mathit{\boldsymbol{h}}^{k + 1}}} \right)$ | (23) |
由于式(21) 为二阶可微函数,可以对其求导并令导数等于0,得
| $\begin{array}{*{20}{c}} {\left( {{{\left( {\nabla {\mathit{\boldsymbol{x}}^J}} \right)}^{\rm{T}}} \otimes \left( {\nabla {\mathit{\boldsymbol{x}}^J}} \right) + \rho + 2\eta {\nabla ^{\rm{T}}}\nabla } \right){\mathit{\boldsymbol{h}}^{k + 1}} = }\\ {\left( {\nabla {\mathit{\boldsymbol{x}}^J}} \right)\nabla y + \rho \left( {{\mathit{\boldsymbol{l}}^k} + {\mathit{\boldsymbol{a}}^k}} \right)} \end{array}$ | (24) |
再利用快速傅里叶变换可得
| $\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}^{k + 1}} = }\\ {{F^{ - 1}}\left( {\frac{{\bar F\left( {\nabla {x^J}} \right) \odot F\left( {\nabla y} \right) + F\left( {\rho \left( {{\mathit{\boldsymbol{l}}^k} + {\mathit{\boldsymbol{a}}^k}} \right)} \right)}}{{\bar F\left( {\nabla {\mathit{\boldsymbol{x}}^J}} \right) \odot \left( {\nabla {\mathit{\boldsymbol{x}}^J}} \right) + \rho \mathit{\boldsymbol{I + }}2\eta \bar F\left( \nabla \right) \odot F\left( \nabla \right)}}} \right)} \end{array}$ | (25) |
式中:F(·)和F-1(·)分别表示傅里叶正逆变换,“⊙”表示对应位置元素间的相乘,F表示复共轭运算,I为单位阵。此外,在求得模糊核后将其归一化,使其满足约束条件。
式(22) 是典型的稀疏l1范数问题,可以通过下式进行求解:
| ${\mathit{\boldsymbol{l}}^{k + 1}} = \max \left( {\left| {{\mathit{\boldsymbol{h}}^{k + 1}} + {\mathit{\boldsymbol{a}}^k}} \right| - \frac{\eta }{\rho },0} \right){\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{h}}^{k + 1}} + {\mathit{\boldsymbol{a}}^k}} \right)$ | (26) |
式中sgn(·)为标准符号函数。
由于模糊核尺寸有限,且其值一般不会很大。因此,为了使算法简洁,模糊核的估计只进行两次迭代即可。
综上所述,将本文所提出的算法总结如下。
初始化:观测图像y,p1=x0,μ=μ0,J=0,Jmax,kmax;
外层循环:
1) 计算∇xJ和∇y,利用式(21) 方法求解模糊核hJ+1;
2) 内层循环:令k=0,t0=1;
① 利用式(17) 计算proxμg(Ψxk);
② 利用式(15)、(18) 分别计算∇f(pk+1)和∇gμ(Ψxk);
③
④
⑤ xk+1=argmin(x:H(x=qk), H(x=xk));
⑥
若k=kmax,转至3);否则,k=k+1;
3) 令xJ+1=xk+1,μ=μ/2;
4) 若J=Jmax,输出复原图像xJ+1;否则,J=J+1。
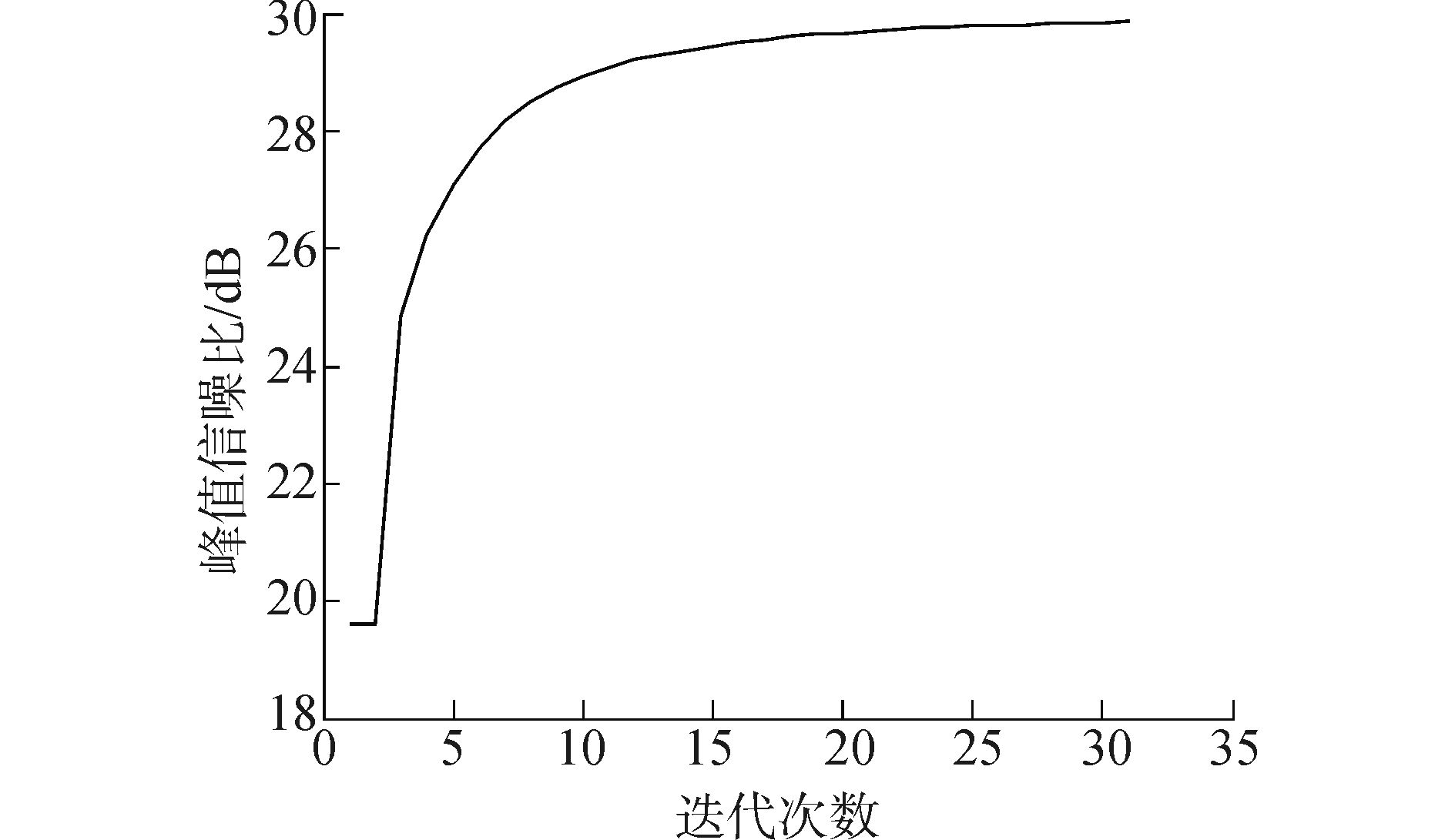
3 实验结果与分析为了验证算法的有效性,本文进行了模糊图像复原的对比实验。对比方法包括基于全变差的FISTA方法,文献[10]中基于字典学习的盲复原方法,文献[15]中基于联合统计模型的复原方法以及本文所提算法。FISTA方法中模糊核的估计采用文献[26]中的方法,文献[15]中的模糊核估计采用文献[11]中的估计方法。实验平台为Matlab7.10.0, Intel© CoreTM 2 Duo CPU, 4GB RAM, Windows操作系统。实验图像分别采用一组256×256的标准归一化测试图像(如图 1所示)和一幅真实模糊图像。对于真实的彩色图像,本文算法中将其由RGB变换到YUV空间,仅对亮度分量Y实施算法,而保持色度分量U和V不变,然后变换回RGB空间,获得复原图像。实验中采用Shearlet作为本文算法的紧框架[27],其相比传统的Wavelet、Curvelet等具有更好的图像稀疏表示能力且计算复杂度低,易于实现。考虑篇幅的有限,这里对标准归一化图像采用两种最经典的模糊方式,分别为均匀模糊和尺度参数为2的高斯模糊,且核尺寸均为7×7。噪声类型为加性高斯白噪声,噪声标准差为0.01。关于迭代参数设置,本文通过实验发现,随着迭代次数的增加,初始阶段复原效果明显提升,而后缓慢趋于收敛。因此,考虑到计算量与计算时间的因素,这里设置内、外两层循环的迭代次数分别为kmax=30,Jmax=5,达到几乎收敛的效果。同时,本文采用峰值信噪比(peak signal to noise rate, PSNR)和结构相似性度量(structural similarity index measurement, SSIM)作为客观评价指标[28]。PSNR越大说明复原图像与原始图像在全部像素上的绝对差之和越小,一定程度上宏观的体现了与原始图像在平均数值上的接近程度, 而SSIM指标越大则说明复原图像与原始图像在细节及纹理结构方面具有更高的相似性。考虑篇幅的有限,这里仅给出Cameraman在高斯模糊核下的复原结果(如图 2),真实模糊图像的核估计以及视觉复原效果如图 3所示。图 4为Cameraman图像以外循环变量k为横轴的PSNR变化图。表 1~4中分别记录了标准归一化测试图像在不同模糊核下的PSNR和SSIM指标。

|
图 1 标准测试图像 Fig.1 Benchmark test images |

|
图 2 Cameraman复原结果 Fig.2 Restoration results of Cameraman |

|
图 3 真实模糊图像复原结果 Fig.3 Restoration results of real blurry image |
|
图 4 Cameraman PSNR迭代变化图 Fig.4 PSNR plot versus iteration of Cameraman |
| 表 1 高斯模糊下标准测试图像的PSNR值 Tab.1 PSNR of benchmark images with gaussian blurry |
| 表 2 高斯模糊下标准测试图像的SSIM值 Tab.2 SSIM of benchmark images with gaussian blurry |
| 表 3 均匀模糊下标准测试图像的PSNR值 Tab.3 PSNR of benchmark images with union blurry |
| 表 4 均匀模糊下标准测试图像的SSIM值 Tab.4 SSIM of benchmark images with union blurry |
从图 2对比结果中可以看出,FISTA方法在平滑区域的复原效果较好,但部分位置出现了本不应有的斑驳和阶梯效应,这主要是由于全变差约束的分片光滑假设前提所导致,丢失了不连续边缘处的部分细节信息,相比紧框架下的稀疏模型,其先验约束缺乏一般性。基于离散余弦变换(discrete cosine transformation, DCT)字典的文献[10]中方法的复原图像有微弱振铃现象产生,这主要是由于通用DCT字典不能针对性的有效表示某一个体图像。此外,该算法中采用的基于l1范数的合成模型相比本文分析模型,在目标函数收敛精度方面的性能较差,细节的复原能力仍有待进一步提高。文献[15]和本文算法相比前两种方法,复原性能有显著提高。尽管文献[15]获得了最优的PSNR值,但该值仅能从宏观上衡量复原结果与原始图像在数值上的的接近程度,而并不能反应局部的细节视觉效果。可以看出,该方法在非局部和全变差的联合约束下,使图像过分的平滑,细节纹理不够突出,因此在SSIM指标方面略低于本文算法。从真实模糊图像复原效果还可以看出,文献[11]尽管较前两种方法在复原性能方面有所提升,但由于估计核并未呈现出细而平滑的特性,使得复原图像仍未获得理想的视觉效果。相比传统算法,本文所提出的方法,一方面由于采用了分析模型,在提高目标函数收敛精度方面具有一定的优势,更好的复原了图像中的细节信息(如图 2中框图部分所示),具有更为锐化的边缘并能够呈现清晰的图像。另一方面,由于同时引入对卷积核稀疏性与一阶平滑特性的约束,优化了估计性能。从图 3中可以看出,白亮点描述了核的实际形状,本文方法所估计的模糊核占据较小的核尺寸面积(即细特征),较好的体现了核的稀疏性。此外,其呈现的线状分段连续形状也有效的反应了其平滑连续性。在客观评价指标方面,本文方法的PSNR与文献[15]中的方法接近,相比FISTA和文献[10]中的方法体现了一定的优越性。从图 4的PSNR迭代变化图中还可以看出本文算法随迭代次数的增加,PSNR呈现升高趋势且具有较好的收敛性能。在SSIM结构化指标中,本文方法在四种对比方法中展现出相对优势(即有较好的视觉复原效果)。同时,在获得估计核后,各复原算法相当于进行非盲复原。因此,好的复原结果也进一步影响着下一次迭代中的核估计精度,达到相互促进的目的,这也从另一方面说明了本文算法中紧框架分析模型的非盲复原能力。
4 结论1) 针对模糊图像的盲复原问题,本文提出一种紧框架下的盲复原方法,该方法通过迭代的进行模糊核估计与非盲图像复原,不仅能够提高在图像细节信息复原方面的能力,还获得了较好的客观评价指标。对于高斯和均匀两种模糊模型,本文在PSNR指标方面尽管均未取得最优值但与最优值较为接近,这可能由于本文方法在个别像素点上的复原值差异较大,但视觉上并未影响总体效果。
2) 在方法上,区别于传统的复原方法,本文分别建立了针对模糊核估计以及紧框架分析非盲复原的有效约束模型。一方面,为了实现准确的核估计,提出同时约束模糊核的稀疏性及其一阶微分的平滑特性。另一方面,为了解决分析模型的不可微性和不可分离性,借鉴FISTA算法,提出一种平滑项替代的迭代数值算法,得到分析模型的近似解。该方法的建立也为模糊图像的盲复原领域提供了新的模型和解决思路,其研究成果可应用于各类成像设备的预处理模块。
此外,通过对本文中迭代优化模型的修改,还可将该方法扩展应用于如图像超分辨、图像压缩传感等其他图像反问题中,这些问题将在以后的研究中进行深入的讨论。
| [1] |
QU Xiaobo, MAYZEL Maxim, CAI Jianfeng, et al. Accelerated NMR spectroscopy with low-rank reconstruction[J]. Angewandte chemie international edition, 2015, 54(3): 852-854. DOI:10.1002/anie.201409291 ( 0) 0)
|
| [2] |
ZHAO YongQiang, YANG Jingxiang. Hyperspectral image denoising via sparse representation and low-rank constraint[J]. IEEE transactions on geoscience and remote sensing, 2015, 53(1): 296-308. DOI:10.1109/TGRS.2014.2321557 ( 0) 0)
|
| [3] |
QI Shan, JIA Jiaya, ASEEM A. High-quality motion deblurring from a single image[J]. ACM transactions on graphics, 2008, 27(3): 1-10. ( 0) 0)
|
| [4] |
李一兵, 付强, 张静. 水下模糊图像参数估计复原方法[J]. 吉林大学学报:工学版, 2013, 43(4): 1133-1138. LI Yibing, FU Qiang, ZHANG Jing. Underwater blurry image restoration based on parameter estimation[J]. Journal of Jilin University:engineering and technology edition, 2013, 43(4): 1133-1138. (  0) 0)
|
| [5] |
JIA Jiaya. Single image motion deblurring using transparency[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Minneapolis(CVPR), USA, 2007:1-8.
( 0) 0)
|
| [6] |
DONG Yiqiu, HINTERMULLER M, MONSERRAT R C. Automated regularization parameter selection in multi-scale total variation models for image restoration[J]. Journal of mathematical imaging and vision, 2011, 40(1): 82-104. DOI:10.1007/s10851-010-0248-9 ( 0) 0)
|
| [7] |
LI Jie, YUAN Qiangqiang, SHEN Huanfeng, et al. Hyperspectral image recovery employing a multidimensional nonlocal total variation model[J]. Signal processing, 2015, 111: 230-248. DOI:10.1016/j.sigpro.2014.12.023 ( 0) 0)
|
| [8] |
CHANG Huibin, ZHANG Xiaoqun, TAI Xuecheng, et al. Domain decomposition methods for nonlocal total variation image restoration[J]. Journal of scientific computing, 2014, 60(1): 79-100. DOI:10.1007/s10915-013-9786-9 ( 0) 0)
|
| [9] |
CAI Jianfeng, JI Hui, LIU Chaoqiang, et al. Blind motion deblurring from a single image using sparse approximation[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Florida USA, 2009:104-111.
( 0) 0)
|
| [10] |
ZHANG Haichao, YANG Jianchao, ZHANG Yanning, et al. Sparse representation based blind image deblurring[C]//IEEE International Conference on Multimedia and Expo (ICME) Barcelona, 2011:1-6.
( 0) 0)
|
| [11] |
KRISHNAN D, TAY T, FERGUS R. Blind deconvolution using a normalized sparsity measure[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado, 2011:233-240.
( 0) 0)
|
| [12] |
ZHANG Haichao, WIPF D, ZHANG Yanning. Multi-image blind deblurring using a coupled adaptive sparse prior[C]//IEEE Conference on Computer Vision and Pattern Recognition. Portland, 2013:1051-1058.
( 0) 0)
|
| [13] |
DONG Weisheng, ZHANG Lei, SHI Guangming, et al. Nonlocally centralized sparse representation for image restoration[J]. IEEE transactions on image processing, 2013, 22(4): 1620-1630. DOI:10.1109/TIP.2012.2235847 ( 0) 0)
|
| [14] |
HANIF M, SEGHOUANE A K. Blind Image deblurring using non-negative sparse approximation[C]//IEEE Conference on Image Processing. Pairs, 2014:4042-4046.
( 0) 0)
|
| [15] |
ZHANG Jian, ZHAO Debin, XIONG Ruiqin, et al. Image restoration using joint statistical modeling in space-transform domain[J]. IEEE transactions on circuits and systems for video technology, 2014, 24(6): 915-928. DOI:10.1109/TCSVT.2014.2302380 ( 0) 0)
|
| [16] |
LIU Jun, HUANG Tingzhu, SELESNICK I W, et al. Image restoration using total variation with overlapping group sparsity[J]. Information sciences, 2015, 295(20): 232-246. ( 0) 0)
|
| [17] |
唐述, 谢显中. 多正则化混合约束的模糊图像盲复原方法[J]. 电子与信息学报, 2015, 3(4): 770-776. TANG Shu, XIE Xianzhong. Multi-regularization hybrid constraints method for blind image restoration[J]. Journal of electronics & information technology, 2015, 3(4): 770-776. DOI:10.11999/JEIT140949 (  0) 0)
|
| [18] |
ELAD M, MILANFAR P, ROBINSTEIN R. Analysis versus synthesis in signal priors[J]. Inverse problem, 2007, 23(3): 947-957. DOI:10.1088/0266-5611/23/3/007 ( 0) 0)
|
| [19] |
DUFFIN R J, SCHAEFFER A C. A class of nonharmonic fourier series[J]. Transactions of the american mathematical society, 1952, 72: 341-366. DOI:10.1090/S0002-9947-1952-0047179-6 ( 0) 0)
|
| [20] |
SELESNICK I W, FIGUEIREDO M A T. Signal restoration with overcomplete wavelet transforms:comparison of analysis and synthesis priors[C]//Wavelets ⅩⅢ of SPIE. San Diego, 2009, 7446:1-15.
( 0) 0)
|
| [21] |
MAJUMDA A, WARD R K. On the choice of compressed sensing priors and sparsifying transforms for MR image reconstruction:an experimental study[J]. Signal processing:image communication, 2012, 27(9): 1035-1048. DOI:10.1016/j.image.2012.08.002 ( 0) 0)
|
| [22] |
CANDEX E J, ELDAR Y, NEEDELL C D, et al. Compressed sensing with coherent and redundant dictionaries[J]. Appl comput harmon anal, 2011, 31(1): 59-73. DOI:10.1016/j.acha.2010.10.002 ( 0) 0)
|
| [23] |
BECK A, TEBOULLE M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems[J]. IEEE transactions on image processing, 2009, 18(11): 2419-2434. DOI:10.1109/TIP.2009.2028250 ( 0) 0)
|
| [24] |
MOUREA J J. Proximitéet dualité dans un espace Hilbertien[J]. Bull soc math france, 1965, 93: 273-299. ( 0) 0)
|
| [25] |
BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and trends in machine learning, 2010, 3(1): 1-122. DOI:10.1561/2200000016 ( 0) 0)
|
| [26] |
CHO Sunghyun, LEE Seungyong. Fast motion deblurring[J]. ACM transactions on graphics, 2009, 28(5): 1120-1132. ( 0) 0)
|
| [27] |
LIM W Q. The discrete shearlet transform:a new directional transform and compactly supported shearlet frames[J]. IEEE transactions on image processing, 2010, 19(5): 1166-1180. DOI:10.1109/TIP.2010.2041410 ( 0) 0)
|
| [28] |
REHMAN A, WANG Z. Reduced-reference image quality assessment by structural similarity estimation[J]. IEEE transactions on image processing, 2012, 21(8): 3378-3389. DOI:10.1109/TIP.2012.2197011 ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


