船模自航试验是预估实船性能和判断船-机-桨匹配好坏的重要手段,对于新设计的船舶来说,还可以对若干方案进行比较,从而选型择优,船模自航试验的具体操作规程和方法已由ITTC(International Towing Conference)[1]给出。近年来,随着计算机技术的高速发展,运用CFD方法已经能成功模拟船模自航试验[2-4],其精度足以满足工程计算的需要,相比水池试验能节省大量的时间和成本。但由于自航试验船模与实船之间只满足傅汝德数和进速系数相等,雷诺数并不相等,导致模型数据换算到实船的过程中因为尺度效应的存在而产生较大的误差,尽管有相关的经验统计方法(ΔCT、Δω法和1978ITTC标准方法等)用来修正,但对不同类型的船舶其可靠性也是堪忧的。目前,船桨一体模型尺度的流场和水动力数值计算方法已经较为成熟[5-7],在此基础上已经开始有学者尝试实尺度船体的CFD计算研究,并取得了一定成果。Alejandro M. Castro等[8]基于动态重叠网格方法,开展了实尺度的KCS数值模拟自航试验研究,对比了船模自航和实船自航推进因子和流场等各方面的不同;熊鹰等[9]提出了不考虑船体兴波的自航船模推进因子计算方法,对实船推进因子做了数值预报研究工作。由于实船自航数值模拟网格数量太大、边界层网格厚度难以保证、收敛时间长等问题,使得气-液两相粘性流计算较船模自航更为复杂和困难,自由液面也不易捕捉,国内在这方面的研究工作还很少,但是开展实尺度船舶自航试验的数值模拟工作对尺度效应的修正方法研究是极具意义的,也是未来CFD方法发展的必然趋势。
本文基于RANS方法,采用VOF方法捕捉自由液面,开展了KCS标模实船自航试验数值模拟。首先进行模型尺度的自航状态计算,通过与水池试验对比验证了该方法的可靠性。由于直接模拟实船自航计算过于复杂,数值模拟分为两阶段进行,先保证螺旋桨静止船体以服务航速航行,待流场收敛稳定后再以强制自航法的方式预报实船自航点,并比较了本次计算结果与试验换算值[10]和文献[8-9]中计算值之间的差异,还分析了模型尺度和实船之间由于尺度效应导致的阻力、流场、波形及推进因子变化。
1 数值方法 1.1 控制方程和湍流模型流体流动要受物理守恒定律的支配,基本的守恒定律包括:质量守恒定律、动量守恒定律和能量守恒定律。计算中介质水为不可压缩流体,热交换很小以至于可以忽略不计,可只对质量守恒方程和动量守恒方程进行求解,详细公式可参考文献[11]。计算中采用的湍流模型为进行螺旋桨水动力性能计算时比较常用的SST(shear stress transmission)[12]模型,该模型有效集成了k-ε和k-ω模型的优点,能够较好地模拟存在流动分离和强逆压梯度的复杂流动问题。
1.2 VOF模型VOF(volume of fluid)方法的基本原理是通过研究网格单元中流体和网格体积比函数来确定自由面,追踪流体的变化,而非追踪自由液面上质点的运动。只要知道函数在流场中每个网格上的值,就可以实现对运动界面的追踪。
将整个计算区域定义为Ω,主相流体区域记为Ω1,副相流体区域记为Ω2。VOF定义这样一个函数:
| $\omega \left( x,t \right)=\left\{ \begin{matrix} 1, & x\in {{\Omega }_{1}} \\ 0, & x\in {{\Omega }_{2}} \\ \end{matrix} \right.$ | (1) |
此外,在由两种互不相溶流体构成的流场中,流体的速度场记为V=(u,v),函数ω满足:
| $\frac{\partial \omega }{\partial t}+u\frac{\partial \omega }{\partial x}+v\frac{\partial \omega }{\partial y}=0$ | (2) |
在每个网格Iij上定义ω(x,t)在网格上的积分为Cij,可以得到VOF函数:
| ${{C}_{ij}}=\frac{1}{\Delta {{V}_{ij}}}\int_{{{I}_{ij}}}{\omega \left( x,t \right)dV}$ | (3) |
VOF函数也满足式(2) :
| $\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=0$ | (4) |
显然,当C=0时,网格中全为副相流体;当C=1的时,网格充满主相流体;当0<C<1时,则是含有流体界面的网格,成为界面网格。
2 计算模型的建立 2.1 计算对象和工况本文研究对象为KCS集装箱船,与之搭配的桨为KP505桨,二者模型如图 1所示。实船具体参数如表 1,本文所有计算工况如表 2所示。

|
| 图1 KCS 船桨模型 Figure 1 Model of KCS ship and propeller |
| KCS集装箱船 | KP505螺旋桨 | ||
| 垂线间长/m | 230.0 | 直径/m | 7.9 |
| 吃水/m | 10.8 | 叶数 | 5 |
| 湿表面积/m2 | 9 424 | 毂径比 | 0.167 |
| 雷诺数 | 2.39×109 | 盘面比 | 0.7 |
| 序号 | 名称 | 航速/(m·s-1) | 雷诺数 | 螺旋桨转速/(r·min-1) | 网格数目 | 计算方法 | CPU并行数目 |
| 1 | 船模裸船体阻力计算 | 2.196 | 1.4×107 | — | 532×104 | 稳态VOF | 96核 |
| 2 | 船模自航试验模拟 | 2.196 | 1.4×107 | 570 | 532×104 | 瞬态VOF | 96核 |
| 3 | 实船裸船体阻力计算 | 12.346 | 2.39×109 | — | 2 240×104 | 稳态VOF | 192核 |
| 4 | 实船自航试验模拟 | 12.346 | 2.39×109 | 89、95、101、107和113 | 2 240×104 | 稳态VOF | 192核 |
本次计算采用混合网格方法,全部网格划分工作在ICEM软件中完成。由于KCS船艉收缩曲率大,划分结构化网格困难,所以将船艉小部分流域划分非结构化网格,以节省网格划分工作量,而其它部分包括螺旋桨在内都采用六面体结构化网格,结构化网格和非结构化网格之间通过interface连接,流场通过interface插值进行信息传递。
数值计算时模型尺度和实尺度网格拓扑结构一致,船体表面网格如图 2(a)所示,区别在于首层网格厚度和三个方向上的网格节点数目。一般来说,模型尺度Y+建议控制在60左右是合适的,由式(5) 可计算出第一层网格厚度为0.8~1 mm:
| ${{Y}^{+}}=0.172\frac{\Delta {{y}_{P}}}{L}R{{e}^{0.9}}$ | (5) |
式中:L为特征长度。实尺度Y+控制范围可参考的文献不多,本文根据大量计算统计和文献[13]建议,发现Y+值在300左右是合理的,对应第一层网格厚度为1~2 mm。结构化网格区域第一层层网格厚度可以直接用参数定义,而船艉非结构化网格则需要通过添加多层棱柱网格完成,如图 2(b)所示。螺旋桨网格如图 2(c)所示。另外值得注意的是,计算划分网格时,船体首尾形状复杂,流场变化剧烈,应给与适当加密;为了较好地捕捉自由液面,自由液面附近也要增加网格节点数目以提高网格分辨率。
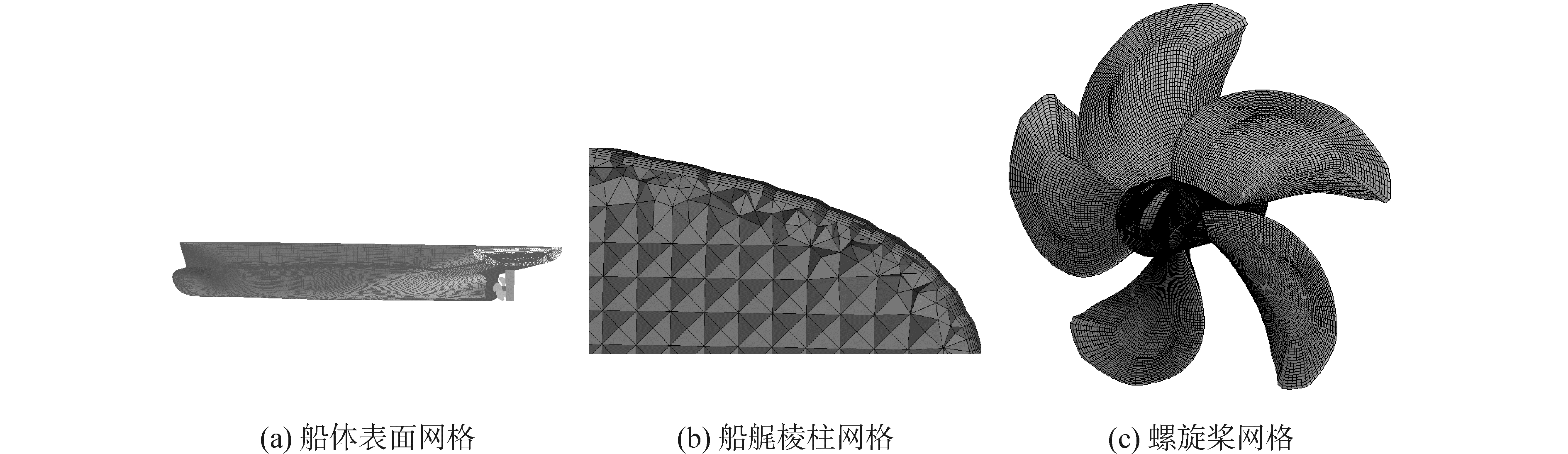
|
| 图2 KCS自航数值计算网格 Figure 2 Computational grid for numerical self-propulsion KCS ship |
流场计算区域为:入口距船艏1.0LPP,出口距船艉2.0LPP,侧面和底面均距船体表面1.0LPP。入口划分为空气速度入口和水流速度入口,二者速度大小一致,模型条件下Vm=2.196 m/s,实尺度条件下VS=12.346 m/s;出口利用Fluent用户自定义函数(UDF)设置为压力出口,出口垂直方向压强按下式变化:
| $p=\left\{ \begin{array}{*{35}{l}} {{p}_{0}}, & z\ge T \\ {{p}_{0}}=\rho g\left( z-T \right), & z<T \\ \end{array} \right.$ | (6) |
式中:p0为一个大气压,ρ为水的密度,g为重力加速度,z为垂直方向坐标值,T为吃水。流域上边界定义为对称面,船体表面、侧面和底面均定义为无滑移壁面,螺旋桨旋转运动采用MRF模型,压力速度耦合迭代采用SIMPLEC方法。
3 计算结果分析 3.1 船模自航点工况数值计算为了验证本文计算方法的准确性,首先开展船模尺度的推进因子数值预报。参考水池自航试验流程,要获得船模推进因子,需要分别进行KCS船模裸船体阻力计算、KP505桨模敞水性能计算和船桨一体自航点工况数值计算,自航点时螺旋桨转速为570 r/min。为了节省计算工作量,仅在KP505桨最高效率点附近取了四个不同进速系数J=0.6,0.7,0.8,0.9分别进行敞水性能计算。
图 3所示为船模尺度裸船体计算自由液面波形与试验值对比图,从图中可以看出二者各处波形和波高基本一致,自由液面总体捕捉效果较好,仅在尾部其波形细节存在一定差异,这可能是因为远离船体流域网格尺度逐渐增大,波能耗散较快。

|
| 图3 自由液面波形图对比 Figure 3 Comparison of free surface wave pattern |
图 4所示为螺旋桨敞水性能曲线,可以看出在最大效率点附近计算值与试验值非常接近,最大误差不超过3%,计算精度满足要求。
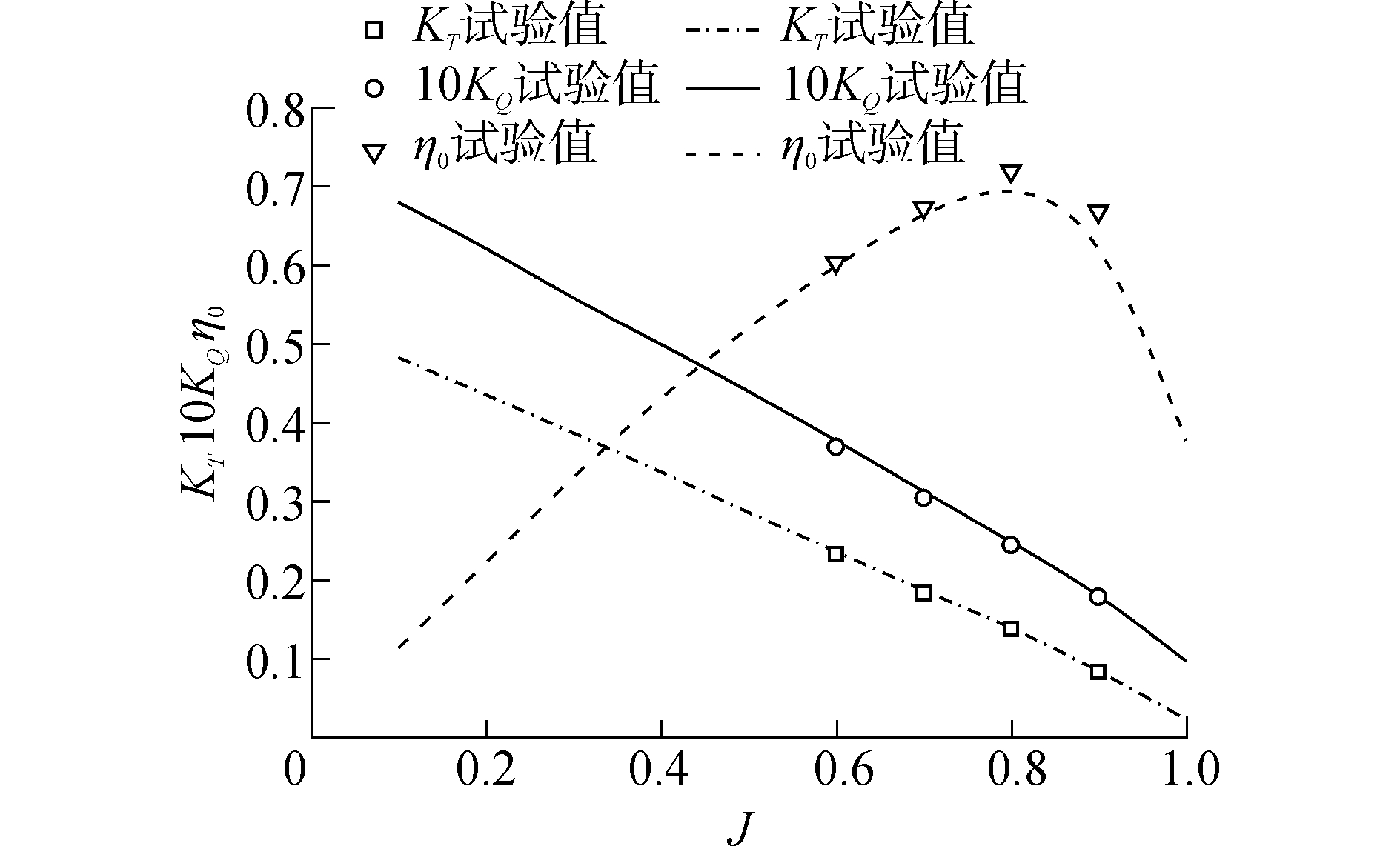
|
| 图4 螺旋桨敞水性能 Figure 4 The open water performance of propeller |
表 3为船模自航点计算结果与试验值对比,表中Ct表示裸船体阻力系数,CtSP表示自航状态下船体阻力系数,KT表示船后螺旋桨推力系数,KQ船后螺旋桨转矩系数,J表示据KT用等推力法查敞水曲线所得进速系数,wm表示伴流分数,tm表示推力减额。通过比较可知,除了推力系数和推力减额外,各项计算结果均与试验值吻合良好,误差在3%以内,推力误差较大有可能是因为螺旋桨旋转域与非结构网格流域相接的这对interface网格节点数目存在一定差异,从而增大了流场数据插值传递误差。
在确定实船自航点之前首先要进行的是服务航速下带自由液面的裸船体阻力计算,其计算结果如表 4所示。表中试验值摩擦阻力修正系数SFC可由式(7) 计算得到,试验总阻力系数可由式(8) 计算得到
| $SFC=\left( 1+k \right)\left( {{C}_{FM}}-{{C}_{FS}} \right)-\Delta {{C}_{F}}$ | (7) |
| ${{C}_{tFull}}={{C}_{tModel}}-SFC$ | (8) |
式中:形状因子取1+k=1.1,摩擦阻力系数根据1957ITTC公式计算得到CFM=2.832×10-3,CFS=1.378×10-3,粗糙度补贴系数由文献[14]提供ΔCF=0.27×10-3。
从表 4中可以看出,这与文献[8]计算结果误差趋势一致,实船总阻力系数计算值要比ITTC换算值要略大,误差为3.83%,摩擦阻力修正系数SFC数值计算值要比计算值(式(6) )要小,误差为2.63%。文献[13]中的计算结果显示形状因子1+k存在较大的尺度效应,随着雷诺数的增大,尺度的增加,形状因子将增大。所以如果按照船模尺度的形状因子进行实船阻力换算,而不考虑其尺度效应,必然导致摩擦阻力修正系数过小,从而换算得到的实船总阻力系数偏大。但是从表中数据来看,试验换算值与本文计算值和文献[8]计算值均吻合良好,其主要原因是船模试验确定的形状因子是偏大的,文献[13]中KCS模型尺度形状因子数值计算值仅为1.05。船模形状因子确定的主要方法有普鲁哈斯卡(Prohaska)方法和第15届ITTC推荐方法,在Fr为0.1~0.2范围内测量得到,但是这都是以休斯假设为基础的,即认为形状因子1+k是与船体形状有关的常数,实际上诸多试验结果都表明形状因子1+k在低速时近似为常数,而在较高航速(Fr>0.16)后,随着Fr增大而减小,本次计算中Fr=0.26,故Fr增大导致的形状因子误差很大程度上抵消了尺度效应所带来的误差,从而使得试验换算值和实船数值计算值非常靠近,这也表明现有的三因次换算方法形状因子的确定方法是可取的,大大降低了尺度效应。
图 5所示为实船与船模纵剖面y/Lpp=0.006处无量纲轴向速度等值线图,从图中可以明显看到实船的边界层要比船模的更薄,船模的低速区要向下游拖延得更远,在相同X轴位置处,实船船艉下游的速度均大于船模。同时可以看到一个有意思的现象,就是实船时船艉还形成了一个船模没有的速度闭合区,说明此纵剖面处有一定的回流出现。另外观察艉封板附近流域,发现实船船艉还有一股相对船模速度更大,波峰更高的急流涌现。

|
| 图5 实船与船模纵剖面(y/Lpp=0.006)无量纲轴向速度对比 Figure 5 Comparison of full-scale and model-scale nondimensional axial velocity at y/Lpp=0.006 |
图 6为实船与船模桨盘面处无量纲轴向速度等值线图,图中也体现出了实船边界层要比船模更薄的特点,实船的轴向速度等值线相比船模要向里收缩,这使得在桨盘面处实船具有更大的轴向速度,也就是说其轴向标称伴流分数要小。观察螺旋桨所在位置区域,可以发现实船与船模之间的伴流差异是很大的,实船船艉后的螺旋桨的进速要大于船模,如果根据船模测量伴流分数来设计螺旋桨,就很容易导致安装在实船上的螺旋桨会产生推力不足的情况,所以根据伴流的尺度效应情况必须留出一定推力余量。

|
| 图6 实船与船模桨盘面(x/Lpp=0.982 5)无量纲轴向速度对比 Figure 6 Comparison of full-scale and model-scale nondimensiona axial velocity at the propeller plane x/Lpp=0.982 5 |
图 7所示为实船与船模波高等值线图,船艏和船舯部分的兴波二者几乎看不出差别,这和兴波阻力与雷诺数无关的假设是相符合的,但是在尾部及其下流区域波形存在一定的差异,主要是雷诺数增大导致的边界层差异增大了实船船艉流速,进而使得实船船艉急流波峰增高,其尾部波形略微有整体向后移动,这与图 5中观察到的现象一致。

|
| 图7 实船与船模自由液面波形图对比 Figure 7 Comparison of full-scale and model-scale free surface wave pattern |
实船自航试验的数值模拟方法和模型基本一致,唯一不同的是确定自航点的过程中不用再考虑因为雷诺数Re的不同而要进行摩擦阻力的修正,当船体阻力和螺旋桨推力达到平衡时即可确定自航点下的螺旋桨转速、推力和转矩,这有效避免了阻力换算和伴流尺度效应等因素带来的误差。确定实船自航点的具体操作步骤如下:
1) 根据船模自航试验结果,预估实船一个实船自航点。为了方便,可以将不做修正的船模自航点根据缩尺比直接换算过来作为实船的预估自航点,本文计算预估的自航点螺旋桨转速为:
2) 在预估的自航点螺旋桨转速Ns0前后适当范围内再各取两个转速,本文取Ns1=89 r/min,Ns2=95 r/min,Ns3=107 r/min,Ns4=113 r/min,然后在服务航速VS=12.346 m/s下,分别对五个不同螺旋桨转速进行数值模拟;
3) 绘制船体阻力和螺旋桨推力随螺旋桨转速的变化曲线,两曲线的交点即为该航速下的自航点。
3.2.3 实船自航点数值计算结果依据3.2.2节中实船自航点确定步骤,数值模拟得到五个不同螺旋桨转速下螺旋桨推力、转矩和船体阻力,其结果如表 5所示,实船自航试验曲线绘制于图 8中。由Rt=T,在实船自航曲线上通过插值可得自航点N=107.3 r/min,Rt=T=1.995×106N,Q=2.589×106,103Ct=2.783,KT=0.161,10KQ=0.264。
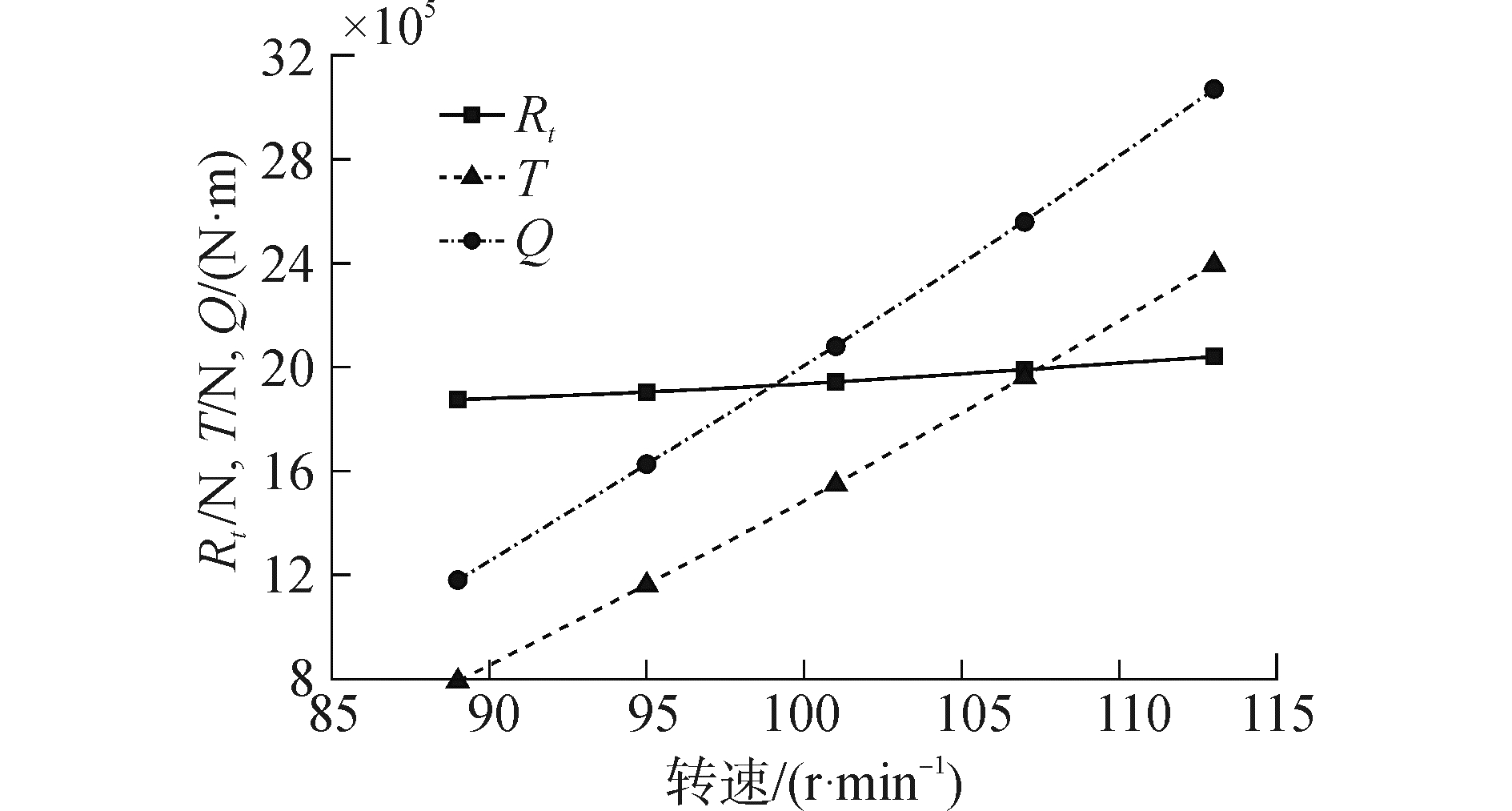
|
| 图8 实船自航试验曲线 Figure 8 Results of full-scale self-propulsion test |
| N/(r·min-1) | Rt/N | 103Ct | T/N | Q/(N·m) | KT | 10KQ |
| 裸船体 | 1.653×106 | 2.306 | — | — | — | — |
| 89 | 1.876×106 | 2.617 | 0.793×106 | 1.181×106 | 0.093 | 0.175 |
| 95 | 1.903×106 | 2.654 | 1.162×106 | 1.627×106 | 0.119 | 0.211 |
| 101 | 1.942×106 | 2.709 | 1.550×106 | 2.080×106 | 0.141 | 0.239 |
| 107 | 1.991×106 | 2.777 | 1.962×106 | 2.559×106 | 0.159 | 0.262 |
| 113 | 2.041×106 | 2.847 | 2.394×106 | 3.069×106 | 0.174 | 0.282 |
为节省计算量,本文没有进行实尺度螺旋桨敞水性能计算,主要是因为推力受尺度作用的影响很小,几乎可以忽略,转矩系数变化一般也在1%左右,文献[8]中的计算值也验证了这一点,实桨和桨模的敞水曲线基本重合。基于以上分析,实船自航点螺旋桨的进速系数可直接利用等推力法在模型桨的敞水特性曲线上插值得到,J0=0.755,10KQ=0.275。
数值模拟最后得到的实船自航推进性能结果具体如表 6所示,表中数据显示实船计算值和船模试验换算值之间差异较大的量为自航点转速和伴流分数,其误差分别为+5.82%和+8.96%。3.2.1节中,通过分析图4和图5可知,由于实船雷诺数与船模雷诺数相差巨大,其边界层厚度也要更薄,实船桨盘面的进速是要大于船模的,故实船自航试验模拟得到实船的伴流分数要小于船模,自航点转速要大于船模是预料之中的结果。这启示在做模型试验时仅考虑螺旋桨载荷的尺度效应是不够的,边界层厚度和伴流分数的尺度效应也是必须引起注意的。
| 103Ct | 103CtSP | KT | 10KQ | N/(r·min-1) | J | 1-wm | 1-tm | |
| 实船计算值 | 2.306 | 2.783 | 0.161 | 0.275 | 107.3 | 0.755 | 0.863 | 0.829 |
| 文献[9]计算值 | 2.334 | 2.773 | 0.166 | 0.261 | 103.3 | 0.714 | 0.793 | 0.842 |
| 试验值 | 2.221 | — | 0.17 | 0.288 | 101.4 | 0.728 | 0.792 | 0.853 |
| 误差/% | +3.83 | — | -5.29 | -4.51 | +5.82 | +3.71 | +8.96 | -2.81 |
本文选用KCS船和KP505桨为计算对象,考虑自由液面的情况下开展了实船自航试验数值模拟和尺度效应研究分析,根据数值模拟结果主要得出了以下结论:
1) 在模型自航点工况下,自由液面波形、船体阻力和螺旋桨推力转矩值和试验吻合良好,表明计算精度满足要求,本文计算方法准确可靠。
2) 对比实船与船模裸船数值计算结果,发现由于雷诺数的巨大差异,实船边界层要比船模薄,桨盘面位置进速要更大,如果依据船模伴流分数来进行螺旋桨设计容易导致实船推力不足。同时实船艉流高速区向后延伸,并有一股相对船模来说速度更大,波峰更高的急流涌现,这使得实船船艉自由液面波形也略微有所整体后移。
3) 运用强制自航法数值预报得到实船自航点,插值计算得到推进因子,与试验换算值对比,误差均在可接受范围之内,尺度效应主要体现在伴流分数和自航点转速,结果显示实船伴流分数要小于船模,自航点转速要大于船模。
4) 实船自航试验数值模拟是数值计算实船螺旋桨诱导激振力的一个必要工作,下面将以此为基础进一步开展实船激振力的相关研究。
| [1] | ITTC. Testing and extrapolation methods, Propulsion, performance propulsion test[R]. Recommended Procedures and Guidelines, Report 7.5-02-03-01.1. Rio de Janeiro:ITTC Secretary, 2002. |
| [2] | CARRICA P M, CASTRO A M, STERN F. Self-propulsion computations using a speed controller and a discretized propeller with dynamic overset grids[J]. Journal of marine science and technology, 2010, 15(4): 316–330. |
| [3] |
戈亮, 顾民, 吴乘胜, 等. 水面船自航因子CFD预报研究[J].
船舶力学, 2012, 16(7): 767–773.
GE Liang, GU Min, WU Chengsheng, et al. CFD prediction of self-propulsion parameters for a surface ship[J]. Journal of ship mechanics, 2012, 16(7): 767–773. |
| [4] | NOBUAKI S, YASUTAKA K, SHOTARO U, et al. Estimation of resistance and self-propulsion characteristics for low L/B twin-skeg container ship by a high-fidelity RANS solver[J]. Journal of ship research, 2013, 57(1): 24–41. |
| [5] | ABDEL-MAKSOUD M, MENTER F, WUTTKE H. Numerical computation of the viscous flow around the series 60 CB=0.6 ship with rotating propeller[C]//Proceedings of the 3rd Osaka colloquium on advanced CFD applications to ship flow and hull form design. Osaka, 1998. |
| [6] |
刘祥珺, 孙存楼. 数值水池船模自航试验方法研究[J].
舰船科学技术, 2011, 33(2): 28–31.
LIU Xiangjun, SUN Cunlou. Research on ship self-propulsion model test in numerical tank[J]. Ship science and technology, 2011, 33(2): 28–31. |
| [7] | CARRICA P M, FU Huiping, STERN F. Computations of self-propulsion free to sink and trim and of motions in head waves of the KRISO container ship (KCS) model[J]. Applied ocean research, 2011, 33(4): 309–320. |
| [8] | CASTRO A M, CARRICA P M, STERN F. Full scale self-propulsion computations using discretized propeller for the KRISO container ship KCS[J]. Computers & fluids, 2011, 51(1): 35–47. |
| [9] |
熊鹰, 刘志华. 自航船模和实船推进因子的数值预报方法研究[J].
船舶力学, 2013, 17(1/2): 14–18.
XIONG Ying, LIU Zhihua. Numerical prediction of propulsion factors of propelled ship model and full scale ship[J]. Journal of ship mechanics, 2013, 17(1/2): 14–18. |
| [10] | LARSSON L, STERN F, VISONNEAU M. CFD in ship hydrodynamics-results of the Gothenburg 2010 workshop[C]//MARINE 2011, IV International Conference on Computational Methods in Marine Engineering. Netherlands:Springer, 2013:237-259. |
| [11] |
王福军.
计算流体动力学分析——CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004: 7 -11.
WANG Fujun. Principle and application of CFD software[M]. Beijing: Tsinghua University Press, 2004: 7 -11. |
| [12] | MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA journal, 1994, 32(8): 1598–1605. |
| [13] |
王展智. 采用混合式CRP推进器的船舶水动力特性及尺度效应研究[D]. 武汉:海军工程大学, 2014.
WANG Zhanzhi. Study on the hydrodynamic characteristic and scale effect of a ship equipped with the hybrid CRP pod propulsion system[D]. Wuhan:Naval University of Engineering, 2014. |
| [14] | National Maritime Research Institute. Tokyo 2015 a workshop on CFD in ship hydrodynamics[EB/OL].(2016-04-15).http://www.t2015.nmri.go.jp/program.html. |



